Дипломная работа: Термодинаміка і синергетика

Дипломна робота

з фізики

на тему

ТЕРМОДИНАМІКА

ЗМІСТ

ВВЕДЕННЯ

РОЗДІЛ 1. ОСНОВНІ ПОНЯТТЯ І ПОЧАТКОВІ ПОЛОЖЕННЯ ТЕРМОДИНАМІКИ

1.1 Закриті і відкриті термодинамічні системи

1.2 Нульовий початок термодинаміки

1.3 Перший початок термодинаміки

1.4 Другий початок термодинаміки

1.4.1 Оборотні і необоротні процеси

1.4.2 Ентропія

1.5 Третій початок термодинаміки

РОЗДІЛ 2. ОСНОВНІ ПОНЯТТЯ І ПОЛОЖЕННЯ СИНЕРГЕТИКИ. САМООРГАНІЗАЦІЯ РІЗНИХ СИСТЕМ

2.1. Загальна характеристика відкритих систем

2.1.1 Диссипативні структури

2.2 Самоорганізація різних систем і синергетики

2.3 Приклади самоорганізації різних систем

2.3.1 Фізичні системи

2.3.2 Хімічні системи

2.3.3 Біологічні системи

2.3.4 Соціальні системи

РОЗДІЛ 3. АНАЛІТИЧНІ І ЧИСЕЛЬНІ ДОСЛІДЖЕННЯ САМООРГАНІЗАЦІЇ РІЗНИХ СИСТЕМ

3.1 Осередки Бенара

3.2 Лазер, як система, що самоорганізовується

3.3 Біологічна система

3.3.1 Динаміка популяцій. Екологія

3.3.2 Система «Жертва - Хижак»

ВИСНОВОК

ЛІТЕРАТУРА

ВВЕДЕННЯ

Наука зародилася дуже давно, на Стародавньому Сході, і потім інтенсивно розвивалася в Європі. У наукових традиціях довгий час залишався недостатньо вивченим питання про взаєминах цілого і частині. Як стало ясно в середині 20 століть частина може перетворити ціле радикальним і несподіваним чином.

З класичної термодинаміки відомо, що ізольовані термодинамічні системи відповідно до другого початку термодинаміки для необоротних процесів ентропія системи S зростає до тих пір, поки не досягне свого максимального значення в стані термодинамічної рівноваги. Зростання ентропії супроводжується втратою інформації про систему.

З часом відкриття другого закону термодинаміки встало питання про те, як можна погоджувати зростання з часом ентропії в замкнутих системах з процесами самоорганізації в живій і не живій природі. Довгий час здавалося, що існує суперечність між виведенням другого закону термодинаміки і виводами еволюційної теорії Дарвіна, згідно якої в живій природі завдяки принципу відбору безперервно відбувається процес самоорганізації.

Суперечність між другим початком термодинаміки і прикладами високоорганізованого навколишнього нас світу була дозволена з появою більше п'ятдесяти років тому і подальшим природним розвитком нелінійної нерівноважної термодинаміки. Її ще називають термодинамікою відкритих систем. Великий внесок до становлення цієї нової науки внесли І.Р. Прігожін, П. Гленсдорф, Г. Хакен. Бельгійський фізик російського походження Ілля Романовіч Прігожін за роботи в цій області в 1977 році був удостоєний Нобелівської премії.

Як підсумок розвитку нелінійної нерівноважної термодинаміки з'явилася абсолютно нова наукова дисципліна синергетика - наука про самоорганізацію і стійкість структур різних складних нерівноважних систем: фізичних, хімічних, біологічних і соціальних.

У справжній роботі досліджується самоорганізація різних систем аналітичними і чисельними методами.

РОЗДІЛ 1. ОСНОВНІ ПОНЯТТЯ І ПОЧАТКОВІ ПОЛОЖЕННЯ ТЕРМОДИНАМІКИ

1.1 ЗАКРИТІ І ВІДКРИТІ ТЕРМОДИНАМІЧНІ СИСТЕМИ

Всякий матеріальний об'єкт, всяке тіло, що складається з великого числа частинок, називається макроскопічною системою . Розміри макроскопічних систем значно більше розмірів атомів і молекул. Всі макроскопічні ознаки, що характеризують таку систему і її відношення до навколишніх тіл, називаються макроскопічними параметрами . До їх числа відносяться такі, наприклад, як щільність, об'єм, пружність, концентрація, поляризована, намагніченість і так далі Макроскопічні параметри розділяються на зовнішніх і внутрішніх .

Величини, визначувані положенням не вхідних в нашу систему зовнішніх тіл, називаються зовнішніми параметрами, наприклад напруженість силового поля ( оскільки залежать від положення джерел поля - зарядів і струмів, що не входять в нашу систему ), об'єм системи ( оскільки визначається розташуванням зовнішніх тіл ) і так далі Отже зовнішні параметри є функціями координат зовнішніх тіл. Величини, визначувані сукупним рухом і розподілом в просторі вхідних в систему частинок, називаються внутрішніми параметрами, наприклад енергія, тиск, щільність, намагніченість, поляризована і так далі ( оскільки їх значення залежать від руху і положення частинок системи і вхідних в них зарядів ).

Сукупність незалежних макроскопічних параметрів визначає стан системи, тобто форму її буття. Величини, які не залежать від передісторії системи і повністю визначувані її станом в даний момент (тобто сукупністю незалежних параметрів ), називаються функціями стану.

Стан називається стаціонарним, якщо параметри системи з часом не змінюються.

Якщо крім того, в системі не тільки всі параметри постійні в часі, але і немає ніяких стаціонарних потоків за рахунок дії яких-небудь зовнішніх джерел, то такий стан системи називається рівноважним ( стан термодинамічної рівноваги). Термодинамічними системами зазвичай називають не всякі, а тільки ті макроскопічні системи, які знаходяться в термодинамічній рівновазі. Аналогічно, термодинамічними параметрами називаються ті параметри, які характеризують систему в термодинамічній рівновазі.

Внутрішні параметри системи розділяються на інтенсивних і екстенсивних . Параметри не залежні від маси і числа частинок в системі, називаються інтенсивними ( тиск, температура і ін.) . Параметри пропорційні масі або числу частинок в системі, називаються адитивними або екстенсивними ( енергія, ентропія і ін.). Екстенсивні параметри характеризують систему як ціле, тоді як інтенсивні можуть приймати певні значення в кожній точці системи.

За способом передачі енергії, речовини і інформації між даної системи і навколишнім середовищем термодинамічні системи класифікуються:

1. Замкнута ( ізольована ) система - це система в якій немає обміну із зовнішніми тілами ні енергією, ні речовиною ( у тому числі і випромінюванням ), ні інформацією.

2. Закрита система - система в якій є обмін тільки з енергією.

3. Адіабатна ізольована система - це система в якій є обмін енергією тільки у формі теплоти.

4. Відкрита система - це система, яка обмінюється і енергією, і речовиною, і інформацією.

1.2 НУЛЬОВИЙ ПОЧАТОК ТЕРМОДИНАМІКИ

Нульовий початок термодинаміки сформульований всього біля 50 років назад, по суті є отриманим «заднім числом» логічним виправданням для введення поняття температури фізичних тіл . Температура - одне з найглибших понять термодинаміки . Температура грає таку ж важливу роль в термодинаміці, як, наприклад процеси. Вперше центральне місце у фізиці зайняв абсолютно абстрактне поняття ; воно прийшло на зміну введеному ще в часи Ньютона ( 17 вік) поняттю сили - на перший погляд конкретнішому і «відчутнішому» і до того ж успішно «математезірованому» Ньютоном.

Перший початок термодинаміки встановлює внутрішня енергія системи є однозначна функція її стану і змінюється тільки під впливом зовнішніх дій.

У термодинаміці розглядаються два типи зовнішніх взаємодій: дія, пов'язана із зміною зовнішніх параметрів системи ( система здійснює роботу W ), і дія не пов'язані із зміною зовнішніх параметрів і обумовлені зміною внутрішніх параметрів або температури ( системі повідомляється деяка кількість теплоти Q ).

Тому, згідно першому початку, зміна внутрішній енергії U2-U1 системи при її переході під впливом цих дій з першого стану в друге рівно сумі алгебри Q і W, що для кінцевого процесу запишеться у вигляді рівняння

U2- U1= Q - W або Q = U2- U1+ W (1.1)

Перший початок формується як постулат і є узагальненням великої кількості досвідчених даних.

Для елементарного процесу рівняння першого початку такого :

dQ = dU + W (1.2)d

dQ і dW не є повним диференціалом, оскільки залежать від шляху проходження.

Залежність Q і W від шляху видно на простому прикладі розширення газу. Робота досконала системою під час переходу її із стану 1 в 2 ( мал. 1) по дорозі а зображується площею, обмеженою контуром А1а2ва :

Wа = p(V,T) dV ;

а робота при переході по дорозі в - площею обмежену контуром А1в2ва:

Wb= p(V,T) dV.

Мал. 1

Оскільки тиск залежить не тільки від об'єму, але і від температури, то при різних змінах температури на шляху а і в під час переходу одного і того ж початкового стану (p1,V1) в одне і теж кінцеве (p2,V2) робота виходить різною. Звідси видно, що при замкнутому процесі (циклі) 1а2в1 система здійснює роботу не рівну нулю. На цьому заснована робота всіх теплових двигунів.

З першого початку термодинаміки виходить, що робота може здійснюватися або за рахунок зміни внутрішній енергії, або за рахунок повідомлення системи кількості теплоти . У випадку якщо процес круга, початковий і кінцевий стан співпадають U2- U1 = 0 і W = Q, тобто робота при круговому процесі може здійснюватися тільки за рахунок отримання системою теплоти від зовнішніх тіл .

Перший початок можна сформулювати в декількох видах :

1. Неможливе виникнення і знищення енергії .

2. Будь-яка форма руху здатна і повинна перетворюватися на будь-яку іншу форму руху .

3. Внутрішня енергія є однозначною формою стану .

4. Вічний двигун першого роду неможливий .

5. Нескінченна мала зміна внутрішній енергії є повним диференціалом.

6. Сума кількості теплоти і роботи не залежить від шляху процесу.

Перший закон термодинаміки, постулювавши закон збереження енергії для термодинамічної системи. не указує спрямування процесів, що відбуваються в природі. Спрямування термодинамічних процесів встановлює другий початок термодинаміки.

1.4 ДРУГИЙ ПОЧАТОК ТЕРМОДИНАМІКИ

Другий початок термодинаміки встановлює наявність в природі фундаментальної асиметрії, тобто одно направленості всіх мимовільних процесів, що відбуваються в ній.

Другий основний постулат термодинаміки пов'язаний так само з іншими властивостями термодинамічної рівноваги як особливого виду теплового руху. Досвід показує, що якщо дві рівноважні системи А і В привести в тепловий контакт, то незалежно від відмінності або рівності у них зовнішніх параметрів вони або залишаються по колишньому в стані термодинамічної рівноваги, або рівновага у них порушується і через деякий час в процесі теплообміну ( обміну енергією ) обидві системи приходять в інший рівноважний стан. Крім того, якщо є три рівноважні системи А, В і З і якщо системи А і В порознь знаходяться в рівновазі з системою З, то системи А і В знаходяться в термодинамічній рівновазі і між собою (властивості транзитивності термодинамічної рівноваги ).

Хай є дві системи. Для того, щоб переконається в тому, що вони знаходяться в стані термодинамічної рівноваги треба зміряти незалежно всі внутрішні параметри цих систем і переконатися в тому, що вони постійні в часі. Це завдання дуже важке.

Виявляється проте, що є така фізична величина, яка дозволяє порівняти термодинамічні стани двох систем і двох частин однієї системи без докладного дослідження і внутрішніх параметрів. Ця величина, що виражає стан внутрішнього руху рівноважної системи, має одне і те ж значення у всіх частин складної рівноважної системи незалежно від числа частинок в них і визначуване зовнішніми параметрами і енергією називається температурою .

Температура є інтенсивним параметром і служить мірою інтенсивності теплового руху молекул.

Викладене положення про існування температури як особливій функції стану рівноважної системи представляє другий постулат термодинаміки.

Інакше кажучи, стан термодинамічної рівноваги визначається сукупністю зовнішніх параметрів і температури.

Р. Фаулер і Е. Гуггенгейм назвали його нульовим початком, оскільки воно подібно до першого і другого початку що визначає існування деяких функцій стану, встановлює існування температури у рівноважних систем. Про це згадувалося вищим.

Отже, всі внутрішні параметри рівноважної системи є функціями зовнішніх параметрів і температур .(Другий постулат термодинаміки).

Виражаючи температуру через зовнішні параметри і енергію, другий постулат можна сформулювати у такому вигляді : при термодинамічній рівновазі всі внутрішні параметри є функціями зовнішніх параметрів і енергії.

Другий постулат дозволяє визначити зміну температури тіла по зміні якого або його параметра, на чому заснований пристрій різних термометрів.

1.4.1 ОБОРОТНІ І НЕОБОРОТНІ ПРОЦЕСИ

Процес переходу системи із стану 1 в 2 називається оборотним, якщо поверненням цієї системи в те, що початкове складається з 2 в 1 можна здійснити без яких би то не було змін навколишніх зовнішніх тілах.

Процес же переходу системи із стану 1 в 2 називається необоротним, якщо зворотний перехід системи з 2 в 1 не можна здійснити без зміни в навколишніх тілах .

Мірою безповоротності процесу в замкнутій системі є зміною новій функції стану - ентропії, існування якої у рівноважної системи встановлює перше положення другого початку про неможливість вічного двигуна другого роду . Однозначність цієї функції стану приводить до того, що всякий необоротний процес є не рівноважним.

З другого початку виходить, що S є однозначною функцією стану. Це означає, що dQ/T для будь-якого кругового рівноважного процесу рівний нулю. Якби це не виконувалося, тобто якби ентропія була неоднозначною функцією стану те, можна було б здійснити вічний двигун другого роду.

Положення про існування у всякої термодинамічної системи новою однозначною функцією стану ентропії S, яка при адіабатних рівноважних процесах не змінюється і складє зміст другого початку термодинаміки для рівноважних процесів.

Математично другий початок термодинаміки для рівноважних процесів записується рівнянням:

dQ/T = dSабо dQ = TDS(1.3)

Інтегральним рівнянням другого початку для рівноважних кругових процесів є рівність Клаузіуса:

dQ/T = 0 (1.4)

Для нерівноважного кругового процесу нерівність Клаузіуса має наступний вигляд :

dQ/T < 0 (1.5)

Тепер можна записати основне рівняння термодинаміки для простої системи що знаходиться під всестороннім тиском :

TDS = dU + pdV(1.6)

Обговоримо питання про фізичний сенс ентропії.

1.4.2 ЕНТРОПІЯ

Другий закон термодинаміки постулював існування функції стану, званого «ентропією» (що означає від грецького «еволюція» ) і що володіє наступними властивостями:

а) Ентропія системи є екстенсивною властивістю . Якщо система складається з декількох частин, то повна ентропія системи рівна сумі ентропії кожної частини .

б) Зміна ентропії d S складається з двох частин . Позначимо через dе S потік ентропії, обумовлений взаємодією з навколишнім середовищем, а через di S - частину ентропії, обумовлену змінами усередині системи, маємо

d S = de S + di S (1.7)

Приріст ентропії di S обумовлений зміною усередині системи, ніколи не має негативного значення . Величина di S = 0, тільки тоді, коли система зазнає оборотні зміни, але вона завжди позитивна, якщо в системі йдуть такі ж необоротні процеси.

Таким чином

di S = 0 (1.8)

(оборотні процеси);

di S > 0 (1.9)

(необоротні процеси);

Для ізольованої системи потік ентропії рівний нулю і вирази (1.8) і (1.9) зводяться до наступного вигляду :

d S = di S > 0 (1.10)

(ізольована система ).

Для ізольованої системи це співвідношення рівноцінне класичному формулюванню, що ентропія ніколи не може зменшуватися, так що в цьому випадку властивості энтропийной функції дають критерій, що дозволяє виявити наявність необоротних процесів . Подібні критерії існують і для деяких інших окремих випадків .

Припустимо, що система, яку ми позначатимемо символом 1, знаходиться усередині системи 2 більші розміри і що загальна система, що полягає системи 1 і 2, є ізольованою.

Класичне формулювання другого закону термодинаміки тоді має вигляд :

d S = d S1 + d S2 ³ 0 (1.11

Прикладаючи рівняння (1.8) і (1.9) окремо кожній частині цього виразу, постулював, що

diS1 ³ 0, diS2 ³ 0

Ситуація при якій

diS1 > 0 і diS2 < 0, а d( S1 + S2 ) >0,

фізично неосуществима . Тому можна стверджувати, що зменшення ентропії в окремій частині системи, що компенсується достатнім зростанням ентропії в іншій частині системи, є забороненим процесом . З такого формулювання витікає, що в будь-якій макроскопічній ділянці системи приріст ентропії, обумовлений перебігом необоротних процесів, є позитивним. Під поняттям « макроскопічна ділянка » системи мається на увазі будь-яка ділянка системи, в якій міститься достатнє велике число молекул, щоб можна було нехтувати мікроскопічними флуктуакціями. Взаємодія необоротних процесів можлива лише тоді, коли ці процеси відбуваються в тих же самих ділянках системи .

Таке формулювання другого закону можна було б назвати « локальною » формулювання в протилежність « глобальною » формулювання класичної термодинаміки . Значення подібному новому формулюванню полягає в тому,что на її основі можливий набагато глибший аналіз необоротних процесів.

1.5 ТРЕТІЙ ПОЧАТОК ТЕРМОДИНАМІКИ

Відкриття третього початку термодинаміки пов'язане із знаходженням хімічного засобу - величини, що характеризують здатність різних речовин хімічно реагувати один з одним . Ця величина визначається роботою W хімічних сил при реакції . Перший і другий початок термодинаміки дозволяють обчислити хімічний засіб W тільки з точністю до деякої невизначеної функції . Щоб визначити цю функцію потрібні в доповненні до обох початків термодинаміки нові досвідчені дані про властивості тіл . Тому Нернстоном були зроблені широкі експериментальні дослідження поведінка речовин при низькій температурі.

В результаті цих досліджень і було сформульовано третій початок термодинаміки : у міру наближення температури до 0 До ентропія всякої рівноважної системи при ізотермічних процесах перестає зависить від яких-небудь термодинамічних параметрів стану і в межі ( Т= 0 До) приймає одну і тугіше для всіх систем універсальну постійну величину, яку можна прийняти рівною нулю .

Спільність цього твердження полягає в тому, що, по-перше, воно відноситься до будь-якої рівноважної системи і, по-друге, що при Т прагнучому до 0 До ентропія не залежить від значення будь-якого параметра системи. Таким чином по третьому початку

lim [ S (T,X2) - S (T,X1) ] = 0 (1.12)

або

lim [ dS/dX ]_T = 0 при Т ® 0 (1.13)

де Х - будь-який термодинамічний параметр (аi або Аi).

Граничне значення ентропії, оскільки воно одне і теж для всіх систем, не має ніякого фізичного сенсу і тому вважається рівним нулю (постулат Планка). Як показує статичний розгляд цього питання, ентропія по своїй істоті визначена з точністю до деякої постійної (подібно, наприклад, електростатичному потенціалу системи зарядів в якій або точці поля). Таким чином, немає сенсу вводити якусь «абсолютну ентропію», як це робив Планк і деякі інші учені.

РОЗДІЛ 2. ОСНОВНІ ПОНЯТТЯ І ПОЛОЖЕННЯ СИНЕРГЕТИКИ. САМООРГАНІЗАЦІЯ РІЗНИХ СИСТЕМ

Близько 50 років тому в результаті розвитку термодинаміки виникла нова дисципліна - синергетика.

Великим є значення цієї науки.

Синергетика займається вивченням систем, що складаються з багатьох підсистем самої різної природи, таких, як електрони, атоми, молекули, клітки, нейтрони, механічні елементи, фотони, органи, тварини і навіть люди.

При виборі математичного апарату необхідно мати зважаючи на, що він повинен бути застосовний до проблем, з якими стикаються фізик, хімік, біолог, електротехнік і інженер механік. Не менш безвідмовний він повинен діяти і в області економіки, екології і соціології.

У всіх цих випадках нам доведеться розглядати системи, що складаються з дуже великого числа підсистем, щодо яких ми можемо не мати в своєму розпорядженні всієї повної інформації.

Для опису таких систем не рідко використовують підходи, засновані на термодинаміки і теорії інформації.

У всіх системах, що представляють інтерес для синергетики, вирішальну роль грає динаміка. Як і які макроскопічні стани утворюються, визначаються швидкістю росту (або розпаду) колективних «мод».

Можна сказати що в певному значенні ми приходимо до свого роду узагальненому дарвенізму, дія якого розпізнається не тільки на органічний,но і на неорганічний світ : виникнення макроскопічних структур обумовлених народженням колективних мод під впливом флуктуацій, їх конкуренцією і, нарешті, відбором «найбільш пристосованої» моди або комбінації таких мод.

Ясно, що вирішальну роль грає параметр «час».

Отже, ми повинні досліджувати еволюцію систем в часі. Саме тому рівняння, що цікавлять нас, іноді називають «еволюційними».

2.1 ЗАГАЛЬНА ХАРАКТЕРИСТИКА ВІДКРИТИХ СИСТЕМ

Відкриті системи - це термодинамічні системи, які обмінюються з навколишніми тілами ( середовищем ), речовиною, енергією і імпульсом . Якщо відхилення відкритої системи від стану рівноваги невелике, то нерівно важний стан можна описати тими ж параметрами (температура, хімічний потенціал та інші), що і рівноважне . Проте відхилення параметрів від рівноважних значень викликають потоки речовини і енергії в системі . Такі процеси перенесення приводять до виробництва ентропії . Прикладами відкритих систем є : біологічні системи, включаючи клітку, системи обробки інформації в кібернетиці, системи енергопостачання та інші . Для підтримки життя в системах від клітки до людини необхідний постійний обмін енергією і речовиною з навколишнім середовищем . Отже живі організми є системами відкритими, аналогічно і з іншими приведеними параметрами. Прігожіним в 1945 році був сформульований розширений варіант термодинаміки.

У відкритій системі зміну ентропії можна розбити на суму двох внесків

d S = d Se + d Si(2.1)

Тут d Se- потік ентропії, обумовлений обміном енергією і речовиною з навколишнім середовищем, d Si- виробництво ентропії усередині системи (мал. 2.1).

Мал. 2.1. Схематичне представлення відкритих

систем : виробництво і потік ентропії.

Х - набір характеристик :

З - склад системи і зовнішнього середовища ;

Р - тиск ; Т - температура.

Отже, відкрита система відрізняється від ізольованої наявністю члена у виразі для зміни ентропії, відповідної обміну . При цьому знак члена d Seможе бути будь-яким у відмінності від d Si .

Для нерівноважного стану :

S < Smax

Нерівноважний стан більш высокоорганизованно, ніж рівноважне, для якого

S = Smax

Таким чином еволюцію до вищого порядку можна представити як процес, в якому система досягає стану з нижчою ентропією в порівнянні з початковою.

Фундаментальна теорема про виробництво ентропії у відкритій системі з незалежними від часу краєвими умовами була сформульована Прігожіним: у лінійній області система еволюціонує до стаціонарного стану, що характеризується мінімальним виробництвом ентропії, сумісним з накладеними граничними умовами .

Отже стан всякої лінійної відкритої системи з незалежними від часу краєвими умовами завжди змінюється у напрямі зменшення виробництва ентропії P = d S / d t поки не буде досягнуте стан поточної рівноваги, при якій виробництво ентропії мінімальне :

d P < 0 (умова еволюції)

P = min, d P = 0 (умова поточної рівноваги)

d P/ d t < 0 (2.2)

2.1.1ДИССИПАТИВНІ СТРУКТУРИ

Кожна система складається з елементів (підсистем). Ці елементи знаходяться в певному порядку і зв'язані певними відносинами. Структуру системи можна назвати організацію елементів і характер зв'язку між ними.

У реальних фізичних системах є просторові і тимчасові структури .

Формування структури - це виникнення нових властивостей і відносин в безлічі елементів системи . У процесах формування структур грають важливу роль поняття і принципи :

1. Постійний негативний потік ентропії .

2. Полягання системи в далечіні від рівноваги .

3. Нелінійність рівнянь тих, що описують процеси .

4. Колективна (кооперативне) поведінка підсистем .

5. Універсальний критерій еволюції Прігожіна - Гленсдорфа.

Формування структур при необоротних процесах повинне супроводжуватися якісним стрибком (фазовим переходом) при досягненні в системі критичних значень параметрів. У відкритих системах зовнішній внесок в ентропію (2.1) d S в принципі можна вибрати довільно, змінюючи відповідним чином параметри системи і властивості навколишнього середовища . Зокрема ентропія може зменшуватися за рахунок віддачі ентропії в зовнішнє середовище, тобто коли d S < 0 . Це може відбуватися, якщо вилучення з системи в одиницю часу перевищує виробництво ентропії усередині системи, тобто

dS dSedSi¾ < 0, якщо > > 0 (2.3)¾ d t dtdt

Щоб почати формування структури, віддача ентропії повинна перевищити деяке критичне значення . У сильно нерівноважній відстані змінні системи задовольняють нелінійним рівнянням.

Таким чином, можна виділити два основні класи необоротних процесів:

1. Знищення структури поблизу положення рівноваги . Це універсальна властивість систем за довільних умов .

2. Народження структури далеко від рівноваги у відкритій системі за особливих критичних зовнішніх умов і при нелінійної внутрішньої динаміки. Ця властивість не універсальна.

Просторові, тимчасові або просторово-часові структури, які можуть виникати далеко від рівноваги в нелінійній області при критичних значеннях параметрів системи називаються дисипативними структурами.

У цих структурах взаємозв'язані три аспекти :

1. Функція стану, що виражається рівняннями .

2. Просторово - тимчасова структура, що виникає із-за нестійкості .

3. Флуктуації, відповідальні за нестійкості .

Мал. 1. Три аспекти дисипативних структур.

Взаємодії між цими аспектами приводить до несподіваних явищ - до виникнення порядку через флуктуації, формуванню високоорганізованої структури з хаосу.

Таким чином, в дисипативних структурах відбувається становлення з буття, формується те, що виникає з того, що існує.

2.2 САМООРГАНІЗАЦІЯ РІЗНИХ СІСТЕМ І СИНЕРГЕТІКА

Перехід від хаосу до порядку, що відбувається при зміні значень параметрів від до критичних до надкритичних, змінює симетрію системи . По цьому такий перехід аналогічний термодинамічним фазовим переходам . Переходи в нерівноважних процесах називаються кінетичними фазовими переходами. У близи нерівноважних фазових переходів не існує несуперечливого макроскопічного опису. Флуктуації такі ж важливі, як і середнє значенні. Наприклад, макроскопічні флуктуації можуть приводити до нових типів не устойчивостей.

Отже, в далечіні від рівноваги між хімічною, кінетичною і просторово-часовою структурою реагуючих систем існує несподіваний зв'язок . Правда, взаємодія, що визначають взаємодію констант швидкостей і коефіцієнтів перенесення, обумовлені короткодіючими силами (силами валентності, водневими зв'язками і силами Ван-Дер-Ваальса). Проте вирішення відповідних рівнянь залежать, крім того, від глобальних характеристик. Для виникнення дисипативних структур зазвичай потрібний, щоб розміри системи перевищували деяке критичне значення - складну функцію параметрів, що описують реакційно-дифузійні процеси . Ми можемо по цьому стверджувати, що хімічні нестійкості задають подальший порядок, за допомогою якого система діє як ціле .

Якщо врахувати дифузію, то математичне формулювання проблем, пов'язаних з дисипативними структурами, зажадає вивченні диференціальних рівнянь в приватних похідних. Дійсно, еволюція концентрації компонент Х з часом визначається рівнянням вигляду

(2.4)

де перший член дає внесок хімічних реакцій в зміні концентрації Хi і зазвичай має простий полиноминальный вигляд, а другий член означає дифузію уздовж осі r.

Дійсно вражаюче, як багато різноманітних явищ описує реакційно-дифузне рівняння (2.4 ), по цьому цікаво розглянути ² основне рішення, яке б відповідала термодинамічній гілці . Інші рішення можна було б отримувати при не послідовних устойчивостях, що виникають у міру видалення від стану рівноваги. Нестійкості такого типу зручно вивчати методами теорії біфуркації [Николіс і Прігожін, 1977]. В принципі, біфуркація є щось інше, як виникнення при деякому критичному значенні параметра нового вирішення рівнянь . Припустимо, що ми маємо хімічну реакцію, відповідну кінетичному рівнянню [ Маклейн і Уоліс, 1974] .

d X ¾ = а X (X-R) (2.5)¾ d t

Ясно що при R < 0 існує тільки одне рішення, незалежне від часу, X = 0. У точці R = 0 відбувається біфуркація, і з'являється нове рішення X = R.

Мал. 2.3. Біфуркационная диограмма для рівняння ( 2.5.)

Суцільна лінія відповідає стійкій гілці

крапки - нестійкої гілки

Аналіз стійкості в лінійному наближенні дозволяє перевірити, що рішення X = 0 під час переходу через R = 0 стає нестійким, а рішення X = R - стійким . Загалом випадки при зростанні деякого характеристичного параметра р відбуваються послідовні біфуркації . На малюнку 2.4. показано єдине рішення при р = р1, але при р = р2 єдиністю поступається місце множинним рішення.

Цікаво відзначити, що біфуркація в деякому розумінні вводить у фізику і в хімію, історію - елемент, який раніше вважався прерогативою наук що займаються вивченням біологічним, суспільних і культурних явищ .

Мал. 2.4. Послідовні біфуркації:

А і А1 - точки первинних біфуркацій з термодинамічній гілці

У і В1 - точки вторинної біфуркації

Відомо, що при зміні параметрів, що управляють, в системі спостерігаються різноманітні перехідні явища. Виділимо тепер з цих спостережень певні загальні риси, характерні для великого числа інших переходів у физико хімічних системах.

З цією метою представимо графічно (мал. 2.5) залежність вертикальною компоненти швидкості перебігу рідини в деякій певній крапці від зовнішнього обмеження, або, в більш загальному вигляді, залежність змінної стан системи Х (або х = Х - Хs ) від параметра, що управляє l. Таким чином ми отримаємо графік, відомий під назвою бифуркационной діаграми.

Мал. 2.5. Біфуркаційна діаграма:

а - стійка частина термодинамічної гілки

а1 - не стійка частина термодинамічної гілки

в1,в2 - дисипативні структури, народжені в

надкритичній області .

При малих значення l можливо лише одне рішення, відповідне поляганню спокою в бенаровському експерименті. Воно є безпосередню екстраполяцію термодинамічної рівноваги, і подібно рівноважне, що характеризується важливою властивістю - асимптотичною стійкістю, оскільки в цій області система здатна гасити внутрішні флуктуації або зовнішнє обурення . З цієї причини таку гілку станів ми називатимемо термодинамічною гілкою. Під час переходу критичного значення параметраl, позначеного l_з на малюнку 2.5., що перебувають на цій гілці стає нестійкими, оскільки флуктуації або малі зовнішні обурення вже не гасяться . Діючи подібно до підсилювача, система відхиляється від стаціонарного стану і переходить до нового режиму, у разі бенаровського експерименту відповідному стану стаціонарної конвекції. Обидва цих режиму зливаються при = _l _з і розрізняються при >_з . Це явище називається біфуркацією . Легко зрозуміти причини, по яких це явище слід асоціювати з катастрофічними змінами і конфліктами. Насправді, у вирішальний момент переходу система повинна зробити критичний вибір ( у околиці = _з ), що в завданні Бенара пов'язане з виникненням право- або лівообертальних осередків в певній області простору ( мал. 2.5., гілки в1 або в2 ).

Поруч з рівноважним станом стаціонарний стан асимптотичних стійкий (по теоремі про мінімальне виробництво ентропії ), по цьому через безперервність ця термодинамічна гілка тягнеться у всій докритичній області. Досягши критичного значення термодинамічна гілка може стати нестійкою, так що будь-яке, навіть мале обурення, перекладає систему з термодинамічної гілки в новий стійкий стан, який може бути впорядкованим. Отже, при критичному значенні параметром відбулася біфуркація і виникла нова гілка рішень і, відповідно, новий стан. У критичній області, таким чином, подія розвивається по такій схемі

Флуктуація ® Біфуркація

нерівноважний фазовий перехід ®

Народження впорядкованої структури

Біфуркація в широкому розумінні - придбанні нової якості рухами динамічної системи при малій зміні її параметрів ( виникнення при деякому критичному значенні параметра нового вирішення рівнянь ) . Відзначимо, що при біфуркації вибір наступного стану носить суто випадковий характер, так що перехід від одного необхідного стійкого стану до іншого необхідного стійкому стану проходить через випадкове (діалектика необхідного і випадкового) . Будь-який опис системи, що зазнає біфуркацію, включає як детерміністичний, так і імовірнісний елементи, від біфуркації до біфуркації поведінці системи детерміновано, а в околиці точок біфуркації вибір подальшого шляху випадковий. Проводячи аналогію з біологічною еволюцією можна сказати, що мутації - це флуктуації, а пошук нової стійкості грає роль природного відбору. Біфуркація в деякому розумінні вводить у фізику і хімію елемент історизму - аналіз стану в1, наприклад, має на увазі знання історії системи, що пройшла біфуркацію.

Загальна теорія процесів самоорганізації відкритих сильно не рівноважних системах розвивається на основі універсального критерію еволюції Прігожіна-Гленсдорфа. Цей критерій є узагальненням теореми Прігожіна про мінімальне виробництво ентропії. Швидкість виробництва ентропії, обумовлена зміною термодинамічних сил Х, згідно цьому критерію підкоряється умові

dx P / t £ 0 (2.6)£

Ця нерівність не залежить не від яких припущень про характер зв'язків між потоками і силами в умовах локальної рівноваги і носить по цьому універсальний характер . У лінійній області нерівність (2.6. ) переходить в теорему Прігожіна про мінімальне виробництво ентропії . Отже, в неравновестной системі процеси йдуть так, тобто система еволюціонує таким чином, що швидкість виробництва ентропії при зміні термодинамічних сил зменшується (або рівна нулю в стаціонарному стані).

Впорядковані структури, які народжуються далеко від рівноваги, відповідно до критерію (2.6.) і є диссипативні структури.

Еволюція біфуркації і подальшої самоорганізації обумовлено, таким чином, відповідними не рівноважними обмеженнями.

Еволюція змінних Х описуватиметься системою рівнянь

(2.7)

де функції F як завгодно складним чином можуть залежать від самих змінних Х і їх просторових похідних координат r і часу t . Крім того, ці функції буду залежать від параметрів, що управляють, тобто тих характеристик, що змінюються, які можуть сильно змінити систему . На перший погляд здається очевидним, що структура функції { F } буде сильна визначаться типом відповідної даної системи . Проте, можна виділити деякі основні універсальні риси, незалежні від типу систем.

Вирішення рівняння (2.7), якщо немає зовнішніх обмежень, повинні відповідати рівновазі при будь-якому виді функції F . Оскільки рівноважний стан стаціонарний, то

Fi ({Xрав},равl ) = 0 (2.8)l

У більш загальному випадку для нерівноважного стану можна аналогічно написати умову

Fi ({X},l) = 0 (2.9)l

Ці умови накладають певні обмеження універсального характеру, наприклад, закони еволюції системи повинні бути такими, щоб виконувалася вимога позитивності температури або хімічної концентрації, що отримуються як вирішення відповідних рівнянь.

Іншою універсальною межею є нелінійним . Хай, наприклад деяка єдина характеристика системи задовольняє рівнянню

(2.10)

де до - деякий параметр, l - зовнішні обмеження, що управляють . Тоді стаціонарний стан визначається з наступного рівняння алгебри

l - kX = 0 (2.11)l

звідки

Xs = l / до (2.12)l

У стаціонарному стані, таким чином, значенні характеристики, наприклад, концентрації, лінійно змінюється залежно від значень обмеженняl, що управляєl, і є для кожного єдиний стан Хs . Абсолютно однозначно можна передбачити стаціонарне значення Х при будь-якомуl,если мати хоч би два експериментальні значення Х(l). Керуючий параметр може, зокрема, відповідати ступеню віддаленості системи від рівноваги . Поведінка в цьому випадку системи дуже схожі на рівновазі навіть за наявності сильно нерівноважних обмежень.

Мал. 2.6. Ілюстрація універсальної межі нелінійності в самоорганізації структур

Якщо ж стаціонарне значення характеристики Х не лінійно залежить від обмеження, що управляє, при деяких значеннях, то при одному і тому ж значенні є декілька різних рішень . Наприклад, при обмеженнях система має три стаціонарні рішення, малюнок 2.6.в. Така універсальна відмінність від лінійної поведінки наступає при досягненні параметром, що управляє, деякого критичного значення l - виявляється біфуркація. При цьому в нелінійній області невелике збільшення може привести до неадекватно сильному ефекту - система може зробити стрибок на стійку гілку при невеликій зміні поблизу критичного значенняl, малюнок 2.6.в. Крім того з перебувань на гілці А1в можуть відбуватися переходи Ав1 ( або навпаки ) навіть раніше, ніж будуть досягнуті полягання В або А, якщо обурення накладаються на стаціонарний стан, більше значення, відповідного проміжній гілці А В . Обуреннями можуть служити або зовнішня дія або внутрішні флуктуації в самій системі. Таким чином, системі з множинними стаціонарними станами властиво універсально властивостям внутрішньо збудливість і мінливості скачкам.

Виконання теореми по мінімально виробництві ентропії в лінійній області, а, як узагальнення цієї теореми, виконання універсального критерію (2.6.) і в лінійній, і в нелінійній області гарантують стійкість стаціонарних нерівноважних станів. В області лінійності необоротних процесів виробництво ентропії грає таку ж роль, як термодинамічні потенціали в рівноважній термодинаміці. У нелінійній області величина dP / dtне має якого або загальної властивості, проте, величина dx P/dt задовольняє нерівності загального характеру (2.6.), яка є узагальненням теореми про мінімальне виробництво ентропії.

2.3 ПРИКЛАДИ САМООРГАНІЗАЦІЇ РІЗНИХ СИСТЕМ

Розглянемо як ілюстрацію деякі приклади самоорганізації систем у фізиці, хімії, біології і соціумі

2.3.1 ФІЗИЧНІ СИСТЕМИ

В принципі навіть в термодинамічній рівновазі можна вказати приклади самоорганізації, як результати колективної поведінки . Це, наприклад, всі фазові переходи у фізичних системах, такі як перехід рідина - газ, феромагнітний перехід або виникнення надпровідності . У нерівноважному стані можна назвати приклади високої організації в гідродинаміці, в лазерах різних типів, у фізиці твердого тіла - осцилятор Ганна, тунельні діоди, зростання кристалів.

У відкритих системах, міняючи потік речовини і енергії із зовні, можна контролювати процеси і направляти еволюцію систем до станів, все більш далеких від рівноваги. В ході нерівноважних процесів при деякому критичному значенні зовнішнього потоку з неврегульованих і хаотичних станів за рахунок втрати їх стійкості можуть виникати впорядковані стани, створюватися дисипативні структури.

2.3.1а ОСЕРЕДКИ БЕНАРА

Класичним прикладом виникнення структури з повністю хаотичної фази є конвективні осередки Бенара . У 1900 році була опублікована стаття Х.Бенара з фотографією структури, що по вигляду нагадувала бджолині соти (мал. 2.7).

Мал. 2.7. Осередки Бенара :

а) - загальний вид структури

б) - окремий осередок.

Ця структура утворилася в ртуті, налитій в плоску широку судину, що підігрівається знизу, після того, як температурний градієнт перевищив деяке критичне значення . Весь шар ртуті (або іншій в'язкій рідині) розпадався на однакові вертикальні шестигранні призми з певним співвідношенням між стороною і висотою (осередки Бенара). У центральній області призми рідина піднімається, а поблизу вертикальних граней - опускається . Виникає різниця температур Т між нижньою і верхньою поверхнею DТ = Т2 - Т1 > 0 .Для малих до критичних різниць Т <DТkp рідина залишається в спокоїD><D, тепло від низу до верху передається шляхом теплопровідності . Досягши температури підігріву критичного значення

Т2 = Тkp (відповідно Т = DТkp )

починається конвекція. Досягши критичного значення параметра Т, народжується, таким чином, просторова диссипативна структура . При рівновазі температури рівні Т2 =Т₁ , DТ = 0 . При короткочасному підігріві (підводі тепла) нижньої площини, тобто при короткочасному зовнішньому обуренні температура швидко стане однорідною і рівною її первинному значенню . Обурення затухає, а стан - асимптотика стійко. При тривалому, але до критичному підігріві ( DТ < Тkp ) в системі знову встановиться простий і єдиний стан, в якому відбувається перенесення до верхньої поверхні і передачі його в зовнішнє середовище (теплопровідність), мал. 2.8, ділянка а . Відмінність цього стану від рівноважного стану полягає в тому, що температура, щільність, тиск стануть неоднорідними. Вони будуть приблизно лінійно змінюватися від теплої області до холодної .

Мал. 2.8. Потік тепла в тонкому шарі рідини

Збільшення різниці температур DТ, тобто подальше відхилення системи від рівноваги, приводить до того, що стан нерухомої теплопроводящей рідини стає нестійким ділянка б на малюнку 2.8. Цей стан змінявся стійким станом (ділянка в на мал. 2.8), утворенням осередків, що характеризується . При великих різницях температур рідина, що покоїться, не забезпечує велике перенесення тепла, рідина ²вимушена рухатися, причому кооперативним колективним узгодженому образом.

Далі це питання розглядається в 3 розділі.

2.3.1б ЛАЗЕР ЯК СИСТЕМА, ЩО САМООРГАНИЗУЄТЬСЯ

Отже, як приклад фізичної системи, впорядкованість якої є наслідок зовнішньої дії, розглянемо лазер.

При найгрубішому описі лазер - це якась скляна трубка, в яку поступає світло від некогерентного джерела (звичайної лампи), а виходить з неї вузьконаправлений когерентний світловий пучок, при цьому виділяється деяке кількості тепла.

При малій потужності накачування ці електромагнітні хвилі, які випускає лазер, некорельовані, і випромінювання подібно до випромінювання звичайної лампи. Таке некогерентне випромінювання - це шум, хаос. При підвищенні зовнішньої дії у вигляді накачування до порогового критичного значення некогерентний шум перетвориться в ²чистий тон, тобто випускає число синусоїдальна хвиля - окремі атоми поводяться строго корельованим чином, само організовуватимуться.

Лампа ® Лазер

Хаос ® Порядок

Шум ® Когерентне випромінювання

У надкритичній області режим ²звичайної лампи ²виявляється не стабільним, а лазерний режим стабільним, малюнок 2.9.

Мал. 2.9. Випромінювання лазера в до критичної (а) і

надкритичній (б) області.

Видно, що утворення структури в рідині і в лазері формально описується вельми схожим чином. Аналогія пов'язана з наявністю тих же самих типів біфуркацій у відповідних динамічних рівнях.

Докладніше це питання розглянемо в практичній частині, в 3 розділі.

2.3.2 ХІМІЧНІ СИСТЕМИ

У цій області синергетика концентрує свою увагу на тих явищах, які супроводжуються утворенням макроскопічних структур. Зазвичай якщо дати реагентам про взаємодіяти, інтенсивно перемішуючи реакційну суміш, то кінцевий продукт виходить однорідний. Але в деяких реакціях можуть виникати тимчасові, просторові або змішані (просторові - тимчасові) структури. Найбільш відомим прикладом може служити реакція Белоусова-Жаботінського.

2.3.2а РЕАКЦІЯ БЕЛАУСОВА-ЖАБОТІНСЬКОГО

Розглянемо реакцію Белоусова-Жаботинского. У колбу зливають в певних пропорціях Ce2(SO4), KBrO3, CH2(COOH)₂ , H2SO4, додають декілька крапель індикатора окислення - відновлення - ферроїна і перемішують. Конкретніше - досліджуються окислювально-відновні реакції

Ce^{3+_ _ _} Ce⁴⁺ ; Ce^{4+_ _ _} Ce³⁺

у розчині сульфату церію, броміду калі, молочної кислоти і сірчаної кислоти . Додавання ферогена дозволяє стежити за ходом реакції по зміні кольору ( по спектральному поглинанню). При високій концентрації реагуючих речовин, що перевищують критичне значення спорідненості, спостерігаються незвичайні явища.

При складі

сульфат церію - 0,12 ммоль/л

броміду калі - 0,60 ммоль/л

молочної кислоти - 48 ммоль/л

3-нормальна сірчана кислота

небагато ферроїна

При 60 Із зміни концентрації іонів церію набуває характер релаксаційних коливанні - колір розчину з часом періодично змінюється від червоного (при надлишку Се3+ ) до синього ( при надлишку Це 4+), малюнок 2.10а.

Мал. 2.10. Тимчасові (а) і просторові (б)

періодичні структури в реакції

Белоусова-Жаботінського

Така система і ефект отримали назву хімічний годинник. Якщо на реакцію Белоусова-Жаботінського накладати обурення - концентраційний або температурний імпульс, тобто вводячи декілька Мілімолей бромату калі або торкаючись до колби в перебігу декількох секунд, то після деякого перехідного режиму знову здійснюватимуться коливання з такою ж амплітудою і періодом, що і до обурення. Дисипативна Белоусова-Жаботінського, таким чином, є асимптотичне стійкою. Народження і існування незгасаючих коливань в такій системі свідчить про те, що окремі частини системи діють погоджено з підтримкою певних співвідношень між фазами. При складі

сульфату церію - 4,0 ммоль/л

броміду калі - 0,35 ммоль/л

молочної кислоти - 1,20 міль/л

сірчаної кислоти - 1,50 міль/л

небагато ферроїна

при 20 З в системі відбуваються періодичні зміни кольору з періодом близько 4 хвилин. Після декількох таких коливань спонтанно виникають неоднорідності концентрації і утворюються на деякий час ( 30 хвилин ), якщо не підводити нові речовини, стійкі просторові структури, малюнок 2.10б . Якщо безперервно підводити реагенти і відводити кінцеві продукти, то структура зберігається необмежено довго.

2.3.3 БІОЛОГІЧНІ СИСТЕМИ

Тваринний світ демонструє безліч високо впорядкованих структур і що прекрасно функціонують. Організм як ціле безперервно отримує потоки енергії (сонячна енергія, наприклад, у рослин) і речовин (живильних) і виділяє в навколишнє середовище відходи життєдіяльності. Живий організм - це система відкрита. Живі системи при цьому функціонують безумовно в далечіні від рівноваги. У біологічних системах, процеси самоорганізації дозволяють біологічним системам ²трансформувати ²енергію з молекулярного рівня на макроскопічний. Такі процеси, наприклад, виявляються в м'язовому скороченні, що приводить до всіляких рухів, в утворенні заряду у електричних риб, в розпізнаванні образів, мови і в інших процесах в живих системах. Складні біологічні системи є одним з головних об'єктів дослідження в синергетиці. Можливість повного пояснення особливостей біологічних систем, наприклад, їх еволюції за допомогою понять відкритих термодинамічних систем і синергетики в даний час остаточно неясна . Проте можна вказати декілька прикладів явного зв'язку між понятійним і математичним апаратом відкритих систем і біологічною впорядкованістю.

Конкретніше біологічні системи ми розглянемо в 3 розділі, подивимося динаміку популяцій одного вигляду і систему ²жертва - хижак².

2.3.4 СОЦІАЛЬНІ СИСТЕМИ

Соціальна система є певним цілісним утворенням, де основними елементами є люди, їх норми і зв'язки. Як ціле система утворює нову якість, яка не зводиться до суми якостей її елементів. У цьому спостерігається деяка аналогія із зміною властивостей при переході від малого до дуже великого числа частинок в статичній фізиці - перехід від динамічних до статичних закономірностей . При цьому вельми очевидно, що всякі аналогії з физико-хімічними і біологічними системами вельми умовні, тому проводити аналогію між людиною і молекулою або навіть щось подібне було б не допустимою помилкою . Проте, понятійний і математичний апарат нелінійної нерівноважної термодинаміки і синергетики виявляються корисними в описі і аналізі елементів самоорганізації в людському суспільстві.

Соціальна самоорганізація - один з проявів спонтанних або вимушених процесів в суспільстві, направлена на впорядкування життя соціальної системи, на більше саморегулювання. Соціальна система є системою відкритої здатна, навіть вимушена обмінюватися із зовнішнім світом інформацією, речовиною, енергією. Соціальна самоорганізація виникає як результат цілеспрямованих індивідуальних дій її складових.

Розглянемо самоорганізацію в соціальної системи наприкладу урбанізації зони. Проводячи аналіз урбанізації географічних зон можна припустити, що зростання локальної заселеності даної території буде обумовлено наявністю в цій зоні робочих місць. Проте, тут існує деяка залежність : стан ринку, що визначає потребу в товарах і послугах і зайнятості . Звідси виникає механізм нелінійного зворотного зв'язку в процесі зростання щільності населення. Таке завдання вирішується на основі логістичного рівняння, де зона характеризується зростанням її продуктивності N, нових економічних функцій S - функція в локальній області i міста. Логістичне рівняння описує еволюцію чисельності населення і може бути тоді представлена у вигляді

dni

¾= Кni(N + åRkSik - ni) - dni( 2.13 )å

dtдо

де Rkвага даної до - ой функції, її значущість. Економічна функція змінюється із зростанням чисельності : визначається попитом на до - й продукт в i - й області залежно від збільшення чисельності населення і конкуренції підприємств в інших зонах міста. Появу нової економічної функції грає роль соціально економічній флуктуації і порушує рівномірний розподіл щільності населення. Такі чисельні розрахунки по логістичних рівняннях можуть бути корисні прогнозуванні багатьох проблем.

У розглянутих прикладах в літературі є лише загальні виводи і висновки, не приведені конкретні аналітичні розрахунки або чисельні.

Метою справжньої дипломної роботи є аналітичні і чисельні дослідження самоорганізації різних систем.

РОЗДІЛ 3. АНАЛІТИЧНІ І ЧИСЕЛЬНІ ДОСЛІДЖЕННЯ САМООРГАНІЗАЦІЇ РІЗНИХ СИСТЕМ

3.1 ОСЕРЕДКИ БЕНАРА

Для того, щоб експериментально вивчити структури, досить мати сковороду, трохи масла і якою ні будь дрібний порошок, щоб було помітно рух рідини . Наллємо в сковороду масло з розмішаним в нім порошком і підігріватимемо її знизу (мал. 3.1)

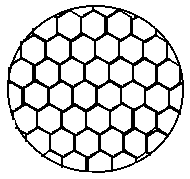
Мал. 3.1. Конвективні осередки Бенара

Якщо дно сковороди плоске і нагріваємо ми її рівномірно, то можна вважати, що у дна і на поверхні підтримуються постійні температури, знизу - Т1, зверху - Т2 . Поки різниця температури DТ = Т1 - Т2 невелика, частинки порошку нерухомі, а отже, нерухома і рідина .

Плавно збільшуватимемо температуру Т1. Із зростанням різниці температур до значення DТc спостерігається все та ж картина, але коли DТ >DТc, все середовище розбивається на правильні шестигранні осередки (див. Мал. 3.1) в центрі кожної з яких рідина рухається вгору, по кроях вниз . Якщо узяти іншу сковороду, то можна переконатися, що величина виникаючих осередків практично не залежить від її форми і розмірів . Цей чудовий досвід вперше був виконаний Бенаром на початку нашого століття, а самі осередки отримали назву осередків Бенара.

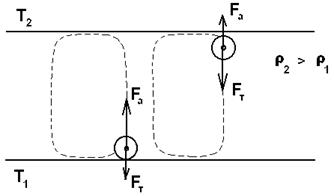
Елементарне якісне пояснення причини руху рідини полягає в наступному . Із-за теплового розширення рідина розшаровується, і в більш нижньому шарі щільність рідини r₁ менше, ніж у верхньому _r ₂ . Виникає інверсний градієнт щільності, направлений протилежно силі тяжіння . Якщо виділити елементарний об'єм V, який трохи зміщується вгору в наслідку обурення, то в сусідньому шарі архімедова сила стане більше сили тяжіння, оскільки _r ₂ >r₁ . У верхній частині малий об'єм, зміщуючись вниз, потрапляє в область зниженої щільності, і архімедова сила буде менше сили тяжіння FA < FT, виникає низхідний рух рідини. Напрям руху низхідного і висхідного потоків в даному осередку випадково, рух же потоків в сусідніх осередках, після вибору напрямів в даному осередку детерміновано. Повний потік ентропії через межі системи негативний, тобто система віддає ентропію, причому в стаціонарному стані віддає стільки, скільки ентропії проводиться усередині системи (за рахунок втрат на тертя).

dSeq q T1 - T2

¾= ¾ - = q *¾¾¾ < 0 (3.1)*¾¾¾

dtT2T1T1*T2

Освіта саме стільникової комірчастої структури пояснюється мінімальними витратами енергії в системі на створення саме такої форми просторової структури . При цьому в центральній частині осередку рідина рухається вгору, а на її периферії - вниз.

Подальше надкритичне нагрівання рідини приводить до руйнування просторової структури - виникає хаотичний турбулентний режим.

Мал. 3.2. Ілюстрація виникнення теплової

конвекції в рідині .

3.2 ЛАЗЕР, ЯК СИСТЕМА, ЩО САМООРГАНИЗУЄТЬСЯ

У другому розділі це питання ми вже розглядали . Тут же, розглянемо просту модель лазера.

Лазер - це пристрій, в якому в процесі випромінювання, що стимулює, породжуються фотони.

Зміна з часом числа фотонів n, або іншими словами, швидкість породження фотонів, визначається рівнянням вигляду :

dn / dt= «Приріст» - «Втрати» (3.2)

Приріст обумовлений так званим що стимулює випромінюванням . Він пропорційний числу вже наявних фотонів і числу збуджених атомів N . Таким чином :

Приріст = G N n (3.3)

Тут G - коефіцієнт посилення, який може бути отриманий з мікроскопічної теорії . Член, що описує втрати, обумовлений відходом фотонів через торці лазера . Єдине допущення, яке ми приймаємо, - це те, що швидкість відходу пропорційна числу наявних фотонів. Отже

Втрати = 2nc (3.4)c

2c = 1/ t0, де t0 - час життя фотона в лазері .

Тепер слід врахувати одну важливу обставину, яка робить (2.1) нелінійним рівнянням вигляду :

(3.5)

Число збуджених атомів зменшується за рахунок випускання фотонів . Це зменшення DN пропорційно числу наявних в лазері фотонів, оскільки ці фотони постійно примушують атоми повертатися в основний стан .

DN = an (3.6)a

Таким чином, число збуджених атомів рівне

N = N0 - DN (3.7)D

де N0 - число збуджених атомів, підтримуване зовнішньою

накачуванням, у відсутності лазерної генерації.

Підставляючи (3.3) - (3.7) в (3.2), отримуємо основне рівняння наший спрощеній лазерній моделі :

(3.8)

де постійна до дає вираз :

k1= aG

до = 2 c- GN0>< 0 (3.9)

Якщо число збуджених атомів N0(створюваних накачуванням) невелике, то до позитивно, тоді як при достатньо великих N0до - може стати негативним . Зміна знаку відбувається коли

GN0= 2c (3.10)c

Ця умова є умова порогу лазерної генерації .

З теорії біфуркації виходить, що при до > 0 лазерної генерації немає, тоді як при до < 0 лазер випускає фотони.

Нижче або вище за поріг лазер працює в здійснено різних режимах .

Вирішимо рівняння (3.8) і проаналізуємо його аналітично :

- це рівняння одномодового лазера .

Запишемо рівняння (3.8) в наступному вигляді :

Розділимо початкове рівняння на n2 .

і введемо нову функцію Z :

1/n = n-1 = Z ÞZ1 = - n-2 отже рівняння прийме вигляд :

перепишемо його в наступному вигляді :

розділимо обидві частини даного рівняння на -1, отримаємо

(3.11)

Рівняння (3.11) - це рівняння Бернуллі, тому зробимо наступну заміну

Z = UV×, де U і V невідомі поки функції n, тоді Z1 = U1 V + U V1 .

Рівняння (3.11), після заміни змінних, приймає вигляд

U1 V + UV1 - до UV= k1

перетворимо, отримаємо

U1 V + U(V1 - до V)= k1 (3.12)

Вирішимо рівняння (3.12)

V1 - до V = 0 ® dV/dt = до V

зробимо розділення змінних

dV/V =k dt®ln V = до t

результат V = ekt(3.13)

Звідси ми можемо рівняння (3.12) переписати у вигляді :

U1 ekt= k1- це те ж саме, що dU/dt = k1e-kt, dU = k1e^- ^kt dtвиразимо звідси U, отримаємо

(3.14)

По рівнянню Бернуллі ми робили заміну Z = U V підставляючи рівняння (3.13) і (3.14) в цю заміну, отримаємо

Раніше вводили функцію Z = n-1, отже

(3.15)

Початкова умова n0=1/(c-k1/k), з цієї умови ми можемо визначити константу з наступним чином

Підставляючи, знайдену нами константу в рівняння (3.15), отримаємо

(3.16)

Досліджуємо функцію (3.16) при до = 0, до < 0, до > 0 .

При k0 ®; ekt® 0 ; (ekt - 1)®0, тобто (ekt - 1)×k1/k0®×¥ (невизначеність), розкриємо цю невизначеність за правилом Лопіталя . Цю невизначеність вигляду 0¥ слід привести до вигляду . При цьому, як і завжди при застосуванні правила Лопіталя, по ходу обчислень рекомендується спрощувати вирази, що вийшли, таким чином :

n(k)_при _k0 _® ® 0, отже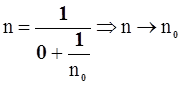

Перепишемо (3.16) в наступному вигляді

Лінеарізуєм нелінійне рівняння, отримаємо

ln n = - kt + з Þ

Побудуємо графік для цих умов

Мал. 3.3 До самоорганізації в одномодовому лазері :

крива 1 : до < 0, режим лазерної генерації

крива 2 : до = 0, точка біфуркації, поріг

крива 3 : до > 0, режим лампи.

При до = 0 рівняння (3.8) прийме вигляд

вирішуючи його, отримаємо

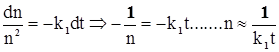
(3.8)

За умови ; n(t)= const, функція (3.8) наближається до стаціонарного стану, не залежно від початкового значення n0, але залежно від знаків до і k1 (дивися малюнок 3.3).

Таким чином, функція (3.8) ухвалює стаціонарне рішення

3.3 ДИНАМІКА ПОПУЛЯЦІЇ

Про розповсюдження і чисельність видів була зібрана велика інформація. Макроскопічною характеристикою, що описує популяцію, може бути число особин в популяції . Це число грає роль параметра порядку. Якщо різні види підтримуються загальним харчовим ресурсом, то починається міжвидова боротьба, і тоді застосуємо принцип Дарвіна: виживає найбільш пристосований вигляд. (Не можна не відзначити сильну аналогію, що існує між конкуренцією лазерних мод і міжвидовою боротьбою). Якщо є однотипні харчові ресурси, то стає можливим співіснування видів. Чисельність видів може бути схильна до тимчасових коливань.

ОДИН ВИГЛЯД.

Розглянемо спочатку одну популяцію з числом особин в ній n . За наявності харчових ресурсів А особини розмножуються з швидкістю :

і гинуть з швидкістю :

Тут до і d - деякі коефіцієнти народжуваності і смертності, в загальному випадку залежне від параметрів зовнішнього місця існування. Якби кількість їжі була необмежено, то еволюційне рівняння виглядало б так:

Введемо позначення a = kA - d

Воно було б лінійним і описувало б необмежене експериментальне зростання (при kA > d), або експериментальну загибель (при kA < d) популяції.

Мал. 3.4 Крива 1: Експоненціальне зростання; >a0, kA>d

Крива 2: Експоненціальна загибель; >a0, kA>d.

У загальному випадку, проте, харчові ресурси обмежені, так що швидкість споживання їжі

Разом з тим в загальному випадку можливе відновлення харчових ресурсів з швидкістю :

Тут, звичайно, розглянутий боковий випадок збереження повної кількості органічної речовини

A + n = N = const

N - здатність місця існування підтримувати популяцію.

Тоді з урахуванням A = N - n вийде наступне рівняння еволюції популяції одного вигляду (логістичне рівняння Ферхюльста ) :

(3.17)

Вирішимо рівняння (3.17) аналітично, перепишемо його таким чином

позначимо kN - d = k1

Отримаємо :

Скористаємося табличним інтегралом ,полученное рівняння прийме вигляд :

вирішимо це рівняння, перетворюючи

скоротимо отриманий вираз на до, і перенесемо змінну k1в праву частину, отримаємо

звідси n(t) ®

Початкові умови :

Звідки

Підставляючи з в рішення, отримаємо рівняння в наступному вигляді

раніше ми означали, що підставляємо і перетворюваний

скоротимо на до - коефіцієнт народжуваності, остаточно отримаємо вирішення рівняння (3.17)

Отже, отримано аналітичне вирішення логістичного рівняння - це рішення указує на те, що зростання популяції зупиняється на деякому кінцевому стаціонарному рівні:

тобто параметр n1указує висоту плато насичення, до якого прагне n(t) з часом .

Параметр n0указує початкове значення чисельності одного виду популяції : n0 = n(t0) . Дійсно ,то є n1 - гранична чисельність вигляду в даному місці існування . Інакше кажучи, параметр n1 характеризує ємкість середовища по відношенню до даної популяції . І нарешті, параметр (kN - d) задає крутизну початкового зростання.

Відзначимо, що при малій початковій чисельності n0 (початкове число особини) початкове зростання популяцій буде майже експоненціальним

Мал. 3.5. Логістична крива.

(еволюція популяції одного вигляду)

Вирішення рівняння (3.17) можна представити за допомогою логістичної кривої (мал. 3.5) . Еволюція повністю детермінована . Популяція перестає рости, коли ресурс середовища виявляється вичерпаним.

Самоорганізація - при обмеженому харчовому ресурсі. Підкреслимо, що при описі даної біологічної системи використовують понятійний і фізико-математичний апарат з нелінійної нерівноважної термодинаміки.

Може трапиться, проте, що завжди за подіями, не керованими в рамках моделі, в тому ж середовищі з'явиться, спочатку в малих кількостях, новий вигляд (що характеризуються іншими екологічними параметрами к,N і d) . У зв'язку з такою екологічною флуктуацією виникає питання про структурну стійкість: новий вигляд може або зникнути, або витіснити первинних мешканців.

Користуючись лінійним аналізом стійкості, не важко показати, що новий вигляд витісняє старі тільки в тому випадку, якщо

Послідовність, в якій види заповнюють екологічну нішу, представлена на малюнку 3.6.

Мал. 3.6. Послідовне заповнення екологічної ніші різними видами .

Ця модель дозволяє додати точним кількісний сенс твердженню про те, що «виживає найбільш пристосований», в рамках завдання про заповнення заданої екологічної ніші .

3.3.2 СИСТЕМА «ЖЕРТВА - ХИЖАК»

Розглянемо систему, що складається з двох видів, - це «жертва» і «хижак» (наприклад, зайці і лисиці), то еволюція системи і її самоорганізація виглядають інакше, ніж у попередньому випадку.

Хай в біологічній системі є дві популяції - «жертви» - кролики (К), і «хижаків» - лисиць (Л), чисельністю До і Л .

Проведемо тепер міркування, яке дозволить нам пояснити існування дисипативних структур .

Кролики (К) поїдають траву (Т). Припустимо, що запас трави постійний і невичерпний. Тоді, одночасна наявність трави і кроликів сприяють необмеженому зростанню кролячої популяції . Цей процес можна символічно зобразити так:

Кролики + Трава ® Більше кроликів

До + Т ®2К

Той факт, що в країні кроликів завжди є в достатку трави, цілком аналогічний безперервному підведенню теплової енергії в завданні з осередками Бенара. Незабаром процес, в цілому, виглядатиме як дисипативний (багато в чому аналогічно процесу Бенара ).

Реакція «Кролики - Трава» відбувається спонтанно у напрямі збільшення популяції кроликів, що є прямим наслідком другого початку термодинаміки.

Але в нашу картину, де мирно пустують кролики, прокралися хижі лисиці (Л), для яких кролики є здобиччю . Подібно до того, як у міру поїдання трави кроликів стає більше, за рахунок поїдання кроликів зростає число лисиць:

Лисиці + Кролики ® Більше лисиць

Л + До ®2Л

У свою чергу лисиці, як і кролики є жертвами - цього разу людини, точніше кажучи відбувається процес

Лисиці ® Хутра

Кінцевий продукт - Хутра, не грає безпосередньої ролі в подальшому ході процесу . Цей кінцевий продукт можна, проте, розглядати як носій енергії, що виводиться з системи, до якої вона була на початку підведена (наприклад, у вигляді трави).

Таким чином, в екологічній системі також існує потік енергії - аналогічно тому, як це має місце в хімічній пробірці або біологічній клітці.

Абсолютно ясно, що насправді відбуваються періодичні коливання чисельності популяції кроликів і лисиць, причому за наростанні чисельності кроликів слідує наростання чисельності лисиць, які змінялися зменшенням чисельності кроликів, таким же різким зниженням чисельності лисиць, що супроводжується, потім підвищеним підйомом чисельності кроликів і так далі (мал. 3.7).

Мал. 3.7. Зміна чисельності популяцій кроликів і лисиць з часом. Наявність періодичності означає виникнення екологічної структури.

З часом чисельність обох популяцій міняється відповідно до послідовного проходження точок графіка . Через деякий час (конкретне значення залежить від швидкості поїдання лисицями кроликів, а так само від швидкості розмноження обох видів) весь цикл починається знов.

Поведінка популяцій при різних ступенях плодючості, а так само різних здібностях уникати винищування можна вивчити кількісно за допомогою програми : ПОПУЛЯЦІЯ (у додатку).

Ця програма реалізує вирішення рівнянь для дисипативної структури «кролики - лисиці». Результат рішення зображується графічно . Вирішується система диференціальних рівнянь

Тут букви До, Л, Т - означають відповідно кількість кроликів, лисиць, трави ; коефіцієнти k1, k2, k3 - позначають відповідно швидкість народження кроликів, швидкість поїдання кроликів лисицями і швидкість загибелі лисиць.

У програмі знадобиться уточнити значення відносин (приблизно рівне 1), постійну кількість трави (що так само приймається зазвичай рівним 1), початкові значення популяції кроликів і лисиць (зазвичай 0,4), тривалість циклу (типове значення 700) і крок по осі часу (зазвичай рівний 1).

Програма популяції - це графік. Він показує поведінку популяцій при різних ступенях плодючості, а так само різних здібностях уникати винищування.

ВИСНОВОК

Ми бачили, що безповоротність часу тісно пов'язана з неустойчивостями у відкритих системах . І.Р. Прігожін визначає два часи. Одне - динамічне, таке, що дозволяє задати опис руху крапки в класичній механіці або зміну хвилевій функції в квантовій механіці . Інший час - нове внутрішні час, який існує тільки для нестійких динамічних систем . Воно характеризує стан системи, пов'язаний з ентропією.

Процеси біологічного або суспільного розвитку не мають кінцевого стану . Ці процеси неограниченны . Тут, з одного боку, як ми бачили, немає якої-небудь суперечності з другим початком термодинаміки, а з іншого боку - чітко видно поступальний характер розвитку (прогресу) у відкритій системі. Розвиток зв'язаний, взагалі кажучи, з поглибленням нерівнованості, а значить, в принципі з удосконаленням структури . Проте з ускладненням структури зростає число і глибина неустойчивостей, вірогідність біфуркації .

Успіхи вирішення багатьох завдань дозволили виділити в них загальні закономірності, ввести нові поняття і на цій основі сформулювати нову систему поглядів - синергетику . Вона вивчає питання самоорганізації і тому повинна давати картину розвитку і принципи самоорганізації складних систем, щоб застосовувати їх в управлінні. Це завдання має величезне значення, і, на нашу думку, успіхи в її дослідженні означатимуть просування в рішенні глобальних завдань : проблеми керованого термоядерного синтезу, екологічних проблем, завдань управління і інших.

Ми розуміємо, що всі приведені в роботі приклади відносяться до модельних завдань, і багатьом професіоналам, що працюють у відповідних областях науки, вони можуть показатися дуже простими . У одному вони мають рацію : використання ідей і представлень синергетики не повинне підміняти глибокого аналізу конкретної ситуації. З'ясувати, яким може бути шлях від модельних завдань і загальних принципів до реальної проблеми - справа фахівців. Стисло можна сказати так : якщо в системі, що вивчається, можна виділити один найважливіший процес (або невелике їх число), то проаналізувати його допоможе синергетика. Вона указує напрям, в якому потрібно рухатися. І, мабуть, це вже багато.

Дослідження більшості реальних нелінійних завдань було неможливе без обчислювального експерименту, без побудови наближених і якісних моделей процесів, що вивчаються (синергетика грає важливу роль в їх створенні). Обидва підходи доповнюють один одного. Ефективність застосування одного часто визначається успішним використанням іншого. Тому майбутнє синергетики тісно пов'язане з розвитком і широким використанням обчислювального експерименту.

Вивчені останніми роками прості нелінійні середовища володіють складними і цікавими властивостями. Структури в таких середовищах можуть розвиватися незалежно і бути локалізовані, можуть розмножуватися і взаємодіяти . Ці моделі можуть виявитися корисними при вивченні широкого круга явищ.

Відомо, що є деяка роз'єднаність природно наукової і гуманітарної культур. Зближення, а надалі, можливо, гармонійне взаємозбагачення цих культур може бути здійснене на фундаменті нового діалогу з природою на мові термодинаміки відкритих систем і синергетики.

ЛІТЕРАТУРА

1. Базаров І.П. Термодинаміка. - М.: Вища школа, 1991 р.

2. Гленсдорф П., Прігожін І. Термодинамічна теорія структури, стійкості і флуктуацій. - М.: Мир, 1973 р.

3. Карері Д. Порядок і безлад в структурі матерії. - М.: Мир, 1995 р.

4. Курдюшов с.П., Малінецкий г.Г. Синергетика - теорія самоорганізації. Ідеї, методи перспективи. - М.: Знання, 1983 р.

5. Николіс Р., Прігожін І. Самоорганізація в нерівноважних системах. - М.: Мир, 1979 р.

6. Николіс Р., Прігожін І. Пізнання складного. - М.: Мир, 1990 р.

7. Перовський і.Г. Лекції з теорії диференціальних рівнянь. - М.: МГУ, 1980 р.

8. Попов д.Е. Міждисциплінарні зв'язки і синергетика. - КГПУ, 1996 р.

9. Прігожін І. Введення в термодинаміку необоротних процесів. - М.: Іноземна література, 1960 р.

10. Прігожін І. Від того, що існує до того, що виникає. - М.: Наука, 1985 р.

11. Синергетика, збірка статей. - М.: Мир, 1984 р.

12. Хакен Р. Синергетика. - М.: Мир, 1980 р.

13. Хакен Р. Синергетика. Ієрархія неустойчивостей в системах, що самоорганизующихся, і пристроях . - М.: Мир, 1985 р.

14. Шелепін л.А. В далечіні від рівноваги. - М.: Знання, 1987 р.

15. Ейген М., Шустер П. Гіперцикл. Принципи самоорганізації макромолекул . - М.: Мир, 1982 р.

16. Еткинс П. Порядок і безлад в природі. - М.: Мир, 1987 г