| Скачать .docx |
Курсовая работа: Разработка асинхронного двигателя с короткозамкнутым ротором
Введение
1. Описание конструкции асинхронного двигателя
2. Выбор главных размеров
2.1 Расчёт высоты вращения и длины железа статора
2.2 Определение числа пазов, витков и сечения провода обмотки статора
2.3 Расчёт размеров зубцовой зоны статора и воздушного зазора
2.4 Расчёт ротора
2.5 Расчёт паза ротора
2.6 Расчёт короткозамыкающих колец
3. Электромагнитный расчёт
3.1 Расчёт магнитной цепи
3.2 Расчёт намагничивающего тока
3.3 Параметры рабочего режима
3.4 Расчёт потерь
3.5 Расчёт рабочих характеристик
3.6 Расчёт пусковых характеристик
4. Круговая диаграмма
5. Тепловой и вентиляционный расчёты
5.1 Тепловой расчёт
5.2 Вентиляционный расчёт
6. Механичский расчёт
6.1 Расчёт вала
6.2 Расчёт подшипников
7. Экономический расчёт
8. Описание технологии сборки
Заключение
Список литературы
Введение
Асинхронные двигатели являются основными преобразователями электрической энергии в механическую и составляют основу электропривода большинства механизмов, используемых во всех производствах.
Асинхронные двигатели общего назначения мощностью от 0,06 до 400кВт на напряжение до 1140В - наиболее широко применяемые электрические машины. В парке всех производств Республики Беларусь они составляют по количеству 90%, по мощности - примерно 55%, а по потреблению электроэнергии более 40%.
При проектировании необходимо учитывать соответствие технико-экономических показателей современному мировому уровню при соблюдении требований государственных и отраслевых стандартов. Приходится также учитывать назначение и условия эксплуатации, стоимость активных и конструктивных материалов КПД, технологию производства, надежность в работе и патентную частоту.
Расчет и конструирование неотделимы от технологии их изготовления. Поэтому при проектировании необходимо учитывать возможности электротехнических заводов, стремиться к максимальному снижению трудоемкости изготовления электрических машин.
Выбрать оптимальный вариант можно, сопоставив многие варианты расчета. Поэтому без применения ЭВМ не обходится ни один серьезный расчет электрических машин.
В данном курсовом проекте все расчеты ведутся на ЭВМ, включая и построение рабочих и пусковых характеристик.
1. Описание конструкции асинхронного двигателя
Опираясь на исходные данные, заданные в задании на проектирование, можно произвести анализ конструкции электродвигателя.
По условию курсовой работы заданы: исполнение по защите, монтажное исполнение и способ охлаждения. Исполнение по защите проектируемого двигателя IP44. Это подразумевает, что двигатель защищен от возможности соприкосновения инструмента с токоведущими частями попадания внутрь двигателя твердых тел диаметром более 1 мм, а также двигатель защищен от брызг, вода, разбрызгиваемая на оболочку в любом направлении, не должна оказывать вредного действия на изделие, т.е. двигатель выполнен в закрытом исполнении.
Способ охлаждения IС0А141 подразумевает, что охлаждение осуществляется воздухом, а машина с ребристой станиной, обдуваемая внешним вентилятором, расположенным на валу двигателя.
Монтажное исполнение IМ2001 говорит о том, что двигатель выполнен на лапах с двумя подшипниковыми щитами и фланцем на одном щите, имеет горизонтальное расположение и один выходной конец вала.
Обмотка короткозамкнутого ротора не имеет изоляции, выполняется заливкой пазов алюминием, одновременно со стержнями отливается замыкающие кольца с вентиляционными лопатками.
В связи с тем, что мощность двигателя 50 кВт, в статор укладываем двухслойную обмотку с укороченным шагом.
Магнитопровод статора выполняют шихтованным из целых листов электротехнической стали 2312 толщиной 0,5 мм.
2. Выбор главных размеров
По условиям курсового проекта заданы следующие параметры проектируемого двигателя:
- мощность двигателя Р2 = 47800 Вт;
- линейное напряжение питания 380/220В;
- исполнение по способу защиты IP44;
- число пар полюсов 2р=10
- частота питающей сети 50 Гц;
- конструктивное исполнение IM2001;
2.1 Расчёты высоты вращения и длины железа статора
Первым шагом при выборе главных размеров асинхронного двигателя является выбор высоты оси вращения h, которая предварительно выбирается по рисунку 8.17 [1,c.274] для двигателя P2 =47,8кВт, IP=44, 2р=10. Принимается h=280 мм.
Внешний диаметр Da магнитопровода статора выбирается из таблицы 8.6 [1, c.275] для h=280 мм. Принимается Da =520 мм.
Внутренний диаметр D магнитопровода статора вычисляется по формуле [1, c. 275]
D=kD ×Da, (1)
где kD – коэффициент характеризующий отклонение внутреннего и внешнего диаметров сердечников статора асинхронных двигателей серий 4А и АИ, таблица 8.7 [1, c. 276].Принимается для 2р=10 kD =0,76.
D=0,76×0,52=0,395 м
Полюсное деление t, мм определяется по формуле8.3 [1, c. 276]:
![]() (2)
(2)
где р – число пар полюсов.
Расчётная мощность ![]() ,В×А:
,В×А:
![]() , (3)
, (3)
где ![]() - номинальная мощность двигателя, Вт;
- номинальная мощность двигателя, Вт; ![]() - отношение ЭДС обмотки статора к номинальному напряжению; h - номинальный расчётный КПД; соsj- номинальный расчётный коэффициент мощности.
- отношение ЭДС обмотки статора к номинальному напряжению; h - номинальный расчётный КПД; соsj- номинальный расчётный коэффициент мощности.
Из рисунка 8.20 [1, c. 276] ![]() =0,945. Из рисунка 8.21 [1, c. 277] принимается h=0,91, соsj =0,78.
=0,945. Из рисунка 8.21 [1, c. 277] принимается h=0,91, соsj =0,78.
![]() (Вт)
(Вт)
Синхронная угловая скорость движения W, рад/с, рассчитывается по формуле:
![]() (4)
(4)
где f1 – частота питающей сети, Гц.
![]()
Расчётная длина магнитопровода определяется по формуле 8.6 [1, c. 279]:
 (5)
(5)
где ![]() - коэффициент формы поля;
- коэффициент формы поля; ![]() - обмоточный коэффициент (выбирается в зависимости от типа обмотки статора); А - электромагнитная нагрузка, А/м;
- обмоточный коэффициент (выбирается в зависимости от типа обмотки статора); А - электромагнитная нагрузка, А/м; ![]() - индукция магнитного поля в воздушном зазоре, Тл.
- индукция магнитного поля в воздушном зазоре, Тл.
![]() принимается равным 1,11.
принимается равным 1,11.
При мощности АД больше 15 кВт используется двухслойная обмотка, поэтому принимается ![]() =0,91. Из рисунка 8.23 [1, c. 279] находим: А=36×103
А/м,
=0,91. Из рисунка 8.23 [1, c. 279] находим: А=36×103
А/м, ![]() =0,8 Тл.
=0,8 Тл.
![]()
Для определения правильности выбора главных размеров D и ld используется значение:
![]() (6)
(6)
Полученное значение находится в пределах указанных на рисунке 8.25 [1, c. 280].
2.2 Определение числа пазов, витков и сечения провода обмотки статора
Следующий этап расчёта включает определение числа пазов статора Z1 и числа витков в фазе обмотки статора W1 .
 (7)
(7)
Значения tZ 1 min , tZ 1 max определяются по графику на рисунке 8.26 [1, c. 282]. Для h=280 мм, 2p=10, t=124 мм, tZ 1 min =0.0138 м, tZ 1 max =0.016 м.
![]()
Окончательное число пазов статора Z1 выбирается в полученных пределах с учётом условий симметрии: q1 есть целое число.
![]() (8)
(8)
где m – число фаз, m=3.
Принимается Z1 =90, q1 =3. Окончательное значение tZ 1 вычисляется по формуле:
![]() (9)
(9)
![]()
![]() входит в выбранный диапазон.
входит в выбранный диапазон.
Далее предварительно определяется число эффективных проводников в пазу u’п по формуле 8.17 [1, c. 284]при условии, что параллельных ветвей в обмотке 4 (a=4).
![]() (10)
(10)
где I1ном – номинальный ток АД, А по формуле 8.18 [1, c. 279].
 (11)
(11)
![]()
![]()
Окончательно принимается a=5.
Число эффективных проводников в пазу равно:
![]() (12)
(12)
Для двухслойной обмотки принимаем ![]() . Относительное число витков в фазе обмотки по формуле 8.20 [1, c. 279]:
. Относительное число витков в фазе обмотки по формуле 8.20 [1, c. 279]:
![]() (13)
(13)
Окончательное значение линейной нагрузки по формуле 8.21 [1, c. 279]:
 (14)
(14)
 (15)
(15)
Пусть шаг обмотки y=7 зубцовых делений, тогда относительный шаг равен:
![]() (16)
(16)
Коэффициент укорочения:
![]() (17)
(17)
Коэффициент распределения определяется по таблице 3.16 [1, c. 113]. Принимается ![]() =0,943.
=0,943.
Обмоточный коэффициент определяется следующим образом:
![]() (18)
(18)
Далее определяется значение потока по формуле 8.22 [1, c. 285]:
 (19)
(19)
Индукция в воздушном зазоре определяется по формуле 8.23 [1, c. 285]:
 (20)
(20)
Выбор допустимой плотности тока производится с учётом линейной нагрузки двигателя:
![]() (21)
(21)
Значение (A·J) для АД различных исполнений приведены на рисунке 8.27 [1, c. 286]. Для проектируемого двигателя выбирается (A·J)=150·109 A2 /м2 .

Сечение эффективных проводников определяется исходя из тока одной параллельной ветви и допустимой плотности тока в обмотке по формуле 8.24 [1, c. 285]:
 (22)
(22)
Принимается число эффективных проводников nэл =3, qэл =1.227 мм2 (таблица П-28 [2, c. 470]), тогда qэф1 =3•1.227=3.68 мм2 , dиз =1,33 мм. Обмотка выполняется круглым проводом.
Далее уточняется плотность тока в обмотке:
 (23)
(23)
2.3 Расчёт размеров зубцовой зоны статора и воздушного зазора
По таблице 8.10 [1, c. 289] Ba =1.1 Тл и BZср =1.6 Тл. По таблице 8.11 [1, c. 290] выбирается коэффициент заполнения сталью магнитопровода kc 1 =0,95. По выбранным значениям Bа и kc 1 рассчитывается высота ярма статора по формуле 8.28 [1, c. 288]:
 (24)
(24)
Минимальная ширина зубца статора:
 (25)
(25)
Размеры паза вначале определяются без учёта размеров и числа проводников обмотки, исходя из допустимых значений индукции в зубцах и ярме статора.
Высота паза определяется по следующей формуле:
![]()
![]() (26)
(26)
Ширина паза:
 (27)
(27)
 (28)
(28)
![]()
где ![]() - высота шлица зуба, м;
- высота шлица зуба, м; ![]() - ширина шлица зуба, м.
- ширина шлица зуба, м.
Принимается ![]() =1 мм,
=1 мм, ![]() =4 мм [1, c. 295-296]. Приведённые расчёты выполнены для трапециидального паза. Форма паза статора представлена в графической части проекта.
=4 мм [1, c. 295-296]. Приведённые расчёты выполнены для трапециидального паза. Форма паза статора представлена в графической части проекта.
 .
.
![]() (29)
(29)
![]()
![]()
Для расчёта коэффициента заполнения паза необходимо определить площадь паза в свету и учесть площадь сечения паза, занимаемую корпусной изоляцией Sиз и прокладками в пазу Sпр . Размеры паза в свету определяются с учётом припусков на шихтовку и сборку сердечников Dbп и Dhп :
 (30)
(30)
Из таблицы 8.12 [1, c. 292] Dbп =Dhп =0,3 мм.

Площадь поперечного сечения трапециидального паза, в которой размещаются обмотки, корпусная изоляция и прокладки:
![]() . (31)
. (31)
Площадь занимаемая корпусной изоляцией в пазу, м2 :
![]() (32)
(32)
где ![]() - односторонняя толщина изоляции в пазу, м.
- односторонняя толщина изоляции в пазу, м.
Из таблицы 3.1 [1, c. 74] выбирается ![]() =0,55·10-3
м2
, тогда:
=0,55·10-3
м2
, тогда:
![]()
Площадь поперечного сечения прокладок по 8.47, м2 :
![]() (м2
) (33)
(м2
) (33)
![]()
Площадь поперечного сечения паза, остающаяся свободной для размещения проводников обмотки, м2 :
![]()
Контролем правильности размещения обмотки в пазах является значение коэффициента заполнения паза:
![]() , (34)
, (34)
где dиз – диаметр изолированного элементарного проводника, мм. dиз =1.33*10-3 м.

Коэффициент заполнения входит в указанные пределы (0.72<![]() <0.74)[1]
<0.74)[1]
Для обмотки статора используется круглый медный эмалированный провод ПЭТ-155 с площадью поперечного сечения 1.227 мм2 .
На следующем этапе выбирается воздушный зазор по рис. 8,31 [1, c.300]:
d = 0,0007 (м)
После выбора величины воздушного зазора выполняется расчёт короткозамкнутого ротора.
Число пазов ротора по таблице 8.16 [1, c.307]: ![]() .
.
Диаметр ротора:
![]() (35)
(35)
Длина магнитопрвода ротора равна длине магнитопровода статора: ![]() .
.
Зубцовое деление:
 (36)
(36)
Внутренний диаметр ротора равен диаметру вала, так как сердечник ротора непосредственно насаживается на вал, по формуле 8.102 [1, c.319]:
![]() ; (37)
; (37)
где ![]() - находим из таблицы 8.17 [1, c.319].
- находим из таблицы 8.17 [1, c.319].
![]() (м).
(м).
Коэффициент привидения токов по формуле 8.66 [1, c.308]
 , (38)
, (38)
Пазы ротора со скосом пазов вычисляем по формулам.
![]() (39)
(39)
![]() (40)
(40)
Угол скоса:
![]() (41)
(41)
Коэффициент скоса равен:
 (42)
(42)
Ток в обмотке ротора по формуле 8.57 [1, c.302]
![]() , (43)
, (43)
где ![]() - коэффициент учитывающий влияние формы тока намагничивания на отношение I2
/I1
находим по формуле 8.58 [1, c.303]
- коэффициент учитывающий влияние формы тока намагничивания на отношение I2
/I1
находим по формуле 8.58 [1, c.303]
![]() . (45)
. (45)
![]()
Плотность поперечного сечения стержня ![]() предварительно по формуле 8.68 [1, c.308], плотность тока в стержне алюминиевой литой клетки принимаем
предварительно по формуле 8.68 [1, c.308], плотность тока в стержне алюминиевой литой клетки принимаем ![]()
![]() (46)
(46)
Принимается ![]() =0,8 мм,
=0,8 мм, ![]() =1,7 мм,
=1,7 мм, ![]() =0,5 мм [1, c. 295-296]. Приведённые расчёты выполнены для трапецеидального закрытого паза. Форма паза ротора представлена в графической части проекта.
=0,5 мм [1, c. 295-296]. Приведённые расчёты выполнены для трапецеидального закрытого паза. Форма паза ротора представлена в графической части проекта.
Определяем допустимое значение индукции по таблице 8.10 [1, c.289] ![]() =1.85.
=1.85.
Допустимая ширина зубца по формуле 8.75 [1, c.314]
 (47)
(47)
Размеры паза по формулам 8.76-8.78 [1, c.314]:
 (48)
(48)
![]()
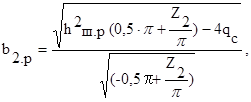 (49)
(49)

![]() (50)
(50)
Уточняем ширину зубцов ротора по формулам таблицы 8.18 [1,c.324]
 (51)
(51)
![]()
Полная высота паза:
![]() (52)
(52)
![]()
 (53)
(53)
Таким образом ![]() Площадь поперечного сечения стержня рассчитываем по формуле 8.79 [1, c. 314]
Площадь поперечного сечения стержня рассчитываем по формуле 8.79 [1, c. 314]
 (54)
(54)
![]()
Плотность тока в стержне:
![]() (55)
(55)
2.6 Расчёт короткозамыкающих колец
Токи в кольце по формуле 8.70 [1, c.309]
![]() (56)
(56)
где ![]() .
.
![]()
Плотность тока в замыкающих кольцах [1, c.309]:
![]() . (57)
. (57)
Площадь поперечного сечения кольца по формуле 8.72 [1, c.309]:
![]() (58)
(58)
Высота сечения кольцах [1, c.310]:
![]() (59)
(59)
Ширина замыкающих колец [1, c.310]:
 . (60)
. (60)
Средний диаметр замыкающих колец по формуле 8.74 [1, c.310]:
![]() . (61)
. (61)

Следующим этапом является электромагнитный расчет.
3. Электромагнитный расчёт
3.1 Расчет магнитной цепи
Для магнитопровода используется сталь 2312.
Магнитное напряжение воздушного зазора определяется по формуле:
 (62)
(62)
где ![]() - коэффициент воздушного зазора;
- коэффициент воздушного зазора; ![]() - магнитная постоянная.
- магнитная постоянная.
Коэффициент воздушного зазора рассчитывается по следующей формуле:
![]() (63)
(63)
 (64)
(64)
где ![]() - зубцовое деление статора;
- зубцовое деление статора;![]() - ширина шлица паза статора.
- ширина шлица паза статора.
Для статора ![]() =14·10-3
м,
=14·10-3
м, ![]() =4·10-3
м,d=0,7·10-3
м.
=4·10-3
м,d=0,7·10-3
м.

![]()
![]()
Далее рассматривается магнитное напряжение зубцовой зоны статора. Для зубцов с параллельными гранями (трапециидальные пазы):
 , (65)
, (65)
 (66)
(66)
![]()
![]()
![]() (67)
(67)
![]()
По таблице 8.15 [1, c. 299] расчетная высота паза hZ 1 =hп =33·10-3 м.
Индукция в зубце, Тл:
 (68)
(68)

Магнитное напряжение зубцовой зоны статора, А:
![]() (69)
(69)
После расчёта магнитной цепи статора рассчитывается магнитная цепь ротора. Общая формула для расчета магнитного напряжения ротора, А:
![]() (70)
(70)
где ![]() - расчётная высота зубца, м;
- расчётная высота зубца, м; ![]() - расчётная напряжённость в зубце, А/м.
- расчётная напряжённость в зубце, А/м.
Для короткозамкнутого ротора с закрытыми пазами
![]() =
=![]() -0,1
-0,1![]() =28-0,1·5.86=27 мм. (71)
=28-0,1·5.86=27 мм. (71)
Индукция в зубце, Тл:
 (72)
(72)

Пусть действительная индукция ![]() =1,85 Тл, соответствующая ей напряжённость
=1,85 Тл, соответствующая ей напряжённость ![]() =3330 А/м (таблица П – 17, [2, c. 330]). Полученные данные нужно подставить в следующие уравнения:
=3330 А/м (таблица П – 17, [2, c. 330]). Полученные данные нужно подставить в следующие уравнения:
Магнитное напряжение зубцовой зоны статора, А:
![]() (73)
(73)
Коэффициент насыщения зубцовой зоны рассчитываем по формуле 8.115 [1, c.328]:
 (74)
(74)
На следующем этапе рассматривается магнитное напряжение ![]() ярма статора по формуле 8.116 [1, c.329]:
ярма статора по формуле 8.116 [1, c.329]:
![]() (75)
(75)
где ![]() - длина средней магнитной силовой линии в ярме статора, м;
- длина средней магнитной силовой линии в ярме статора, м; ![]() - напряжённость поля при индукции
- напряжённость поля при индукции ![]() по кривой намагничивания стали ярма, А/м.
по кривой намагничивания стали ярма, А/м.
Индукция в ярме статора, определяется по следующей формуле, Тл:
![]() (76)
(76)
где ![]() - расчётная высота ярма статора, м.
- расчётная высота ярма статора, м.
При отсутствии аксиальных вентиляционных каналов в статоре:
![]() (77)
(77)
Длина средней магнитной силовой линии в ярме статора:
![]() (78)
(78)
![]()
По таблице П – 16 [2, c. 460] для ![]() =1.1 Тл для стали 2212
=1.1 Тл для стали 2212 ![]() =332 А/м.
=332 А/м.
![]()
Магнитное напряжение ярма ротора, А по формуле 8.121 [1, c.329]:
![]() (79)
(79)
где ![]() - напряжённость поля в ярме при индукции
- напряжённость поля в ярме при индукции ![]() по кривой намагничивания;
по кривой намагничивания;![]() - длинна силовой линии в ярме, м.
- длинна силовой линии в ярме, м.
Для двигателей с непосредственной посадкой ротора на вал (Dj =DB ) без вентиляционных аксиальных каналов по формуле 8.123 [1, c.330]:
 (80)
(80)
Индукция в ярме ротора по формуле 8.122 [1, c.329]:

Для ![]() =0.44 Тл,
=0.44 Тл, ![]() =108 А/м.
=108 А/м.
Длина средней магнитной силовой линии в ярме ротора, м:
 (81)
(81)
 . (82)
. (82)
![]()
![]()
Суммарное магнитное напряжение на пазу полюсов по формуле 8.128 [1, c.330]:
![]()
![]() (83)
(83)
Коэффициент насыщения магнитной цепи по формуле 8.129 [1, c.330]:
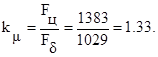 (84)
(84)
3.2 Расчёт намагничивающего тока
Намагничивающий ток по формуле 8.130 [1, c.331]:
 (85)
(85)
Относительное значение намагничивающего тока определяется по формуле 8.131 [1, c.331]:
 (86)
(86)
![]() - находится в допустимых пределах
- находится в допустимых пределах
На следующем этапе рассчитываются параметры асинхронной машины для номинального режима.
3.3 Параметры рабочего режима
Для номинального режима АД активное сопротивление обмотки статора определяется по формуле 8.132 [1, c.332]:
 (87)
(87)
где ![]() – общая длинна эффективных проводников фазы обмотки, м;
– общая длинна эффективных проводников фазы обмотки, м; ![]() - площадь поперечного сечения эффективного проводника, м2;
- площадь поперечного сечения эффективного проводника, м2; ![]() – удельное сопротивление материала обмотки при расчётной температуре,Ом·м;
– удельное сопротивление материала обмотки при расчётной температуре,Ом·м; ![]() -коэффициент увеличения активного сопротивления фазы обмотки от действия эффекта вытеснения тока.
-коэффициент увеличения активного сопротивления фазы обмотки от действия эффекта вытеснения тока.
Значение ![]() для номинальных режимов принимается равным единице. Для класса изоляции F
для номинальных режимов принимается равным единице. Для класса изоляции F![]() =(1/41)·10-6
Ом·м.
=(1/41)·10-6
Ом·м.
Общая длина проводников фазы обмотки определяется по формуле:
![]() (88)
(88)
где ![]() - средняя длина витка обмотки статора, м;
- средняя длина витка обмотки статора, м; ![]() - число витков фазы.
- число витков фазы.
Средняя длинна витка есть сумма прямолинейных пазовых и изогнутых лобовых частей катушки:
![]() (89)
(89)
Длина пазовой части равна конструктивной длине сердечника, для всыпной обмотки статора длина лобовой части равна:
![]() (90)
(90)
Вылет лобовых частей, м:
![]() (91)
(91)
где ![]() - средняя ширина катушки, м, определяемая по дуге окружности, проходящей по серединам высоты пазов; B - длины вылета прямолинейной части катушек из паза, м.
- средняя ширина катушки, м, определяемая по дуге окружности, проходящей по серединам высоты пазов; B - длины вылета прямолинейной части катушек из паза, м.
![]() , (92)
, (92)
где ![]() - относительное укорочение шага обмотки статора.
- относительное укорочение шага обмотки статора. ![]() ,
,![]() – коэффициенты в зависимости от числа полюсов машины и наличия изоляции в лобовых частях (таблица 8.21[1, с.334]).
– коэффициенты в зависимости от числа полюсов машины и наличия изоляции в лобовых частях (таблица 8.21[1, с.334]).
Для машин, обмотки которых укладываются после запрессовки сердечника в корпус, вылет прямолинейной части B=0,01 м. Из таблицы 8.21 [1, с. 334] ![]() =1,9,
=1,9, ![]() =0,72.
=0,72.
![]() (м),
(м),
![]() (м),
(м),
![]() (м),
(м),
![]() (м),
(м),
![]() (м).
(м).
Активное сопротивление фазы статора:
![]() (Ом).
(Ом).
Относительное значение:
 (93)
(93)
Далее рассчитывается активное сопротивление фазы ротора, Ом:
 (94)
(94)
где ![]() -сопротивление стержня;
-сопротивление стержня; ![]() - сопротивление участка замыкающего кольца, заключенного между двумя соседними стержнями.
- сопротивление участка замыкающего кольца, заключенного между двумя соседними стержнями.
Сопротивление стержня:
 (95)
(95)
Сопротивление участка замыкающего кольца, заключенного между двумя соседними стержнями:
 . (96)
. (96)

Для дальнейших расчётов ![]() должно быть приведено к числу витков первичной обмотки:
должно быть приведено к числу витков первичной обмотки:
 . (97)
. (97)
 ( Ом).
( Ом).
Относительное значение сопротивления:
 (98)
(98)
Далее рассчитываются индуктивные сопротивления, обмоток статора и ротора двигателя.
Индуктивное сопротивление фазы обмотки статора:
 (99)
(99)
где ![]() - расчётная длина магнитопровода, м;
- расчётная длина магнитопровода, м; ![]() - коэффициенты магнитной проводимости пазового, лобового и дифференциального рассеяния соответственно.
- коэффициенты магнитной проводимости пазового, лобового и дифференциального рассеяния соответственно.
При отсутствии вентиляционных каналов ![]() =
= ![]() ,
, ![]() =
=![]() =1,
=1, ![]() =0.024.
=0.024.
Коэффициент ![]() рассчитывается для двухслойной обмотки в трапециидальном пазу.
рассчитывается для двухслойной обмотки в трапециидальном пазу.
 (100)
(100)
![]()
Коэффициент магнитной проводимости лобового рассеяния:
 (101)
(101)
![]()
Коэффициенты магнитной проводимости дифференциального рассеяния:
 (102)
(102)
 (103)
(103)
Из рисунка 8.51 [1, c. 340] ![]() =0,9
=0,9![]() =1.
=1.
![]()
![]() .
.
![]()
Относительное значение:
 (104)
(104)
Индуктивное сопротивление фазы обмотки ротора по 8.177 [1, c.343]:
![]() (105)
(105)
где ![]() - коэффициент магнитной проводимости пазового рассеяния обмотки короткозамкнутого ротора;
- коэффициент магнитной проводимости пазового рассеяния обмотки короткозамкнутого ротора; ![]() - коэффициент магнитной проводимости дифференциального рассеяния обмотки короткозамкнутого ротора;
- коэффициент магнитной проводимости дифференциального рассеяния обмотки короткозамкнутого ротора; ![]() - коэффициент магнитной проводимости лобового рассеяния ротора.
- коэффициент магнитной проводимости лобового рассеяния ротора.
![]() (106)
(106)
![]() так как режим номинальный.
так как режим номинальный.
Коэффициент магнитной проводимости пазового рассеяния обмотки короткозамкнутого ротора:
 (107)
(107)

Коэффициент магнитной проводимости лобового рассеяния для ротора с литыми обмотками при замыкающих кольцах, прилегающих к торцам сердечника ротора:
 (108)
(108)
![]()
Коэффициент магнитной проводимости дифференциального рассеяния обмотки короткозамкнутого ротора:
 (109)
(109)
![]()
Приводим ![]() к числу витков статора по формуле:
к числу витков статора по формуле:
 (110)
(110)
Относительное значение:
 (111)
(111)
На следующем этапе проектирования рассчитываются потери и КПД.
3.4 Расчет потерь
Основные потери в стали определяются по формуле:
![]() (112)
(112)
где ![]() - удельные потери, Вт/кг; b - показатель степени, учитывающий зависимость потерь в стали от частоты перемагничивания, b=1,5;
- удельные потери, Вт/кг; b - показатель степени, учитывающий зависимость потерь в стали от частоты перемагничивания, b=1,5;![]() ,
,![]() - коэффициенты, учитывающие влияние на потери в стали, неравномерности распределения потока по сечениям участков магнитопровода и технологических факторов;
- коэффициенты, учитывающие влияние на потери в стали, неравномерности распределения потока по сечениям участков магнитопровода и технологических факторов;![]() ,
,![]() - масса стали ярма и зубьев статора, кг. Для стали 2312 по таблице 8.26 [1, c. 348] принимается
- масса стали ярма и зубьев статора, кг. Для стали 2312 по таблице 8.26 [1, c. 348] принимается ![]() =1,3 Вт/кг. Для машины мощностью менее 250 кВт
=1,3 Вт/кг. Для машины мощностью менее 250 кВт ![]() =1,6 и
=1,6 и ![]() =1,8.
=1,8.
![]() (113)
(113)
![]() (114)
(114)
где ![]() =
= ![]() - расчётная высота зубца статора, м;
- расчётная высота зубца статора, м; ![]() - удельная плотность стали,
- удельная плотность стали, ![]() =7800 кг/м3.
=7800 кг/м3.
![]()
![]()
![]()
Затем рассчитываются добавочные потери в стали.
Амплитуда пульсации индукции в воздушном зазоре над коронками зубцов статора и ротора, Тл:
![]() (115)
(115)
![]() .
.
![]() =0,16 из рисунка 8.53 [1, c.349].
=0,16 из рисунка 8.53 [1, c.349].
![]()
По ![]() и частоте пульсаций индукции под зубцами, равной
и частоте пульсаций индукции под зубцами, равной ![]() , определяются удельные поверхностные потери для ротора. Для проектируемого двигателя n=600 мин-1
.
, определяются удельные поверхностные потери для ротора. Для проектируемого двигателя n=600 мин-1
.
![]() (116)
(116)
где ![]() – коэффициент учитывающий влияние обработки поверхности зубцов ротора на удельные потери.
– коэффициент учитывающий влияние обработки поверхности зубцов ротора на удельные потери.
Принимается ![]() =1,5.
=1,5.
![]()
Полные потери ротора, Вт:
![]() (117)
(117)
![]()
Для определения пульсационных потерь вначале находится амплитуда пульсаций индукции в среднем сечении зубцов ротора, Тл:
 (118)
(118)
 .
.
Пульсационные потери в зубцах статора и ротора, Вт:
![]() (119)
(119)
Масса стали зубцов ротора:
![]() (120)
(120)
![]()
![]()
Добавочные потери в стали, Вт:
![]() , (121)
, (121)
![]()
Полные потери в стали, Вт:
![]() (122)
(122)
![]()
Механические потери, Вт:
![]() (123)
(123)
![]() (124)
(124)
![]()
Добавочные потери, Вт при номинальном режиме:
![]() (125)
(125)
Суммарные потери в двигателе ,Вт:
![]() (126)
(126)
Коэффициент полезного действия двигателя:
 (127)
(127)
Рассчитываем холостой ход двигателя.
Электрические потери статора при холостом ходе, Вт:
![]() (128)
(128)
Ток холостого хода двигателя, А:
![]() (129)
(129)
где ![]() - активная составляющая тока, А;
- активная составляющая тока, А; ![]() - реактивная составляющая тока, А.
- реактивная составляющая тока, А.
 (130)
(130)
![]()
![]()
![]() .
.
![]() - при холостом ходе:
- при холостом ходе:
 (131)
(131)
На следующем этапе необходимо рассчитать рабочие характеристики асинхронной машины.
3.5 Расчет рабочих характеристик
Методы расчёта характеристик основаны на системе уравнений токов и напряжений, которой соответствует схема замещения.

Рисунок 3.1- Cхема замещения.
Рассчитаем сопротивление взаимной индукции обмоток статора и ротора:
 (132)
(132)
 (133)
(133)
Комплексный коэффициент ![]() для машин мощностью более 3 кВт с большой точностью можно определить по формуле:
для машин мощностью более 3 кВт с большой точностью можно определить по формуле:
 (134)
(134)
![]() (135)
(135)
![]() (136)
(136)
![]()
![]() (137)
(137)
Активная составляющая тока синхронного холостого хода, А:
 (138)
(138)
![]()
Номинальное скольжение (предварительно) принимаем s=0,02
Для расчёта рабочих характеристик необходимы следующие формулы:
![]() (139)
(139)
![]() (140)
(140)
![]() (141)
(141)
![]() (142)
(142)
![]() (143)
(143)
![]() (144)
(144)
![]() (145)
(145)
![]() (146)
(146)
![]() (147)
(147)
![]() (148)
(148)
![]() (149)
(149)
![]() (150)
(150)
![]() (151)
(151)
![]() (152)
(152)
![]() (153)
(153)
![]() (154)
(154)
![]() (155)
(155)
 (156)
(156)
![]() (157)
(157)
Результаты расчёта рабочих характеристик представлены в таблице 3.4.1 и 3.4.2
Таблица 3.4.1
| Si | m1 i | zi | I1 ai | I1 pi | I1 i | I2 i | P1 i |
| 0.0001 | 619.587 | 619.962 | 1.577 | 37.149 | 37.18 | 0.373 | 1.041 |
| 0.0019 | 32.61 | 32.718 | 7.945 | 37.253 | 38.09 | 7.065 | 5.244 |
| 0.0038 | 16.305 | 16.417 | 14.616 | 37.563 | 40.3 | 14.081 | 9.647 |
| 0.0057 | 10.87 | 10.986 | 21.226 | 38.073 | 43.5 | 21.043 | 14.009 |
| 0.0076 | 8.152 | 8.272 | 27.767 | 38.778 | 47.69 | 27.945 | 18.326 |
| 0.0095 | 6.522 | 6.645 | 34.231 | 39.673 | 52.39 | 37.786 | 22.592 |
| 0.011 | 5.435 | 5.562 | 40.61 | 40.751 | 57.53 | 41.56 | 26.803 |
| 0.013 | 4.659 | 4.79 | 46.898 | 42.007 | 62.9 | 48.265 | 30.952 |
| 0.015 | 4.076 | 4.211 | 53.087 | 43.434 | 68.59 | 54.897 | 35.038 |
| 0.017 | 3.623 | 3.762 | 59.173 | 45.025 | 74.35 | 61.453 | 39.054 |
| 0.019 | 3.261 | 3.403 | 65.15 | 46.773 | 80.2 | 67.93 | 42.868 |
| 0.021 | 2.965 | 3.11 | 71.013 | 48.67 | 86.09 | 74.326 | 46.868 |
| 0.023 | 2.717 | 2.867 | 76.757 | 50.71 | 91.99 | 80.638 | 50.659 |
| 0.024 | 2.592 | 2.744 | 80.027 | 51.954 | 95.41 | 84.254 | 52.818 |
| 0.026 | 2.383 | 2.538 | 86.153 | 54.448 | 101.91 | 91.075 | 56.861 |
| 0.029 | 2.174 | 2.334 | 93.243 | 57.612 | 109.6 | 99.054 | 61.54 |
Таблица 3.4.2
| Ri | I``2i | P2i | P’э2i | P’э1i | Pдоб i | |||
| 619.962 | 0.355 | 0.124 | 0.00002 | 0.411 | 0.0052 | 0.119 | 0.042 | 1.164 |
| 32.718 | 6.724 | 4.03 | 0.0084 | 0.431 | 0.026 | 0.768 | 0.209 | 1.214 |
| 16.417 | 13.401 | 8.334 | 0.033 | 0.483 | 0.048 | 0.864 | 0.363 | 1.313 |
| 10.986 | 20.026 | 12.552 | 0.075 | 0.565 | 0.07 | 0.896 | 0.487 | 1.458 |
| 8.272 | 26.595 | 16.679 | 0.131 | 0.676 | 0.092 | 0.91 | 0.582 | 1.647 |
| 6.645 | 33.105 | 20.711 | 0.204 | 0.816 | 0.113 | 0.917 | 0.653 | 1.881 |
| 5.562 | 39.553 | 24.646 | 0.291 | 0.984 | 0.134 | 0.92 | 0.706 | 2.157 |
| 4.79 | 45.933 | 28.479 | 0.392 | 1.178 | 0.155 | 0.92 | 0.745 | 2.473 |
| 4.211 | 52.245 | 32.208 | 0.507 | 1.399 | 0.175 | 0.919 | 0.774 | 2.829 |
| 3.762 | 58.484 | 35.832 | 0.636 | 1.644 | 0.195 | 0.917 | 0.796 | 3.223 |
| 3.403 | 64.648 | 39.347 | 0.77 | 1.912 | 0.215 | 0.915 | 0.812 | 3.652 |
| 3.11 | 70.735 | 42.753 | 0.93 | 2.203 | 0.234 | 0.912 | 0.825 | 4.116 |
| 2.867 | 76.743 | 46.048 | 1.095 | 2.516 | 0.253 | 0.909 | 0.834 | 4.612 |
| 2.744 | 80.184 | 47.904 | 1.195 | 2.706 | 0.264 | 0.907 | 0.839 | 4.913 |
| 2.538 | 86.675 | 51.345 | 1.396 | 3.088 | 0.284 | 0.903 | 0.845 | 5.517 |
| 2.334 | 94.269 | 55.261 | 1.652 | 3.571 | 0.308 | 0.989 | 0.851 | 6.279 |

3.6 Расчет пусковых характеристик
Расчет токов с учетом влияния изменения параметров под влиянием эффекта вытеснения тока (без учета влияния насыщения от полей рассеяния).
Расчет проводим для значения s=1.
Находим высоту стержня по рисунку 2.1:
![]() (158)
(158)
При литой алюминиевой обмотке ротора при расчетной температуре 75o имеем по 8.244 [1, c.364]:
![]() (159)
(159)
Находим параметры для ![]() =1.76 из графиков на рисунках 8.57-58 [1, c. 366]:
=1.76 из графиков на рисунках 8.57-58 [1, c. 366]:
![]() ;
; ![]()
![]()
Глубина проникновения тока по формуле 8.246 [1, c.367]:
![]() (160)
(160)
Тогда площадь сечения по 8.253 [1, c.367]:
 (161)
(161)
 (162)
(162)
![]()
![]() .
.
Коэффициент ![]() определяется по формуле 8.247 [1, c.365]:
определяется по формуле 8.247 [1, c.365]:
![]() (163)
(163)
Коэффициент общего увеличения сопротивления фазы ротора под влиянием вытеснения тока по 8.257 [1, c.368]:
 (164)
(164)
Приведенное активное сопротивление фазы ротора под действием эффекта вытеснения тока по 8.260 [1, c.369]:
![]() (165)
(165)
Коэффициент магнитной проводимости пазового рассеяния с учетом вытеснения тока:
 (167)
(167)

Рассчитываем коэффициент уменьшения индуктивного сопротивления фазы ротора:
 (168)
(168)
Приведенное индуктивное сопротивление фазы ротора под действием эффекта вытеснения тока по 8.260 [1, c.369]:
![]() (169)
(169)
Пусковые параметры:
![]() (170)
(170)
![]() (171)
(171)
![]() . (172)
. (172)
![]() (173)
(173)
Токи без учета влияния эффекта насыщения:
 (174)
(174)
 (175)
(175)

Расчет токов с учетом влияния вытеснения тока и насыщения от полей рассеяния.
Зададимся кратностью увеличения тока, обусловленного уменьшением индуктивного сопротивления из-за насыщения зубцовой зоны:
![]() . (176)
. (176)
Средняя МДС обмотки, отнесенная к одному пазу статора:
 ; (177)
; (177)
![]()
Фиктивная индукция потока рассеяния:
 (178)
(178)
где ![]() коэффициент, который находится следующим образом:
коэффициент, который находится следующим образом:
 (179)
(179)
![]()
По рисунку 8.61 [1, c.370] выбираем для ![]() =3.4
=3.4 ![]() .
.
Значение дополнительного раскрытия паза статора:
![]() (180)
(180)
Уменьшение коэффициента магнитной проводимости пазового рассеяния обмотки статора с учетом влияния насыщения по 8.266 [1, c.371]:
 (181)
(181)
![]()
Коэффициент магнитной проводимости пазового рассеяния обмотки статора с учетом влияния насыщения по 8.271 [1, c.372]:
![]() (182)
(182)
Коэффициент проводимости дифференциального рассеяния участков зубцов статора с учетом влияния насыщения по 8.274 [1, c.373]:
![]() (183)
(183)
Индуктивное сопротивление обмотки статора с учетом насыщения от полей рассеяния:
 (184)
(184)
Значение дополнительного раскрытия паза ротора:
![]() (185)
(185)
Уменьшение коэффициента магнитной проводимости пазового рассеяния обмотки ротора с учетом влияния насыщения по 8.271 [1, c.371]:
![]() (186)
(186)
Коэффициент магнитной проводимости пазового рассеяния обмотки статора с учетом влияния насыщения по 8.271 [1, c.372]:
![]() (187)
(187)
Коэффициент проводимости дифференциального рассеяния участков зубцов ротора с учетом влияния насыщения по 8.274 [1, c.373]:
![]() (188)
(188)
Приведенное индуктивное сопротивление обмотки статора с учетом насыщения от полей рассеяния:
![]() (189)
(189)
Пусковые параметры:
![]() (190)
(190)
![]() (191)
(191)
![]() (192)
(192)
Ток в обмотке ротора:
 (193)
(193)
Ток в обмотке статора:
 (194)
(194)

Кратность пускового тока:
 (195)
(195)
Кратность пускового момента:
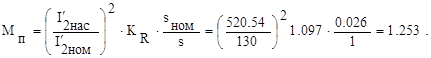 (196)
(196)
Формулы для расчета токов в пусковом режиме асинхронного двигателя с КЗ ротором с учетом эффекта вытеснения тока.
![]() (197)
(197)
![]() . (198)
. (198)
![]() (199)
(199)
 (200)
(200)
![]() (201)
(201)
![]() (202)
(202)
 (203)
(203)
![]() (204)
(204)
 (205)
(205)
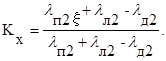 (206)
(206)
![]() (207)
(207)
![]() (208)
(208)
![]() (209)
(209)
 (210)
(210)
 (211)
(211)
Результаты расчёта токов в пусковом режиме асинхронного двигателя с КЗ ротором учетом влияния эффекта вытеснения тока представлены в таблице 3.5.1 и 3.5.2
Таблица 3.5.1 – Расчет токов в пусковом режиме асинхронного двигателя с КЗ ротором учетом влияния эффекта вытеснения тока
| Si | hri | kri | Kri | ||||
| 1 | 1.743 | 0.55 | 0.018 | 1.43 | 1.34 | 0.075 | 0.8 |
| 0.8 | 1.559 | 0.42 | 0.019 | 1.32 | 1.25 | 0.07 | 0.9 |
| 0.6 | 1.35 | 0.309 | 0.021 | 1.22 | 1.17 | 0.066 | 0.9 |
| 0.5 | 1.233 | 0.259 | 0.022 | 1.18 | 1.14 | 0.064 | 0.9 |
| 0.4 | 1.102 | 0.213 | 0.023 | 1.14 | 1.11 | 0.062 | 0.95 |
| 0.35 | 1.031 | 0.193 | 0.023 | 1.12 | 1.09 | 0.061 | 0.95 |
| 0.3 | 0.955 | 0.173 | 0.023 | 1.103 | 1.08 | 0.061 | 0.95 |
| 0.25 | 0.872 | 0.156 | 0.024 | 1.09 | 1.07 | 0.06 | 0.95 |
| 0.2 | 0.78 | 0.14 | 0.024 | 1.07 | 1.058 | 0.059 | 0.97 |
| 0.151 | 0.677 | 0.126 | 0.024 | 1.06 | 1.05 | 0.059 | 0.97 |
| 0.146 | 0.666 | 0.125 | 0.024 | 1.06 | 1.048 | 0.059 | 0.97 |
| 0.1 | 0.551 | 0.114 | 0.025 | 1.05 | 1.041 | 0.058 | 0.97 |
| 0.05 | 0.39 | 0.105 | 0.025 | 1.044 | 1.034 | 0.058 | 0.99 |
| 0.001 | 0.055 | 0.1 | 0.025 | 1.04 | 1.031 | 0.058 | 0.99 |
Таблица 3.5.2
| Si | Kxi | Xni | I`2i | I1i | Rni | ||
| 1 | 1.474 | 0.929 | 0.173 | 0.466 | 441.351 | 451.6 | 0.177 |
| 0.8 | 1.6 | 0.964 | 0.18 | 0.473 | 431.68 | 442.1 | 0.19 |
| 0.6 | 1.6 | 0.964 | 0.18 | 0.473 | 424.233 | 434.5 | 0.213 |
| 0.5 | 1.6 | 0.964 | 0.18 | 0.473 | 4117.8 | 427.9 | 0.232 |
| 0.4 | 1.662 | 0.982 | 0.183 | 0.476 | 405.3 | 415.3 | 0.26 |
| 0.35 | 1.662 | 0.982 | 0.183 | 0.476 | 397.8 | 407.7 | 0.281 |
| 0.3 | 1.662 | 0.982 | 0.183 | 0.476 | 387.5 | 397.3 | 0.309 |
| 0.25 | 1.662 | 0.892 | 0.183 | 0.476 | 372.9 | 382.4 | 0.348 |
| 0.2 | 1.687 | 0.989 | 0.185 | 0.478 | 350.5 | 359.6 | 0.41 |
| 0.151 | 1.687 | 0.989 | 0.185 | 0.478 | 316.9 | 325.4 | 0.5 |
| 0.146 | 1.687 | 0.989 | 0.185 | 0.478 | 312.3 | 320.8 | 0.52 |
| 0.1 | 1.687 | 0.989 | 0.185 | 0.478 | 258.3 | 265.6 | 0.71 |
| 0.05 | 1.712 | 0.996 | 0.186 | 0.479 | 158.3 | 164.4 | 1.3 |
| 0.001 | 1.712 | 0.996 | 0.186 | 0.479 | 3.657 | 28.4 | 60.2 |
Формулы для расчета токов в пусковом режиме асинхронного двигателя с КЗ ротором с учетом эффектов вытеснения и насыщения.
 . (212)
. (212)
 (213)
(213)
![]() (214)
(214)
![]() (215)
(215)
![]() (216)
(216)
 (217)
(217)
![]() (218)
(218)
![]() (219)
(219)
![]() (220)
(220)
 (221)
(221)
Пусковые параметры:
![]() (222)
(222)
![]() (223)
(223)
![]() (224)
(224)
 (225)
(225)
 (226)
(226)
 (227)
(227)
 (228)
(228)
Результаты расчёта токов в пусковом режиме асинхронного двигателя с КЗ ротором учетом влияния эффекта вытеснения тока представлены в таблице 3.5.3 и 3.5.4.
Таблица 3.5.3 – Расчет пусковых характеристик асинхронного двигателя с КЗ ротором учетом эффекта вытеснения тока и насыщения от полей рассеяния
| 1 | 1.35 | 4013 | 3.432 | 0.68 | 0.0031 | 0.246 | 1.033 | 1 |
| 0.8 | 1.3 | 3783 | 3.235 | 0.68 | 0.0031 | 0.246 | 1.033 | 0.8 |
| 0.6 | 1.25 | 3575 | 3.057 | 0.68 | 0.0031 | 0.246 | 1.033 | 0.6 |
| 0.5 | 1.25 | 3521 | 3.011 | 0.68 | 0.0031 | 0.255 | 1.033 | 0.5 |
| 0.4 | 1.15 | 3144 | 2.689 | 0.75 | 0.0024 | 0.255 | 1.034 | 0.4 |
| 0.35 | 1.15 | 3086 | 2.639 | 0.75 | 0.0024 | 0.255 | 1.034 | 0.35 |
| 0.3 | 1.15 | 3007 | 2.572 | 0.75 | 0.0024 | 0.261 | 1.034 | 0.3 |
| 0.25 | 1.15 | 2894 | 2.475 | 0.3 | 0.0019 | 0.261 | 1.035 | 0.25 |
| 0.2 | 1.05 | 2485 | 2.125 | 08 | 0.0019 | 0.279 | 1.035 | 0.2 |
| 0.151 | 1.05 | 2249 | 1.923 | 0.95 | 0.00049 | 0.279 | 1.037 | 0.151 |
| 0.146 | 1.05 | 2217 | 1.896 | 0.95 | 0.00049 | 0.279 | 1.037 | 0.146 |
| 0.1 | 1.05 | 1836 | 1.57 | 0.95 | 0.00049 | 0.283 | 1.037 | 0.1 |
| 0.05 | 1.05 | 1136 | 0.972 | 0.98 | 0.00019 | 0.283 | 1.038 | 0.05 |
| 0.001 | 1.05 | 196.5 | 0.168 | 0.98 | 0.00019 | 0.283 | 1.038 | 0.001 |
Таблица 3.5.4
| 0.537 | 0.177 | 0.385 | 519.3 | 528.69 | 1.171 | 1.033 | 1.216 | 5.541 |
| 0.563 | 0.19 | 0.39 | 505.3 | 514.9 | 1.165 | 1.033 | 1.343 | 5.39 |
| 0.563 | 0.212 | 0.392 | 493.6 | 502.9 | 1.157 | 1.033 | 1.603 | 5.27 |
| 0.563 | 0.231 | 0.392 | 483.6 | 492.8 | 1.152 | 1.033 | 1.793 | 5.165 |
| 0.601 | 0.26 | 0.41 | 453.2 | 462.5 | 1.113 | 1.034 | 1.915 | 4.848 |
| 0.601 | 0.308 | 0.41 | 442.8 | 451.9 | 1.109 | 1.034 | 2.064 | 4.737 |
| 0.601 | 0.347 | 0.41 | 428.9 | 437.8 | 1.102 | 1.034 | 2.231 | 4.589 |
| 0.621 | 0.406 | 0.421 | 403 | 411.7 | 1.077 | 1.035 | 2.338 | 4.315 |
| 0.626 | 0.503 | 0.422 | 375.4 | 383.7 | 1.067 | 1.035 | 2.509 | 4.021 |
| 0.699 | 0.517 | 0.461 | 322.4 | 330.6 | 1.016 | 1.037 | 2.431 | 3.465 |
| 0.699 | 0.71 | 0.461 | 317.7 | 325.8 | 1.016 | 1.037 | 2.44 | 3.415 |
| 0.699 | 1.3 | 0.461 | 261.3 | 268.4 | 1.01 | 1.037 | 2.392 | 2.813 |
| 0.726 | 1.5 | 0.472 | 158.7 | 164.7 | 1.002 | 1.038 | 1.754 | 1.726 |
| 0.726 | 60.137 | 0.472 | 3.658 | 28.45 | 1 | 1.038 | 0.046 | 0.298 |
Кратность максимального момента для
![]()
![]()
Круговая диаграмма представлена на листе Д1.
Круговая диаграмма изображена в графической части курсового проекта. Исходными данными для её построения являются:
Ток синхронного холостого хода по формуле 8.236 [1, стр.360]:
![]() , (229)
, (229)
![]() А.
А.
Коэффициент c1 = 1.0348.
Сопротивление короткого замыкания по формуле 8.237 [1,стр.360]:
![]() , (230)
, (230)
![]() Ом;
Ом;
![]() , (231)
, (231)
![]() Ом;
Ом;
Диаметр круговой диаграммы: Dk = 200 мм.
Рассчитаем масштабы.
Масштаб тока:
![]() , (232)
, (232)
![]() А/мм.
А/мм.
Масштаб мощности:
![]() , (233)
, (233)
![]() Вт/мм;
Вт/мм;
Масштаб момента:
![]() , (234)
, (234)
![]() Н·м/м;
Н·м/м;
Вектор тока синхронного холостого хода:
![]() , (235)
, (235)
![]() мм;
мм;
![]() , (236)
, (236)
![]() 0
.
0
.
Определим длинны отрезков:
![]() , (237)
, (237)
![]() ; мм
; мм
![]() , (238)
, (238)
![]() ;м
;м
![]() м;
м;
![]() , (239)
, (239)
![]() м;
м;
![]() , (240), где:
, (240), где:
![]() , (241)
, (241)
![]() Вт.
Вт.
Тогда:
![]() мм.
мм.
По круговой диаграмме для тока статора , которому соответствует точка А на окружности, можно рассчитать необходимые для построения рабочих характеристик данные:
1. Ток статора, А: ![]() , (242)
, (242)
2. Ток ротора, А: ![]() , (243)
, (243)
3. Первичная мощность, Вт: ![]() , (244)
, (244)
4.Электромагнитныймомент:![]() (245)
(245)
5. Полезная мощность, Вт: ![]() ; (246)
; (246)
6. КПД:  ; (247)
; (247)
7. Коэффициент мощности: ![]() ,
,
8.Скольжение двигателя: . (248)
. (248)
Полученная круговая диаграмма представлена в графической части проекта.
5 Тепловой и вентиляционный расчеты
Превышение температуры внутренней поверхности сердечника статора над температурой воздуха внутри двигателя:
 (249)
(249)
где K=0,17 – коэффициент, определяемый из таблицы 8.33 [1, c.402];![]() =74 – коэффициент теплоотдачи по рисунку 8.71 [1, c.401];
=74 – коэффициент теплоотдачи по рисунку 8.71 [1, c.401];![]() - электрические потери в пазовой части статора.
- электрические потери в пазовой части статора.

![]() (250)
(250)
![]()
Перепад температуры в изоляции пазовой части обмотки статора по 8.331 [1, c.400]:
 (251)
(251)
где ![]() - расчетный параметр поперечного сечения паза статора;
- расчетный параметр поперечного сечения паза статора;![]() - средняя эквивалентная теплопроводность изоляции класса B;
- средняя эквивалентная теплопроводность изоляции класса B;![]() - среднее значение коэффициента теплопроводности внутренней изоляции обмотки из эмалированных проводников с учетом неплотности прилегания проводников друг к другу по рисунку 8.72 [1, c.402].
- среднее значение коэффициента теплопроводности внутренней изоляции обмотки из эмалированных проводников с учетом неплотности прилегания проводников друг к другу по рисунку 8.72 [1, c.402].
![]() (252)
(252)
![]() =0,16 Вт/м2
.
=0,16 Вт/м2
.
![]() =1,4 Вт/м2
.
=1,4 Вт/м2
.
![]()
Перепад температуры по толщине изоляции лобовых частей по 8.335 [1, c.402]:
 (253)
(253)
где ![]() - расчетный параметр поперечного сечения паза статора;
- расчетный параметр поперечного сечения паза статора; ![]() - электрические потери в лобовых частях статора.
- электрические потери в лобовых частях статора.
 (254)
(254)
![]()
![]() =0.05
=0.05
![]()
Повышение температуры наружной поверхности лобовых частей над температурой воздуха внутри двигателя:
 (255)
(255)
![]()
Среднее превышение температуры обмотки статора над температурой воздуха внутри двигателя:
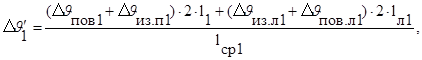 (256)
(256)
![]()
Превышение температуры воздуха внутри двигателя над температурой окружающей среды по 8.338 [1, c.403]:
 (257)
(257)
где ![]() - эквивалентная поверхность охлаждения;
- эквивалентная поверхность охлаждения; ![]() - коэффициент подогрева воздуха, определяется по рисунку 8.70 [1 c. 400];
- коэффициент подогрева воздуха, определяется по рисунку 8.70 [1 c. 400];
![]() - сумма потерь, отводимых в воздух двигателя.
- сумма потерь, отводимых в воздух двигателя.
![]() Вт/
Вт/![]()
![]() (258)
(258)
![]() (259)
(259)
![]() =1,07 - коэффициент нагревостойкости.
=1,07 - коэффициент нагревостойкости.
![]()
![]()
![]() (260)
(260)
![]()
![]()
Среднее превышение температуры обмотки статора над температурой окружающей среды по 8.344 [1, c.404]:
![]() (261)
(261)
Для двигателей со степенью защиты IP44, требуемый для охлаждения расход воздуха вычисляется по формуле 8.356 стр. 407 [1]:
![]() м3
/с, (262)
м3
/с, (262)
где ![]() - коэффициент, учитывающий изменение условий охлаждения по всей длине поверхности корпуса, вычисляется по формуле 8.357 стр. 407 [1]:
- коэффициент, учитывающий изменение условий охлаждения по всей длине поверхности корпуса, вычисляется по формуле 8.357 стр. 407 [1]:
![]() м3
/с, (263)
м3
/с, (263)
![]() -Коэффициент, зависящий от высоты вращения и числа пар полюсов стр. 407 [1].
-Коэффициент, зависящий от высоты вращения и числа пар полюсов стр. 407 [1].
Определяем расход воздуха, обеспечиваемый наружным вентилятором по формуле 8.358 стр. 407 [1]:
![]() м3
/с. (264)
м3
/с. (264)
Т.к. ![]() , то требуемый для охлаждения объем воздуха наружным вентилятором обеспечивается.
, то требуемый для охлаждения объем воздуха наружным вентилятором обеспечивается.
Принимаем ![]() . По выбранному диаметру вентилятора мы определяем окружную скорость по формуле 7.49 стр. 236 [1]:
. По выбранному диаметру вентилятора мы определяем окружную скорость по формуле 7.49 стр. 236 [1]:
![]() (265)
(265)
Номинальный расход воздуха ![]() .
.
Сечение на выходной кромке вентилятора найдем по формуле 7.51 стр. 237 [1]:
![]() . (267)
. (267)
Ширина колеса вентилятора вычисляется по формуле 7.52 стр. 237 [1]:
![]() . (268)
. (268)
Выберем аэродинамическое сопротивление по рисунку 7.5 стр. 231 [1]:![]()
Окружная скорость на внутренней кромке вентилятора по формуле 7.55 стр. 237 [1]:
 . (269)
. (269)
где ![]() -для радиальных лопаток стр. 237 [1].
-для радиальных лопаток стр. 237 [1].
![]() -плотность охлаждающей среды.
-плотность охлаждающей среды.
Давление развиваемое вентилятором в режиме холостого хода вычисляется по формуле 7.42 стр. 234 [1]:
![]() (270)
(270)
Рассчитаем внутренний диаметр по формуле:
![]() (271)
(271)
Число лопаток вентилятора по формуле:
![]() (272)
(272)
Примем число лопаток равное 26.
6.1 Расчёт вала

Рисунок 6.1 – Вал двигателя.
Расчет вала на жесткость.
Вал имеет следующие размеры (рисунок 6.1):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Сила тяжести сердечника ротора с обмоткой и участком вала по его длине по формуле 8 [3, c.17]:
Массу ротора можно представить как:
![]() (кг) (273)
(кг) (273)
Расчет прогиба вала проводят исходя из приведенной силы тяжести
![]() (H) (274)
(H) (274)
Hоминальный вращающий момент для двигателя:
![]() (275)
(275)
Прогиб вала посредине сердечника ротора от реакции передачи по формуле 9 [3, c.17]:
![]() (H). (276)
(H). (276)
Модуль упругости E=2,06![]() Па.
Па.
Момент инерции находим по формуле 13 [3, c.17]:
 (277)
(277)

Для определения прогиба вала рассчитываем вспомогательные значения ![]() ,
, ![]() ,
, ![]() по формулам 10, 11, 12 [3, c.17]:
по формулам 10, 11, 12 [3, c.17]:
![]() (278)
(278)
![]()
![]()
![]() (278)
(278)
![]()
![]()
![]() (280)
(280)
 (281)
(281)

Прогиб вала посредине сердечника ротора от реакции передачи по формуле 9 [3, c.17]:

 (282)
(282)
Прогиб вала посредине сердечника ротора под действием силы тяжести по формуле 7 [3, c.15]:
Начальный расчетный эксцентриситет ротора по формуле 13 [3, c.17]:
![]() (283)
(283)
Начальная сила одностороннего магнитного притяжения по формуле 14 [3, c.18]:
![]() (284)
(284)
Прогиб вала под действием силы ![]() по формуле 16 [3, c.18]:
по формуле 16 [3, c.18]:
 (285)
(285)
Установившийся прогиб вала от одностороннего магнитного притяжения по формуле 17 [3, c.18]:
 (286)
(286)
 (287)
(287)
Результирующий прогиб вала от силы тяжести ротора, реакции передачи и магнитного притяжения по формуле 18 [3, c.18]:
![]() (288)
(288)
Суммарный прогиб вала посредине магнитопровада ротора в процента
![]() . (289)
. (289)
Прогиб составляет примерно 3.51% воздушного зазора, т.е. прогиб не влияет на вал.
Критическая частота вращения:
 (290)
(290)
Превышение критической частоты вращения относительно номинальной
 (291)
(291)
Рабочая частота вращения ротора отличается от критической более чем 45 раза.
В расчете на прочность принимаем коэффициент перегрузки:![]() k=2;
k=2;
Напряжение на свободном конце вала в сечении А:
![]()
Момент сопротивления при изгибе :
![]() (292)
(292)

![]()
Напряжение в сечении Б :

![]() (294)
(294)
Момент сопротивления при изгибе:
 (295)
(295)
 (296)
(296)

Напряжение в сечении В :
 (297)
(297)![]()
Момент сопротивления при изгибе :
 (298)
(298)

Напряжение в сечении Г
 (300)
(300)
Момент сопротивления при изгибе


Напряжение в сечении Д:

Момент сопротивления при изгибе :


Напряжение в сечении Е:

Момент сопротивления при изгибе :306


Из сопоставлениия полученных данныч следует, что наиболее нагруженным является сечение Б, для которого ![]()
![]() выполняется условие нагруженности.
выполняется условие нагруженности.
В соответствии с рекомендациями, выбираем для P=18,8 кВт со стороны выходного вала подшипники качения роликовые,а с другой стороны шариковые.
6.2 Выбор подшипников
В соответствии с рекомендациями, выбираем для P=47.8 кВт со стороны выходного вала подшипники качения роликовые, а с другой стороны шариковые.
![]()
Определяем радиальную нагрузку на подшипники RA , RB по формуле 26 [3, c.24]:
![]() (309)
(309)
![]() (310)
(310)
Динамическая приведенная нагрузка по формуле 27 [3, c.24]:
![]() (311)
(311)
![]() (312)
(312)
Динамическая грузоподъемность по формуле 27 [3, c.24]:
 (313)
(313)
 (314)
(314)
Выбираем по каталогу, с учетом надежности шарикоподшипник № 218 средней серии со значением С=75500 Н, роликоподшипник № 22218 средней узкой серии со значением С=55500 Н.
Масса меди статора:
![]() (315)
(315)
где ![]() - плотность меди.
- плотность меди.
![]() =8900 кг/м3.
=8900 кг/м3.
![]() (316)
(316)
Масса статора:
![]() (317)
(317)
Масса стали ротора:
![]() (318)
(318)
где ![]() - плотность стали.
- плотность стали.
![]() =7800 кг/м3.
=7800 кг/м3.
![]() (319)
(319)
Масса алюминия ротора:
![]() (320)
(320)
где ![]() - плотность алюминия.
- плотность алюминия.
![]() =2700 кг/м3.
=2700 кг/м3.
![]()
Масса ротора:
![]() (321)
(321)
Масса корпуса электродвигателя:
![]() (322)
(322)
где ![]() - толщина корпуса;
- толщина корпуса; ![]() - длина корпуса двигателя.
- длина корпуса двигателя.
![]() =0.02.
=0.02.
![]() =0.7
=0.7
![]() (323)
(323)
Масса подшипников: ![]()
Масса подшипниковых щитов:
 (324)
(324)
где ![]() - внешний диаметр подшипникового щита;
- внешний диаметр подшипникового щита; ![]() - ширина подшипникового щита.
- ширина подшипникового щита.
![]() =0.45.
=0.45.
![]() =0.005.
=0.005.
![]() (325)
(325)
Масса выводной коробки ![]()
Масса вала:

Масса электродвигателя:
 (327)
(327)
Отношение массы к полезной мощности:
![]() (328)
(328)
8 Описание технологии сборки
Сердечник статора и ротора шихтуются из электротехнической стали толщиной 0,5 мм, сердечник выполняется без вентиляционных каналов.
Для изоляции листов друг от друга их лакируют. Для стали 2312 листы подвергают термообработке, в результате которой стабилизируются потери в стали и образуется поверхностный оксидный изолирующий слой.
Магнитопровод ротора насаживается непосредственно на гладкий вал.
Для предотвращения деформации (распушения) относительно тонких листов крайние торцевые листы магнитопровода штампуют из более тонких листов стали.
Собранный таким образом магнитопровод прессуют. После укладки обмотки в статор и пропитки ее лаком сердечник запрессовывают в станину.
Обмотки короткозамкнутых роторов не имеют изоляции. Они выполняются заливкой пазов алюминием, причем одновременно со стержнями обмотки отливают замыкающие кольца с вентиляционными лопатками.
На ротор напрессовывают подшипники, заводят его в статор. После этого устанавливают передний фланец и фиксируют в нем подшипник ротора. Затем устанавливают задний подшипниковый щит.
После этого устанавливают на задний конец вала надевают крыльчатку вентилятора. Затем защищают вентилятор кожухом.
На завершающем этапе сборки устанавливают клемную коробку.
Перед пробным пуском проверяют точность установки вала путем прокручивания его на несколько оборотов.
К корпусу ЭД с помощью болтов на коробку выводов крепится верхняя крышка.
Заключение
В результате проектирования был разработан асинхронный двигатель с короткозамкнутым ротором, который полностью отвечает требованиям, поставленным в курсовом проекте. Все проверяемые параметры отвечают критериям, рекомендуемым ГОСТ. Из-за перехода на меньшую высоту оси вращения, разработанный двигатель по некоторым технико-экономическим параметрам уступает существующим двигателям аналогичной мощности.
1. Проектирование электрических машин: Учебник для вузов Книга 1. Под редакцией Копылова И.П.Москва: Энергоатомиздат 1993. – 464 с.
2. Проектирование электрических машин: Учебник для вузов Книга 2. Под редакцией Копылова И.П.Москва: Энергоатомиздат 1993. – 384 с.
3. Электрические машины. Методические указания по курсовому проектированию для студентов специальности Т.11.02.00 "Автоматизированный электропривод".- Могилев: УО МГТУ, 2002. – 51 с.
4. Электрические машины: Асинхронные машины: Учеб. Для электромех. спец. вузов/ Радин В.И., Брускин Д.Э., Зорохович А.Е.; Под ред. И.П. Копылов-М.: Высшая школа, 1988,-328 с.