| Скачать .docx |
Реферат: Кинематика
Кинематика
тема 1 кинематика точки
1.1 п редмет изучения
С самого рождения и на протяжении всей своей жизни мы встречаемся с движением материи. Простейшей формой движения материи является механика. В разделе «кинематика» мы будем изучать только одну сторону механического движения – геометрическую, т.е. мы будем изучать геометрию движения тела без учета его массы и сил, действующих на него. Механически движение в общем смысле будет изучаться в разделе «динамика».
Под движением в механике мы будем понимать перемещение данного тела в пространстве и времени по отношению к другим телам.
Для определения положения движущего тела вводится система отсчета, связанная с телом, условно принимаемым за неподвижное. Движение тела происходит в пространстве и времени. Мы будем рассматривать трехмерное эвклидо пространство. За единицу длины в нем принимается 1 метр. Время считается универсальным, т. е. не зависящим от выбранной системы отсчета. За единицу времени принимается 1 секунда. В задачах механики время принимается за независимую переменную. Все остальные кинематические величины (расстояния, скорости, ускорения и т.д.) являются функциями времени.
Прежде чем изучать движение его необходимо задать, т.е. описать каким-либо математическими формулами так, чтобы можно было узнать положение тела и все его кинематические характеристики в любой момент времени.
Основная задача кинематики заключается в том, чтобы по известному закону движения тела (или какой-либо его точки) найти все остальные
кинематические характеристики движения.
Изучение кинематики мы начнем с изучения движения простейшего тела – точки, т.е. такого тела, размерами которого можно пренебречь и рассматривать его как геометрическую точку.
1.2 Способы задания движения точки
Мы будем рассматривать три способа задания движения: векторный, координатный и естественный.
1.2.1 Векторный способ
Положение движущейся точки М
определяется с помощью радиуса вектора ![]() , проведенного из некоторого неподвижного центра О
в эту точку (рис. 1.1). В процессе движения этот вектор изменяется по величине и направлению, т.е. является функцией времени. Зависимость
, проведенного из некоторого неподвижного центра О
в эту точку (рис. 1.1). В процессе движения этот вектор изменяется по величине и направлению, т.е. является функцией времени. Зависимость
![]() (1.1)
(1.1)
называется уравнением движения (или законом движения) в векторной форме. Линия, описываемая концом этого вектора называется траекторией движения.
|
1.2.2 Координатный способ
С неподвижным центром О связывается неподвижная система координат ОХ у Z . Положение точки определяется тремя координатами: х , у , z (рис. 1.2). В процессе движения эти координаты изменяются, т.е. они являются функциями времени.
|
Зависимости
х=f1 (t); у=f2 (t); z=f3 (t) (1.2)
называются уравнениями движения точки в координатной форме. Эти уравнения являются одновременно параметрическими уравнениями траектории движения (параметром является t ).
Чтобы получить уравнение траектории в явной форме, надо из уравнений (1.2) исключить параметр t.
1.2.3 Естественный способ
При естественном способе задания движения траектория заранее известна. На траектории выбирается начало отсчета (т. 0) и устанавливается положи-тельное и отрицательное направления отсчета.
Положение точки на траектории однозначно определяется криволинейной координатой S , измеряемой вдоль траектории. Зависимость
S = f(t) (1.3)
называется уравнением движения в естественной форме.
|
1.2.4 Связь между способами задания движения
Координатный векторный способы связаны зависимостью:
![]() (1.4)
(1.4)
где ![]() - единичные орты координатных осей.
- единичные орты координатных осей.
Переход от координатного способа к естественному:

здесь: ![]() ;
; 
![]()
(т.е. здесь и в дальнейшем производная по времени обозначается точкой над буквой).
1.3 Определение скорости и ускорение точки при векторном задании движения
Пусть точка за время ![]() переходит из положения М
в положение М1
, двигаясь вдоль траектории (Рис. 1.4)
переходит из положения М
в положение М1
, двигаясь вдоль траектории (Рис. 1.4) ![]() называется вектором перемеще-ния.
называется вектором перемеще-ния. 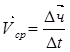 - средняя скорость.
- средняя скорость.
Например, вектор ![]() по хорде М М1
. если уменьшать промежуток времени
по хорде М М1
. если уменьшать промежуток времени ![]() , то хорда будет приближаться к касательной, а средняя скорость к мгновенной.
, то хорда будет приближаться к касательной, а средняя скорость к мгновенной.

Рис. 1.4

![]() (1.6)
(1.6)
Направлен вектор скорости по касательной к траектории.
Определение ускорения:
Пусть в положении М
скорость ![]() , а в положении М1
(через время
, а в положении М1
(через время ![]() ) скорость
) скорость ![]() . Приращение скорости
. Приращение скорости ![]() (рис. 1.5).
(рис. 1.5).
Среднее ускорение:
![]()
Ускорение в данный момент

 (1.7)
(1.7)
Лежит вектор ускорения в плоскости, проведенных через касательной к траектории в двух бесконечно близких точках. Эта плоскость называется соприкасающейся или плоскостью главной кривизны.
1.4 Определение скорости и ускорения точки при координатном способе задания движения
при координатном способе задания движения:
![]() (а)
(а)
с другой стороны:
![]() (б)
(б)
Сравнивая (а) и (б) находим:
 ;
;  ;
;  (1.8)
(1.8)
т.е. проекция вектора скорости на оси координат равны первым производным по времени от соответствующих координат.
Величина скорости:
![]() (1.9)
(1.9)
направление вектора скорости определяется с помощью направляющих косинусов, т.е. косинусов углов между вектором скорости и осями координат (рис. 1.6).
|
 (1.10)
(1.10)
Аналогично ищем ускорения:

Сравнивая (в), (г), (д) находим:
 (1.11)
(1.11)
Проекция ускорения равны первым производным по времени от соответствующих проекций скорости или вторым производным по времени от соответствующих координат.
Величина ускорения:
![]() (1.12)
(1.12)
Направляющие косинусы:
![]() ;
; ![]() ;
; ![]() ; (1.13)
; (1.13)
1.5 Определение скорости и ускорения точки при естественном задании движения
Пусть за время ![]() точка переместилась из положения М
в положение М1
, совершив перемещение
точка переместилась из положения М
в положение М1
, совершив перемещение ![]() (рис. 1.17).
(рис. 1.17).
|
величина скорости точки:
![]()
![]()
![]() (1.14)
(1.14)
Направлена скорость по касательной к траектории:
Найдем ускорение точки.
Пусть в положении М
точка имеет скорость ![]() (рис. 1.8).
(рис. 1.8).
Полное ускорение точки будет:
![]()
![]()
![]()
Обозначим угол между касательными через ![]() (угол смежности). Спроецируем вектор ускорения
(угол смежности). Спроецируем вектор ускорения ![]() на касательную
на касательную ![]() и нормам п
.
и нормам п
.
![]()
![]()
|
Найдем эти пределы, учитывая, что при ![]() одновременно и
одновременно и ![]() и
и ![]() .
.

где ρ – радиус кривизны траектории в данной точке.
Подставив эти значения в ап получим:

Т.о. величины касательного, нормального и полного ускорений определяется формулами:
|
|
|

Касательное ускорение направлено по касательной к траектории (в сторону скорости при ускоренном движении и противоположно скорости – при замедленном) и характеризует изменение величины скорости.
Нормальное ускорение направлено по нормам к траектории к центру кривизны и характеризует изменение направления скорости.
1.6 Частные случаи движения точки
По виду траектории движение делится на прямолинейное и криволинейное. При прямолинейном движении ап = 0, т.к. ρ = ∞.
По изменению величины скорости движения делится на равномерные и неравномерные.
Движение называется равномерным, если величина скорости постоянна (V=const ).
Закон равномерного движения:
S=S0 +Vt (1.18)
Движение называется равномерным, если величина касательного ускорения постоянна.

Т.о. равномерное движение описывается двумя формулами:
 (1.19)
(1.19)
Нормальное ускорение направлено от данной точки к оси вращения
Тема 2 Простейшие движения тела
К простейшим движениям твердого тела относятся поступательное движение и вращательное движение вокруг неподвижной оси.
2.1 Поступательное движение твердого тела
Поступательным называется такое движение тела, при котором любой отрезок прямой проведенной в теле перемещается параллельно самому себе.
Это самое простое движение тела.
Оно описывается одной теоремой:
При поступательном движении тела все его точки описывают одинаковые, при наложении совпадающие траектории, и имеют одинаковые скорости и одинаковые ускорения.
Доказательство:
Проведем в теле произвольный отрезок АВ . При движении тела он остается параллельным самому себе (рис. 2.1). траектория точки А на величину АВ , т.е. они одинаковые.
|
Проведем из неподвижного центра О
радиусы-векторы точек А
и В
(![]() ), а также вектор
), а также вектор ![]() из точки А
в точку В
.
из точки А
в точку В
.
Очевидно, что
![]()
Продифференцируем это векторное равенство по времени, учитывая, что ![]() .
.
![]() ; но
; но ![]() , значит
, значит
![]() (2.1)
(2.1)
дифференцируя (2.1) по времени: ![]() , получаем:
, получаем:
![]() (2.2)
(2.2)
Так как точки А и В взяты произвольно, то все выводы справедливы для всех точек тела.
Следовательно, при поступательном движении тела его можно считать точкой и пользоваться формулами кинематики точки.
2.2 Вращение тела вокруг неподвижной оси
Вращательным называется такое движение тела, при котором хотя бы две точки, принадлежащие телу или жестко с ним связанные, во все время движения остаются неподвижными. Прямая, проходящая через эти две неподвижные точки называется осью вращения.
Проведем через ось вращения две полуплоскости: неподвижную І и подвижную II, жестко связанную с телом и вращающуюся вместе с ним (рис. 2.2).
Положением тела будет однозначно определяться углом φ между этими полуплоскостями. Угол φ называется углом поворота. Измеряется он в радианах. Положительное направление φ – против часовой стрелки, если смотреть навстречу оси Z .
Зависимость
φ = φ(t) (2.3)
называется уравнением вращательного движения.
|
Быстрота вращения характеризуется угловой скоростью ω . Средняя угловая скорость определяется как отношения приращения угла поворота ∆φ к промежутку времени ∆t , за который оно произошло.
![]()
Угловая скорость в данный момент времени:
 (2.3)
(2.3)
Вектор угловой скорости ![]() направлен по оси вращения в ту сторону, чтобы, глядя навстречу ему, мы видели вращение происходящей против часовой стрелки. Изменяется ω
в радиан/сек. На производстве угловую скорость измеряют в об/мин. В этом случае она обозначается буквой «п».
направлен по оси вращения в ту сторону, чтобы, глядя навстречу ему, мы видели вращение происходящей против часовой стрелки. Изменяется ω
в радиан/сек. На производстве угловую скорость измеряют в об/мин. В этом случае она обозначается буквой «п».
Формула перехода:
 (2.4)
(2.4)
Изменение угловой скорости характеризуется угловым ускорением ε , которая определяется как первая производная от угловой скорости или вторая производная от угла поворота по времени:
 (2.5)
(2.5)
Направлен вектор ![]() также по оси вращения в сторону
также по оси вращения в сторону ![]() при ускоренном и противоположном
при ускоренном и противоположном ![]() при замедленном вращении. Единица измерения – 1Рад/с2
.
при замедленном вращении. Единица измерения – 1Рад/с2
.
2.3 Равномерное и равнопеременное вращение
Вращение называется равномерным, если угловая скорость постоянна, т.е. ω = const .
Закон равномерного вращения:
φ=φ0 +ωt (2.6)
Вращение называется равнопеременным, если угловое ускорение постоянно, т.е. ε = const .
Но ![]() . Разделяя переменные и интеграции
. Разделяя переменные и интеграции  находим, что
находим, что
![]() (2.7)
(2.7)
Подставив сюда ![]() и еще раз интегрируя
и еще раз интегрируя  , получим уравнение переменного вращения:
, получим уравнение переменного вращения:
![]() (2.8)
(2.8)
2.4 Скорости и ускорение точек вращающегося тела
пусть за время dt тело повернулось на угол dφ , а точка М , находящаяся на расстоянии R от оси вращения, получила перемещение dS =ч* dφ (рис. 2.3).
Тогда скорость точки
 (2.9)
(2.9)
Направлен вектор скорости ![]() по касательной к траекториям, т.е. по касательной к окружности радиуса R
, центр которой лежит на оси вращения, а ее плоскость перпендикулярна оси вращения.
по касательной к траекториям, т.е. по касательной к окружности радиуса R
, центр которой лежит на оси вращения, а ее плоскость перпендикулярна оси вращения.
Найдем нормальное и касательное ускорение точки:
|

|
|
Нормальное ускорение направлено от данной точки к оси вращения.
Касательное ускорение направлено по касательной к округлости, которую описывает точка и совпадает с направлением скорости при ускоренном вращении, а при немедленном – противоположно скорости.
Рассмотрим векторное произведение ![]() (рис. 2.4). Его модуль
(рис. 2.4). Его модуль ![]() , а направление совпадает с направлением скорости. Из этого делаем вывод, что вектор скорости:
, а направление совпадает с направлением скорости. Из этого делаем вывод, что вектор скорости:
![]() (2.11)
(2.11)
взяв от этого выражения производную по времени, получим:
![]()
Первое произведение по величине и направлению совпадает с касательным, а вторая – с нормальным ускорением.
Таким образом, касательная и нормальная составляющие вектора полного ускорения при вращательном движении определяется формулами:
 (2.12)
(2.12)
|
Отметим, что радиус-вектор ![]() точки М
можно проводить из любой точки О1
, лежащей на оси вращения (все точки оси вращения неподвижны) и что этот вектор постоянный по модулю (у него меняется только направление).
точки М
можно проводить из любой точки О1
, лежащей на оси вращения (все точки оси вращения неподвижны) и что этот вектор постоянный по модулю (у него меняется только направление).
2.5 Простейшие передаточные механизмы
Передаточными называют механизмы, служащие для передачи вращения с одного вала на другой. К простейшим из них относятся: зубчатые, ременные, цепные и фрикционные. Схематическое изображение зубчатых и фрикционных механизмов показано на рис. 2.5а , а ременных и цепных на рис. 2.5.б .
Найдем скорость точки а
: ![]() на колесе І и
на колесе І и ![]() на колесе ІІ. Так как проскальзывание отсутствует, то
на колесе ІІ. Так как проскальзывание отсутствует, то ![]() .
.
Отсюда:
 (2.13)
(2.13)
т.е. угловые скорости обратно пропорциональны радиусом колес. Величина i 1-2 называется передаточным отношением.
У зубчатых и цепных передач – передаточное отношение точное, у ременных и фрикционных – может быть проскальзывание. Ременные и цепные передачи позволяют передавать вращение на большие расстояния, чем зубчатые и фрикционные. С устройством передаточных механизмов, их изготовлением, расчетами и эксплуатацией вы познакомитесь в курсах «Теория механизмов и машин» и «Детали машин».
Тема 3 Сложное движение точки
3.1 Основные определения
До сих пор мы рассматриваем движение точки в одной, неподвижной системе отсчета. Однако, часто встречаются случаи, когда точка движется по определенному закону в некоторой системе отсчета, которая, в свою очередь, перемещается относительно неподвижной системы отсчета. Такое движение точки называется сложным. Введем основные определения сложного движения точки.
Движение точки в подвижной системе отсчета называется относительным. Скорость и ускорение точки в этом движении называются относительными и обозначаются: ![]() (или
(или ![]() ).
).
Движение точки вместе с подвижной системой называется переносным. Скорость и ускорение той точки М/
подвижной системы, в которой в данный момент находится движущаяся точка М
, являются для данной точки переносной скоростью и переносным ускорением и обозначаются ![]() (или
(или ![]() ).
).
Движение точки относительно неподвижной системы отсчета называется абсолютным. Скорость и ускорение точки в этом движении называются абсолютными и обозначаются ![]() (или
(или ![]() ).
).
Пусть точка М движется в подвижной системе отсчета оху z . Ее координаты х, у, z являются функциями времени, а координаты х/ , у/ , z / точки М/ подвижной системы, в которой в данный момент находится движущая точка М , являются константами. Но в любой момент времени
х = х/ , у = у/ , z = z / (3.1)
Введем в рассмотрение радиусы-векторы, определяющие положение точек М и М/ в подвижной и неподвижной системах отсчета (рис. 3.1).

![]() - радиус-вектор, определяющий положение начала подвижной системы оху
z
в неподвижной системе отсчета о1
х1
у1
z
1
.
- радиус-вектор, определяющий положение начала подвижной системы оху
z
в неподвижной системе отсчета о1
х1
у1
z
1
.
![]() =
=
![]() - радиус-вектор, определяющий положение движущейся точки М
в подвижной системе отсчета. Он описывает относительное движение точки.
- радиус-вектор, определяющий положение движущейся точки М
в подвижной системе отсчета. Он описывает относительное движение точки.
![]() - радиус-вектор, определяющий положение точки М/
подвижной системы в этой же системе.
- радиус-вектор, определяющий положение точки М/
подвижной системы в этой же системе.
![]() - радиус-вектор, определяющий положение точки М/
подвижной системы в неподвижной системе отсчета. Он описывает переносное движение точки.
- радиус-вектор, определяющий положение точки М/
подвижной системы в неподвижной системе отсчета. Он описывает переносное движение точки.
![]() - радиус-вектор, определяющий положение движущейся точки М
в неподвижной системе отсчета. Он описывает абсолютное движение.
- радиус-вектор, определяющий положение движущейся точки М
в неподвижной системе отсчета. Он описывает абсолютное движение.
3.2 Теоремы о схождении скоростей и ускорений
Скорости и ускорения точки в различных движениях будем определять как первую и вторую производные по времени от соответствующих радиусов-векторов.
1. Относительную скорость и относительное ускорение находим как первую и вторую производные по времени от радиус-вектора ![]() , считая единичные орты
, считая единичные орты ![]() константами (в подвижной системе – они постоянны).
константами (в подвижной системе – они постоянны).
|
|

2. Переносную скорость и переносное ускорение находим как первую и вторую производные по времени от радиус-вектора ![]() , считая координаты х/
, у/
,
z
/
константами, а единичные орты – переменными.
, считая координаты х/
, у/
,
z
/
константами, а единичные орты – переменными.

так как дифференцирование проведено, то мы можем воспользоваться равенствами (3.1), т.е. заменить х/ на х , у/ на у , z / на z :
|
|

3. Абсолютную скорость и абсолютное ускорение находим как первую и вторую производные по времени от радиус-вектора ![]() , считая все величины переменными:
, считая все величины переменными:
![]()
Таким образом доказана теорема сложения скоростей:
Абсолютная скорость равна геометрической сумме переносной и относительной скоростей.
![]() (3.6)
(3.6)
находим абсолютное ускорение:

где введено обозначение:
 (3.7)
(3.7)
Величина ![]() , определяемая равенством (3.7) называется поворотным ускорением или ускорением Кориолиса, по имени французского ученого, доказавшего теорему сложения ускорений:
, определяемая равенством (3.7) называется поворотным ускорением или ускорением Кориолиса, по имени французского ученого, доказавшего теорему сложения ускорений:
Абсолютное ускорение точки равно геометрической сумме переносного, относительного и Кориолисов ускорений.
![]() (3.8)
(3.8)
3.3 Ускорение Кориолиса, его величина направление и физический смысл
Рассмотрим ускорение Кориолиса, определяемое равенством (3.7). Если подвижная система движется относительно неподвижной поступательно (т.е. переносное движение поступательное), то единичные орты будут постоянны и по модулю и по направлению и их производные по времени будут равны нулю, следовательно и ускорение Кориолиса равно нулю.
Теорема о сложении ускорений при поступательном переносном движении будет выражаться равенством:
![]()
![]() (3.9)
(3.9)
Рассмотрим переносное вращательное движение. Пусть подвижная система вращается вокруг оси О3 с угловой скоростью ![]() (рис. 3.2). единичные орты
(рис. 3.2). единичные орты ![]() можно рассматривать как радиус-векторы точек А
, В
и С
соответственно. А производные по времени от радиус-векторов точек дают скорости точек.
можно рассматривать как радиус-векторы точек А
, В
и С
соответственно. А производные по времени от радиус-векторов точек дают скорости точек.
|
Следовательно:
![]() ;
; ![]() ;
; ![]() (а
)
(а
)
с другой стороны, скорости точек А, В и С мы можем найти как во вращательном движении по формуле (2.11):
![]() ;
; ![]() ;
; ![]() (б
)
(б
)
сравнивая (а ) и (б ) находим, что:
 ;
;  ;
;  ;(в
)
;(в
)
Подставим эти значения в формулу (3.7)

Таким образом ускорение Кориолиса равно удвоенному векторному произведению вектора угловой скорости переносного движения на вектор относительной скорости.
![]() (3.10)
(3.10)
Его величина
![]() (3.11)
(3.11)
|
В соответствии с правилом векторного произведения ускорения Кориолиса направлено перпендикулярно плоскости, в которой лежат векторы ![]() и
и ![]() , в ту сторону, чтобы, глядя навстречу ему, мы видим поворот вектора
, в ту сторону, чтобы, глядя навстречу ему, мы видим поворот вектора ![]() к вектору
к вектору ![]() на меньший угол происходящим против часовой стрелки.
на меньший угол происходящим против часовой стрелки.
Другое правило: чтобы найти направление ускорения Кориолиса, надо вектор ![]() спроецировать на плоскость, перпендикулярно оси переносного вращения, и полученную проекцию повернуть на 90о
в сторону вращения. Эти и будет направление вектора
спроецировать на плоскость, перпендикулярно оси переносного вращения, и полученную проекцию повернуть на 90о
в сторону вращения. Эти и будет направление вектора ![]() .
.
Физический смысл ускорения Кориолиса выясним на таком примере. Пусть круглая платформа вращается с постоянной угловой скоростью ![]() , а по радиусу платформы двигается точка М
с постоянной относительной скоростью V
ч
(рис. 3.3). В некоторый момент точка занимает положение Мо
,а через промежуток времени
, а по радиусу платформы двигается точка М
с постоянной относительной скоростью V
ч
(рис. 3.3). В некоторый момент точка занимает положение Мо
,а через промежуток времени ![]() положение М1.
При этом произошло изменение относительной скорости за счет переносного движения (изменилось направление вектора
положение М1.
При этом произошло изменение относительной скорости за счет переносного движения (изменилось направление вектора ![]() ) и изменение переносной скорости за счет относительного движения (изменилась величина
) и изменение переносной скорости за счет относительного движения (изменилась величина ![]() в результате удаления точки от оси вращения). Эти два изменения и характеризуются ускорением Кориолиса.
в результате удаления точки от оси вращения). Эти два изменения и характеризуются ускорением Кориолиса.
Таким образом, ускорение Кориолиса характеризует изменение относительной скорости в результате переносного движения и изменение переносной скорости в результате относительного движения.
В общем случае движения формулы (3.8) удобнее использовать в таком виде:
![]() (3.12)
(3.12)
Задача кинематики плоского движения твердого тела - найти характеристики движения самого тела и отдельных его точек. В данном задании к таким характеристикам относятся векторы угловой скорости и углового ускорения тела.

![]() Рис. 1
Рис. 1
Основные формулы кинематики плоского движения твердого тела - векторные формулы, связывающие соответственно скорости и ускорения двух произвольных точек плоской фигуры, например, точек А и В (рис. 1)
![]() B
=
B
= ![]() A
+
A
+ ![]() BA
=
BA
= ![]() A
+
A
+ ![]() ´
´![]() ;(1)
;(1)
![]() B
=
B
= ![]() A
+
A
+ ![]() +
+ ![]() =
= ![]() A
+
A
+ ![]() × (
× (![]() ´
´![]() ) +
) + ![]() ×
× ![]() ;(2)
;(2)
где ![]() ,
, ![]() , - векторы угловой скорости и углового ускорения вращения плоской фигуры вокруг любой оси, например Az' перпендикулярной плоскости движения Oxy относительно системы координат Ax'y'z', оси которой параллельны осям неподвижной системы координат Оxyz.На рис.1 оси Оz. и Аz' не изображены, так как считается, что они перпендикулярны к плоскости рисунка и направлены на наблюдателя, а плоскости Охy и Аx'y' совпадают с плоскостью рисунка.
, - векторы угловой скорости и углового ускорения вращения плоской фигуры вокруг любой оси, например Az' перпендикулярной плоскости движения Oxy относительно системы координат Ax'y'z', оси которой параллельны осям неподвижной системы координат Оxyz.На рис.1 оси Оz. и Аz' не изображены, так как считается, что они перпендикулярны к плоскости рисунка и направлены на наблюдателя, а плоскости Охy и Аx'y' совпадают с плоскостью рисунка.
Левые части выражений
![]() BA
=
BA
= ![]() ´
´![]() ;
;![]() =
=![]() × (
× (![]() ´
´![]() ) =
) = ![]() ×
× ![]() BA
;
BA
; ![]() =
= ![]() ×
× ![]() ;
;
являются соответственно векторамискорости, нормального и касательного ускорения точки В относительно системы координат Ax'y'z'при вращении отрезка АВ в плоскости рисунка вокруг точки A, называемой в таком случае полюсом, с угловой скоростью ![]() и угловым ускорением
и угловым ускорением ![]() . Индексы n и t
,
в выражениях
. Индексы n и t
,
в выражениях ![]() и
и ![]() указывают, что эти векторы направлены соответственно по внутренней нормали и касательной в точке Bк окружности радиуса r = AB с центром в точке А. Модули упомянутых векторов
указывают, что эти векторы направлены соответственно по внутренней нормали и касательной в точке Bк окружности радиуса r = AB с центром в точке А. Модули упомянутых векторов ![]()
![]() находятся по формулам
находятся по формулам
½![]() BA
½ =
BA
½ = ![]() ´AB;½
´AB;½![]() ½ =
½ = ![]() =
= ![]() ´AB;½
´AB;½![]() ½ =
½ = ![]() ´AB;(3)
´AB;(3)
Векторы ![]() BA
,
BA
, ![]() ,
, ![]() лежат в плоскости движения плоской фигуры тела, причем ненулевые векторы
лежат в плоскости движения плоской фигуры тела, причем ненулевые векторы ![]() BA
,
BA
, ![]() перпендикулярны отрезку AB, а ненулевой вектор
перпендикулярны отрезку AB, а ненулевой вектор ![]() направлен от точки В к точке А . Таким образом, для этих векторов всегда известны линии действия.
направлен от точки В к точке А . Таким образом, для этих векторов всегда известны линии действия.
Поскольку модуль ускорения ![]() может быть вычисленпо формуле (3) через угловую скорость тела
может быть вычисленпо формуле (3) через угловую скорость тела ![]() , обычно известную к этапу нахождения ускорений, целесообразно в формуле (2) вектор
, обычно известную к этапу нахождения ускорений, целесообразно в формуле (2) вектор ![]() записывать вслед за известным вектором
записывать вслед за известным вектором![]() А
, т.е. перед вектором
А
, т.е. перед вектором ![]() .
.
Векторы ![]() и
и ![]() параллельны оси Оz и поэтому полностью определяются своими проекциями на эту ось
параллельны оси Оz и поэтому полностью определяются своими проекциями на эту ось
Модуль проекции равен модулю вектора ![]() ;
;![]() , а знак проекции указывает на направление вектора. Например, если проекции векторов положительны (
, а знак проекции указывает на направление вектора. Например, если проекции векторов положительны (![]() , то векторы
, то векторы ![]() направлены так же, как и
направлены так же, как и ![]() , или ось Oz. Таким образом, при плоском движении тела задача нахождения векторов
, или ось Oz. Таким образом, при плоском движении тела задача нахождения векторов ![]() сводится к задаче отыскания их проекций на ось Oz или Az'.
сводится к задаче отыскания их проекций на ось Oz или Az'.
Если ![]() (рад) - угол между осью Ax' (Ох) и вектором
(рад) - угол между осью Ax' (Ох) и вектором ![]() (рис. 1) и за положительное направление отсчета угла
(рис. 1) и за положительное направление отсчета угла ![]() для выбранной системы координат принято направление против хода часовой стрелки, то
для выбранной системы координат принято направление против хода часовой стрелки, то
![]()
![]() рад/с;
рад/с;![]() =
= ![]()
![]() =
= ![]()
![]() рад/с.(4)
рад/с.(4)
О направлении векторов ![]() и
и ![]() судят по круговым стрелкам
судят по круговым стрелкам ![]() и
и ![]() согласно правилу: "круговая стрелка, направленная против хода стрелки часов, соответствует вектору, направленному так же, как ось Oz".
согласно правилу: "круговая стрелка, направленная против хода стрелки часов, соответствует вектору, направленному так же, как ось Oz".
Из формул, использующих понятие МЦС (точка Р) на рис.2,
![]() ´
´![]() ;
;![]() B
=
B
= ![]() ;
;![]() ;
;
![]() ;
;![]() ,(5)
,(5)
следует, что в данный момент времени распределение скоростей точек тела при плоском движении таково, как если бы тело вращалось вокруг оси Рz
с угловой скоростью ![]() .
.
 |
![]()

![]()
![]() Если отсчитывать угол 90 от направления вектора скорости точки
Если отсчитывать угол 90 от направления вектора скорости точки ![]() A
к направлению АР от этой точки до МЦС, то направление отсчета угла совпадает с направлением круговойстрелки
A
к направлению АР от этой точки до МЦС, то направление отсчета угла совпадает с направлением круговойстрелки ![]() . Этот факт можно использовать для определения направления вектора
. Этот факт можно использовать для определения направления вектора ![]() .
.
Из формул, использующих понятие МЦУ (точка Q на рис. 3),
![]()
![]() ;
;![]()
![]() ;(6)
;(6)
![]() ,
,
следует, что в данный момент времени распределение ускорений точек тела при плоском движении таково, как если бы тело вращалось вокруг оси Qz
с угловой скоростью ![]() и угловым ускорением
и угловым ускорением ![]() .
.
Угол ![]() отсчитывается от вектора ускорения какой-либоточки в направлении круговой стрелки
отсчитывается от вектора ускорения какой-либоточки в направлении круговой стрелки ![]() . При отыскании положения МЦУ по ускорениям двух точек, например по
. При отыскании положения МЦУ по ускорениям двух точек, например по ![]() и
и![]() , под углом
, под углом ![]() к соответствующим ускорениям проводят лучи AQ и BQ. Точка пересечения лучей (точка Q) является МЦУ плоской фигуры в данный момент времени.
к соответствующим ускорениям проводят лучи AQ и BQ. Точка пересечения лучей (точка Q) является МЦУ плоской фигуры в данный момент времени.
Направления векторов ![]() и
и ![]() помимо формул (4) могут быть найдены из отдельных векторных формул
помимо формул (4) могут быть найдены из отдельных векторных формул
![]() ;
;![]() ;
;![]() .(7)
.(7)

Рис. 4
Чтобы избежать анализа расположения трех взаимно перпендикулярных векторов формул (7) при известных ![]() ,
, ![]() ,
, ![]() направления
направления ![]() и
и ![]() находят аналогично случаю вращательного движения тела вокруг неподвижной оси (рис. 4).
находят аналогично случаю вращательного движения тела вокруг неподвижной оси (рис. 4).
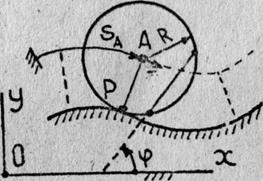
Рис. 5![]()
Кинематика плоского движения
катка радиуса R. при отсутствии скольжения по направляющей (в общемслучае криволинейной), имеет некоторые особенности вследствие того,что мгновенный центр скоростей катка (точка Р ) совпадает с точкой окружности касающейся направляющей (рис. 5). Поэтому при движении каткарасстояние от его центра (точкиА) до МЦС является неизменным во времени и равнымR.
AP(t) = const = R(8)
Свойство неизменности расстояния АР позволяет установить дополнительные соотношения, удобные для расчетов кинематических характеристик катка. Представим вектор скорости точки А с помощью:
а) формулы естественного способа задания движения точки
![]() , где
, где ![]() - единичный вектор естественного трехгранника, касательный в точке A к кривой ее движения; SA
- криволинейная координата точки;
- единичный вектор естественного трехгранника, касательный в точке A к кривой ее движения; SA
- криволинейная координата точки;
б) формулы (7) плоского движения тела
![]() ,
,
![]() ;
;
![]() - орт оси Оz
, перпендикулярной плоскости движения катка Qxy;j - угол, задающий направление какого-либо отрезка плоской фигуры катка. Ввиду произвольности выбора такого отрезка, обычно собственно отрезок, не указывают на рисунках, а изображают лишь круговую стрелку положительного направления отсчета угла j, называя его углом поворота катка.
- орт оси Оz
, перпендикулярной плоскости движения катка Qxy;j - угол, задающий направление какого-либо отрезка плоской фигуры катка. Ввиду произвольности выбора такого отрезка, обычно собственно отрезок, не указывают на рисунках, а изображают лишь круговую стрелку положительного направления отсчета угла j, называя его углом поворота катка.
Приравнивая правые части последних формул, имеем
![]() .
.
Поскольку вектoр ![]() коллинеарен результату векторного произведения
коллинеарен результату векторного произведения
![]() (
(![]() ^
^![]() ,
, ![]() ^
^![]() ), то
), то
![]() .
.
Откуда, используя свойство (8), получим формулы
![]() , или
, или ![]() , (9)
, (9)
справедливые для любого момента времени t.
В правой части формулы (9) берется знак "+", если при мысленном увеличении угла поворота катка jв направлении против хода стрелки часов наблюдается возрастание координаты SА центра движущегося катка в положительном направлении ее отсчета, иначе берется знак "-".
Так, например, для случая отсчетов SА и j, изображенном на рис.5, в формуле (9) необходимо брать знак "-".
Дифференцируя и интегрируя по времени соотношения (9), придем к выражениям
![]() , или
, или ![]() ,(10),
,(10),
а также ![]() ,
,
где С - некоторая константа, значение которой зависит от выбора начал отсчетов SА и j. Обычно принимают С=0, так как считают, что когда SА =0, j также равно нулю. Из произведения соответствующих частей формул (9), (10),
![]() (11)
(11)
![]()
![]()
![]()
![]()
![]()
![]() следует, что если векторы
следует, что если векторы ![]() ,
, ![]() сонаправлены, то сонаправлены и векторы
сонаправлены, то сонаправлены и векторы ![]() ,
, ![]() .
.
Таким образом, с помощью формул (1-4), (8-9) могут быть найдены характеристики векторов скоростей и ускорений точек, векторов угловых скоростей и ускорений звеньев механизма, а с помощью формул (5, 6), (11) осуществлена их проверка.
Нахождение кинематических характеристик движения (![]() ,
, ![]() ,
, ![]() ,
, ![]() ) при помощи векторных формул (1), (2) рекомендуется проводить следующим образом:
) при помощи векторных формул (1), (2) рекомендуется проводить следующим образом:
1) написать формулу (1) или (2) применительно к конкретным точкам рассматриваемого звена механизма. При этом в качестве полюса следует взять точку с известными кинематическими характеристиками движения;
2) установить, известны или неизвестны на данном этапе решения две независимые характеристики {проекции на две оси или модуль и направляющий угол) для каждого вектора, входящего в уравнение (1) или (2). Найти значения тех независимых характеристик векторов, которые могут быть установлены из условий движения звена без решения рассматриваемого векторного уравнения;
3) решить векторное уравнение графоаналитическим или аналитическим методом (метод проекций).











