| Скачать .zip |
Реферат: Курс лекции по Физике
Фотоны.
В теории равновесного излучения абсолютно черного тела Планка вводится понятие фотона – кванта света или порции излучения, которая может поглощаться или излучаться только целиком. С другой стороны, по средствам фотонов осуществляется электромагнитное взаимодействие. Энергия фотона ![]() , импульс
, импульс ![]() . Масса покоя фотона равна нулю. Докажем это утверждение.
. Масса покоя фотона равна нулю. Докажем это утверждение.
Рассмотрим фотон в покоящейся и движущейся системах отсчета. Энергия в покоящейся системе ![]() , в движущейся
, в движущейся ![]() . Частоты в движущейся и покоящейся системах отсчета связаны соотношением
. Частоты в движущейся и покоящейся системах отсчета связаны соотношением  , тогда энергия в движущейся и покоящейся системах
, тогда энергия в движущейся и покоящейся системах  . Энергия связана с импульсом
. Энергия связана с импульсом  . Энергия фотона в движущейся и покоящейся в системах отсчета должны быть равны, поэтому,
. Энергия фотона в движущейся и покоящейся в системах отсчета должны быть равны, поэтому,  , из связи энергии и импульса
, из связи энергии и импульса ![]() .
.
Фотоэффект
Фотоэффект наблюдается при передаче энергии фотона электрону, находящемуся вещества, то есть связанному электрону. Поглощение фотона электроном может привести либо к перераспределению электронной плотности в веществе, либо к вырыванию электрона с поверхности вещества. В связи с этим, для различных материалов имеют место два вида фотоэффекта: для металлов – внешний, для диэлектриков и полупроводников – внутренний (в частности, в полупроводниках наблюдается один из видов внутреннего фотоэффекта – вентильный). При внутреннем фотоэффекте валентные электроны либо становятся электронами проводимости, что наблюдается в полупроводниках, либо переходят на более высокий энергетический уровень, оставаясь в связанном состоянии.
Внешним фотоэффектом называется явление вырывания электронов с поверхности металлов. Энергия фотона, падающего на поверхность металла, переходит валентному электрону

Экспериментально фотоэффект описывается законами Столетова:
Фототок насыщения не зависит от частоты падающего света, а определяется только его интенсивностью
Задерживающее напряжение не зависит от интенсивности, а определяется только частотой падающего света
Для любого металла существует минимальная частота, называемая красной границей, при которой только начинается фотоэффект
Теоретически закон внешнего фотоэффекта описывается выражением, представляющим собой закон сохранения энергии:  (1) – формула Эйнштейна, где Ав – работа выхода электрона из металла, - частота света, освещающего фотокатод, - максимальная скорость фотоэлектрона.
(1) – формула Эйнштейна, где Ав – работа выхода электрона из металла, - частота света, освещающего фотокатод, - максимальная скорость фотоэлектрона.
С учетом законов Столетова  (2), и условие красной границы
(2), и условие красной границы ![]() (3), тогда уравнение (1) можно переписать в виде
(3), тогда уравнение (1) можно переписать в виде ![]()
Световое давление
Квант света, попадая на поверхность, передает ей импульс. При отражении от поверхности переданный импульс равен удвоенному импульсу фотона ![]() , а при поглощении – импульсу фотона
, а при поглощении – импульсу фотона ![]() . Вводя коэффициент отражения – относительное число фотонов, отраженных поверхностью, полный импульс, переданный N падающими фотонами перпендикулярной единичной поверхности
. Вводя коэффициент отражения – относительное число фотонов, отраженных поверхностью, полный импульс, переданный N падающими фотонами перпендикулярной единичной поверхности ![]() . Импульс, переданный за единицу времени единице поверхности, равен нормальной силе, действующей на единицу поверхности, а это величина называется давлением. Таким образом, давление света на перпендикулярную поверхность равно
. Импульс, переданный за единицу времени единице поверхности, равен нормальной силе, действующей на единицу поверхности, а это величина называется давлением. Таким образом, давление света на перпендикулярную поверхность равно ![]() (4), где Nts – число фотонов ежесекундно падающих на единицу площади поверхности.
(4), где Nts – число фотонов ежесекундно падающих на единицу площади поверхности.
Эффект Комптона
При отражении высокоэнергичных рентгеновских лучей от металлических поверхностей наблюдается изменение их длины волны. Такое явление имеет место только при отражении от металлов, следовательно необходимо рассмотреть взаимодействие фотона с электроном проводимости металла. Как известно, валентные электроны в металле обобществляются и их можно считать свободными, то есть способными перемещаться под действием внешних полей.
Р ассмотрим взаимодействие падающего фотона с импульсом
ассмотрим взаимодействие падающего фотона с импульсом ![]() и покоящегося валентного электрона. В результате возникает отраженный фотон с импульсом
и покоящегося валентного электрона. В результате возникает отраженный фотон с импульсом ![]() и электрон отдачи с импульсом
и электрон отдачи с импульсом ![]() . По закону сохранения импульса
. По закону сохранения импульса ![]() (рис.3) или по теореме косинусов
(рис.3) или по теореме косинусов ![]() (4).
(4).
По закону сохранения энергии ![]() (5), здесь учтено, что электрон является релятивистской частицей и до взаимодействия обладает только энергией покоя. Зная связь релятивистской энергии и импульса
(5), здесь учтено, что электрон является релятивистской частицей и до взаимодействия обладает только энергией покоя. Зная связь релятивистской энергии и импульса ![]() , тогда,
, тогда,  . Возведем в квадрат обе части уравнения и, учитывая
. Возведем в квадрат обе части уравнения и, учитывая ![]() , получим
, получим ![]() или, приводя подобные,
или, приводя подобные, ![]() разделим обе части на kk и учтем, что
разделим обе части на kk и учтем, что ![]() ,
,  , где комптоновская длина волны
, где комптоновская длина волны ![]() .
.
Спектр водорода. Формула Бальмера. Постулаты Бора.
В конце 19 начале 20 веков бурно развивалась спектроскопия. Самым простым для изучения материалом является водород, поэтому наибольшее число работ было посвящено изучению спектров атома водорода. Исследуемые спектры были линейчатыми. Особенность водородных спектров заключалась в том, что линии излучения и поглощения располагались группам, которые были названы сериями. Одна из спектральных серий лежит в видимой области, одна – в ультрафиолетовой, остальные – в инфракрасной.Частоты спектральных линий хорошо описывались обобщенной формулой Бальмера.
 (1)
(1)
Где R = 3,291015 с-1 – константа Ридберга, а n и m – целые числа. Аналогичная формула имеет место для длин волн, где R = 1,10107 м-1:
 (2)
(2)
Целое число m определяет спектральную серию: n = 1 серия Лаймана
n = 2 серия Бальмера
n = 3 серия Пашена
n = 4 серия Бреккета
n = 5 серия Пфунда
n = 6 серия Хэмфри
n = 7 серия Пиккеринга
Для объяснения полученных формул, а именно физического смысла чисел n и m были разработаны атомные модели.
Модель Томпсона.
Атом представляет собой массивный положительный заряд, занимающий практически весь объем атома, а точечные электроны равномерно распределены по его поверхности. Предполагалось, что электроны колеблются около положения равновесия и частота их колебания совпадает с частотой излучения света. Проблема заключалась в том, что согласно законам классической электродинамики, ускоренно движущаяся частица должна излучать. Если колеблющиеся электроны излучают – теряется энергия, следовательно, должна равномерно уменьшаться частота их колебания, и спектр излучения должен быть сплошным. Таким образом, модель объясняет сам факт излучения, но не объясняет физический смысл чисел n и m.
Модель атома Резерфорда.
На основании проведенного эксперимента Резерфорд заключил, что размер атома, в основном, определяется электронной оболочкой, масса атома определяется ядром, размер которого значительно меньше размеров оболочки. Электроны вращаются вокруг ядра по круговым орбитам, как планеты вокруг Солнца, поэтому, модель атома Резерфорда была названа планетарной. Предполагалось, что при переходе электронов между орбитами атом излучает или поглощает свет, в результате этих переходов формируется спектр атома. Целые числа в формуле Бальмера соответствуют номерам орбит, между которыми происходит переход: m – уровень, на который осуществляется переход, n – уровень, с которого осуществляется переход.
Проблема объяснения формирования спектров осталась прежней – ускоренно движущиеся по орбитам электроны должны излучать, следовательно, терять энергию, что должно приводить к уменьшению радиусов их орбит. В результате электроны должны были опуститься на ядро. Однако, последняя модель не только описывала факт излучения атома, но и объясняла сериальные закономерности, поэтому, для правомерности ее применения Бор сформулировал три постулата:
а) Существуют такие стационарные состояния, в которых атом не поглощает и не излучает энергию
б) При переходе между двумя стационарными состояниями атом излучает или поглощает квант света, энергия которого равна разности энергий состояний
![]() (3)
(3)
в) Момент импульса электрона в атоме является квантованной величиной
![]() (4)
(4)
Где n – скорость электрона на n-ной боровской орбите, rn – радиус соответствующей боровской орбиты, n – номер орбиты, m – масса электрона.
Применяя постулаты Бора к модели атома водорода (рис.1) легко получить обобщенную формулу Бальмера:
Р ассмотрим электрон, движущийся по n-ной боровской орбите. Кулоновская сила взаимодействия электрона с ядром сообщает электрону нормальное ускорение и по второму закону Ньютона
ассмотрим электрон, движущийся по n-ной боровской орбите. Кулоновская сила взаимодействия электрона с ядром сообщает электрону нормальное ускорение и по второму закону Ньютона 
Согласно третьему постулату Бора ![]() , отсюда радиус n-ной боровской орбиты
, отсюда радиус n-ной боровской орбиты  (5); скорость на этой орбите
(5); скорость на этой орбите  (6)
(6)
Полная энергия электрона на n-ной боровской орбите складывается из кинетической энергии электрона и его потенциальной энергии кулоновского взаимодействия с ядром:  . Подставляя (5) и (6) получим:
. Подставляя (5) и (6) получим:  , для атома водорода заряд ядра Z = 1. Таким образом, электрон в атоме водорода способен принимать строго дискретный набор энергий, определенный целым числом n – главным квантовым числом.
, для атома водорода заряд ядра Z = 1. Таким образом, электрон в атоме водорода способен принимать строго дискретный набор энергий, определенный целым числом n – главным квантовым числом.
Применяя второй постулат Бора, получим обобщенную формулу Бальмера  , тогда значение постоянной Ридберга
, тогда значение постоянной Ридберга  (7). Расчет последней дает хорошее согласование с экспериментальным значением.
(7). Расчет последней дает хорошее согласование с экспериментальным значением.
Корпускулярно волновой дуализм
Экспериментальные факты свидетельствуют, что в ряде явлений свет проявляет сугубо волновые свойства (дифракция, интерференция, поляризация, дисперсия), а в ряде – чисто корпускулярные (фотоэффект, эффект Комптона). Рассматривая эти факты, де Бройль предположил, что аналогичные проявления двойственности свойств должны иметь место для любого материального объекта. Импульс объекта определяет его длину волны  (1).
(1).
Данное утверждение было экспериментально подтверждено Дэвидсоном и Джермером, которые исследовали дифракцию электронных пучков на атомных плоскостях кристалла. Электронные пучки разгонялись в электрическом поле и их скорость определялась выражением  (2). Тогда длина волны де Бройля электрона
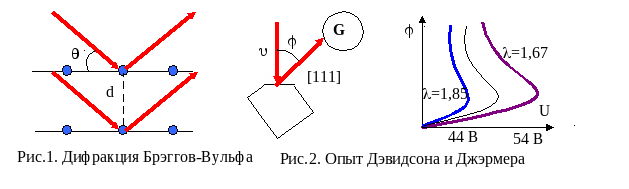
(2). Тогда длина волны де Бройля электрона  (3). Предполагалось, что дифракция электронных пучков будет аналогична дифракции рентгеновских лучей (рис.1) и условие дифракционных максимумов будет удовлетворять формуле Брэггов-Вульфа
(3). Предполагалось, что дифракция электронных пучков будет аналогична дифракции рентгеновских лучей (рис.1) и условие дифракционных максимумов будет удовлетворять формуле Брэггов-Вульфа ![]() (4). Длина волны рентгеновского излучения 1,67 нм. В опыте Девидсона и Джермера электронный пучок падал на кристалл перпендикулярно кристаллографической плоскости [111], отражался под углом и фототок фиксировался гальванометром (рис.2). В зависимости от напряжения, при прохождении которого разгонялись электроны, максимум дифракции фиксировался под углом . Для напряжений 44, 48, 54 В длина волны де Бройля составила 1,85 нм, 1,77 нм, 1,67 нм, что соответствовало рентгеновской длине волны, дифрагировавшей под заданными углами в опыте Брэггов-Вульфа.
(4). Длина волны рентгеновского излучения 1,67 нм. В опыте Девидсона и Джермера электронный пучок падал на кристалл перпендикулярно кристаллографической плоскости [111], отражался под углом и фототок фиксировался гальванометром (рис.2). В зависимости от напряжения, при прохождении которого разгонялись электроны, максимум дифракции фиксировался под углом . Для напряжений 44, 48, 54 В длина волны де Бройля составила 1,85 нм, 1,77 нм, 1,67 нм, что соответствовало рентгеновской длине волны, дифрагировавшей под заданными углами в опыте Брэггов-Вульфа.
Второй опыт был проделан Томпсоном. Электронный пучок дифрагировал на тонкой фольге, при этом наблюдалось полное совпадение электронных и рентгеновских максимумов. Тартаковский усовершенствовал опыт, увеличив время экспозиции и сведя электронный пучок к одиночным электронам и снова зафиксировал совпадение электронных и рентгеновских максимумов.
Таким образом, для вещества, как и для света, имеет место корпускулярно-волновой дуализм.
Принцип неопределенности Гейзенберга
В макромире работают законы классической механики и электродинамики, поэтому, для любого макрообъекта определено понятие траектории и любые кинематические и динамические параметры движения объекта могут быть измерены одновременно.
Для микрочастиц имеют место волновые свойства, поэтому, законы макромира при переходе в микромир претерпевают существенные изменения. Рассмотрим двухщелевой интерферометр, на который падает пучок гипотетических параллельно движущихся частиц. Если перекрыть одну из щелей, на экране, расположенном за щелью, частицы после ее прохождения симметрично распределятся по обе стороны от центра щели (рис.3). Вероятность для частицы занять на экране координату х будет определяться некой функцией 1(x, t). Перекрывая вторую щель, получим аналогичную картину и вероятность для частицы определится функцией 2(x, t). Если открыть обе щели, на экране окажется интерференционная картина с максимумом в центре экрана, симметрично по отношению к щелям и вероятность обнаружения частицы в точке с координатой x в момент времени t будет равна сумме вероятностей ![]()

В микромире принципиально отсутствует понятие траектории, поэтому, координата и импульс микрочастицы могут быть одновременно измерены только с точностью до некоторой величины. Данное утверждение носит название принципа неопределенности Гейзенберга, а выражения
![]() (5)
(5)
![]() (6)
(6)
называются соотношениями неопределенности Гейзенберга. Выражение (6) легко получить из выражения (5), записав, что  , так как импульс
, так как импульс ![]() , а скорость
, а скорость ![]() , заменяя дифференциалы величин на их приращения, приходим к идентичности выражений (5) и (6).
, заменяя дифференциалы величин на их приращения, приходим к идентичности выражений (5) и (6).
Уравнение Шредингера
Для описания микрочастицы необходимо, чтобы были определены:
величины, задающие состояние частицы;
уравнение движения, определяющее изменение состояния частицы;
физические величины, доступные измерению и способ получения их значений в данном состоянии.
Для микрочастиц из-за соотношений неопределенности классическое определение состояния (координата и импульс, а следовательно и сила) не подойдет. В соответствии с корпускулярно-волновым дуализма в квантовой теории состояния частицы задается волновая функция ![]() , которая является комплексной величиной и формально обладает волновыми свойствами. Для волновой функции характерны следующие свойства:
, которая является комплексной величиной и формально обладает волновыми свойствами. Для волновой функции характерны следующие свойства:
1) с помощью волновой функции определяется вероятность ![]() (7), то есть вероятность нахождения частицы в единице объема
(7), то есть вероятность нахождения частицы в единице объема ![]()
2) волновая функция нормирована на единицу  (8), то есть, во всем пространстве, где волновая функция отлична от нуля, частица может быть достоверно найдена
(8), то есть, во всем пространстве, где волновая функция отлична от нуля, частица может быть достоверно найдена
3) для волновых функций имеет место принцип суперпозиции ![]() что объясняет проявление волновых свойств частицы
что объясняет проявление волновых свойств частицы
4) так как волновая функция описывает реальные частицы, она должна быть конечной, непрерывной, гладкой и однозначно определяемой.
Рассмотрим свободную частицу, способную двигаться вдоль оси x в отсутствии внешних полей. Такая частица должна описываться плоской волной ![]() (9) или, учитывая связь волнового числа и импульса
(9) или, учитывая связь волнового числа и импульса ![]() , а также частоты и энергии
, а также частоты и энергии ![]() , тогда выражение (9) примет вид
, тогда выражение (9) примет вид  (10).
(10).
Продифференцируем (10) по времени и по координате:
 (11)
(11)
 ;
;  (12)
(12)
Учитывая связь энергии и импульса  для свободной частицы и следствия уравнений (11) и (12)
для свободной частицы и следствия уравнений (11) и (12)  , получим одномерное уравнение
, получим одномерное уравнение  (13).
(13).
В общем случаи  и в левой части берется сумма производных по координатам.
и в левой части берется сумма производных по координатам.
Последнее уравнение может быть записано, используя операторную форму. Вводя оператор полной энергии частицы – оператор Гамильтона - сумму операторов кинетической и потенциальной энергии  (14) и оператор импульса
(14) и оператор импульса ![]() , в декартовых координатах он примет вид
, в декартовых координатах он примет вид  , в одномерном случаи
, в одномерном случаи  . Действие оператора потенциальной энергии сводится к его домножению на волновую функцию поэтому выражение (13) примет вид:
. Действие оператора потенциальной энергии сводится к его домножению на волновую функцию поэтому выражение (13) примет вид:  (14) – временное уравнение Шредингера.
(14) – временное уравнение Шредингера.
В случаи, когда потенциальная энергия частицы не зависит от времени волновую функцию можно представить как произведение чисто временной и чисто координатной частей ![]() , тогда переменные в (14) разделяются и задача сводится к нахождению собственных функций и собственных значений оператора Гамильтона
, тогда переменные в (14) разделяются и задача сводится к нахождению собственных функций и собственных значений оператора Гамильтона ![]() (15) –стационарное уравнение Шредингера. Решая уравнение Шредингера находят волновую функцию и плотность вероятности положения частицы в пространстве.
(15) –стационарное уравнение Шредингера. Решая уравнение Шредингера находят волновую функцию и плотность вероятности положения частицы в пространстве.
Тепловое излучение и люминесценция
Энергия, расходуемая светящимся телом на излучение, может пополняться из различных источников. Окисляющийся на воздухе фосфор светится за счет энергии, выделяемой при химическом превращении. Такой вид свечения называется хемилюминесценцией. Свечение, возникающее при различных видах самостоятельного газового разряда, носит название электролюминесценции. Свечение твердых тел, вызванное бомбардировкой их электронами, называют катодо-л юм и не сцен цией. Испускание телом излучения некоторой характерной для него длины волны λ1 можно вызвать, облучая это тело (или облучив предварительно) излучением длины волны λ2, меньшей чем λ1. Такие процессы объединяются под названием фотолюминесценции.
Самым распространенным является свечение тел, обусловленное их нагреванием. Этот вид свечения называется тепловым (или температурным) излучением. Тепловое излучение имеет место при любой температуре, однако при невысоких температурах излучаются практически лишь длинные (инфракрасные) электромагнитные волны.
Окружим излучающее тело непроницаемой оболочкой с идеально отражающей поверхностью (рис. 154). Воздух из оболочки удалим. Отраженное оболочкой излучение, упав на тело, поглотится им (частично или полностью). Следовательно, будет происходить непрерывный обмен энергией между телом и заполняющим оболочку излучением. Если распределение энергии между телом и излучением остается неизменным для каждой длины волны, состояние системы тело — излучение будет равновесным. Опыт показывает, что единственным видом излучения, которое может находиться в равновесии с излучающими телами, является тепловое излучение. Все остальные виды излучения оказываются неравновесными.

Способность теплового излучения находиться в равновесии с излучающими телами обусловлена тем, что его интенсивность возрастает при повышении температуры. Допустим, что равновесие между телом и излучением (см. рис. 1) нарушено и тело излучает энергии больше, чем поглощает. Тогда внутренняя энергия тела будет убывать, что приведет к понижению температуры. Это в свою очередь обусловит уменьшение количества излучаемой телом энергии. Температура тела будет понижаться до тех пор, пока количество излучаемой телом энергии не станет равным количеству поглощаемой энергии. Если равновесие нарушится в другую сторону, т. е. количество излучаемой энергии окажется меньше, чем поглощаемой, температура тела будет возрастать до тех пор, пока снова не установится равновесие. Таким образом, нарушение равновесия в системе тело — излучение вызывает возникновение процессов, восстанавливающих равновесие.
Иначе обстоит дело в случае любого из видов люминесценции. Покажем это на примере хемилюминесценции. Пока протекает обусловливающая излучение химическая реакция, излучающее тело все больше и больше удаляется от первоначального состояния. Поглощение телом излучения не изменит направления реакции, а наоборот приведет к более быстрому (вследствие нагревания) протеканию реакции в первоначальном направлении. Равновесие установится лишь тогда, когда будет израсходован весь запас реагирующих веществ и свечение, обусловленное химическими процессами, заменится тепловым излучением.
Итак, из всех видов излучения равновесным может быть только тепловое излучение. К равновесным состояниям и процессам применимы законы термодинамики. Следовательно, и тепловое излучение должно подчиняться некоторым общим закономерностям, вытекающим из принципов термодинамики. К рассмотрению этих закономерностей мы и перейдем.
Закон Кирхгофа
Для характеристики теплового излучения, мы будем пользоваться величиной потока энергии, измеряемой в ваттах.
Поток энергии, испускаемый единицей поверхности излучающего тела по всем направлениям (в пределах телесного угла 2π), называют энергетической светимостью тела Rэ.
Излучение состоит из волн различных частот ω (или длин λ). Обозначим поток энергии, испускаемый единицей поверхности тела в интервале частот dω, через dRω (чтобы не усложнять обозначений, мы опустили индекс «э» при R). При малой величине интервала dω поток dRω будет пропорционален dω
![]() (1)
(1)
Величина rω называется испускательной способностью тела. Опыт показывает, что испускательная способность сильно зависит от температуры тела. Таким образом, rω есть функция частоты и температуры. Соответственно и энергетическая светимость является функцией температуры.
Зная испускательную способность, можно вычислить энергетическую светимость:
![]() (2)
(2)
(чтобы подчеркнуть, что энергетическая светимость и испускательная способность зависят от температуры, мы их снабдили индексом «T»).
Излучение можно характеризовать вместо частоты со длиной волны λ. Участку спектра dω будет соответствовать интервал длин волн dλ. Определяющие один и тот же участок величины dω и dλ связаны простым соотношением, вытекающим из формулы: λ = c/v = 2πс/ω. Дифференцирование дает:
![]() (3)
(3)
Знак минус в этом выражении не имеет существенного значения, он лишь указывает на то, что с возрастанием одной из величин, ω или λ, другая величина убывает. Поэтому знак минус в дальнейшем мы не будем писать.
Доля энергетической светимости, приходящаяся на интервал dλ, может быть по аналогии с (1) представлена в виде:
![]() (4)
(4)
Если интервалы d и d, входящие в выражения (1) и (4), связаны соотношением (3), т. е. относятся к одному и тому же участку спектра, то величины dRω и dRλ, должны совпадать:
![]() .
.
Заменив в последнем равенстве d согласно (3), получим:
![]() ,
,
откуда
![]()
С помощью (5) можно перейти от rλ к rω и наоборот.
Пусть на элементарную площадку поверхности тела падает поток лучистой энергии dΦω, обусловленный электромагнитными волнами, частота которых заключена в интервале dω. Часть этого потока dΦ′ω будет поглощена телом. Безразмерная величина
![]() (6)
(6)
называется поглощательной способностью тела. Поглощательная способность зависит от температуры тела. Следовательно, аωТ есть функция частоты и температуры.

По определению аωТ не может быть больше единицы. Для тела, полностью поглощающего упавшее на него излучение всех частот, аωТ = 1. Такое тело называют абсолютно черным. Тело, для которого аωТ = аТ = const < 1, называется серым.
Между испускательной и поглощательной способностью любого тела имеется определенная связь. В этом можно убедиться, рассмотрев следующий эксперимент. Пусть внутри замкнутой оболочки, поддерживаемой при постоянной температуре Т, помещены несколько тел (рис. 2). Полость внутри оболочки эвакуирована, так что тела могут обмениваться энергией между собой и с оболочкой лишь путем испускания и поглощения электромагнитных волн. Опыт показывает, что такая система через некоторое время придет в состояние теплового равновесия — все тела примут одну и ту же температуру, равную температуре оболочки T. В таком состоянии тело, обладающее большей испускательной способностью rωТ, теряет в единицу времени с единицы поверхности больше энергии, чем тело, обладающее меньшей rωТ. Поскольку температура (а следовательно и энергия) тел не меняется, то тело; испускающее больше энергии, должно и больше поглощать, т. е. обладать большей аωТ. Таким образом, чем больше испускательная способность тела rωТ, тем больше и его поглощательная Способность аωТ. Отсюда вытекает соотношение:
![]() ,
,
где индексы 1, 2, 3 и т. д. относятся к разным телам.
Кирхгоф сформулировал следующий закон: отношение испускательной и поглощательной способностей не зависит от природы тела, оно является для всех тел одной и той же, (универсальной) функцией частоты (длины волны) и температуры:
![]() (7)
(7)
Сами величины rωТ и аωТ, взятые отдельно, могут меняться чрезвычайно сильно при переходе от одного тела к другому. Отношение же их оказывается одинаковым для всех тел. Это означает, что тело, сильнее поглощающее какие-либо лучи, будет эти лучи сильнее и испускать (не следует смешивать испускание лучей с их отражением).
Для абсолютно черного тела по определению аωТ = 1. Следовательно, нз формулы (7) вытекает, что rωТ для такого тела равна f(ω,Т). Таким образом, универсальная функция Кирхгофа f(ω,Т) есть не что иное, как испускательная способность абсолютно черного тела.
При теоретических исследованиях для характеристики спектрального состава равновесного теплового излучения удобнее пользоваться функцией частоты — f(ω,Т). В экспериментальных работах удобнее пользоваться функцией длины волны — φ(λ,Т). Обе функции связаны друг с другом формулой
![]() , (8)
, (8)
аналогичной формуле (5). Согласно (8) для того, чтобы по известной функции f(ω,Т) найти φ(λ,Т), нужно заменить в f(ω,Т) частоту ω через 2πс/λ и получившееся выражение умножить на 2πс/λ2:
![]() (9)
(9)
Для нахождения f(ω,Т) по известной φ(λ,Т) нужно воспользоваться соотношением:
![]() (10)
(10)
Абсолютно черных тел в природе не существует. Сажа или платиновая чернь имеют поглощательную способность аωТ, близкую к единице, лишь в ограниченном интервале частот; в далекой инфракрасной области их поглощательная способность заметно меньше единицы. Однако можно создать устройство, сколь угодно близкое по своим свойствам к абсолютно черному телу.

Такое устройство представляет собой почти замкнутую полость, снабженную малым отверстием (рис. 3). Излучение, проникшее внутрь через отверстие, прежде чем выйти обратно из отверстия, претерпевает многократные отражения. При каждом отражении часть энергии поглощается, в результате чего практически все излучение любой частоты поглощается такой полостью. Согласно закону Кирхгофа испускательная способность такого устройства очень близка к f(ω,Т), причем Т означает температуру стенок полости. Таким образом, если стенки полости под-церживать при некоторой температуре Т, то из отверстия выходит излучение, весьма близкое по спектральному составу к излучению абсолютно черного тела при той же температуре. Разлагая это излучение в спектр с помощью дифракционной решетки и измеряя болометром интенсивность различных участков спектра, можно найти экспериментально вид функции f(ω, Т) или φ(λ,Т). Результаты таких опытов приведены на рис. 4. Разные кривые относятся к различным значениям температуры Т абсолютно черного тела. Площадь, охватываемая кривой, дает энергетическую светимость абсолютно черного тела при соответствующей температуре.
К ривые на рис. 4 очень похожи на кривые распределения молекул газа по скоростям. Правда, есть и существенное отличие. В то время как кривые распределения по скоростям для разных температур пересекают друг друга (охватываемые ими площади одинаковы), кривые спектрального распределения излучения абсолютно черного тела для более низких температур целиком лежат внутри кривых, соответствующих более высоким температурам (как мы увидим в следующем параграфе, площадь, охватываемая этими кривыми, пропорциональна четвертой степени температуры).
ривые на рис. 4 очень похожи на кривые распределения молекул газа по скоростям. Правда, есть и существенное отличие. В то время как кривые распределения по скоростям для разных температур пересекают друг друга (охватываемые ими площади одинаковы), кривые спектрального распределения излучения абсолютно черного тела для более низких температур целиком лежат внутри кривых, соответствующих более высоким температурам (как мы увидим в следующем параграфе, площадь, охватываемая этими кривыми, пропорциональна четвертой степени температуры).
Из рис. 4 следует, что энергетическая светимость абсолютно черного тела сильно возрастает с температурой. Максимум испускательной способности с увеличением температуры сдвигается в сторону более коротких волн.
Закон Стефана — Больцмана и закон Вина
Теоретическое объяснение излучения абсолютно черного тела имело огромное значение в истории физики — оно привело к понятию квантов энергии.
Долгое время многочисленные попытки получить теоретически вид функции f(ω, Т) не давали общего решения задачи. Стефан (1879), анализируя экспериментальные данные, пришел к выводу, что энергетическая светимость Rэ любого тела пропорциональна четвертой степени абсолютной температуры. Однако последующие более точные измерения показали ошибочность его выводов. Больцман (1884), исходя из термодинамических соображений, получил теоретически для энергетической светимости абсолютно черного тела следующее значение:
![]() (11)
(11)
где σ —постоянная величина, Т — абсолютная температура. Таким образом, заключение, к которому Стефан пришел для нечерных тел (с абсолютно черными телами он не экспериментировал), оказалось справедливым лишь для абсолютно черных тел.
Соотношение (11) между энергетической светимостью абсолютно черного тела и его абсолютной температурой получило название закона Стефана — Больцмана. Константу σ называют постоянной Стефана — Больцмана. Ее экспериментальное значение равно:
![]() (12)
(12)
Вин (1893), воспользовавшись, кроме термодинамики, электромагнитной теорией, показал, что функция спектрального распределения должна иметь вид:
![]() (13)
(13)
где F — неизвестная функция отношения частоты к температуре.
Согласно формуле (9) для функции φ(λ,Т) получается выражение:
![]() (14)
(14)
где ψ(λТ) — неизвестная функция произведения КТ.
Соотношение (4) позволяет установить зависимость между длиной волны λm, на которую приходится максимум функции φ(λ,Т), и температурой. Продифференцируем (14) по λ:
![]() (15)
(15)
Выражение в квадратных скобках представляет собой некоторую функцию ψ(λT). При длине волны λт, соответствующей максимуму функции φ(λ,T), выражение (15) должно обращаться в нуль:
![]() .
.
Поскольку, как следует из опыта, λm≠∞, должно выполняться условие: Ψ(λтТ) = 0. Решение последнего уравнения относительно неизвестного λтТ дает для этого неизвестного некоторое число, которое мы обозначим буквой b. Таким образом, получается соотношение:
![]() (16)
(16)
которое носит название закона смещения Вина. Экспериментальное значение константы b равно:
b=2,90∙107Е∙град=2,90∙103мк∙град (17)
Формула Рэлея — Джииса
Рэлей и Джинс сделали попытку определить функцию f(ω,T), исходя из теоремы классической статистики о равнораспределении энергии по степеням свободы. Они предположили, что на каждое электромагнитное колебание приходится в среднем энергия, равная двум половникам kT— одна половинка на электрическую, вторая—на магнитную энергию волны (напомним, что по классическим представлениям на каждую колебательную степень свободы приходится в среднем энергия, равная двум половинкам kT).
Рассмотрим излучение, находящееся в равновесии с веществом. Для этого представим себе эвакуированную полость, стенки которой поддерживаются при постоянной температуре Т. В равновесном состоянии энергия излучения будет распределена в объеме полости с определенной плотностью и = и(Т). Спектральное распределение этой энергии можно охарактеризовать функцией и (ω,Т), определяемой условием: duω = и(ω,Т)dω, где duω — доля плотности энергии, приходящаяся на интервал частот dω. Полная плотность энергии может быть представлена в виде:
![]() (18)
(18)
Р авновесная плотность энергии излучения и(Т) зависит только от температуры и не зависит ют свойств стенок полости. Это следует из термодинамических соображений. Рассмотрим две полости, стенки которых изготовлены из разных материалов и имеют первоначально одинаковую температуру. Допустим, что равновесная плотность энергии в обеих полостях различна и, скажем, u1(Т)> u2(Т). Соединим полости с помощью небольшого отверстия (рис. 5) и тем самым позволим стенкам полостей вступить в теплообмен через излучение. Так как по предположению u1 > u2, поток энергии из первой полости во вторую должен быть больше, чем поток, текущий во встречном направлении.
авновесная плотность энергии излучения и(Т) зависит только от температуры и не зависит ют свойств стенок полости. Это следует из термодинамических соображений. Рассмотрим две полости, стенки которых изготовлены из разных материалов и имеют первоначально одинаковую температуру. Допустим, что равновесная плотность энергии в обеих полостях различна и, скажем, u1(Т)> u2(Т). Соединим полости с помощью небольшого отверстия (рис. 5) и тем самым позволим стенкам полостей вступить в теплообмен через излучение. Так как по предположению u1 > u2, поток энергии из первой полости во вторую должен быть больше, чем поток, текущий во встречном направлении.
В результате стенки второй полости станут поглощать больше энергии, чем излучать, и температура их начнет повышаться. Стенки же первой полости станут поглощать меньше энергии, чем излучать, так что они будут охлаждаться. Однако два тела с первоначально одинаковой температурой не могут вследствие теплообмена друг с другом приобрести различные температуры — это запрещено вторым началом термодинамики. Поэтому наше допущение о неодинаковости u1 и и2 должно быть признано неправомерным. Вывод о равенстве u1(Т) и и2(Т) распространяется на каждую спектральную составляющую u(ω,Т).
Независимость равновесного излучения от природы стенОк полости можно пояснить следующими соображениями. Абсолютно черные стенки поглощали бы всю упавшую на них энергию Фэ и испускали бы такой же по величине поток энергии Фэ. Стенки с поглощательной способностью а поглотят долю аФэ упавшего на них потока Фэ и отразят поток, равный (1—а)Фэ. Кроме того, они излучат поток аФэ (равный поглощенному потоку). В итоге стенки полости вернут излучению поток энергии Фэ = (1—а)Фэ + аФэ, такой же, какой возвращали бы излучению абсолютно черные стенки.
Равновесная плотность энергии излучения и связана с энергетической светимостью абсолютно черного тела R*э простым соотношением, которое мы сейчас выведем.
В случае плоской волны (т. е. когда энергия переносится волной в одном, определяемом вектором k направлении) плотность потока энергии I может быть представлена как произведение плотности энергии и на скорость волны с: I = си. Через каждую точку внутри полости проходит бесчисленное количество волн, направления которых равномерно распределены в пределах телесного угла 4л. Поток энергии I = си также распределен равномерно в пределах этого телесного угла. Следовательно, в пределах телесного угла dQ будет заключен поток энергии, плотность которого равна:
![]() .
.
Возьмем на поверхности полости элементарную площадку ΔS . Эта площадка посылает в пределах телесного угла ![]() в направлении, образующем с нормалью угол
в направлении, образующем с нормалью угол ![]() , поток энергии:
, поток энергии:

По всем направлениям, заключенным в пределах телесного угла 2π, площадка ΔS посылает поток энергии:
 .
.
Вместе с тем поток Фэ должен быть таким, какой излучали бы абсолютно черные стенки. Последний же поток по определению равен R*эΔS. Следовательно,
![]() (19)
(19)
Соотношение (19) должно выполняться для каждой спектральной составляющей излучения. Отсюда вытекает, что
![]() (20)
(20)
Рэлей и Джине исходили из того, что равновесное излучение в полости представляет собой систему стоячих волн. Такое представление оправдывается тем, что замена поглощающих стенок полости идеально отражающими стенками не изменяет плотности энергии равновесного излучения. Возникновение стоячих волн возможно лишь при выполнении определенных условий. Пусть полость имеет форму прямоугольного параллелепипеда со сторонами a, b и с. Совместим с ребрами параллелепипеда координатные оси х, у, z . Условие возникновения стоячей волны вдоль оси х имеет вид:
 (21)
(21)
г
![]() де kx — модуль волнового вектора, совпадающий в дан
де kx — модуль волнового вектора, совпадающий в дан
ном случае с проекцией волнового вектора на ось х. За-
метим, что данная стоячая волна образована наложением двух бегущих волн, для которых значения kx отличаются знаком. Для стоячих волн, устанавливающихся вдоль оси у или оси z, должны выполняться условия, аналогичные (21). Если волновой вектор к не совпадает с направлением ни одной из координатных осей, условия, аналогичные (21), должны выполняться одновременно для всех трех проекций вектора к:
 (22)
(22)
В этом случае стоячая волна с данным значением "к (т. е. k) представляет собой суперпозицию восьми бегущих волн одинаковой длины, но различных направлений, для которых проекции волнового вектора равны:

Одинаковые по модулю векторы k, соответствующие восьми приведенным выше комбинациям чисел kx, ky и kz, располагаются в разных октантах. Векторы (1) и (8) имеют противоположные направления; то же самое относится к векторам (2) и (7), (3) и (6), а также (4) и (5). Векторы (1) и (2) симметричны относительно координатной плоскости yz, векторы (1) и (3) — относительно плоскости xz и т. д.
Каждая тройка чисел т1 т2 и т3 определяет возможное значение волнового числа:
![]()
По определению k = 2π/λ = ω/с. Следовательно, каждой тройке чисел m1 m2 и m3 соответствует возможное значение частоты стоячей волны ω (или длины волны λ). Определим количество возможных частот dNω, попадающих в интервал dω. Для этого возьмем прямоугольную систему координат с осями kx, ky, kz (рис. 6). Такую систему называют координатной системой в k-пространстве. Каждой стоячей волне с данным значением k будет соответствовать в k-пространстве точка с координатами, определяемыми условиями (22) (точки размещаются в октанте с положительными kx, ky, kz). Плотность этих точек в к-пространстве равна ![]() (объем прямоугольного параллелепипеда с вершинами, помещающимися в соседних точках, равен
(объем прямоугольного параллелепипеда с вершинами, помещающимися в соседних точках, равен ![]() ; в пределы такого параллелепипеда попадает одна точка).
; в пределы такого параллелепипеда попадает одна точка).
К оличество волн dNk, для которых мо
оличество волн dNk, для которых мо
дуль волнового вектора лежит в пределах от k до k + dk, равно количеству точек в ⅛ объема шарового слоя толщины dk (см рис. 6):
![]() (23)
(23)
(V — объем полости). Произведя в (23) замену: k = ω/с, dk = dω/c, найдем число волн dNω, частоты которых попадают в интервал от ω до ω + dω:
![]() (24)
(24)
Вдоль заданного направления могут распространяться две электромагнитные волны одинаковой частоты, отличающиеся направлением поляризации (поляризованные во взаимно перпендикулярных направлениях). Чтобы учесть это обстоятельство, нужно выражение (52.7) умножить на два. Число колебаний (52.7) пропорционально объему полости V. Поэтому можно говорить о числе колебаний dnω, приходящихся на единицу объема полости. Учтя оба направления поляризации, получим:
![]() (25)
(25)
Умножив (25) на среднюю энергию одного колебания, получим приходящуюся на интервал частот dω энергию излучения, заключенную в единице объема, т. е. u(ω,T)dω. Исходя из закона равнораспределения энергии по степеням свободы, Рэлей и Джине приписали каждому колебанию энергию, равную kT (см. выше). В этом случае
![]()
или
![]() (26)
(26)
Перейдя от и(ω,Т) к f(ω,Т) по формуле (26), получим:
![]()
Выражение (26), равно как и (25), называется формулой Рэлея — Джинеса. Заметим, что функция (26) удовлетворяет полученному Вином условию (25).
Формула Рэлея — Джинса удовлетворительно согласуется с экспериментальными данными лишь при больших длинах волн, и резко расходится с опытом для малых длин волн (см. рис. 7), на котором сплошной линией изображена экспериментальная кривая, пунктиром — кривая, построенная по формуле Рэлея — Джинса).

Интегрирование выражения (23) или (24) по со в пределах от 0 до ∞ дает для равновесной плотности энергии и(Т) и для энергетической светимости R*э бесконечно большие значения.- Этот результат, получивший название ультрафиолетовой катастрофы, также находится в противоречии с опытом. Равновесие между излучением и излучающим телом устанавливается при конечных значениях и(Т).
Формула Планка
Вывод формулы Рэлея — Джинса с классической точки зрения является безупречным. Поэтому расхождение этой формулы с опытом указывало на существование каких-то закономерностей, несовместимых с представлениями классической статистической физики и электродинамики.
В 1900 г. Планку удалось найти вид функции f(ω,T), в точности соответствующий опытным данным. Для этого ему пришлось сделать предположение, совершенно чуждое классическим представлениям, а именно допустить, что электромагнитное излучение испускается в виде отдельных порций энергии ε (квантов), величина которых пропорциональна частоте излучения:
![]() (27)
(27)
Коэффициент пропорциональности ħ получил впоследствии название постоянной Планка. Определенное из опыта значение равно:
![]() (28)
(28)
В механике есть имеющая размерность «энергиях X время» величина, которая называется действием. Поэтому постоянную Планка иногда называют квантом действия. Заметим, что размерность ħ совпадает с размерностью момента импульса.
Если излучение испускается порциями ħω, то его энергия εn должна быть кратной этой величине:
![]() (29)
(29)
Согласно закону Больцмана вероятность Рп того, что энергия излучения имеет величину еп, определяется выражением:
![]() (30)
(30)
Нормировочный множитель А можно найти, исходя из условия, что сумма всех Рп должна быть равна единице. Действительно, сумма Рп представляет собой вероятность того, что энергия имеет одно из возможных для нее значений. Такое событие является достоверным и, следовательно, имеет вероятность, равную единице. Итак,
 ,
,
откуда
 .
.
Подставив найденное значение А в формулу (53.4), получим:
 .
.
Предположим, что мы имеем возможность измерить значение энергии данной спектральной составляющей излучения в любой момент времени. Произведем через равные промежутки времени Δt очень большое число таких измерений N. Разделив сумму полученных значений на число измерений N, мы найдем среднее по врег мени значение энергии ![]() . При очень большом N количество измерений Nn, которые дадут результат εп, будет равно NPn. Поэтому
. При очень большом N количество измерений Nn, которые дадут результат εп, будет равно NPn. Поэтому
 (31)
(31)
Таким образом, среднее значение энергии излучения частоты со определяется следующим выражением:
 (32)
(32)
Чтобы произвести вычисления, обозначим bw/kT = х и допустим, что величина х может изменяться, принимая непрерывный ряд значений. Тогда выражение для ё можно записать в виде:
 (33)
(33)
Выражение, стоящее под знаком логарифма, представляет собой сумму членов бесконечной геометрической прогрессии с первым членом, равным единице, и знаменателем прогрессии, равным е-x. Так как знаменатель меньше единицы, прогрессия будет убывающей, и по известной из алгебры формуле
 .
.
Подставив это значение суммы в (53.7) и выполнив дифференцирование, получим:
 .
.
Наконец, заменив х его значением ħω/kT, получим окончательное выражение для средней энергии излучения частоты ω:
![]() (34)
(34)
Заметим, что при ħ, стремящемся к нулю, формула (26) переходит в классическое выражение ![]() . В этом можно убедиться, положив
. В этом можно убедиться, положив ![]() , что выполняется тем точнее, чем меньше ħ. Таким образом, если бы энергия могла принимать непрерывный ряд значений, ее среднее значение было бы равно kT.
, что выполняется тем точнее, чем меньше ħ. Таким образом, если бы энергия могла принимать непрерывный ряд значений, ее среднее значение было бы равно kT.
Заменив в формуле Рэлея — Джинса kT выражением (34), получим формулу, найденную Планком:
 (35)
(35)
Эта формула, как уже отмечалось, точно согласуется с экспериментальными данными во всем интервале частот от 0 до ∞. Она удовлетворяет критерию Вина (26). При условии, что ħω/kT<1 (малые частоты или большие длины волн), ![]() можно положить равным приближенно 1 + ħω/kТ, в результате чего формула (53.9) переходит в формулу Рэлея — Джинса. Это следует также непосредственно из того, что при указанном условии выражение (35) приближенно равняется kT.
можно положить равным приближенно 1 + ħω/kТ, в результате чего формула (53.9) переходит в формулу Рэлея — Джинса. Это следует также непосредственно из того, что при указанном условии выражение (35) приближенно равняется kT.
Осуществив преобразование по формуле (35), получим:
 (36)
(36)
На рис. 8 сопоставлены графики функций (35) и (36), построенные для одной и той же температуры (5000° К). Масштабы по оси абсцисс логарифмические и выбраны так, что связанные соотношением λ = 2πс/ω значения λ и ω совмещены друг с другом. Из рисунка видно, что частота ωm, соответствующая максимуму f(ω,Т), не совпадает с 2πс/λm, где λm — длина волны, отвечающая максимуму φ(λ,Т).

Для энергетической светимости абсолютно черного тела получается выражение:
 .
.
Введем вместо ω безразмерную переменную х = ħω/kT. Подстановка ω = (kT/ħ)x, dω = (kT/ħ)dx преобразует формулу для R*э к виду:
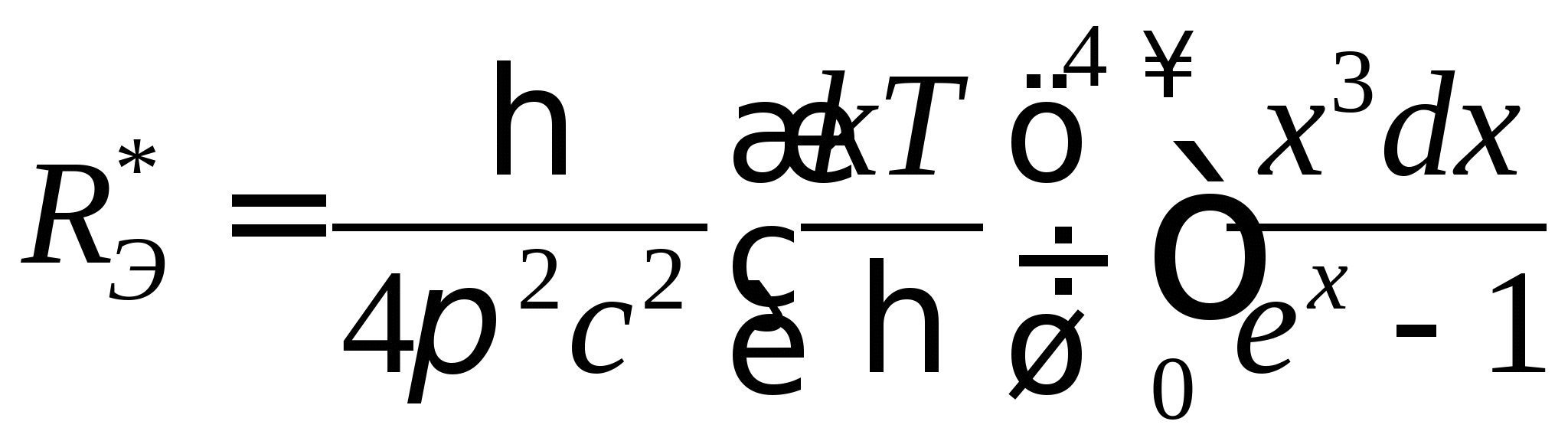 .
.
Определенный интеграл в последнем выражении может быть вычислен. Он равен π4/15 = 6,5. Подставив его значение, мы придем к закону Стефана — Больцмана:
 (37)
(37)
Подстановка в эту формулу численных значений k, с и ħ дает для постоянной Стефана — Больцмана величину 5,6696∙10-8 вт/м2∙град4, очень хорошо согласующуюся с экспериментальным значением (37).
В заключение найдем значение постоянной в законе смещения Вина (16). Для этого продифференцируем функцию (36) по λ и приравняем получившееся выражение нулю:
 .
.
Удовлетворяющие этому уравнению значения λ = 0 и λ = ∞ соответствуют минимумам функции φ(λ,T). Значение λm, при котором функция достигает максимума, обращает в нуль выражение, стоящее в числителе в квадратных скобках. Обозначив 2πħc/kTλm = x, получим уравнение:
![]() .
.
Решение этого трансцендентного уравнения дает х = 4,965. Следовательно, 2πħc/kTλm = 4,965, откуда
 .
.
Подстановка численных значений ħ, с и k дает для b величину 2,90∙103 мк∙град, совпадающую с экспериментальным значением (17).
Таким образом, формула Планка дает исчерпывающее описание равновесного теплового излучения.
Применение уравнения Шредингера
Частица в потенциальной яме с бесконечно высокими стенками.
П усть в одномерном пространстве создано силовое поле, потенциальная энергия которого бесконечна везде, кроме области 0 < x < l и не зависит от времени. Пусть электрон попадает в это поле, тогда его движение описывается волновой функцией, которая является решением уравнения Шредингера. Так как потенциальная энергия не зависит от времени, решается стационарное уравнение Шредингера
усть в одномерном пространстве создано силовое поле, потенциальная энергия которого бесконечна везде, кроме области 0 < x < l и не зависит от времени. Пусть электрон попадает в это поле, тогда его движение описывается волновой функцией, которая является решением уравнения Шредингера. Так как потенциальная энергия не зависит от времени, решается стационарное уравнение Шредингера ![]() , где Е – разрешенные значения энергии в потенциальной яме. Расписывая оператор Гамильтона, получим
, где Е – разрешенные значения энергии в потенциальной яме. Расписывая оператор Гамильтона, получим  (1).
(1).
В областях 1 и 3 (рис.1) потенциальная энергия бесконечна, для ее преодоления частица должна иметь бесконечную скорость, а так как волновая функция описывает только реальные частицы, она не может иметь сингулярности, поэтому, в этих областях ![]() .
.
В области 2 U=0, поэтому  (2). Решение уравнения ищем в виде
(2). Решение уравнения ищем в виде ![]() , где
, где ![]() (3). Решение можно записать в виде
(3). Решение можно записать в виде ![]() (4), где константы А и определим из граничных условий. Так как волновая функция должна быть непрерывна и однозначно определяема во всем пространстве,
(4), где константы А и определим из граничных условий. Так как волновая функция должна быть непрерывна и однозначно определяема во всем пространстве, ![]() и
и ![]() . Применим условия
. Применим условия ![]() .
. ![]() , тогда энергия электрона на n-ном уровне
, тогда энергия электрона на n-ном уровне  (5), таким образом, электрон в потенциальной яме может занимать только дискретный набор уровней. Тогда волновая функция имеет вид
(5), таким образом, электрон в потенциальной яме может занимать только дискретный набор уровней. Тогда волновая функция имеет вид ![]() . Константу А найдем из условий нормировки
. Константу А найдем из условий нормировки  или в одномерном случаи
или в одномерном случаи  (6).
(6).
 Плотность вероятности электрона в потенциальной яме с бесконечно высокими стенками можно представить графически (рис.2)
Плотность вероятности электрона в потенциальной яме с бесконечно высокими стенками можно представить графически (рис.2)
Прохождение через барьер.
Пусть частица, движущаяся слева направо, падает на потенциальный барьер

высоты Uo и ширины l (рис. 3). По классическим представлениям поведение частицы имеет следующий характер. Если энергия частицы больше высоты барьера (E>U0), частица беспрепятственно проходит «над» барьером (на участке 0![]() x
x![]() l лишь уменьшает скорость частицы, но затем при х > I снова принимает первоначальное значение). Если же Е меньше Uo (как изображено на рисунке), то частица отражается от барьера и летит в обратную сторону; сквозь барьер частица проникнуть не может.
l лишь уменьшает скорость частицы, но затем при х > I снова принимает первоначальное значение). Если же Е меньше Uo (как изображено на рисунке), то частица отражается от барьера и летит в обратную сторону; сквозь барьер частица проникнуть не может.
Совершенно иначе выглядит поведение частицы согласно квантовой механике. Во-первых, даже при Е>U0 имеется отличная от нуля вероятность того, что частица отразится от барьера и полетит в обратную сторону. Во-вторых, при Е < Uo имеется отличная от нуля вероятность того, что частица проникнет «сквозь» барьер и окажется в области, где х>l. Такое, совершенно невозможное с классической точки зрения, поведение микрочастицы вытекает непосредственно из уравнения Шредингера.
Рассмотрим случай Е<Uo. В этом случае уравнение Шредингера имеет вид: ![]() , для областей I и III и
, для областей I и III и ![]() для области
для области![]() , причем Е — U0<0. Легко убедиться (хотя бы подстановкой), что общее решение уравнения Шредингера для каждой из трех областей имеет вид:
, причем Е — U0<0. Легко убедиться (хотя бы подстановкой), что общее решение уравнения Шредингера для каждой из трех областей имеет вид:
 (7)
(7)
причем ![]() и
и![]() определяются из выражений:
определяются из выражений: ![]()
![]() (8)
(8)
Заметим, что решение вида eiax соответствует волне, распространяющейся в направлении оси х, а решение вида e-iax — волне, распространяющейся в противоположном направлении. Чтобы это понять, вспомним, что обычная (звуковая, электромагнитная и т. п.) плоская волна, распространяющаяся в направлении оси х, имеет вид cos(at—kx), а волна, распространяющаяся в направлении убывания х,— вид cos (![]() - kx) [см. т. I, формулы (78.2) и (78.5)]. В § 65 мы установили, что волновая функция свободной частицы, движущейся в направлении оси х, имеет вид (65.5). Если отбросить в этой формуле временной множитель, то для
- kx) [см. т. I, формулы (78.2) и (78.5)]. В § 65 мы установили, что волновая функция свободной частицы, движущейся в направлении оси х, имеет вид (65.5). Если отбросить в этой формуле временной множитель, то для ![]() получится значение
получится значение ![]() . Для частицы, движущейся в противоположном направлении, нужно, очевидно, взять e-i(p/h)x.
. Для частицы, движущейся в противоположном направлении, нужно, очевидно, взять e-i(p/h)x.
В области III имеется только волна, прошедшая через барьер и распространяющаяся слева направо. Поэтому коэффициент В3 следует положить равным нулю. Для нахождения остальных коэффициентов воспользуемся условиями, которым должна удовлетворять функция ![]() . Для того чтобы
. Для того чтобы ![]() была непрерывна во всей области изменений х от
была непрерывна во всей области изменений х от ![]() до
до ![]() , должны выполняться условия:
, должны выполняться условия: ![]() =
= ![]() и
и ![]() 2(l) =
2(l) =![]() (l). Для того, чтобы
(l). Для того, чтобы ![]() была гладкой, т. е. не имела изломов, должны выполняться условия:
была гладкой, т. е. не имела изломов, должны выполняться условия: ![]() =
= ![]() и
и ![]() ’2(l) =
’2(l) =![]() ’(l) .Из этихусловий вытекают соотношения:
’(l) .Из этихусловий вытекают соотношения:

(9)
Разделим все уравнения на А1 и введем обозначения:
![]()
а также ![]() (10), Тогда уравнения (9) примут вид:
(10), Тогда уравнения (9) примут вид:
 (11)
(11)
Отношение квадратов модулей амплитуд отраженной и падающей волны

определяет вероятность отражения частицы от потенциального барьера и может быть названо коэффициентом отражения.
Отношение квадратов модулей прошедшей и падающей волны 
определяет вероятность прохождения частицы через барьер и может быть названо коэффициентом прохождения (или коэффициентом прозрачности).
Нас будет интересовать только прохождение частиц через барьер, и мы ограничимся нахождением величины D. Правда, найдя D, легко найти R, поскольку эти коэффициенты связаны очевидным соотношением: R+D=1.
Умножим первое из уравнений (11) на i и сложим с третьим. В результате получим: 2i = (п + i) a2-(n- i) b2. (13)
Теперь умножим второе из уравнений (11) на i и вычтем его из четвертого. Получим: ![]() (14)
(14)
Решая совместно уравнения (68.13) и (68.14), найдем, что ![]() и
и ![]()
Наконец, подставив найденные нами значения а2 и b2 во второе дз уравнений (68.11), получим выражение для а3: ![]()
Величина ![]() обычно бывает много больше единицы. Поэтому в знаменателе выражения для а3 слагаемым, содержащим множитель
обычно бывает много больше единицы. Поэтому в знаменателе выражения для а3 слагаемым, содержащим множитель ![]() , можно пренебречь по сравнению со слагаемым, содержащим множитель
, можно пренебречь по сравнению со слагаемым, содержащим множитель ![]() (комплексные числа п+i и п-i имеют одинаковый модуль). Итак, можно положить
(комплексные числа п+i и п-i имеют одинаковый модуль). Итак, можно положить ![]() Согласно (12) квадрат модуля этой величины дает вероятность прохождения частицы через потенциальный барьер. Учтя, что
Согласно (12) квадрат модуля этой величины дает вероятность прохождения частицы через потенциальный барьер. Учтя, что ![]() , получим:
, получим: ![]() где
где ![]()
Выражение 16п2/(п2 + 1)2 имеет величину порядка единицы1). Поэтому можно считать, что ![]() (15).
(15).
Как следует из полученного нами выражения, вероятность прохождения частицы через потенциальный барьер сильно зависит от ширины барьера l и от его превышения над Е, т.е. от Uo — Е. Если при какой-то ширине барьера коэффициент прохождения D равен, допустим, 0,01, то при увеличении ширины в два раза D станет равным 0,012 = 0,0001, т.е. уменьшается в 100 раз. Тот же эффект в этом случае вызвало бы возрастание в четыре раза величины Uo — Е. Коэффициент прохождения резко уменьшается при увеличении массы частицы m. В случае потенциального барьера произвольной формы (см., например, (рис. 2) формула (15) должна быть заменена более общей формулой: ![]() (16) где U= U(x),
(16) где U= U(x),
При преодолении потенциального барьера частица как бы проходит через «туннель» в этом барьере (см. заштрихованную область на рис. 197,6), в связи с чем рассмотренное нами явление часто называют туннельным эффектом.
С классической точки зрения туннельный эффект представляется абсурдным, так как частица, «находящаяся в туннеле», должна была бы обладать отрицательной кинетической энергией (в туннеле E<U). Однако туннель — явление специфически квантовое, не имеющее аналога в классической физике. В квантовой же механике деление полной энергии на кинетическую и потенциальную не имеет смысла, так как противоречит принципу неопределенности. Действительно, тот факт, что частица обладает определенной кинетической энергией T, был бы равнозначен тому, что частица имеет определенный импульс р. Аналогично тот факт, что частица имеет определенную потенциальную энергию U, означал бы, что частица находится в точно заданном месте пространства. Поскольку координата и импульс частицы не могут одновременно иметь определенных значений, не могут быть одновременно точно определены Т и U. Таким образом, хотя полная энергия частицы Е имеет вполне определенное значение, она не может быть представлена в виде суммы точно определенных энергий Т и U. Ясно, что при такой ситуации заключение об отрицательности Т в туннеле становится беспочвенным.
Мультиплетность спектров и спин электрона
Исследование спектров щелочных металлов при помощи приборов с большой разрешающей силой показало, что каждая линия этих спектров является двойной (дублет). Так, например, характерная для натрия желтая линия ЗР ![]() 3S состоит из двух линий с длинами волн 5890 А и 5896 А. То же относится и к другим линиям главной серии, а также к линиям других серий. В табл. 4 приведены некоторые дублеты натрия. В четвертом столбце указаны волновые числа линий
3S состоит из двух линий с длинами волн 5890 А и 5896 А. То же относится и к другим линиям главной серии, а также к линиям других серий. В табл. 4 приведены некоторые дублеты натрия. В четвертом столбце указаны волновые числа линий ![]() '. В последнем столбце дано расщепление компонент дублетов (разность волновых чисел).
'. В последнем столбце дано расщепление компонент дублетов (разность волновых чисел).
Расщепление спектральных линий, очевидно, обусловлено расщеплением энергетических уровней. Поскольку расщепление линий главной серии nP![]() 3S различно, а для линий резкой серии nS
3S различно, а для линий резкой серии nS![]() 3P одно и то же
3P одно и то же

(см. табл. 4), приходится предположить, что уровни S являются одиночными (синглетами), а уровни Р — двойными (дублетными) (см. рис. 204). Дальнейший анализ спектра натрия показал, что уровни D и F также являются двойными.
Структура спектра, отражающая расщепление линий на компоненты, называется тонкой структурой. Сложные линии, состоящие из нескольких компонент, получили название мультиплетов. Тонкая структура обнаруживается, кроме щелочных металлов, также и у других элементов, причем число компонент в муль-типлете может быть равно двум (дублеты), трем (триплеты), четырем (квартеты), пяти (квинтеты) и т. д. В частном случае спектральные линии даже с учетом тонкой структуры могут быть одиночными (синглеты).
Для объяснения мультиплетной структуры спектров и аномального эффекта Зеемана Гаудсмит и Юленбек выдвинули в 1925 г. гипотезу о том, что электрон обладает собственным моментом импульса Ms, не связанным с движением электрона в пространстве. Этот собственный момент был назван спином.
Первоначально предполагалось, что спин обусловлен вращением электрона вокруг своей оси. Согласно этим представлениям электрон уподоблялся волчку или веретену. Кстати, отсюда происходит и сам термин «спин»: по-английски spin означает «верчение». Однако очень скоро пришлось отказаться от подобных модельных представлений, в частности по следующей причине. Вращающийся заряженный шарик должен обладать магнитным моментом, причем отношение магнитного момента к механическому должно иметь значение : ![]() (1)
(1)
Действительно, было установлено, что электрон, наряду с собственным механическим моментом, обладает также и собственным магнитным моментом ![]() . Однако ряд опытных фактов, в частности аномальный эффект Зеемана, свидетельствует о том, что отношение собственных магнитного и механического моментов в два раза больше, чем для орбитальных моментов:
. Однако ряд опытных фактов, в частности аномальный эффект Зеемана, свидетельствует о том, что отношение собственных магнитного и механического моментов в два раза больше, чем для орбитальных моментов: ![]() (2)
(2)
Таким образом, представление об электроне как о вращающемся шарике оказалось несостоятельным. Спин следует считать внутренним свойством, присущим электрону подобно тому, как ему присущи заряд и масса.
Предположение о спине электрона было подтверждено большим количеством опытных фактов и должно, считаться совершенно доказанным. Оказалось также, что наличие спина и все его свойства автоматически вытекают из установленного Дираком уравнения квантовой механики, удовлетворяющего требованиям теории относительности. Таким образом, выяснилось, что спин электрона является свойством одновременно квантовым и релятивистским. В настоящее время также установлено, что спином обладают и другие элементарные частицы: протоны, нейтроны, фотоны и др.
Величина собственного момента импульса электрона определяется по общим законам квантовой механики так называемым спиновым квантовым числом s, равным 1/2:  . (3)
. (3)
Составляющая механического момента по заданному направлению может принимать квантованные значения, отличающиеся друг от друга на h:
![]() где
где ![]() (4)
(4)
Чтобы найти величину собственного магнитного момента электрона, умножим Ms на отношение (2) ![]() к Ms:
к Ms:
 . (5)
. (5)
Знак минус указывает на то, что механический Ms и магнитный ц,5 моменты электрона направлены в противоположные стороны.
Проекция собственного магнитного момента электрона на заданное направление может иметь следующие значения:

(минус получается, если ms = + ![]() , плюс — если ms = = -
, плюс — если ms = = -![]() ).
).
Таким образом, проекция собственного момента импульса электрона может принимать значения +![]() и -
и -![]() , а собственного магнитного момента — значения +
, а собственного магнитного момента — значения + ![]() и .
и .![]() В ряд формул, в частности в выражение для энергии, входят не сами моменты, а их проекции. Поэтому принято говорить, что собственный механический момент (спин) электрона равен половине (подразумевается в единицах h), а собственный магнитный момент равен одному магнетону Бора.
В ряд формул, в частности в выражение для энергии, входят не сами моменты, а их проекции. Поэтому принято говорить, что собственный механический момент (спин) электрона равен половине (подразумевается в единицах h), а собственный магнитный момент равен одному магнетону Бора.
Рассмотрим теперь на примере атома натрия, как существование спина электрона может объяснить мультиплетную структуру спектра. Поскольку момент атомного остатка равен нулю, момент атома натрия равен моменту оптического электрона. Момент же электрона будет слагаться из двух моментов: орбитального Mi, обусловленного движением электрона в атоме, и спинового Ms, не связанного с движением электрона в пространстве. Результирующая этих двух моментов дает полный момент импульса оптического электрона. Сложение орбитального и спинового моментов в полный момент осуществляется по тем же квантовым законам, по которым складываются орбитальные моменты разных электронов. Величина полного момента Mj определяется квантовым числом j:
![]() причем / может иметь значения:
причем / может иметь значения: ![]()
где l и s соответственно азимутальное и спиновое квантовые числа. При l=0 квантовое число j имеет только одно значение: j = s = ![]() . При l, отличном от нуля, возможны два значения: j = l +
. При l, отличном от нуля, возможны два значения: j = l +![]() и j = l-
и j = l-![]() , которые соответствуют двум возможным взаимным ориентациям моментов Ml и Ms — «параллельной» и «антипараллельной».
, которые соответствуют двум возможным взаимным ориентациям моментов Ml и Ms — «параллельной» и «антипараллельной».
Теперь учтем, что с механическими моментами связаны магнитные моменты, которые взаимодействуют друг с другом подобно тому, как взаимодействуют два тока или две магнитные стрелки. Энергия этого взаимодействия (называемого спин-орбитальным взаимодействием) зависит от взаимной ориентации орбитального и собственного моментов. Следовательно, состояния с различными j должны обладать различной энергией.
Таким образом, каждый терм ряда Р(l=1) расщепляется на два, соответствующих j = ![]() и j = 3/2; каждый терм ряда D (l = 2) расщепляется на термы с j = 3/2 и j =
и j = 3/2; каждый терм ряда D (l = 2) расщепляется на термы с j = 3/2 и j = ![]() , и т. д. Каждому терму ряда S(l= 0) соответствует только одно значение j=
, и т. д. Каждому терму ряда S(l= 0) соответствует только одно значение j= ![]() ; поэтому термы ряда S не расщепляются.
; поэтому термы ряда S не расщепляются.
Итак, каждый ряд термов, кроме S, распадается на два ряда—структура термов оказывается дублетной (двойной). Термы принято обозначать символами:
![]()
Рис.1


Рис.2
С учетом тонкой структуры схема термов выглядит более сложно, о чем дают представление схемы уровней натрия (рис. 1) и цезия (рис. 2). Поскольку мультиплетное расщепление термов D и F для натрия очень мало, подуровни D и F, отличающиеся значениями /, изображены на схеме слитно. Мультиплетное расщепление у цезия значительно больше, чем у натрия. На схеме цезия видно, что тонкая структура диффузной серии состоит не из двух линий, а из трех:
![]()


Возникновение этих линий пояснено дополнительно на рис. 206, Изображенный пунктиром переход ![]() запрещен правилом отбора:
запрещен правилом отбора:
![]() = 0, ±1. (7)
= 0, ±1. (7)
В нижней части схемы на рис. 3 показано, как выглядит сам мультиплет. Толщина линий на, схеме примерно соответствует" интенсивности спектральных линий. Совокупность получающихся линий выглядит как дублет, у которого одна из компонент в свою очередь оказывается двойной. Такая группа линий называется не триплетом, а сложным дублетом, так как она возникает в результате комбинации дублетных термов.
З
Рис. 3
аметим в заключение, что в связи с существованием спина электрона естественно возникает вопрос о том, что и у водородного атома уровни с l> 0 должны быть двойными, а спектральные линии — дублетными. Тонкая структура водородного спектра действительно была обнаружена экспериментально.Атом водорода
В атоме водорода или водородоподобном ионе потенциальная энергия электрона равна ![]() где Ze — заряд ядра, r — расстояние между ядром и электроном.
где Ze — заряд ядра, r — расстояние между ядром и электроном.
Уравнение Шредингера имеет в этом случае вид ![]() (1)
(1)
Поскольку поле является центрально-симметричным, удобно воспользоваться сферической системой координат: r, ![]() ,
, ![]() . Подставив в (1) выражение оператора Лапласа в сферических координатах, получим уравнение:
. Подставив в (1) выражение оператора Лапласа в сферических координатах, получим уравнение:
![]()
 (2)
(2)
Можно показать, что уравнение (2) имеет требуемые (т. е. однозначные, конечные и непрерывные) решения в следующих случаях: 1) при любых положительных значениях Е; 2) при дискретных отрицательных значениях энергии, равных ![]() (n=1, 2, 3,…). (3)
(n=1, 2, 3,…). (3)
Случай Е > 0 соответствует электрону, пролетающему вблизи ядра и удаляющемуся вновь на бесконечность. Случай Е < 0 соответствует электрону, находящемуся в пределах атома. Сравнение (3) с (5) показывает, что квантовая механика приводит к таким же значениям энергии водородного атома, какие получались и в теории Бора. Однако в квантовой механике эти значения полу- чаются логическим путем из основного предположения о том, что движение микрочастиц описывается уравнением Шредингера. Бору же для получения такого результата пришлось вводить специальные дополнительные предположения.
Собственные функции уравнения (2) содержат три целочисленных параметра. Один из них совпадает с номером уровня энергии п, два других принято обозначать буквами l и т. Эти числа называются квантовыми:
п — главное квантовое число,
l — азимутальное квантовое число,
т — магнитное квантовое число.
При данном п числа l и т могут принимать следую» щие значения:
L = 0, 1, 2, …, п -1,
т. е. всего п различных значений;
т=-l, -l+1, .... -1, 0, +1, .... l-1, l,
т. е. всего 2l + 1 различных значений.
Таким образом, каждому Еп (кроме Е1) соответствует несколько волновых функций ![]() отличающихся значениями квантовых чисел l и т. Это означает, что атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях.
отличающихся значениями квантовых чисел l и т. Это означает, что атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях.
Состояния с одинаковой энергией называются вырожденными, а число различных состояний с каким-либо значением энергии называется кратностью вырождения соответствующего энергетического уровня.
Кратность вырождения уровней водорода легко вычислить, исходя из возможных значений для l и т. Каждому из п значений квантового числа l соответствует 2l + 1 значений квантового числа т. Следовательно, число различных состоя-
н ий, соответствующих данному п, равно
ий, соответствующих данному п, равно
![]()
Таким образом, каждый уровень энергии водородного атома имеет вырождение кратности п2.
В табл. 3 приведены состояния, соответствующие первым трем энергетическим уровням.
Как мы выяснили, состояние электрона в водородном атоме зависит от трех квантовых чисел п, l и т, причем значение главного квантового числа п. определяет энергию состояния. Естественно предположить, что и два других квантовых числа определяют какие-то физические величины. Действительно, в квантовой механике доказывается, что азимутальное квантовое число l определяет величину момента импульса электрона в атоме, а магнитное квантовое число т — величину проекции этого момента на заданное направление в пространстве. Под заданным направлением (мы будем обозначать его буквой z) понимают направление, выделенное физически,путем создания, например магнитного или электрического поля.
Момент импульса М оказывается равным: ![]() (4)
(4)
Проекция момента импульса на заданное направление равна: Мz = mh. (5)
Соотношения (4) и (5) показывают, что момент импульса электрона в атоме и проекция этого момента являются, как и энергия, квантованными величинами. Постоянную h можно рассматривать как естественную единицу момента импульса.
Итак, состояния с различными значениями азимутального квантового числа l отличаются величиной момента импульса. В атомной физике применяются заимствованные из спектроскопии условные обозначения состояний электрона с различными значениями момента импульса. Электрон, находящийся в состоянии с l = 0, называют s-электроном (соответствующее состояние — s-состояни-ем), с l = 1 — р-электроном, с l = 2 — d-электроном, с l = 3 — f-электроном, затем идут g, h и т. д. уже по алфавиту. Значение главного квантового числа указывается перед условным обозначением квантового числа l. Таким образом, электрон в состоянии с п = 3 и l = 1 обозначается символом Зр и т. д.
Поскольку l всегда меньше п, возможны следующие состояния электрона:
1s
2s, 2p,
3s, 3p, 3d,
4s, 4p, 4d, 4f
и.т.д.
Схему уровней энергии можно изобразить пользуясь схемой, показанной на рис. 1. На этой схеме отражено (правда, частично) вырождение уровней; кроме того, она имеет еще ряд существенных преимуществ, которые вскоре станут очевидными.
Мы знаем, что испускание и поглощение света происходит при переходах электрона с одного уровня на другой. В квантовой механике доказывается, что возможны только такие переходы, при которых квантовое число / изменяется на единицу: ![]() . (6)
. (6)
Условие, выраженное соотношением (6), называется правилом отбора. Существование правила (6) обусловлено тем, что фотон обладает собственным моментом импульса (спином), равным примерно h (в дальнейшем мы уточним его значение). При испускании фотон уносит из атома этот момент, а при поглощении привносит, так что правило отбора (6) есть просто следствие закона сохранения момента импульса.
На рис. 198 показаны переходы, разрешенные правилом (6). Пользуясь условными обозначениями состояний электрона, переходы, приводящие к возникновению серии Лаймана, можно записать в виде:
np![]() 1s (n = 2, 3, ...); серии Бальмера соответствуют переходы:
1s (n = 2, 3, ...); серии Бальмера соответствуют переходы:
ns![]() 2p и nd
2p и nd![]() 2p (n = 3, 4, ...),
2p (n = 3, 4, ...),
и т. д.
Состояние 1s является основным состоянием атома водорода. В этом состоянии атом обладает минимальной энергией. Чтобы перевести атом из основного состояния в возбужденное (т. е. в состояние с большей энергией), ему необходимо сообщить энергию. Это может быть осуществлено за счет теплового соударения атомов (по этой причине нагретые тела светятся — атомы излучают, возвращаясь из возбужденного в основное состояние), или оптического возбуждения. Кроме обозначенных квантовых чисел имеет место спиновое квантовое число, характеризующее собственный механический момент электрона в атоме.
Нормальный эффект Зеемана
Если атомы, излучающие свет, поместить в магнитное поле, то линии, испускаемые этими атомами, расщепляются на несколько компонент. Это явление было обнаружено голландским физиком Зееманом в 1896 г. при наблюдении свечения паров натрия и носит его имя. Расщепление весьма невелико — при Н = 20 ![]() 30 тысяч эрстед оно достигает лишь несколько десятых долей ангстрема.
30 тысяч эрстед оно достигает лишь несколько десятых долей ангстрема.
Напрашивается предположение, что расщепление линий обусловлено расщеплением под действием магнитного поля энергетических уровней атома. Причину такого расщепления легко понять, если учесть, что вращающийся по орбите электрон обладает, наряду с механическим моментом М, также и магнитным моментом: ![]() (6)
(6)
Хотя представление об орбитах, как и вообще представление о траекториях микрочастиц, является неправильным, соотношение (6) остается, как показывает опыт, справедливым.
Известно, что магнитный момент обладает в магнитном поле энергией:
![]() (7) где
(7) где ![]() — проекция магнитного момента на направление поля.
— проекция магнитного момента на направление поля.
Вычислим величину орбитального магнитного момента электрона и величину проекции момента на направление поля. Подставим в соотношение (7) квантово-механическое выражение для механического момента:
![]()
Величина ![]() эрг/гаусс (8) называется магнетоном Бора.
эрг/гаусс (8) называется магнетоном Бора.
Проекция магнитного момента на направление поля равна: где ![]() т — магнитное квантовое число.
т — магнитное квантовое число.

![]()
Рис.1.
Согласно (7) атом получает в магнитном поле добавочную энергию: ![]()
Следовательно, энергетический уровень Enl расщепляется на 2l + 1 равноотстоящих друг от друга подуровней (магнитное поле снимает вырождение по т), в связи с чем расщепляются и спектральные линии.
На рис. 1 показано рacщепление уровней и спектральных линий для перехода между состояниями сl = 1 и l = 0 (для Р ![]() S-перехода). В отсутствие поля наблюдается одна линия, частота которой обозначена
S-перехода). В отсутствие поля наблюдается одна линия, частота которой обозначена ![]() . При включении поля, кроме линии o, появляются две
. При включении поля, кроме линии o, появляются две

Рис.2
расположенные симметрично относительно нее линии с частотами ![]() и
и ![]() .
.
На рис. 202 дана аналогичная схема для более сложного случая — для перехода D![]() P. На первый взгляд может показаться, что первоначальная линия должна в этом случае расщепиться на семь компонент. Однако на самом деле получается, как и в предыдущем случае, лишь три компоненты: линия с частотой ю0 и две симметрично расположенные относительно нее линии с частотами
P. На первый взгляд может показаться, что первоначальная линия должна в этом случае расщепиться на семь компонент. Однако на самом деле получается, как и в предыдущем случае, лишь три компоненты: линия с частотой ю0 и две симметрично расположенные относительно нее линии с частотами ![]() и
и ![]() . Это объясняется тем, что для магнитного квантового числа т также имеется правило отбора, согласно которому возможны только такие переходы, при которых квантовое число т либо остается неизменным, либо изменяется на единицу:
. Это объясняется тем, что для магнитного квантового числа т также имеется правило отбора, согласно которому возможны только такие переходы, при которых квантовое число т либо остается неизменным, либо изменяется на единицу:
![]() (8)
(8)
Происхождение этого правила можно пояснить следующим образом. Если механический момент электрона

![]()
Рис.3
при излучении изменяется на единицу (фотон уносит с собой момент, равный единице), то изменение проекции момента не может быть больше единицы.
С учетом правила (9) возможны только переходы, указанные на рис. 3. В результате получаются три компоненты с частотами, указанными выше. Опыт показывает, что эти компоненты поляризованы. Характер поляризации зависит от направления наблюдения. При поперечном наблюдении (т. е. при наблюдении в направлении, перпендикулярном к вектору Н ) световой (электрический) вектор несмещенной компоненты (ее называют я-компонентой) колеблется в направлении, параллельном вектору Н, а в смещенных с-компонентах — в направлении, перпендикулярном к Н (рис. 3, а). При продольном наблюдении получаются только две смещенные компоненты. Обе поляризованы по кругу: смещенная в сторону меньших частот — против часовой стрелки, смещенная в сторону больших частот — по часовой стрелке (рис. 3, б).
Получающееся в рассмотренных случаях смещение компонент называется нормальным или лоренцевым смещением. Величина нормального смещения, очевидно, равна:
![]() (9)
(9)
О
Рис.4
ценим величину расщепления компонент ДХ для поля порядка 104 эрстед. ПосколькуЧастота и для видимого света имеет порядок 3-1015 сек-1 .Следовательно,
![]()

за счет столкновения атома с достаточно быстрым электроном, или, наконец, за счет поглощения атомом фотона.
Фотон при поглощении его атомом исчезает, передавая атому всю свою энергию. Атом не может поглотить только часть фотона, ибо фотон, как и электрон, как и

Рис.5
другие элементарные частицы, является неделимым. Поэтому атом может поглощать только те фотоны, энергия которых в точности соответствует разности энергий двух его уровней. Поскольку поглощающий атом обычно находится в основном состоянии, спектр поглощения водородного атома должен состоять из линий, соответствующих переходам 1s![]() np (n = 2, 3, ...). Этот результат полностью согласуется с опытом.
np (n = 2, 3, ...). Этот результат полностью согласуется с опытом.
Собственные функции s-состояний (т. е. состояний с l = 0) оказываются не зависящими от углов ![]() и
и ![]() . Это можно записать следующим образом:
. Это можно записать следующим образом:
![]()
Вероятность найти электрон в тонком шаровом слое радиуса r и толщины dr согласно (66.1) равна ![]() .
.
Выражение ![]() представляет собой плотность вероятности нахождения электрона на расстоянии r от ядра.
представляет собой плотность вероятности нахождения электрона на расстоянии r от ядра.
Волновые функции для l, отличных от нуля, распадаются на два множителя, один из которых зависит только от r, а другой — только от углов ![]() и
и ![]() . Таким образом, и в этом случае можно ввести понятие плотности вероятности нахождения электрона на расстоянии r от ядра, подразумевая под R(r) ту часть функции
. Таким образом, и в этом случае можно ввести понятие плотности вероятности нахождения электрона на расстоянии r от ядра, подразумевая под R(r) ту часть функции ![]() , которая зависит только от r.
, которая зависит только от r.
На рис. 5 приведены плотности вероятности для случаев: 1) п = 1, l = 0; 2) п = 2, l = 1 и 3) п = 3, l = 2. За единицу масштаба для оси r принят радиус первой боровской орбиты. На графиках отмечены радиусы соответствующих боровских орбит. Как видно из рисунка, эти радиусы совпадают с наиболее вероятными расстояниями электрона от ядра.