Реферат: Оптическая физика

СОДЕРЖАНИЕ

Лабораторная работа №1 Определение расстояния между щелями в опыте Юнга

Лабораторная работа №2 Определение длины световой волны интерференционным методом

Лабораторная работа №3 Определение длины световой волны дифракционным методом

Лабораторная работа №4 Исследование закона Малюса

Лабораторная работа №5 Определение концентрации сахара в водном растворе поляризационным методом

Лабораторная работа №1 ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ МЕЖДУ ЩЕЛЯМИ В ОПЫТЕ ЮНГА

Цель работы: экспериментально определить расстояние между щелями в опыте Юнга с использованием лазерного источника излучения.

Приборы и принадлежности: оптическая скамья, полупроводниковый (GaAs) лазерный источник света, фотолитографический тест-объект МОЛ-02 с нанесенными на него парами щелей, зеркало, экран.

Теоретическая часть работы

1.Общая теория явления интерференции

В обычных условиях в пространстве распространяется одновременно бесчисленное множество световых волн от различных источников излучения или волн, отраженных и рассеянных поверхностями предметов. Из опыта мы знаем, что такое взаимное наложение друг на друга всего бесконечного множества излучений не мешает их распространению в пространстве, так как видимые нами предметы совершенно не искажаются, несмотря на то, что свет, приносящий в глаз информацию о внешних предметах, на своем пути много раз пересекался с другими световыми лучами.

При взаимодействии световых излучений особый интерес представляет сложение двух волн одинаковой частоты. Это явление называется интерференцией, и заключается в том, что в одних местах волны усиливают друг друга, а в других ослабляют.

Рассмотрим математически сложение двух волн одинаковой частоты, имеющих одно и то же направление колебаний, так как это наиболее простой случай сложения двух линейно-поляризованных монохроматических волн. Ради упрощения математических выкладок мы предположим, что амплитуды волн равны. Тогда уравнения обеих волн запишутся в виде:

, (1)

где r₁ и r₂ - расстояния от источников I₁ и I₂ до точки наблюдения сложения волн; Ф₁ и Ф₂ - начальные фазы колебаний в источниках излучений; k - волновое число. Согласно принципу суперпозиции напряженность результирующего колебания Е будет равна алгебраической сумме напряженностей рассматриваемых колебаний, т. е.:

. (2)

Величину называют разностью хода интерферирующих лучей.

В формуле (2) первый тригонометрический множитель представляет собой выражение, определяющее зависимость Е от времени. Он показывает, что результирующее поле изменяется с той же самой частотой, что и слагаемые поля, а фаза, зависящая от расстояния и от начальных условий в источнике, есть среднее арифметическое аналогичных фаз у отдельных источников. Второй множитель не зависит от времени, поэтому величину

, (3)

считают амплитудой результирующей волны в рассматриваемой точке. Если теперь подсчитать амплитуду мощности волны, определяемую для 1 см² поверхности волны вектором Умова-Пойтинга, то будем иметь:

. (4)

Заменим через интенсивность волны I,а через амплитуду интенсивности I₀ , тогда выражение (4) примет вид:

. (5)

Из формулы (5) вытекают важные следствия. Если Ф₁ и Ф₂ не зависят от времени, то их разность представляет постоянную величину (в частном случае она равна нулю). Вся разность фаз в формуле (5) в таком случае не зависит от времени. Обозначим ее через ,то есть

. (6)

Если

, (6*)

где р = 0,1,2,3,…, то cos=1. В этом случае результирующая интенсивность максимальна и равна 4I₀ . Если же при тех значениях

(7)

то интенсивность имеет минимум (I=0). При промежуточных значениях разности фаз интенсивность будет принимать промежуточные значения от 0 до 4 I₀ .

Так, в результате сложения излучений, у которых начальная разность фаз источников излучения Ф₁ - Ф₂ не зависит от времени, получается стабильная интерференция света с независящими от времени максимумами и минимумами интенсивности. Формула (5) дает, таким образом, распределение интенсивности в полосах интерференции. Такая устойчивая интерференционная картина обычно наблюдается, если два интерферирующих пучка света получены из светового пучка, исходящего от одного и того же источника. Затем получившиеся пучки заставляют сходиться в одном месте, где и наблюдается интерференция. Так как пучки возникли из одного источника, то разность "начальных" фаз пучков Ф₁ -Ф₂ всегда равна нулю, независимо от того, меняются ли во времени фазы Ф₁ и Ф₂ или нет. Если несколько световых волн имеют постоянную разность фаз, то они называются когерентными.Только когерентные световые волны могут давать устойчивую во времени интерференционную картину.

Найдем условие, которое определяет получение максимумов и минимумов интерференции при сложении когерентных световых пучков, в зависимости от разности хода лучей . Максимумы будут иметь место (см. формулу 5), когда

, (8)

где p = 0,1,2,3,… (Ф₁ -Ф₂ = 0). Отсюда, учитывая, что получаем:

, (9)

т. е. разность хода первого и второго луча от источников до точки наблюдения равна целому числу волн (четному числу полуволн).

Минимумы света будут в тех местах, для которых выполняется условие:

(10)

или

, (11)

т. е. разность хода равна нечетному числу полуволн.

Формулы (9) и (11) не ограничивают величины , сколь бы велика она ни была. Поэтому можно подумать, что наблюдение интерференционной картины возможно при любой разности хода. Однако это не так. Чем больше разность хода, тем менее высокими становятся максимумы и тем менее глубоко опускаются минимумы. С повышением разности хода видимость интерференции постепенно ухудшается и затем интерференционная картина исчезает совсем.

2. Схема опыта Юнга

Одним из первых ученых, кто наблюдал это явление интерференции, был Томас Юнг, который в 1802 году получил интерференционную картину в опыте, показанном на рисунке 1.Свет, предварительно прошедший через светофильтр, проходя через экран А, падал на экран В, в котором были проделаны две тонкие щели S₁ и S₂ . Эти щели являлись когерентными источниками света и давали достаточно четкую картину интерференции на экране С.

В настоящей лабораторной установке вместо обычного источника света со светофильтром для повышения степени когерентности используется полупроводниковый(GaAs) лазер.

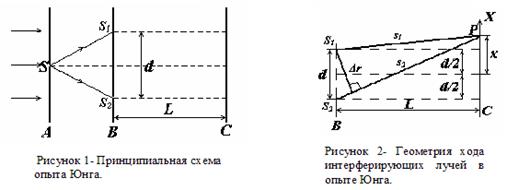
Геометрия хода лучей в опыте Юнга показана на рисунке 2. Где S₁ и S₂ - источники когерентного излучения, s₁ и s₂ - пути света от источников до точки наблюдения Р, d - расстояние между щелями, L - расстояние между экранами В и С. Разность фаз колебаний возбужденных волнами, приходящими в точку Р от источников S₁ и S₂ равна:

, (12)

где ∆r = ns₂ - ns₁ , n - показатель преломления среды.

Отсюда следует, что если в ∆r укладывается целое число длин волн (±рλ₀ ), где λ₀ - длина волны в вакууме, то разность фаз оказывается кратной 2, и в этой точке будет наблюдаться интерференционный максимум.

Если в ∆r укладывается целое число длин волн (±(р+) λ₀ ), то будет возникать интерференционный минимум. Из геометрии (рис. 2) видно, что:

откуда:

. (13)

Учитывая, что d<<L, а s₁ + s₂ 2L и умножив равенство (4.13) на n - показатель преломления среды, получим оптическую разность хода:

. (14)

Подставив в это выражение условия наблюдения максимума и минимума интерференции, получим соответственно:

(15)

где p=0,1,2,… .

Таким образом, ширина интерференционной полосы на экране будет определяться соотношением:

. (16)

Описание экспериментальной установки

Схема экспериментальной установки представлена на рисунке 3.

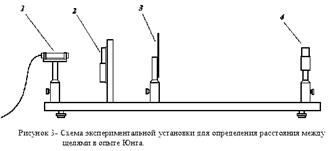
Источником света служит полупроводниковый (GaAs) лазер. Параллельный световой пучок, испускаемый лазером 1, освещает интерференционный объект 2, представляющий собой тонкий стеклянный диск с непрозрачным покрытием, на котором по кругу, параллельно радиусу, нанесены пары щелей с разными расстояниями между ними. Пары щелей равной ширины объединены в группы по четыре. Свет, интерферируя на паре щелей, проходит через отверстие в экране 3, падает на зеркало 4 и, отражаясь от него, дает на экране 3 интерференционную картину, по которой и будут проводиться измерения.

Выполнение работы

Перед началом выполнения работы необходимо добиться четкого изображения интерференционных полос. Для этого нужно включить лазер 1 и без интерференционного объекта 2, получить световое пятно на экране 3 при отражении от зеркала 4 путем его поворота на небольшой угол и регулируя винтами горизонтальность расположения установки. После этого, поставив интерференционный объект на место, получить четкое изображение на экране 3, на котором устанавливается миллиметровая бумага для измерения параметров интерференционной картины (∆х).

Далее измерения проводятся в следующем порядке.

1. Измерить ширину интерференционной полосы (∆х) для каждой из пар щелей (не менее 3 раз). Полученные данные усреднить и занести в таблицу 1, где ∆х_i - значение ширины интерференционной полосы для i-ой пары щелей. Измерение ширины интерференционной полосы целесообразно провести при различных расстояниях от интерференционного объекта до экрана. Изменения расстояния между интерференционным объектом и экраном добиваются путем изменения положения зеркала 4 на установке (рис.3).

Таблица 1.

N^* _{измерения}

для

1 пары щелей

для

2 пары щелей

для

3 пары щелей

для

4 пары щелей

(L₁ =110см)

(L₂ =90см)

(L₃ =70см)

(L₄ =50см)

^* Проводятся 4 серии измерений для различных положений зеркала L на оптической скамье. (L₁ =110 см; L₂ =90 см; L₃ =70 см; L₄ =50 см).

2. По результатам измерений, зная величину L (она равна сумме расстояний между экраном 3 и зеркалом 4 и зеркалом и интерференционным объектом 2), и длину волны излучения полупроводникового лазера (λ=632,8нм) рассчитать расстояние между щелями по формуле:

. (17)

3. Определить средние значения для каждой пары щелей и найти погрешность нахождения расстояния между щелями для каждой пары щелей.

Полученные средние значения для каждой пары щелей из группы занести в таблицу 2.

Таблица 2.

Номер пары щелей

d, мкм

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем состоит явление интерференции?

2. Какие волны называются когерентными? Как на практике осуществляются когерентные источники света?

3. Запишите условие усиления и ослабления результирующих колебаний при интерференции?

4. Выведите формулу для ширины интерференционной полосы в опыте Юнга?

5. Как изменяется интерференционная картина в опыте Юнга при изменении расстояния от интерференционного объекта до экрана?

6. Как изменится интерференционная картина в опыте Юнга, если на пути одного из интерферирующих лучей установить плоскопараллельную стеклянную пластинку? Ответ обоснуйте.

ЛИТЕРАТУРА

1. Ландсберг Г.С. Оптика.- М.: Наука, 1976.- 927с.

2. Сивухин Д.В. Общий курс физики. Оптика.- М.: Наука, 1980.- 752с.

3. Годжаев Н.М. Оптика.- М.: Высшая школа, 1977.- 495с.

4. Дитчберн Р. Физическая оптика.- М.: Наука. 1965.- 632с.

Лабораторная работа №2 ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ ИНТЕРФЕРЕНЦИОННЫМ МЕТОДОМ

Цель работы: 1) вычислить радиус кривизны выпуклой поверхности линзы; 2) измерить длину световой волны.

Приборы и принадлежности: микроскоп, микрометрическое устройство для измерения диаметра колец Ньютона, плосковыпуклая линза, плоскопараллельная пластинка, ртутная лампа (или электролампа), светофильтры.

Теоретическая часть работы

Общая теория явления интерференции описана в лабораторной работе №6.

Рисунок 1 – Принципиальная схема наблюдения интерференционной картины колец Ньютона

В данной работе определение длины световой волны осуществляется методом интерференционных колец Ньютона. Схема опыта для получения интерференционной картины в виде колец Ньютона приведена на рис.1. Плосковыпуклая линза L большого радиуса кривизны (1-2 м) накладывается выпуклой стороной на плоскую стеклянную пластинку P. Между соприкасающимися в точке A поверхностями L линзы и пластинки P образуется клинообразный воздушный слой. С помощью наклоненного под углом 45⁰ полупрозрачного зеркала S свет от источника I направляется на объектив O, превращающий падающий на него от зеркала S световой пучок в параллельный, который и освещает линзу L и пластинку P, причем угол падения равен нулю. После отражения от выпуклой поверхности L и соприкасающейся с ней поверхности пластинки P свет проходит в обратном направлении в объектив О, затем в полупрозрачное зеркало S и собирается в точке I’, являющейся изображением точки I. Получившиеся два когерентные световые пучка дают интерференционную картину в виде колец с центром в точке соприкосновения линзы и пластинки P. Т.к. изображение колец Ньютона, даваемое объективом в плоскости P^’ , очень мало, то его рассматривают через окуляр О^’ . В случае освещения белым светом кольца будут окрашены. При освещении монохроматическим светом получаются светлые и темные кольца с убывающей шириной (рис.2).

Рисунок 2 – Схема обозначения правых и левых краев колец Ньютона при измерениях с помощью микрометра.

При отражении от нижней пластинки, представляющей оптически более плотную среду по сравнению с воздухом, волны меняют фазу на противоположную, что эквивалентно изменению пути на l/2. В месте соприкосновения линзы с пластинкой остается тонкая воздушная прослойка, толщина которой значительно меньше длины волны. Поэтому разность хода между лучами, возникающими в этой точке, определяется лишь потерей полуволны при отражении от пластинки, т.е. D=l/2. Следовательно, в центре интерференционной картины наблюдается темное пятно. Т.к. между линзой L и пластинкой P находится воздух (показатель преломления воздуха равен 1) и пучок света падает нормально к пластинке и, практически, к нижней поверхности линзы (кривизна линзы мала), то разность хода в этом случае будет равна D=2h + l/2.

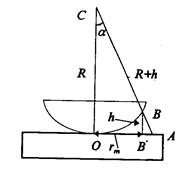
Рисунок 3 – Геометрические построения для вычисления радиусов колец Ньютона.

Для вычисления радиусов колец дополним выпуклую поверхность линзы до полной сферы (рис.3). Если BС - диаметр, то квадрат длины отрезка АО, который мы обозначим через x² , по известной геометрической теореме x² =АО² =(СB + h)² -CO ² . Поскольку СO = CB = R (R - радиус сферы), и, в силу того, что R >> h, выражение для x² можно записать следующим образом: x² =2Rh. Тогда D=x² /R+l/2. Светлые кольца получатся при D=ml, где m - целое число. Из этого условия можно найти радиус r_m m- го светлого кольца:

. (1)

Аналогично для радиуса m - го темного кольца:

. (2)

Т.о, измерив экспериментально радиус темного или светлого m- го кольца r_m и радиус кривизны линзы R можно вычислить длину световой волны. Однако вычислять по формулам (1) или (2) длину световой волны на практике не удобно, поскольку в измерениях может присутствовать большая систематическая ошибка. Для того, чтобы ее избежать, измеряют радиусы m - го и k - го колец и, вычитая их друг из друга (это вычитание приводит к уничтожению ошибки), получают следующее выражение для длины световой волны:

. (3)

Описание экспериментальной установки

Для наблюдения и измерения радиусов колец Ньютона применяется микроскоп с длиннофокусным объективом и микрометрическим винтом. На предметный столик микроскопа помещается стеклянная пластинка с подложенной под нее черной бумагой или же пластинка из черного стекла. Поверх пластинки кладется плосковыпуклая линза с большим радиусом кривизны (R»1,5м). Вся эта система заключена в металлическую оправу, имеющую винты для регулировки ширины колец Ньютона.

При выполнении работы, прежде всего, нужно получить картину колец Ньютона на установке с линзой и плоской пластинкой. При визуальном наблюдении эти кольца в отраженном свете будут выглядеть как маленькое темное пятнышко на поверхности линзы. Затем установка помещается на предметный столик микроскопа. После этого добиваются, чтобы свет, падающий из объектива, освещал это пятнышко и, сфокусировав микроскоп, наблюдают кольца Ньютона в окуляр микроскопа.

Выполнение работы

1. Вычисление радиуса кривизны выпуклой поверхности линзы.

1. Поместите на предметный столик стеклянную пластинку с линзой так, чтобы свет от ртутной лампы падал на линзу. Получите отчетливое изображение колец Ньютона.

2. Установите оранжевый светофильтр (l_оранж. =630 нм).

3. Произведите отсчеты по барабану микрометра левого и правого краев пяти темных колец, видимых в окуляре. Для этого переместите столик микроскопа путем вращения микрометрического винта, так, чтобы нить, натянутая в окуляре, совпала с наружным краем левого (правого) темного кольца. Запишите показания барабана микрометрического винта. Затем совместите нить с правым (левым) наружным краем этого же кольца, и, в свою очередь, запишите показания барабана микрометрического винта. Вычислите радиус r интерференционного кольца. Отсчеты производить в соответствии с рис.2. Результаты измерений занести в таблицу №1.

Таблица 1

4. Вычислить радиус кривизны линзы R по формуле (4):

. (4)

2. Определение длины световой волны.

1. Вместо оранжевого светофильтра поочередно установить другие светофильтры, для которых длина волны неизвестна.

2. Как и в первом задании для каждого светофильтра произвести отсчеты по барабану микрометра левого и правого краев пяти видимых колец Ньютона. Результаты измерений занести в таблицу, аналогичную таблице №1, предварительно указав цвет светофильтра.

3. Используя формулу (3) и известное из первого задания значение радиуса кривизны линзы R вычислите длину волны света l, считая, что k=1, а m пробегает значения 2, 3, 4, 5. Произведите усреднение l по числу рассчитанных значений.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Почему наблюдаемая интерференционная картина состоит из ряда темных и светлых колец?

2. Запишите условия максимумов и минимумов света при интерференции когерентных световых пучков.

3. Чем различаются картины колец Ньютона в отраженном и проходящем свете?

4. Почему в данной работе радиус кривизны линзы выбран большим?

5. Можно ли для наблюдения колец Ньютона пользоваться достаточно протяженными источниками света?

6. Что произойдет в данной работе с интерференционной картиной, если линзу слегка приподнять над пластинкой?

7. Как изменится картина колец Ньютона, если пространство между линзой и пластинкой заполнить водой?

ЛИТЕРАТУРА

1. Сивухин Д. В. Общий курс физики. Т.3. Оптика. М.: Наука, 1985.- 752с.

2. Савельев И. В. Курс общей физики. Т.2. Электричество и магнетизм. Волны. Оптика. М.: Наука, 1988.- 496c.

3. Фейнман Р., Лейтон Р., Сэндс М. Феймановские лекции по физике. Т.3-4. Излучение. Волны. Кванты. М.: Мир, 1977.- 496 с.

4. Крауфорд Ф. Берклеевский курс физики. Волны. М.: Наука, 1984.- 512с.

Лабораторная работа №3 ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ ДИФРАКЦИОННЫМ МЕТОДОМ

Цель работы: измерить длину световой волны с помощью дифракционной решетки.

Приборы и принадлежности: спектрометр, дифракционная решетка, неоновая лампа.

Теоретическая часть работы

Под дифракцией света понимают всякое отклонение от прямолинейного распространения световых лучей, если оно не может быть истолковано как результат их отражения, преломления или изгибания в средах с непрерывно меняющимся показателем преломления. Решение дифракционной задачи заключается в нахождении распределения освещенности на экране в зависимости от размеров и формы препятствий, вызывающих отклонение света от прямолинейного распространения. Строгое математическое решение дифракционной задачи возможно только на основе электромагнитной теории Максвелла. Однако оно является очень сложным. В упрощенном варианте решение дифракционной задачи может быть получено путем использования принципа Гюйгенса-Френеля.

Принцип Гюйгенса заключается в следующем. Каждую точку всякой волны можно рассматривать как центр новой сферической элементарной волны. Волна, получающаяся в результате наложения этих элементарных волн, совпадает с непосредственно распространяющейся первоначальной волной. Гюйгенс считал, что результирующая волна является просто огибающей всей совокупности сферических элементарных волн.

Френель усовершенствовал принцип Гюйгенса тем, что учел различие фаз элементарных волн. Измененный таким образом принцип Гюйгенса называют принципом Гюйгенса-Френеля. Согласно этому принципу при распространении волн с ограниченным фронтом свет будет наблюдаться только в тех местах, где элементарные волны от всех точек распространяющейся волны складываются в фазе, усиливая друг друга. Наоборот, в местах, где элементарные волны, будучи в противофазе, при сложении гасят друг друга, будет наблюдаться ослабление света. На основе принципа Гюйгенса-Френеля можно дать объяснение всем явлениям дифракции. Дифракционные явления по своему характеру разбиваются на два больших класса. Первый класс явлений, называемый дифракцией Френеля, относится к случаю, когда дифракционная картина наблюдается на конечном расстоянии от ограничивающих падающую волну экранов. Второй класс явлений, называемый дифракцией Фраунгофера, относится к случаю, когда дифракционная картина наблюдается на бесконечном расстоянии от экранов, ограничивающих падающую волну, т.е. дифрагирующие пучки света являются параллельными.

В данной лабораторной работе рассматривается только дифракция Фраунгофера, т.е. когда дифракционная картина образована системой параллельных лучей.

Дифракционная решетка как спектральный прибор

Дифракционная решетка очень часто используется для разложения света в спектр и является одним из важнейших спектральных приборов, с помощью которого можно, в частности, определить длину световой волны. Она представляет собой плоскую стеклянную или металлическую поверхность, на которой делительной машинкой нарезано очень много (до сотен тысяч) прямых равноотстоящих штрихов. На стеклянных решетках наблюдения можно производить как в проходящем, так и в отраженном свете, на металлических - только в отраженном.

Рассмотрим простейшую идеализированную решетку, состоящую из одинаковых равноотстоящих параллельных щелей, сделанных в непрозрачном экране (рис.1). Ширину щели обозначим через b,, ширину непрозрачной части экрана между двумя соседними щелями - через a. Величина d=a+b называется периодом решетки. В решетке осуществляется многолучевая интерференция когерентных дифрагировавших пучков света, исходящих от щелей решетки при ее освещении. Дифракционная картина наблюдается по методу Фраунгофера, т.е. либо на бесконечно удаленном экране, либо в фокальной плоскости линзы, поставленной на пути дифрагировавшего света.

Пусть на решетку перпендикулярно к ее поверхности падает плоская монохроматическая волна (рис.1). Вследствии наложения элементарных волн от всех щелей дифракционной решетки в фокальной плоскости линзы, поставленной на пути лучей, возникает сложная дифракционная картина. При освещении белым светом она имеет вид цветных полос, параллельных щели, и носит название спектра. Распределение интенсивности дифргировавшего света в зависимости от угла дифракции Ө имеет вид:

, (1)

где I₀ – интенсивность света под углом Ө=0^о ; N – число щелей; , . Первая функция в формуле (1) описывает дифракцию Фраунгофера на одной щели, вторая – вклад других щелей в дифракционную картину. Формула (1) – основная в теории дифракционной решетки.

При освещении дифракционной решетки пучком параллельных и когерентных лучей в результате дифракции произойдет отклонение световых волн в различных направлениях. Если в фокальной плоскости линзы, на которую происходит падение дифрагировавших световых волн, поместить экран, то в определенных участках экрана получатся дифракционные максимумы и минимумы. Если решетку осветить белым светом, то после дифракции на решетке белый свет разложится на составляющие, т.е. каждая световая волна отклонится на определенный угол, который зависит от ее длины. И на экране в местах максимумов будут наблюдаться изображения щелей, окрашенные в различные цвета. В данном случае вся картина на экране носит название дифракционного спектра.

В направлениях, определяемых условием

dsinΘ =ml (m = 0, ± 1, ± 2, ...), (2)

получаются максимумы, интенсивность которых в N² превосходит интенсивность волны от одной щели в том же направлении. Они называются главными максимумами. Целое число m называется порядком главного максимума или порядком спектра (рис.2). Условие (2) определяет направления, в которых излучения от всех щелей решетки приходят в точку наблюдения в одинаковых фазах, а потому усиливают друг друга Однако, в таких направлениях при отдельных значениях m могут и не возникнуть максимумы. Это будет, когда I₁ =0, т.е. в направлениях на дифракционные минимумы от одной щели. Например, если a=b, то все главные максимумы четных порядков не появятся, поскольку условие появление главного максимума порядка 2n имеет вид dsinΘ=2nl. При d=2b оно переходит в bsinΘ=nl, т.е. в условие дифракционного минимума на щели. Т.о. в рассматриваемом направлении, ни одна щель, а потому и решетка в целом не пропускают свет. Минимумы дифракционной картины, получающиеся при обращении I₁ в нуль называются главными минимумами.

Кроме того выражения (1) обращается в нуль, если sin(Nd/2)=0, но sin(d)¹0, т.е. при Nd=(Nm+p)p, или

dsinΘ=(m+p/N)l(p=1, 2, ..., N-1). (3)

В соответствующих направлениях получаются дифракционные минимумы, в которых интенсивность света равна нулю. Они называются побочными минимумами. Между двумя соседними побочными минимумами получается максимум. Такие максимумы называются добавочными. Между двумя соседними главными максимумами располагается (N-1) минимумов и (N-2) добавочных максимумов.

Интенсивности главного максимума и ближайших к нему второстепенных максимумов находятся в следующих отношениях

1:4/(9p² ):4/(25p² ):4/(49p² ):.. =1:0.045:0.016:0.0083:...

Добавочные максимумы слабы по сравнению с главными. При большом числе щелей они обычно не играют роли. Второстепенные максимумы создают более или менее равномерный слабый фон, на нем выступают узкие и резкие главные максимумы, в которых концентрируется практически весь дифрагировавший свет.

Из условия (2) следует, что при m=0, sinΘ =0. На экране получается дифракционный максимум, называемый нулевым. При m=±1 по обе стороны от нулевого возникают два дифракционных максимума первого порядка. При освещении дифракционной решетки белым светом каждый максимум будет представлять собой спектр, отделенный от других темными промежутками.

Число дифракционных спектров ограничено и определяется условием

sinΘ =ml/d£1. (4)

Из (4) следует, что чем больше постоянная решетки, тем большее число максимумов можно наблюдать, однако максимумы становятся в данном случае менее яркими.

Описание экспериментальной установки

В работе используется распространенная в лабораторной практике решетка, представляющая собой стеклянную пластинку, на которой с помощью делительной машины специальным алмазным резцом нанесен ряд параллельных штрихов.

Для измерения угла отклонения применяется гониометр, схема которого представлена на рисунке 3.

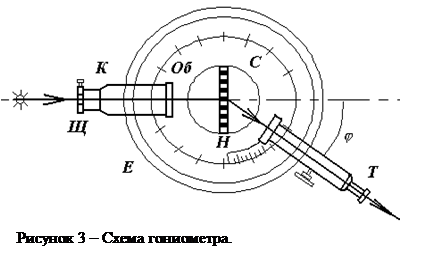
Гониометр состоит из зрительной трубы Т, коллиматора К, столика С, лимба Е, нониуса Н. Коллиматор служит для создания параллельного пучка света. Он состоит из наружного тубуса с объективом Об и внутреннего тубуса с входной щелью Щ устанавливаемой в фокальной плоскости объектива. Из коллиматора выходит плоская световая волна (параллельный пучок света) и падает на дифракционную решетку. Пучки света собираются объективом зрительной трубы и образуют в фокальной плоскости действительное изображение щели коллиматора. В поле зрения окуляра одновременно видны крест нитей и действительное изображение щели (дифракционный максимум). Перемещая зрительную трубу, можно совместить крест нитей с любым из дифракционных максимумов. Источником исследуемого излучения является неоновая лампа.

Выполнение работы

При работе с дифракционной решеткой основной задачей является точное измерение углов, на которых наблюдаются максимумы для разных длин волн.

Приступая к выполнению работы, необходимо произвести юстировку гониометра. Для этого нужно:

1. Произвести установку зрительной трубы на бесконечность, т. е. на отчетливое видение удаленных предметов;

2. Источник света (неоновую лампу) расположить против щели коллиматора;

3. Установить зрительную трубу так, чтобы ее оптическая ось была продолжением оси коллиматора. Эта будет достигнуто тогда, когда вертикальная линия окуляра трубы будет находиться посередине изображения щели;

4. Поместить решетку на столике таким образом, чтобы нить окуляра была посередине центральной наиболее яркой полосы (спектра нулевого порядка). Чтобы получить хорошие спектры решетка должна быть установлена перпендикулярно пучку лучей так, чтобы ее штрихи шли параллельно щели коллиматора.

Дифракционная решетка с известным периодом может быть использована для измерения длин волн. При выполнении работы решетка остается неподвижной, а зрительная труба поворачивается так, чтобы изображение исследуемой спектральной линии совпало с нитью окуляра.

Длину волны определяют из формулы решетки. Здесь d=0,01мм; m- порядок спектра или номер максимума. Это уравнение является основной расчетной формулой для вычисления длин световых волн при помощи дифракционных решеток.

Измерение длины волны сводится к определению угла отклонения лучей от первоначального направления. Далее работа выполняется в следующем порядке.

1. Произвести отсчет положения нулевой линии n₀ . Для этого нить окуляра нужно совместить с серединой спектра нулевого порядка (центральной яркой полосой) и, с помощью кругового лимба и нониуса, определить значение n₀ .

2. Аналогично произвести отсчеты для красной, желтой и зеленой линий спектров 1 и 2 порядков, каждый раз совмещая нить окуляра с соответствующей линией. Измерения проводить в порядке, показанном на рисунке 4.

3. Результаты измерений занести в таблицу 1.

4. Если все отсчеты справа обозначить через , а слева – , то угол для одной и той же линии может быть подсчитан тремя способами (формулы приведены ниже):

Для зеленой линии, например I порядка, n₁ =n₁ , а n’₁ =n₂ , для желтой линии I порядка n₁ =n₃ , n’₁ =n₄ и т.д. (см. таблицу 1).

5. Зная угол, определить длину волны для каждой линии спектра.

6. Подсчитать относительные погрешности измерений ,%

Таблица 1.

Линия спектра	порядок спектра	номер линии по рисунку	отсчет по лимбу справа	отсчет по лимбу слева	,нм	,%
0	0	n₀
зеленая	I	1 2	n₁	n₂
желтая	I	1 2	n₃	n₄
красная	I	1 2	n₅	n₆
зеленая	II	1 2	n₇	n₈
желтая	II	1 2	n₉	n₁₀
красная	II	1 2	n₁₁	n₁₂

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие волны называются когерентными?

2. В чем заключается явление дифракции?

3. Сформулируйте принцип Гюйгенса-Френеля.

4. Какого типа дифракция наблюдается в работе?

5. Какого цвета линия в спектре 1-го и более высоких порядков будет ближайшей к центральному максимуму?

6. Чем будут отличаться дифракционные картины, полученные от решеток с различными постоянными, но с одинаковым числом штрихов?

7. Как изменится дифракционная картина, если закрыть часть решетки как на рисунке?

8. Каков порядок следования цветов в дифракционных спектрах?

9. Какова окраска нулевого максимума? Почему она такая?

10. Как изменится дифракционная картина, если изменить ширину щели, не меняя постоянную решетки?

ЛИТЕРАТУРА

1. Сивухин Д. В. Общий курс физики. Т.3. Оптика. М.: Наука, 1985.- 752с.

2. Савельев И. В. Курс общей физики. Т.2. Электричество и магнетизм. Волны. Оптика. М.: Наука, 1988.-496 c.

3. Фейнман Р., Лейтон Р., Сэндс М. Феймановские лекции по физике. Т.3-4. Излучение. Волны. Кванты. М.: Мир, 1977.- 496 с.

4. Ландсберг Г. С. Оптика. М.: Наука, 1976.- 823 с.

5. Калитеевский Н. И. Волновая оптика. М.: Высшая школа, 1978.- 321с.

Лабораторная работа №4 ИССЛЕДОВАНИЕ ЗАКОНА МАЛЮСА

Цель работы: экспериментальная проверка закона Малюса.

Приборы и принадлежности: полупроводниковый (GaAs) лазерный источник света, фотоприеменик, гальванометр, анализатор с нанесенной на него угловой разметкой (цена одного деления 1^о ).

Теоретическая часть работы

С точки зрения электромагнитной теории свет представляет собой поперечные электромагнитные волны, в которых векторы напряженностей электрического E и магнитного H полей колеблются во взаимно перпендикулярных плоскоcтях. Электромагнитная волна (э/м) называется линейно поляризованной или плоскополяризованной, если электрический вектор E все время лежит в одной плоскости, в которой расположена также нормаль k к фронту волны (рис.1). Плоскость, которая содержит нормаль k к фронту, и в которой лежит электрический вектор Е э/м волны, называется плоскостью поляризации. Естественный свет не поляризован, он представляет собой совокупность световых волн, излучаемых множеством отдельных атомов, и векторы Е и Н колеблются беспорядочно во всех направлениях, перпендикулярных лучу. В естественном свете все направления колебаний вектора Е оказываются равновероятными. К естественному свету относятся дневной свет, свет лампы накаливания и др.

Для получения линейно поляризованного света на практике часто применяют поляроиды, изготовленные из кристаллов турмалина или геропатита. Каждый поляроид характеризуется оптической осью U, которая представляет собой выделенное направление. Физический смысл выделенного направления в данном случае заключается в следующем. Пусть на поляроид перпендикулярно его плоскости, содержащей оптическую ось, падает свет. Электрический вектор Е э/м волны можно разложить на две составляющих. Эти составляющие всегда можно выбрать так, что одна из них, например, Е_y будет параллельна оптической оси U, а другая, назовем ее Е_x , перпендикулярна U. Если на поляроид направить естественный свет, то через поляроид пройдут только те э/м волны, электрические векторы E которых имеют составляющие Е_y (параллельные оптической оси поляроида). При этом происходит поляризация естественного света.

Т.о. поляризация света при помощи поляроидов состоит в выделении из светового пучка колебаний определенного направления. Если на поляризатор падает естественный свет, интенсивность которого I_ест , то интенсивность I прошедшего поляризованного света не зависит от ориентации поляризатора (его поворота вокруг луча) и равна половине интенсивности падающего естественного света:

. (1)

Глаз человека не отличает поляризованный свет от естественного. Устройство, способное пропускать колеблющуюся только в определенной плоскости составляющую светового вектора Е, может также использоваться и для анализа поляризованного света; в этом случае оно называется анализатором. Если на анализатор падает частично поляризованный свет, то поворот анализатора вокруг луча сопровождается изменением интенсивности проходящего света от максимальной (плоскость анализатора совпадает с направлением уу) до минимальной.

Если плоскополяризованный свет падает на анализатор А (рис. 3), то будет пропущена составляющая

, (1)

где a - угол между плоскостью колебаний падающего света рр и плоскостью анализатора аа. Так как интенсивность света пропорциональна E² , то с учетом (1) получим:

, (2)

где I — интенсивность света, вышедшего из анализатора, I_о —интенсивность падающего света. Формула (2) выражает закон Малюса. При повороте анализатора вокруг луча можно найти такое его положение, при котором свет совсем сквозь него не проходит (интенсивность I становится равной нулю). Это надежный способ убедиться в том, что падающий свет полностью поляризован. Если естественный свет с интенсивностью I_ест проходит последовательно сквозь поляризатор и анализатор, выходящий пучок имеет интенсивность.

. (3)

При α=0 (плоскости поляризатора и анализатора параллельны) интенсивность I максимальна и равна . "Скрещенные" поляризатор и анализатор свет не пропускают вовсе.

Описание экспериментальной установки

Установка для исследования закона Малюса представлена на рисунке 4. Установка состоит из лазера 1, установленного на основании 2, фотоприёмника 4 и анализатора 6, установленного на основании 3. Основания 2 и 3 скреплены между собой при помощи алюминиевых стержней 5. Вертикальность установки регулируется при помощи ножек 7. Для этого ножки 7 снабжены резьбой. Вращая ножки вокруг своей оси можно регулировать вертикальность положения установки. Интенсивность лазерного луча, падающего на фотоприёмник 4, регистрируется при помощи миллиамперметра 8, подключенного к фотоприемнику. Анализатор можно вращать вокруг своей оси. Угол поворота анализатора регистрируется по угловой шкале, нанесенной на анализатор. Точность определения угла достигает 1⁰ . Поворачивая анализатор, изменяем интенсивность света, падающего на фотоэлемент ФЭ (рис.5), соединенного с миллиамперметром.

В зависимости от интенсивности света I сила фототока i в гальванометре будет меняться, так как свет, падающий на поляризатор, плоскополяризованный. Плоскость колебаний вектора E показана на рисунке 3 направлением PP. Направление плоскости колебаний анализатора АА. В данной работе снимают графики зависимости фототока i от квадрата косинуса угла a, для чего поворачивают анализатор вокруг оси ОО^′ .

Выполнение работы

Рассмотрим методику исследования закона Малюса. Свет, испускаемый лазером, является плоскополяризованным. Его интенсивность при выходе из анализатора определяется законом Малюса I=I₀ cos² a. Угол aизменяется вращением анализатора. Свет, прошедший через анализатор, попадает на фотоэлемент, подключенный к вольтметру. Показания вольтметра пропорциональны световому потоку, попадающему на фотоэлемент.

Порядок измерений

1. Установить лазер 1 на установке таким образом, чтобы его луч попадал в отверстие фотоэлемента.

2. Установить анализатор в положение, соответствующее a=0⁰

3. Включить гальванометр, подключенный к фотоэлементу в режим тока.

4. Поворачивая анализатор вокруг оси ОО^/ снять показания тока через каждые 15⁰ .

5. Полученные данные занести в таблицу 1.

6. Произвести указанные в п.4 измерения ещё раз и рассчитать средние значения I_ср по результатам измерений.

7. Подсчитать отношения I_ср /I_ср0 и занести в таблицу 1.

8. На основе полученных результатов построить график зависимости I_ср /I_ср0 =f(a.).

9. На том же графике постройте теоретическую кривую f(a)=I/I₀ и сравните полученные результаты.

10. Определите среднюю погрешность d расхождения между расчетными и экспериментальными данными, выраженную в %.

Таблица 1.

Угол a	0	15	30	45	60	75	90	105	120	135	150	165	180
I мА
I мА
I_ср мА
I_ср /I_ср0

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте определение плоскополяризованного света? В чем состоит основное отличие естественного света от плоскополяризованного?

2. Назовите основные методы получения поляризованного света?

3. Сформулируйте закон Малюса?

4. Чему равна интенсивность естественного света после прохождения им анализатора? Зависит ли эта интенсивность от вращения анализатора?

ЛИТЕРАТУРА

1. Сивухин Д. В. Общий курс физики. Т.3. Оптика. М.: Наука, 1985.- 752с.

2. Савельев И. В. Курс общей физики. Т.2. Электричество и магнетизм. Волны. Оптика. М.: Наука, 1988.- 496 c.

3. Фейнман Р., Лейтон Р., Сэндс М. Феймановские лекции по физике. Т.3-4. Излучение. Волны. Кванты. М.: Мир, 1977.- 496 с.

4. Крауфорд Ф. Берклеевский курс физики. Волны. М.: Наука, 1984.- 512с.

Лабораторная работа №5 ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ САХАРА В ВОДНОМ РАСТВОРЕ ПОЛЯРИЗАЦИОННЫМ МЕТОДОМ

Цель работы: определить концентрацию сахара в водном растворе.

Приборы и принадлежности: поляриметр круговой (модель СМ), набор трубок с растворами сахара.

Теоретическая часть работы

С точки зрения электромагнитной теории свет представляет собой поперечные электромагнитные волны, в которых векторы напряженностей электрического E и магнитного H полей колеблются во взаимно перпендикулярных плоскоcтях. Электромагнитная волна (э/м) называется линейно поляризованной или плоскополяризованной, если электрический вектор E все время лежит в одной плоскости, в которой расположена также нормаль k к фронту волны (рис.1). Плоскость, которая содержит нормаль k к фронту, и в которой лежит электрический вектор Е э/м волны, называется плоскостью поляризации. Естественный свет представляет собой совокупность э/м волн, электрические векторы E которых перпендикулярны вектору k и колеблются во всевозможных направлениях. К естественному свету относятся дневной свет, свет лампы накаливания и др.

Если линейно поляризованный свет проходит через плоскопараллельный слой вещества, то в некоторых случаях плоскость поляризации света оказывается повернутой относительно своего исходного положения (рис.2). Это явление называется вращением плоскости поляризации или оптической активностью.

Как было отмечено выше, система из двух скрещенных поляроидов не пропускает естественный свет. Однако, если между скрещенными поляроидами ввести пластинку кварца, вырезанную таким образом, что при прохождении через нее света происходит поворот плоскости поляризации на 90⁰ , то система, состоящая из скрещенных поляроидов и кварцевой пластинки, будет пропускать свет.

В физической оптике, поляроид, предназначенный для поляризации естественного света, принято называть поляризатором. Анализатором называют поляроид, который предназначен для анализа поляризованного света Следовательно, в данной работе ближайший к источнику света поляроид является поляризатором, второй поляроид - анализатором. Рассмотрим прохождение света через систему поляризатор - кварцевая пластинка - анализатор более подробно.

1. При освещении естественным светом через поляризатор пройдут только те э/м волны, векторы E которых имеют составляющие Е_y, параллельные оптической оси поляризатора U. При этом, электрический вектор E, каждой прошедшей через поляризатор э/м волны будет равен по абсолютной величине электрическому вектору Е_y .

2. В дальнейшем, прошедшие поляризатор э/м волны проходят через кварцевую пластинку. Отметим, что прошедшие поляризатор световые э/м волны линейно поляризованы, причем таким образом, что плоскость поляризации э/м волн параллельна оптической оси поляризатора. При прохождении через кварцевую пластинку э/м волн их плоскость поляризации поворачивается на 90⁰ , в результате чего она становится параллельной оптической оси анализатора, и, как следствие, все э/м волны, прошедшие через кварцевую пластинку, пройдут через анализатор без ослабления интенсивности.

Кроме некоторых твердых тел способностью вращать вектор E э/м волн обладают также и некоторые жидкие тела, например раствор сахара, виннокаменная кислота, растворы ее солей и др..

В зависимости от пространственной структуры молекул или кристаллической решетки вещество может вращать плоскость поляризации по часовой стрелке (вправо, если смотреть навстречу лучу)или против часовой стрелки (влево).Поэтому говорят о двух модификациях оптически активных веществ (оптических изомерах) — правовращающих веществах (d – типа) и левовращающих (i - типа). Пространственные формы молекул i- и d-типа являются зеркальными отображениями друг друга: их нельзя совместить ни поворотом, ни перемещением (трансляцией). Оптическую активность многих веществ связывают с наличием асимметрического атома углерода, который, присоединяя различные атомы или радикалы, образует молекулы с зеркальной симметрией.

Модели зеркально-симметричных молекул яблочной кислоты изображены на рисунке 3. Молекулы сахара и других органических соединений содержат по нескольку асимметричных атомов углерода, что обусловливает возможность существования различных зеркально-симметричных структурных форм этих молекул.

Био установил на опыте, что угол поворота a плоскости поляризации пропорционален толщине l оптически активного вещества:

a=a₀ Сl. (1)

Величина a₀ характеризует оптическую активность жидкостей и называется постоянной удельного вращения. С – объёмная концентрация раствора активного вещества в неактивном растворителе. Следовательно, a₀ есть угол на который повернется плоскость поляризации при прохождении э/м волной единичной длины в растворе с единичной концентрацией вещества. Следует отметить, что в общем случае постоянная удельного вращения a₀ зависит от температуры оптически активного вещества и длины э/м волны. Поэтому при определении a указывают для какой длины волны и при какой температуре определялось a_ 

Т.о., измерив экспериментально угол поворота плоскости поляризации a, длину оптически активного вещества l и зная константу удельного вращения a, _ можно из _ формулы (1) определить концентрацию раствора С. Если же константа удельного вращения a_ _о неизвестна, но известна концентрация раствора С, то из формулы (1) можно найти константу удельного вращения a_ ₀

Описание экспериментальной установки

Установка для определения концентрации сахара в водном растворе представлена на рисунке 4:

Установка состоит из: источника света (лампа накаливания)-1, поляризатораа-2, изготовленного из поляроидной пленки, кварцевой пластинки-3 , зрительной трубы-4, трубки с исследуемым раствором или жидкостью-5, системы анализатора, которая состоит из неподвижного лимба-6, вращающегося фрикциона -7, анализатора -8, ручки настройки резкости -9.

В круговом поляриметре применен принцип выравнивания контрастов полей зрения, которые имеют место в поляриметре без трубки 5 и с трубкой 5, содержащей исследуемый раствор или жидкость.

В общем случае при вращении анализатора в поляриметре можно наблюдать три основных (наиболее контрастных) поля зрения:

1. Если оптические оси поляризатора и анализатора параллельны, то та площадь поля зрения, которая освещается световыми волнами, прошедшими через кварцевую пластинку, будет наиболее темной, в то время, как площадь, освещаемая световыми волнами, которые не проходили через кварцевую пластинку - наиболее светлой, т.е. освещенность данной площади будет максимальной (рис.5а).

2. Если оптические оси поляризатора и анализатора перпендикулярны, то площадь поля зрения, которая освещается световыми волнами, прошедшими через кварцевую пластинку, будет характеризоваться максимальной освещенностью, в то время как площадь освещаемая, световыми волнами, которые не проходили через кварцевую, пластинку - наиболее темной, т.е. освещенность данной площади будет минимальной (рис.5б).

3. Если угол между оптическим осями поляризатора и анализатора составляет 45⁰ , то все поле зрения будет освещено равномерно, причем освещенность в данном случае составит величину приблизительно равную 0.7 от максимально возможной (рис.5в).

Три наиболее контрастных поля зрения (рис.5(а-в)) в поляриметре можно наблюдать путем вращения фрикциона 7 (рис.4) по или против часовой стрелки, в результате чего также будет вращаться анализатор. Каждое из указанных полей зрения характеризуется определенным положением нониуса I или II на шкале лимба (в градусах). Таким образом, настроив поляриметр без трубки с исследуемым раствором сахара на какое-либо одно из тpёx указанных выше полей зрения, мы можем по нониусу I или II определить его положение в градусах a₀ _I или a₀ _II . Здесь a₀ _I - положение данного поля зрения по нониусу I, a₀ _II положение данного поля зрения по нониусу II. При введении в поляриметр трубки с раствором сахара контрастность поля зрения изменяется (ухудшается). Изменение контрастности происходит в результате вращения сахарным раствором плоскости поляризации, т.е. при прохождении э/м волной в растворе определённого пути плоскость поляризации поворачивается на определенный угол a. Для того, чтобы определить a, нужно путем вращения фрикциона 7 повернуть анализатор так, чтобы восстановить поле зрения (и его контрастность), которое наблюдалось в поляриметре до введения в него трубки с исследуемым раствором сахара. При этом положение нониуса I составит a₁ _I , а положение нониуса II - a₁ _II . Т.о. искомый угол поворота плоскости поляризации a будет равен:

или . (2)

Выполнение работы

1. Путем вращения фрикциона 7 настроить поляриметр (без трубки с исследуемым раствором) на одно из полей зрения, приведенных на рис.5(а-в).

2. Определить a₀ _I или a₀ _II .

3. Ввести в трубу поляриметра трубку с исследуемым раствором. Вращая фрикцион 7 настроить на изображение в поле зрения и определить a₁ _I или a₁ _II .

4. По формуле (1) вычислим угол вращения плоскости поляризации a, и затем из формулы найдём концентрацию С сахара в растворе (в данном эксперименте). Для водного раствора сахара константу удельного вращения a₀ , считать равной 0.08⁰ л/(г см) или 0.08⁰ см² /г. a₀ определяется при комнатной температуре. Источник света - лампа накаливай. Длина трубки составляет 20 см.

5.Для получения точного результата последовательность действий необходимо выполнить не менее 8-10 раз и произвести усреднение концентрации С по числу измерений.

6. Полученные результаты занести в таблицу 1.

Таблица 1

№ п/п	a₀ _I (a₀ _II )	a_II (a_III )	a=a_II -a₀ _I (a=a_III -a₀ _II )	C (кг/м³ )	C_ср (кг/м³ )	DС (кг/м³ )	δ(%)
1
….
10

7. Перечисленную в пунктах 1-5 последовательность действий повторите для других полей зрения и вычислите среднюю концентрацию на основе измерений, выполненных для каждого из трех полей зрения.

Большое число измерений обусловлено необходимостью, которая заключается в том, что настройка человеком поляриметра на выбранное поле зрения производится очень грубо, поскольку человеческий глаз обладает определенной "погрешностью". Например, погрешность отдельного измерения, в некоторых случаях, может составлять приблизительно 30 %. Известно, что с увеличением числа измерений ошибка убывает как , где N-число измерений. Т.о, проделав 30 измерений, Вы уменьшите ошибку приблизительно в 5,5 раз.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какой свет называется плоскополяризованным?

2. Для каких целей в данной работе используются поляроиды?

3. Какой угол должен быть между оптическими осями поляризатора и анализатора, чтобы в окуляре было видно:

а) поле зрения, изображенное на рис.5(а)?

б) поле зрения, изображенное на рис.5(б)?

в) поле зрения, изображенное на рис.5(в)?

4. В каких единицах выражается размерность постоянной удельного вращения?

5. От каких физических параметров зависит константа удельного вращения?

ЛИТЕРАТУРА

1. Сивухин Д. В. Общий курс физики. Т.3. Оптика. М.: Наука, 1985.- 752с.

2. Савельев И. В. Курс общей физики. Т.2. Электричество и магнетизм. Волны. Оптика. М.: Наука, 1988.- 496 c.

3. Фейнман Р., Лейтон Р., Сэндс М. Феймановские лекции по физике. Т.3-4. Излучение. Волны. Кванты. М.: Мир, 1977.- 496 с.

4. Крауфорд Ф. Берклеевский курс физики. Волны. М.: Наука, 1984.-512с.