| Скачать .docx |
Реферат: Елементи квантової фізики
1. Елементи квантової фізики
1.1. Корпускулярно - хвильовий дуалізм речовини
1.1.1. Ядерна модель атома. Теорія Бора і її затруднення.
1.1.2. Гіпотеза і формула де Бройля. Дослідне обгрунтування
корпускулярно - хвильового дуалізму речовини.
1.1.3. Співвідношення невизначеностей. Межі використання
законів класичної фізики.
1.1.1. Ядерна модель атома. Теорія Бора і її затруднення
До кінця 19-го сторіччя атом вважали неподільним. Однак відкриття цілого ряду нових фізичних явищ поставили це ствердження під сумнів. На початку 20-го сторіччя було висунуто кілька моделей будови атома. При допомозі цих моделей вчені пробували пояснити ряд незрозумілих експериментальних фактів - лінійність спектрів випромінювання газів при високій температурі, електричну нейтральність і стійкість атомів.
Першу спробу побудувати теорію будови атома в межах класичної фізики зробив у 1903 р. англійський фізик Д.Томсон. За гіпотезою Томсона атом уявлявся у вигляді сфери, яка рівномірно заповнена позитивним зарядом, в середині якої містяться електрони. Проте ця модель була неспроможна пояснити спектральні закономірності атомів. За цією гіпотезою число ліній у спектрі не повинно було перевищувати число електронів в атомі, тоді як в дійсності навіть у спектрі атома водню число ліній перевищувало 30. Крім того гіпотеза Томсона не спиралась на будь які дослідні дані.
Вирішальне значення для теорії будови атома мали досліди Резерфорда, який у 1913 році вивчав розсіяння пучка a - частинок при проходженні їх через тонку металеву фольгу. Ці досліди показали, що при проходженні через фольгу переважна більшість a - частинок зазнає дуже незначних відхилень, але знаходиться чимале число і таких частинок, які зазнають дуже великих відхилень на кут, більший 150°. Таке значне розсіяння a - частинок могло статися тільки під дією позитивного заряду атома. Електрони, маса яких майже у 8000 разів менша від a - частинки, не могли помітно вплинути на її рух. Проходження переважної більшості a - частинок вказували на те, що розміри позитивного заряду атома повинні бути значно меншими від розмірів атома. Знаючи заряд атома q = Z e можна було визначити для різних кутів розсіювання так звані прицільні відстані a - частинок від центрів атомів. Виявилося, що для золотої фольги для кутів розсіювання 150° прицільна відстань дорівнює 10-14 м. Якщо на такій відстані a - частинка і атом не взаємодіють, то це може означати лише одне - розміри позитивно зарядженої частини атома не перевищують 10-15 м.
Ці дослідні факти дали можливість Резерфорду описати ядерну модель атома: в центрі атома міститься позитивно заряджене ядро атома, розміри якого мають величину порядку 10-15 м, навколо ядра по замкнутих орбітах в об’ємі сфери радіусом порядку 10-10 м обертаються електрони, причому їх кількість дорівнює порядковому номеру елемента.
В такому вигляді ядерна модель атома зберегла своє значення і до нашого часу, хоч і зазнала багатьох уточнень.
На кожний рухомий електрон в атомі діє доцентрова сила ядра, яка дорівнює кулонівській силі притягання електрона до ядра. Ця сила забезпечує стійкий орбітальний рух електрона в атомі, подібно орбітальному руху планет в сонячній системі.
Однак планетарна модель атома незабаром виявилась неприйнятною. Дійсно, електрони рухаючись в атомі з доцентровими прискореннями, згідно теорії Максвелла повинні випромінювати енергію у вигляді електромагнітних хвиль, що робить атоми не стійкими. Насправді атоми досить стійкі і при невисоких температурах енергії не випромінюють і не поглинають. В той же час при високих температурах будь-які атоми, перебуваючи у газоподібному стані, випромінюють електромагнітні хвилі у вигляді лінійчатих спектрів.
Вихід із затруднень знайшов датський фізик Нільс Бор. В основу нової моделі атома була покладена планетарна модель Резерфорда. Бор висунув припущення, що рух електронів в атомі, випромінювання і поглинання атомами електромагнітних хвиль підпорядковуються не класичним законам, а квантовим.
Ці закони Бор сформулював у вигляді наступних постулатів:
1. Електрони, які рухаються в атомі на окремих стаціонарних рівнях, не випромінюють і не поглинають електромагнітних хвиль. В стаціонарних станах атома електрони рухаються вздовж колових орбіт, які мають дискретні значення моменту імпульсу.
m
u
rn
= n![]() , (1.1)
, (1.1)
де m
- маса електрона; u
![]() - лінійна швидкість орбітального руху; rn
- радіус n-ї колової орбіти; n
- порядковий номер стаціонарного рівня - головне квантове число;
- лінійна швидкість орбітального руху; rn
- радіус n-ї колової орбіти; n
- порядковий номер стаціонарного рівня - головне квантове число; ![]() - стала Планка поділена на 2
p
(
- стала Планка поділена на 2
p
(![]() =
h
/ 2
p
).
=
h
/ 2
p
).
2. При переході електрона з однієї стаціонарної орбіти на іншу випромінюється або поглинається квант енергії
h n = En2 - En1 , (1.2)
який дорівнює різниці енергій двох стаціонарних рівнів атома .
Зміст формули (1.2) має принципове значення. Він виражає два нових фундаментальних ствердження:
а) енергетичний c спектр атома дискретний;
б) частоти атомного випромінювання пов’язані з атомними рівнями.
Величезна заслуга Нільса Бора перед наукою полягає в тому, що він вперше усвідомив дискретність енергетичного спектра атома. Історичний дослід Франка і Герца був першою дослідною перевіркою цих передбачень.
Однак теорія Бора має ряд внутрішніх протиріч:
З одного боку в ній використовуються закони класичної фізики, а з іншого боку вона базується на квантових постулатах. Так результати теорії вивчення випромінювання атома водню і воднево подібних атомів блискуче співпали з експериментом. Теорія Бора також пояснила причину випромінювання лінійчатих спектрів складними атомами, періодичний закон Менделєєва і закон Мозлі. Однак залишалось не виясненим: Чому рух електронів в атомах підпорядкований двом постулатам Бора? Чому одні лінії спектра досить інтенсивні, а інші ні? Чому здійснюються лише певні переходи електронів в атомах при випромінюванні і поглинанні ними енергії?
Досить значним недоліком теорії Бора була неможливість описати з її допомогою будову атома гелію, наступного за атомом водню елемента.
Відповіді на поставлені запитання дала квантова механіка, в якій на принципово новій основі установлені закономірності руху електронів в атомах і будь-яких частинок в інших системах.
1.1.2. Гіпотеза і формула де Бр o йля. Дослідне обґрунтування
корпускулярно хвильового дуалізму речовини
Дослідження Макса Планка і Альберта Ейнштейна взаємодії світла з речовиною є початком квантової теорії електромагнітного випромінювання. З квантової точки зору світло - це фотони з енергією Е і імпульсом Р :
Е = h n ,
Р = h / l . (1.3)
Ліві частини системи (1.3) є ознаками частинок (корпускул), а праві частини (частота і довжина хвилі) є ознаками електромагнітних хвиль. В формулах (1.3) відображено дуалізм (хвиля-частинка) світла. Світло з одного боку схоже на газ, який складається з фотонів з енергією Е і імпульсом Р . З другого боку він є неперервною електромагнітною хвилею з частотою v . В різних експериментальних умовах світло проявляє або корпускулярні, або хвильові властивості.
В 1924 році французький фізик Луї де Бройль висунув гіпотезу, яка незабаром знайшла дослідне підтвердження, згідно якої кількісні співвідношення частинок, такі ж, як і для фотонів. Сміливість гіпотези де Бройля полягає якраз в тому, що співвідношення (1.3) постулюються не лише для фотонів, але і для інших мікрочастинок, які мають масу спокою. Таким чином, будь-якій мікрочастинці, імпульс якої Р= m u , відповідає хвиля з імпульсом P = h / l .
Тому
![]()
![]() ,
, ![]() (1.4)
(1.4)
де m - маса частини; u - швидкість руху частинки.
Формула (1.4) називається формулою де Бройля. Вона дає можливість оцінити довжину хвилі мікроскопічної частинки масою m , яка рухається з швидкістю u . У макроскопічних тіл ці властивості не проявляються. Так, у тіла масою 1 г, яке летить з швидкістю 10 м/с довжина хвилі де Бройля дорівнює
|
|
Жоден прилад не зможе зареєструвати таку коротку хвилю (на сьогодні реєструють довжини порядку 10-18 м).
У мікрочастинок (електрон, протон, нейтрон і ін.) маса співрозмірна з атомною одиницею маси, а тому довжина хвилі де Бройля при невеликих швидкостях може бути досить великою. Так, довжина хвилі електрона з кіне-тичною енергією 1 еВ дорівнює 13,3 . 10-10 м. Із збільшенням швидкості мікрочастинки довжина хвилі де Бройля зменшується, а при дуже великих швидкостях мікрочастинка веде себе як класична частинка.
В 1925 році після ознайомлення з дисертацією де Бройля, де описується корпускулярно-хвильовий дуалізм матерії, Ейнштейн пише Максу Борну так: «Прочитайте її! Хоч і відчувається, що цю дисертацію писав божевільний, але як солідно вона написана». Це говорить про те що в ті часи ідея де Бройля виглядала досить неправдоподібно із-за відсутності дослідного обґрунтування, яке б підтверджувало хвильові властивості елементарних частинок.
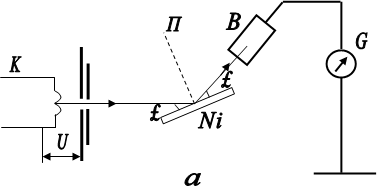
Лише в 1927 році американські фізики Девісон і Джермер виявили, що пучок електронів, який розсіювався від природної дифракційної гратки - монокристал нікелю - дає чітку дифракційну картину. Схема установки зображена на рис.1.1.
 |
Д
Рис. 1. 1
Електронний пучок, який вилітав з нагрітої нитки катода К, прискорювався полем з різницею потенціалів U , і проходячи через ряд діафрагм Д у вигляді досить вузького пучка падав на монокристал нікелю а . Іонізаційна камера В , яка з’єднувалась з гальванометром G , вимірювала величину струму І , пропорційну числу електронів, відбитих від грані монокристала нікелю. Кут a під час досліду залишався сталим.
![]() Дослід полягав в тому, що вимірювався струм І
через гальванометр, як функція прискорюваної різниці потенціалів U
. В результаті досліду було установлено, що при монотонній зміні прискорюваної різниці потенціалів U
, струм гальванометра змінювався не монотонно, а давав ряд максимумів. Графік залежності струму І
від величини Ö
U
показано на рис.2.
Дослід полягав в тому, що вимірювався струм І
через гальванометр, як функція прискорюваної різниці потенціалів U
. В результаті досліду було установлено, що при монотонній зміні прискорюваної різниці потенціалів U
, струм гальванометра змінювався не монотонно, а давав ряд максимумів. Графік залежності струму І
від величини Ö
U
показано на рис.2.
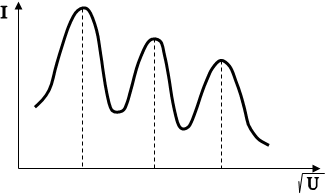 |
Рис. 1.2
Одержана залежність I
=
f
(
![]() )
характеризується рядом майже однаково віддалених максимумів сили струму. Звідси випливає, що відбивання електронів здійснюється лише при певних різницях потенціалів, тобто при відповідних швидкостях електронів.
)
характеризується рядом майже однаково віддалених максимумів сили струму. Звідси випливає, що відбивання електронів здійснюється лише при певних різницях потенціалів, тобто при відповідних швидкостях електронів.
Аналогічне явище спостерігається при відбиванні рентгенівських променів від кристала кварцу. Відбивання у певному напрямі характеризується кутом a згідно закону Вульфа-Брегга
2d sin a = k l , (1.5)
де l - довжина рентгенівської хвилі ; d - стала кристалічної гратки; k - порядок відбивання.
Порівнявши наведені факти, можна зробити висновок, що електронний пучок проявляє хвильові властивості і при цьому довжина хвилі електронного пучка залежить від швидкості електронів.
Дійсно, oскільки d й a в умовах досліду є незмінними, виконання умови (1.5) з хвильової точки зору визначається значенням довжини хвилі l . Числову відповідність результатів розсіювання електронного пучка з умовою (1.5) можна одержати, якщо довжину хвилі електронного пучка l зв’язати з швидкістю u електронів за допомогою формули де Бройля
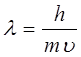 ,
(1.6)
,
(1.6)
де h - стала Планка ; m - маса електрона.
Швидкість електронів u , які пройшли прискорювану різницю потенціалів U знайдемо з умови
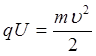 . (1.7)
. (1.7)
Звідки
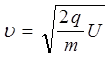 . (1.8)
. (1.8)
Підставивши (1.8) в (1.6), одержимо:
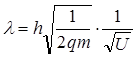 . (1.9)
. (1.9)
Довжину хвилі з (1.9) підставимо в (1.5)
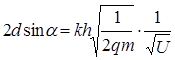 . (1.10)
. (1.10)
Рівність (1.10) визначає ті значення різниці потенціалів U , при яких струм І через гальванометр досягає максимумів.
Так як в умовах досліду кут a є сталим, то для різних максимумів, при певних значеннях k з (1.10) маємо
![]() , (1.11)
, (1.11)
де 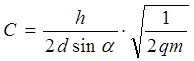 - стала величина в умовах цього досліду.
- стала величина в умовах цього досліду.
Таким чином, значення U , які відповідають максимумам струму І , відрізняються між собою на сталу величину С .
Дещо інший варіант цього досліду здійснив Тартаковський, який спостерігав дифракцію повільних електронів при проходженні ними тонкої алюмінієвої фольги. Схему досліду Тартаковського зображено на рис.1.3.
 |
Рис.1.3.
На рис.1.3 К - нагрітий катод, який є джерелом електронів; А - сітка, яка створює прискорюване поле для цих електронів; Д - діафрагма, яка дозволяє виділити вузький пучок електронів; В - алюмінієва фольга; Е - пластинка з двома круглими отворами, через які можуть пройти лише ті електрони, які розсіялись під кутом a . Далі розміщена пластина F , з’єднана з електрометром G , за допомогою якого вимірюють електричний струм I .
Дослід полягав у вимірюванні електричного струму I , як функції прискорюваної різниці потенціалів U . В цьому випадку розрахунок дифракційної картини повністю співпадає з експериментальними результатами, якщо довжина хвилі електрона визначається формулою (1.6).
Слід відмітити, що експериментальним методом виявлено хвильові властивості у нейтральних атомів і молекул, а також і у нейтронів.
1.1.3. Співвідношення невизначеностей. Межі використання
законів класичної фізики
В класичній механіці траєкторія руху тіла характеризується точними значеннями координати x ( t ) і імпульсу p ( t ) в довільний момент часу t , причому ці два параметри зв’язані між собою. Наприклад, рівномірний і прямолінійний рух тіла масою m з швидкістю u виражається координатою х( t ) = u t і імпульсом p ( t )= m u , звідки одержуємо, що х( t )= p ( t ) t / m .
В мікросвіті частинки проявляють при одних умовах хвильові властивості, при інших умовах - корпускулярні. Якщо виходити лише з корпускулярних властивостей , то згідно теорії Н. Бора можна визначити точне значення координати частинки в просторі. У випадку хвильових властивостей елементарних частинок поняття координати хвилі немає фізичного змісту.
В квантовій фізиці з урахуванням хвильових властивостей частинок показано, що у частинки не існує одночасно точних значень координат і імпульсу і що ці величини між собою навіть не пов’язані. Якщо імпульс частинки має точне значення, то її місце знаходження невизначене і навпаки. Така закономірність мікросвіту відображена співвідношеннями невизначеностей Гейзенберга.
Розглянемо дифракцію електронів на одній щілині. Нехай пучок електронів з швидкістю u летить в напрямі осі OY так, як це показано на рис. 1.4.
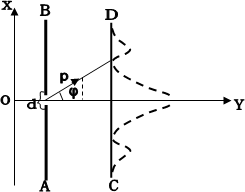 |
Рис.1.4
Екран АВ з щілиною шириною d розміщено перпендикулярно до пучкаa. На другому екрані СД одержано розподіл інтенсивності, який співпадає з розподілом інтенсивності при дифракції світла від однієї щілини. На рис. 1.4 цей розподіл зображено пунктирною лінією. Максимум нульового порядку одержано при куті дифракції j , який задовольняє умові :
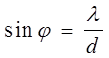 , (1.12)
, (1.12)
де l - довжина хвилі, яка відповідає пучку електронів.
З рис. 1.4 видно, що переважна більшість електронів формують нульовий максимум, тому вторинними максимумами в цьому випадку можна знехтувати. Якщо уявити електрони у вигляді механічних частинок, то можна стверджувати, що при їх русі з швидкістю u в напрямі осі OX їх положення визначається з точністю до ширини щілини, тобто
![]() . (1.13)
. (1.13)
В той же час, внаслідок дифракції змінюється напрям швидкості частинок. Враховуючи лише ті електрони, які формують центральний максимум дифракції, похибку у визначенні проекції імпульсу на напрям осі OX знайдемо із умови
![]() . (1.14)
. (1.14)
З урахуванням (1.12) і (1.13) одержимо
![]() . (1.15)
. (1.15)
А так як не всі електрони формують центральний максимум, тому
![]() , (1.16)
, (1.16)
де Dx і Dpx - похибки у визначені координати і імпульсу частинки; h - стала Планка.
Співвідношення (1.16) можна узагальнити для всіх напрямків, тому:
![]() ,
,
![]() , (1.17)
, (1.17)
![]() .
.
Це і є співвідношення невизначеностей Гейзенберга.
Так як точні значення координати і імпульсу для мікрочастинки не існують, то про траєкторію частинки в мікросвіті можна говорити лише з певним наближенням. З цієї точки зору електрони в атомі не мають точних значень електронних орбіт.
В квантовій теорії використовується також співвідношення невизначеностей для енергії Е і часу t , тобто невизначеності цих параметрів задовольняють умові
![]() , (1.18)
, (1.18)
де D E - похибка у визначенні енергії частинки; D t - похибка у визначенні часу, коли частинка має енергію E .
Cпіввідношення невизначеностей неодноразово були предметом філо-софських дискусій. Однак вони не виражають собою яких небуть обмежень пізнання мікросвіту, а лише указують межі використання в таких випадках понять класичної механіки.
1.2.Основні поняття квантової механіки
1.2.1. Поняття стану частинки в квантовій механіці. Хвильова
функція і її статистичний зміст. Стандартні умови.
1.2.2 Загальне (часове) рівняння Шредінгера.
1.2.3. Рівняння Шредінгера для стаціонарних станів.
1.2.1. Подання стану частинки в квантовій механіці. Хвильова
функція і її статистичний зміст. Стандартні умови
В класичній механіці при одномірному русі вздовж осі х
стан частинки в кожний момент часу t
задається двома величинами: координатою частинки x
(
t
)
і її швидкістю ![]() або імпульсом частинки
або імпульсом частинки ![]() . Таке визначення стану частинки є головним вихідним моментом побудови класичної механіки.
. Таке визначення стану частинки є головним вихідним моментом побудови класичної механіки.
В фізиці мікрочастинок з наявністю у них хвильових властивостей, класичне визначення стану частинки втрачає будь-який зміст, а з ним і поняття сили, яка за визначенням є функцією класичного стану.
Встановити фізичний зміст квантового стану допомогло відкриття корпускулярно-хвильового дуалізму матерії. В квантовій фізиці стан частинки задається хвильовою функцією, яка є комплексною величиною і визначається у всіх точках простору і в будь-який момент часу.
Аналогічно класичним хвилям рух елементарних частинок характеризується хвилями де Бройля.
Рівняння хвилі де Бройля елементарної частини називається хвильовою функцією і позначається![]() . Хвильова функція Y
(
r
,
t
)
не має жодного відношення до механічних хвиль. Класичні хвилі поширюються в пружних середовищах, а елементарні частинки можуть рухатись також і у вакуумі. Слід мати на увазі, що хвилі де Бройля властиві будь-яким частинкам, як зарядженим так і нейтральним, в той час як електромагнітні хвилі випромінюються лише зарядженими частинками при їх прискореному русі.
. Хвильова функція Y
(
r
,
t
)
не має жодного відношення до механічних хвиль. Класичні хвилі поширюються в пружних середовищах, а елементарні частинки можуть рухатись також і у вакуумі. Слід мати на увазі, що хвилі де Бройля властиві будь-яким частинкам, як зарядженим так і нейтральним, в той час як електромагнітні хвилі випромінюються лише зарядженими частинками при їх прискореному русі.
Для класичних хвиль характерні найбільш суттєві властивості, такі як енергія, імпульс, інтенсивність, яка визначається квадратом амплітуди хвилі.
Поняття фізичного змісту хвильової функції прийшло після того, як вияснилось, що в інтерференції хвиль де Бройля проявляються властивості окремих частинок, а не їх системи. Це підтверджується незалежністю інтерференції від інтенсивності частинок в пучку. Інтерференція спостерігається навіть в тих випадках, коли за час польоту від джерела до детектора пролітає лише одна частинка. Цей факт можна тлумачити так лише у випадках, коли рух будь-якої мікрочастинки підпорядковується статистичним закономірностям.
За аналогією з класичними хвилями знайдемо фізичний зміст квадрата модуля хвильової функції
![]() , (1.19)
, (1.19)
де ![]() -функція, комплексно спряжена до
-функція, комплексно спряжена до ![]()
![]()
В досліді Девісона і Джермера, схема якого показана на рис.1.1 встановлено, що струм, який реєструється гальванометром, пропорційний квадрату модуля хвильової функції
![]() . (1.20)
. (1.20)
З іншого боку величина цього струму пропорційна також об’єму детектора dV
![]() . (1.21)
. (1.21)
З урахуванням (1.20) і (1.21) маємо:
![]() . (1.22)
. (1.22)
Якщо імовірність попадання частинок в детектор дорівнює dp , то величина струму гальванометра буде також пропорційною величині цієї імовірності
I = k 2 dp . (1.23)
Прирівнявши рівності (1.22) і (1.23), одержимо:
![]() . (1.24)
. (1.24)
Завжди можна вибрати значення хвильової функції такою, щоб k 1 = k 2. Тоді (1.24) набуде вигляду
![]() . (1.25)
. (1.25)
Звідки
![]() . (1.26)
. (1.26)
Квадрат модуля хвильової функції (1.26) визначає густину імовірності виявити частинку в точці з радіусом-вектором ![]() в момент часу t
. Квантова механіка на відміну від класичної дає імовірнісне пояснення квантового стану, а хвильова функція має статичний зміст.
в момент часу t
. Квантова механіка на відміну від класичної дає імовірнісне пояснення квантового стану, а хвильова функція має статичний зміст.
При відомій хвильовій функції рівність (1.26) дозволяє визначити імовірність виявити частинку в об’ємі dV
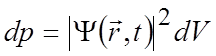 .
(1.27)
.
(1.27)
Якщо частинка знаходиться в довільній точці простору, то ця подія є достовірною, а імовірність такої події дорівнює одиниці, тобто
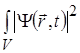 dV
=1.
(1.28)
dV
=1.
(1.28)
Умова (1.28) називається умовою нормування.
Як бачимо, квантова механіка має статистичний характер; у ній не ставиться питання про знаходження положення частинки або її траєкторії в просторі, так як завдяки хвильових властивостей мікрочастинок такі питання взагалі втрачають зміст. В квантовій механіці за допомогою хвильової функції ![]() визначається лише імовірність виявлення мікрочастинки в різних точках простору. З сказаного випливає, що хвильова функція
визначається лише імовірність виявлення мікрочастинки в різних точках простору. З сказаного випливає, що хвильова функція ![]() повинна задовольняти певним обмежувальним умовам, які ще називаються стандартними умовами
: воно має бути скінченою, однозначною і неперервною
, так як імовірність не може бути більшою за 1; бути неоднозначною і змінюватись стрибкоподібно.
повинна задовольняти певним обмежувальним умовам, які ще називаються стандартними умовами
: воно має бути скінченою, однозначною і неперервною
, так як імовірність не може бути більшою за 1; бути неоднозначною і змінюватись стрибкоподібно.
1.2.2. Загальне часове рівняння Шредінгера і його аналіз
В класичній механіці рівняння одновимірного руху частинки дозволяє
одержати її координату x ( t ) і імпульс p ( t ) за їх початковими значеннями x (0) і p (0) . Таким рівнянням руху є другий закон Ньютона.
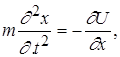 (1.29)
(1.29)
де m
- маса частинки; ![]() - прискорення руху частинки;
- прискорення руху частинки;
![]() - градієнт потенціальної енергії, зміна якої визначається діючою силою.
- градієнт потенціальної енергії, зміна якої визначається діючою силою.
З визначення квантового стану рівняння руху квантової частинки має задавати зміну в часі хвильової функції ![]() . Так як квантовий стан характеризує лише одна хвильова функція, то відповідне квантове рівняння руху повинно містити лише першу похідну за часом від хвильової функції. В інших випадках таке рівняння не буде погоджуватись з визначенням квантового стану .
. Так як квантовий стан характеризує лише одна хвильова функція, то відповідне квантове рівняння руху повинно містити лише першу похідну за часом від хвильової функції. В інших випадках таке рівняння не буде погоджуватись з визначенням квантового стану .
Рівняння руху квантової нерелятивістської частинки в силовому полі називається рівнянням Шредінгера, так як вперше в 1926 році було сформульовано німецьким фізиком Е. Шредінгером.
Справедливість цього рівняння обгрунтована тим, що всі висновки які випливають із нього, знайшли своє експериментальне підтвердження. Рівняння Шредінгера відіграє в квантовій механіці таку ж роль, як і рівняння Ньютона в класичній.
В загальному випадку рівняння Шредінгера має вигляд
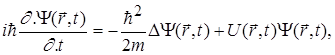 (1.30)
(1.30)
де m
- маса частинки ; ![]() - потенціальна енергія частинки в силовому полі;
- потенціальна енергія частинки в силовому полі;![]() - уявна одиниця;
- уявна одиниця; ![]() - стала Дірка;
- стала Дірка;
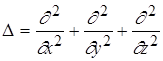 - оператор Лапласа.
- оператор Лапласа.
Із-за присутності в рівнянні Шредінгера (1.30) уявної одиниці хвильова функція ![]() , яка задовольняє цьому рівнянню, завжди комплексна. Не кожна функція може бути розв’язком рівняння (1.30). Перш за все ця функція повинна бути скінченою, неперервною і мати неперервні перші похідні. Ці вимоги мають чисто математичний характер. Крім того - хвильова функція повинна бути однозначною , інакше буде порушений її фізичний зміст.
, яка задовольняє цьому рівнянню, завжди комплексна. Не кожна функція може бути розв’язком рівняння (1.30). Перш за все ця функція повинна бути скінченою, неперервною і мати неперервні перші похідні. Ці вимоги мають чисто математичний характер. Крім того - хвильова функція повинна бути однозначною , інакше буде порушений її фізичний зміст.
Рівняння Шредінгера за часом є лінійним диференціальним рівнянням 1-го порядку. Із теорії диференціальних рівнянь відомо, що кожне лінійне рівняння в частинних похідних повинно мати безліч розв’язків, причому таких, що всяка лінійна комбінація будь-якої сукупності розв’язків теж буде його розв’язком.
Слід зауважити, що рівняння Шредінгера, подібно до законів Ньютона в класичній механіці, не є результатом якогось теоретичних доведень, а є узагальненням багатьох дослідних фактів, встановлених при вивченні мікросвіту. Відмітимо також, що рівняння Шредінгера описує рух частинок, швидкість яких значно менша швидкості світла, так як співвідношення між кінетичною енергією і імпульсом справедливе лише при цих умовах. В релятивістському випадку для описання хвильових властивостей мікрочастинок слід користуватись іншими рівняннями, наприклад рівняннями Дірака чи Клейна-Гордона.
1.2.3. Рівняння Шредінгера для стаціонарних станів
Потенціальна енергія частинки залежить від координат x
,
y
,
z
і часу t
. Якщо потенціальна енергія U
від часу не залежить і відповідно повна енергія також не змінюється з часом, то хвильову функцію ![]() можна подати у вигляді добутку двох співмножників
можна подати у вигляді добутку двох співмножників
![]() . (1.31)
. (1.31)
Перший співмножник в (1.31) залежить лише від часу, а другий - лише від координат (![]() ).
).
Розв’язки рівняння Шредінгера, для яких потенціальна енергія, а також густина імовірностей не змінюються з часом, називаються стаціонарними. Стаціонарні стани не виключають залежності хвильової функції від часу, а лише обмежують її гармонічним законом ![]() .
.
Підставимо хвильову функцію (1.31) в рівняння Шредінгера (1.30)
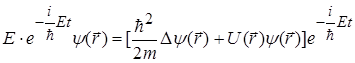 .
.
Після скорочення на експоненту, одержуємо:
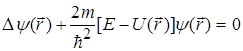 , (1.32)
, (1.32)
де 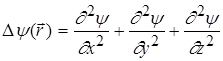 ; Е
- повна енергія частинки;
; Е
- повна енергія частинки; ![]() - потенціальна енергія частинки , яка є функцією лише координат;
- потенціальна енергія частинки , яка є функцією лише координат; ![]() - хвильова функція; m
- маса частинки;
- хвильова функція; m
- маса частинки; ![]() - стала Дірака (
- стала Дірака (![]() ).
).
Стаціонарне рівняння Шредінгера (1.32) є однорідним лінійним диференціальним рівнянням другого порядку відносно координат x
,
y
,
z
. У випадку, коли ![]() =0
, це рівняння не має фізичного змісту. В рівнянні Шредінгера для стаціонарних станів є єдиний вільний параметр - повна енергія частинки Е
. При деяких значеннях повної енергії це рівняння може мати нульові розв’язки. Ті значення повної енергії, при яких рівняння (1.32) буде мати нульові розв’язки, називаються власними значеннями. Кожному такому власному значенню енергії відповідає свій розв’язок рівняння (1.32).
=0
, це рівняння не має фізичного змісту. В рівнянні Шредінгера для стаціонарних станів є єдиний вільний параметр - повна енергія частинки Е
. При деяких значеннях повної енергії це рівняння може мати нульові розв’язки. Ті значення повної енергії, при яких рівняння (1.32) буде мати нульові розв’язки, називаються власними значеннями. Кожному такому власному значенню енергії відповідає свій розв’язок рівняння (1.32).
Стаціонарне рівняння Шредінгера дає не лише значення хвильової функції, але й значення цієї функції в стаціонарних станах.
1.3. Найпростіші задачі квантової механіки
1.3.1. Рух вільної частинки.
1,3.2. Частинка в одновимірному потенціальному ящику.
1.3.3. Гармонічний квантовий осцилятор.
1.3. 4. Проходження частинки крізь потенціальний бар’єр.
Тунельний ефект.
1.3.1. Рух вільної частинки
Найпростішим рухом квантової частинки є вільний рух. Прикладом такого руху є рух електронів в металах і напівпровідниках. В цьому випадку потенціальна енергія частинок дорівнює нулю. При вільному русі повна енергія частинки збігається з кінетичною, а її швидкість є сталою величиною. Такому рухові в класичній механіці відповідає рівномірний і прямолінійний рух.
Нехай рівномірний рух квантової частинки відбувається в напрямі осі х , яка співпадає з напрямком вектора швидкості. Стаціонарне рівняння Шредінгера для вільної частинки запишеться:
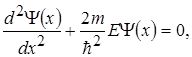 (1.33)
(1.33)
де m - маса частинки; Е - повна енергія частинки.
Рівняння (1.33) є диференціальним рівнянням другого порядку з сталими коефіцієнтами, розв’язком якого може бути функція
![]() (1.34)
(1.34)
де А і к - сталі величини; і - уявна одиниця.
Підстановка (1.34) в (1.33) дасть тотожність
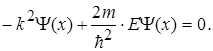
Звідки 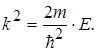 (1.35)
(1.35)
В співвідношенні (1.35) к - хвильове число хвиль де Бройля; Е - повна енергія частинки; m - маса частинки.
Енергія вільної частинки із рівності (1.35) дорівнює
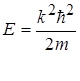 (1.36)
(1.36)
Хвильове число к може набувати довільних значень, так як вільні частинки в системі можуть мати практично будь-які постійні швидкості. Це говорить про те, що енергетичний спектр вільних частинок є суцільним.
Густина імовірності перебування вільної частинки в довільних точках осі х дорівнює
![]()
де ![]() - комплексна спряжена хвильова функція. Звідки
- комплексна спряжена хвильова функція. Звідки
![]()
Густина імовірності вільної частинки в будь-якій точці осі х є сталою величиною. Невизначеності вільної частинки в координаті в такому випадку дорівнюють безмежності. Цей висновок є добрим підтвердженням співвідношення невизначеностей Гейзенберга.
1.3.2. Частинка в одновимірному потенціальному ящику
Розглянемо приклад просторово-обмеженого одновимірного руху квантової частинки в глибокому потенціальному ящику з вертикальними стінками, шириною l . Потенціальна енергія електрона зовні і всередині такого ящика має наступні значення:
![]()
![]() U
(
x
)=0
при 0
<
x
<
l
, (1.37)
U
(
x
)=0
при 0
<
x
<
l
, (1.37)
U ( x )= ¥ при x £ 0 й x ³ l
![]()
Графік залежності потенціальної енергії частинки U ( x ) від х показаний на рис 1.5.
Частинка в такому ящику може вільно рухатись на ділянці 0<х<l . На кінцях цього інтервалу вона стикається з абсолютно твердими стінками. Непрозорість цих стінок визначається необмеженим ростом потенціальної енергії U ( x ) в точках х=0 і х =l .
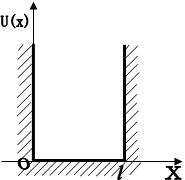 |
Рис. 1.5
Прикладом руху електрона в потенціальному ящику може бути рух колективізованих електронів усередині металу. Як відомо, в класичній електронній теорії вважали, що поза металом потенціальна енергія електрона дорівнює нулю, а всередині металу - вона від’ємна і чисельно дорівнює роботі виходу електрона з металу. Інакше кажучи, вважали, що рух електронів обмежений потенціальним бар’єром прямокутної форми з плоским дном. В нашому випадку потенціальний ящик значно простішої форми ніж реальний випадок електрона в металі.
Так як частинка не виходить за межі ділянки 0
<
х
<
l
, то імовірність знайти її за межами цієї ділянки дорівнює нулю. Це означає, що рівняння Шредінгера для стаціонарних станів можна доповнити граничними умовами ![]() і
і ![]()
Запишемо рівняння Шредінгера для частинки в потенціальному ящику
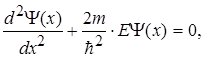 (1.38)
(1.38)
де m
- маса частинки; ![]() - стала Дірака; Е
- повна енергія частинки; Y
(х)
- хвильова функція.
- стала Дірака; Е
- повна енергія частинки; Y
(х)
- хвильова функція.
Введемо позначення
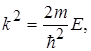 (1.39)
(1.39)
де к - хвильове число хвиль де Бройля для електрона, який перебуває усередині потенціального ящика.
Рівняння (1.38) набуде вигляду
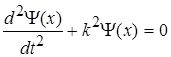 (1.40)
(1.40)
Знайдемо розв’язок рівняння (1.40), подібно до аналогічних диференціальних рівнянь гармонічних коливань, в тригонометричній формі
![]() (1.41)
(1.41)
де А,В і С - сталі величині.
З граничних умов одержуємо:
а) Y (0)=0 ; 0=А cosB . 0+ CsinB . 0
Звідки А=0 ; В ¹ 0 і С ¹ 0 .
б) Y ( l)=0 ; 0=CsinB. l .
звідки при С
¹
0, В
l
=
n
p
, або ![]() де n
= 1,2,3.
.......
де n
= 1,2,3.
.......
Хвильова функція з урахуванням граничних умов набуде вигляду:
![]() (1.42)
(1.42)
Константу С у формулі (1.42) знайдемо із умови нормування
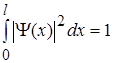 (1.43)
(1.43)
або
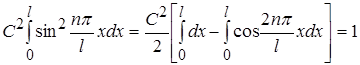 . (1.44)
. (1.44)
Другий інтеграл у виразі (1.44) при будь-яких значеннях n дорівнює нулю, тому
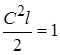 звідки
звідки 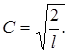
Хвильова функція, яка описує квантовий рух частинки в потенціальному ящику має вигляд:
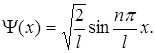 (1.45)
(1.45)
При підстановці (1.45) в (1.38) одержуємо тотожність:
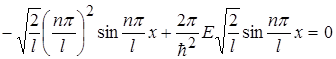 .
.
Звідки
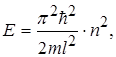 (1.46)
(1.46)
тобто енергія Е електрона в потенціальному ящику не може бути довільною. Вона набуває лише дискретних власних значень Е(n). Імовірність виявити в межах потенціального ящика електрон з іншою енергією, ніж (1.46) дорівнює нулю.
Енергетичний спектр і густина імовірності частинки в потенціальному ящику показана на рис. 1.6.
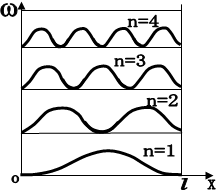 |
Рис.1.6
Число n в формулі (1.46) визначає вид хвильової функції і енергію частинки в стані з цією хвильовою функцією, називається квантовим числом
. Покажемо, що для частинки в потенціальному ящику можливі лише такі енергетичні рівні, на яких викладається ціле число півхвиль де Бройля. При аналізі граничних умов було показано, що kl
=
n
p
, де ![]() - хвильове число хвиль де Бройля. З урахуванням останнього маємо:
- хвильове число хвиль де Бройля. З урахуванням останнього маємо:
![]() (1.47)
(1.47)
Співвідношення (1.47) показує, що в потенціальному ящику можливі лише такі стани частинки, при яких на ширині потенціального ящика l вкладається ціле число півхвиль де Бройля (Рис.1.7).
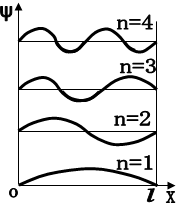 |
Рис 1.7
Незбуреному стану частинки відповідає енергія
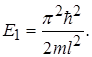 (1.48)
(1.48)
Значення цієї енергії Е1 > 0 свідчить про те, що частинка в потенціальному ящику ніколи не зупиняється і що невизначеність D Рх імпульсу частинки не може бути меншою за величину
![]() (1.49)
(1.49)
Однак в потенціальному ящику шириною l положення частинки визначається похибкою, яка співрозмірна з шириною ящика Dх»l
Тому
D
х.
D
Рх
³
p
![]() ,
(1.50)
,
(1.50)
що перебуває у повній відповідності із співвідношенням невизначеностей імпульс - координата.
Покажемо, як залежить ширини енергетичного інтервалу D Е від розмірів потенціального ящика. У потенціальному ящику з розмірами l =10-9 м. Власні значення енергії електрона утворюють послідовність енергетичних рівнів, енергетична відстань між якими дорівнює
D E=En+1 -En .
Або
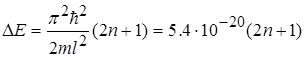 Дж.
Дж.
В електрон-вольтах ця енергія дорівнює
![]()
Коли ширина потенціального ящика співрозмірна з розмірами атома, енергетичний інтервал між сусідніми енергетичними рівнями досить значний, а спектр є дискретним.
У випадку, коли потенціальний ящик має мікроскопічні розміри l » 10-2 м ., енергетичний інтервал між сусідніми рівнями дорівнює
![]() Дж=0,34.
10-14
(2n+1) eB.
Дж=0,34.
10-14
(2n+1) eB.
Для такого потенціального ящика квантуванням енергії можна знехтувати. Вона нічим не відрізняються від значень енергії, одержаних класичними методами.
Аналогічні результати можна одержати для великих квантових чисел n . У цьому випадку проявляється принцип відносності, встановлений Бором у 1923р.
При великих квантових числах висновки і результати квантової механіки збігаються з відповідними класичними результатами.
1.3.3. Гармонічний квантовий осцилятор.
Просторово-обмеженим є також рух квантового осцилятора. З класичної точки зору осцилятором може бути будь-яка матеріальна точка, яка здійснює гармонічні коливання під дією квазіпружної сили.
F
=-
kx
, де k
=
m
![]() (1.51)
(1.51)
Потенціальна енергія класичного осцилятора знаходиться за формулою
![]()
де m
- маса частинки; ![]() - циклічна частота осцилятора.
- циклічна частота осцилятора.
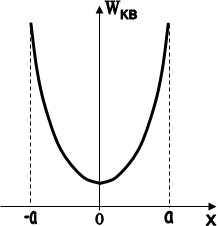 Графічна залежність енергії класичного осцилятора показана на рис.1.8.
Графічна залежність енергії класичного осцилятора показана на рис.1.8.
Рис. 1.8
.
З рисунка видно, що осцилятор може мати практично довільну енергію, навіть рівну нулю. В точках -а і +а кінетична енергія осцилятора дорівнює нулю, а потенціальна енергія досягає свого максимуму. За межі області (-а, +а) класичний осцилятор вийти не може.
Квантовим осцилятором може бути лише елементарна частинка, яка поряд з корпускулярними властивостями проявляє і хвильові властивості. Прикладом квантового осцилятора може бути коливний рух атомів і молекул у вузлах кристалічної гратки. Потенціальна енергія квантового осцилятора має таку ж математичну залежність, що і класичний осцилятор (1.52).
Стаціонарне рівняння Шредінгера для лінійного гармонічного осцилятора має вигляд:
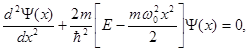 (1.53)
(1.53)
де m
- маса квантової частинки; ![]() - циклічна частота; Е
- повна енергія частинки.
- циклічна частота; Е
- повна енергія частинки.
Знаходження хвильових функцій квантового осцилятора є досить складною математичною задачею. Тому, опускаючи такі розв’язки, наводимо енергетичний спектр квантового осцилятора. Він має вигляд
![]() (1.54)
(1.54)
де n
= 0,1,2,3,
..... - любе ціле число, починаючи з нуля; ![]() - циклічна частота;
- циклічна частота; ![]() - стала Дірака.
- стала Дірака.
Аналіз рівняння (1.54) показує, що енергетичний спектр квантового осцилятора є дискретним і що власні значення енергії дорівнюють:
![]()
![]()
![]()
В енергетичному спектрі (1.54) проміжки між енергетичними рівнями не залежать від квантового числа n , а є однаковими
![]() (1.55)
(1.55)
Як показано на рис. 1.9, де енергетичний спектр квантового осцилятора суміщається з аналогічним спектром класичного осцилятора, квантовий осцилятор не має значень енергії, рівних нулю.
Найменше значення енергії квантового осцилятора дорівнює
![]() (1.56)
(1.56)
Меншої енергії квантовий осцилятор не може мати навіть при абсолютному нулі температур.
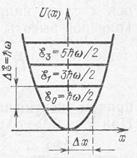
Рис. 1.9
Покажемо наближеним способом, що енергія квантового осцилятора квантується. З рис 1.10 видно, що на відрізку l =2х0 вкладається ціле число півхвиль де Бройля, тобто
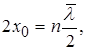 (1.57)
(1.57)
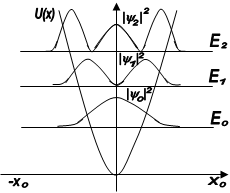 |
Рис 1.10
де ![]() - середнє значення довжини хвилі де Бройля.
- середнє значення довжини хвилі де Бройля.
Звідки
![]() (1.58)
(1.58)
Середнє значення імпульсу кванта хвилі де Бройля
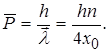 (1.59)
(1.59)
Середня кінетична енергія такого осцилятора
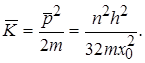 (1.60)
(1.60)
Відомо, що повна енергія Е перевищує середнє значення кінетичної енергії в два рази, тобто
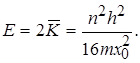 (1.61)
(1.61)
З іншої точки зору повна енергія квантового осцилятора дорівнюватиме максимальній потенціальній енергії
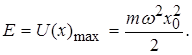 (1.62)
(1.62)
Перемножимо рівності (1.61) і (1.62)
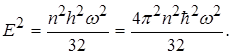 (1.63)
(1.63)
Або
![]() (1.64)
(1.64)
В межах точності наших міркувань ![]() »1, тому
»1, тому
![]() (1.65)
(1.65)
де n =1,2,3 ,... - цілі числа.
Наближений розрахунок показує, що енергія квантового осцилятора набуває ряду дискретних значень, тобто квантується.
Точне значення енергії квантового осцилятора для не збудженого, нульового рівня можна одержати із рівняння Шредінгера (1.53), якщо згідно рис. (1.10) скористатись функцією Гаусса, яка дорівнює
![]() (1.66)
(1.66)
де а - стала величина, яку слід визначити.
Другу похідну від (1.66) підставимо в (1.53)
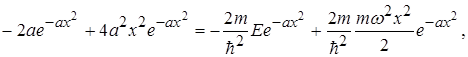
звідки
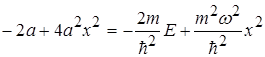 . (1.67)
. (1.67)
Тотожність (1.67) має місце при рівності коефіцієнтів при х2 і вільних членів, тобто
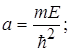
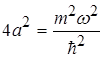 (1.68)
(1.68)
Система рівнянь (1.68) дає значення енергії Е і сталої величини а
![]()
![]() (1.69)
(1.69)
Таким чином функція Гаусса є розв’язком рівняння Шредінгера (1.53) лише за умови, коли ![]() .
.
В цьому випадку
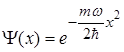 . (1.70)
. (1.70)
Слід відмітити, що так як відстань між суміжними рівнями енергії квантового осцилятора дорівнює ![]() то з урахуванням
то з урахуванням ![]() одержуємо енергетичний спектр квантового осцилятора у вигляді
одержуємо енергетичний спектр квантового осцилятора у вигляді
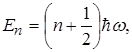 (1.71)
(1.71)
де n = 0,1,2,3. ...
1.3.4.Проходження частинки крізь потенціальний бар’єр. Тунельний ефект.
Класична частинка не може перебувати в тих місцях, де її потенціальна енергія U ( x ) перевищувала б повну енергію частинки E . Щодо квантової частинки, то вона має таку властивість із-за того, що існує відмінна від нуля імовірність проникнення її крізь потенціальний бар’єр, тобто в область, де U ( x ) > E
Проведемо оцінку цієї імовірності шляхом розв’язування наступної задачі. Нехай квантова частинка з масою m , рухаючись в напрямі осі х , вдаряється в потенціальний бар’єр кінцевої висоти U 0 , тобто
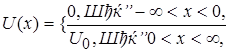
причому енергія частинки e менша висоти бар’єра U 0 , (рис. 1.11).
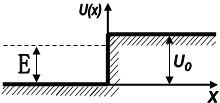
Рис. 1.11
В області потенціального бар’єра рівняння Шредінгера для стаціонарних станів набуде вигляду
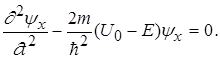 (1.72)
(1.72)
Якщо позначити вираз ![]() через
через ![]() , то рівняння (1.72) перепишеться
, то рівняння (1.72) перепишеться
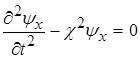 . (1.73)
. (1.73)
Розв’язком рівняння (1.34) може бути функція
![]() , (1.74)
, (1.74)
де А і В - деякі константи, і - уявна одиниця.
Експонента з додатним знаком фізичного змісту не має і може бути відкинута, так як не повинно бути зростання імовірності в області потенціального бар’єра. Тому в області потенціального бар’єра (х >0), хвильова функція частинки Y x визначається рівністю
Y
x
= Be-i![]() x
(1.75)
x
(1.75)
Коефіцієнт В у виразі (1.75) пов’язаний з інтенсивністю променя частинок, які рухаються в напрямі бар’єра, а тому задається довільно. Як правило х > 0 координати частинок розподіляються з густиною імовірності
![]() , (1.76)
, (1.76)
де w ( 0 ) дорівнює значенню |Y x |2 при х=0.
Рівняння (1.76) показує, що із збільшенням глибини проникнення в область потенціального бар’єра, густина імовірності w ( х ) зменшується експоненційно. Це зменшення буде тим швидше, чим більша різниця енергій U 0 - E .
Знайдемо глибину проникнення елементарної частинки в область потенціального бар’єра при умові, що m = 9,1 10-31 кг (електрон), U 0 - E = 10-4 eB , а густина імовірності w (х ) на цій відстані зменшується в е разів
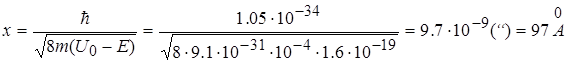 .
.
Ця відстань перевищує на два порядки діаметр атома водню. Глибина проникнення зменшується на порядок, якщо різниця енергій U 0 - E зросте до 10-2 еВ .
Здатність квантових частинок проникати в область потенціального бар’єра приводить до тунельного ефекту. Його суть полягає в проникненні частинки із однієї області в іншу область, які поділені потенціальним бар’єром навіть в тих випадках, коли енергія частинки Е менше висоти потенціального бар’єра U 0 .
Таке проходження частинки виявляється можливим дякуючи існуванню під бар’єром хвильової функції, яка «прокладає» шлях частинки на будь-яку відстань. Тунельний ефект є головною причиною a - розпаду радіоактивних ядер.
2. Фізика атомів і молекул
2.1. Атом водню
2.1.1. Використання рівняння Шредінгера до атома водню.
Хвильова функція. Квантові числа.
2.1.2. Енергія атома водню і його спектр. Виродження рівнів.
Правила відбору.
2.1.3. Механічний і магнітний моменти атома водню.
2.1.1.Використання рівняння Шредінгера до атома водню.
Хвильова функція. Квантові числа.
Теорія Бора будови і властивостей енергетичних рівнів електронів у воднево подібних системах знайшла своє підтвердження в квантовій механіці. Квантова механіка також стверджує, що:
a) електрони в атомах водню знаходяться лише в дискретних енергетичних станах. При переході електронів із одних станів в інші випромінюється або поглинається фотон;
б).не існує певних колових орбіт електронів. В силу хвильової природи електрони «розмиті» в просторі подібно до хмарки негативного заряду. Розміри і форму такої хмарки в заданому стані можна розрахувати.
Розглянемо рух електрона в кулонівському полі ядра з зарядом Ze , потенціальна енергія якого виражається формулою
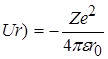 , (2.1.1)
, (2.1.1)
де r - відстань між електроном і ядром.
Стан електрона в атомі водню або воднево подібному атомі описується деякою хвильовою функцією Y , яка задовольняє стаціонарному рівнянню Шредінгера:
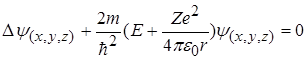 , (2.1.2)
, (2.1.2)
де 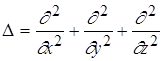 - оператор Лапласа; Е
- значення повної енергії електрона в атомі; m
- маса частинки;
- оператор Лапласа; Е
- значення повної енергії електрона в атомі; m
- маса частинки; ![]()
![]() (
x
,
y
,
z
)
- хвильова функція в декартові системі координат.
(
x
,
y
,
z
)
- хвильова функція в декартові системі координат.
![]() Для розв’язування рівняння Шредінгера (2.1.2), тобто знаходження виду хвильової функції для електрона в атомі водню слід перейти від декартових координат до сферичних. В цьому випадку зв’язок між параметрами цих систем координат визначається з рис.2.1.
Для розв’язування рівняння Шредінгера (2.1.2), тобто знаходження виду хвильової функції для електрона в атомі водню слід перейти від декартових координат до сферичних. В цьому випадку зв’язок між параметрами цих систем координат визначається з рис.2.1.
Рис.2.1.
Співвідношення, які зв’язують координати x,y,z декартової прямокутної системи координат з сферичними координатами r , q , j наступні:
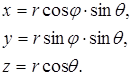 (2.1.3)
(2.1.3)
Таким чином можна вважати, що хвильова функція y електрона в атомі водню залежить від сферичних координат, тобто y = y ( r , q , j ) .
Опустивши не складні, але досить громіздкі перетворення переходу від декартової системи координат до сферичної, одержимо:
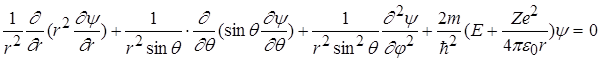 .
.
(2.1.4)
Якщо розглядати основний (не збуджений) стан атома водню, то другою і третьою складовими в рівнянні (2.1.4) можна знехтувати. Електрон в такому стані рухається лише по коловій траєкторії, і хвильова функція не залежить від q і j . Тому
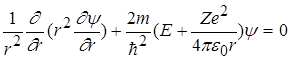 . (2.1.5)
. (2.1.5)
Хвильова функція y електрона в основному стані (2.1.5) є функцією лише r , тобто y = y ( r ). Такий стан називається s-станом; він має сферично-симетричний характер. Імовірність виявити електрон у заданій точці атома - залежатиме лише від r . Умовам стаціонарного стану відповідає легко диференціруєма центральносиметрична функція, яка має вигляд:
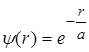 , (2.1.6)
, (2.1.6)
де a - деяка стала величина, яка має розмірність довжини.
Необхідні похідні від (2.1.6) підставимо в (2.1.5). Після скорочення на ![]() одержимо:
одержимо:
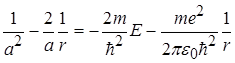 . (2.1.7)
. (2.1.7)
Рівність (2.1.7) має місце для будь-яких значень r при виконанні наступних умов:
![]()
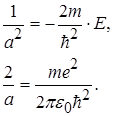 (2.1.8)
(2.1.8)
З рівностей (2.1.8) одержуємо
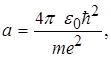 (2.1.9)
(2.1.9)
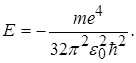 (2.1.10)
(2.1.10)
Покажемо, що вираз (2.1.9) є найбільш імовірною відстанню електрона в атомі водню до ядра. Імовірність знайти електрон на відставні r від ядра, точніше в інтервалі відстаней від r до r + dr , тобто в кульковому шарі з об¢ємом dV =4 p r 2 dr , дорівнює:
![]() . (2.1.11)
. (2.1.11)
З урахуванням (2.1.6), хвильової функції основного стану маємо:
![]() , (2.1.12)
, (2.1.12)
де 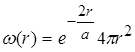 - густина імовірності.
- густина імовірності.
Дослідимо вираз (2.1.12) на максимум, тобто похідну від w(r) прирівняємо до нуля
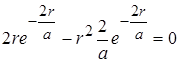 .
.
Звідки
r = a . (2.1.13)
Цей результат є окремим випадком загального висновку: борівські орбіти електрона в атомі водню є геометричними місцями точок, в яких з найбільшою імовірністю можна виявити електрон.
Залежність густини імовірності w ( r ) виявити електрон на різних відстанях від ядра показана на рис.2.2.
![]()
Рис.2.2.
За теорією Бора імовірність виявити електрон у стані з n =1 відмінна від нуля лише для r = a , а згідно з висновками квантової механіки ця відстань є лише найбільш імовірною.
Теорія Бора дає можливість визначити значення енергії електрона в будь-якому енергетичному стані, а також радіус відповідних борівських орбіт:
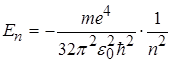 , (2.1.14)
, (2.1.14)
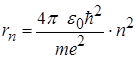 , (2.1.15)
, (2.1.15)
де m
- маса електрона; e
- заряд електрона; e
0
- діелектрична проникність вакууму; ![]() - стала Планка, поділена на 2
p
;
n
=1,2,3...
- головні квантові числа.
- стала Планка, поділена на 2
p
;
n
=1,2,3...
- головні квантові числа.
Співставлення (2.1.9) і (2.1.14), а також (2.1.9) і (2.1.15) показують, що висновки квантової механіки і теорії Бора повністю співпадають. Це співподання підкреслює значну історичну роль теорії Бора, яка ще не є квантовою, однак і не класичною теорією.
Хвильові функції для наступних двох енергетичних рівнів електронів в атомі водню мають вигляд
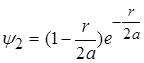 , (2.1.16)
, (2.1.16)
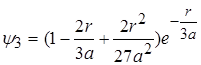 . (2.1.17)
. (2.1.17)
Ці хвильові функції також є розв¢язками рівняння (2.1.4) при умові, що ![]() і
і ![]() . Можна показати, що формула (2.1.14) є значенням енергії електрона на будь-якому енергетичному рівні.
. Можна показати, що формула (2.1.14) є значенням енергії електрона на будь-якому енергетичному рівні.
Однак для повного пояснення стану електрона в атомі водню необхідні ще два квантові числа, які входять у відповідні рівняння хвильових функцій і які характеризують момент імпульсу електрона в атомі.
Для збуджених атомів хвильові функції не є центрально симетричними і залежать не лише від r , а і від q і j . Ці хвильові функції містять три цілочислові параметри, які називають квантовими числами. Серед них:
n - головне квантове число, співпадає з аналогічним квантовим числом теорії Бора і набуває значень від 1 до ¥;
l - орбітальне квантове число, квантує момент імпульсу
![]() . (2.1.18)
. (2.1.18)
Орбітальне квантове число набуває значень l =0,1,2,... .
ml - магнітне квантове число, квантує проекцію орбітального моменту імпульсу на вісь Z напрямку зовнішнього магнітного поля
![]() . (2.1.19)
. (2.1.19)
Магнітне квантове число набуває значень ml = 0, ± 1, ± 2 , ± 3... .
2.1.2. Енергія атома водню і його спектр. Виродження рівнів.
Правила відбору.
Знаючи кількісне співвідношення для енергії електрона на енергетичному рівні в атомі водню, можна розрахувати весь його спектр. Нехай енергія більш високого збудженого енергетичного рівня дорівнює
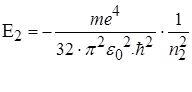 (2.1.19)
(2.1.19)
а енергія нижчого рівня
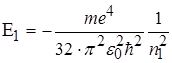 (2.1.19)
(2.1.19)
Частоти, які відповідають різним спектральним лініям, можна записати у вигляді
![]() ,
,
або
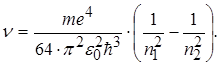 (2.1.21)
(2.1.21)
Серія спектральних ліній, яким відповідає n 1 =1 , називається серією Лаймана. Всі лінії цієї серії розміщені в ультрафіолетовій області спектра електромагнітного випромінювання. У випадку, коли n 1 =2, виникає друга серія випромінювання, яка називається серією Бальмера. Перші чотири лінії цієї серії знаходяться у видимій області спектра. Інші спектральні лінії цієї серії перебувають на межі видимої і ультрафіолетової області спектра.
Формула (2.1.21) називається формулою Бальмера. У цій формулі вираз перед дужками є сталою величиною, яку називають сталою Рідберга. Стала Рідберга R розрахована з великою точністю. Її величина дорівнює
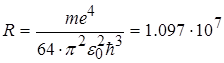 м-1
.
м-1
.
Число знаків, до яких визначена стала Рідберга показує рівень точності сучасної спектроскопії і ілюструє повне співпадання розрахунків за формулою Бальмера з результатами спостережень.
Якщо n 1 =3 , то за формулою (2.1.21) можна розрахувати наступну серію випромінювання - серію Пашена. Всі лінії цієї серії перебувають в інфрачервоній області спектра.
Наступна серія випромінювання для n 1 =4 носить назву серії Бреккета. Лінії цієї серії перебувають в інфрачервоній області спектра.
Характер утворення спектральних серій атомом водню наведено на рис. 2.3.
Кожному значенню енергії електрона в атомі водню E
n
(за винятком Е1
)
відповідає декілька значень хвильової функції ![]() .
Вони відрізняються значеннями квантових чисел l
i
ml
.
Це означає, що атом водню може мати однакове значення енергії і перебувати в кількох різних квантових станах.
.
Вони відрізняються значеннями квантових чисел l
i
ml
.
Це означає, що атом водню може мати однакове значення енергії і перебувати в кількох різних квантових станах.
Стани з однаковою енергією називаються виродженими, а число таких станів з одним значенням енергії, називається порядком виродження.
Порядок виродження легко обчислити виходячи з числа можливих значень l i ml . Кожному значенню числа n відповідає 2 l +1 значень квантового числа ml . Тому число різноманітних станів для даного значення n, дорівнює
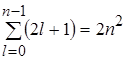 (2.1.22)
(2.1.22)
Таким чином кожен рівень енергії атома водню має порядок виродження 2n 2 .
В квантовій механіці доводиться, що можливі лише такі переходи електронів між енергетичними рівнями, для яких виконується умова зміни орбітального квантового числа l на одиницю:
D l =±1 . (2.1.23)
![]()
Рис. 2.3.
Умова, яка виражена співвідношенням (2.1.23) називається правилом відбору. Існування цього правила обумовлено тим, що фотон має власний момент імпульсу, який називають спіном
, рівним наближено ![]() .
При випромінюванні фотон забирає від атома цей момент, а при поглинанні віддає атому. Тому правило відбору є відповідним наслідком закону збереження моменту імпульсу.
.
При випромінюванні фотон забирає від атома цей момент, а при поглинанні віддає атому. Тому правило відбору є відповідним наслідком закону збереження моменту імпульсу.
Переходи електронів в атомі водню, які дозволені правилом відбору показані на рис. 2.3.
Серії Лаймана відповідають переходи
np®1s, (n=2,3,4,...).
Серії Бальмера відповідають переходи
np®2s, ns®2p i nd®2p, (n=3,4,5,...).
Стан 1 s є основним станом атому водню. В цьому стані атом має найменшу енергію. Для виведення атома з основного стану йому слід надати необхідної енергії за рахунок зовнішнього джерела. Таким джерелом енергії може бути нагрівання, електричний розряд або опромінення.
При опромінені водню фотонами від зовнішнього джерела їх енергія поглинається повністю лише у випадку коли енергія фотонів в точності співпадає з різницею енергії двох енергетичних рівнів. В цьому випадку фотон зникає повністю, передаючи атому всю свою енергію. Атом не може поглинути частину фотона, так як фотон є неподільним.
2.1..3. Механічний і магнітний моменти атома водню.
Орбітальне квантове число l визначає стан електрона в атомі. Якщо рух електрона характеризується значенням квантового числа l =0, то електрон перебуває в s - стані, а сам електрон називається s-електроном. Квантовому числу l = 1 відповідає р-стан електрона, l =2 - d-стан, l =3 - f-стан і т. д.
Для електрона, що знаходиться в атомі водню на n-му енергетичному рівні, можливі одна колова орбіта при l = n -1 i n -1 еліптичних орбіт. Із зменшенням l збільшується ступінь витягнутості орбіти. Отже, при заданому головному квантовому числі орбітальне квантове число l визначає форму орбіти.
У квантовій механіці орбітальний момент імпульсу електрона визначається таким співвідношенням:
![]() , де (l
=0,1,2,...n-1). (2.1.24)
, де (l
=0,1,2,...n-1). (2.1.24)
Цей вираз свідчить про можливість таких рухів електрона, для яких (при l =0) орбітальний момент імпульсу електрона дорівнює нулю.
Третє квантове число ml , яке називається магнітним квантовим числом, визначає просторовий розподіл траєкторії руху електрона, а також і проекцію вектора механічного моменту або моменту імпульсу орбіти на заданий напрям.
Орбіту, по якій рухається електрон, можна розглядати як контур струму. Такий контур характеризується певним значенням орбітального магнітного моменту електрона ![]() , векторною величиною, що направлена вздовж осі орбіти в той бік, куди направлена індукція магнітного поля, створюваного цим контуром. Між вектором
, векторною величиною, що направлена вздовж осі орбіти в той бік, куди направлена індукція магнітного поля, створюваного цим контуром. Між вектором ![]() і
і ![]() існує наступний зв’язок
існує наступний зв’язок
![]() = -
= - 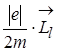 =-g
=-g
![]() , (2.1.25)
, (2.1.25)
де е
- заряд електрона; m
- маса електрона; g
![]() - гіромагнітне відношення.
- гіромагнітне відношення.
Враховуючи значення Ll з (2.1.24) одержимо:
![]() =-g
=-g
![]() =-
=-![]() б
б![]() , (2.1.26)
, (2.1.26)
де ![]() б=
g
б=
g
![]() - магнетон Бора.
- магнетон Бора.
Як видно з (2.1.26) вектори ![]() і
і ![]() мають протилежні напрямки.
мають протилежні напрямки.
Вектор ![]() може мати 2
l
+1
просторових орієнтацій, а це означає, що при даному l
електрон в атомі, який вміщено в зовнішнє магнітне поле, може рухатися по 2
l
+1
орбітах, які відрізняються своєю орієнтацією щодо напрямку магнітного поля.
може мати 2
l
+1
просторових орієнтацій, а це означає, що при даному l
електрон в атомі, який вміщено в зовнішнє магнітне поле, може рухатися по 2
l
+1
орбітах, які відрізняються своєю орієнтацією щодо напрямку магнітного поля.
![]() , (2.1.27)
, (2.1.27)
де m l - магнітне квантове число.
На рис. 2.4. зображено можливі значення проекції орбітального механічного моменту на напрям осі z зовнішнього магнітного поля для випадків l =1 i l =2.
![]()
Рис. 2.4.
Таким чином просторове квантування приводить до розчеплення в магнітному полі енергетичного рівня електрона на ряд підрівнів, а отже, і до розчеплення спектральних ліній. Таке явище спостерігав Зеєман. Розчеплення спектральних ліній також можливе в електричному полі - дослід Штарка.
![]()
Рис. 2.5
Між розщепленими рівнями можливі переходи електронів згідно правил відбору (рис. 2.5)
Dl =±1 i Dml =0 ; ±1.
2.2 Багатоелектронні атоми.
2.2.1 . Досліди Штерна і Герлаха. Спін електрона.
2.2.2 . Принцип нерозрізненості тотожних частинок. Принцип
Паулі.
2.2.3 . Розподіл електронів за станами. Періодична система
елементів.
2.2.4 . Рентгенівські промені. Суцільний спектр і його межі.
Характеристичний спектр. Закон Мозлі.
2.2.1 . Досліди Штерна і Герлаха. Cпін електрона
Висновки квантової механіки про просторове квантування потребували експериментального підтвердження . Виявилось, що всі електронні лінії мають так звану «тонку структуру», яка спостерігається навіть при відсутності зовнішнього магнітного поля. Так, всі спектральні лінії водню і лужних металів є дублетами, тобто складаються з двох окремих, близько розташованих ліній. Була висунута гіпотеза про наявність у електронів власного механічного моменту, пов’язаного з обертанням його навколо власної осі. Пізніше власний механічний момент електронів S назвали спіном. Чисельно спін електрона дорівнює 1/2
![]() . Електрону властивий також магнітний момент, що дорівнює магнетону Бора m
Б
=
. Електрону властивий також магнітний момент, що дорівнює магнетону Бора m
Б
=![]() g
, де g
- гіромагнітне відношення, рівне e
/2
m
; Власний механічний і магнітний моменти електрона можуть бути орієнтовані лише двома способами: паралельно або антипаралельно відносно вибраного напрямку. Ці дві орієнтації визначаються четвертим квантовим числом, яке називається спіновим
. Спінове квантове число може набувати значень 1/2
і -1/2
. Отже, на ряду з уже введеними раніше трьома квантовими числами n
, l
, ml
є ще четверте квантове число ms
- яке квантує власний механічний момент електрона.
g
, де g
- гіромагнітне відношення, рівне e
/2
m
; Власний механічний і магнітний моменти електрона можуть бути орієнтовані лише двома способами: паралельно або антипаралельно відносно вибраного напрямку. Ці дві орієнтації визначаються четвертим квантовим числом, яке називається спіновим
. Спінове квантове число може набувати значень 1/2
і -1/2
. Отже, на ряду з уже введеними раніше трьома квантовими числами n
, l
, ml
є ще четверте квантове число ms
- яке квантує власний механічний момент електрона.
Гіпотезу про існування власного механічного моменту (спіну) і власного магнітного моменту було пояснено в дослідах Штерна і Герлаха, виконаних ними ще в 1921-1923р.р.
Для дослідження були використані нейтральні атоми срібла, на зовнішніх оболонках яких рухається по одному електрону. Схема установки дослідів Штерна і Герлаха показана на рис. 2.6.

Рис. 2.6
В установці на рис. 2.6. було створено досить неоднорідне магнітне поле за рахунок особливої конструкції магнітних полюсів постійного магніту.
Потенціальна енергія атомів срібла пов’язана з Рм і В співвідношенням
![]() (2.1.28)
(2.1.28)
де ![]() - вектор магнітного моменту атому срібла:
- вектор магнітного моменту атому срібла:
![]() - вектор індукції зовнішнього магнітного поля.
- вектор індукції зовнішнього магнітного поля.
Якщо зовнішнє магнітне поле буде постійним, то магнітні моменти атомів срібла, здійснювали б прецесію навколо вектора ![]() , а магнітні сили були б відсутні.
, а магнітні сили були б відсутні.
В сильно неоднорідному магнітному полі цього не спостерігається, так як
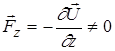 , тому що
, тому що ![]()
Отже
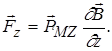 (2.1.29)
(2.1.29)
Під дією цієї магнітної сили (2.1.29.) повинно бути розчеплення спектральних рівнів.
Якщо просторового квантування немає, тобто орієнтація магнітних моментів атомів у зовнішньому магнітному полі довільна, то на екрані спостерігатиметься неперервний розподіл атомів. При просторовому квантуванні пучок атомів після проходження неоднорідного поля розчеплюється на кілька пучків. Таке розчеплення атомних пучків спостерігали Штерн і Герлах і тим самим довели справедливість положення про просторове квантування магнітних моментів атомів. Проте виявилося, що в окремих дослідах є розбіжність між результатами експерименту і вимогами теорії.
Так, в експерименті з атомами срібла спостерігалось розчеплення пучка атомів, що проходили неоднорідне магнітне поле на два пучки, тоді як за теорією ці атоми не повинні зазнавати дії магнітного поля, оскільки їх орбітальні магнітні моменти в основному стані дорівнюють нулю.
Аномальне розчеплення атомних пучків водню, літію, срібла на два пучки неоднорідним магнітним полем пов’язане з квантуванням власного магнітного моменту атомів.
![]() (2.1.30)
(2.1.30)
де ms - спінове квантове число, рівне 1/2 і -1/2.
В дослідах Штерна і Герлаха було встановлено, що власний магнітний момент електронів дорівнює
![]() (2.1.31)
(2.1.31)
Спінове гіромагнітне відношення в два рази перевищує орбітальне. Наявність власного механічного моменту електрона заборонена теорією відносності. Це говорить про те, що класичної інтерпретації власний механічний момент немає.
З квантової точки зору цю властивість частинок називають спіном, і інтерпретують як невід’ємну властивість елементарних частинок.
Спін та власний магнітний момент мають протони, нейтрони та інші елементарні частинки.
2.2.2. Принцип нерозрізненості тотожних частинок. Принцип Паулі
До цих пір ми розглядали рух лише однієї квантової частинки. Незвичайні, з класичної точки зору властивості, проявляються при вивченні руху системи квантових частинок. Квантова теорія систем частинок полягає в тому, що в цій теорії поняття хвильової функції відноситься лише до системи частинок. Кожна окрема частинка системи не знаходиться в певному квантовому стані і не може бути охарактеризована своєю хвильовою функцією, яка б залежала лише від параметрів даної частинки.
Система квантових частинок набуває властивостей, яким не має аналога ні в класичній фізиці ні в квантовій механіці однієї частинки. Специфічна особливість квантової теорії систем частинок полягає в їх принциповій нерозрізненості. Всі частинки такої квантової системи є тотожними.
Нерозрізненість тотожних частинок в квантових системах не властива для систем класичних частинок, де кожна частинка системи має свою індивідуальність.
В квантовій фізиці однакові частинки втрачають свою індивідуальність, так як рухаються не по траєкторіях. Поняття траєкторії квантових частинок із за хвильових властивостей втрачає будь-який фізичний зміст.
Із принципової нерозрізненості однакових частинок випливає, що перестановка місцями двох однакових частинок в системі не впливає ні на одну із фізичних величин, що характеризують цю систему.
Слід відмітити, що при перестановці місцями двох частинок в системі хвильова функція, яка є функцією всіх параметрів частинок цієї системи, змінюється з Y на Y 1 . Однак густина імовірності при цьому не змінюється, тобто
|Y |2 = |Y 1 |2 .
В той же час хвильова функція Y 1 відрізняється від Y на множник ei a , де a - деяка дійсна величина. Переставимо ті ж частинки ще раз місцями, тобто повернемось в попередній стан. Густина імовірностей знову ж не зміниться, а от хвильова функція Y буде відрізнятись від Y в початковий момент на е2і a . Для рівності імовірностей необхідно, щоб е2і a =1 , а еі a = ± 1. З цих міркувань видно, що при перестановці місцями довільної пари частинок системи хвильова функція може залишитися такою ж, або змінювати знак.
Хвильова функція, яка при перестановці місцями двох частинок системи свого знаку не змінює - називається симетричною . В тих випадках, коли при аналогічній перестановці частинок системи хвильова функція змінює знак, вона є антисиметричною .
Симетрія хвильової функції системи однакових частинок зберігається з часом. Тому тип симетрії хвильової функції є властивістю тільки самих частинок.
Системи однакових частинок з нульовими, або цілочисловими спінами описуються лише симетричними хвильовими функціями і називаються бозонами .
Системи однакових частинок з напівцілими спінами описуються лише антисиметричними хвильовими функціями і називаються ферміонами .
До ферміонів відносяться електрони (![]() ), протони і нейтрони (
), протони і нейтрони (![]() ) й інші частинки.
) й інші частинки.
До бозонів відносяться p
- мезони (![]() ), фотони (
), фотони (![]() ) і інші частинки.
) і інші частинки.
Спін мікроскопічної частинки є її найважливішою характеристикою. Так від спінів частинок залежать статистичні властивості квантових систем, які складаються з багатьох частинок. Статистичні властивості частинок з нульовими і цілочисловими спінами вперше вивчали Бозе й Ейнштейн ще в 1924 році, від чого відповідна квантова статистика дістала назву статистики Бозе і Ейнштейна . Статистичні властивості частинок з напівцілими спінами вивчали в 1926 році Фермі і Дірак - звідки назва відповідної квантової статистики Фермі і Дірака .
Зупинимось на розподілі електронів в атомі на відповідних енергетичних рівнях. Відомо, що стан кожного із електронів можна характеризувати чотирма квантовими числами: n , l , ml , ms , де n - головне квантове число, яке квантує енергію електрона в атомі і визначає розміри орбіти електрона; l - орбітальне квантове число, що визначає (квантує) орбітальний момент імпульсу (механічний момент); ml - магнітне квантове число, квантує проекцію вектора механічного моменту на заданий напрям зовнішнього магнітного поля; ms - спінове квантове число, що визначає орієнтацію власного механічного і магнітного моментів електрона.
За принципом Паулі (1924 р.) електрони, які входять до складу якої-небудь системи, зокрема електрони атомних оболонок, не можуть перебувати в тотожних станах руху. Інакше кажучи, в будь-якому стаціонарному стані, що характеризується сукупністю чотирьох квантових чисел n , l , ml , ms , не може перебувати більше одного електрона .
Принцип Паулі має використання лише для систем, частинок з антисиметричними хвильовими функціями, тобто до ферміонів.
2.2.3. Розподіл електронів за станами.
Періодична система елементів.
Сукупність електронів, які перебувають у всіх можливих станах з однаковим значенням головного квантового числа n , утворює електронну оболонку (електронний шар). Енергетичні шари прийнято позначати великими латинськими літерами відповідно до значень головного квантового числа.
Найближче до ядра в будь-якому атомі розташований К-шар, для якого n=1. Далі йдуть L- шар (n=2), M- шар (n=3), N- шар (n=4) тощо. Кількість електронів в шарі визначається формулою
![]() (2.2.1)
(2.2.1)
де n - головне квантове число.
Згідно формули (2.2.1), в К-шарі міститься не більше двох електронів (два s- електрони); в L- шарі не більше восьми електронів (з них два в s- стані і шість в p-стані); в М-шарі не більше вісімнадцяти електронів (з яких два в s-стані, шість в р-стані і десять в d-стані) і т. д. Число електронів в тому чи іншому квантовому стані визначається за формулою
![]() (2.2.2)
(2.2.2)
де l - орбітальне квантове число.
Згідно формули (2.2.2), в s-стані перебуває не більше двох електронів (l =0); в p-стані перебуває не більше шeсти електронів (l =1); в d- стані перебуває не більше десять електронів (l =2); в f- стані не більше чотирнадцяти електронів (l = 3), тощо.
Для станів з фіксованими квантовими числами n і l використовують позначення типу 1s,2s,2p і т.д.: значення n вказується цифрою, яка стоїть зліва від букви, що вказує значення числа l . Як уже було відмічено в кожній такій групі є 2(2l +1) станів. Вони відрізняються один від одного значеннями магнітного квантового числа ml - значення спінового квантового числа можуть бути лише ms =1/2 і ms =-1/2.
Наприклад, у кожного стану із групи 1s орбітальне квантове число l =0, так що група 1s містить лише два окремі квантові стани. В цих станах
n=1, l =0, ml =0, ms =1/2,
n=1, l =0, ml =0, ms =-1/2.
Група 2s також містить два стани, оскільки в ній також l =0; група 2p містить уже 2(21 +1)=6 станів. В цих станах:
n=2, l =1, ml =1, ms =1/2,
n=2, l =1, ml =1, ms =-1/2,
n=2, l =1, ml =0, ms =1/2,
n=2, l =1, ml =0, ms =-1/2,
n=2, l =1, ml =-1, ms =-1/2,
n=2, l =1, ml =-1, ms =-1/2.
Аналогічно можна показати, що в d- стані число електронів не може перевищувати 10 електронів; в f- стані - не більше 14 електронів.
Розподіл електронів за одночастинковими станами називається електронною конфігурацією. Електронні конфігурації позначаються символами типу 1s2 2s2 2p6 3s2 . Тут цифрою над s i p справа, указують число електронів в станах 1s, 2s, 2p i 3s.
Якщо шар повністю заповнений то він називається замкнутим.
Кожен період таблиці Менделєєва починається елементом, який перебуває в стані 1s1 , 2s1 , 3s1 , і т.д. Закінчується період елементом з повністю заповненим зовнішнім електронним шаром.
Процес забудови електронних оболонок у елементів перших двох періодів таблиці Менделєєва показано нижче:
1H - 1s1
2He - 1s2
3Li - 1s2 2s1
4Be – 1s2 2s2
5B - 1s2 2s2 2p1
6C - 1s2 2s2 2p2
7N - 1s2 2s2 2p3
8O - 1s2 2s2 2p4
9F - 1s2 2s2 2p5
10Ne –1s2 2s2 2p6
18Ar – 1s2 2s2 2p6 3s2 3p6
36Kr – 1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6
Електронні оболонки в інертних газів є повністю заповненими.
Періодичність властивостей атомів пояснюється періодичністю заповнення їх електронних оболонок, яка випливає з принципу Паулі. Періодичність у фізичних властивостей окремих хімічних елементів виявляється насамперед в структурі лінійчатих спектрів, які випромінюють атоми цих елементів. Подібність спектрів лужних металів обумовлена подібністю забудови зовнішніх електронних оболонок. Це пояснюється тим, що оптичні лінійчаті спектри випромінюються електронами зовнішніх електронних оболонок. Періодичність властивостей хімічних елементів проявляється також і в електричних властивостях атомів.
В основі періодичного закону лежить не лише уявлення про періодичну залежність властивостей елементів, а й уявлення про закономірний зв’язок між властивостями елементів у кожному періоді і в кожній групі періодичної системи, а також всередині цієї системи по діагональних напрямках. Саме цей закономірний зв’язок між кількісними і якісними характеристиками елементів, вперше відкритий і досліджений Менделєєвим, дав змогу йому передбачити існування і властивості невідомих на той час хімічних елементів.
Періодичний закон став одним з основних законів природознавства, які становлять фундамент сучасного фізичного вчення про будову матерії.
2.2.4. Рентгенівські промені. Суцільний спектр і його межі. Характеристичний спектр. Закон Мозлі.
Випромінювання, яке було відкрите в 1895 році німецьким фізиком Рентгеном і пізніше назване на його честь рентгенівським відіграє велику роль у дослідженнях будови електронних оболонок і властивостей складних атомів, при вивченні будови молекул, а особливо твердих тіл.
Рентгенівське випромінювання виникає при гальмуванні речовиною швидких електронів внаслідок перетворення кінетичної енергії цих електронів в електромагнітне випромінювання. Довжини хвиль рентгенівського випромінювання перебувають в межах від 0.01 до 80 нм.
Для одержання рентгенівського випромінювання використовують рентгенівські трубки. Вони мають скляний або металевий корпус в якому вмонтовано катод і анод і створено глибокий вакуум. Катод рентгенівської трубки є джерелом електронів, а анод - джерелом рентгенівського випромінювання. Між катодом і анодом створюють електричне поле, яке здатне прискорювати електрони до 104 - 105 еВ.
Досліди показують, що при бомбардуванні високо енергетичними електронами тіло аноду виникають два типи рентгенівського випромінювання. Перший тип називають білим, власний спектр якого є суцільним, подібним до спектру білого світла. Біле рентгенівське випромінювання утворюється при гальмуванні швидких електронів тілом анода. Тому це випромінювання називають ще гальмівним. Гальмівний рентгенівський спектр має короткохвильову межу lmin , яка визначається величиною анодної напруги, прикладеної між катодом і анодом.
Завдяки випадковому характеру зіткнень електронів з атомними оболонками анода, втрати енергії електронів на теплоту і випромінювання розподіляються довільно. Тому енергія фотонів гальмівного випромінювання може бути різною, а його спектр - суцільним.
При підвищенні напруги на рентгенівській трубці інтенсивність випромінювання зростає. Примітним також є те, що спектр рентгенівського випромінювання при всякій напрузі в короткохвильовій частині різко обривається (рис.2.7).
![]()
Рис. 2.7
Для короткохвильової межі гальмівного спектра маємо
![]() . (2.2.3)
. (2.2.3)
Звідки
![]() , (2.2.4)
, (2.2.4)
де h - стала Планка; с - швидкість світла; q - заряд електрона U - анодна напруга. Формула (2.2.4) добре узгоджується з дослідними даними. В свій час вона виявилась одним з найточніших методів експериментального визначення сталої Планка. Це співвідношення добре збігається з рівнянням Ейнштейна для фотоефекту, якщо в ньому знехтувати роботою виходу електрона з металу.
Другим типом випромінювання є характеристичне рентгенівське випромінювання. Його називають так через те, що воно характеризує речовину анода рентгенівської трубки. Спектр характеристичного рентгенівського випромінювання - лінійчатий. Особливість цих спектрів полягає в тому, що кожний хімічний елемент дає певний характеристичний рентгенівський спектр незалежно від того, чи збуджується атом у вільному стані, чи він входить до хімічної сполуки. Спектр характеристичного рентгенівського випромінювання істотно відрізняється від оптичних електронних спектрів тих же атомів. Вплив хімічного зв’язку на оптичні спектри досить значний, так як оптичні спектри випромінюються якраз валентними електронами. В той же час характеристичне рентгенівське випромінювання здійснюється електронами глибоких енергетичних рівнів.
В 1913р.Англійський фізик Мозлі встановив закон, який виражає частоти у характеристичних спектрах речовини залежно від її атомного номера, а саме:
![]() , (2.2.5)
, (2.2.5)
де R - стала Рідберга в,с-1 ; m і n - номери числа рівнів, між якими здійснюється перехід електрона; s - стала екранування, яка зберігає своє значення в межах даної серії для всіх елементів. Для К-серії s=1; для L- серії s=7.5 і т.д.
Інколи закон Мозлі пишуть в такій формі
![]() , (2.2.6)
, (2.2.6)
де n*
=1/l - хвильове число; R1
- стала Рідберга в м-1
; ![]() - стала величина; s - стала екранування.
- стала величина; s - стала екранування.
Для довжини хвиль, які характеризують переходи електронів на Кa рівень Мозлі дістав таке співвідношення
![]() =
=![]() (2.2.7)
(2.2.7)
Співставляючи (2.2.6) і (2.2.7), маємо, що для цих ліній
![]() і s=1.
і s=1.
Застосування закону Мозлі до атомів хімічних елементів періодичної системи Менделєєва підтвердило закономірне зростання електричного заряду ядра на одиницю при послідовному переході від одного елемента до іншого.
2.3 Молекула
2.3.1. Взаємодія атомів. Іонний ковалентний зв’язок атомів у
молекулах. Поняття про теорію обмінних сил.
2.3.2. Енергетичні рівні молекул. Молекулярні спектри.
Парамагнітний резонанс.
2.3.3. Комбінаційне розсіювання світла.
2.3.4. Поглинання, спонтанне і вимушене випромінюва-ння.
Оптичні квантові генератори.
2.3.1 Взаємодія атомів. Іонний і ковалентний зв’язок атомів у
молекулах. Поняття про теорію обмінних сил.
Молекули складаються з однакових або різних атомів, сполучених між собою в одне ціле міжатомними зв’язками. Саме існування молекул як стійких систем показує, що хімічні зв’язки атомів у молекулах повинні бути зумовлені наявністю між атомами деяких сил взаємодії, що зв’язує атоми в молекулах один з одним. Для роз’єднання молекули на атоми слід виконати певну роботу. Це підтверджує факт виділення енергії при утворенні молекули. Так, наприклад, два атоми водню у вільному стані мають більшу енергію ніж ті самі атоми, сполучені в двохатомну молекулу. Це є доказом наявності сил, які зв’язують атоми в молекулах, причому енергія, яка виділяється при утворенні молекули, є мірою тих сил взаємодії.
Експерименти показують, що сили міжатомної взаємодії в молекулах виникають між зовнішніми, валентними електронами атомів. Про це свідчить різка зміна оптичного спектра атомів при утворенні ними молекул і, навпаки, збереження особливостей рентгенівського характеристичного спектра атомів незалежно від того чи атоми вільні чи утворюють молекулярні сполуки.
Важливо відмітити, що атоми на значних відстанях не взаємодіють один з одним. Із зменшенням відстані r між ядрами атомів зростають сили взаємного притягування. Проте ці сили не єдині. На малих відстанях між атомами виникають сили взаємного відштовхування, величина яких різко зростає в момент перекриття електронних оболонок. Сили відштовхування більш короткодіючі, ніж сили притягування. На рис.2.8 наведено криві залежності від відстані r сил притягування F2 ; відштовхування F1 і результуючої сили F взаємодії атомів у такій молекулі, причому сили відштовхування вважаються додатними.
![]()
Рис. 2.8
Bнаслідок протилежної дії сил F1 i F2 на деякій відстані r0 між атомами обидві сили врівноважуються і її геометрична сума стає рівною нулю. На цій відстані найменша взаємна потенціальна енергія W(r) атомів двохатомної молекули. На рис. 2.9 зображено криву залежності від r потенціальної енергії W(r) взаємодії двох атомів у молекулі.
![]()
Рис. 2.9
Величина D (на рис. 2.9) чисельно дорівнює роботі, яку потрібно виконати, щоб розірвати зв’язки атомів у молекулі, тобто роз’єднати молекулу на атоми. Цю роботу ще називають енергією дисоціації молекули або енергією зв’язку. Зрозуміло, що при утворенні молекули з окремих атомів така енергія повинна звільнитись.
Нехай один із атомів в результаті взаємодії приєднує до себе один або кілька електронів стає негативним іоном, а інший атом, віддає відповідну кількість електронів і перетворюється в позитивний іон. Такі атоми за рахунок електростатичного притягування утворюють молекулу. Молекули, в яких здійснюється такий тип зв’язку називають іонними або гетерополярними молекулами.
Однак більшість молекул в природі утворенні із електрично нейтральних атомів. Хімічний зв’язок, який здійснюється між електрично нейтральними атомами в молекулі називають ковалентним, або гемополярним. Природу ковалентного зв’язку вдалось з’ясувати лише на основі квантової механіки.
Зупинимось більш детально на механізмі утворення іонних молекул. Типовим прикладом такої молекули є кухонна сіль NaCl. Метали першої групи таблиці Менделєєва мають порівняно невеликі величини потенціалу іонізації. Так для натрію потенціал іонізації становить 5.1 еВ. З другого боку електронна спорідненість атома хлору має значну величину, порядку 3.8 еВ. Перехід електрона від атома Na до атома Cl приводить до утворення іонів Na+ i Cl- , які притягуючись між собою за допомогою електростатичних сил, утворюють стійку молекулу з іонним зв’язком. Електростатичне притягування між іонами Na+ i Cl- на певній відстані зрівноважується електростатичним відштовхуванням оболонок обох іонів. Іонний зв’язок не може бути насиченим.
Порівняння потенціалу іонізації атомів натрію і електронної спорідненості атомів хлору показує, що майже завжди величина еj енергії іонізації трохи перевищує електронну спорідненість. Для кухонної солі це перевищення становить 1.3 еВ. Отже електрон від атома натрію не може самочинно перейти до атома хлору. В той же час, при утворенні молекули NaCl енергія виділяється. Пояснити цей процес можна лише значним зближенням іонів, від чого виділяється електростатична енергія їх взаємодії. Утворення іонів і їх зближення - це єдиний процес, який відбувається одночасно і лише після того, як атоми так наблизилися, що разом з утворенням іонів виділяється потрібна для цього кількість енергії.
Ковалентний хімічний зв’язок здійснюється між нейтральними атомами. Цей зв’язок має властивість насичення. Атом водню може вступити у взаємодію лише з одним атомом водню. Атом вуглецю може при взаємодії зв’язати лише чотири атома водню і т.д.
Таким чином, насичення ковалентних зв’язків є істотно не класичним ефектом. Можливість його пояснення за допомогою гравітаційних сил в цьому випадку повністю виключається.
Кількісну теорію ковалентного зв’язку, стосовно молекули водню, розробили Гейтлер і Лондон у 1927р. на основі квантової механіки. Розглянемо два атоми водню, ядра яких перебувають у точках ![]() і
і ![]() на відстані R. Якщо відстань R дуже велика, то атоми не взаємодіють і повна енергія системи із двох атомів водню дорівнюватиме подвійній енергії основного стану атома водню, тобто:
на відстані R. Якщо відстань R дуже велика, то атоми не взаємодіють і повна енергія системи із двох атомів водню дорівнюватиме подвійній енергії основного стану атома водню, тобто:
W=2W1 ,
де ![]() .
.
При наближенні атомів між ними виникає взаємодія, яка характеризується деякою енергією Wp ( R ), що залежить від відстані між атомами. Загальна енергія тоді буде рівною
W=2W1 +WP ( R ). (2.3.1)
Якщо R®¥, то Wp (R)®0. При наближенні двох атомів водню один до одного Wp (R) спочатку буде зменшуватись від 0 (при R=¥) до деяких від’ємних значень (при скінчених R), що відповідає притяганню атомів. Потім при зменшенні R Wp (R) буде зростати, що відповідає відштовхуванню атомів. Такий характер зміни Wp (R) не залежить від природи хімічного зв’язку і показаний на рис. 2.9.
На рис. 2.10 зображено електронні хмари двох атомів водню, які при скінченній відстані R між ядрами частково перекриваються.
Обидва електрони в молекулі водню є тотожні й нерозрізнені частинки. Згідно принципу Паулі при переміні місцями цих електронів система не зміниться.
![]()
Рис. 2.10
Однак стан такої системи в квантовій механіці може визначатись або симетричною або антисиметричною хвильовою функцією. В цьому випадку хвильова функція повинна бути обов’язково антисиметричною. При цьому енергія взаємодії Wp (R) буде визначатись з урахуванням обох можливих станів молекули водню за формулою:
![]() , (2.3.2)
, (2.3.2)
де знак плюс стосується випадку опису стану молекули симетричною координатною хвильовою функцією, а мінус - антисиметричною координатною функцією.
Безрозмірний інтеграл S(R) називають інтегралом перекривання; він характеризує перекривання електронних хмар при наближенні атомів один до одного. При R®¥, коли атоми не взаємодіють, інтеграл S(R) перетворюється в нуль. Найбільшого значення S(R)=1 цей інтеграл досягає при R=0, коли обидва атоми сумістяться своїми ядрами і оболонками. Зрозуміло, що таких випадків не буває. В молекулі водню Н2 інтеграл S(R) має додатне значення менше за одиницю. На знак енергії Wp (R) інтеграл S(R) не впливає.
Інтеграл C(R) називають кулонівським інтегралом. Він характеризує кулонівську взаємодію ядер і електронів у молекулі Н2 . Найбільший інтерес становить інтеграл А(R) , який називають обмінним інтегралом. Наявність цього інтеграла пов’язана з нерозрізненістю електронів у молекулі і можливістю їх перестановки місцями. Інтеграл А( R ) має розмірність енергії і характеризує особливу квантово-механічну взаємодію, яка виникає між двома тотожними електронами, і яку умовно називають «обмінною взаємодією». «Обмінну взаємодію» електронів в молекулі водню розуміють так, що електрон кожного із її атомів періодично перебуває то біля одного атома, то біля іншого атома, здійснюючи тим самим зв’язок обох атомів. Сили, які проявляються при цьому, називають «обмінними».
Розрахунки показують, що на великих відстанях R C(R) i A(R) мають зникаюче мале значення. На великих відстанях взаємодія між окремими атомами водню відсутня. На середніх відстанях, співрозмірних з борівським радіусом водневого атома, обидва інтеграли C(R) i A(R) є від’ємні, причому çA(R)ç>çC(R)ç. Тому енергія в формулі (2.3.2) матиме такі два значення:
![]() ;
; ![]() . (2.3.3)
. (2.3.3)
Перше з них W+ p (R) відповідає притяганню і характеризує стійкий стан молекули водню. Друге W- p (R) відповідає відштовхуванню і визначає нестійкий стан молекули. Для стійкого стану молекули, координатна хвильова функція є симетричною, а спіни електронів повинні бути антипаралельними. Лише в такому випадку за принципом Паулі повна хвильова функція буде антисиметричною* . У нестійкому стані молекули водню координатні хвильові функції є антисиметричними. Для збереження антисиметричного характеру повної хвильової функції необхідно щоб спіни електронів в обох атомах молекули були паралельними.
* Y( r ) - координатна хвильова функція
Y( r,q,j ) - повна хвильова функція.
2.3.2. Енергетичні рівні молекул. Молекулярні спектри. Парамагнітний резонанс.
У попередніх лекціях були розглянуті спектри атомів, що складаються з окремих ліній, які утворюють серії. В середині кожної серії атомного спектра спектральні лінії розміщені на різніх відстанях одна від одної, при чому до межі кожної із серій вони зближуються. Молекулярні спектри вже за зовнішнім виглядом значно відрізняються від атомних. Молекулярні спектри являють собою широкі смуги, які утворені досить тісно розміщеними окремими лініями. Короткохвильовий край кожної із смуг має розмитий характер. Це пов’язано з тим, що окремі спектральні лінії так близько розміщені одна від одної, що сучасними спектральними приладами вже не розділяються.
Молекулярні спектри за їх характерний вигляд називають смугастими спектрами. Смуги і групи смуг молекулярних спектрів розміщуються як в інфрачервоній, видимій, так і в ультрафіолетовій області довжин електромагнітних хвиль. З ускладненням молекул ускладнюються і їх молекулярні спектри. В досить складних молекул в різних областях довжин хвиль спостерігаються суцільні широкі смуги поглинання або випромінювання.
Розглянемо механізм утворення молекулярних спектрів. Повна енергія молекули W може бути розглянута, як суперпозиція: Wпост - енергії поступального руху центра інерції молекули; Wел - енергії руху електронів в атомах молекули; Wкол - енергії коливального руху ядер атомів, що входять до складу молекули, біля їх положення рівноваги; Wоб - енергії обертального руху молекули як цілого; Wяд - енергія ядер атомів у молекулі. Тобто
W = Wпост + Wел + Wкол + Wоб + Wяд. (2.3.4)
Енергія Wпост не квантується, тому її зміна на молекулярні спектри не впливає. Енергія, пов’язана з впливом ядра Wяд на процеси в молекулі, досить мала й істотної ролі не відіграє. Тому надтонка структура в молекулярних спектрах пов’язана з впливом ядра, практично нехтується. Тому енергія молекули, яка визначає її оптичні властивості, складається з суми трьох доданків:
W1 =Wел +Wкол +Wоб (2.3.5)
За правилом Бора частота n кванта, який випускає молекула при зміні її енергетичного стану дорівнює:
![]() (2.3.6)
(2.3.6)
де DWел , DWкол , DWоб - зміни відповідних частин енергії молекули.
Оскільки кожний з доданків (2.3.5) набуває ряду дискретних квантових значень, тобто їх зміни також мають дискретні значення і тому спектр молекул складається з густо розміщених спектральних ліній. Як показують досліди і теоретичні розрахунки, зміни енергій DWел , DWкол , i DWоб мають різну величину
DWоб <<DWкол <<DWел .
Для виділення частот, які відповідають змінам різних видів енергії в молекулі зручніше розглянути її спектр поглинання. Припустимо, на речовину, яка складається з молекул, що не взаємодіють між собою, падає довгохвильове випромінювання з мало енергетичними квантами hn. До тих пір, доки енергія кванта hn не стане рівною найменшій різниці енергії між двома найближчими енергетичними рівнями молекул, поглинання не буде. Поглинання настане при довжинах хвиль зовнішнього опромінення порядку (0.1-1) мкм, тобто в далекій інфрачервоній області спектра. Кванти енергії таких хвиль можуть перевести молекулу з одного обертального енергетичного рівня на інший, вищий. А це призведе до виникнення спектра поглинання.
Довжини хвиль в кілька мікрон мають енергію, з допомогою якої можна збуджувати відповідні переходи коливальних рівнів. В цьому випадку будуть також збуджуватись відповідні обертальні рівні. Виникне коливально-обертальний спектр (рис.2.11).
![]()
Рис. 2.11
У видимій і ультрафіолетовій області енергії квантів достатньо для збудження в молекулах переходів між відповід-ними електронними рівнями.
![]()
Рис. 2.12
Одночасно з цими переходами будуть збуджуватись коливальні і обертальні енергетичні рівні. Це дасть можливість одержати електронно-коливальний спектр, який показано на (рис.2.12).
Отже, кожному електронно-коливальному переходу відповідатиме певна смуга, тому весь електронно-коливальний спектр у видимій і близькій до неї області є системою з кількох груп смуг, розміщених в цих ділянках спектра.
У 1996р. Зеєман знайшов, що коли джерело світла помістити між полюсами електромагніту, відбувається розчеплення спектральних ліній, а відповідно і атомних рівнів речовини джерела, на ряд компонентів. Цей ефект було названо на честь Зеємана - зеєманівським.
Якщо направити промінь світла перпендикулярно до напрямку силових ліній магнітного поля, то спектральні лінії частотою n0 симетрично розчеплюються на три компоненти n0 +Dn, n0 і n0 -Dn.
Ефект Зеємана (нормальний) спостерігається лише у парамагнітних атомів, так як лише ці атоми мають нульовий орбітальний магнітний момент і можуть взаємодіяти із зовнішнім магнітним полем.
Відстань між середньою і крайніми лініями зеєманівського розчеплення виявляється рівною
![]()
де ![]() - магнетон Бора; m0
- магнітна стала; h - стала Планка.
- магнетон Бора; m0
- магнітна стала; h - стала Планка.
Нормальний ефект Зеємана пов’язаний з розчепленням атомних рівнів і відповідно спектральних ліній завдяки взаємодії орбітальних магнітних моментів з зовнішнім магнітним полем. У випадку слабих магнітних полів можна спостерігати розчеплення пов’язане із взаємодією спінових магнітних моментів електронів. В цьому випадку ефект Зеємана називається аномальним. З ним пов’язана тонка структура спектральних ліній.
При типічних для лабораторних умов значеннях магнітного поля в 1 Тл енергія зеєманівського розчеплення рівнів DЕ»0.5. 104 еВ. Цій енергії відповідає частота
![]()
яка перебуває в мікрохвильовому діапазоні радіохвиль. Тому в магнітних полях порядку 1Тл зеєманівські рівні можна збуджувати за допомогою радіочастотного випромінювання.
В парамагнітному середовищі такі переходи приводять до електронного парамагнітного резонансу, який вперше спостерігався Завойським у 1944р.
Електронний парамагнітний резонанс полягає в поглинанні парамагнітною речовиною, яка перебуває в магнітному полі, енергії радіочастотного випромінювання.
Використання електронного парамагнітного резонансу пов’язане з вивченням властивостей парамагнітних речовин. В цьому випадку визначаються магнітні моменти атомів, резонансні частоти, орбітальне квантове число. Якщо ці параметри відомі, то можна вимірювати величину індукції магнітного поля. Магнітометри, які працюють на явищі парамагнітного резонансу, широко використовуються.
2.3.3 Комбінаційне розсіювання світла.
Комбінаційне розсіювання світла було відкрите в 1928 р. індійськими фізиками Раманом і Кришнаном. Одночасно над цим явищем працювали російські фізики Ландсберг і Мандельштам. В сучасній зарубіжній літературі комбінаційне розсіювання називається раманівським.
Суть комбінаційного розсіювання полягає в тому, що в спектрі розсіяного монохроматичного світла, після проходження його через гази, рідини або прозорі кристалічні тіла, поряд незміщених спектральних ліній містяться нові лінії, частоти яких є комбінацією частот n0 і nі коливних або обертальних переходів розсіюванних молекул:
n=n0 ±nі .
Комбінаційне розсіювання, як і всі інші явища взаємодії світла з речовиною, має квантовий характер. Нехай молекула розсіюваної речовини може знаходитися в ряді коливальних енергетичних станів W0 , W1 , ... ,Wi ,...,а нормальний стан молекули відповідає енергії W0 . При взаємодії такої молекули з квантом зовнішнього випромінювання енергією e0 =hn0 , молекула може виявитись в більш високому енергетичному стані з енергією Wi . На цей перехід буде затрачена енергія DW=Wi -W0 . Тому енергія фотона зменшиться на величину DW; в той же час появиться новий фотон (розсіяний) з енергією
e = h n =h n 0 - D W .
З останньої рівності видно, що
![]() (2.3.7)
(2.3.7)
де ![]() - частота, якій відповідає перехід між рівнями W0
i Wi
. Тому n
=
n
0
-
n
і
,
що відповідає появі «червоного» супутника. Поява фіолетового супутника пояснюється взаємодією падаючого фотона частотою n0
з молекулою, яка перебуває у збудженому стані з енергією Wi
. Взаємодія падаючого фотона з молекулою в збудженому стані стимулює її перехід в нормальний енергетичний стан. Тому:
- частота, якій відповідає перехід між рівнями W0
i Wi
. Тому n
=
n
0
-
n
і
,
що відповідає появі «червоного» супутника. Поява фіолетового супутника пояснюється взаємодією падаючого фотона частотою n0
з молекулою, яка перебуває у збудженому стані з енергією Wi
. Взаємодія падаючого фотона з молекулою в збудженому стані стимулює її перехід в нормальний енергетичний стан. Тому:
e = h n 0 + D W ,
звідки n = n 0 + n / - фіолетовий супутник.
Очевидно, що число молекул у збудженому стані буде зростати з підвищенням температури. А це сприяє зростанню інтенсивності фіолетових супутників. Указані висновки добре погоджуються з експериментом.
Комбінаційне розсіювання є важливим методом вивчення власних частот коливань в складних молекулах, особливо в органічних сполуках. В останні роки цей метод є невід’ємною частиною молекулярного спектрального аналізу.
2.3.4 Поглинання, спонтанне і вимушене випромінювання. Оптичні підсилювачі і квантові генератори.
Як уже було відмічено, атоми можуть знаходитись лише у строго визначених квантових станах, яким відповідають дискретні значення енергії W 1 , W 2 , W 3 ,..., Wn .
З точки зору квантової механіки стаціонарний стан атома повинен зберігатися як завгодно довго, якщо немає зовнішніх причин, які спричиняють зміну енергії атома. Проте дослід показує, що атом у збудженому енергетичному стані сам собою переходить у нормальний, не збуджений стан, випромінюючи світло. Таке випромінювання називається самочинним, або спонтанним випромінюванням.
Крім самочинних (спонтанних) переходів з одного енергетичного рівня на другий, спостерігаються також вимушені (індуковані) переходи, обумовлені дією падаючого випромінювання. Самочинні переходи відбуваються лише в одному напрямі - з більш високих енергетичних рівнів на нижчі енергетичні рівні. Вимушене випромінювання рівнозначно відбувається як в одному, так і в другому напрямі. У випадку переходу на більш високий енергетичний рівень атом поглинає квант енергії. При вимушеному випромінюванні із збуджених енергетичних рівнів випромінюються додаткові фотони, які називаються вимушеними або індукованими. На рис 2.13 показано ці процеси для атомів, які мають умовно лише два енергетичні стани - основний W 0 і збуджений W 1 .
![]()
Рис 2.13
Важливо відмітити, що при вимушеному випромінюванні первинний і вторинний фотони є точними копіями один одного. Ще в 1916р. Ейнштейн і Дірак доказали, що вимушені (вторинні) фотони мають однакову частоту, фазу, поляризацію і напрям поширення. Вимушене випромінювання строго когерентне до падаючого. Ця особливість вимушеного випромінювання покладена в основу дії підсилювачів і генераторів світла, які називають лазерами.
Методи підсилення світла за рахунок вимушеного випромінювання були запропоновані ще в 1939р. російським фізиком Фабрикантом, а в 1954р. вже були побудовані прилади підсилення електромагнітних хвиль фізиками Басовим і Прохоровим і незалежно від них американським фізиком Таунсом. Ці прилади були названі мазерами. Вони працювали у сантиметровому діапазоні електромагнітних хвиль.
Перший лазер (оптичний квантовий генератор) створив Мейман (США) у 1960р.
Для підсилення світла необхідно, щоб на вищому енергетичному рівні W 1 знаходилось більше електронів, ніж на нижчому, тобто N 1 > N 0 при W 1 > W 0 . Вважають, що в цьому випадку відбувається інверсна заселеність рівнів W 1 i W 0 . Тоді при проходженні через таку речовину електромагнітної хвилі з частотою n =( W 1 - W 0 )/ h ця хвиля буде не слабшати, а навпаки, підсилюватись за рахунок індукованого випромінювання.
Новий фотон, що з’явиться внаслідок індукованого випромінювання, підсилює світло, яке проходить крізь середовище. Однак необхідно мати на увазі, що крім індукованого випромінювання відбувається процес поглинання світла. Внаслідок поглинання фотона атомом, що перебуває на енергетичному рівні W 0 , фотон зникає і атом перейде на енергетичний рівень W 1 (рис 2.13. «а»). Цей процес зменшує потужність світла, що проходить крізь середовище. Внаслідок актів вимушеного випромінювання фотон з енергією h n переводить атом із рівня W 1 на W 0 і замість одного фотона далі летять два фотони (рис 2.13 «б»). Дія підсилюючого середовища визначається тим, який з двох процесів переважає. Якщо переважають акти поглинання, то середовище ослаблює падаюче випромінювання і навпаки, якщо переважають акти вимушеного випромінювання, то середовище підсилює світло.
Досліди показали, що використання дворівневого середовища для побудови оптичних квантових генераторів не є ефективним. Перший квантовий генератор був створений за схемою трьох рівнів. Підсилюючим середовищем у ньому є кристал рубіну, який за хімічним складом є окисом алюмінію AL2 O3 з домішками окису хрому Cr2 O3 в кількості біля 0.03%. При цьому в кристалічній гратці Al2 O3 певну кількість іонів Al3+ замінено на іони Cr3+ . Активною речовиною, в якій здійснюються вимушені переходи в рубіні є іони Cr3+ . Енергетична схема Cr3+ складається з трьох рівнів: основний стан W 0 і дві широкі енергетичні смуги W 1 , і подвійний метастабільний рівень W 2 . Перехід з метастабільного рівня W 2 в основний стан W 0 супроводжується випромінюванням червоного світла з довжинами хвиль 6927 і 6943 А0 . (рис.2.14)
 W1
W1
W2
W0
Рис 2.14
Якщо рубін інтенсивно опромінюють світлом потужної імпульсної лампи (криптон-ксенонова лампа), то іони хрому переходять з основного стану W 0 на рівні широкої смуги W 1 , звідки найімовірнішим є безвипромінювальний перехід іонів на подвійний рівень W 2 з переданням частини енергії кристалічній гратці рубіну. Важливо те, що рівні W 2 i W 0 заселені інверсно. Головним в цьому випадку є різний час збудженого стану рівнів W 1 (приблизно 10-7 с.) і метастабільного стану W 2 ( приблизно 10-3 с.). За час 10-4 с. на рівнях W 2 відбувається нагромадження енергії, тобто створюється інверсний стан. Кожний фотон, який випадково може виникнути при самочинних переходах в принципі може ініціювати в активному середовищі лавину вимушених переходів W 2 ® W 0 . Однак спонтанні переходи носять випадковий характер, а ініційовані ними вимушені фотони випромінюються в різних напрямках. Таке випромінювання не може бути високо когерентним.
Для лазерної генерації використовують ще один елемент - оптичний резонатор. Оптичним резонатором в найпростішому випадку можуть бути два дзеркала, між якими розміщують рубіновий стержень. Одне із дзеркал є напівпрозорим. Всі ті фотони, які зародились і рухаються в напрямку осі лазера багаторазово відбиваються від дзеркал і в певний момент часу (кожні 10-3 с.) разом з черговою лавиною вимушених фотонів при переході W 2 - W 0 , випромінюються через напівпрозоре дзеркало у вигляді лазерного імпульсу. Потужність такого випромінювання в імпульсі може досягати 106 - 109 Вт, а густина потоку світлової енергії 104 - 107 кВт/м2 .
Першим газовим лазером безперервної дії став гелій-неоновий лазер, який було створено в 1961р. В гелій-неоновому лазері накачку створюють в два етапи: гелій є носієм енергії збудження, а лазерне випромінювання дає неон. На рис 2.15 показана енергетична схема гелій-неонового лазера.

W1
W2
W0
Рис. 2.15
За рахунок співударів з електронами атоми гелію переходять у збуджений стан W
1
. При зіткненнях збуджених атомів гелію з атомами неону останні також збуджуються і переходять на один з верхніх рівнів неону, розташованих поблизу відповідних збуджених рівнів гелію. Перехід атомів з цього рівня на один з нижчих рівнів W
2
супроводиться випромінюванням лазера. Час збудженого стану He W
1
становить близько 10-7
с., час збудженого стану Ne W
1
приблизно 10-3
с. Різниця в часі дає можливість в певній мірі концентрувати світлову енергію. Довжина хвилі гелій-неонового лазера становить 6328![]() .
.
Основні властивості лазерного випромінювання:
1. Високі часова і просторова когерентність. Час когерентності біля 10-3 с., а довжина когерентності - 105 м.
2. Висока монохроматичність (D l = 10-11 м.)
3. Велика потужність випромінювання (до 109 Вт)
4. Мала кутова розходженість в променях.
У більшості відомих на сьогодні лазерів ККД не перевищує 1%. Однак є лазери на основі неодиму з ККД біля 75% і потужний СО2 - лазер з ККД до 30%.
Лазери знайшли широке використання у різних галузях науки і техніки.
Серед прикладів використання лазерів слід відмітити слідуючи:
а) обробка металів, мікрозварювання, обробка алмазних виробів;
б) безкровний лазерний скальпель на основі СО2 - лазера в медицині;
в) створення високотемпературної плазми, можливість термоядерного синтезу в майбутньому;
г) різноманітна вимірювальна техніка, лазерні інтерферометри;
д) створення і відтворення голограм;
е) створення сучасних засобів зв’язку і т.д.