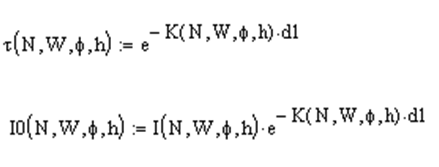Дипломная работа: Оптична нестабільність кристалів

Дипломна робота

ОПТИЧНА НЕСТАБІЛЬНІСТЬ КРИСТАЛІВ

Реферат

Розглянуто явище оптичної нестабільності, основні її види та моделі представлення, умови та середовища реалізації. Проаналізовано особливості будови шаруватих кристалів, як можливого середовища реалізації оптичної нестабільності. Представлено моделі нестабільних оптичних пристроїв. Теоретично досліджено вплив слабких магнітних полів на умови реалізації оптичної нестабільності в області екситонного поглинання шаруватих напівпровідників. На прикладі кристалу 2H-PbI₂ розраховано область реалізації магнітооптичної нестабільності при змінній температурі і частоті.

Кількість сторінок - 54, кількість рисунків – 27, посилань на літературні джерела - 25

Ключові слова: оптична нестабільність, магнітооптична нестабільність, шаруваті кристали, нестабільний оптичний пристрій.

Зміст

Список умовних позначень, скорочень

Вступ

Розділ 1. Теоретична частина

1.1 Означення оптичної нестабільності

1.2 Модель оптично нестабільної системи

1.2.1 Дисперсійна оптична нестабільна система

1.2.2 Абсорбуюча оптична нестабільна система

1.3 Механізми оптичної нелінійності в напівпровідникових матеріалах

1.4 Оптичні нестабільні пристрої

1.4.1 Модель резонаторного нестабільного пристрою

1.4.2 Оптичні нестабільні пристрої на напівпровідникових кристалах

1.4.3 Модель березонаторного нестабільного пристрою на шаруватих кристалах

Розділ 2. Експериментальна частина

2.1 Математична модель безрезонаторної оптичної нестабільності шаруватих кристалів

2.2 Магнітооптична нестабільність

2.3 Обговорення результатів розрахунку області реалізації магнітооптичної нестабільності в шаруватих кристалах

Висновки

Література

Додаток 1

Список умовних позначень, скорочень

ОН – оптична нестабільність

ШК – шаруваті кристали

МОН – магнітооптична нестабільність

Вступ

Актуальним та одним із найцікавіших напрямків розвитку сучасної фізики є можливість створення оптичних комп’ютерних мереж. Побудова чисто оптичної інформаційної системи потребує розв’язання двох задач: шляхів передачі оптичних сигналів та методів запису, зберігання і відтворення оптичної інформації. На сьогодні, перша задача повністю технологічно розв’язана. Перспектива ж створення оптичного логічного елементу пов’язана із використанням оптичних бістабільний пристроїв.

Явище оптичної нестабільності (ОБ) проявляється в тому, що при певних умовах проходження світла через середовище, при фіксованому значенню вхідної інтенсивності , реалізується два (або більше) стабільних стани, що відповідають різним значенням вихідного сигналу, тобто має місце гістерезисна залежність [1]. Механізм ж виникнення ОБ і середовище реалізації можуть бути різними. Але обов’язковою умовою є нелінійне середовище і обернений зв'язок. Останнє може бути забезпечено як накладанням зовнішніх умов так і специфічним характером внутрішніх умов, тобто можна організувати резонаторну та безрезонаторну ОБ. Остання виникає без зовнішнього оберненого зв’язку в результаті збільшення поглинаючої здатності середовища при зростанні інтенсивності вхідного сигналу.

В роботі розглянуто екситонний механізм нелінійності, з особливістю керування динамікою зміни густини екситонів. Це в свою чергу призводить до виникнення безрезонаторної оптичної нестабільності. Її реалізація пов’язана з процесами релаксації екситонного збудження [2].

Для особливого класу речовин – шаруватих кристалів, процеси екситон-фононної релаксації мають певні особливості, зумовлені їх будовою [3].

Шаруваті кристали (ШК) за своєю будовою займають проміжне місце між кристалічними і склоподібними структурами, між двомірними і тримірними сполуками, між іонними і молекулярними речовинами. Шаруватим напівпровідникам властива істотна анізотропія їх фізичних властивостей вздовж шару і між шарами. Це приводить до особливостей фононного спектру: існуванню хвиль згину в акустичному спектрі фононів, які являють собою мембранні коливання шару. Екситонний спектр у таких речовинах формується звичайними тримірними екситонами Ваньє-Мотта з радіусом, який охоплює декілька шарових пакетів [3].

Однією з причин виникнення оптичної нестабільності в шаруватих кристалах є динамічна нелінійність оптичного поглинання в екситонній області частот (внутрішня ОБ), що пояснюється конкуренцією процесів збудження екситонних станів і їх релаксацією внаслідок екситон-фононної взаємодії [4]. Можливість реалізації двох або більше стабільних оптичних станів кристалу в області екситонних резонансів відкриває нові можливості не тільки запису і зберігання оптичної інформації, але й керуванням нелінійними явищами, шляхом зміни зовнішніх факторів.

Мета роботи: Аналіз можливості і умов реалізації магнітооптичної нестабільності (МОБ) в шаруватих напівпровідниках в області екситонних резонансів.

Завдання, які підлягають вирішенню:

1. Розгляд особливостей явища ОБ, видів, механізмів та середовищ реалізації;

2. Дослідження реалізації ОБ в ШК;

3. Аналіз умов реалізації МОБ;

4. Розрахунок області реалізації МОБ при змінній температурі і частоті.

Розділ 1. Теоретична частина

1.1 Означення оптичної нестабільності

Під оптичною нестабільністю розуміють наявність в оптичній системі двох або більше сталих станів при дії на неї випромінюванням визначеної інтенсивності і спектрального складу [5].

Залежність між випромінюванням, що пройшло крізь бістабільний оптичний пристрій І_прох від І_о , характеризується наявністю гістерезису за певних умов. Змінюючи умови роботи пристрою, змінюють ширину гістерезису, тобто змінюють область нестабільності. Тоді, коли область нестабільності зовсім пропадає, має місце однозначна залежність І_прох від І_о , на всьому інтервалі зміни І_о . При наявності гістерезису, перехід між станами слабого і сильного пропускання відбувається стрибкоподібно, а при відсутності – без стрибка [5].

Рис. 1. Схема оптичного нестабільного пристрою

Явище оптичної нестабільності відкриває можливості для керування оптичним випромінюванням, що дозволяє реалізовувати аналоги різних електронних пристроїв в оптичному діапазоні [5].

Оптично бістабільний пристрій (характеристика якого зображена на рис. 2а може працювати як елемент оптичної пам’яті [5]. Світловий імпульс, інтенсивність якого перевищує величину , переводить систему зі стану малого пропускання (стан А) в стан сильного пропускання. Після припинення дії даного світлового імпульсу цей стан буде збережено, тобто він “ запам’ятовується ” .

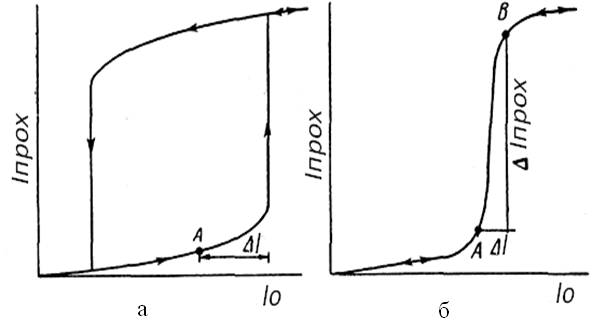Рис. 2. Характеристики оптичних нестабільних пристроїв: а – 1-й; б – 2-й

Оптично бістабільний пристрій (характеристика якого зображена на рис. 2б може працювати як оптичний транзистор [5]. При дії на систему достатньо потужного випромінювання спостерігається точка переходу між станом слабого пропускання у стан сильного пропускання. Зовнішній світловий сигнал малої інтенсивності І переводить оптично нестабільні систему в стан сильного пропускання. Тобто за допомогою випромінювання малої інтенсивності контролюють випромінюванням із значною інтенсивністю (І_прох /І1).

1.2 Модель оптично нестабільної системи

Як модель розглянемо резонатор Фабрі-Перо [6]. На одне з його дзеркал перпендикулярно падає когерентне випромінювання інтенсивності І₀ . Середовище резонатора являє собою речовину з коефіцієнтом поглинання і показником заломлення n для випромінювання довжини хвилі, що використовується.

В результаті багатопроменевої інтерференції інтенсивність світла всередині і на виході резонатора залежить від співвідношень між його довжиною L (відстань між дзеркалами резонатора) і довжиною хвилі випромінювання. Якщо довжина резонатора дорівнює цілому числу N півхвиль випромінювання (умова резонатора), то інтенсивність випромінювання всередині і на виході резонатора має максимум, якщо ( N + ) = nL – інтенсивність мінімальна.

В області резонансу величина поглинаючої в резонаторі потужності зі збільшенням коефіцієнта поглинання може зменшуватися. Це відбувається за рахунок того, що в області резонансу збільшення коефіцієнта поглинання призводить до різкого зменшення інтенсивності світла в резонаторі, що перекомпенсовує ріст самого коефіцієнта поглинання.

Якщо даний резонатор заповнити середовищем, показник заломлення якого змінюється зі зміною інтенсивності світла в ньому, або середовищем із насиченим поглинанням, то за допомогою такого резонатора можна отримати ОБ.

ОБ може бути абсорбуючою чи диспергуючою, у відповідності з тим чи виникає зворотній зв'язок, тобто чи коефіцієнт поглинання залежить від інтенсивності або коефіцієнт заломлення. Однак цей поділ не є різким, ці два механізми можуть існувати одночасно. Виділяють нестабільні системи власні і гібридні. Для власної притаманна залежність характеристик системи від інтенсивності, що є результатом безпосередньої взаємодії випромінювання з речовиною. В гібридній (оптоелектронній) - така залежність формується електричним сигналом. Основою для створення обох типів оптично нестабільних систем, в багатьох випадках, є резонатор Фабрі-Перо.

1.2.1 Дисперсійна оптична нестабільна система

Нехай резонатор Фабрі-Перо заповнений речовиною, яка непоглинає випромінювання, показник заломлення якої залежить від інтенсивності світла, за законом n = n₀ +n_2Iвн (‘керрівське’ середовище) [6]. На рис. 3 представлений графічний розв’язок, залежності інтенсивності світла I_вн і І_прох від зміни І₀ , I_вн =(nL-n0L)/n2L.

Рис. 3. Залежність інтенсивності випромінювання всередині резонатора Iвн від оптичної довжини шляху (nL): для різних І0 і R=0.3 (осцилографічні криві)

Точки перетину цієї прямої (певне значення І₀ ), визначає значення функцій I_вн (І₀ ) і І_прох (І₀ ). При плавному збільшені І₀ , I_вн спочатку збільшується теж плавно (точки 1-4), потім при значенні І₀ , що відповідає точці 5, відбуваються стрибок (5-6). Далі спостерігається плавне зменшення І₀ , I_вн (6-8) і стрибок (8-3).

Отже залежність I_вн (І₀ ) є гістерезисною, спостерігається ОБ. При збільшені І₀ , області нестабільності можуть повторюватися. В системі наявний зворотній зв'язок, що приводить до ОБ. Стан системи в точці 5, характеризується тим, що будь-яке збільшення І₀ приводить до росту I_вн , а відповідно і nL. За рахунок наближення системи до резонансу відбувається подальше збільшення I_вн , nL. Як наслідок проявляється стрибкоподібний перехід між точками 5 – 6. Точка 6 являється точкою стійкої рівноваги.

Рис. 4. Характеристики оптичної нестабільної системи при реалізації дисперсійної оптичної нестабільності

1.2.2 Абсорбуюча оптична нестабільна система

Нехай резонатор Фабрі-Перо заповнений речовиною, коефіцієнт поглинання якої зменшується зі збільшенням інтенсивності світла, за законом

де - параметри насичення поглинання, що не залежать від І₀ [7].

Будемо вважати, що , тоді Р, при резонансі різноманітних І₀ представлено на рис. 4а. Також на цьому рисунку наведена пряма Р, яка описується рівнянням

(де – робочий об’єм резонатора).

Точки перетину цих прямих визначають залежності P(I₀ ), (I₀ ), I_прох (I₀ ) (рис. 4 б, в, г ). Тут наявний гістерезис, тобто формується ОБ. Але в даному випадку при збільшенні I₀ , область нестабільності не повторюється.

Рис. 5. Залежність поглинання потужності в резонаторі Р від (для різних I0 і R = 0.99): а - залежності, що описують поглинання в матеріалі з насиченим поглиначем (суцільна пряма - L/(1+R)>8, штрихові - L/(1+R)<8); б, в, г - характеристики нестабільного оптичного пристрою при абсорбуючій оптичній нестабільності

За допомогою резонатора Фабрі-Перо забезпечується позитивний зворотній зв'язок, який призводить до ОБ [6]. При плавному збільшенні I₀ , Р збільшується плавно, але при переході системи із стану 6 – 7, спостерігається лавиноподібний процес. Система знаходиться в стані 6, при цьому будь яке збільшення I₀ , визначає збільшення Р, що в свою чергу забезпечує зменшення , і навпаки зменшення - до збільшення Р (властивість резонатора). Коли система буде знаходитися в стані 7, плавне зменшення I₀ , зменшує Р і відповідно збільшує але це не викликає лавиноподібного процесу, а лише збільшує Р. Після досягнення системою стану 9, ріст створює умови зменшення Р (властивість резонатора). Тобто відбудеться лавиноподібний процес і стрибок системи із стану 9 – 4.

При малих значеннях ОБ в резонаторі із насиченим поглинаючим середовищем, не може бути реалізована, вона має місце, якщо

де Т – пропускання дзеркала резонатора.

Наявність фонового поглинання сильно ускладнює можливість отримання абсорбуючої оптичної нестабільності.

Отже резонатор, який заповнений насиченим поглинаючим середовищем або нелінійним матеріалом, у якого n залежить від І, може виступати, як оптично бістабільний пристрій. В напівпровідниках достатньо просто реалізувати умови необхідні для насичення оптичного середовища [7].

1.3 Механізми оптичної нелінійності в напівпровідникових матеріалах

Характерною особливістю всіх достатньо чистих напівпровідників є те, що на певній довжині хвилі, коефіцієнт поглинання починає різко зменшуватися, і на довших хвилях матеріал стає доволі прозорим [7]. Цю ділянку значного зниження поглинання називають краєм власного поглинання (фундаментального поглинання). При фундаментальному поглинанні випромінювання, в напівпровідниках концентрація електронів у зоні провідності і дірок у валентній зоні збільшується.

Ріст повної концентрації нерівноважних носіїв заряду приводить до зменшення числа вільних станів в зоні провідності і до зменшення зайнятих електронами станів у валентній зоні. Віддаленість відповідних зон, між якими здійснюються оптичні переходи, збільшує кількість нерівноважних носіїв. Відповідно насичення поглинання за рахунок динамічного ефекту Бурштейна-Мосса [8], буде найбільш сильним, якщо енергія квантів випромінювання, що використовується, буде порядку ширини забороненої зони напівпровідника ().

Позначивши коефіцієнт поглинання випромінювання малої інтенсивності через , отримаємо

де визначають імовірності заповнення енергетичних станів електронами і дірками відповідно в зоні провідності і валентній зоні, між якими відбуваються оптичні переходи.

У напівпровідниках густина станів в зоні провідності значно менша, ніж у валентній зоні [8], тому зміни заповнення дірками станів у валентній зоні можна не враховувати, тоді

де - квазірівень Фермі, який визначається концентрацією електронів в зоні провідності, – рівноважна концентрація електронів. Також концентрацію нерівноважних електронів , можна отримати з рівняння балансу

де - час життя, що залежить від конкретного механізму рекомбінації і параметрів напівпровідника.

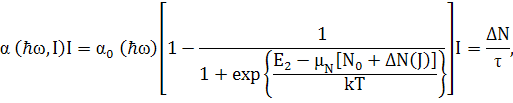
де - ефективна густина станів в зоні провідності.

Експерименти по дослідженню та спостереженню динамічного ефекту Бурштейна-Мосса проводилися на різноманітних напівпровідниках[8] .

На рис. 6, 7 наведено спектри поглинання деяких напівпровідників, для різних концентрацій в області фундаментального поглинання.

Нелінійність спектрів поглинання, як свідчать численні експерименти, пояснюється екситонними процесами формування відповідних спектрів. Тут, форма краю фундаментального поглинання у значній мірі визначається кулонівською взаємодією електронів і дірок, яка призводить до утворення екситонних максимумів в спектрі поглинання і до суттєвого збільшення коефіцієнта поглинання поблизу краю [8]. В тому випадку, коли в напівпровіднику висока концентрація вільних носіїв струму, то кулонівська взаємодія екранується і відповідно змінюється форма краю поглинання. На рис. 7 приведені експериментальні залежності коефіцієнта поглинання Gе при прямих оптичних переходах від концентрації дрібних донорів (тобто від концентрації електронів в умовах експерименту).

Рис. 6. Спектр поглинання германія для декількох концентрацій домішок (при Т = 77 К): 1 – 3 1013 см-1; 2 – 2 1015 см-1; 3 – 1 1016 см-1; 4 – 2 1017 см-1; 5 – 1.5 1018 см-1; 6 – спектр поглинання чистого германія

Відносна зміна поглинання особливо суттєва в області екситонного максимуму, який практично зникає при концентрації електронів см-3, що відповідає виконанню умови де - радіус екранування, - боровський радіус екситона [9]. Якщо інтенсивність падаючого на напівпровідник випромінювання з енергією кванта значна, то створена цим випромінюванням концентрація нерівноважних носіїв може виявитися достатньою, щоб заекранувати кулонівську взаємодію електронів і дірок. В цьому випадку повинно спостерігатися зменшення коефіцієнта поглинання по відношенню до коефіцієнта поглинання випромінювання того ж спектрального складу, але малої інтенсивності. Цей ефект насичення поглинання, експериментально спостерігається в області екситонного резонансу і розглядався в [9].

Рис. 7. Спектри лінійного поглинання (Т=300К): а – GaAs; б - GaAs–AlGaAs

Ефект насичення поглинання при не дуже значних І обумовлений екрануванням кулонівської взаємодії електрона і дірки нерівноважними носіями [9]. Насичення поглинання при фотопереходах з домішковим центрів в одну із дозволених зон і при фотопереходах між підзонами валентної зони може бути використано для отримання ОБ [10]. В обох випадках насичення поглинання, в основному, обумовлено виснаженням початкових станів, з яких ідуть фото переходи.

Рис. 8. Схема оптоелектронного насичуючого поглинача

Рис. 9. Залежність коефіцієнта поглинання , насичуючого поглинача, від падаючої на його робочу частину, потужності випромінювання Р0

Рис. 10. Залежність Рпрох від Р0: 1 – L = 200 мкм; 2 – L = 500 мкм

1.4 Моделі нестабільних напівпровідникових пристроїв

1.4.1 Модель резонаторного нестабільного пристрою

Явище оптичної нестабільності лежить в основі створення оптичних бістабільний пристроїв. ОБ, яка обумовлена зміною показника заломлення при динамічному ефекті Бурштейна-Мосса, може спостерігатися при використанні резонатора [9].

Як джерело випромінювання використовувався CO-лазер, енергія квантів світла якого, в умовах експерименту, була дещо меншою за ширину забороненої зони InSb. Результати експерименту для резонатора із InSb (L=200мкм) при 77 К приведені на рис. 11. Вперше ОБ, за рахунок зміни показника заломлення при насиченні поглинання в області екситонного резонансу спостерігалася при низьких температурах в експериментах з резонаторами із GaAs.

Рис. 11. Ефект резонаторної ОБ, зареєстрований експериментально

При кімнатній температурі оптична НЕСТАБІЛЬНІСТЬ, зв’язана із зникненням екситонного резонансу, спостерігалася в експериментах з резонаторами із CdSe [10].

1.4.2 Нестабільні оптичні пристрої на напівпровідникових кристалах

Зображений на рис. 12, оптичний бістабільний пристрій формується із фотодіоду (ФД) і лазерного діоду (ЛД), розміщених на напівпровідниковій підкладці 1 [11].

Комбінація шарів фотодіода і лазерного діода наступна:

1 – n-тип GaAs підкладка;

3 – n-тип шар GaAlAs;

4 – p-тип шар GaAs;

5 – p-тип шар GaAlAs;

6 – p-тип шар GaAs.

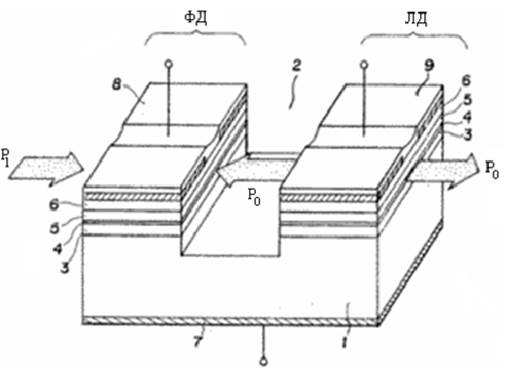
Рис. 12. Будова нестабільного оптичного пристрою

Рис. 13. Еквівалентна схема оптичного нестабільного пристрою

Лазерний діод випромінює частину світла , в прямому напрямку, а частину в зворотному, яка повертається до фотодіоду [11].

Як видно, із еквівалентної схеми пристрою, зображеної на рис. 13, додатній полюс джерела живлення під’єднаний до анодного електроду лазерного діоду 9, а від’ємний полюс – до електроду фотодіоду 8. Одночасно, вони з’єднанні із загальним електродом 7.

При опроміненні фотодіоду вхідним світловим сигналом P₁ , струм у фотодіоді протікає у зворотному напрямку, що створює потік струму в прямому напрямку в лазерному діоді і генерацію випромінювання P₀ , лазерним діодом [12].

Світло отримане фотодіодом, збільшує струм, а отже підсилює вихідне випромінювання P₀ за додатнім оберненим зв'язком.

Інтенсивність вихідного сигналу лазерного діоду зазнає незначного росту, до досягнення деякого граничного значення А вхідного струму, після чого швидко збільшується.

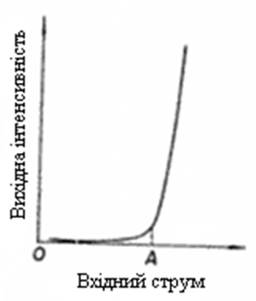
Рис. 14. Залежність вихідної інтенсивності від вхідного струму лазерного діоду

Вихідний струм фотодіода майже пропорційно збільшується, аж до досягнення певного значень B вхідної інтенсивності і як тільки це значення перевищено - струм стабілізується на фіксованому рівні С [13].

Рис. 15. Залежність вихідного струму фотодіода від вхідної інтенсивності

Коли вхідний сигнал P₁ досягає певного значення X₁ , вихідний сигнал P₀ швидко зростає до певного максимального рівня. Після чого, вихідний сигнал P₀ випромінюється лазерним діодом на стабільному рівні Y, як зображено на рис. 16.

Якщо вхідний промінь P₁ зменшується, то вихідний струм фотодіода зазнає зменшення також. Однак частина вихідного сигналу P₀ лазерного діода надходить назад до фотодіоду, тому вихідний струм зменшується за малим градієнтом. Коли вхідний сигнал падає нижче значення змінної X₂ , інтенсивність вихідного світла P₀ , лазерного діода швидко змінюється від високого до низького рівня. Значення X₂ менше ніж X₁ .

Щоб змінити значення X₁ і X₂ для умовного оптичного нестабільного пристрою, потрібно змінювати значення величин резисторів R₁ , R₂ і R₃ .

Отже, після того як опір було обрано і резистори зібрано в ланцюг, змінити значення X₁ і X₂ , надзвичайно важко.

Напруга джерела живлення ділиться на резисторах R₁ , R₂ і R₃ та подається на фотодіод у зворотньому напрямку, а на лазерний діод, відповідно, в прямому [14].

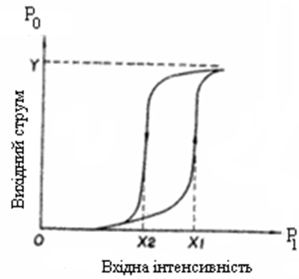
Рис. 16. Залежність вихідного струму оптичного нестабільного пристрою від вхідної інтенсивності

Світломодулюючий елемент складається із:

шару GaAs n-типу 13;

шару GaAlAs n-типу 14;

шару GaAlAs p-типу 15.

Рис. 17. Електрична схема оптичного нестабільного пристрою

Рис. 18 та 19 ілюструють модель оптичного нестабільного пристрою, що формується за допомогою світломодулюючого елемента, розміщеного в каналі 2 [14].

На рис. 18, світло, що випромінюється від лазерного діода передається через світломодулюючий елемент зліва на право, відповідно, узгоджено із рівнем напруги між електродами 16 і 17.

Рис. 18. Переріз оптичного нестабільного пристрою

Світло передається через світломодулюючий елемент уздовж напрямку Z. Кількість переданого випромінювання контролюється напругою, прикладеною між електродами 16 і 17. Чим більше значення напруги - тим менше випромінювання передається.

Рис. 19. Еквівалентна схема оптичного нестабільного пристрою зображеного на рис. 18

Рис. 20. Схематичний вигляд модулюючого елемента

В цілому, світломодулюючий елемент працює як хвилевід із додатнім оберненим зв’язком, частина вихідного випромінювання від лазерного діода потрапляє на фотодіод [14]. В результаті, циклічність додатнього оберненого зв'язку може бути досягнуто, контролем подання напруги сигналу і зміною точок X₁ і X₂ без зміни зовнішніх зв’язків.

1.4.3 Модель безрезонаторного нестабільного пристрою на прикладі шаруватих кристалів

ШК - це структури побудовані специфічними структурними елементам (шаровими пакетами), які складаються з одного або декількох моношарів [15]. Завдяки цьому, вони займають проміжне місце між іонними та молекулярними кристалами, між двовимірними та тривимірними сполуками. В межах шарового пакету зв'язок між атомами сильний (іонно-ковалентний), а між шаровими пакетами – слабкий (типу ван-дерваальсового). Істотна анізотропія міжатомних взаємодій може пояснити значну кількість оптичних властивостей [15]. В залежності від типу об’єднань окремих шарів (поворот відносно головної осі кристалу або зсув шару відносно один одного) з’являються різні поліпептидні модифікації кристала. Саме явище поліпептизму і визначає анізотропію міжатомних взаємодій у кристалах даного типу, адже існування слабкої взаємодії реалізує різні способи їх розшарування відносно головної осі кристала [16]. За рахунок різної величини сил міжатомного зв’язку, діючих в межах шарового пакету і між ними, при описанні пружних властивостей таких структур необхідно враховувати поперечну жорсткість шарових пакетів. Така відмінність зв’язків призводить до аномалії коливних спектрів – виникнення в них специфічних низькоенергетичних коливань акустичного типу – хвиль згину, які призводять до зміни форми і розмірів кристалу: видовженню вздовж головної оптичної осі і скороченню в перпендикулярному напрямку (мембранний ефект) [16].

В шаруватих кристалах, при поглинанні ними кванту світла, утворюється такий стан, коли електрон і дірка, притягуються один до одного, утворюючи зв’язаний збуджений стан, який може рухатися вздовж кристала, що отримав назву екситонного. В шаруватих кристалах збуджуються звичайні тримірні екситони Ваньє-Мотта з радіусом, який охоплює декілька шарових пакетів, які характеризуються анізотропією електрон-дірка [17]. Це є причиною виникнення дипольного моменту утвореного екситона, який відіграє істотну роль у процесах взаємодії падаючого фотону з фононною підсистемою кристала [18].

Особливостями фононного спектру шаруватих кристалів є наявність низькоенергетичних оптичних фононів, що відповідають коливанням шарових пакетів один відносно одного та існуванню хвиль згину в акустичному спектрі фононів, які являють собою мембранні коливання шару [19]. Сильна відмінність внутрішньошарових і міжшарових взаємодій у шаруватих кристалах спричинює те, що процеси розсіювання екситонів на хвилях згину істотно залежать від напрямку поширення світла відносно кристалографічної осі кристалу. Розповсюдження світла вздовж шарового пакету, або перпендикулярно до нього, дозволяє формувати відгук кристалу у різних частотних областях вихідного сигналу з різною динамікою зміни гістерезисної петлі, до того ж знак функції екситон-фононного зв’язку буде різним для різних напрямків поширення світла [20].

В ідеальних кристалах, при відсутності домішок та дефектів, спектр поглинання представляється у вигляді вузьких резонансних ліній [20]. Така ситуація відповідає прямому перетворенню енергії фотону в енергію екситону і навпаки. Але в дійсності спостерігаються широкі смуги поглинання із значно меншим часом життя екситонного збудження.

У випадку опромінення ШК лазерним світлом відгук буде залежати від чисел заповнення екситонних станів, які в свою чергу, визначаються інтенсивністю зовнішнього випромінювання. Відбувається зміна оптичних властивостей кристала, що є вже нелінійним оптичним процесом, адже індукується оптично. Однією із причин виникнення оптичної нестабільності в ШК є динамічна нелінійність оптичного поглинання в екситонній області частот, що пояснюється конкуренцією процесів збудження екситонних станів і їх релаксацією внаслідок екситон-фононної взаємодії. Кристали з шаруватістю структури являються вдалою моделлю для спостереження різноманітних нелінійних процесів, зокрема і нелінійної екситон-фононної взаємодії.

Для реалізації явища ОБ необхідний зворотній зв'язок (внутрішній чи зовнішній) [20]. Довільне оптичне явище, яке задає нелінійність вихідного сигналу із вхідного параметра, може бути використано для демонстрації оптичної нестабільності. На рис. 21 наведено одну із експериментальних установок для реалізації ОБ.

Рис. 21. Експериментальна схема некогерентного безрезонаторного нестабільного оптичного пристрою з використанням електрооптичного поляризаційного модулятора: 1 - лазер; 2 - змінний послаблювач; 3 - поляризатор; 4 - світоподільна пластинка; 5 - аналізатор із призми Глана; 6 - вихідний пучок; 7 - фотопровідник; 8 - детектор

Але підхід може бути різноманітним, різноманітним може бути і середовище, де ОБ організовується. Наприклад, середовищем з істотною нелінійністю поглинання є шаруваті кристали [20].

Можливість реалізації декількох стабільних оптичних станів кристалу в області екситонних резонансів дає можливість керування процесом розвитку нелінійних явищ шляхом зміни зовнішніх факторів [21].

Розділ 2. Експериментальна частина

2.1 Математична модель безрезонаторної ОБ ШК

Розглядають переважно такий механізм взаємодії падаючого випромінювання з ШК, коли поглинання фотону кристалом сприяє народженню екситона з формуванням відповідного спектра, а зміна його енергії зв’язана з наявністю оптичних фононів й виникненням особливого типу акустичних фононів (хвиль згину). Це приводить до кінцевого часу життя екситонного збудження і визначає розширення резонансної смуги пропускання. Хвилі згину визначають особливості екситон-фононної взаємодії [21].

Процеси розсіювання екситонів на хвилях згину істотно залежать від напрямку поширення світла відносно кристалографічної осі кристалу. Розповсюдження світла вздовж шарового пакету, або перпендикулярно до нього, дозволяє формувати відгук кристалу у різних частотних областях вихідного сигналу з різною динамікою зміни гістерезисної петлі, до того ж знак функції екситон-фононного зв’язку буде різним для різних напрямків поширення світла.

Для теоретичного дослідження взаємодії кристалу із електромагнітним випромінювання, розглянемо систему, яка складається із зовнішнього поля та досліджуваного макроскопічного тіла. За допомогою кулонівської калібровки векторного потенціалу поперечне електромагнітне поле відокремиться в окрему підсистему. Кристал будемо вважати другою підсистемою.

Тоді гамільтоніан цієї взаємодії набуде вигляду:

, (1)

де - оператор енергії екситонів.

де - відповідно оператори народження і знищення оптичних фононів, з енергією ;

де – число атомів кристалу.

Релаксація енергії екситонного збудження забезпечується двома механізмами:

- взаємодією з оптичними фононами (частота збудження ); взаємодія лінійна

, (2)

- взаємодією з хвилями згину (частота збудження ). Взаємодія є нелінійною з функцією зв’язку

де,- константи лінійної та нелінійної взаємодії; знак “+” відповідає поширенню світла вздовж шару, знак “-“ перпендикулярно до нього; α_i = (a_ex m_i )² /[2(m_e +m_h )]² (i = e, h; a_ex – радіус екситону; m_e , m_h – ефективні маси електрона та дірки відповідно).

Згідно з методом функції Гріна вираз для функції форми екситонного поглинання

, (3)

де - Фур’є-компонента часової запізнюючої функції Гріна

(4)

Права частина рівності при слабкому екситон-фононному зв’язку задовольняє рівнянню Дайсона:

G( , (5)

(6)

- масовий оператор екситонів, який у загальному випадку є комплексною функцією частоти.

– описує внесок процесів лінійної взаємодії екситонів з оптичними фононами;

- описує внесок нелінійної взаємодії екситонів із хвилями згину.

(7)

- дійсна частина масового оператору, визначає зміну енергії екситону (тобто зсув екситонного рівня), - описує лінійну складову, а - нелінійну.

- уявна частина масового оператору, пов’язана зі згасанням екситонного збудження внаслідок взаємодії з фононами і визначає півширину спектральної лінії.

Тоді функція форми екситонного поглинання згідно з теорією екситонного поглинання визначається як

. (8)

Величина поглинання в системі у наближенні слабкого екситон-фононного зв’язку і збудженням найнижчого екситонного стану, має наступний вигляд

, (9)

де D₀ – параметр екситон-фотонної взаємодії.

Для прикладу розрахуємо масовий оператор лінійної взаємодії екситонів з оптичними фононами. Відповідно до рівняння (8), запізнюючу функцію Гріна можна представити набором більш простих, згідно з методом Боголюбова-Тяблікова:

Складаємо систему зчіплюючих рівнянь і обриваємо її на величинах, пропорційних квадрату функції екситон-фононного зв’язку.

(10)

За традиційною схемою, що ґрунтується на послідовному диференціюванні функції Гріна, продиференціювавши за виразами (10) та , отримаємо рівняння руху для даної функції

де - функції Гріна більш високого порядку.

Продиференціюємо і

(11)

Більш складніші функції Гріна

(12)

При диференціюванні й далі будуть отримуватися рівняння, що містять функції Гріна ще більш високих порядків, тобто отримується безкінечна система рівнянь [22].

Обриваємо цей безкінечний ланцюг і здійснюємо спарювання однотипних операторів, які належать до одного моменту часу, згідно теореми Віка.

Тут – густина оптичних фононів з квазіімпульсом , - густина екситонів з квазіімпульсом , а

Якщо , тоді

Підставивши знайдені значення у рівняння (12), переходимо до Фур’є-образу функції Гріна

З цієї системи рівнянь можна визначити необхідну функцію Гріна

- масовий оператор екситон-фононної системи.

. (13)

Зараз знайдемо величини півширини та зсуву екситонного рівня.

Проаналізувавши вираз (13), для дійсної частини масового оператора отримаємо

. (14)

Уявна частина масового оператору запишеться

, (15)

де

Для безпосереднього розрахунку величини зсуву та півширини екситонної спектральної лінії, перейдемо у виразах (14) та (15) від сумування по квазіімпульсу до інтегрування по безрозмірному параметру ( – постійна гратки кристала).

Із врахуванням того, що - тримірний вектор, то правило переходу набуде вигляду

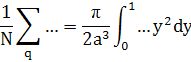
Обмежимо розгляд екситонів першої найнижчої зони із квадратичним законом дисперсії

, (16)

які взаємодіють із довгохвильовим електромагнітним випромінюванням (.

У виразі (16) – ширина екситонної зони, - ефективна маса екситона.

Здійснюючи перехід до інтегрування з урахуванням всіх вище зазначених наближень, отримаємо:

. (17)

Нормуємо всі енергетичні величини на ширину екситонної зони L і перейдемо до таких безрозмірних параметрів:

; ; ; ; . (18)

Функція зв’язку екситонів з оптичними фононами у стандартному наближенні:

Кінцевий вигляд півширини та зсуву екситонного рівня:

, (19)

.Для нелінійної взаємодії екситонів з хвилями згину, півширина та зсув екситонного рівня розраховуються аналогічно за допомогою методу функції Гріна і набувають вигляду

де .

Отримані вирази дають змогу визначити коефіцієнт поглинання світла.

Але опромінення кристалу потужним лазерним випромінюванням, змінює умову формування поглинаючої здатності кристалу. Виникає її залежність від інтенсивності падаючого світла I₀ . Спостерігається нелінійність поглинання в області екситонних резонансів. Причиною цієї нелінійності є нелінійний ріст концентрації екситонів зі зростанням інтенсивності I₀ . Наслідком цієї нелінійності буде внутрішній зворотний зв’язок і оптична НЕСТАБІЛЬНІСТЬ вихідних параметрів опроміненого кристалу [22].

Наявність внутрішнього зворотного зв’язку випливає з рівняння балансу екситонів [22]

яке дає змогу прослідкувати за динамікою зміни концентрації екситонів в залежності від інтенсивності опромінення.

Знаходимо залежність N(I₀ ), яка в певній частотній області має S-подібний характер. Слід очікувати в цій області нелінійність відгуку і оптичну НЕСТАБІЛЬНІСТЬ [23]. Використовуючи тотожність, знаходимо . Замикаємо систему наведених рівнянь, використовуємо закон Бугера, який дозволяє визначити залежність , а отже , де (– інтенсивність світла на виході кристалу).

2.2 Магнітооптична НЕСТАБІЛЬНІСТЬ

Вплив магнітного поля на конденсоване середовище є дуже різноманітний. Магнітне поле може: 1) зумовлювати енергетичний зсув екситонного рівня; 2) змінювати щільність екситонних станів; 3) деформувати спектри екситонного поглинання; 4) впливати на величину екситон-фононної взаємодії; 5) змінювати динаміку екситон-екситонних зіткнень і т.п. Експериментально діамагнітний зсув екситонного рівня було зареєстровано, понад 30 років тому Б. Евансом [23].

Нас цікавлять тільки первинні ефекти прояву впливу магнітного поля, тобто зміни енергій екситонного збудження та чисел заповнення екситонів під дією слабкого зовнішнього магнітного поля. Оскільки всі інші ефекти можна отримати лише у другому порядку міжквазічастинкових взаємодій [23].

Дія сильних магнітних полів на напівпровідник, зумовлює розщеплення кожного енергетичного рівня електрона (дірки) на ряд підрівнів Ландау. В такому випадку утворюється діамагнітний екситон, з енергією, що залежить від того, як і які підрівні Ландау електрона в зоні провідності і дірки у валентній зоні зв’язані між собою. Слабкі магнітні поля зумовлюють появу звичайної воднеподібної серії екситона Ваньє, положення якої залежить від H (напруженості зовнішнього магнітного поля) [24].

Розрахунок цієї залежності здійснюється за допомогою методів теорії збурень, при цьому імпульс зарядженої частинки (електрона і дірки) зв’язаний з магнітним полем співвідношенням:

Обмежившись другим порядком теорії збурень слабким магнітним полем, енергія екситона набуде вигляду:

, (20)

де - енергія дна екситонної зони у відсутності магнітного поля, - її ширина, а – параметр діамагнітного зсуву екситонного рівня; - приведена маса екситона.

Згідно із (20), зміна напруженості магнітного поля H приводить до зміни енергії екситонних станів і тому визначає числа їх заповнення

тут - постійна Больцмана, - хімічний потенціал.

Отож, напруженість магнітного поля є ще одним (як і частота падаючого світла, його інтенсивності, поляризація і температура кристалу) зовнішнім параметром, що може впливати на динаміку екситонного поглинання. Однією з особливостей спектрів екситонного поглинання в шаруватих напівпровідниках є їх залежність від напрямку розповсюдження і поляризації падаючого світла відносно кристалографічної осі [24]. Така залежність дозволяє впливати на умови реалізації ОБ, шляхом зміни - кутів між кристалографічною віссю с і напрямками векторів та , при фіксованих значеннях решти параметрів, тобто має місце поляризаційна оптична НЕСТАБІЛЬНІСТЬ. Зміною даних кутів можна управляти розмірами і положення петлі гістерезису.

Використовуючи наближення слабкого екситон-фононного зв’язку з урахуванням слабкого зовнішнього магнітного поля і можливості збудження різних екситонних станів, вираз для коефіцієнта поглинання (9) запишеться як:

де - функція форми і-тої смуги поглинання.

Розрахунки дозволяють переписати вираз (8) у вигляді:

де - визначає кількість збуджених зон.

Дійсна та уявна частина Г масового оператора функції Гріна для кожного випадку визначається стандартним способом, як зазначалося раніше, через параметри екситон-фононної взаємодії. Вигляд масового оператора екситонів ускладнюється залежностями від частоти, температури і напруженості зовнішнього магнітного поля:

Далі розрахунок проводиться за, описаною раніше схемою, із врахуванням ускладнення, що вноситься накладанням зовнішнього магнітного поля та температури. Отриманні вирази дозволяють визначити коефіцієнт поглинання.

Таким чином, визначається коефіцієнт поглинання в залежності від частоти лазерного випромінювання, температури, напруженості зовнішнього магнітного поля та поляризації.

Закон Бугера-Ламберта замикає систему наведених рівнянь, дозволяє визначити залежність , а отже .

Під впливом слабких магнітних полів, форма смуги поглинання напівпровідника, не деформується, а лише в цілому переноситься в область більших енергій з ростом напруженості зовнішнього магнітного поля.

де - частота екситонного резонансу у відсутності магнітного поля.

Тобто дія магнітного поля зводиться до частотної селекції оптичних властивостей кристалу [24]. Характер поглинання кристалом світла заданої частоти, істотно залежить від того до якої спектральної області належить дана частота. Якщо вона знаходить в довгохвильовій області, то зсув смуги поглинання в бік більших енергій з ростом напруженості магнітного поля, призводить до автоматичного зменшення коефіцієнта поглинання на даній частоті. А зменшення поглинання, означає зростання пропускання, тобто кристал стає більш прозорішим для відповідної частоти. Саме цей ефект і призводить до виникнення магнітооптичної нестабільності шаруватих кристалів в області екситонного резонансу. При ввімкненні зовнішнього магнітного поля є дві можливості одержання функціональної залежності щільності екситонних станів (а отже і реалізацію ОБ):

1) фіксацією величини напруженості зовнішнього магнітного поля і відповідною зміною частоти лазерного випромінювання;

2) фіксацією всіх параметрів і частоти та відповідною зміною напруженості магнітного поля.

1.2. Обговорення і результати отримання області реалізації магнітооптичної нестабільності

Теоретично розглянуто вплив слабких магнітних полів на умови реалізації ОБ в області екситонних резонансів шаруватого кристалу. Розраховано область реалізації магнітооптичної нестабільності ШК, на прикладі 2H-Pb₂ . Програма розрахунку наведена в додатку 1.

Розрахунок області реалізації МОБ здійснюється за наступною схемою [25]:

· розраховується коефіцієнт поглинання для різних концентрацій екситонів N і значень напруженості зовнішнього магнітного поля h;

· проводиться розрахунок залежності N(h), по відомим уже значенням ;

· останній етап розрахунків заключається у визначенні залежності .

В області екситонного резонансу функція N(h) має S-подібний характер, що забезпечує можливість існування трьох розв’язків рівняння балансу, два з яких відповідають стабільним станам із різними рівнями поглинання.

Із рис. 22 та 23 видно, що існує певна область інтенсивностей лазерного сигналу для першої і другої екситонних зон шаруватого кристалу, для якої можливі різні значення пропускної здатності кристалу, що в свою чергу залежить від напрямку зміни інтенсивності лазерної хвилі, при фіксованому значенні напруженості зовнішнього магнітного поля. Ця залежність зображується петлею гістерезису і забезпечує реалізацію стабільних станів на виході кристалу, з різними значеннями пропускання.

Рис. 22. Залежність пропускання від інтенсивності І0. При , на частоті відн. од., у зовнішньому магнітному полі h = 3274 відн. од.

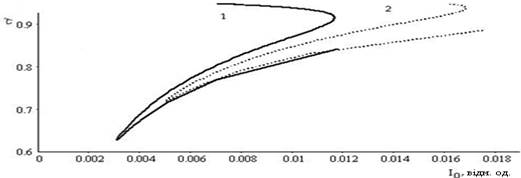
Рис. 23. Залежність пропускання від інтенсивності І0: 1 - ; 1 - . На частоті відн. од., у зовнішньому магнітному полі h = 3274 відн. од.

На рис. 24 і 25 зображена розрахована область реалізації МОБ при змінній температурі, для першої і другої екситонних зон. Із зростанням температури відбувається зсув петлі гістерезису в напрямку зростання магнітного поля, а також зміна форми. Ширина області нестабільності по магнітному полю, складає =450 відн. од. (T = 0.085 – 0.054 відн. од. – для першої екситонної зони; T = 0.071 – 0.040 відн. од. - для другої екситонної зони). Область нестабільності для першої зони зазнає більшого зсуву в бік зростання напруженості магнітного поля ніж друга. Абсолютна ширина області реалізації МОБ і температурний інтервал однакові для двох екситонних зон. Перехід від однієї до іншої зони дозволяє здійснювати корекція напруженості зовнішнього магнітного поля.

Рис. 24. Область реалізації магнітооптичної нестабільності при різних температурах: 1 - T = 0.055 відн. од.; 2 - T = 0.069 відн. од.; 3 - T = 0.073 відн. од. Розрахована для першої екситонної зони, відн. од.

Рис. 25. Область реалізації магнітооптичної нестабільності при різних температурах: 1 - T = 0.041 відн. од.; 2 - T = 0.055 відн. од.; 3 - T = 0.07 відн. од. Розрахована для другої екситонної зони, відн. од.

Розрахунок області реалізації МОБ для різних частот, при опроміненні першої і другої екситонних зон зображено на рис. 26 і 27. Ширина області нестабільності по магнітному полю, складає =690 відн. од. ( відн. од. - для першої зони та відн. од. - для другої зони). Збільшення частоти (для відповідної екситонної зони) зсовує петлю гістерезису в напрямку зростання напруженості магнітного поля, зі зміною самих розмірів петлі.

При переході від однієї зони до іншої, значення інтервала частот залишається незмінним, що дозволяє зберегти область реалізації ОБ лише за рахунок зміни напруженості магнітного поля.

Р ис. 26. Область реалізації магнітооптичної нестабільності при різних частотах: 1 - = 0.017 відн. од.; 2 - = 0.02 відн. од.; 3 - = 0.023 відн. од. Розрахована для першої екситонної зони відн. од.

Рис. 27. Область реалізації магнітооптичної нестабільності при різних частотах: 1 - = 0.057 відн. од.; 2 - = 0.06 відн. од.; 3 - = 0.063 відн. од . Розрахована для другої екситонної зони відн. од.

Розміри області реалізації МОБ не залежать від частоти лазерного випромінювання. При зміні частоти на величину , можливе збереження області нестабільності незмінною, шляхом відповідної зміни напруженості зовнішнього магнітного поля. Так забезпечується вибір області ОБ без зміни джерела випромінювання [25].

Наявність декількох екситонних зон в шаруватих напівпровідниках, створює можливість керування розмірами і положенням петлі гістерезису, значенням поглинання (пропускання) кожного із стабільних станів, шляхом зміни напруженості зовнішнього магнітного поля, що створює перспективи для створення оптичних логічних і запам’ятовуючих пристроїв.

Висновки

1. Теоретично досліджено можливість реалізації магнітооптичної нестабільності в області екситонних резонансів в шаруватих напівпровідниках на прикладі кристалу 2H-PbI₂ .

2. Проведено розрахунок області реалізації магнітооптичної нестабільності для двох екситонних зон зі зміною температури і частоти. З ростом температури петля гістерезису зміщується в бік зростання напруженості магнітного поля.

3. Розміри області реалізації МОБ не залежать від частоти. Отримання багаторівневого відгуку на виході не потребує зміни джерела випромінювання, а лише зміну напруженості магнітного поля.

Література

1. Zenkova C.Yu. The dynamics of optical bistability layer crystals / C.Yu. Zenkova // Proc. SPIE. – 2009. - Vol. 7297, No. 5. – P. 654-657.

2. Дерев’янчук А.В. Оптическая бистабильность слоистого полупроводника в области экситонного поглощения / А.В. Дерев’янчук, К. Ю. Зенкова, Н.К. Крамар, В.М. Крамар // Оптика и спектроскопия. – 2006. - Т. 101, №1. - С.789-794.

3. Nitsovich B.M. Magneto-optical correlation of the exciton series / B. M. Nitsovich, C.Yu. Zenkova, O.V. Derevyanchuk // Proc. SPIE. – 2002. – Vol. 4607, No. 3. – P. 332-338.

4. Дерев’янчук О.В. Особливості реалізації оптичної нестабільності в області екситонного поглинання шаруватих напівпровідників / О.В. Дерев’янчук, К.Ю. Зенкова, Н.К. Крамар, В.М. Крамар // Актуальні проблеми фізики напівпровідників: матеріали V міжнар. конф, 27-30 червня 2005 р. – Дрогобич, 2005. – С. 108-109.

5. Гиббс Х. Оптическая бистабильность. Управление светом с помощью света: пер. с англ. / Х. Гиббс. - М. : Мир, 1988. - 520 с.

6. Рывкин Б.С. Оптическая бистабильность в полупроводниках / Б.С. Рывкин // ФТП. - 1985. - Т. 19, № 1. - С. 3.

7. Бонч-Бруєвич В.Л., Физика полупроводников / В. Л. Бонч-Бруэвич, С.Г. Калашников. - М. : Наука, 1990. - 685 с.

8. Бродин М.С. Экситонные процессы в слоистых кристаллах / М.С. Бродин, И.В. Блонский. – Киев : Наукова думка, 1986. - 236 с.

9. Днепровский В.С. Экситоны перестают быть экзотическими квазичастицами / В.С. Днепровский // СОЖ. - 2000. - Т. 6, № 8. - С. 88.

10. Henneberger F.B. Optical bistability in the absorption edge of semiconductor / F.B. Henneber // Phys. stat. sol. (b). – 1986. – Vol. 137, No. 2. – P. 371-432.

11. Pat. 4675518, G01J 132. Optical bistable device / Katsuhiko Oimura, Haruo Misumi, Hiroshi Ogawa, Naotake Nagao. ; Mar 4, 1983; Jun 23, 1987.

12. Garmire B. L. Moving Toward Integrated Optics / B. L. Garmire // Laser Focus. – 1975. – Vol. 25, No. 15. – P. 55-59.

13. Бакієв М.В. Нестабільні напівпровідникові прилади / М.В. Бекієв // РЖКЕ. – 1985. – Вип. 15. – С. 430-433.

14. Strandley E.A. Optical Waveguides / E.A. Strandley // Applied Physics Letters. – 1975. – Vol. 25, No. 15. – P. 711-713.

15. Zenkova C Yu. Dynamics of layer crystal light absorption and the formation of optical bistability / C.Yu. Zenkova // Proc. SPIE. - 2008. – Vol. 7138, No. 1. – P. 564-579.

16. Nitsovich B.M. Nonlinearity of absorption in an exciton-phonon system / B.M. Nitsovich ., O.V. Krechivskii ., G.M. Pestryakov // Phys. stat. sol. (b). – 1988. – Vol. 148, No. 1. – P. 165-168.

17. Lyubchanskii I. L. Optical bistability in one-dimensional magnetic photonic crystal with two defect layers / I. L. Lyubchanskii, N. N. Dadoenkova, A.E. Zabolotin // J. Appl. Phys. – Vol. 103, No. 8. – P. 43-46.

18. Joannopoulos D.J. Optical bistability in axially modulated / D.J. Joannopoulos // Optics letters. – 2003. - Vol. 28, No. 7. P. 516-518.

19. Esnaashari Y. Theory of Increasing Absorption Optical Bistability and Self-Focusing in Bulk ZnSe / Y. Esnaashari, A. Koohian, S. Jelvani, S. Abolhosseini // Laser Physics. – 2005. - Vol. 15, No. 3. P. 415–418.

20. Зенкова К.Ю. Магнитооптическая бистабильность слоистого полупроводиника в области экситонного поглощения / К.Ю. Зенкова, А.В. Деревянчк, В. М. Крамар, Н. К. Крамар // Оптика и спектроскопия. – 2008. - 104, №2. - С. 260-265.

21. Zenkova С.Yu. Magnetooptical bistability of layer crystals / C.Yu. Zenkova, V.M. Kramar, N.K. Kramar // Proc. SPIE. – 2008. – Vol. 7008, No. 8. – P. 651-655.

22. Minde R. Charge transport in layer semiconductors / R. Minde, C. Ottaviani, C. Canaly // J.Phys. Chem. – 1976. – Vol. 37, No. 2. – P. 417-655.

23. Evans B. L. Exciton spectra in thin crystals: the diamagnetic effect / B.L. Evans, P.A. Young // Proc. Phys. Soc. – 1967. – Vol. 91, No. 3. – P. 475-482.

24. Xu Z. Y. Temperature switch based on optical bistability / Z.Y. Xu, J. Tann, M. Gal, P.C. Taylor // Optical and Quantum Electronics. – 1992. – Vol. 24, No. 1. – P. 587-590.

25. Зенкова К.Ю. Магнітооптична НЕСТАБІЛЬНІСТЬ напівпровідників / К.Ю. Зенкова, Б.М. Ніцович // Укр. фіз. жур. – 2000. – Т. 45, № 2. – С. 246-250.

Додаток
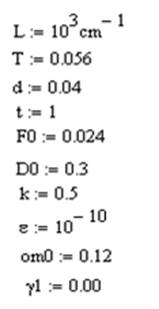