Реферат: Стохастический резонанс

7 Список литературы

Анищенко В.С. «Стохастический резонанс как индуцированный шумом эффект увеличения степени порядка»: УФН/ Анищенко В.С., Нейман А.Б., Мосс Ф., Шиманский-Гайер Л..- Т. 169 – стр.8-38

Gammaitoni L. «Stochastic resonance»: Reviews of Modern Physics/ Gammaitoni L., Hanggi P., Jung P., Marchesoni F..-Т.70 - №1

Гоноровский И.С. Радиотехнические цепи и сигналы. Учебник для ВУЗов.- М., «Советское радио», 1977, 608стр.

1 Введение

С понятием "шум" в обыденном сознании ассоции­руется термин "помеха", наличие которой может только ухудшить функционирование любой системы. Хорошо известны классические проблемы радиофи­зики, связанные с ограничением чувствительности уси­лителей и конечностью ширины спектральной линии генераторов, что обусловлено воздействием естествен­ных и технических шумов. В силу дискретности строения материи флуктуационные явления присущи всем реальным системам и принципиально неустра­нимы. Со времен Больцмана стала ясной ограниченно­сть чисто детерминистского описания эволюционных процессов, и это ускорило развитие статистической физики. Основатели теории нелинейных колебаний также сознавали ограниченность детерминированного описания. Уже в 1933 г. ими был поставлен вопрос о статистическом рассмотрении динамических систем, что послужило основой для развития исследований в обла­сти статистической радиофизики.

Было установлено, что наличие источников шума в нелинейных динамических системах может индуциро­вать принципиально новые режимы функционирования, которые не могут быть реализованы в отсутствие шума, например, индуцированные шумом незатухающие коле­бания. Эффекты указанного типа получили название индуцированных шумом переходов. Многообразие и сложность типов таких переходов в нелинейных динами­ческих системах вызвали постановку удивительных до недавнего времени вопросов: всегда ли воздействие шума приводит к ухудшению характеристик динамиче­ских систем и возможны ли случаи, когда действие шума вызывает увеличение степени упорядоченности движе­ний в системе или улучшение ее рабочих характеристик? Исследования последних лет убедительно показали, что в нелинейных системах воздействие шума может инду­цировать новые более упорядоченные режимы, приво­дить к образованию более регулярных структур, увели­чивать степень когерентности, вызывать рост усиления и увеличение отношения сигнал/шум и т.д. Другими сло­вами, шум в нелинейных системах может играть кон­структивную роль, вызывая рост степени порядка в системе.

Одним из наиболее ярких и относительно простых примеров указанного типа поведения нелинейных систем при воздействии шума является эффект стохастического резонанса (СР). Эффект СР определяет группу явлений, при которых отклик нелинейной системы на слабый внешний сигнал заметно усиливается с ростом интенсив­ности шума в системе. При этом интегральные характе­ристики процесса на выходе системы, такие как коэффи­циент усиления и отношение сигнал/шум, имеют отчет­ливо выраженный максимум при некотором оптималь­ном уровне шума. В то же время энтропия как мера степени беспорядка достигает минимума, свидетель­ствуя о возрастании степени индуцированного шумом порядка.

Термин "стохастический резонанс" был введен в 1981 -1982 гг. на основе исследований модели бистабильного осциллятора, предложенной для описания периодичности в наступлении ледниковых периодов на Земле. Модель описывала движение частицы в симметричном двухъямном потенциале под действием периодической силы в условиях большого трения. Устойчивые положения частицы соответство­вали ледниковому периоду и нормальному климату Земли. Периодическая сила соответствовала колеба­ниям эксцентриситета орбиты Земли. Расчеты показали, что реальная амплитуда периодический силы оказалась малой и не обеспечивала переключений системы из одного состояния в другое. Возможность переключений была достигнута путем введения дополнительной слу­чайной силы, индуцирующей переходы через потенци­альный барьер.

В 1983 г. эффект СР был исследован в триггере Шмитта, где для описания явления впервые использо­вано отношение сигнал/шум. В этой работе устано­влено, что отношение сигнал/шум на выходе триггера при возбуждении его слабым периодическим и шумовым сигналами возрастает с ростом шума, достигает макси­мума и затем убывает. Таким образом, существует некий оптимальный уровень интенсивности шума, при кото­ром периодическая компонента сигнала усиливается максимально.

Впоследствии эффект СР был обнаружен и исследован во многих бистабильных системах: в кольцевом лазере, в магнитных системах, в пассивных оптических бистабильных системах, в системах с электронным парамагнитным резонансом, в экспе­риментах с броуновскими частицами, в эксперимен­тах с магнитоупругой лентой, в туннельном диоде, в сверхпроводящих квантовых интерферометрах, в ферромагнетиках и сегнетоэлектриках, СР наблюдался не только в физических, но и в химических системах и даже в социологических моделях.

Исследования показали, что эффект СР представляет собой фундаментально общее физическое явление, типичное для нелинейных систем, в которых с помощью шума можно контролировать один из характерных временных масштабов системы. Физическая же картина явления СР достаточно наглядна и проста.

Рассмотрим качест­венно движение броуновской частицы в системе с сим­метричным бистабильным потенциалом типа U(x) = -0.5х2 + 0,25х4 в условиях действия слабого периоди­ческого возмущения Asin(wt). Система имеет два харак­терных временных масштаба: один обусловлен случай­ными блужданиями частицы в окрестности одного из состояний равновесия (внутриямная динамика), другой временной масштаб характеризует среднее время пере­хода через потенциальный барьер (глобальная дина­мика). Отметим, что амплитуда периодического воздей­ствия предполагается малой настолько, что исключает переходы через барьер в отсутствие шума. Второму временному масштабу в частотной области отвечает средняя скорость (или частота) выхода из метастабильного состояния скорость Крамерса.

Д
ля случая белого шума, параболических потенци­альных ям и относительно высоких потенциальных барьеров скорость Крамерса дается законом Аррениуса:

г

де U" = d2U(x)/dx2, с — координата минимума потен­циала, Uo — потенциальный барьер, D — интенсив­ность шума. Скорость Крамерса будет определять и вероятности переходов.

Рисунок 1 - Бистабильный потенциал под действием слабой периодиче­ской модуляции. Потенциал может иметь как "жесткую", так и "мягкую" форму. Частица, отмеченная шариком, может преодолеть потенциальный барьер только в присутствии внешнего или внутреннего шума.

В присутствии периодической силы потенциальные ямы будут периодически колебаться (рис. 1), вероятности перехода также станут периодическими функциями вре­мени, и выходной сигнал будет включать периодическую компоненту.

На рисунке 2 представлены сигналы на выходе бистабильной системы с учетом внутриямной динамики (а) и с учетом исключительно моментов времени пере­сечения барьера (приближение двух состояний) (б), а также спектр мощности (в) сигнала, показанного на графике (б).

П

Рис. 2- Полный сигнал на выходе бистабильной системы (а), отфильтрованный методом двух состояний сигнал (б) и спектр мощности отфильтрованного сигнала (в).

3 Стохастический резонанскак фундаментальный пороговый эффект

С точки зрения передачи информации биcтабильными системами в режиме СР основную роль играют исклю­чительно переходы через потенциальный барьер. Внутриямная динамика может не оказывать существенного влияния на процесс переключений. Поэтому при обра­ботке выходного сигнала с успехом используется метод динамики двух состояний. Выходной сигнал предста­вляется в виде случайного телеграфного процесса, в котором путем фильтрации выделяется составляющая основной частоты. Можно вообще отказаться от анализа бистабильных динамических систем и представить СР как фундаментальный пороговый эффект. В этом случае процесс рассматривается в виде последовательности случайных событий, появляющихся в случае, когда сумма регулярной и шумовой компонент входного сигнала пересекает некоторый заданный пороговый уровень P:

[Asinwt+(t)]> P или < P.

Рассмотрим явление СР, используя концепцию неди­намическою порогового эффекта. Временные диаграммы моделирования данного процесса получены с помощью пакета Microcap 7.0. Схема моделирования представлена на рисунке 3. Она включает в себя два генератора сигналов: гармонического сигнала и шума. С них сигнал поступает на сумматор и далее на компаратор. На инвертирующий вход компаратора подается постоянное напряжение, определяющее уровень порога срабатывания. На выходе компаратора находится фильтр низких частот, состоящий из RC-цепи.

Н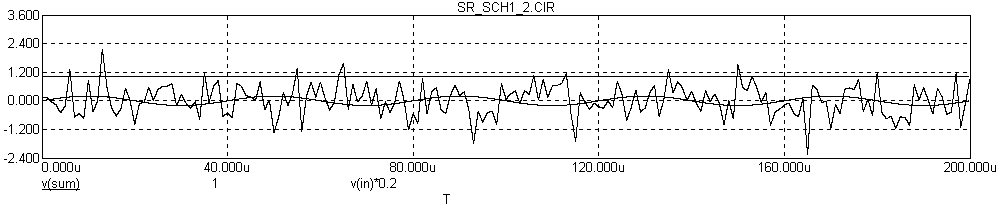
а рисунке 4 представлен подпороговый регулярный гармонический сигнал и аддитивный шум. В отсутствие шума амплитуды сигнала недостаточно для достижения порога. С доба­влением шума преодоление порога становится возмож­ным и происходит случайный образом.

Всякий раз, когда уровень порога пересекается в одном направлении, генерируется импульс стандартной формы. Процесс пересечений порога порождает во времени случайную последовательность импульсов на выходе компаратора, как это показано на рисунке 5.

На рисунке 6 находится амплитудный спектр данной последовательности импульсов, полученный с помощью быстрого преобразования Фурье. На фоне шума четко видна гармоника с частотой сигнала.

Р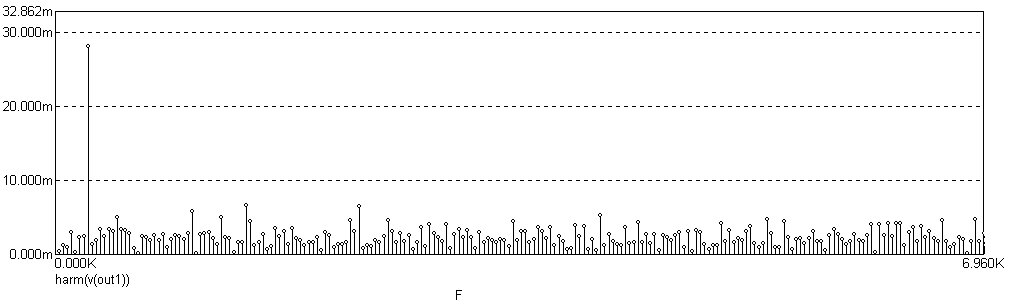
исунок 6 – График амплитудного спектра выходного сигнала

Для того чтобы получить сигнал, наиболее похожий на исходный, необходимо отфильтровать высокочастотные составляющие спектра. Для этих целей используется фильтр низких частот в виде RC-цепи. Временная диаграмма сигнала на выходе фильтра и его амплитудный спектр представлены на рисунке 7.

На данном графике видно , что на выходе фильтра получился сигнал с искажениями, но совпадающий по форме и частоте со входным сигналом. Для наилучшего восстановления сигнала на выходе, необходимо найти параметры схемы и сигналов, соответствующие максимальному отношению энергии сигнала к энергии шума.

Для этого необходимо найти оптимальный уровень шума, который добавляется к сигналу. Поэтому будем считать порог срабатывания компаратора и амплитуду входного сигнала величинами постоянными, а находить будем зависимость отношения энергии сигнала к энергии шума на выходе компаратора в зависимости от уровня шума на входе.

Моделирование будем производить в пакете Mathcad 2000. Зададим шум на входе как сумму нескольких случайных величин с равномерным распределением плотности вероятности. В результате мы получим случайный процесс, похожий по свойствам на гауссовский белый шум, так как по центральной предельной теореме распределение плотности вероятности суммы большого количества независимых случайных величин близко к нормальному распределению.

Определим зависимость сигналов на входе и выходе порогового элемента условием

где x(t) – сигнал на входе,

y(y) – сигнал на выходе,

P – порог срабатывания порогового элемента.

Тогда во все моменты времени, в которые входной сигнал выше порогового, на выходе будет уровень единицы.

Б
удем находить зависимость отношения энергий сигнала и шума на выходе схемы от уровня шума на входе, тогда данная зависимость будет определяться выражением

В результате моделирования были получены графики для трех частот входного сигнала: w0=4 кГц, w0=16кГц, w0=64кГц. Порог срабатывания и амплитуда входного сигнала постоянны. Уровень шума показан как отношение его амплитуды к амплитуде сигнала. Зависимости представлены на рисунках 8-10.

Р
исунок 8 – Результаты моделирования эффекта СР для частоты входного сигнала w0=4кГц

Рисунок 9 - Результаты моделирования эффекта СР для частоты входного сигнала w0=16кГц

Рисунок 10 - Результаты моделирования эффекта СР для частоты входного сигнала w0=64кГц

4 Синхронизация стохастических систем

Применение теории линейного отклика даст хорошие результаты, вскрывающие физический механизм явле­ния СР. Возникает вопрос: почему? Ведь все стохастиче­ские системы, демонстрирующие эффект СР, принципи­ально нелинейны! Дело в том, что основные нелинейные свойства стохастических систем учитываются в том или ином приближении при определении корреляционной функции не возмущенной системы. Нелинейность системы проявляется в зависимости корреляционной функции от интенсивности шума D, в результате чего от D зависит и восприимчивость. Ограничения теории линейного отклика ведут к требованию малости ампли­туды сигнала возмущения. Отказ от этого условия переводит проблему в класс принципиально нелиней­ных, и теория линейного отклика становится непримени­мой.

Одним из важных нелинейных эффектов, сопровож­дающих эффект СР, является синхронизация. Синхрони­зация стохастических систем, не имеющих собственных периодических компонент во временных реализациях процесса, — явление нетривиальное. Однако недавно были открыты эффекты как внешней, так и взаимной стохастической синхронизации.

4.1 Синхронизация стохастического бистабильного осциллятора

Для рассмотрения эффекта синхронизации стохастиче­ских систем обратимся к результатам исследований неавтономного генератора Ван дер Поля — классиче­ской автоколебательной системы с предельным циклом, находящейся под воздействием периодической силы и флуктуации. Как известно, наличие шума ведет к флуктуациям амплитуды и фазы колебаний. В результате разность фаз колебаний генератора и внешней гармони­ческой силы ф(t)=(t)-(t) также будет флуктуиро­вать. В приближении постоянной амплитуды медленная динамика разности фаз ф(t) описывается следующим СДУ:

= - е*sin+(t)

где =-0 есть разность частот генератора и внешней силы (расстройке по частоте), е – параметр нелинейности, (t) – гауссов шум. Разность фаз ф(t) совершает броуновское движение в передемпфи­рованном осцилляторе c наклонным периодическим потенциалом U(ф) = -ф-e* cos ф. При малом уровне шума разность фаз флуктуирует длительное время внутри одной из потенциальных, ям (эффект захвата фаз) и редко совершает перескажи через потенциальный барьер (нарушение синхронизации),

В отличие от классической синхронизации детерми­нированных систем, в случае стохастических колебаний необходимо использовать понятие "эффективной син­хронизации" с учетом ограничений на флуктуации фазы, частоты и отношения сигнал/шум. Будем использо­вать наиболее жесткое определение эффективной синхро­низации: система функционирует в режиме эффективной синхронизации, если среднее время захвата фазы много больше периода внешней гармонической силы. Количе­ственной мерой степени эффективной синхронизации будет коэффициент эффективной диффузии разности фаз Deff.

Можно показать, что Deff пропорциональна средней скорости r перехода через барьер

Deff = 4*2*r

и обратно пропорциональна среднему интервалу времени захвата разности фаз :

(Т) = н2/0. n>> 1.

Таким образом, критерий эффективной синхронизации можно опреде­лить как:

Эффект воздействия шума на синхронизируемый авто­генератор хорошо изучен: с ростом интенсивности шума условия синхронизации ухудшаются, так что коэффициент эффективной диффузии возрастает с увели­чением интенсивности шума. Области синхронизации в пространстве параметров системы сужаются с ростом шума. Иными словами, шум действует против синхронизации, внося беспорядок (стохастическую диф­фузию фазы). Как мы увидим из дальнейшего, в систе­мах, демонстрирующих СР, шум играет принципиально иную роль.

4.2 Внешняя стохастическая синхронизация триггера Шмитта

При изучении синхронизирующего действия внешнего периодического сигнала на стохастические бистабильные системы основной интерес представляет глобальная динамика переходов между метастабильными состоя­ниями. Поэтому для исследований синхронизации удобно использовать идеальную бистабильную систему - триггер Шмитта.

Проведем моделирование эксперимента измерения средней частоты от интенсивности шумового сигнала. На триггер Шмитта с порогом срабатывания U=200мВ будем подавать шумовой сигнал и периодический сигнал с частотой 100Гц. При слабом сигнале зависимость средней частоты от интенсивности шума не зависит от сигнала и экспоненциально возрастает. С увеличением амплитуды сигнала зависимость средней частоты от интенсивности шума качественно иная: появляется область значений интенсивности шума, в котором средняя частота переключений практически не меняется сростом шума и в пределах погрешности моделирования остается равной частота сигнала. Наблюдается эффект захвата частоты. На рисунке 11 представлены графики зависимости переключений триггера Шмитта от интенсивности шума с амплитудой сигнала А=0мВ, А=50мВ и А=100мВ.

Рисунок 11 – Зависимость частоты выходного сигнала триггера Шмитта от интенсивности шума для различных значений амплитуды А сигнала.

Из приведенного примера следует, что внешний периодический сигнал достаточной амплитуды синхронизирует стохастическую динамику процессов. Хотя амплитуда сигнала находится за приделами применимости теории линейного отклика, она остается малой настолько, что в отсутствии шума переключений не происходит. Шум таким образом, является необходимым компонентом рассматриваемого явления. Это явление сопровождается захватом мгновенной фазы и средней частоты.

5 Стохастический резонанс и количественная оценка восприятия информации

Практически во всех экспериментах по изучению СР используются методы компьютерного анализа сигна­лов на входе и выходе изучаемых систем, с помощью которых обосновывается усиление (или увеличение информации) при действии оптимального уровня шума. Можно попытать­ся протестировать общий интегральный эффект в каких-либо поведенческих, т.е. психологических, эксперимен­тах с человеком. Другими словами, можно заменить сложное программное обеспечение обработки данных на ЭВМ на человеческое восприятие (интерпретацию). Такие эксперименты были разработаны и проведены специально для исследования способности человека воспринимать зрительно информацию на фоне воздей­ствия шума. Будет ли визуально воспринимаемая инфор­мация зависеть от интенсивности шума нелинейным образом, подобно эффекту СР? Возможно ли ввести количественный критерий оптимальности зрительного восприятия информации? Ответ на эти вопросы дан и является утвердительным.

Произвольно выбранную фотографию оцифруем на 256 уровней серого цвета и выведим на экран в качестве изображения 200*200 точек. Затем поместим ее ниже порогового уровня, так что бы ее не было видно. К подпороговому уровню добавим гауссов шум с нулевым средним, который действовал на каждый дискретный элемент независимо (источники шума в каждом элементе не коррелированны). Если в каком-либо конкретном пикселе преодолевался пороговый уровень-то он становится черного цвета. При малом уровне шума лишь небольшое количество точек появляется на экране и картинку не возможно распознать. Если шум слишком большой распознавание образа также невозможно. Однако всегда существует некоторое оптимальное значение интенсивности шума, когда информация о картинке максимальная и ее можно воспринять. Один из примеров приведен на рисунках , из которого видно, что наиболее отчетливо воспринимается изображение на рисунке , когда интенсивность внешнего шума оптимальна. Эффект восприятия картинки на самом деле динамический, ведь человеческий глаз обладая определенной инерцией более четко воспринимает те области изображения где появление черных точек больше белых. Этот эффект можно использовать для создания примитивного фильтра восстановления изображения.

Перед выводом на экран точки добавим полученный результат (о пересечении или нет порога) в таблицу памяти, где хранится информация о предыдущих результатах (если сигнал пересек порог то добавляем единицу в таблицу, если сигнал не пересек порога, то единица вычитается). Далее в соответствии с полученной статистикой выводим изображение на экран. Данный способ позволяет выводить не только контрастные, черно-белые изображения, но и серые, что повышает восприимчивость. На рисунке , приведено изображение сигнала на входе этого фильтра, а на рисунке после фильтра. На рисунке приведен еще один результат, когда интенсивность шума еще выше. Результат представляется очень оптимистичным. Единственным, но пожалуй наиболее значимым недостатком такой фильтрации является, то что пока фильтр накапливает информацию сигнал на его входе должен оставаться постоянным, а вся фильтрации занимает довольно-таки продолжительное время.

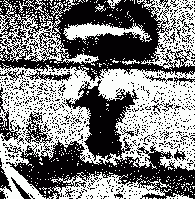
Рисунок .- Изображения на экране при различных уровнях шума, добавленному к подпороговому сигналу

а б в

Рисунок - Изображения полученные при использовании статической фильтрации б и в. Смесь сигнала с шумом на входе фильтра-а.

7 Список литературы

Анищенко В.С. «Стохастический резонанс как индуцированный шумом эффект увеличения степени порядка»: УФН/ Анищенко В.С., Нейман А.Б., Мосс Ф., Шиманский-Гайер Л..- Т. 169 – стр.8-38

Gammaitoni L. «Stochastic resonance»: Reviews of Modern Physics/ Gammaitoni L., Hanggi P., Jung P., Marchesoni F..-Т.70 - №1

Гоноровский И.С. Радиотехнические цепи и сигналы. Учебник для ВУЗов.- М., «Советское радио», 1977, 608стр.

Введение

С понятием "шум" в обыденном сознании ассоции­руется термин "помеха", наличие которой может только ухудшить функционирование любой системы. Хорошо известны классические проблемы радиофи­зики, связанные с ограничением чувствительности уси­лителей и конечностью ширины спектральной линии генераторов, что обусловлено воздействием естествен­ных и технических шумов. В силу дискретности строения материи флуктуационные явления присущи всем реальным системам и принципиально неустра­нимы. Со времен Больцмана стала ясной ограниченно­сть чисто детерминистского описания эволюционных процессов, и это ускорило развитие статистической физики. Основатели теории нелинейных колебаний также сознавали ограниченность детерминированного описания. Уже в 1933 г. ими был поставлен вопрос о статистическом рассмотрении динамических систем, что послужило основой для развития исследований в обла­сти статистической радиофизики.

Было установлено, что наличие источников шума в нелинейных динамических системах может индуциро­вать принципиально новые режимы функционирования, которые не могут быть реализованы в отсутствие шума, например, индуцированные шумом незатухающие коле­бания. Эффекты указанного типа получили название индуцированных шумом переходов. Многообразие и сложность типов таких переходов в нелинейных динами­ческих системах вызвали постановку удивительных до недавнего времени вопросов: всегда ли воздействие шума приводит к ухудшению характеристик динамиче­ских систем и возможны ли случаи, когда действие шума вызывает увеличение степени упорядоченности движе­ний в системе или улучшение ее рабочих характеристик? Исследования последних лет убедительно показали, что в нелинейных системах воздействие шума может инду­цировать новые более упорядоченные режимы, приво­дить к образованию более регулярных структур, увели­чивать степень когерентности, вызывать рост усиления и увеличение отношения сигнал/шум и т.д. Другими сло­вами, шум в нелинейных системах может играть кон­структивную роль, вызывая рост степени порядка в системе.

Одним из наиболее ярких и относительно простых примеров указанного типа поведения нелинейных систем при воздействии шума является эффект стохастического резонанса (СР). Эффект СР определяет группу явлений, при которых отклик нелинейной системы на слабый внешний сигнал заметно усиливается с ростом интенсив­ности шума в системе. При этом интегральные характе­ристики процесса на выходе системы, такие как коэффи­циент усиления и отношение сигнал/шум, имеют отчет­ливо выраженный максимум при некотором оптималь­ном уровне шума. В то же время энтропия как мера степени беспорядка достигает минимума, свидетель­ствуя о возрастании степени индуцированного шумом порядка.

Термин "стохастический резонанс" был введен в 1981 -1982 гг. на основе исследований модели бистабильного осциллятора, предложенной для описания периодичности в наступлении ледниковых периодов на Земле. Модель описывала движение частицы в симметричном двухъямном потенциале под действием периодической силы в условиях большого трения. Устойчивые положения частицы соответство­вали ледниковому периоду и нормальному климату Земли. Периодическая сила соответствовала колеба­ниям эксцентриситета орбиты Земли. Расчеты показали, что реальная амплитуда периодический силы оказалась малой и не обеспечивала переключений системы из одного состояния в другое. Возможность переключений была достигнута путем введения дополнительной слу­чайной силы, индуцирующей переходы через потенци­альный барьер.

В 1983 г. эффект СР был исследован в триггере Шмитта, где для описания явления впервые использо­вано отношение сигнал/шум. В этой работе устано­влено, что отношение сигнал/шум на выходе триггера при возбуждении его слабым периодическим и шумовым сигналами возрастает с ростом шума, достигает макси­мума и затем убывает. Таким образом, существует некий оптимальный уровень интенсивности шума, при кото­ром периодическая компонента сигнала усиливается максимально.

Впоследствии эффект СР был обнаружен и исследован во многих бистабильных системах: в кольцевом лазере, в магнитных системах, в пассивных оптических бистабильных системах, в системах с электронным парамагнитным резонансом, в экспе­риментах с броуновскими час гидами, в эксперимен­тах с магнитоупругой лентой, в туннельном диоде, в сверхпроводящих квантовых интерферометрах, в ферромагнетиках и сегнетоэлектриках, СР наблюдался не только в физических, но и в химических системах и даже в социологических моделях.

Исследования показали, что эффект СР представляет собой фундаментально общее физическое явление, типичное для нелинейных систем, в которых с помощью шума можно контролировать один из характерных временных масштабов системы. Физическая картина явления СР достаточно наглядна и проста. Для иллю­страции рассмотрим модель стохастического бистабильного осциллятора.

2 Физические основы эффекта СР

Рассмотрим качест­венно движение броуновской частицы в системе с сим­метричным бистабильным потенциалом типа U(x) = —0.5х2 + 0,25х4 в условиях действия слабого периоди­ческого возмущения Asin(wt). Система имеет два харак­терных временных масштаба: один обусловлен случай­ными блужданиями частицы в окрестности одного из состояний равновесия (внутриямная динамика), другой временной масштаб характеризует среднее время пере­хода через потенциальный барьер (глобальная дина­мика). Отметим, что амплитуда периодического воздей­ствия предполагается малой настолько, что исключает переходы через барьер в отсутствие шума. Второму временному масштабу в частотной области отвечает средняя скорость (или частота) выхода из метастабильного состояния скорость Крамерса.

Для случая белого шума, параболических потенци­альных ям и относительно высоких потенциальных барьеров скорость Крамерса дается законом Аррениуса:

г
де U" = d2U(x)/dx2, с — координата минимума потен­циала, Uo — потенциальный барьер, D — интенсив­ность шума. Скорость Крамерса будет определять и вероятности переходов.

Рисунок 1 - Бистабильный потенциал под действием слабой периодиче­ской модуляции. Потенциал может иметь как "жесткую", так и "мягкую" форму. Частица, отмеченная шариком, может преодолеть потенциальный барьер At/o только в присутствии внешнего или внутреннего шума.

В присутствии периодической силы потенциальные ямы будут периодически колебаться (рис. 1), вероятности перехода также станут периодическими функциями вре­мени, и выходной сигнал будет включать периодическую компоненту.

На рисунке 2 представлены сигналы на выходе бистабильной системы с учетом внутриямной динамики (а) и с учетом исключительно моментов времени пере­сечения барьера (приближение двух состояний) (б), а также спектр мощности (в) сигнала, показанного на графике (б).

П

Рис. 2. Полный сигнал на выходе бистабильной системы (а), отфильтрованный методом двух состояний сигнал (б) и спектр мощности отфильтрованного сигнала (в).