| Скачать .docx |
Курсовая работа: Трехмерное напряжение и деформированное состояние
ТРЕХМЕРНОЕ НАПРЯЖЕННОЕ И ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ
1. Напряжённое состояние в точке
Вспомним, как нами было введено понятие напряжения. Рассмотрим тело, находящееся под действием системы уравновешенных сил (рис.48).
 |
Рис.48
Будем исследовать внутренние силы в малой области окружающей точку 
,
для чего проведём через данную точку сечение, рассекая тело на две части, и отбросим одну из них. Действие отброшенной части заменим внутренними силами (рис.49).
Рис. 49
Выделим малую площадку 
, содержащую точку . Внешнюю нормаль этой площадки обозначим 
.
Результирующую внутренних сил, действующих на площадку , обозначим
. Деля результирующую на получим величину среднего напряжения по площадке
Величина 
зависит от размеров площадки. Чтобы избавиться от влияния размеров площадки , перейдём к пределу и будем стягивать площадку к точке
(1)
Величину 
будем называть полным напряжением в точке по площадке с внешней нормалью .
Совершенно очевидно, что если мы выберем другую площадку, проходящую через точку , но ориентированную другим образом, то в общем случае вектор полного напряжения окажется иным.
Совокупность всех векторов полного напряжения по всем площадкам, проходящим через данную точку, составляет напряженное состояние в данной точке.
Напряжённое состояние в данной точке известно, если известны напряжения по трём взаимно перпендикулярным площадкам, проходящим через данную точку.
Докажем это важнейшее положение.
Нас интересует напряжённое состояние в точке . Выделим в окрестности этой точки малый прямоугольный параллелепипед (рис.50). Размеры параллелепипеда настолько малы, что напряжённое состояние в пределах параллелепипеда можно считать однородным, и что грани параллелепипеда являются площадками, проходящими через точку и имеющими внешними нормалями оси 
Рис. 50
Полное напряжение можно разложить на три составляющие, направленные по координатным осям. Всего будем иметь 9 компонент напряжённого состояния: три нормальных и шесть касательных напряжений. Нормальные напряжения обозначим 
и припишем индекс, указывающий внешнюю нормаль.
Например: 
— нормальное напряжение по площадке с внешней нормалью 
.
Касательные напряжения обозначаются 
с двумя индексами. Первый индекс указывает площадку, второй – направление напряжения.
Например 
— касательное напряжение по площадке с внешней нормалью , параллельное оси Y
.
Нормальное напряжение считается положительным, если оно направлено по внешней нормали, т.е. является растягивающим.
Касательные напряжения считаются положительными, если при положительной внешней нормали они направлены в сторону положительных координатных осей.
Совершенно очевидно, что по противоположным граням параллелепипеда действуют равные по величине и противоположные по направлению напряжения.
Заметим также, что хотя на рис.50 компоненты напряжённого состояния показаны в виде векторов, они являются величинами скалярными.
Докажем, что касательные напряжения по взаимно перпендикулярным площадкам равны. Т.к. тело, из которого вырезан элементарный параллелепипед, находится в равновесии, то условия равновесия применимы и к элементу объёма. Запишем условие, что сумма моментов всех сил приложенных к элементарному параллелепипеду относительно координатных осей равна нулю
Раскроем первое из этих уравнений
,
откуда 
т.е. закон парности касательных напряжений.
Два других уравнения дадут равенства:
;
Таким образом, независимых составляющих 6.
А теперь докажем положение высказанное на стр.2 о том, что зная напряжения, действующие по любым трём взаимно перпендикулярным площадкам, можно определить напряжения по любой площадке, проходящей через данную точку.
Вырежем в окрестности исследуемой точки элементарный тетраэдр с бесконечно малыми рёбрами. Три грани тетраэдра параллельны координатным плоскостям, а четвёртая наклонна к первым трём и её внешняя нормаль 
(рис.51).
 |
Рис. 51
Напряжения
(2)
возникающие по площадкам с внешними нормалями 
считаем известными.
Нужно найти полное напряжение по площадке с внешней нормалью 
—
. Составляющие полного напряжения, направленные по координатным осям обозначим 
.
Направляющие косинусы нормали обозначим:
;
;
(3)
Если принять площадь грани 
—
, то площади остальных граней
;
;
Составим уравнения равновесия для тетраэдра
Используя также условия
;
, получаем следующие соотношения
(4)
Совокупность 6 компонент напряжённого состояния (2) составляет тензор напряжений. Зная тензор напряжений (2), можно с помощью соотношений (4) определить напряжения по любой площадке в данной точке.
Величина полного напряжения определится
Для того чтобы определить нормальное напряжение по площадке с внешней нормалью , надо спроектировать на нормаль составляющие полного напряжения 
(рис.52).
 |
Рис. 52
Подставляя выражение (4), получаем:
(5)
Касательное напряжение определяется
2. Главные напряжения
В окрестности любой точки существуют три взаимно перпендикулярные площадки, касательные напряжения по которым равны нулю. Эти площадки называются главными, а напряжения, действующие на них главными напряжениями.
Покажем, как находить главные напряжения и главные площадки в общем случае.
Допустим, что главная площадка существует и её внешняя нормаль 
. Главное напряжение совпадает по направлению с внешней нормалью и составляющие напряжения 
по координатным осям равны:
(6)
Внесём выражения (6) в уравнения (4) и получим систему трёх уравнений однородных относительно направляющих косинусов 
,
,
:
(7)
Кроме того, направляющие косинусы связаны между собой соотношением
(8)
В силу соотношения (7) система (6) не может иметь тривиального решения:
, 
,
, следовательно, определитель системы (6) должен быть равен нулю.
Раскроем определитель
Или
Полученное кубическое уравнение перепишем:
, (9)
где коэффициенты имеют следующее выражение
т.е.
равняется сумме миноров элементов, стоящих на главной диагонали определителя, составленного из компонентов тензора напряжений (2)
т.е. 
равняется определителю, составленному из компонентов тензора напряжений (2). Т.к. матрица, составленная из компонентов тензора напряжений симметрична, уравнение (9) имеет три действительных корня — три главных напряжения, которые пронумеруем в порядке их алгебраической величины
Главные напряжения в данной точке при заданном напряжённом состоянии не могут зависеть от выбора исходных площадок, т.е. от выбора координатных осей, следовательно, коэффициенты уравнения (8) инварианты по отношению к выбору системы координат. Они называются инвариантами тензора напряжений
— линейный инвариант
— квадратичный инвариант
— кубичный инвариант
Найдя из уравнения (9) главные напряжения и внося их в любые 2 уравнения (7) и добавляя соотношение (8) находим направляющие косинусы главных площадок.
3. Главные касательные напряжения
Экстремальные касательные напряжения возникают по площадкам, проходящим через рёбра параллелепипеда, гранями которого являются главные площадки, и делящим пополам прямые углы между гранями (рис.54).
 |
Рис. 54
Наибольшим из главных касательных напряжений является напряжение
(10)
4. Пример
Определить величину главных напряжений и наибольшее касательное напряжение для заданного (рис.55) напряжённого состояния
;
;
;
Тензор напряжений в этом случае будет выглядеть
Вычисляем инварианты напряжённого состояния
;
Рис. 55
;
Составляем кубическое уравнение
Решим кубическое уравнение, для чего рассмотрим функцию
;
методом попыток устанавливаем, что один из корней многочлена 
равняется приблизительно 
.
Уточним этот корень с помощью итерационного метода Ньютона
Примем 
Проделывая ещё раз ряд итераций, получаем
т.е. практически точный результат.
Найдём два других корня. На основании следствия из теоремы Безу:
многочлен 
должен делиться без остатка на двучлен 
,
где 
— корень многочлена.
Разделим 
на 
Многочлен разделился практически без остатка. Для того чтобы найти другие два корня, решим квадратное уравнение
;
Сопоставляя 
,
и 
устанавливаем
;
;
Проверим полученное решение, вычислив для этого инварианты через главные напряжения
(точное значение 3200).
(точное значение 48000).
Наибольшие касательные напряжения равны
5. Классификация напряжённых состояний
Частные случаи определения главных напряжений:
1) Если все три главные напряжения отличны от нуля, то напряжённое состояние называется объёмным или трехосным.
2) Когда два главные напряжения отличны от нуля, напряжённое состояние называется плоским или двуосным. Кубичный инвариант при этом равен нулю: 
.
В этом случае уравнение (8) принимает вид:
откуда следует, что один из корней равен нулю. Два остальных найдутся из решения квадратичного уравнения.
(11)
Если напряжения действуют только лишь в одной плоскости, например, в плоскости, параллельной координатной плоскости X — Y , то тензор напряжений будет состоять из трёх независимых компонент (ненулевых).
Инварианты напряжённого состояния будут равны:
;
подставим эти выражения в (11)
получаем главные напряжения:
(12)
3) Если кубичный и квадратичный инварианты одновременно равны нулю, то уравнение (8) даёт лишь один корень отличный от нуля.
;
Напряжённое состояние называется в этом случае линейным или одноосным.
Приведённая выше классификация не является исчерпывающей, и поэтому принято классифицировать напряжённые состояния ещё в зависимости от знака главных напряжений. В этом случае все напряжённые состояния можно разделить на три класса:
1. Трёхосные растяжения. В этом случае ни одно из главных напряжений не является сжимающим.
2. Трёхосные сжатия, когда ни одного из главных напряжений не является растягивающим.
3. Смешанные напряжённые состояния, когда наибольшее и наименьшее главные напряжения имеют разные знаки.
Примеры различных типов напряжённых состояний см. в учебнике В.И.Феодосьева “Сопротивление материалов”, 1986 г. стр.270-274.
6. Определение напряжений по площадкам параллельным направлению одного из главных напряжений
В практических задачах часто сталкиваются с таким положением, когда положение одной из главных площадок заранее известно. Решение в этом случае значительно упрощается.
Рассмотрим элемент в виде параллелепипеда. Грани параллелепипеда являются главными площадками (рис.56).
Выделим из параллелепипеда треугольную призму. Наклонная к координатным плоскостям грань параллельна направлению главного напряжения 
. Составим условия равновесия элементарной призмы.
Рис. 56
Проектируя на направление нормали к площадке, получаем:
Сумма проекций всех сил на направление 
даст:
Упрощая полученные выражения, получаем окончательно:
(12)
Если рассматривать 
и 
как декартовы координаты на плоскости, то легко обнаружить, что уравнения (12) представляют собой уравнение окружности в параметрическом виде:
Возводя оба равенства в квадрат и складывая, получаем:
т.е. уравнение окружности с центром находящимся на оси на расстоянии 
от начала координат и радиусом 
(рис.57).
Рис. 57
Полученный круг называется круговой диаграммой Мора. Если не принимать во внимание знак касательного напряжения, то можно ограничиться построением только верхней половины круга Мора.
Построенная диаграмма имеет следующий смысл: каждой площадке параллельной направлению напряжения 
соответствует точка на окружности.
Площадкам общего положения, не параллельным ни одному из главных напряжений, соответствуют точки расположенные в заштрихованной области (рис.59).
Наложим круговые диаграммы на один чертёж.
Рис. 59
7. Определение главных напряжений в случае, когда известно положение одной из главных площадок
Пускай 
— главное напряжение. Требуется найти величину двух других главных напряжений. Введём систему координат ,
, и нанесём точки, соответствующие площадкам I и II (рис.61)
Рис.61
Проведём через точки I и II окружность, центр которой лежит на оси . Точки пересечения круговой диаграммы с осью дадут значения главных напряжений 
и 
.
Определяя 
и 
из чертежа, приходим к знакомой формуле (12).
8. Дифференциальные уравнения равновесия
Пусть 
— произвольный объём тела ограниченный замкнутой поверхностью 
.
Вектор массовых сил, отнесённый к единичному объёму, обозначим 
, а вектор поверхностных сил, действующих на единичную площадь 
, где 
— нормаль к поверхности в данной точке.
Главный вектор внешних сил, действующих на тело, состоящий из главного вектора объёмных сил равен нулю:
Спроектируем это равенство на ось X :
Используя первую из формул (4) и учитывая (3) получим
С помощью формулы Грина-Остроградского преобразуем поверхностный интеграл к объёмному.
Т.к. условия равновесия должны соблюдаться для любого объёма, то подынтегральная функция должна быть равной нулю в любой точке тела. Аналогичным образом, проектируя векторное равенство (*) на оси Y и Z получим систему дифференциальных уравнений равновесия.
9. Деформированное состояние в точке
Деформированное состояние в точке определяется тензором деформаций. Т.е. удлинение в данной точке по любому направлению может быть вычислено, если заданы удлинения по трём взаимно перпендикулярным осям и углы сдвига по трём взаимно перпендикулярным площадкам, нормалями к которым служат оси.
Тензор деформаций выглядит
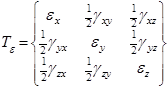
Здесь 
,
,
— деформации относительного удлинения в направлении соответствующих осей.
,…,
— углы сдвига в соответствующих координатных плоскостях.
10. Связь между компонентами тензора деформаций и перемещениями
Рассмотрим малый элемент, который в процессе деформации изменил свою конфигурацию. На рисунке показана одна из граней, совпадающая с плоскостью осей X и Y :
аналогично 
Угол сдвига — это угол, на который изменится первоначально прямой угол, т.е.
Аналогично определяется и другие компоненты тензора деформаций. Итак! Соотношения Коши:
;
;
;
;
;
Шесть компонент тензора деформаций выражаются через три компоненты вектора перемещения. Отсюда следует, что компоненты тензора деформаций не являются независимыми. И в самом деле, они связаны соотношениями называемыми уравнениями совместности деформаций.
Условиям совместности деформаций можно придать следующий смысл. Разрежем тело на малые элементы, деформируем каждый из элементов в отдельности и соберём из деформированных элементов тело. Тогда, если деформации правильные, т.е. удовлетворяющие уравнениям совместности, то собранное тело не будет иметь разрывов и пустот.
11. Обобщённый закон Гука
Будем основываться на известном нам законе Гука для одноосного состояния
,
и принципе независимости действия сил.
Обратим внимание на такой факт, что с точностью до малых высшего порядка, нормальные напряжения не вызывают сдвигов, а в свою очередь касательные напряжения не вызывают удлинений.
Рассмотрим малый элемент (рис.50).
Воспользуемся принципом независимости действия сил.
1) Пусть действуют только напряжения 
.
, тогда 
; 
2) 
; 
; 
; 
3) 
; 
; 
; 
При совместном действии всех трёх напряжений
Аналогично определяется и деформации 
и 
.
В результате получаем уравнения называемые обобщённым законом Гука.
;
;
;
К таким уравнениям нужно добавить ещё три соотношения
; 
; 
Три дифференциальных уравнения равновесия, шесть соотношений Коши и шесть соотношений обобщённого закона Гука составляют систему уравнений теории упругости, в которых неизвестными будут шесть компонент тензора напряжений, шесть компонент тензора деформаций и три компоненты перемещения.