| Скачать .docx |
Реферат: Изучение законов вращательного движения
![]() Министерство общего и профессионального образования
Министерство общего и профессионального образования
Российской Федерации
Уральский Государственный Технический Университет
Краснотурьинский Общетехнический Факультет
Кафедра физики
ОТЧЁТ
по лабораторной работе №9
«Изучение законов вращательного движения»
Студент Ивашова Н. С.
Группа С 171К
Дата
г.Краснотурьинск
2000г.
1. Расчетные формулы:
1.1. Момент силы натяжения нити

где <d> ‑ средний диаметр шкива;
![]() ‑ масса опускающегося груза, N=0,1,2,3,4;
‑ масса опускающегося груза, N=0,1,2,3,4;
![]() ‑ высота падения груза;
‑ высота падения груза;
<t> ‑ среднее время опускания груза.
1.2. Угловое ускорение маятника
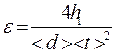 .
.
1.3. Момент инерции маятника

где ![]() , N=const ‑ задаётся преподавателем;
, N=const ‑ задаётся преподавателем;
<![]() > ‑ средняя высота подъема платформы с перегрузками.
> ‑ средняя высота подъема платформы с перегрузками.
2. Эскиз установки.

3. Средства измерений и их характеристики.
Таблица 1
| Наименование средства измерения |
Предел измерения или номинальное Значение |
Цена деления шкалы |
Класс точности |
Предел основной погрешности
|
| Электросекундомер Металлическая линейка |
99,999 с 50 см |
0,001 с 1 мм |
0,0005 с 0,5 мм |
4. Результаты измерений: Установка № 21.
Задача 1.
Определения момента инерции ![]() вала и крестовины без грузов и момента сил трения.
вала и крестовины без грузов и момента сил трения.
4.1. Массы платформы ![]() перегрузков
перегрузков ![]() и их погрешности приводятся в таблице, находящейся в лаборатории.
и их погрешности приводятся в таблице, находящейся в лаборатории.
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]()
![]()
![]()
![]()
4.2. Измерения высоты опускания груза
![]() =
= ![]() =
=
4.3. Измерения диаметра шкива. (Диаметр шкива может быть задан преподавателем)
Таблица 2
| d , мм |
|
|
<d>=
![]()

4.4. Измерение времени опускания груза, расчет ![]() и М
.
и М
.
Таблица 3
| Масса опускающегося груза, (г) |
|
|
|
|
|
| Время t опускания груза, (с) |
|||||
| <t> , c |
|||||
| Угловое ускорение |
|||||
| Момент М силы натяжения, Нм |


![]()
4.5. Построение графика ![]() определение
определение ![]() и
и ![]() .
.
4.6. Расчет границ погрешностей результатов измерений.
Использование ЭВМ позволяет оценить средние квадратические отклонения ![]() и
и ![]() , по которым можно вычислить доверительные границы случайных погрешностей
, по которым можно вычислить доверительные границы случайных погрешностей

где ![]() ‑ коэффициент Стьюдента при доверительной вероятности
‑ коэффициент Стьюдента при доверительной вероятности
Р=0,95 и числе наблюдений ![]() (в нашем случае
(в нашем случае ![]() ).
).
Неисключенными систематическими погрешностями пренебрегаем.
Следовательно,

4.7. Окончательные результаты

Задача 2. Определение момента инерции системы четырех цилиндров,
симметрично расположенных относительно оси вращения.
4.8. Измерение массы цилиндра m1 (производится в таблице, прилагаемой к установке ) и массы m падающего груза
m 1 =
m = m 0 + Nmn (рекомендуется N =4).
4.9. Измерение расстояние R от оси вращения до центра тяжести цилиндра на крестовине
R
= ![]() R
=1,1
R
=1,1![]()
4.10. Измерение времени t опускания груза и высоты h 2 его подъема
Таблица 4
| |
|
|
|
|
|
<t>= <h2 >=
![]()
![]()
Средние квадратические отклонения ![]() и
и ![]() :
:

Доверительные границы случайных погрешностей:

Границы неисключенных систематических погрешностей: 
4.11. Вычисление момента инерции < I > крестовины с четырьмя цилиндрами по формуле (3).
4.12. Расчет момента инерции < I 1 > четырех цилиндров
<I1 >=<I>-<I0 >=
4.13. Вычисление границы относительной погрешности определения I

где ![]()
4.14. Граница абсолютной погрешности определения I равна
![]()
4.15. Граница относительной погрешности результата измерения момента инерции I четырех цилиндров вычисляется по формуле

4.16. Граница абсолютной погрешности результата измерения I 1 равна
![]()
4.17. Окончательный результат:
![]()
4.18. Вычисление теоритического значения момента инерции I 2 четырех цилиндров относительно оси вращения в предложении, что они являются материальными точками
![]()
где m 1 – масса цилиндра;
R ‑ расстояние от оси вращения до центра тяжести цилиндра,
расположенного на крестовине.
4.19. Сравнение результата I 2 с полученными из опыта I 1 и оценка относительной погрешности, возникающей при допущении, что цилиндры являются материальными точками

4.20. Выводы: