Реферат: Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях

Задание K 2. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях

Дано :

x=c₂ t² +c₁ t+c₀ ,

R₂ =40см,

r₂ =25 см,

R₃ =20 см,

x₀ =9 см,

V₀ =8 см/с,

x₂ =65 см,

t₁ =1с,

t₂ =2с.

c₁ -? c₂ -? c₃ -?

V-? a-? -?

-? V_M -?

Уравнение груза 1 имеет вид: (1)

x=c₂ t² +c₁ t+c₀ .

Коэффициенты c₂ , c₁ , c₀ могут быть определены из следующих условий:

При t=0c x=9 =V₀ =8; (2)

При t=2c x=65. (3)

Скорость груза 1

V == 2c₂ t+c₁ (4)

Подставляя (2) и (3) в (1) и (4) получим систему уравнений, из которой найдем коэффициенты

c₂ , c₁ , c₀

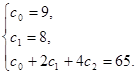
Таким образом, уравнение движения груза 1 имеет вид:

x= 10 t² +8t+9. (5)

Скорость груза 1:

V ==20t+8

При t=1c V =28см/ c . (6)

Ускорение груза 1:

a =20см/с² .

Для определения скорости и ускорения точки М запишем уравнения, связывающие скорость груза V и угловые скорости колес и .

откуда имеем:

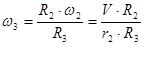(7)

Т.к. V =20t+8 , то

;

При t=1c =2,24рад/с.

Угловое ускорение колеса 3:

Скорость точки М, ее вращательное, центростремительное и полное ускорения определяются по формулам:

V_М =см/с.

см/с² .

см/с²


28	20	2,24	1,6	44,8	100,35	32	105,33

Задание:

Найти скорость 1 тела в конце отрезка s.

Дано :

кг

Решение:

Применим теорему об изменении кинетической энергии системы

(т.к. система состоит из абсолютно твёрдых тел)

T₀ =0(т.к. в начальный момент времени система покоилась)

Определим кинетическую энергию системы в конечный момент времени

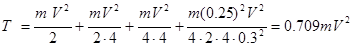
Определим работу сил в конечный момент времени

Определим скорость в конечный момент времени

(м/с)

Ответ: м/с

К4. Кинематический анализ многозвенного механизма

Дано :

=2рад/с.

a=50см

b=30см

O₁ A=14см

O₂ B=29см

AB=45см

BC=54см

CD=34см

DE=37см

Найти:

1) скорости точек А, В, С и D механизма и угловые скорости всех его звеньев с помощью плана скоростей;

2) скорости точек А, В, С и D механизма и угловые скорости всех его звеньев с помощью мгновенных центров скоростей;

3) ускорения точек А и В и угловое ускорение звена АВ;

4) положение мгновенного центра ускорений звена АВ;

5) ускорение точки М, делящей звено АВ пополам.

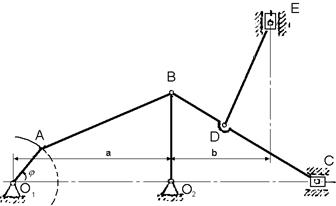
Определние скоростей точек и угловых ускорений звеньев с помощью плана скоростей.

Определяем скорости точек.

Строим схему механизма в выбранном масштабе (рис1). Вычисляем модуль скорости точки А кривошипа О₁ А:

=м/с.

Вектор перпендикулярен О₁ А и направлен в сторону вращения кривошипа.

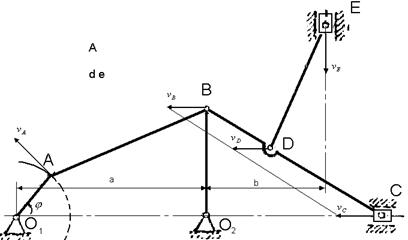
Строим план скоростей. Из произвольно выбранного полюса О проводим луч Оа, изображающий в выбранном масштабе скорость точки А.

Для определения скорости точки В через

полюс О проводим прямую, параллельную

скорости , через точку а- прямую,

перпендикулярную АВ. Получаем точку b;

отрезок Оbопределяет скорость точки В.

Измеряем длину луча Оb и, пользуясь масштабом скоростей, находим =13см/с

Продолжая построение плана скоростей, находим , ,

=13 см/с.

=5,3 см/с.

Определяем угловые скорости звеньев механизма.

Отрезок ab плана скоростей выражает вращательную скорость точки В вокруг точки А:

ab=;

отсюда угловая скорость звена АВ

=ab/AB=14,5/45=0,32 рад/с

Аналогично определяются угловые скорости звеньев ВС и ED:

=bc/BC=0/54=0

=ed/ED=14/37=0,38 рад/с

Угловая скорость звена О₂ В определяется по вращательной скорости точки В вокруг неподвижного центра О₂ .

=13/29=0,45 рад/с

Определение скоростей точек и угловых ускорений звеньев с помощью мгновенных центров скоростей.

а) Определяем положения мгновенных центров скоростей звеньев механизма.

Строим схему в выбранном масштабе(рис3)

Звенья О₁ А, O₂ B вращаются вокруг неподвижных центров О₁ и О₂ .

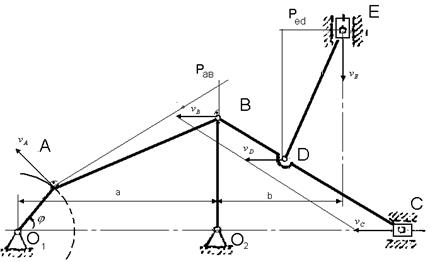
Рис3

Мгновенный центр скоростей Р_АВ звена АВ находится на как точка пересечения перпендикуляров, проведенных из точек А и В к их скоростям. Аналогично определяется положение мгновенного центра скоростей Р_DE . Мгновенный центр скоростей звена АВ находится в бесконечности.

Б) Определяем скорости точек . Скорости точек звеньев механизма пропорциональны расстояниям от этих точек до мгновенных центров скоростей соответствующих звеньев. Эти расстояния измеряются на чертеже.

Для определения скорости точки В звена АВ имеем пропорции

АР_АВ /ВР_АВ .

Следовательно ,

ВР_АВ /АР_АВ .

см/с.

Т.к. мгновенный центр скоростей звена ВС находится в бесконечности, то

Для определения скорости точки Е звена ED имеем пропорции

ЕР_ED /DP_ED _.

Следовательно,

DP_ED /EP_ED .

см/с.

Одновременно с определением модулей скоростей точек находим их направления, а также направления вращений звеньев механизма. Например, по направлению скорости точки А и положению мгновенного центра скоростей Р_АВ устанавливаем, что вращение звена АВ происходит по часовой стрелке. Поэтому скорость точки В при данном положении механизма направлена влево.

Аналогично определяем направления вращений остальных звеньев и направления скоростей точек механизма.

в) Определяем угловые скорости звеньев механизма

Скорость любой точки звена равна произведению угловой скорости этого звена на расстояние от точки до мгновенного центра скоростей:

АР_АВ .

28/64=0,43 рад/с.

Угловая скорость звена О₂ В определяется по скорости точки В:

13,1/29=0,45 рад/с.

Угловая скорость звена ВС равна нулю, т.к. мгновенный центр скоростей звена ВС находится в бесконечности:

Аналогично вычисляем угловую скорость звена ED:

EP_ED _.

5,4/14=0,38 рад/с.

3. Определение ускорений точек A и B и угловое ускорение звена АВ.

Определяем и .

С помощью теоремы об ускорениях точек плоской фигуры определяем ускорение точки В:

Т.к. кривошип О₁ А вращается равномерно, то ускорение точки А направлено к центру О₁ и равно

см/с² .

Центростремительное ускорение точки В во вращательном движении шатуна АВ вокруг полюса А направлено от точки В к точке А и равно

0,43=19,43 см/с² .

Откладываем от точки В в соответствующем масштабе ускорение полюса . Из конца вектора строим вектор , проводя его параллельно ВА. Через конец вектора проводим прямую JK, перпендикулярную ВА, т.е. параллельную вращательному ускорению . Однако определить ускорение этим построением невозможно, т.к. его направление неизвестно.

Чтобы найти ускорение точки В, необходимо выполнить второе построение, рассматривая эту точку как принадлежащую О₂ В. В этом случае

Центростремительное ускорение точки В:

см/с² .

Откладываем от точки В вектор , направив его к центру О₂ . Через конец вектора проводим прямую LN перпендикулярно О₂ В, т.е. параллельно вращательному ускорению .

Точка пересечения этой прямой с JK определяет концы векторов ,

Измерением на чертеже получаем

80 см/с² .

49 см/с² .

Т.к. =АВ, то угловое ускорение звена АВ

/АВ=49/45=1,09 рад/с² .

4)Определение положения мгновенного центра ускорений звена АВ.

Примем точку А за полюс. Тогда ускорение точки В

Строим параллелограмм ускорений при точке В по диагонали и стороне . Сторона параллелограмма выражает ускорение точки В во вращении АВ вокруг полюса А. Ускорение составляет с отрезком АВ угол , который можно измерить на чертеже.

Направление вектора относительно полюса А позволяет определить направление , в данном случае соответствующее направлению часовой стрелки Отложив угол от векторов и в этом направлении и проводя два луча, найдем точку их пересечения - мгновенный центр ускорений звена АВ.

5) Определение ускорения точки М.

Найдем ускорение точки М с помощью МЦУ.

Ускорения точек плоской фигуры пропорциональны их расстояниям до мгновенного центра ускорений:

Подставив расстояния, определенные по чертежу

К7. Определение абсолютной скорости и абсолютного ускорения точки

Дано :

OM=Sr(t)=25sin(t/3);

a=25см

v-?

a-?

Положение точки М на теле D определяется расстоянием Sr=ОМ.

При 4c Sr=25 sin(4/3)= -21,65 см.

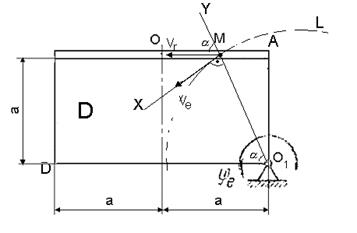
Абсолютную скорость точки М найдем как геометрическую сумму относительной и переносной скоростей:

Модуль относительной скорости , где dSr/dt=25cos(t/3) /3

При t=4c -13,08см/с.

13,08см/с.

Отрицательный знак у показывает, что вектор направлен в сторону убывания Sr.

Модуль переносной скорости =, где

-радиус окружности L, описываемой той точкой тела, с которой в данный момент совпадает точка М,

-модуль угловой скорости тела.

Найдем .

Рассмотрим прямоугольный треугольник .

АМ=ОА-ОМ.

АМ=25-21,65=3,35см.

=25см.

По теореме Пифагора имеем:

=25,22см.

Найдем .

, где

=d/dt =4t-0,5

При t=4c =15,5рад/с.

Знак ”+” у величины показывает, что вращение тела D происходит в ту же сторону, в которую ведется отсчет угла .

Тогда модуль переносной скорости

==390,91 см/с.

Модуль абсолютной скорости v найдем способом проекций.

Через точку М проводим оси X и Y.

Из треугольника :

=AM/

=3,35/25,22=0,13

Тогда

1,704 см/с

403,86см/с.

Значит v =

403,86см/с.

Абсолютное ускорение точки М равно геометрической сумме относительного, переносного и кориолисова ускорений.

, где в свою очередь

Относительное движение.

Это движение происходит по закону Sr(t)=25sin(t/3);

Модуль относительного касательного ускорения ,

где =d² Sr/dt=

При t=4c 23,72см/с² .

23,72см/с² .

Модуль относительного центростремительного ускорения =0, т.к. радиус кривизны относительной траектории стремится к бесконечности.

Переносное движение.

Это движение происходит по закону

Модуль переносного вращательного ускорения , где

= - модуль углового ускорения тела D

d² /dt² =4рад/с²

Знаки у и одинаковые. Значит вращение тела D ускоренное.

Тогда см/с²

Модуль переносного центростремительного ускорения

=6059,1 см/с² .

Кориолисово ускорение.

Модуль кориолисова ускорения определяем по формуле

, где

- угол между вектором и осью вращения (вектором ).

В нашем случае =, т.к. ось вращения перпендикулярна плоскости вращения тела D.

Тогда 12118,21 см/с² .

Направление вектора найдем по правилу Н.Е.Жуковского: т.к. вектор лежит в плоскости, перпендикулярной оси вращения, то повернем его на в направлении , т.е. против хода часовой стрелки.