| Скачать .docx |
Реферат: Електромагнітна сумісність
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ДОНЕЦЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
Кафедра ЕПМ
РОЗРАХУНКОВО-ГРАФІЧНА РОБОТА
З «ЕЛЕКТРОМАГНІТНОЇ СУМІСНОСТІ»
Виконав:
ст.гр. ЕСЕ – 08м
Овсянніков М.А.
Перевірив:
проф. Курінний Е.Г.
Донецьк – 2008
ІМІТАЦІЯ БАЗОВОГО ГРАФІКА ЗАВАДИ
|
|
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
75 |
80 |
| у,мм |
70 |
77 |
90 |
115 |
133 |
145 |
144 |
110 |
70 |
48 |
43 |
57 |
70 |
85 |
100 |
95 |
70 |
Таблиця 1 – Початкові дані для обробки базового графіка, мм
|
|
85 |
90 |
95 |
100 |
105 |
110 |
115 |
120 |
125 |
130 |
135 |
140 |
145 |
150 |
155 |
| у,мм |
66 |
78 |
105 |
120 |
139 |
110 |
50 |
37 |
42 |
55 |
68 |
61 |
40 |
23 |
27 |
|
|
160 |
165 |
170 |
175 |
180 |
185 |
190 |
195 |
200 |
205 |
210 |
215 |
220 |
225 |
| у,мм |
43 |
75 |
98 |
114 |
122 |
120 |
110 |
100 |
140 |
90 |
56 |
38 |
41 |
86 |
|
|
230 |
235 |
240 |
245 |
250 |
255 |
260 |
265 |
270 |
275 |
280 |
285 |
290 |
295 |
300 |
| у,мм |
97 |
80 |
57 |
80 |
116 |
134 |
141 |
138 |
106 |
120 |
140 |
135 |
100 |
77 |
57 |
|
|
305 |
310 |
315 |
320 |
325 |
330 |
335 |
340 |
345 |
350 |
355 |
360 |
365 |
370 |
375 |
| у,мм |
75 |
112 |
118 |
100 |
76 |
52 |
37 |
47 |
72 |
98 |
112 |
90 |
74 |
87 |
110 |
|
|
380 |
385 |
390 |
395 |
400 |
405 |
410 |
415 |
420 |
425 |
430 |
435 |
440 |
445 |
| у,мм |
135 |
143 |
135 |
114 |
60 |
31 |
43 |
60 |
61 |
37 |
20 |
18 |
32 |
50 |
|
|
450 |
455 |
460 |
465 |
470 |
475 |
480 |
485 |
490 |
495 |
500 |
505 |
510 |
515 |
| у,мм |
84 |
113 |
127 |
135 |
124 |
98 |
110 |
120 |
94 |
42 |
55 |
70 |
98 |
110 |
|
|
520 |
525 |
530 |
535 |
540 |
545 |
550 |
555 |
560 |
565 |
570 |
575 |
580 |
585 |
| у,мм |
116 |
125 |
128 |
121 |
90 |
74 |
73 |
76 |
88 |
96 |
82 |
65 |
54 |
43 |
|
|
590 |
595 |
600 |
605 |
610 |
615 |
620 |
625 |
630 |
635 |
640 |
645 |
650 |
655 |
| у,мм |
56 |
71 |
85 |
103 |
117 |
127 |
133 |
134 |
124 |
90 |
80 |
80 |
38 |
37 |
|
|
660 |
665 |
670 |
675 |
680 |
685 |
690 |
695 |
700 |
705 |
710 |
715 |
720 |
| у,мм |
50 |
60 |
53 |
35 |
28 |
41 |
54 |
70 |
80 |
92 |
103 |
115 |
119 |
Графік завад є випадковим, тому що він утворюється великою кількістю електроприймачів.
Практичне заняття № 2
СТАТИСТИЧНА ОБРОБКА БАЗОВОГО ГРАФІКА
Мета – визначення статистичної функції розподілу і її характеристик.
2.1 За даними табл.1 розраховую наступні числові характеристики базового графіка:
- середнє значення
y
c
= ![]() = 85 мм;
= 85 мм;
- ефективне значення
y
е
= 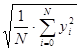 = 91 мм;
= 91 мм;
- дисперсія
Dy
= ![]() = 912
– 852
= 1056 мм2
;
= 912
– 852
= 1056 мм2
;
- стандарт
σy
= ![]() =
=![]() = 33 мм;
= 33 мм;
- коефіцієнт форми
k
ф
= ![]() =
= ![]() = 1,07 ,
= 1,07 ,
де i – індекс підсумування від 0 до N .
2.2 Знаходжу статистичну функцію F розподілу ординат базового графіка.
Таблиця 2 – Статистична функція розподілу базового графіка
| Інтервал, мм |
n |
|
|
| 0 |
0 |
0 |
0 |
| 0-5 |
0 |
0 |
0,000 |
| 5-10 |
0 |
0 |
0,000 |
| 10-15 |
0 |
0 |
0,000 |
| 15-20 |
2 |
2 |
0,014 |
| 20-25 |
2 |
3 |
0,021 |
| 25-30 |
2 |
5 |
0,034 |
| 30-35 |
3 |
8 |
0,055 |
| 35-40 |
8 |
15 |
0,103 |
| 40-45 |
9 |
24 |
0,166 |
| 45-50 |
5 |
29 |
0,200 |
| 50-55 |
6 |
35 |
0,241 |
| 55-60 |
8 |
43 |
0,297 |
| 60-65 |
3 |
46 |
0,317 |
| 65-70 |
7 |
53 |
0,366 |
| 70-75 |
7 |
60 |
0,414 |
| 75-80 |
10 |
70 |
0,483 |
| 80-85 |
4 |
74 |
0,510 |
| 85-90 |
8 |
82 |
0,566 |
| 90-95 |
3 |
85 |
0,586 |
| 95-100 |
10 |
95 |
0,655 |
| 100-105 |
3 |
98 |
0,676 |
| 105-110 |
7 |
105 |
0,724 |
| 110-115 |
7 |
112 |
0,772 |
| 115-120 |
9 |
121 |
0,834 |
| 120-125 |
5 |
126 |
0,869 |
| 125-130 |
3 |
129 |
0,890 |
| 130-135 |
8 |
137 |
0,945 |
| 135-140 |
4 |
141 |
0,972 |
| 140-145 |
4 |
145 |
1,000 |
За даними стовпців 1 (абсциси) і 4 (ординати) викреслюю графік 1.
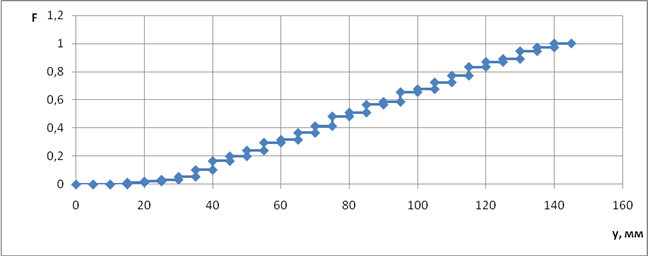
Рисунок 2.1 – Статистична функція розподілу базового графіка
2.3 Знаходжу ymin мінімальне і ymax максимальне значення випадкової величини згідно з інтегральною імовірністю 95%, якій відповідають імовірності Ex = 0,05 для мінімального і Ex = 0,95 для максимального значень.
ymin =32,5 мм;
ymax =132,5 мм.
З табл. 1 виписую найменшу у м і найбільшу у М ординати – повинно бути:
у м < y min , у М > y max .
у м =18 мм;
у М =145 мм.
18<32,5
145>132,5
Умова виконується.
Висновки:
1. Випадковий графік має невипадкові характеристики.
2. Використання згідно з ГОСТ 13109-97 практично достовірних значень показників ЕМС дозволяє заощаджувати капітальні вкладення на забезпечення ЕМС.
Практичне заняття № 3
АПРОКСИМАЦІЯ СТАТИСТИЧНОЇ ФУНКЦІЇ РОЗПОДІЛУ
Мета – перевірка можливості апроксимації статистичної (опитної) функції розподілу теоретичними імовірнісними розподілами: рівномірним і нормальним.
Критерій перевірки.
Відповідність теоретичної функції розподілу F (у)
статистичній ![]() (у)
виконується за найбільш простим критерієм Колмогорова:
(у)
виконується за найбільш простим критерієм Колмогорова:
![]() . (3.1)
. (3.1)
де N – кількість дослідів (N 0 = 50)
3.1 Рівномірний закон розподілу характеризується прямолінійною функцією розподілу F п (у) у межах
![]() мм,
мм,
![]() мм. (3.2)
мм. (3.2)
де – y c = 85 мм, σy = 33 мм беремо з практичної роботи №2.
Теоретичний діапазон змінення
k п = y пМ – y пм =142-28=114 мм. (3.3)
Наносимо точки а і b з координатами (у пм , 0) і (у пМ , 1) на графік статистичної функції, який зображений на рис. 3.1. Ці точки з'єднуємо прямою.
Перевіряємо можливість прийняття рівномірного розподілу для апроксимації статистичної функції розподілу за критерієм Колмогорова:
![]() ,
,
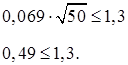
3.2 Нормальний закон розподілу характеризується функцією розподілу F
н
(у
) від –![]() до
до ![]() . Для цього розрахуємо необхідні величини та занесемо їх
. Для цього розрахуємо необхідні величини та занесемо їх
до табл. 3.1.
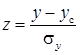 . (3.4)
. (3.4)
У верхній частині таблиці у < у с , тому ці значення є від'ємними. З таблиці Б.1 по абсолютним величинам | z | знаходимо значення Φ(| z | ) і заносимо їх до табл. 3.1. Шукані значення функції нормального розподілу
![]() при y
< y
c
. (3.5)
при y
< y
c
. (3.5)
У нижній частині таблиці при у > у с аргумент z є позитивним. У цьому випадку знайдені з таблиці Б.1 значення Φ (| z | ) заносимо зразу в останній стовпець, оскільки
![]() при y
> y
c
(3.6)
при y
> y
c
(3.6)
Нижня частина стовпця Φ(| z | ) не заповнюється.
Перевіряємо можливість прийняття рівномірного розподілу для апроксимації статистичної функції розподілу за критерієм Колмогорова:
![]() ,
,
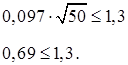
Таблиця 3.1 – Функція розподілу нормального закону
| y , мм |
z |
Φ(|z| ) |
F н |
| 0 |
-2,58 |
0,9951 |
0,0049 |
| 5 |
-2,42 |
0,9922 |
0,0078 |
| 10 |
-2,27 |
0,9884 |
0,0116 |
| 15 |
-2,12 |
0,9826 |
0,0174 |
| 20 |
-1,97 |
0,9756 |
0,0244 |
| 25 |
-1,82 |
0,9656 |
0,0344 |
| 30 |
-1,67 |
0,9525 |
0,0475 |
| 40 |
-1,36 |
0,9099 |
0,0901 |
| 50 |
-1,06 |
0,8554 |
0,1446 |
| 60 |
-0,76 |
0,7764 |
0,2236 |
| 70 |
-0,45 |
0,6736 |
0,3264 |
| 80 |
-0,15 |
0,5596 |
0,4404 |
| 85 |
0 |
0,5 |
0,5 |
| 90 |
0,15 |
0,5596 |
|
| 100 |
0,45 |
0,6736 |
|
| 110 |
0,76 |
0,7764 |
|
| 120 |
1,06 |
0,8554 |
|
| 125 |
1,21 |
0,8869 |
|
| 130 |
1,36 |
0,9099 |
|
| 135 |
1,52 |
0,9345 |
|
| 140 |
1,67 |
0,9525 |
|
| 145 |
1,82 |
0,9656 |
|
| 150 |
1,97 |
0,9756 |
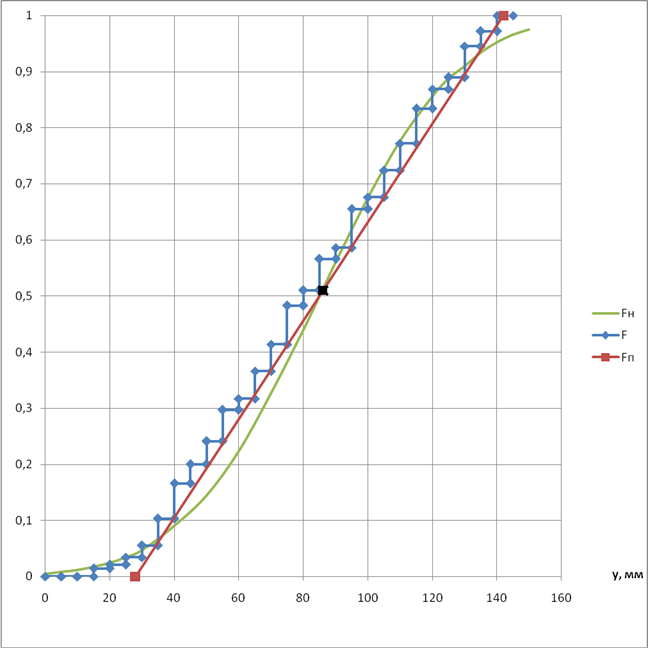
Рисунок 3.1 – Функції розподілу: ![]() – статистична, F
п
– рівномірного і F
н
– нормального законів розподілу
– статистична, F
п
– рівномірного і F
н
– нормального законів розподілу
3.3 Зіставляємо розрахункові значення: статистичні і теоретичні. Розходження вважається прийнятим, якщо воно не перевищує 10% від найбільш можливої ординати – 150 мм.
Таблиця 3.2 – Зіставлення розрахункових значень
| Розподіл |
Розрахункові значення |
Розбіжності, % |
||
| min, мм |
max, мм |
min |
max |
|
| Статистичний |
32,5 |
132,5 |
||
| Рівномірний |
33,5 |
136,5 |
0,67 |
2,9 |
| Нормальний |
30,5 |
139,5 |
-1,3 |
4,7 |
Мінімальні і максимальні розрахункові значення:
- для рівномірного розподілу
![]() =
=![]() мм,
мм,
![]() мм, (3.7)
мм, (3.7)
де дані беремо з п.3.1,
- для нормального розподілу
![]() мм. (3.8)
мм. (3.8)
Розраховуємо відносні розходження:
- для рівномірного розподілу
![]() ,
,
![]() , (3.9)
, (3.9)
- для нормального розподілу
![]() ;
;
![]() . (3.10)
. (3.10)
Висновки:
1. Згідно до розрахунків рівномірний і нормальний розподіли є прийнятними за критерієм Колмогорова, тому ми приймаємо нормальний закон, як такий, що за фізичним змістом більш відповідає умовам опиту.
2. За розрахунками абсолютні величини не перевищують допустиме значення розходження 10%.
Практичне заняття № 4
ОЦІНЮВАННЯ ЕМС ЗА НОРМАМИ НА ВІДХИЛЕННЯ НАПРУГИ
Мета – перевірка дотримання норм стандарту [1] на однохвилинні відхилення напруги.
4.1 Базовий графік (гр. з пр. з. № 1) вважається графіком змінення за часом t діючих значень U напруги у відносних одиницях (в.о.). Зв'язок між ординатами у у мм і напругою дається співвідношеннями:
U = 1 + 0,0008·y . (4.1)
4.2 Базовий графік напруги розбиваємо на однохвилинні ділянки: для цього через кожні 40 мм проводимо вертикальні лінії. Для першої ділянки перевіряємо точність візуальної обробки шляхом розрахунку точного значення:
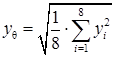 , (4.2)
, (4.2)
де підсумовуються квадрати 8 перших значень з табл. 1.
Таким чином, графік у θ (t) є ступеневим з кількістю ступенів Ν = 720/40 =18. Величини ступенів заносимо у стовпець 2 табл. 4,1, у якій i – номер ступеня (стовпець 1). В стовпці 3 їх розташовуємо у порядку зростання – позначення у θз . У стовпець 4 заносять значення функції розподілу
![]() , (4.3)
, (4.3)
перше з яких дорівнює 1/40 = 0,025, а останнє – одиниці.
Таблиця 4.1 – Дані для розрахунку однохвилинних напруг
| i |
y θ , мм |
y θ з , мм |
|
| 1 |
111,2 |
40 |
0,056 |
| 2 |
75 |
50 |
0,11 |
| 3 |
100 |
55 |
0,17 |
| 4 |
50 |
70 |
0,22 |
| 5 |
95 |
70 |
0,28 |
| 6 |
80 |
75 |
0,33 |
| 7 |
115 |
75 |
0,39 |
| 8 |
95 |
75 |
0,44 |
| 9 |
75 |
80 |
0,5 |
| 10 |
100 |
90 |
0,56 |
| 11 |
40 |
95 |
0,61 |
| 12 |
95 |
95 |
0,67 |
| 13 |
70 |
95 |
0,72 |
| 14 |
90 |
100 |
0,78 |
| 15 |
70 |
100 |
0,83 |
| 16 |
100 |
100 |
0,89 |
| 17 |
55 |
111,2 |
0,94 |
| 18 |
75 |
115 |
1 |
Мінімальне розрахункове значення у θmin та максимальне значення у θmax знаходимо з табл. 4.1. Підставивши їх в одну з формулу (4.1), отримаємо мінімальне U θmin і максимальне U θmax розрахункові значення однохвилинних напруг U θ у в.о. ( в стандарті [1] – U у ):
у θmin =40 мм,
у θmax =115 мм,
U θmin = 1 + 0,0008 · у θmin =1+0,0008·40=1,03,
U θmax = 1 + 0,0008· у θmax =1+0,0008·115=1,09.
U θmin ≥ 0,95 – виконується,
U θmax ≤ 1,05 – не виконується.
Порівняємо значення U min та U max (які перерахуємо за формулою (4.1) для у min =32,5 мм та у max =132,5 мм) з U θmin і U θmax :
U min = 1 + 0,0008·32,5 =1,026,
U max = 1 + 0,0008·132,5=1,11.
U θmin ≥ U min , U θmax ≤ U max
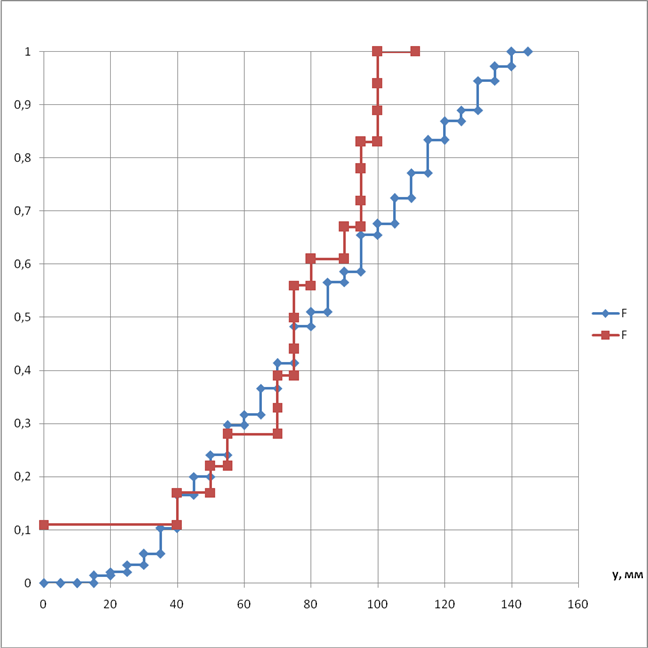
Рисунок 4.1 – Статистична функція розподілу базового графіка та функція розподілу відхилення напруги
Висновки:
3. Норми стандарту [1] на однохвилинні відхилення напруги не виконуються, тому що максимальне значення відхилення напруги перевищує допустимі 5%.
4. Однолінійне усереднення зменшує диапозон змінення графіка.