Реферат: Задачи по физике

Заказ №1448

Контрольная по физике.

1. Два велосипедиста выехали из пункта в пункт одновременно. Скорость первого велосипедиста , а скорость второго . Во время движения первый велосипедист был вынужден остановиться в пункте , расположенном на расстоянии от пункта , на . С какой минимальной скоростью должен двигаться первый велосипедист на оставшемся участке пути, чтобы приехать в пункт первым, если все расстояние между пунктами и равно ?

Дано:

Найти:

Решение

Общее время движения первого велосипедиста равно

,

а второго

Согласно условию задачи . Тогда

Подставив числовые значения, получим

Ответ:

2. Из одной точки одновременно бросают с одинаковыми скоростями два тела: одно вертикально вверх, второе горизонтально. Найти расстояние между телами через t = 2 с после бросания. Сопротивлением воздуха пренебречь.

Дано:

Найти:

Решение

Зависимость координат первого тела, кинутого вертикально вверх, от времени

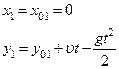
Для второго тела соответственно имеем

Расстояние между телами можем найти как

или

Поскольку согласно условию задачи , то

Подставив числовые значения, получаем

Ответ:

3 .Строительный кран поднимает груз массой . С каким ускорением можно производить подъем, если стальные тросы крана рассчитаны на силу натяжения . Какой груз можно будет поднять, если уменьшить ускорение вдвое?

Дано:

Найти:

Решение

Согласно второму закону Ньютона имеем:

Спроецировав уравнение на ось х , получаем

(1)

Откуда находим

Подставив числовые значения, находим

Перепишем равенство (1) для второго случая

Подставив числовые значения, получим

Ответ: ;

4. Однородный цилиндр массы и радиуса вращается без трения вокруг горизонтальной оси под действием веса груза , прикрепленного к легкой нити, намотанной на цилиндр. Найти угол поворота цилиндра в зависимости от времени, если при .

Дано:

Найти:

Решение

Согласно закону динамики вращательного движения имеем:

где - угловое ускорение. Тогда

откуда

Интегрируя последнее равенство с учетом пределов интегрирования, получаем

Подставив числовые значения, находим

Ответ:

5. Материальная точка совершает гармонические колебания согласно уравнению . Определите: амплитуду, период, начальную фазу колебаний, максимальную скорость точки, максимальное ускорение точки. Через сколько времени после начала отсчета точка будет проходить через положение равновесия?

Дано:

Найти:

Решение

Согласно уравнению колебания можем определить:

- амплитуда колебаний ;

- период колебаний: ; т.к. , то ;

- начальная фаза: ;

- максимальная скорость:

- максимальное ускорение:

В момент прохождения положения равновесия . Тогда

Ответ: ; ; ; ; ;

6. Сосуд разделен на две равные части полупроницаемой неподвижной перегородкой. В первую половину сосуда введена смесь аргона и водорода при давлении , во второй половине вакуум. Через перегородку может диффундировать только водород. После окончания процесса диффузии давление в первой половине оказалось равным . Во время процесса температура поддерживалась постоянной. Определите отношение масс аргона и водорода в смеси, которая была первоначально введена в первую половину сосуда.

Дано:

Найти:

Решение

Согласно закону Дальтона и в соответствии с уравнением Менделеева – Клапейрона можем для каждого состояния записать

Разделив первое равенство на второе, получаем

Подставив числовые значения, получаем

Ответ:

7. Оцените длину свободного пробега молекулы в воздухе при нормальных условиях. Диаметр молекулы .

Дано:

Найти:

Решение

Средняя длина свободного пробега определяется как

Согласно основному уравнению молекулярно кинетической теории газов

Откуда концентрация газа равна

Следовательно,

Подставив числовые значения, находим

Ответ:

8. Тепловая машина Карно, имеющая КПД , начинает использоваться при тех же тепловых резервуарах как и холодильная машина. Сколько тепла ΔQ₂ эта машина может перевести от холодильника к нагревателю за один цикл, если к ней за каждый цикл подводится работа ?

Дано:

Найти: ΔQ₂

Решение

КПД тепловой машины, работающей по циклу Карно, равен

Количество теплоты, отданное холодильнику, равно

.

Цикл Карно обратим, поэтому его можно провести в обратном направлении. Это будет уже не тепловая машина, а идеальная холодильная. Ее КПД определяется как

.

Так как

то

Подставив числовые значения, находим

Ответ: