Реферат: Решение уравнений движения материальных точек

СОДЕРЖАНИЕ

1. Решение по движении материальных точек

2. Решение по уравнению изменения кинетической энергии

3. Решение по движению системы (по принципу Даламбера)

1. Решение по движении материальных точек

Груз D массой m , получив в точкеА начальную скорость движется в изогнутой трубе АВС, расположенной в вертикальной плоскости: участок АВ – наклонный; участок ВС – горизонтальный.

На участке АВ на груз кроме силы тяжести действует постоянная сила (ее направление показано на рисунке) и сила сопротивления среды R , зависящая от скорости V груза (направлена против движения): трение груза о трубу на участке АВ пренебречь.

В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действует сила трения (коэффициент трения о трубу f = 0,2) и переменная сила , проекция которой F1 задана в таблице.

Считая груз материальной точкой и зная расстояние АВ = t или время t 1 движение груза от точки А до точки В , найти закон движения груза на участке ВС , т.е. x = f ( t ), где x = BD .

Дано :

m =1,8 кг.

= 24 м/с

Q = 5 H

R = 0,3 V

t = 2 c

F = 2

F = 0,2

Составляю дифференциальное уравнение движения точки на участке АВ :

Интегрируя, получaю:

При t=0;⟶

При t=2c :

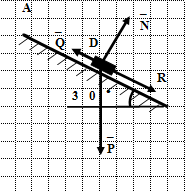
На участке BC:

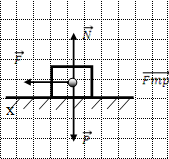
Составляю дифференциальное уравнение:

Fmp = fN; N=P=18 Н

Fmp = 0,2 * 18=3,6 Н

Интегрируя, получаю:

При t=0;

Интегрируя, получаю:

При t=0; ⟶x=0;

Таким образом уравнение движения примет вид:

2. Решение по уравнению изменения кинетической энергии

Механическая система состоит из грузов 1 и 2 , ступенчатого шкива 3 с радиусами ступеней = 0,3 м ., = 0,1 м . и радиусом инерции относительно оси вращения = 0,2 м . блока 4 радиуса = 0,2 м ., и катка (или подвижного блока) 5 .

Тело 5 считать сплошным однородным цилиндром, а массу блока 4 – равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 ; участки нитей параллельны соответствующим плоскостям. К телу 5 прикреплена пружина с коэффициентом жесткости c .

Под действием силы F = f ( s ), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент M сил сопротивления (от трения в подшипниках).

Определить значение искомой величины в тот момент времени, когда перемещение s станет равным = 0,2 м.

Все катки, включая и катки обмотанные нитями катятся по плоскостям без скольжения.

В данной задаче не буду изображать груз 2 , т.к. = 0.

Дано:

= 8 кг.

= 0

= 5 кг.

= 0

= 6 кг.

С = 280 Н/м.

М = 0,8Н*м.

𝝎 3 -?

Решение: Тело 1 совершает поступательное движение; тела 3,4 – вращательное; тело 5 – плоскопараллельное движение.

Из теоремы об изменении кинетической энергии материальной точки следует: - =

= 0, т. к. в начальном движение система находилась в покое.

Так как Т = + + , то кинетическая энергия для тела 1 (поступательное движение):= ;

Для тела 3 ⟶ = , момент инерции тела 3 относительно оси проходящей ч/з центр масс будет равен = =0,2;

Для тела 5 ⟶ = момент инерции тела 5 будет равен

= = 0,03

= = = 3,33

= * = 3,33 *0,1 =0,333

= = 0,3 ⟶ 0,3 = 0,1

= = = 0,5

= = = 0,05

= ; = = 0,1м. ⟶ = = 0,5

= = 0,36

= = 0,1

= + = 0,003 +0,0075 = 0,01125

T =0,36 = 0,47125

Далее определяю работу сил:

A ( F ) = =320*0,2+180* = 64+7,2 = 71,2 Дж.

= = = 0,67 рад.

= 0,67*0,1 = 0,067 м.

= = = 0,335 рад.

= 0,067 м .

= = 0,0335 м .

A( )= *cos 60˚ * g* cos 60˚ = 8*10*0,5*0,2 = 8 Дж .

A( ) = - *

= f* *cos 30˚=8*10*0,87 = 69,6 Н .

69,6 = 6,96 Н

A( ) = - 6,96 *

A( = - М * = - 0,8 * 0,67 = - 0,536 Дж .

A( )= *cos 45 ˚ *

A() = - = - = -0,157 Дж .

= 71,2+8-1,392- 0,536 – 1,4271 – 0,157 = 75,6879 Дж .

0,47125 = 75,6879 Дж .

= = 12,67

3. Решение по движению системы (по принципу Далавера)

Вертикальный вал АК, вращающийся с постоянной угловой скоростью 𝝎=10 , закреплен подпятником в точке А и цилиндрическим подшипником в точке Е(АВ=BD=DE=EK=a). К валу жестко прикреплены тонкий однородный ломаный стержень m =10 кг , состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунке, где b=0,1м, а их массы пропорциональны длинам), и невесомый стержень длинной l =4 b с точечной массой на конце; оба стержня лежат в одной плоскости. Точки крепления стержней D и К, а углы 𝜶=, 𝜸, 𝝋 =.