| Скачать .docx |
Реферат: Процессы в теплотехнике
Балтийская государственная академия рыбопромыслового флота
Расчётно-графическая работа №1
Дисциплина: Теплотехника
Калининград
2008
Дано
P1 =0,3; T1 =313; T3 =523; P4 =0,6; T1-2 =const; S2-3 =const; V3-4 =const; S4-1 =const, что соответствует давлению и температуре в начальной точке изотермического процесса, соответственно P1 =0,3 МПа и Т1 =313 К; температуре в конечной точке адиабатного процесса T3 =523К; давлению в конце изохорного процесса, а также заданы процессы цикла: изотермический, адиабатный, изохорный. Требуется найти все недостающие параметры цикла и его основные характеристики.
В этой работе требуется для 1 кг воздуха:
1. Определить параметры P, V, T, S, U, I для основных точек цикла.
2. Построить цикл: а) в координатах P – V, б) координатах T–S.
3. Найти l, ∆s, q, ∆i, ∆u для каждого процесса, входящего в состав цикла.
4. Определить работу цикла lц , термический к. п. д. ηt и среднее индикаторное давление Pi .
Решение
Для решения задачи заполним поля таблицы в соответствии с заданием (см. табл. 1).
Таблица 1
| Процесс | Начало | Конец | Р | V | T | ∆u | ∆s | ∆i | l | q |
| T | 1 | 0,3 | 313 | |||||||
| 2 | ||||||||||
| S | 2 | |||||||||
| 3 | 523 | |||||||||
| V | 3 | |||||||||
| 4 | 0,6 | |||||||||
| S | 4 | |||||||||
| 1 |
Далее, используя закономерности изменения параметров в процессах, продолжим заполнять графы таблицы (см. табл. 2).
Таблица 2
| Процесс | Начало | Конец | Р | V | T | ∆u | ∆s | ∆i | l | q |
| T | 1 | 0,3 | 0,30 | 313 | ||||||
| 2 | 0,15 | 0,70 | 313 | |||||||
| S | 2 | |||||||||
| 3 | 0,83 | 0,18 | 523 | |||||||
| V | 3 | |||||||||
| 4 | 0,6 | 0,18 | 376 | |||||||
| S | 4 | |||||||||
| 1 | 0,3 | 0,30 | 313 |
Подсчитываем Cv – теплоёмкость при постоянном объёме.
Она численно равна ![]()
Следующим шагом будет последовательное рассмотрение заданных участков цикла.
1. 1 – 2: T = const; T1 = T2 = 313 K
т. к.![]()
то ![]()
![]()
2. 4 – 1:
![]() , где
, где ![]() – показатель адиабаты.
– показатель адиабаты.
Для адиабатного процесса характерно следующее уравнение:
![]()
В данном случае мы можем записать:
Выразив отсюда ![]() , получим
, получим ![]()

Также мы можем посчитать величину ![]() , которая составит:
, которая составит:
![]()
3. 3 – 4:
![]() , для изохорного процесса справедливо отношение:
, для изохорного процесса справедливо отношение: ![]()
Отсюда можно выразить величину давления
![]()
4. 2 – 3:
![]() , где
, где ![]() – показатель адиабаты.
– показатель адиабаты.
Связь между параметрами дается выражениями ![]()
Выражая отсюда ![]() , получим
, получим

В данном случае мы можем записать:
![]()
Выразив отсюда ![]() , получим
, получим 
5. Находим изменение удельной энтропии в заданных процессах:

Изменение энтропии находится по формуле ![]() , где
, где

Так как процесс 2–3 адиабатный, происходит без теплообмена с окружающей средой, то справедливо записать ![]() , т.е.
, т.е. ![]() = 0,069
= 0,069 ![]()
Изменение энтропии находится по формуле ![]() ,
,
где ![]() ,
,
т.е. ![]()
Для проверки сравним ![]() . Они должны быть равны, т. к. процесс 4 – 1 – адиабатный. Что мы и видим.
. Они должны быть равны, т. к. процесс 4 – 1 – адиабатный. Что мы и видим.
6. Следующим этапом следует вычислить работу изменения удельного объёма газа, а также изменение его внутренней энергии, энтальпии и теплоты.
1–2:
![]()
![]()
![]()
![]()
2–3:
![]() ,
, ![]()
Вся работа идёт на изменение внутренней энергии.
![]()
![]()
![]()
![]()
3-4
![]()
Работа по изменению объёма не производится
![]()
![]()
![]()
![]()
4–1
![]() ,
, ![]()
Вся работа идёт на изменение внутренней энергии.
![]()
![]()
![]()
![]()
Теперь можно заполнить оставшиеся графы таблицы (см. табл. 3).
Таблица 3
| Процесс | Начало | Конец | Р | V | T | ∆u | ∆s | ∆i | l | q |
| T | 1 | 0,3 | 0,30 | 313 | 0 | 0,244 | 0 | 76,4 | 76,4 | |
| 2 | 0,15 | 0,70 | 313 | |||||||
| S | 2 | – 73 | 0 | 215,25 | – 73 | 0 | ||||
| 3 | 0,83 | 0,18 | 523 | |||||||
| V | 3 | -108,5 | -0,244 | -150,7 | 0 | -108,5 | ||||
| 4 | 0,6 | 0,18 | 376 | |||||||
| S | 4 | 46,5 | 0 | -64,5 | 46,5 | 0 | ||||
| 1 | 0,3 | 0,30 | 313 |
7. Рассчитываем подведённое в цикле количество теплоты. В данном случае подведённое тепло
![]()
Отведённое количество теплоты равно
![]()
Судя по характерам подвода и отвода тепла, делаем вывод о том, что заданный цикл является холодильным циклом.
Рассчитаем холодильный коэффициент цикла:
![]()
Где работа в цикле определится
l
ц
=![]()
Строим диаграммы с циклом в координатах P-V и T-S (см. рис. 1 и 2).
Для проверки точности построения T-S диаграммы и точности определения холодильного коэффициента цикла, можно воспользоваться графическим методом подсчёта холодильного коэффициента, который основывается на расчётах соответствующих площадей.
Для нахождения холодильного коэффициента графическим методом для заданного цикла, можно воспользоваться следующей формулой:
![]() ,
,
где S1 и S2 площади, соответствующие площади цикла и площади под циклом в мм2 (см. рис. 2).
T – S: S2 = 476478,45 мм2 P – V: S2 = 15,3175 мм2
S1 = 142232,37 мм2 S1 = 4,61 мм2
![]()
![]()
Дано
t1
= 950˚C температура газов ![]() = 2,1·10-
³м, толщина слоя сажи
= 2,1·10-
³м, толщина слоя сажи
t2
= 190˚C температура воды ![]() = 9·10-
³м, толщина стенки из металла
= 9·10-
³м, толщина стенки из металла
![]() = 5·10-
³ м, толщина слоя накипи
= 5·10-
³ м, толщина слоя накипи
![]() = 1,2·10-
³ м, толщина слоя масла
= 1,2·10-
³ м, толщина слоя масла
Коэффициенты теплоотдачи:
![]() = 60 Вт/(м2
*К)
= 60 Вт/(м2
*К)
![]() = 3000 Вт/(м2
*К)
= 3000 Вт/(м2
*К)
Коэффициенты теплопроводности:
![]() = 0,2 Вт/м*К – для сажи;
= 0,2 Вт/м*К – для сажи;
![]() = 50 Вт/м*К – для стенки;
= 50 Вт/м*К – для стенки;
![]() = 2 Вт/м*К – для накипи;
= 2 Вт/м*К – для накипи;
![]() = 0,1 Вт/м*К – для масла
= 0,1 Вт/м*К – для масла
Рассчитать теплообмен от нагретых газов к воде через многослойную стенку, состоящую из слоёв сажи, накипи, металла и масла с заданными геометрическими размерами, а также коэффициентами теплопроводности и теплоотдачи со стороны газа и со стороны воды.
Решение
1. Подсчитаем ![]() - коэффициента теплопередачи для многослойной
- коэффициента теплопередачи для многослойной
плоской стенки, разделяющей жидкости с различными температурами.
Для данного коэффициента справедливо выражение:
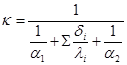
которое для данного вида теплообмена запишется:

тогда можно рассчитать коэффициент теплопередачи:

2. Определим интенсивность теплового потока, которая для всех слоев одинакова:
![]()
Подставив в данное выражение значение температур и коэффициента теплопередачи, получим:
![]()
![]()
3. Выразим баланс тепла для перехода от газов к 1-му слою:

Тогда температура на поверхности первого слоя со стороны теплоотдающей среды будет вычисляться по формуле:

Подставляя численные значения, получим:

Аналогично эти зависимости на границе между первым и вторым слоем выразятся:
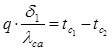 , откуда
, откуда 
Что позволяет получить:

Температура на границе второго и третьего слоя, будет вычисляться по формулам:
 , откуда
, откуда 

Запишем баланс тепла на границе третьего и четвертого слоя:
 , откуда
, откуда 
Таким образом 
Для поверхности последнего слоя баланс тепла выразится:
 , откуда
, откуда 
Что позволяет найти температуру на поверхности последнего слоя, соприкасающегося с тепловоспринимающей средой:

Для проверки запишем баланс тепла на поверхности последнего слоя:
 , откуда
, откуда 
Что позволяет получить:
