| Скачать .docx |
Реферат: Трансформаторы 4
Глава 2. Трансформаторы
2-1. Общие определения
Трансформатор представляет собой статический электромагнитный аппарат с двумя (или больше) обмотками, имеющими между собой магнитную связь, осуществляемую переменным магнитным полем, и служит для преобразования переменного тока одного напряжения в переменный ток другого напряжения при сохранении частоты тока неизменной.
Для усиления магнитной связи между обмотками они помещаются на стальном сердечнике (рис. 2-1). Трансформаторы, не имеющие стального сердечника, называются воздушными. Они применяются в специальных случаях при преобразовании переменных токов высокой частоты (от 10000— 20000 Гц и выше). Мы будем рассматривать трансформаторы со стальным сердечником.
Рис. 2-1. Двухобмоточный трансформатор.
Г
— генератор переменного тока.
Трансформатор имеет не меньше двух обмоток; из них первичной обмоткой 1 называется обмотка, которая получает энергию преобразуемого переменного тока, вторичными обмотками 2 — обмотки, которые отдают энергию преобразованного переменного тока.
Трансформаторы применяются в основном для преобразования однофазного и трехфазного тока. В соответствии с этим различают однофазные и трехфазные трансформаторы.
Впервые трансформаторы получили техническое применение в схемах со свечами Яблочкова. П. Н. Яблочков разработал конструкцию однофазного трансформатора с разомкнутым сердечником и при своих опытах, а также при эксплуатации своих осветительных установок выявил основные его свойства.
Техническое применение для передачи электрической энергии на дальние расстояния трансформаторы начинают получать в конце 80-х годов прошлого столетия.
В системе электропередачи трансформаторы являются необходимыми элементами. Передача большой мощности на дальние расстояния практически может быть осуществлена только при относительно небольшом значении тока и, следовательно, при высоком напряжении.
В начале линии электропередачи устанавливаются трансформаторы, повышающие напряжение переменного тока, вырабатываемого на электрических станциях. Напряжение в начале линии электропередачи берут тем выше, чем больше длина линии и передаваемая мощность. Оно достигает 220—250 кВ при расстоянии 200— 400 км и при мощности 300— 200 тыс кВт. При расстоянии около 1000 км и мощности порядка 1 млн кВт (например, для электропередачи Куйбышев — Москва и Волгоград — Москва) требуется напряжение 400—500 кВ.
В конце линии электропередачи, устанавливаются понижающие напряжение трансформаторы, так как для распределения энергии по заводам, фабрикам, жилым домам и колхозам необходимы сравнительно низкие напряжения.
Впервые трехфазная линия электропередачи высокого напряжения (15000 В; из Лауфена на Неккаре до Франкфурта-на-Майне, протяженность около 175 км), положившая начало широким работам по электрификации, была построена при ближайшем участии русского инженера М.О. Доливо-Добровольского. Им же были разработаны конструкции трехфазных трансформаторов, основные черты которых сохранились до настоящего времени.
В настоящее время трансформаторы находят себе самое широкое применение. Существует очень много разнообразных типов их, различающихся как по назначению, так и по выполнению.
Прежде всего нужно выделить группу силовых трансформаторов, которым будет уделено основное внимание в последующем изложении. Это те трансформаторы, которые устанавливаются в начале и конце линий электропередачи, на заводах и фабриках, в жилых домах, при электрификации сельского хозяйства. Такие трансформаторы строятся на мощности от нескольких до десятков тысяч киловольт-ампер.
Переменный ток по пути от электрической станции, где он создается, до потребителя обычно приходится трансформировать 3—4 раза. Отсюда следует, что мощность силовых трансформаторов, необходимых для передачи и распределения электроэнергии, в 3—4 раза больше мощности установленных на электрических станциях генераторов.
Каждый трансформатор снабжается щитком, прикрепленным на видном месте, с указанными на нем номинальными величинами. Последние характеризуют режим работы, для которого трансформатор предназначен. На щитке трансформатора указываются следующие номинальные величины:
1. кажущаяся мощность, ВА или кВА;
2. линейные напряжения, В или кВ;
3. линейные токи, А, при номинальной мощности;
4. частота, Гц;
5. число фаз;
6. схема и группа соединений (§ 2-12);
7. напряжение короткого замыкания (§ 2-7);
8. режим работы (длительный или кратковременный);
9. способ охлаждения.
Кроме того, на щитке трансформатора приводятся дополнительные данные, необходимые при установке и эксплуатации трансформатора:
10. полный вес трансформатора;
11. вес масла;
12. вес выемной (внутренней, опущенной в масло) части трансформатора.
2-2. Основные элементы устройства
Основными частями трансформатора являются его сердечник и обмотки. Сердечник для уменьшения потерь от вихревых токов собирается из листов специальной электротехнической стали с относительным содержанием кремния до 4—5%. Толщина стали берется 0,5 или 0,35 мм (еще более тонкие листы применяются при повышенной частоте тока). Листы перед сборкой сердечника покрываются с обеих сторон лаком, что дает более прочную и тонкую изоляцию между листами, чем бумага, которой иногда оклеиваются листы до нарезки их на полосы.
Сердечник состоит из стержней, на которых помещаются обмотки, и ярм, которые замыкают стержни и не имеют обмоток. Сборка листов (полос) сердечника производится, как правило, "внахлестку". Таким путем удается свести до весьма малого значения магнитные сопротивления стыков между стержнями и ярмами.
На рис. 2-2 показаны отдельные слои листов, из которых состоит сердечник однофазного трансформатора, а на рис. 2-3 — два слоя листов сердечника трехфазного трансформатора.
Рис. 2-2. Листы сердечника однофазного трансформатора при сборке их «внахлестку».
Рис. 2-3. Листы сердечника трехфазного трансформатора при сборке их «внахлестку».
Листы сердечника стягиваются при помощи накладок и шпилек, изолированных от листов (рис. 2-4). Листы верхнего ярма окончательно закладываются и затем стягиваются, после того как помещены обмотки на стержнях сердечника (рис. 2-5).
Рис. 2-4 Изоляция шпильки, стягивающей листы сердечника.
Рис. 2-5. Сборка сердечника трехфазного трансформатора.
Различные формы сечения стержня и ярма представлены на рис. 2-6 и 2-7. Сечение по рис. 2-6,а применяется лишь для небольших трансформаторов; сечения по рис 2-6,б и в применяются для трансформаторов средней и большой мощности. При большом числе ступеней сечения его периметр приближается к окружности, и, следовательно, при том же сечении стержня уменьшается средняя длина витка обмоток, а при этом и количество расходуемой обмоточной меди.
Рис. 2-6. Форма сечения стержней.
Рис. 2-7. Формы сечения ярма.
По выполнению сердечника принято различать два типа трансформаторов: стержневой и броневой. Стержневой тип трансформатора (рис. 2-5) получил преобладающее применение на практике. Однофазный броневой трансформатор показан на рис. 2-8. Из броневых трансформаторов в Советском Союзе получили некоторое распространение однофазные броневые трансформаторы малой мощности: радиотехнические, звонковые и др.
Рис. 2-8. Однофазный броневой трансформатор с дисковыми чередующимися обмотками.
Обмотки трансформаторов выполняются в виде цилиндрических катушек из проводников круглого или прямоугольного сечения, изолированных хлопчатобумажной пряжей или специальной (кабельной) бумагой.
В зависимости от номинального напряжения следует различать обмотку низшего напряжения и обмотку высшего напряжения Обмотка низшего напряжения (НН) помещается ближе к стержню, а обмотка высшего напряжения (ВН) — снаружи; она охватывает обмотку низшего напряжения (рис. 2-9). При таком расположении обмоток уменьшается расход изоляционных материалов, так как обмотка высшего напряжения относительно стержня будет иметь собственную изоляцию и изоляцию обмотки низшего напряжения. Обмотки, показанные на рис. 2-9, называются концентрическими.
Рис. 2-9. Однофазный стержневой трансформатор с концентрическими обмотками.
Иногда каждую из обмоток разделяют на отдельные катушки и располагают их на стержне в чередующемся порядке, как показано на рис. 2-10. Такие обмотки называются дисковыми чередующимися. Они на практике встречаются редко и применяются главным образом для броневых трансформаторов (рис. 2-8).
Рис.2.10. Дисковая чередующаяся обмотка.
Трансформаторы выполняются с воздушным и масляным охлаждением. Первые называются сухими, вторые — масляными. В масляных трансформаторах сердечник вместе с обмотками помещается в баке с маслом. Масляные трансформаторы более надежны в работе. Масло предохраняет изоляцию обмоток от вредного воздействия воздуха, улучшает условия охлаждения обмоток и сердечника, так как имеет большую теплопроводность, чем воздух; кроме того, вследствие большой диэлектрической прочности позволяет сократить изоляционные расстояния, т. е. расстояния от меди обмоток до стали сердечника.
2-3. Холостой ход трансформатора
Под холостым ходом трансформатора понимается режим его работы при разомкнутой вторичной обмотке. В этих условиях трансформатор со стороны первичной обмотки во всем подобен катушке со стальным сердечником.
Обратимся к рис. 2-11, где схематически изображен однофазный трансформатор. Здесь первичная обмотка с числом витков w 1 и вторичная обмотка с числом витков w 2 расположены для наглядности на разных стержнях.
Рис. 2-11. Холостой ход трансформатора.
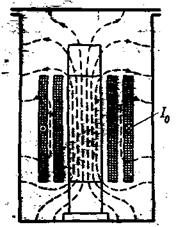
Пусть к первичной обмотке при разомкнутой вторичной подведено напряжение и 1 . По первичной обмотке будет протекать ток i 0 . В трансформаторе возникнет магнитное поле, которое будет создаваться намагничивающей силой (н.с.) i 0 w 1 первичной обмотки. Магнитным полем вне сердечника можем вначале пренебречь, так как магнитная проницаемость стали во много раз больше магнитной проницаемости воздуха (или масла).
Полю в сердечнике соответствует магнитный поток Ф, сцепляющийся со всеми витками обеих обмоток. Он будет наводить в первичной обмотке э.д.с.
и вторичной обмотке э.д.с.
Напряжение на зажимах первичной обмотки
![]()
Активное падение напряжения ![]() в первичной обмотке имеет практически ничтожное значение. Поэтому можно считать, что первичное напряжение
в первичной обмотке имеет практически ничтожное значение. Поэтому можно считать, что первичное напряжение ![]() в любой момент времени уравновешивается только э.д.с.
в любой момент времени уравновешивается только э.д.с.![]() . Если напряжение
. Если напряжение ![]() представляет собой синусоидальную функцию времени, то, следовательно, э.д.с.
представляет собой синусоидальную функцию времени, то, следовательно, э.д.с. ![]() и наводящий её поток Ф — также синусоидальные функции времени. Подставив в (2-1) и (2-2) Ф = Фм
sin ωt
, где Фм
—амплитуда потока, ω = 2πf
— угловая частота тока, t
— время, c, получим:
и наводящий её поток Ф — также синусоидальные функции времени. Подставив в (2-1) и (2-2) Ф = Фм
sin ωt
, где Фм
—амплитуда потока, ω = 2πf
— угловая частота тока, t
— время, c, получим:
Полученные уравнения показывают, что ![]() и
и ![]() отстают по фазе от потока Ф
отстают по фазе от потока Ф
на угол ![]() . Действующие значения обеих э.д.с. соответственно равны:
. Действующие значения обеих э.д.с. соответственно равны:
где Фм — в В∙с.
Из (2-5) и (2-6) следует:
Так как при холостом ходе ![]() и
и ![]() , то можем написать:
, то можем написать:
Отношение напряжений при холостом ходе трансформатора называется коэффициентом трансформации. Обычно берется отношение высшего напряжения к низшему. Если при холостом ходе трансформатора к его первичной обмотке подведено номинальное напряжение U 1н , указанное на щитке трансформатора, то на зажимах вторичной обмотки должно получиться вторичное номинальное напряжение U 20 = U 2н .
Вследствие перемагничивания стали сердечника в нем возникают магнитные потери, т. е. потери от гистерезиса и вихревых токов. Можно считать, что мощность P
0
, потребляемая трансформатором при холостом ходе и напряжении U
1
= U
1н
, идет только на покрытие магнитных потерь Р
с
, так как при этом электрические потери ![]() практически ничтожны. Следовательно, ток холостого хода I
0
наряду с реактивной составляющей I
0
p
имеет активную составляющую I
0а
, т. е.
практически ничтожны. Следовательно, ток холостого хода I
0
наряду с реактивной составляющей I
0
p
имеет активную составляющую I
0а
, т. е.
Реактивная составляющая I 0 р , которую называют также намагничивающим током, идет на создание магнитного поля в сердечнике трансформатора. Ее значение определяется из расчета магнитной цепи трансформатора (§2-14).
Активная составляющая тока холостого хода I 0 а определяется по формуле
Магнитные потери могут быть рассчитаны по обычным формулам (§ 2-14).
Приложенное к первичной обмотке напряжение ![]() , как отмечалось, уравновешивается в основном э.д.с.
, как отмечалось, уравновешивается в основном э.д.с. ![]() . Поэтому при синусоидальном
. Поэтому при синусоидальном ![]() мы можем написать векторное (комплексное) уравнение
мы можем написать векторное (комплексное) уравнение![]()
Следовательно, векторная диаграмма трансформатора при его холостом ходе будет иметь вид, представленный на рис. 2-12.
Рис. 2-12. Векторная диаграмма трансформатора при холостом ходе.
Она отличается от диаграммы для реактивной катушки со стальным сердечником только наличием вектора вторичной э.д.с. Так же как и для реактивной катушки со стальным сердечником, можно написать:
здесь
![]()
![]()
2-4. Работа при нагрузке
а) Первичный ток.
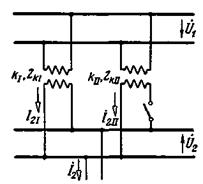
Работа трансформатора при нагрузке характеризуется наличием тока I 2 во вторичной обмотке, увеличение которого (как будет ясно из последующего) вызывает увеличение тока I 1 в первичной обмотке.
При нагрузке трансформатора магнитный поток Ф в его сердечнике, называемый главным потоком, создается согласно закону полного тока совместным действием н.с. обеих обмоток:
где ![]() — мгновенные значения токов, причем в общем случае
— мгновенные значения токов, причем в общем случае ![]() отличается от мгновенного значения тока холостого хода.
отличается от мгновенного значения тока холостого хода.
Так как мы принимаем токи синусоидальными, то можем написать (рис. 2-1):
Результирующая н.с. ![]() должна иметь такое значение, чтобы создаваемый ею поток наводил в первичной обмотке э.д.с. Е\
,
почти полностью уравновешивающую приложенное напряжение U
1
. Поток в сердечнике трансформатора и результирующая н.c.
должна иметь такое значение, чтобы создаваемый ею поток наводил в первичной обмотке э.д.с. Е\
,
почти полностью уравновешивающую приложенное напряжение U
1
. Поток в сердечнике трансформатора и результирующая н.c. ![]() при нагрузке, не превышающей значительно номинальную, мало отличаются от тех же потока и н.с. первичной обмотки при холостом ходе, если в обоих случаях напряжение U
1
сохраняет свое значение.
при нагрузке, не превышающей значительно номинальную, мало отличаются от тех же потока и н.с. первичной обмотки при холостом ходе, если в обоих случаях напряжение U
1
сохраняет свое значение.
Разделив обе части равенства (2-15) на w 1 , получим:
![]() (2-16)
(2-16)
или
где
— вторичный ток, приведенный к числу витков первичной обмотки.
Очевидно, что вторичная обмотка с током ![]() должна иметь число витков w
1
, чтобы ее н.с.
должна иметь число витков w
1
, чтобы ее н.с. ![]() была равна н.с.
была равна н.с. ![]() действительной вторичной обмотки. При этом вместо уравнения н.с. (2-15) можно пользоваться уравнением токов (2-17).
действительной вторичной обмотки. При этом вместо уравнения н.с. (2-15) можно пользоваться уравнением токов (2-17).
Из (2-17) получаем значение первичного тока I1
Мы видим, что первичный ток ![]() имеет две составляющие: одна из них (
имеет две составляющие: одна из них (![]() ) идет на создание потока в сердечнике трансформатора, другая (
) идет на создание потока в сердечнике трансформатора, другая (![]() ) компенсирует размагничивающее действие вторичного тока. Следовательно, при увеличении вторичного тока будет увеличиваться и первичный ток, чтобы поток оставался почти равным потоку при холостом ходе.
) компенсирует размагничивающее действие вторичного тока. Следовательно, при увеличении вторичного тока будет увеличиваться и первичный ток, чтобы поток оставался почти равным потоку при холостом ходе.
Так как ток I 0 имеет относительно небольшое значение, то при токах, близких к номинальным, можно принять
![]()
б) Уравнения напряжений.
Будем вначале считать, что потокосцепления обмоток трансформатора пропорциональны их токам и что магнитные потери в сердечнике отсутствуют (такие условия получаются в воздушном трансформаторе). При этом, так же как для двух магнитно связанных контуров, можем написать следующие уравнения напряжений первичной и вторичной обмоток трансформатора:
где u
1
и u
2
— мгновенные значения первичного и вторичного напряжений;
L
1
, L
2
и М
— полные индуктивности и взаимная индуктивность обмоток;
r
1
и r
2
— их активные сопротивления.
Первичное напряжение u
1
имеет составляющие, уравновешивающие э.д.с. cамоиндукции ![]() и взаимоиндукции
и взаимоиндукции ![]() , и составляющую, равную активному падению напряжения i
1
r
1
. Вторичное напряжение u
2
получается после вычитания из результирующей э.д.с. самоиндукции и взаимоиндукции
, и составляющую, равную активному падению напряжения i
1
r
1
. Вторичное напряжение u
2
получается после вычитания из результирующей э.д.с. самоиндукции и взаимоиндукции ![]() активного падения напряжения i
2
r
2
.
активного падения напряжения i
2
r
2
.
Полагая, так же как и в предыдущем, что в сердечнике трансформатора имеет место главный поток Ф, который создается результирующей н.с. i 0 w 1 мы можем для токов i 1 , и i 2 согласно (2-14) написать следующие равенства:
Подставив (2-23) в (2-20) и (2-22) в (2-21), получим:
или
где ![]() и
и ![]() — индуктивности рассеяния первичной и вторичной обмоток; им соответствуют э.д.с. рассеяния:
— индуктивности рассеяния первичной и вторичной обмоток; им соответствуют э.д.с. рассеяния:
Электродвижущие силы
рассматриваются как э.д.с., наведенные главным потоком Ф.
Приведем здесь уравнения, относящиеся к общей теории двух магнитно связанных обмоток. Для потокосцеплении этих обмоток можем написать:
Вычтем и прибавим с правой стороны написанных равенств одни и те же величины:
![]()
![]()
Здесь коэффициенты ![]() и
и ![]() имеют произвольные значения.
имеют произвольные значения.
Будем называть величины
![]() и
и ![]()
главными потокосцеплениями обмоток, а величины
![]() и
и ![]()
их потокосцеплениями рассеяния.
Главными индуктивностями обмоток назовем величины
![]()
Общий коэффициент рассеяния равен:
Коэффициенты рассеяния обмоток равны отношениям индуктивностей рассеяния к главным индуктивностям:
Между произвольными значениями коэффициентов λ1
и λ2
можно установить простое соотношение. Для этого примем (с физической стороны это легко себе представить), что общий коэффициент рассеяния стремится к нулю (σ → 0), если при этом индуктивности рассеяния стремятся к нулю. Вводя ![]() и
и ![]() в (2-32) и принимая
в (2-32) и принимая ![]() и
и ![]() равными нулю, получим для σ → 0:
равными нулю, получим для σ → 0:
Отсюда имеем: ![]()
Мы видим, следовательно, что, хотя общий коэффициент рассеяния σ определяется однозначно, отдельные коэффициенты рассеяния σ1 и σ2 являются произвольными, так же как λ1 и λ2 .
Подразделяя произведение λ1 λ2 любым образом на λ1 и λ2 можно потокосцепления рассеяния приписать одной или другой обмотке или обеим обмоткам. Мы не имеем также достаточно данных, чтобы однозначно определить главный поток, о котором говорилось ранее. Однако внести определенность в понятия индуктивностей рассеяния мы можем только в том случае, если допустим, что в трансформаторе существует главный поток Ф, созданный н.с. обеих обмоток и сцепляющийся со всеми их витками. Такое допущение, очевидно, в большой степени оправдывается в применении к нормальным трансформаторам со стальным сердечником.
Мы можем теперь написать:
![]()
![]()
Отсюда получаем:
![]()
Так как полученное равенство должно быть справедливо при любых значениях ![]() и
и ![]() , то выражения в скобках по отдельности должны быть равны нулю; следовательно,
, то выражения в скобках по отдельности должны быть равны нулю; следовательно,![]()
![]() и
и ![]() что мы и получили ранее в дифференциальных уравнениях, допустив, что в трансформаторе существует главный поток Ф, созданный результирующей н.с.
что мы и получили ранее в дифференциальных уравнениях, допустив, что в трансформаторе существует главный поток Ф, созданный результирующей н.с. ![]()
Теория электрических машин также основана, как мы покажем в дальнейшем, на допущении существования главного потока, не зависящего от полей рассеяния.
Считая, что токи и э.д.с. уравнений (2-26)—(2-29) изменяются во времени по закону синуса, мы можем эти уравнения переписать в комплексной форме:
![]()
![]()
![]()
В равенствах (2-35) ![]() и
и ![]() — индуктивные сопротивления рассеяния обмоток, а
— индуктивные сопротивления рассеяния обмоток, а ![]() — индуктивное сопротивление взаимоиндукции обмоток.
— индуктивное сопротивление взаимоиндукции обмоток.
Ранее при рассмотрении режима холостого хода мы пренебрегали полем вне сердечника трансформатора. В действительности это поле согласно закону полного тока должно существовать. Оно называется полем рассеяния. Созданные им потокосцепления обмоток малы по сравнению с потокосцеплениями обмоток, созданными главным потоком. С большим приближением к действительным условиям можно считать, что поле рассеяния и поле в сердечнике, соответствующее главному потоку, существуют независимо одно от другого.
На рис. 2-13 представлена приближенная картина поля рассеяния, которую кладут в основу расчета потокосцеплений рассеяния. Здесь пунктирной линией показан путь главного потока Ф, сплошными линиями показаны индукционные линии поля рассеяния. Они могут быть условно разделены на две группы: сцепляющиеся с первичной обмоткой и сцепляющиеся со вторичной обмоткой. Магнитные сопротивления для потоков соответствующих индукционных трубок рассеяния определяются в основном сопротивлениями тех их частей, которые проходят вдоль обмоток и в промежутке между ними Их можно принять постоянными, поскольку потоки трубок проходят по материалам (медь, изоляция, воздух или масло), для которых μ = const. Магнитными сопротивлениями потоков трубок вне обмоток и промежутка между ними можно пренебречь, так как здесь они проходят в основном по стали сердечника.
Рис. 2-13. Приближенная картина поля рассеяния трансформатора с концентрическими обмотками, где крестиками и точками условно показаны направления токов в обмотках для рассматриваемого момента времени.
Таким образом, потокосцепления рассеяния и созданные ими э.д.с. рассеяния можно принять пропорциональными н.с. или токам соответствующих обмоток и считать индуктивности L
σ1
и L
σ2
, а следовательно ![]() и
и ![]() , постоянными величинами. Индуктивное сопротивление взаимоиндукции
, постоянными величинами. Индуктивное сопротивление взаимоиндукции ![]() зависит от Ф, однако в пределах небольшого изменения Фм
и, следовательно, Е
1
можно принять
зависит от Ф, однако в пределах небольшого изменения Фм
и, следовательно, Е
1
можно принять ![]() также постоянным.
также постоянным.
С учетом приведенных равенств (2-35) уравнения напряжений (2-24а ) и (2-25а ) для установившегося режима могут быть написаны в комплексной форме:
Уравнения (2-36) и (2-37) называются векторными уравнениями напряжений трансформатора (здесь имеются в виду временные векторы напряжений, э.д.с. и токов).
В реальном трансформаторе со стальным сердечником при его работе возникают магнитные потери. Для их учета мы должны считать, так же как при холостом ходе, что ток ![]() имеет наряду с реактивной составляющей
имеет наряду с реактивной составляющей ![]() активную составляющую
активную составляющую ![]() [см. уравнения (2-9) — (2-13)]; однако обе эти составляющие мы должны отнести не к
[см. уравнения (2-9) — (2-13)]; однако обе эти составляющие мы должны отнести не к ![]() а к
а к ![]() , так как они зависят от Фм
.
, так как они зависят от Фм
.
Вследствие нелинейной связи между потоком Ф и результирующим током ![]() кривая последнего при синусоидальном потоке Ф будет несинусоидальной (§ 2-13). Для облегчения анализа зависимостей, характеризующих работу трансформатора, ток
кривая последнего при синусоидальном потоке Ф будет несинусоидальной (§ 2-13). Для облегчения анализа зависимостей, характеризующих работу трансформатора, ток ![]() принимается синусоидальным с действующим значением, равным тому же значению действительного тока. Такое допущение не может привести к заметной ошибке из-за относительной малости тока
принимается синусоидальным с действующим значением, равным тому же значению действительного тока. Такое допущение не может привести к заметной ошибке из-за относительной малости тока ![]() .
.
в) Приведение величин вторичной обмотки к числу витков первичной обмотки.
Указанное приведение получим, если помножим уравнение (2-37) на отношение чисел витков ![]()
![]()
соответственно будем иметь
где
![]() ;
; ![]() [согласно (2-8)];
[согласно (2-8)];
![]()

представляют собой величины вторичной обмотки, приведенные к числу витков первичной обмотки. Такое приведение величин вторичной обмотки облегчает исследование работы трансформатора: делает более удобным построение для него векторных диаграмм (§ 2-4,г ), позволяет построить удобную для расчетов схему соединения его активных и индуктивных сопротивлений, называемую схемой замещения трансформатора, где магнитная связь между обмотками заменена электрической связью между ними (§ 2-5).
Можно считать, что приведение величин вторичной обмотки к числу витков первичной обмотки сводится к замене действительной обмотки с числом витков ![]() обмоткой с числом витков
обмоткой с числом витков ![]() , причем при такой замене н.с.
, причем при такой замене н.с. ![]() должна остаться, как отмечалось, неизменной и равной
должна остаться, как отмечалось, неизменной и равной ![]() , а также должны остаться неизменными относительные значения падений напряжения и электрические потери в обмотке:
, а также должны остаться неизменными относительные значения падений напряжения и электрические потери в обмотке:
![]()
![]()
![]()
![]()
Из этих равенств, учитывая, что ![]() и
и ![]() , мы можем также найти соотношения между приведенными и действительными величинами вторичной обмотки. Они получаются такими же, как и (2-39).
, мы можем также найти соотношения между приведенными и действительными величинами вторичной обмотки. Они получаются такими же, как и (2-39).
г) Векторные диаграммы.
Векторные диаграммы наглядно показывают соотношения между токами, э.д.с. и напряжениями обмоток. Они строятся в соответствии с уравнениями (2-19), (2-36) и (2-38).
На рис. 2-14 — 2-16 представлены диаграммы трансформатора, работающего с различными нагрузками.
Рис. 2-14. Векторная диаграмма трансформатора работающего с отстающим током.
Рис. 2-15. Векторная диаграмма трансформатора, работающего с ![]() 1.
1.
Рис. 2-16. Векторная диаграмма трансформатора, работающего с опережающим током.
Векторная диаграмма трансформатора, работающего, например, с отстающим током (рис. 2-14), при заданных ![]()
![]()
![]() может быть построена следующим образом.
может быть построена следующим образом.
Зная ![]() найдем
найдем ![]() и
и ![]() . Построим в выбранном масштабе для токов и напряжений векторы
. Построим в выбранном масштабе для токов и напряжений векторы ![]() и
и ![]() так, чтобы они были сдвинуты на угол
так, чтобы они были сдвинуты на угол ![]() Прибавляя к
Прибавляя к ![]() векторы падений напряжения
векторы падений напряжения ![]() и
и ![]() найдем э.д.с.
найдем э.д.с. ![]() (мы предполагаем, что сопротивления
(мы предполагаем, что сопротивления ![]() и
и ![]() , а также
, а также ![]() и
и ![]() известны). Вектор потока
известны). Вектор потока ![]() опережает э.д.с.
опережает э.д.с. ![]() на 90°. Ток
на 90°. Ток ![]() опережает поток на угол
опережает поток на угол ![]() . Вторая составляющая
. Вторая составляющая ![]() первичного тока
первичного тока ![]() равна и противоположна по фазе вторичному току
равна и противоположна по фазе вторичному току ![]() следовательно, вектор первичного тока определяется геометрическим сложением:
следовательно, вектор первичного тока определяется геометрическим сложением: ![]() . Первичное напряжение
. Первичное напряжение ![]() , имеет составляющую
, имеет составляющую ![]() , уравновешивающую э.д.с.
, уравновешивающую э.д.с. ![]() , и составляющие
, и составляющие ![]() и
и ![]() равные соответственно активному и индуктивному падениям напряжения в первичной обмотке (
равные соответственно активному и индуктивному падениям напряжения в первичной обмотке (![]() совпадает по фазе с током
совпадает по фазе с током ![]()
![]() опережает ток
опережает ток ![]() на 90°).
на 90°).
Обратная задача, с которой обычно приходится иметь дело на практике, когда заданы ![]()
![]() и cos φ2
и требуется найти
и cos φ2
и требуется найти ![]() решается в большинстве случаев аналитически, как показано в § 2-8.
решается в большинстве случаев аналитически, как показано в § 2-8.
Диаграммы на рис. 2-14 и 2-15 показывают, что напряжение ![]() при нагрузке меньше, чем напряжение
при нагрузке меньше, чем напряжение ![]() при холостом ходе, и тем меньше, чем больше сопротивления обмоток r
1
, x
1
, r
2
, и угол φ2
.
при холостом ходе, и тем меньше, чем больше сопротивления обмоток r
1
, x
1
, r
2
, и угол φ2
.
Значение тока ![]() зависит от значения э.д.с.
зависит от значения э.д.с. ![]() ; следовательно, оно изменяется с изменением тока нагрузки, если
; следовательно, оно изменяется с изменением тока нагрузки, если ![]() = const. Однако это изменение невелико, и при практических расчетах можно принять Фм
=const и
= const. Однако это изменение невелико, и при практических расчетах можно принять Фм
=const и ![]() =const.
=const.
Диаграмма на рис. 2-16 показывает, что при работе трансформатора с опережающим током напряжение ![]() на его зажимах может быть выше, чем при холостом ходе, так как в этом случае э.д.с.
на его зажимах может быть выше, чем при холостом ходе, так как в этом случае э.д.с. ![]() возрастает и, кроме того, результирующая э.д.с.
возрастает и, кроме того, результирующая э.д.с. ![]() +
+![]() больше, чем
больше, чем ![]() (
(![]() ― э.д.с. рассеяния вторичной обмотки, приведенная к числу витков первичной обмотки).
― э.д.с. рассеяния вторичной обмотки, приведенная к числу витков первичной обмотки).
Приведенные ранее уравнения напряжений и токов, а также векторные диаграммы относятся к однофазному трансформатору или к одной фазе трехфазного трансформатора. Различие токов холостого хода отдельных фаз трехфазного трансформатора вследствие несимметрии их магнитных цепей не имеет практического значения, так как токи холостого хода составляют обычно небольшую долю номинального тока; параметры же отдельных фаз r
1
, ![]() , x
1
,
, x
1
, ![]() можно считать одинаковыми.
можно считать одинаковыми.
2-5. Схема замещения
Расчеты, связанные с исследованием работы трансформатора, можно свести к расчетам простых цепей переменного тока. Для этого заменим трансформатор некоторой схемой, сопротивление которой Z экв определим; из уравнений напряжений (2-36) и (2-38) и уравнения токов (2-17). Перепишем эти уравнения в следующем виде:
где![]() [см. уравнение (2-12)];
[см. уравнение (2-12)]; ![]()
![]()
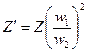 ― приведенное к числу витков первичной обмотки сопротивление внешней вторичной цепи, падение напряжения
― приведенное к числу витков первичной обмотки сопротивление внешней вторичной цепи, падение напряжения ![]() в котором, очевидно, и есть
в котором, очевидно, и есть ![]() .
.
Подставив в (2-41) значение тока ![]() из (2-42), найдем:
из (2-42), найдем:
![]()
Подставив в (2-40) найденное значение ![]() , получим:
, получим:
Сопротивлению Z
экв
соответствует схема, представленная на рис. 2-17. Она называется схемой замещения трансформатора. Здесь ветвь с сопротивлением ![]() может быть названа ветвью намагничивания. Очевидно, что уравнения напряжений и токов, составленные согласно законам Кирхгофа для этой схемы, будут такими же, как и уравнения (2-40) — (2-42).
может быть названа ветвью намагничивания. Очевидно, что уравнения напряжений и токов, составленные согласно законам Кирхгофа для этой схемы, будут такими же, как и уравнения (2-40) — (2-42).
Рис. 2-17. Схема замещения трансформатора.
В схеме замещения переменным параметром является сопротивление ![]() ; остальные ее параметры можно считать постоянными. Они могут быть определены путем расчета, а также опытным путем. В последнем случае обращаются к данным опытов холостого хода и короткого замыкания.
; остальные ее параметры можно считать постоянными. Они могут быть определены путем расчета, а также опытным путем. В последнем случае обращаются к данным опытов холостого хода и короткого замыкания.
2-6. Опыт холостого хода
По данным опыта холостого хода определяются коэффициент трансформации ![]() , магнитные потери Р
с
и параметры ветви намагничивания
, магнитные потери Р
с
и параметры ветви намагничивания ![]() Магнитные потери Р
с
, как указывалось, могут быть приняты равными мощности Р
0
, потребляемой трансформатором при холостом ходе.
Магнитные потери Р
с
, как указывалось, могут быть приняты равными мощности Р
0
, потребляемой трансформатором при холостом ходе.
При опыте холостого хода собирается схема по рис. 2-18 для однофазного трансформатора или по рис. 2-19 для трехфазного трансформатора. При номинальном напряжении ![]() (линейном в случае трехфазного трансформатора) измеряют
(линейном в случае трехфазного трансформатора) измеряют ![]()
![]() и
и ![]() Опыт холостого хода должен производиться при синусоидальном напряжении. Если напряжение заметно отличается от синусоидального, то в данные измерений необходимо внести некоторые поправки (согласно ГОСТ). При исследовании малых трансформаторов следует учитывать потери в приборах, так как они могут быть соизмеримы с потерями холостого хода.
Опыт холостого хода должен производиться при синусоидальном напряжении. Если напряжение заметно отличается от синусоидального, то в данные измерений необходимо внести некоторые поправки (согласно ГОСТ). При исследовании малых трансформаторов следует учитывать потери в приборах, так как они могут быть соизмеримы с потерями холостого хода.
Рис. 2-18 Схема при опыте холостого хода для однофазного трансформатора.
Рис. 2-19. Схема при опыте холостого хода для трехфазного трансформатора.
Измерения U
1
и U
20
производятся при помощи вольтметров или при высоком напряжении, при помощи вольтметров и измерительных трансформаторов напряжения. По данным измерений находят коэффициент трансформации: U
20
/U
1
![]()
![]() По амперметру и ваттметру находят ток
По амперметру и ваттметру находят ток ![]() и мощность P
0
в случае однофазного трансформатора. В случае трехфазного трансформатора необходимо измерить токи во всех трех фазах, так как вследствие несимметрии магнитных цепей отдельных фаз токи в них будут различны. За ток холостого хода здесь принимается среднее арифметическое токов отдельных фаз, т. е.
и мощность P
0
в случае однофазного трансформатора. В случае трехфазного трансформатора необходимо измерить токи во всех трех фазах, так как вследствие несимметрии магнитных цепей отдельных фаз токи в них будут различны. За ток холостого хода здесь принимается среднее арифметическое токов отдельных фаз, т. е.
Мощности отдельных фаз также различны; поэтому мощность, потребляемую трехфазным трансформатором при холостом ходе, следует измерять двумя ваттметрами по схеме рис. 2-19.
Для нормальных силовых трансформаторов ток холостого хода составляет (0,10—0,04) I Н при номинальных мощностях от 5 до нескольких тысяч киловольт-Ампер.
Холостому ходу будет соответствовать схема замещения рис. 2-17 при ![]() =∞. Следовательно, по данным опыта холостого хода получаем:
=∞. Следовательно, по данным опыта холостого хода получаем:
![]()
Так как для нормальных трансформаторов r 12 больше r 1 и x 12 больше х 1 в сотни раз, то можно принять:
![]()
![]()
![]()
2-7. Опыт короткого замыкания
По данным опыта короткого замыкания определяются потери короткого замыкания Р к , которые могут быть приняты равными электрическим потерям в обмотках, и параметры трансформатора, к которым приходится обращаться при решении многих практических задач.
Под коротким замыканием трансформатора здесь понимается такой режим его работы, при котором вторичная обмотка замкнута накоротко, а к первичной обмотке подведено напряжение. Этому режиму работы соответствует схема замещения (рис. 2-17) при ![]() =0.
=0.
Так как сопротивления z
1
и ![]() в сотни раз меньше сопротивления z
12
, то при коротком замыкании трансформатора можно пренебречь током в этом сопротивлении, т. е. принять
в сотни раз меньше сопротивления z
12
, то при коротком замыкании трансформатора можно пренебречь током в этом сопротивлении, т. е. принять ![]() . В этом случае получаем схему замещения, представленную на рис. 2-20.
. В этом случае получаем схему замещения, представленную на рис. 2-20.
Рис. 2-20. Схема замещения короткозамкнутого трансформатора.
Векторная диаграмма короткозамкнутого трансформатора приведена на рис. 2-21.
Рис. 2-21. Векторная диаграмма короткозамкнутого трансформатора.
От этой диаграммы мы можем перейти к диаграмме, представленной на рис. 2-22.
Рис. 2-22. Треугольник короткого замыкания.
Прямоугольный треугольник ОАВ называется треугольником короткого замыкания трансформатора. Один его катет ![]() другой катет
другой катет ![]() и гипотенуза
и гипотенуза ![]()
Сопротивления
![]()
![]()
![]()
называются соответственно активным, индуктивным и полным сопротивлениями короткого замыкания трансформатора. Параметры короткого замыкания z
к
, r
к
и x
к
определяются по данным опыта короткого замыкания. При этом опыте собирается одна из схем, приведенных на рис. 2-18 и 2-19, но вторичные зажимы замыкаются накоротко. Измеряют U
1к
, I
1
, P
к
. Напряжение U
1к
устанавливают такое, чтобы ток ![]() был приблизительно равен номинальному току
был приблизительно равен номинальному току ![]() Оно для нормальных трансформаторов мощностью от 20 до 10000 кВА составляет от 5 до 10% номинального напряжения
Оно для нормальных трансформаторов мощностью от 20 до 10000 кВА составляет от 5 до 10% номинального напряжения ![]() В соответствии с указанными значениями
В соответствии с указанными значениями ![]() и
и ![]() подбирают при опыте короткого замыкания измерительные приборы.
подбирают при опыте короткого замыкания измерительные приборы.
Так как при этом опыте ![]() а следовательно, и поток Ф (E
1
≈ 0,5 U
1к
, рис. 2-21) составляют всего несколько процентов от их значений при номинальном напряжении (а потери в стали приблизительно пропорциональны Ф2
), то магнитными потерями можно пренебречь и считать, что мощность P
к
, потребляемая трансформатором при коротком замыкании, идет на покрытие электрических потерь в обмотках трансформатора:
а следовательно, и поток Ф (E
1
≈ 0,5 U
1к
, рис. 2-21) составляют всего несколько процентов от их значений при номинальном напряжении (а потери в стали приблизительно пропорциональны Ф2
), то магнитными потерями можно пренебречь и считать, что мощность P
к
, потребляемая трансформатором при коротком замыкании, идет на покрытие электрических потерь в обмотках трансформатора:
Отсюда находим:
Согласно ГОСТ активные сопротивления обмоток трансформаторов, по которым определяются электрические потери и активные падения напряжения, должны быть приведены к температуре 75° С. Это приведение делаем согласно соотношению
где ![]() — температура обмоток, °С, при опыте короткого замыкания.
— температура обмоток, °С, при опыте короткого замыкания.
Далее определяем:
![]()
![]()
(можно принять, что ![]() от температуры не зависит) и
от температуры не зависит) и
![]()
После этого определяем номинальное напряжение короткого замыкания U к = I 1н z к75 . Оно, очевидно, равно напряжению, которое, будучи приложено к одной обмотке трансформатора при замкнутой накоротко его другой обмотке, создаст в обеих обмотках номинальные токи.
Напряжение U к = I 1н z к75 выражается в процентах номинального напряжения той обмотки, со стороны которой производились измерения при опыте короткого замыкания:
Процентное значение номинального напряжения короткого замыкания указывается на щитке трансформатора. Оно для нормальных трансформаторов лежит в пределах 5 — 10%. Также выражаются в процентах номинального напряжения реактивная и активная составляющие напряжения короткого замыкания:
Если числитель и знаменатель правой части равенства (2-50) умножить на I 1н и число фаз т , то получим:
т. е. ![]() в то же время дает процентное значение электрических потерь в обмотках трансформатора или потерь короткого замыкания при номинальных токах.
в то же время дает процентное значение электрических потерь в обмотках трансформатора или потерь короткого замыкания при номинальных токах.
Значения r 1 и r 2 могут быть измерены при постоянном токе, например при помощи амперметра и вольтметра Полученные при этом сопротивления будут несколько меньше активных сопротивлений обмоток. Активные сопротивления больше сопротивлений, измеренных при постоянном токе, в 1,03 — 1,07 раза вследствие наличия вихревых токов в проводниках обмоток и в других металлических частях трансформатора, вызванных полями рассеяния.
Определить отдельно значения х 1 и x 2 довольно трудно. Практически достаточно найти только х к .
2-8. Изменение вторичного напряжения
Вторичное напряжение ![]() при нагрузке в общем случае отличается от вторичного напряжения U
20
при холостом ходе. Изменение вторичного напряжения при переходе от холостого хода к нагрузке при
при нагрузке в общем случае отличается от вторичного напряжения U
20
при холостом ходе. Изменение вторичного напряжения при переходе от холостого хода к нагрузке при ![]() принято выражать в процентах номинального напряжения.
принято выражать в процентах номинального напряжения.
Полученное значение
называется процентным изменением напряжения трансформатора. Оно может быть найдено при помощи векторной диаграммы, представленной на рис. 2-23 и соответствующей схеме замещения на рис. 2-24.
Рис. 2-23. Упрощенная векторная диаграмма трансформатора (для определения изменения напряжения).
Рис. 2-24. Упрощенная схема замещения (для определения изменения напряжения).
При построении диаграммы мы пренебрегли током I
0
, так как он не превышает 5—10% номинального тока (при этом ![]() ). На диаграмме ∆ОАВ
— треугольник короткого замыкания со сторонами
). На диаграмме ∆ОАВ
— треугольник короткого замыкания со сторонами ![]()
![]()
![]() Из точки А
мы опустили перпендикуляр
Из точки А
мы опустили перпендикуляр ![]() на продолжение вектора
на продолжение вектора ![]() .
.
Теперь можем написать:
или
где ![]() и
и ![]()
Так как n
составляет в обычных случаях небольшую долю единицы, то можно воспользоваться приближенным равенством ![]() . Подставляя в (2-54) приближенное значение радикала, получим:
. Подставляя в (2-54) приближенное значение радикала, получим: ![]() или в процентах
или в процентах
где m
к
= m
·100 и n
к
= n·100. Значения m
к
и n
к
можно найти при помощи графического построения, представленного на рис. 2-25. Здесь ![]() — треугольник короткого замыкания, стороны которого выражены в процентах от номинального напряжения:
— треугольник короткого замыкания, стороны которого выражены в процентах от номинального напряжения:
где
значения u
к
и u
o
и u
а
рассчитываются по (2-48), (2-49) и (2-50). На гипотенузе ![]() как на диаметре построим окружность Проведем линию
как на диаметре построим окружность Проведем линию ![]() под заданным углом
под заданным углом ![]() к катету
к катету ![]() до пересечения с этой окружностью. Отсюда найдем искомые значения m
к
и n
к
:
до пересечения с этой окружностью. Отсюда найдем искомые значения m
к
и n
к
:
![]() ;
; ![]() .
.
Рис. 2-25 Диаграмма для определения ![]() и
и ![]() .
.
Непосредственное определение ![]() из рис. 2-23 не может быть точным, так как отрезки
из рис. 2-23 не может быть точным, так как отрезки ![]() ,
, ![]() во много раз меньше U
1н
и
во много раз меньше U
1н
и ![]() . На основе рис. 2-25 может быть получена формула для
. На основе рис. 2-25 может быть получена формула для ![]() рекомендованная ГОСТ на трансформаторы.
рекомендованная ГОСТ на трансформаторы.
Из рис. 2-25 и равенств (2-56) имеем:
Подставляя найденные значения m к и n к в (2-55), получим искомую формулу:
При многих практических расчетах можно пренебречь вторым слагаемым, так как оно по сравнению с первым слагаемым незначительно.

 При помощи диаграммы, приведенной на рис. 2-25, или при помощи формулы (2-60) определяются важные в практическом отношении кривые, выражающие зависимости
При помощи диаграммы, приведенной на рис. 2-25, или при помощи формулы (2-60) определяются важные в практическом отношении кривые, выражающие зависимости ![]() от
от ![]() от cos
от cos![]() при
при ![]() Указанные кривые приведены на рис. 2-26 и 2-27.
Указанные кривые приведены на рис. 2-26 и 2-27.
Рис. 2-26. Кривые U% = f (b) при cosφ2 = const. Рис. 2-27. Кривая U% = f (cosj2 ) при b = const.
Здесь отрицательные значения ![]() при работе трансформатора с опережающим током соответствуют повышению напряжения при переходе от холостого хода к нагрузке (ср. с рис. 2-16).
при работе трансформатора с опережающим током соответствуют повышению напряжения при переходе от холостого хода к нагрузке (ср. с рис. 2-16).
Наибольшее значение ![]() получается при cos φ2
= cos φк
, что следует из рис. 2-23.
получается при cos φ2
= cos φк
, что следует из рис. 2-23.
2-9. Потери и коэффициент полезного действия
При работе трансформатора в нем возникают потери — магнитные и электрические.
Магнитные потери, или потери в стали Р с , принимаются, как отмечалось, равными потерям холостого хода P 0 . Они зависят от частоты тока, от индукций В с в стержне и В я в ярме сердечника, а также от весов стержней и ярм. Для уменьшения магнитных потерь и реактивной составляющей тока холостого хода сечение ярма берут несколько больше (на 5—10%) сечения стержня. Потери P 0 приблизительно пропорциональны квадрату индукции (В 2 ) и частоте тока в степени 1,3 (f1,3 ).
Электрические потери, или потери короткого замыкания, пропорциональны квадрату тока.
Коэффициент полезного действия (к.п.д.) трансформатора имеет высокие значения: от 0,96 при S ≈ 5 кВА до 0,995 при номинальной мощности, составляющей десятки тысяч кВА. Поэтому определение его непосредственным методом по формуле
где Р 2 — полезная (вторичная) мощность; Р 1 — затраченная (первичная) мощность, практически не может дать точных результатов.
Так как потери в трансформаторе невелики, то следует определять к.п.д. трансформатора косвенным методом и пользоваться при этом формулой
где ![]() — сумма всех потерь в трансформаторе;
— сумма всех потерь в трансформаторе;
m
— число фаз;
r
к75
и P
0
— активное сопротивление короткого замыкания при 75°С и потери холостого хода, которые определяются, как указывалось ранее, по данным опытов короткого замыкания и холостого хода. Можно считать в обычных условиях U2
= U
2н
= const, ![]() P
0
= const.
P
0
= const.
Тогда, обозначив ![]() , получим:
, получим:
где S н = mU 2 I 2н — номинальная мощность; Р к н — потери короткого замыкания при номинальных токах в обмотках трансформатора.
В правой части (2-63) переменной величиной является только ![]() . Обычным путем можно найти максимум функции
. Обычным путем можно найти максимум функции ![]() . Для этого приравняем ее первую производную нулю:
. Для этого приравняем ее первую производную нулю:
![]()
В полученной дроби знаменатель при реальных значениях ![]() не может быть равным бесконечности. Поэтому нужно приравнять нулю числитель. Отсюда найдем, что к.п.д. будет максимальным, когда потери короткого замыкания будут равны потерям холостого хода:
не может быть равным бесконечности. Поэтому нужно приравнять нулю числитель. Отсюда найдем, что к.п.д. будет максимальным, когда потери короткого замыкания будут равны потерям холостого хода:
т. е. при равенстве переменных потерь постоянным потерям (при изменении нагрузки практически изменяются только потери короткого замыкания).
Для трансформаторов, выпускаемых заводами Советского Союза, имеем:
P
0
: P
к.н
= 0,5÷0,25 , что дает: = 0,7
= 0,7![]()
Следовательно, к.п.д. получается максимальным при нагрузке, составляющей 50—70% от номинальной. Такая нагрузка обычно и соответствует средней нагрузке при эксплуатации трансформатора.
При вычислении к.п.д. пользуются формулой
2-10. Трансформирование трехфазного тока
Для трансформирования трехфазного тока применяются или трехфазные трансформаторы, или «трехфазные группы», состоящие из трех однофазных трансформаторов.
Наибольшее распространение на практике получили трехфазные стрежневые трансформаторы с расположением стержней в одной плоскости.
Сердечник одного из таких трансформаторов показан на рис. 2-28.
Рис. 2-28. Сердечник трехфазного стержневого трансформатора.
Здесь же указаны потоки (в соответствии с векторным уравнением потоков ![]() , причем за положительное их направление условно принято направление снизу вверх. Очевидно, амплитуда потока в ярме равна амплитуде потока в стержне.
, причем за положительное их направление условно принято направление снизу вверх. Очевидно, амплитуда потока в ярме равна амплитуде потока в стержне.
Трехфазная группа, состоящая из трех однофазных трансформаторов, представлена на рис. 2-29.
Рис. 2 29. Трехфазная группа.
Одна из ее обмоток соединена в звезду, другая, как правило, соединяется в треугольник (§ 2-13).
На рис. 2-30,а представлен трехфазный броневой трансформатор.
Рис. 2-30. Трехфазный броневой трансформатор и распределение потоков в его сердечнике.
Обычно его стержни располагаются горизонтально с помещенными на них дисковыми чередующимися обмотками (рис. 2-8). Здесь различают продольные ярма, расположенные параллельно стержням, и поперечные ярма, расположенные перпендикулярно стержням. Продольные и поперечные ярма выполняются обычно с сечением, равным примерно половине сечения стержня. В трехфазном броневом трансформаторе средняя фаза первичной и вторичной обмоток должна быть соединена в обратном порядке по сравнению с крайними фазами. На рис. 2-30,а показано соединение обмотки высшего напряжения в звезду. Здесь правый зажим средней фазы принят за начало фазы, а левый — за ее конец в противоположность тому, что принято для крайних фаз. Только в этом случае поток в промежуточных поперечных ярмах равен полусумме потоков соседних стержней (рис. 2-30,б и в ).
Неправильным будет соединение, при котором за начало и конец средней фазы приняты такие же зажимы, что и для крайних фаз, так как в этом случае в промежуточных поперечных ярмах поток будет равен полуразности потоков в соседних стержнях, т. е. в ![]() раз больше, чем в предыдущем случае.
раз больше, чем в предыдущем случае.
2-11. Соединения обмоток трансформаторов
Обратимся к однофазному трансформатору, обмотки которого показаны на рис. 2-31.
Рис. 2-31. Обозначения зажимов обмоток однофазного трансформатора.
Согласно ГОСТ зажимы обмоток обозначаются так, как указано на этом рисунке. Начало и конец обмотки высшего напряжения обозначаются соответственно прописными буквами А и X . Для обмотки низшего напряжения берутся строчные буквы: а — начало и х — конец обмотки.
Зажимы обмоток трехфазных трансформаторов обозначаются, как указано на рис. 2-32.
Рис. 2-32. Обозначения зажимов обмоток трех фазного трансформатора.
Зная обозначения зажимов обмоток, мы можем правильно соединить обмотки трехфазного трансформатора и трехфазной группы в звезду или треугольник. Их необходимо также знать при включении трансформаторов на параллельную, работу.
Соединение обмотки, например, высшего напряжения в звезду показано на рис. 2-33.
Рис. 2-33. Соединение обмотки в звезду.
Напомним, что в этом случае линейное напряжение в ![]() раз больше фазного, а линейный ток равен фазному.
раз больше фазного, а линейный ток равен фазному.
На рис. 2-34 показано соединение обмотки в треугольник.
Рис. 2-34. Соединение обмотки в треугольник.
Здесь линейное напряжение равно фазному, а линейный ток в ![]() раз больше фазного.
раз больше фазного.
Соединение обмоток в звезду и звезду обозначают Y/Y и называют "звезда — звезда" или "игрек — игрек". Соединение обмоток в звезду и треугольник обозначают Y/D и называют "звезда — треугольник" или "игрек — дельта". Если от обмотки, соединенной в звезду, выводится нулевая точка, то такое соединение обозначают Y0 и называют «звезда с нулем» или «игрек нулевое».
Следует иметь в виду, что отношение линейных напряжений U л1 и U л2 трансформатора зависит не только от чисел витков обмоток w 1 и w 2 (на фазу), но и от способов их соединения:
при Y/Y ![]()
при Y/∆ ![]()
при ∆/Y ![]()
2-12. Группы соединений
В зависимости от сдвига по фазе между линейными первичной и вторичной э.д.с. на одноименных зажимах трансформаторы разделяются на группы соединений, причем каждую группу составляют трансформаторы с одинаковым сдвигом по фазе между указанными э.д.с.
Для обозначения группы соединений выбирается ряд целых чисел от 1 до 12; здесь условно принято, что единица соответствует 30° по аналогии с углами между минутной и часовой стрелками часов в 1, 2,..., 12 ч. При определении группы соединений с вектором э.д.с. обмотки высшего напряжения нужно совместить минутную стрелку, а с вектором э.д.с. обмотки низшего напряжения — часовую стрелку. Отсчет угла производится от минутной стрелки к часовой по направлению их вращения.
Обратимся к однофазному трансформатору, обмотки которого представлены на рис. 2-35.
Рис. 2-35. Однофазный трансформатор 1/1-12.
Если они выполнены при одинаковом направлении намотки (например, по часовой стрелке, если смотреть от А к X и от a к х ), то наведенные в них э.д.с. изобразятся векторами, направленными в одну и ту же сторону (рис. 2-35). Такой трансформатор принадлежит к группе соединений, обозначаемой числом 12. Его условное обозначение: 1/1-12.
Если тот же трансформатор будет иметь обмотку, например, низшего напряжения, у которой будут переставлены обозначения зажимов по сравнению с предыдущим случаем, то сдвиг между э.д.с. будет равен 180° (рис. 2-36).
Рис. 2-36. Однофазный трансформатор 1/1-6.
Такой трансформатор принадлежит к группе соединений, обозначаемой числом 6.
Обратимся к трехфазному трансформатору, представленному на рис. 2-37.
Рис. 2-37. Трехфазный трансформатор Y/Y-12.
Здесь обе обмотки соединены в звезду и намотаны в одинаковом направлении от начал к концам фаз. Векторные диаграммы э.д.с. показывают, что сдвиг между линейными э.д.с. АВ и ab в данном случае равен 0°. В этом мы убеждаемся, совместив при наложении диаграмм точки А и а. Следовательно, рассматриваемый трансформатор принадлежит к группе 12. Его полное обозначение: Y/Y-12.
Если у трехфазного трансформатора группы 12 поменять местами начала и концы фаз, например обмотки низшего напряжения, то получается трансформатор группы 6 (рис. 2-38). Его обозначают: Y/Y-6.
Рис. 2-38. Трехфазный трансформатор Y/Y-6.
Трехфазные трансформаторы с соединением обмоток Y/Y принадлежат к группам 6 и 12, если на каждом стержне сердечника помещены одноименные фазы. Если же у одной из обмоток сделать круговое перемещение обозначений зажимов, например вместо а —b —с сделать с —а —b и затем b —с —а , то при каждом перемещении будем поворачивать звезду вторичных э. д. с. на 120° и, следовательно, переходить от группы 12 к группам 4 и 8, а от группы b — к группам 10 и 2. Таким образом, при соединении обмоток Y/Y можем получить все четные группы соединений 2, 4, 6, 8, 10, 12.
Обратимся к трехфазному трансформатору с соединением обмоток Y/∆ представленному на рис. 2-39.
Рис. 2-39. Трехфазный трансформатор Y/∆-5.
Векторные диаграммы э.д.с., приведенные на этом же рисунке, показывают, что сдвиг между линейными э.д.с. здесь равен 330°. Следовательно, трансформатор принадлежит к группе 11. Он обозначается: Y/∆ -11.
Если у рассмотренного трансформатора (рис. 2-39) поменять местами начала и концы фаз обмотки низшего напряжения, то получается трансформатор группы 5 (рис. 2-40) со сдвигом между линейными э.д.с., равным 150°. Такой трансформатор обозначается Y/∆-5.
Рис. 2-40. Трехфазный трансформатор Y/∆-5.
Если сделать круговое перемещение обозначений зажимов для обмотки низшего напряжения трансформаторов, представленных на рис. 2-39 и 2-40, то перейдем соответственно от группы 11 к группам 3 и 7 и от группы 5 к группам 9 и 1. Следовательно, при соединении обмоток Y/∆ (или ∆/Y) можем noлучить все нечетные группы 1, 3, 5, 7, 9, 11.
Такое большое разнообразие групп соединений трансформаторов не только не требуется, но вызывало бы большие затруднения на практике, например при осуществлении параллельной работы трансформаторов (§ 2-17).
В СССР стандартизованы только две группы соединений: 12 и 11. Все выпускаемые советскими заводами нормальные однофазные трансформаторы и трехфазные с соединением обмоток Y/Y принадлежат к группе 12, а трехфазные трансформаторы с соединением обмоток Y/∆ — к группе 11.
2-13. Третьи гармоники в кривых тока холостого хода, магнитного потока и электродвижущих сил
Рассмотрим вначале процесс намагничивания однофазного трансформатора. Как отмечалось, вследствие нелинейной связи между потоком Ф в стальном сердечнике трансформатора и создающей его н.с. i 0 w 1 кривая i 0 = f (t ) отличается от синусоиды. Мы эту кривую найдем, пренебрегая потерями в стали и рассматривая вместо тока i o намагничивающий ток i μ , практически равный i 0 .
Кривую Ф = f (t ) можно принять синусоидальной, если приложенное напряжение u 1 и, следовательно, уравновешивающая его э.д.с. е 1 — синусоидальные функции времени. В этом случае кривая i μ = f (t ) определяется графически, как показано на рис. 2-41.
Рис. 2-41. Построение кривой намагничивающего тока i μ = f (t ) однофазного трансформатора при синусоидальном потоке.
Слева мы имеем кривую намагничивания Ф = f (i μ ) (здесь пренебрегаем гистерезисом). Справа для заданной синусоидальной кривой Ф = /(t ) мы получаем кривую i μ = f (t ), ординаты которой a , b , с , d и т. д. равны абсциссам кривой Ф = f (i μ ) для соответствующих значений потока Ф.
Мы видим, что кривая тока искажена. Она имеет наряду с первой гармоникой довольно резко выраженные третью и пятую гармоники. Кривая тока построена для нормального трансформатора, имеющего, как это обычно бывает, максимальную индукцию в сердечнике около 14 500 Гс. В этом случае гармоники с номером выше пятого имеют небольшие значения.
Гистерезис мало искажает кривую тока. При разложении на гармоники кривой тока, построенной с учетом гистерезиса, мы получили бы, кроме синусоид, еще косинусоиды с малыми амплитудами. Они дают активную составляющую тока i о , соответствующую потерям от гистерезиса.
При некоторых схемах соединения обмоток трехфазного трансформатора в кривой намагничивающего тока отсутствуют третья гармоника и гармоники с номером, кратным трем. Если принять кривую i μ = f (t ) синусоидальной, то кривая Ф = /(t ) будет отличаться от синусоиды. Из высших гармоник в ней наиболее резко будет выражена 3-я гармоника. На рис. 2-42 приведено построение кривой Ф = /(t ) при синусоидальной кривой i μ = f (t ).
 Рис. 2-42. Построение кривой Ф = /(t
) при синусоидальном намагничивающем токе.
Рис. 2-42. Построение кривой Ф = /(t
) при синусоидальном намагничивающем токе.
Здесь по абсциссам а , b , с и т. д., равным ординатам кривой i μ = f (t ), найдены соответствующие значения потока Ф.
Обратимся к трехфазному трансформатору с соединением обмоток Y0 /Y. Будем считать, что с первичной стороны трансформатора выведена нулевая точка, которая соединена с нулевой точкой обмотки генератора трехфазного тока рис. 2-43.
Рис. 2-43. Третьи гармоники намагничивающих токов трехфазного трансформатора при соединении обмоток Y0 /Y.
В этом случае намагничивающие токи фаз будут иметь третьи гармоники. Они совпадают по фазе и, следовательно, будут все направлены или oт генератора к трансформатору, или обратно. По нулевому проводу будет проходить ток, равный тройному значению третьей гармоники тока.
При отсутствии нулевого провода (при Y/Y) в кривых фазных намагничивающих токов третьи гармоники не могут иметь места, так как теперь для них нет замкнутого пути. Следовательно, в кривых фазных потоков появятся третьи гармоники, которые будут наводить в фазах обмотки третьи гармоники э.д.с.
Наиболее резко третьи гармоники будут проявляться в кривых фазных э.д.с. трехфазной группы и трехфазного броневого трансформатора. Здесь магнитное сопротивление для третьей гармоники потока мало, так как она проходит по стальному, сердечнику, как и первая гармоника; поэтому она может достичь относительно больших значений: при обычных насыщениях сердечником указанных трансформаторов амплитуда третьей гармоники фазной э.д.с. достигает 40—50% амплитуды первой гармоники той же э.д.с.
В трехфазном стержневом трансформаторе при соединении обмоток Y/Y в кривых фазных э.д.с. также будут иметь место третьи гармоники. Однако здесь вследствие большого магнитного сопротивления для третьих гармоник потоков фаз они относительно малы: их амплитуда обычно не превышает 5—7% амплитуды первой гармоники фазной э.д.с. Увеличение магнитного сопротивления для третьих гармоник фазных потоков объясняется тем, что они в любой момент времени будут направлены по стержням трансформатора или вверх, или вниз и не могут, следовательно, замыкаться по стальному сердечнику, а принуждены часть пути проходить по воздуху или маслу, как показано на рис. 2-44.
Рис. 2-44. Приближенная картина поля, соответствующего третьим гармоникам фазных потоков.
Из рис. 2-44 также следует, что наличие третьих гармоник в фазных потоках трехфазного стержневого трансформатора несколько повышает потери в стали (в стенках бака, конструктивных деталях трансформатора).
Наличие третьих гармоник в фазных э.д.с. не нарушает необходимого условия работы трансформатора — равновесия приложенного напряжения и наведенной в обмотке э.д.с. Действительно, хотя фазная э.д.с. будет иметь третью гармонику, но междуфазная э.д.с. ее иметь не будет, так как при соединении обмотки звездой третьи гармоники фазных э.д.с. при обходе двух фаз, встречно соединенных, направлены друг против друга.
Если одна из обмоток трехфазного трансформатора соединена треугольником, то третьи гармоники в кривых потоков, а следовательно, и фазных э.д.с. практически пропадают. Это объясняется тем, что в обмотке, соединенной треугольником, третьи гармоники фазных э.д.с. направлены по контуру в одну сторону; они создадут третью гармонику тока, при наличии которой поток становится почти синусоидальным.
Теперь должно быть ясным, почему обмотки трехфазной группы и трехфазного броневого трансформатора выполняются, как правило, с соединением Y /D или ∆/Y . Обмотки трехфазного стержневого трансформатора часто имеют соединение Y /Y . Однако и здесь при большой мощности (больше 1800 кВА) выбирается соединение Y /∆ или ∆/Y .
Ранее иногда, в случае необходимости иметь соединение обеих обмоток мощного трехфазного трансформатора в звезду, снабжали такой трансформатор третьей обмоткой, соединенной треугольником, причем никаких выводов от этой обмотки не делалось, она служила только для компенсации третьей гармоники в кривой фазной э.д.с. Такую обмотку будем называть компенсационной. В настоящее время она используется как третья рабочая обмотка (см. § 2-16).
2-14. Расчет тока холостого хода
Ток холостого хода I о имеет активную составляющую I оа и реактивную составляющую I ор
![]()
Активная составляющая тока холостого хода, как указывалось, зависит от потерь Р с в стали сердечника:
для однофазного трансформатора ![]()
для трехфазного трансформатора ![]()
где U 1 — фазное напряжение.
В действительности потери в стали зависят от потока Фм
и, следовательно, от э.д.с. Е
1
; однако практически при определении потерь Р
с
можно считать ![]()
Потери в стали сердечника зависят от: В с ─ индукции в стержнях, Гс; В а ─ в ярмах, Гс; веса G я ─ стержней и G я ─ ярм, кг; f ─ частоты перемагничивания, Гц. Приближенно можно принять:
где p 10/50 — удельные потери в листовой стали, Вт/кг, из которой выполнен сердечник трансформатора, при максимальной индукции 10000 Гс и частоте 50 Гц.
Для силовых трансформаторов обычно выбирается сталь марок Э41, Э42 и холоднокатаная Э320 (при толщине листа ∆ = 0,5 или 0,35 мм); для указанных марок стали р 10/50 соответственно равняется 1,6; 1,4 и 1,15 — 1,20 Вт/кг (при ∆ =0,5 мм) и 1,35; 1,2; 0,9—0,95 Вт/кг (при ∆ = 0,35 мм).
Значения индукций определяются по формулам
![]()
![]()
где S c и S я — площади сечения стержня и ярма, см2 (берется площадь без изоляции между листами); значение Фм , мкс, рассчитывается по уравнению
Веса G c и Gя определяются по геометрическим размерам и удельному весу для листовой стали γс = 7,6 кг/дм3 .
Из (2-65) следует, что при увеличении частоты f сверх номинальной и при сохранении неизменным номинального первичного напряжения потери Р с будут уменьшаться, так как при этом согласно (2-66) поток Фм , а следовательно, и В изменяются обратно пропорционально f .
Реактивная составляющая тока холостого хода I 0р определяется из расчета магнитной цепи трансформатора следующим образом.
На рис. 2-45,а представлен сердечник однофазного трансформатора.
Рис. 2-45. Эскизы магнитных цепей.
а
—однофазного трансформатора (п
в
= 4); б
—трехфазного трансформатора (для крайних фаз п
в
= 3; для средней n
в
=1).
Здесь жирным пунктиром показан путь главного потока Ф. Согласно закону полного тока н.с. ![]() I
0р
w
1
, необходимая для создания в сердечнике потока Фм
, определяется из уравнения
I
0р
w
1
, необходимая для создания в сердечнике потока Фм
, определяется из уравнения
![]() I
0р
w
1
= 2H
c
l
c
+ 2H
я
l
я
+ 0,8
B
c
n
в
δв
, (2-67) где H
с
и Н
я
— напряженности поля в стержне и ярме, А/см, которые определяются по кривым намагничивания (рис. 2-46) соответственно для индукций В
с
и В
я
; n
в
— число зазоров, которое принимается равным четырем для однофазного трансформатора при сборке его сердечника «внахлестку»; δв
≈ 0,0035
I
0р
w
1
= 2H
c
l
c
+ 2H
я
l
я
+ 0,8
B
c
n
в
δв
, (2-67) где H
с
и Н
я
— напряженности поля в стержне и ярме, А/см, которые определяются по кривым намагничивания (рис. 2-46) соответственно для индукций В
с
и В
я
; n
в
— число зазоров, которое принимается равным четырем для однофазного трансформатора при сборке его сердечника «внахлестку»; δв
≈ 0,0035![]() 0,005 см — зазор при той же сборке сердечника.
0,005 см — зазор при той же сборке сердечника.
Рис. 2-46. Кривые намагничивания трансформаторной листовой стали: сплошная — для Э41 и Э42; пунктирная — для Э320.
Из (2-67) реактивная составляющая тока холостого хода, А:
На рис. 2-45,б представлен сердечник трехфазного стержневого трансформатора. При расчете I 0р такого трансформатора сначала определяется I 0р(кр) для крайних фаз по формуле
![]()
где n в = 3; затем для средней фазы по формуле
![]()
где n в = 1. Ток I 0р принимается равным среднему арифметическому:
![]()
При расчете I
0р
мы пренебрегаем высшими гармониками тока i
0р
![]() i
μ
, так как они при обычных значениях индукций мало влияют на действующее значение I
0р
.
i
μ
, так как они при обычных значениях индукций мало влияют на действующее значение I
0р
.
Из кривых намагничивания рис. 2-46 мы видим, как сильно влияет насыщение стали (значение В
) на Н
, а следовательно, и на I
0р
. Обычно при стали Э41 и Э42 значения B
с
= 10000 ![]() 14500 Гс и при стали Э320 В
с
= 13000
14500 Гс и при стали Э320 В
с
= 13000 ![]() 16500 Гс, В
я
= (0,90
16500 Гс, В
я
= (0,90 ![]() 0,95) В
с
для масляных трансформаторов мощностью от 5 до 100000 кВА; для сухих трансформаторов они снижаются на 10
0,95) В
с
для масляных трансформаторов мощностью от 5 до 100000 кВА; для сухих трансформаторов они снижаются на 10 ![]() 20%. При таких индукциях ток I
0р
(I
0р
20%. При таких индукциях ток I
0р
(I
0р
![]() I
0
) составляет от 10 до 4% номинального тока I
1н
.
I
0
) составляет от 10 до 4% номинального тока I
1н
.
2-15. Определение параметров трансформатора расчетным путем
Расчет активных сопротивлений r j и r 2, Ом, может быть произведен, если известны сечения проводников обмоток s 1 и s 2 , мм2 , число витков w l и w 2 и средние длины витков l ср1 и l ср2 , м. Тогда имеем:
![]()
![]()
где k
r
= 1,03 ![]() 1,05 — коэффициент, учитывающий потери, вызванные полями рассеяния обмоток;
1,05 — коэффициент, учитывающий потери, вызванные полями рассеяния обмоток;
![]() — удельное сопротивление меди при 75° С;
— удельное сопротивление меди при 75° С;
![]() — тоже для алюминия.
— тоже для алюминия.
Активное сопротивление короткого замыкания
![]()
Потери в обмотках при номинальных токах (сюда же относятся и потери, вызванные полями рассеяния), Вт
![]()
![]()
![]()
Формулы для потерь можно преобразовать следующим образом:
![]()
подставив ![]() ─ квадрат плотности тока первичной обмотки, А/мм2
;
─ квадрат плотности тока первичной обмотки, А/мм2
;![]()
![]()
![]() ─ удельный вес меди;
─ удельный вес меди; ![]() ─ вес меди первичной обмотки, кг, получим:
─ вес меди первичной обмотки, кг, получим:
аналогично будем иметь.
при алюминиевых обмотках (γа
![]() 2,65)
2,65)
![]()
![]()
где G al и G a2 — веса обмоток, кг.
Расчет индуктивных сопротивлений рассеяния х 1 и х 2 может быть произведен только приближенно, так как не представляется возможным точно установить распределение поля рассеяния. Мы рассмотрим метод расчета х 1 и х 2 для цилиндрических обмоток. Они в разрезе с одной стороны стержня показаны на рис. 2-47. Здесь же показана часть стержня, на котором помещены обмотки.
Рис. 2-47. К расчету х к = х 1 + х '2 (см. рис. 2-13).
Мы считаем, что поле рассеяния создается н.с. i
1
w
1
и равной ей н.с. i
2
w
2
= ![]() (пренебрегаем при этом н.с. i
0
w
1
) и что индукционные линии этого поля направлены, как показано на рис. 2-47, параллельно стенкам обмоток, равным по высоте. Примем, что магнитные сопротивления индукционных трубок поля обусловлены только их частью вдоль обмоток и промежутка между ними. Магнитным сопротивлением остальных частей индукционных трубок пренебрегаем. Кривая н.с., создающей поле рассеяния, в этом случае изобразится трапецией, а так как μ для воздуха (или масла), меди и изоляции — величина постоянная, то кривая распределения индукции вдоль пунктирной линии также изобразится трапецией.
(пренебрегаем при этом н.с. i
0
w
1
) и что индукционные линии этого поля направлены, как показано на рис. 2-47, параллельно стенкам обмоток, равным по высоте. Примем, что магнитные сопротивления индукционных трубок поля обусловлены только их частью вдоль обмоток и промежутка между ними. Магнитным сопротивлением остальных частей индукционных трубок пренебрегаем. Кривая н.с., создающей поле рассеяния, в этом случае изобразится трапецией, а так как μ для воздуха (или масла), меди и изоляции — величина постоянная, то кривая распределения индукции вдоль пунктирной линии также изобразится трапецией.
Найдем индуктивность рассеяния первичной обмотки:
![]()
Будем условно считать, что потокосцепление, определяющее L σ1 создается индукционными линиями, находящимися слева от штрихпунктирной линии, разделяющей промежуток δ пополам. Оно рассчитывается следующим образом.
Поток в промежутке ![]() сцепляется со всеми w
1
витками (здесь для определения площади, через которую проходит поток, нужно было бы взять средний диаметр
сцепляется со всеми w
1
витками (здесь для определения площади, через которую проходит поток, нужно было бы взять средний диаметр ![]() а не D
, но в дальнейшем при определении потока промежутка, сцепляющегося со вторичной обмоткой, мы возьмем также D
, а не
а не D
, но в дальнейшем при определении потока промежутка, сцепляющегося со вторичной обмоткой, мы возьмем также D
, а не ![]() что до некоторой степени компенсирует допущенную ошибку). Индукционные линии, проходящие вдоль обмотки, дают различные сцепления с витками обмотки. Поток в стенке цилиндра с толщиной dx
равен Bx
dx
πD
(здесь также приближенно взят постоянный диаметр D
), где
что до некоторой степени компенсирует допущенную ошибку). Индукционные линии, проходящие вдоль обмотки, дают различные сцепления с витками обмотки. Поток в стенке цилиндра с толщиной dx
равен Bx
dx
πD
(здесь также приближенно взят постоянный диаметр D
), где ![]() Он сцепляется с
Он сцепляется с ![]() витками. Следовательно, полное потокосцепление первичной обмотки
витками. Следовательно, полное потокосцепление первичной обмотки
Аналогично определяется потокосцепление ![]() вторичной обмотки, от которого зависит индуктивность рассеяния L
σ2
:
вторичной обмотки, от которого зависит индуктивность рассеяния L
σ2
:
Индукция в промежутке между обмотками, В·с/см2 ,
Индуктивность короткого замыкания
![]()
Подставляя сюда (2-71) — (2-73), получим:
Следовательно, индуктивное сопротивление короткого замыкания, Ом,
где промежуток, см
Мы видим, что х к зависит от геометрических размеров δ, а b , l . Однако в нормальных трансформаторах эти размеры выбираются таким образом, чтобы обеспечить надежную работу трансформатора (достаточные изоляционные расстояния и охлаждение) и получить по возможности меньший расход металлов. Наиболее радикальным способом изменения х к является изменение w 1 . Число витков w 1 зависит от потока Фм , следовательно, от сечения S c (Фм = B с S с ).
Выбор этого сечения должен производиться таким образом, чтобы получились надлежащие значения Фм , w 1 , х к и u к .
Высоты обмоток всегда выбираются по возможности равными друг другу. Только при таких обмотках поле рассеяния распределяется в соответствии с рис. 2-47. В противном случае оно возрастает, что нежелательно из-за увеличения х к , увеличения потерь от полей рассеяния и возрастания электромагнитных сил, действующих на обмотки при внезапном коротком замыкании (§ 2-20,б ).
Параметры трансформатора можно выразить в долях сопротивления, принимаемого за единицу и равного отношению номинальных фазных напряжения и тока U 1н /I 1н . Тогда они будут выражены в долях единицы (д.е.) или в относительных единицах измерения, о.е. Будем их обозначениям приписывать звездочку наверху справа, которые в о.е. измерения равны:
![]()
![]()
![]()
![]()
![]()
где сопротивления, Ом,
![]()
![]()
Токи, напряжения, мощности в о.е. измерения
![]()
![]()
![]()
![]()
Процентные значения параметров получим, если их значения в о.е. измерения умножим на 100. Очевидно, что ![]()
![]()
![]()
Значения указанных величин для нормальных силовых трансформаторов в зависимости от номинальной мощности и верхнего предела номинального высшего напряжения приведены в табл. 2-1 (I
0
% = I
0
/I
н
![]() 100).
100).
Таблица 2-1
| S н |
10 |
100 |
1000 |
10000 |
60000 |
кВт |
| U н |
6,3 |
6,3 ─ 35 |
10 ─ 35 |
38,5 ─ 121 |
121 |
кВ |
| I 0 % |
10 |
6 ─ 8 |
5 ─ 5,5 |
3 ─ 3,5 |
2,7 |
% |
| u а |
3,35 |
2,4 |
1,5 |
0,92 ─ 0,97 |
0,5 |
% |
| u р |
4,36 |
4,94 ─ 6,05 |
5,3 ─6,25 |
7,45 ─ 10,5 |
10,5 |
% |
| u к |
5,5 |
5,5 ─ 6,5 |
5,5 ─ 6,5 |
7,5 ─ 10,5 |
10,5 |
% |
|
|
1,05 |
1,42 |
1,96 ─ 1,68 |
3,23 ─ 3,14 |
3,7 |
о.е. |
|
|
10 |
16,6 ─ 12,5 |
20 ─ 18,2 |
33,3 ─ 28,7 |
37 |
о.е. |
2-16. Автотрансформатор
Автотрансформатор отличается от трансформатора тем, что у него обмотка низшего напряжения является частью обмотки высшего напряжения, причем она выполняется из проводников, в общем случае отличающихся по сечению от проводников другой части, и обычно располагается относительно другой части, как показано на рис. 2-48.
Рис. 2-48. Схема понижающего автотрансформатора (а ); расположение частей его обмоток относительно стержня сердечника (б ).
Следовательно, части Аа и аХ можно рассматривать как обмотки двухобмоточного трансформатора, имеющие между собой не только магнитную связь, но и электрическую.
Автотрансформаторы могут служить как для понижения, так и для повышения напряжения. Они выполняются для небольших коэффициентов трансформации, не сильно отличающихся от единицы, и в этом случае, как показано в дальнейшем, экономичнее в работе и требуют на изготовление меньше материалов, чем обычные двухобмоточные трансформаторы на ту же номинальную мощность.
За номинальную мощность автотрансформатора принимается мощность S н = U 1н I 1н = U 2н I 2н .
Приложенное к обмотке А
— X
напряжение ![]() , уравновешивается в основном э.д.с.
, уравновешивается в основном э.д.с. ![]() . Электродвижущая сила
. Электродвижущая сила ![]() создает ток во вторичной цепи, при этом
создает ток во вторичной цепи, при этом ![]() следовательно,
следовательно,
![]()
Пренебрегая током холостого хода, согласно закону полного тока можем написать:
![]()
отсюда
Ток в общей части обмотки а
— X
равен геометрической сумме первичного и вторичного токов:
![]() (2-78)
(2-78)
Для понижающего трансформатора I 2 >I 1 следовательно, ток общей части обмотки равен
![]()
что дает возможность соответственно уменьшить сечение ее проводников.
Учитывая (2-77), получим:

Части обмотки А — а и а — X магнитно уравновешены, т. е. их н.с. равны и противоположно направлены, что следует из соотношений
Для того чтобы можно было сравнить автотрансформатор с двухобмоточным трансформатором, найдем расчетную мощность S а автотрансформатора.
Расчетная мощность S а1 части обмотки А — а равна:
расчетная мощность Sa 2 части обмотки а — X равна:
Следовательно, S al = S a2 , так как E 1 I 1 = E 2 I 2 .
Отсюда найдем расчетную мощность автотрансформатора при номинальных значениях токов и напряжений:
Размеры автотрансформатора рассчитываются для мощности
![]()
тогда как размеры двухобмоточного трансформатора рассчитываются для мощности S н .
Таким образом, расчетная мощность автотрансформатора меньше его номинальной мощности, называемой также полной или проходной:
Размеры трансформатора определяются значением электромагнитной мощности при cos φ2
= 1, т. е. мощности, которая при этом передается магнитным полем с первичной на вторичную обмотку. Действительно, для данной частоты тока эта мощность ![]() По магнитному потоку Ф определяются сечения стержней и ярм трансформатора (сечение
По магнитному потоку Ф определяются сечения стержней и ярм трансформатора (сечение ![]() где B
= 12000
где B
= 12000 ![]() 14500 Гс при f
= 50 Гц); по току — сечения проводников (
14500 Гс при f
= 50 Гц); по току — сечения проводников (![]() , где для масляных трансформаторов
, где для масляных трансформаторов ![]() ); по числу витков, сечению проводников и их изоляции — размеры окна трансформатора (площадь окна равна произведению высоты стержня на расстояние между соседними стержнями).
); по числу витков, сечению проводников и их изоляции — размеры окна трансформатора (площадь окна равна произведению высоты стержня на расстояние между соседними стержнями).
В двухобмоточном трансформаторе магнитным полем передается мощность S н = E 1н I 1н = E 2н I 2н , а в автотрансформаторе — только часть этой мощности
![]()
другая часть мощности
![]()
передается во вторичную внешнюю цепь непосредственно по проводам.
Очевидно, что автотрансформаторы тем экономичнее по сравнению с двухобмоточными трансформаторами, чем ближе w 2 к w 1 , т. е. чем ближе коэффициент трансформации к единице. Так как веса обмотки и стали сердечника автотрансформатора меньше весов тех же материалов двухобмоточного трансформатора, то и потери в нем меньше, а к.п.д. выше при той же мощности S н . Параметры, а следовательно, и изменение напряжения также имеют меньшие значения.
Изменение напряжения автотрансформатора определяется по аналогии с двухобмоточным трансформатором. Напишем в соответствии с рис. 2-48,а уравнения напряжений:
где ZA
= rА
+ jхА
— сопротивление части обмотки А — а
;
Zx
= rx
+ jxx
— сопротивление части обмотки а —
X
.
Так как ![]() то (2-85) можем переписать в следующем виде:
то (2-85) можем переписать в следующем виде:
Заменив в (2-84) и (2-86) ![]() через
через ![]() по (2-78а
) получим;
по (2-78а
) получим;
Отсюда найдем изменение напряжения для понижающего автотрансформатора:
где  =
=  — сопротивление Zx
части а —
X
с числом витков w
2
, приведенное к числу витков (w
1
, — w
2
) части обмотки А — а
.
— сопротивление Zx
части а —
X
с числом витков w
2
, приведенное к числу витков (w
1
, — w
2
) части обмотки А — а
.
Параметры ZА и Zx могут быть рассчитаны как для двухобмоточного трансформатора, имеющего с первичной стороны (w 1 — w 2 ) витков и со вторичной стороны w 2 витков при тех же сечениях проводников, размерах сердечника и обмоток, что и для частей обмоток А — а , а — X и сердечника автотрансформатора.
Значение

может быть найдено также по данным опыта короткого замыкания, при котором автотрансформатор следует использовать как двухобмоточный трансформатор: пониженное напряжение (порядка 5—10% от ![]() должно быть подведено к части обмотки А — а
, а часть обмотки а—
X
должна быть замкнута накоротко.
должно быть подведено к части обмотки А — а
, а часть обмотки а—
X
должна быть замкнута накоротко.
Ток короткого замыкания I 1к найдем из (2-89), приравняв U 2 = 0:
Номинальное напряжение короткого замыкания автотрансформатора
Для двухобмоточного трансформатора при том же токе I 1н , имеющего первичную обмотку с (w 1 – w 2 ) витками, номинальное напряжение короткого замыкания u к будет определяться отношением
Следовательно,
Отсюда следует, что и к.а автотрансформатора меньше, чем и к двухобмоточного трансформатора при тех же значениях
Z
1
=
ZA
и Z
2
=

Поэтому токи короткого замыкания автотрансформатора могут иметь очень большие значения, если w 2 близко к w 1 . Следует также принять во внимание, что в этом случае может сильно возрасти намагничивающий ток в части обмотки А — а , которым мы пренебрегали в предыдущих выводах.
Для повышающего автотрансформатора, схема которого показана на рис. 2-49, можем написать следующие уравнения напряжений:
Рис. 2-49. Схема повышающего автотрансформатора.
Учитывая (2-78а ) и (2-76), получим:
Отсюда имеем:
Приравняв в (2-99) ![]() = 0, найдем ток короткого замыкания:
= 0, найдем ток короткого замыкания:
Номинальное напряжение короткого замыкания u а к автотрансформатора
При сравнении с двухобмоточным трансформатором последний надо взять с числами витков во вторичной обмотке (w
2
— w
1
,) и в первичной обмотке w
1
, но с номинальным током в первичной обмотке ![]() Тогда номинальное напряжение короткого замыкания такого двухобмоточного трансформатора
Тогда номинальное напряжение короткого замыкания такого двухобмоточного трансформатора
Следовательно, и для повышающего автотрансформатора
Недостатком автотрансформатора является то, что здесь вторичная цепь оказывается электрически соединенной с первичной цепью. Она должна иметь такую же изоляцию по отношению к земле, как и первичная цепь. Это обстоятельство заставляет выбирать значение коэффициента трансформации автотрансформатора при высоких напряжениях не выше 2—2,5.
Схема трехфазного автотрансформатора представлена на рис. 2-50.
Рис. 2-50. Схема трехфазного автотрансформатора.
Автотрансформаторы находят себе применение в качестве пусковых для пуска больших синхронных двигателей и короткозамкнутых асинхронных двигателей, для осветительных установок (для дуговых ламп переменного тока), для связи сетей с напряжениями, мало отличающимися одно от другого. В последнем случае трехфазные автотрансформаторы снабжаются еще одной обмоткой, соединенной треугольником, для подавления третьей гармоники в кривых магнитных потоках и, следовательно, в кривых фазных э.д.с. (см. § 2-13).
Автотрансформаторы выполняются также с устройством, позволяющим плавно регулировать их вторичное напряжение. Регулирование напряжения осуществляется путем изменения числа витков обмотки при помощи специальных переключателей или контакта, перемещаемого непосредственно по обмотке, очищенной с одной стороны от изоляции.
2-17. Трехобмоточный трансформатор
а) Общие сведения.
Большие трансформаторы, устанавливаемые в начале или конце длинных линий электропередачи и иногда на мощных промежуточных подстанциях, часто выполняются с тремя обмотками на каждую фазу, причем одна из них обычно служит в качестве первичной, а две другие — в качестве вторичных (рис. 2-51).
Рис. 2-51. Трехобмоточный трансформатор.
Например, на электрических станциях, от которых отходят две линии электропередачи, часто устанавливаются трехобмоточные трансформаторы с первичным напряжением 10,5 кВ и вторичными напряжениями 121 и 38,5 кВ (для линий электропередачи).
Трансформаторы с тремя (и больше) обмотками малой мощности применяются также в радиотехнических устройствах.
Трехобмоточный трансформатор заменяет собой два двухобмоточных трансформатора. Его применение, очевидно, выгоднее, чем последних.
Если пренебречь током холостого хода, то можно написать, что сумма н.с. всех трех обмоток равна нулю:
или
где ![]() и
и ![]() ― токи второй и третьей обмоток, приведенные к числу витков первой обмотки.
― токи второй и третьей обмоток, приведенные к числу витков первой обмотки.
Пусть первая обмотка будет первичной, а вторая и третья — вторичными. Из (2-105) получаем:
т. е. первичный ток равен не арифметической, а геометрической сумме приведенных вторичных токов (взятой с обратным знаком). Учитывая это равенство, а также то, что вторичные обмотки обычно не имеют одновременно и длительно полной нагрузки, номинальная мощность первичной обмотки берется меньше суммы номинальных мощностей обеих вторичных обмоток.
б) Уравнения напряжений и схема замещения.
Будем по-прежнему считать первую обмотку за первичную, а две другие обмотки — за вторичные и примем, что все обмотки имеют одинаковые числа витков: w 1 = w 2 = w 3 .
В этом случае согласно (2-104) имеем:
Уравнения напряжений обмоток напишутся в следующем виде
![]()
![]()
Учитывая (2-107), найдем из 1-го и 2-го уравнений (2-109) падение напряжения в обмотках 1–2:
![]() (2-110)
(2-110)
Учитывая (2-108), из 1-го и 3-го уравнений (2-109) найдем падение напряжения в обмотках 1—3:
![]() (2-111)
(2-111)
Для каждой пары обмоток имеем равенства:
![]()
![]()
![]()
Полученные в (2-110) и (2-111) величины
![]()
![]()
условно могут рассматриваться как индуктивные сопротивления рассеяния обмоток; каждое из них обусловлено индуктивностью обмотки и взаимными индуктивностями всех трех пар обмоток.
Из (2-110) и (2-111) следует:
Равенствам (2-113) соответствует схема замещения трехобмоточного трансформатора, представленная на рис. 2-52.
Рис. 2-52. Схема замещения трехобмоточного трансформатора.
Ее параметры могут быть определены как опытным, так и расчетным путем.
При опытном определении Z 1 , Z 2 , Z 3 нужно иметь данные трех опытов короткого замыкания.
При первом опыте замыкается накоротко обмотка 2 , обмотка 3 оставляется разомкнутой, пониженное напряжение подводится к обмотке 1 (рис. 2-53,а ); измеряются, так же как при опыте короткого замыкания двухобмоточного трансформатора, U , I , Р . По данным измерений находим:
Рис. 2-53. Схемы трех опытов короткого замыкания для трехобмоточного трансформатора.
При втором опыте замыкается накоротко обмотка 3 , обмотка 2 остается разомкнутой, пониженное напряжение подводится к обмотке 1 (рис. 2-53,б ). По данным измерений находим:
При третьем опыте замыкается накоротко обмотка 3 (или 2 ), обмотка 1 остается разомкнутой, пониженное напряжение подводится к обмотке 2 (или 3 ) (рис. 2-53,в ). По данным измерений находим:
Для реального трансформатора ![]() поэтому в (2-114)—(2-117) войдут величины,
поэтому в (2-114)—(2-117) войдут величины, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , приведенные к числу витков обмотки 1.
, приведенные к числу витков обмотки 1.
B (2-118) и (2-119) войдут величины ![]() и
и ![]() , приведенные к числу витков обмотки 2. Для последующих расчетов x
к23
и r
к23
должны быть приведены к числу витков обмотки 1, т. е. умножены на
, приведенные к числу витков обмотки 2. Для последующих расчетов x
к23
и r
к23
должны быть приведены к числу витков обмотки 1, т. е. умножены на ![]() Все активные сопротивления должны быть приведены к температуре 75°С (§ 2-6).
Все активные сопротивления должны быть приведены к температуре 75°С (§ 2-6).
Складывая (2-114) и (2-116) и вычитая (2-118), найдем:
Складывая (2-114) и (2-118) и вычитая (2-116), найдем:
Складывая (2-116) и (2-118) и вычитая (2-114), найдем:
Аналогично из (2-115), (2-117) и (2-119) находим:
![]()
![]()
![]()
Если в (2-120) —(2-122) подставить соответственно двухобмоточному трансформатору
![]()
![]()
![]()
то мы получим для х 1 , х 2 , х 3 такие же выражения, что и в (2-112).
При расчетном определении параметров трехобмоточного трансформатора сначала рассчитываются х к12 , x к13 и х к23 так же, как для двухобмоточного трансформатора [формула (2-75)], затем по (2-120) — (2-122) определяются х 1 , х 2 , х 3 . Расчет r 1 , r 2 , r 3 производится обычными методами. Отметим особенности трехобмоточного трансформатора, имеющего коаксиальное расположение обмоток, наиболее часто применяемое на практике (рис. 2-51). Здесь следует различать одностороннее расположение вторичных обмоток относительно первичной, когда первичной является обмотка 1 или 3 , и двустороннее расположение вторичных обмоток относительно первичной, когда первичной является обмотка 2 . В первом случае изменение нагрузки одной вторичной обмотки заметно влияет на напряжение другой вторичной обмотки, во втором случае это влияние почти исчезает. Сказанное может быть подтверждено следующими приближенными расчетами.
Примем, что толщина каждой обмотки бесконечно мала, длины их по оси одинаковы и что диаметры окружностей D 12 , D 13 , D 23 приблизительно равны между собой (рис. 2-54).
Рис. 2-54. К определению х 1 , х 2 , х 3 .
Тогда в соответствии с формулой (2-75) можем написать:
где с — согласно допущениям постоянная величина.
Если подставить в (2-120) — (2-122) приближенные равенства (2-123), то получим:
В действительности при учете толщины обмоток и различия D 12 , D 13 , D 23 величина х 2 получается немного отличающейся от нуля (часто имеет отрицательное значение), но все же она обычно в десятки раз меньше х 1 и х 3 . Приведенные соотношения лишний раз подтверждают условный характер величин х 1 , х 2 , x 3 как индуктивных сопротивлений рассеяния обмоток.
Так как для большого трансформатора значения r 1 , r 2 , r 3 относительно малы, то можно в схеме замещения такого трансформатора (рис. 2-52) с расположением обмоток, показанным на рис. 2-51, принять Z 2 » 0.
в) Векторные диаграммы и процентные изменения вторичных напряжений.
В соответствии с уравнениями (2-110) и (2-111), которые с учетом равенства ![]() можно написать в следующем виде:
можно написать в следующем виде:
на рис. 2-55,а , б и в построены векторные диаграммы трехобмоточного трансформатора.
Рис. 2-55. Векторные диаграммы трехобмоточного трансформатора (к определению изменения вторичных напряжений).
При помощи этих диаграмм могут быть определены изменения вторичных напряжений:
При определении DU
12
и DU
13
угол b (рис. 2-55,а
) принимается равным нулю и расчет производится по формулам, составленным аналогично формулам (2-55) и (2-60) для двухобмоточного трансформатора. Значения m
к
и n
к
[см. (2-55)] находим, проектируя падения напряжения в обмотках на линии, являющиеся продолжениями векторов ![]() и
и ![]() и на линии, им перпендикулярные (рис. 2-55,б
и в
). Расчетные формулы получаются в следующем виде:
и на линии, им перпендикулярные (рис. 2-55,б
и в
). Расчетные формулы получаются в следующем виде:
Здесь
![]()
![]()
![]()
![]()
![]() и
и ![]()
в формуле (2-130);
![]() и
и ![]()
в формуле (2-131).
г) Соотношение мощностей.
За номинальную мощность трехобмоточного трансформатора принимается мощность наиболее мощной обмотки. К этой мощности приводятся все напряжения короткого замыкания u к12 , u к23 , u к13 , которые указываются на щитке трансформатора. Для трехфазных трехобмоточных трансформаторов обычно применяется схема соединения обмоток Y0 /Y0 /D-12-11, а для однофазных — 1/1/1-12-12.
Мощности отдельных обмоток устанавливаются в зависимости от условий эксплуатации. Наиболее часто встречаются следующие соотношения мощностей отдельных обмоток в процентах от номинальной мощности:
| 1-я обмотка |
2-я обмотка |
3-я обмотка |
| 100 |
100 |
100 |
| 100 |
100 |
66,7 |
| 100 |
66,7 |
100 |
| 100 |
66,7 |
66,7 |
2-18. Параллельная работа трансформаторов
Параллельное соединение трансформаторов необходимо для обеспечения бесперебойного энергоснабжения при выключении трансформаторов для ремонта. Далее оно целесообразно в тех случаях, когда мощность нагрузки сильно изменяется в течение суток; тогда можно в зависимости от общей нагрузки оставлять в работе столько трансформаторов, чтобы потери в них были наименьшими. При расширении подстанций, а также на мощных подстанциях устанавливается несколько трансформаторов, которые включаются на параллельную работу. При такой работе обмотки трансформаторов с первичной и вторичной стороны присоединяются к общим шинам, как показано на рис. 2-56.
Рис. 2-56. Схема включения на параллельную работу трансформаторов.
Здесь обмотки высшего напряжения служат в качестве первичных.
На параллельную работу трансформаторы могут быть включены только при соблюдении определенных условий. Эти условия практически сводятся к следующим:
1. равенство номинальных напряжений — первичных и вторичных (равенство коэффициентов трансформации);
2. трансформаторы должны принадлежать к одной и той же группе соединений;
3. равенство номинальных напряжений короткого замыкания.
При соблюдении первых двух условий напряжение между зажимами рубильника (рис. 2-56) до его замыкания равно нулю. В этом случае после включения рубильника никакого уравнительного тока в обмотках трансформаторов не получится.
Можно допустить различие в коэффициентах трансформации трансформаторов, включаемых на параллельную работу, не больше 0,5% от их среднего значения.
Недопустимо включение на параллельную работу трансформаторов, принадлежащих к разным группам соединений, так как результирующая э.д.с. в контуре вторичных обмоток вызовет при этом большой ток, который быстро приведет к чрезмерному нагреванию обмоток трансформаторов.
Соблюдение третьего условия необходимо для того, чтобы общая нагрузка распределялась пропорционально номинальным мощностям параллельно работающих трансформаторов.
Пренебрегая токами холостого хода, можем написать следующие уравнения напряжений:
где ![]() и
и ![]() — коэффициенты трансформации;
— коэффициенты трансформации;
![]() и
и ![]()
— сопротивления корoткoго замыкания со стороны вторичных обмоток.
Так как I2 = I 2 I + I 2 II , то вместо (2-132) и (2-133) можно написать:
Решая (2-132) и (2-132а ) в отношении I 21 , а (2-133) и (2-133а ) в отношении I 211 , получим:
![]()
Полученные равенства показывают, что ток каждого трансформатора состоит из уравнительного тока, обусловленного различием коэффициентов трансформации, и тока нагрузки. Очевидно, что уравнительный ток будет меть место и при отсутствии нагрузки (при I 2 = 0).
Из (2-134) также видно, что при k I = k II токи распределяются обратно пропорционально сопротивлениям короткого замыкания. В этом случае мы можем написать в соответствии со схемой, представленной на рис. 2-57,
![]()
Рис. 2-57. Схема для определения токов параллельно работающих трансформаторов.
Значение разности углов (φк II – φк I ) в обычных случаях (если мощности параллельно работающих трансформаторов не сильно отличаются одна от другой) близко к нулю.
Переходя от отношения комплексов к отношению их модулей, имеем:
![]()
Если обе части равенства умножить на ![]() и левую часть, кроме того, на
и левую часть, кроме того, на ![]() , то получим:
, то получим: ![]()
Из полученного соотношения следует, что мощности параллельно работающих трансформаторов, выраженные в долях их номинальных мощностей, относятся друг к другу, как обратные значения номинальных напряжений короткого замыкания. Если u
к
I
![]() u
к
II
, то относительная нагрузка будет больше у того трансформатора, у которого u
к
меньше. Практически допускается различие между номинальными напряжениями короткого замыкания трансформаторов, включаемых на параллельную работу, в ±10% от их среднего значения.
u
к
II
, то относительная нагрузка будет больше у того трансформатора, у которого u
к
меньше. Практически допускается различие между номинальными напряжениями короткого замыкания трансформаторов, включаемых на параллельную работу, в ±10% от их среднего значения.
Приведенные выводы могут быть распространены на любое число параллельно, работающих трансформаторов.
При включении на параллельную работу трехобмоточных трансформаторов необходимо соблюдение указанных условий для соответствующих пар обмоток обоих трансформаторов и, кроме того, необходимо, чтобы оба трансформатора имели одинаковое расположение вторичных обмоток относительно первичной. При включении двухобмоточного трансформатора на параллельную работу с трехобмоточным должны быть соблюдены те же условия для двухобмоточного трансформатора и соответствующих двух обмоток трехобмоточного трансформатора и, кроме того, последний должен иметь двустороннее расположение вторичных обмоток относительно первичной (§ 2-17).
2-19. Несимметричная нагрузка трехфазных трансформаторов
В обычных условиях эксплуатации трехфазной сети нагрузку удается распределить достаточно равномерно на все три фазы Однако бывают случаи, когда нагрузки фаз сильно отличаются одна от другой, например при питании мощных однофазных печей При этом системы токов и напряжений получаются несимметричными. Резко несимметричную систему токов получим, очевидно, при несимметричных коротких замыканиях: двухфазном и однофазном.
При исследовании работы трансформаторов, имеющих несимметричную нагрузку, применяется метод симметричных составляющих. Он также широко применяется при исследовании несимметричных режимов работы трехфазных генераторов и двигателей и позволяет наиболее просто и достаточно точно разрешить многие из возникающих при этом вопросов.
а) Метод симметричных составляющих.
Мы здесь сообщим краткие сведения о методе симметричных составляющих. Сущность этого метода состоит в том, что каждый фазный ток (или фазное напряжение) заменяется тремя его составляющими:
Величины ![]() принимаются равными друг другу и равными одной трети суммы фазных токов:
принимаются равными друг другу и равными одной трети суммы фазных токов:
Эти величины называются составляющими нулевой последовательности, так как они образуют три равных временных вектора с нулевым сдвигом между ними.
Если из каждого тока данной несимметричной системы вычесть его нулевую составляющую, то получим новую систему токов, сумма которых согласно (2-138) равна нулю:
Учитывая теперь (2-135) — (2-137), можем написать:
Здесь системы токов, стоящих в скобках, будем считать трехфазными симметричным системами. Однако, если принять, что порядки чередования фаз той и другой систем одинаковы, то их сумма даст симметричную систему, что в общем случае не будет соответствовать системе токов уравнения (2-139). Следовательно, мы должны считать, что одна из систем токов (2-140) имеет порядок чередования фаз, обратный по отношению к порядку чередования фаз другой. В соответствии с этим система токов ![]() называется системой прямой последовательности [порядок чередования этих токов обычно такой же, как и токов уравнения (2-139)], а система токов
называется системой прямой последовательности [порядок чередования этих токов обычно такой же, как и токов уравнения (2-139)], а система токов ![]() — системой обратной последовательности.
— системой обратной последовательности.
Для удобства вычислений вводится комплексный коэффициент
Умножение вектора на этот коэффициент не изменяет его абсолютного значения, но изменяет его аргумент на ![]() т. е. поворачивает вектор на угол
т. е. поворачивает вектор на угол ![]() в сторону вращения векторов. Очевидно, что умножение на а
2
дает поворот вектора на угол
в сторону вращения векторов. Очевидно, что умножение на а
2
дает поворот вектора на угол ![]() в ту же сторону. Также очевидно, что
в ту же сторону. Также очевидно, что
Уравнения (2-135) — (2-137) после введения в них коэффициентов а и а 2 и с учетом (2-138) перепишем в следующем виде
Написанные уравнения позволяют при заданных токах найти их симметричные составляющие. Составляющие нулевой последовательности ![]() определяются по (2-138). Составляющие прямой и обратной последовательностей определяются следующим образом.
определяются по (2-138). Составляющие прямой и обратной последовательностей определяются следующим образом.
Умножим (2-144) на а и (2-145) на а 2 . Сложив полученные уравнения с (2-143) и учитывая (2-142), будем иметь:
Если умножить (2-144) на а 2 и (2-145) на а , то, сложив три уравнения, получим:
Таким образом, по (2-138), (2-146) и (2-147) при заданных токах ![]() могут быть определены их симметричные составляющие (на рис 2-58 показаны токи
могут быть определены их симметричные составляющие (на рис 2-58 показаны токи ![]() и их симметричные составляющие).
и их симметричные составляющие).
Рис. 2-58. Несимметричная система таков ![]() и их симметричные составляющие.
и их симметричные составляющие.
Аналогичные уравнения получаются для симметричных составляющих заданной системы напряжений ![]() Фазные токи или напряжения в общем случае имеют составляющие всех трех последовательностей: линейные токи (при соединении треугольником) и напряжения могут иметь только составляющие прямой и обратной последовательностей.
Фазные токи или напряжения в общем случае имеют составляющие всех трех последовательностей: линейные токи (при соединении треугольником) и напряжения могут иметь только составляющие прямой и обратной последовательностей.
В обычных случаях системы симметричных составляющих токов или напряжений можно рассматривать независимо одна от другой и при исследовании несимметричной нагрузки исходить из принципа наложения. Если, например, трехфазная система сопротивлений симметрична, то можно считать, что токи любой последовательности вызовут падения напряжения — активные и реактивные — только той же самой последовательности. В применении к трехфазным трансформаторам мы должны считать Z 12 = const, т. е пренебречь изменением насыщения, или считать Z 12 = ∞, т е. пренебречь током холостого хода.
б) Несимметричная нагрузка трехфазного трансформатора при соединении его обмоток Y/ Y0 .
Будем пренебрегать током холостого хода при всех случаях несимметричной нагрузки трансформатора и при всех соединениях его обмоток и будем считать, что нам заданы линейные первичные напряжения и вторичные токи.
В трансформаторах сопротивления Z 1 , Z 2 и Z к для токов прямой последовательности равны тем же сопротивлениям для токов обратной последовательности Это следует из того, что сопротивления трансформатора не изменятся, если мы при его симметричной нагрузке поменяем местами два провода на его первичной стороне.
Рассматриваемому здесь случаю соответствует схема, показанная на рис 2-59.
Рис. 2-59. Несимметричная нагрузка трансформатора при соединении его обмоток Y/Y0 .
Согласно этой схеме напишем уравнения токов:
Система вторичных токов согласно (2-138) имеет составляющие нулевой последовательности
Соотношения между первичными и вторичными токами определяются следующим образом.
Обратимся к рис. 2-60, где схематически изображен трансформатор с условными положительными направлениями токов в его обмотках.
Рис. 2-60. К определению соотношений между первичными и вторичными токами.
Так как мы пренебрегаем током холостого хода, то согласно закону полного тока полный ток сквозь любой магнитный контур по сердечнику (например, показанный пунктиром на рис. 2-60) равен нулю. Поэтому, считая w 1 = w 2 , мы можем написать для контуров, образованных стержнями А — В и А — С и соответствующими ярмами, уравнения:
Из этих уравнений и уравнений (2-148) и (2-149) получаем:
![]()
![]()
Заменяя токи их симметричными составляющими и учитывая (2-150), будем иметь:
![]()
![]()
Из (2-154) следует, что в трансформаторе при данном соединении его обмоток трансформируются только токи прямой и обратной последовательностей, токи же нулевой последовательности будут иметь место только во вторичной обмотке. Поэтому в магнитном контуре, проходящем по любому из стержней сердечника и вне его, н.с. обмоток не будут уравновешены. Здесь возникает магнитное поле, созданное н. с. I a0 . На рис. 2-61 показана приближенная картина этого поля масляного трансформатора.
Рис. 2-61. Приближенная картина поля, созданной токами нулевой последовательности.
Мы можем считать, что в стержнях трансформатора имеют место потоки нулевой последовательности Ф0
, созданные токами нулевой последовательности и накладывающиеся на потоки в стержнях ![]() соответствующие напряжениям прямой и обратной последовательностей, приложенным с первичной стороны. Очевидно, что
соответствующие напряжениям прямой и обратной последовательностей, приложенным с первичной стороны. Очевидно, что ![]() так же как и наведенные ими э.д.с.
так же как и наведенные ими э.д.с.
![]() (2-155)
(2-155)
На рис. 2-62 представлена диаграмма э.д.с., наведенных в фазах обмоток указанными потоками.
Рис. 2-62. Векторная диаграмма э.д.с. в oбмотках трансформатора при несимметричной нагрузке.
Теперь уравнения напряжений для первичной обмотки напишутся следующим образом:
![]()
![]()
Заменим
где Z 0 = r 0 + jx 0 — полное сопротивление нулевой последовательности (x 0 обусловлено полем тока Ia 0 , а r 0 — магнитными потерями от этого поля).
Сложив уравнения (2-156) и, учитывая при этом (2-155), (2-148) и (2-157), получим:
Для линейных (междуфазных) напряжений можем написать:
![]()
![]()
Отсюда с учетом (2-158) получим:
![]()
![]()
В соответствии с (2-160) на рис. 2-63 построена векторная диаграмма первичных напряжений.
Рис. 2-63. Векторная диаграмма первичных напряжений.
Из нее мы видим, что вследствие наличия токов нулевой последовательности потенциал нулевой точки первичной обмотки сместился на величину ![]() из центра тяжести треугольника линейных напряжений.
из центра тяжести треугольника линейных напряжений.
Учитывая (2-160) в (2-154) напишем уравнения напряжений для вторичной обмотки:
![]()
или, так как ![]() и
и ![]() , а
, а ![]()
где
Для двух других фаз уравнения напряжений напишутся аналогично:
Уравнения (2-161), (2-163) и (2-164) показывают, что смещение потенциала нулевой точки вторичной обмотки, вызванное токами нулевой последовательности, равно ![]() . Оно несколько больше, чем для первичной обмотки, где это смещение равняется
. Оно несколько больше, чем для первичной обмотки, где это смещение равняется ![]() . Оба сопротивления Z
0
и Z
н
называются сопротивлениями нулевой последовательности; они практически мало отличаются одно от другого. Для трехфазных стержневых трансформаторов с масляным охлаждением
. Оба сопротивления Z
0
и Z
н
называются сопротивлениями нулевой последовательности; они практически мало отличаются одно от другого. Для трехфазных стержневых трансформаторов с масляным охлаждением
Если первичные линейные напряжения образуют симметричную систему, то, очевидно, и фазные напряжения ![]()
![]() ,
, ![]() образуют симметричную систему. Из уравнении: (2-161), (2-163) и (2-164) следует, что в этом случае симметрия линейных вторичных напряжений
образуют симметричную систему. Из уравнении: (2-161), (2-163) и (2-164) следует, что в этом случае симметрия линейных вторичных напряжений ![]() будет нарушаться только из-за наличия токов обратной последовательности: в системе линейных вторичных напряжение мы будем иметь наряду с составляющими прямой последовательности составляющие обратной последовательности, модуль которых равен
будет нарушаться только из-за наличия токов обратной последовательности: в системе линейных вторичных напряжение мы будем иметь наряду с составляющими прямой последовательности составляющие обратной последовательности, модуль которых равен ![]()
В системе фазных вторичных напряженна мы будем иметь, как это следует из (2-161), (2-163) и (2-164), все три симметричные составляющие:
![]()
![]()
![]()
Если поставить условием, чтобы было ![]() то необходимо иметь ток I
0
в нулевом проводе при
то необходимо иметь ток I
0
в нулевом проводе при ![]() [см (2-165)] не больше 0,25I
н
, что вытекает из следующих соотношений:
[см (2-165)] не больше 0,25I
н
, что вытекает из следующих соотношений:
![]()
![]()
Для расчета сопротивления нулевой последовательности z
н
мы не имеем надежных методов, однако опытным путем величина zн
определяется достаточно точно. Для этого нужно собрать схему, показанную на рис. 2-64. Вторичная обмотка должна быть присоединена к источнику однофазного тока. Ток в ее фазах будет соответствовать току нулевой последовательности. Следовательно, измерив ток I
, напряжение U
и мощность P
при разомкнутой первичной обмотке (рубильник разомкнут), найдем ![]() а также r
н
и x
н
. Справа на рис. 2-64 показана соответствующая схема замещения [см. (2-162)].
а также r
н
и x
н
. Справа на рис. 2-64 показана соответствующая схема замещения [см. (2-162)].
Рис. 2-64. Схема для опытного определения сопротивления нулевой последовательности.
В трехфазной группе, состоящей из трех однофазных трансформаторов, мы не имеем магнитной связи между фазами. В трехфазном броневом трансформаторе эта связь выражена очень слабо. Поэтому при соединении обмоток Y/Y0 в таких трансформаторах мы имели бы незначительное магнитное сопротивление для потока Ф0 , который здесь полностью проходил бы по стальному сердечнику, и сопротивление z н было бы очень велико: z н = z 12 . Следовательно, даже при малом значении I а0 мы получили бы значительные смещения потенциалов нулевых точек вторичной и первичной обмоток. Поэтому ни трехфазная группа, ни трехфазный броневой трансформатор с соединением обмоток Y/Y0 на практике не применяются.
Рассмотрим крайний случай несимметричной нагрузки — однофазное короткое замыкание (рис. 2-65).
Рис. 2-65. Однофазное короткое замыкание.
Здесь имеем ![]()
![]()
![]() следовательно, согласно (2-138), (2-146) в (2-147) получим:
следовательно, согласно (2-138), (2-146) в (2-147) получим:
Подставив в (2-161)
![]()
![]()
![]()
получим формулу для тока однофазного короткого замыкания:
Токи в первичной обмотке согласно (2-153) с учетом (2-166):
в) Несимметричная нагрузка трехфазного трансформатора при соединении обмоток
![]() /Y0
.
/Y0
.
Рассматриваемому случаю соответствует схема, представленная на рис. 2-66.
Рис. 2-66. Несимметричная нагрузка трансформатора при соединения его обмоток ![]() /Y0
.
/Y0
.
На вторичной стороне мы имеем такие же токи, как в предыдущем случае (рис. 2-59). Для них действительно уравнение (2-149), т. е. в общем случае система вторичных токов имеет все три симметричные составляющие.
В первичной обмотке, соединенной треугольником, фазные токи также будут иметь наряду с составляющими прямой и обратной последовательностей составляющие нулевой последовательности. Последние возникнут потому, что э.д.с. ![]() (э.д.с. нулевой последовательности) в фазах, соединенных треугольником, направлены все в одну сторону в любой момент времени. В магнитном отношении они должны уравновесить токи нулевой последовательности вторичной обмотки. Следовательно, н.с. обмоток на каждом стержне будут взаимно уравновешиваться, первичная и вторичная обмотки каждой фазы могут рассматриваться как обмотки отдельного однофазного трансформатора.
(э.д.с. нулевой последовательности) в фазах, соединенных треугольником, направлены все в одну сторону в любой момент времени. В магнитном отношении они должны уравновесить токи нулевой последовательности вторичной обмотки. Следовательно, н.с. обмоток на каждом стержне будут взаимно уравновешиваться, первичная и вторичная обмотки каждой фазы могут рассматриваться как обмотки отдельного однофазного трансформатора.
Первичные фазные токи равны:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Линейные токи, конечно, не будут иметь составляющих нулевой последовательности:
![]()
![]()
![]()
Связь между вторичными и первичными напряжениями устанавливается уравнениями (2-161), (2-163) и (2-164). Здесь ![]() ,
, ![]() ,
, ![]() — напряжения, приложенные к фазам первичной обмотки: сопротивление Zн
при соединении обмоток Y/Y0
значительно меньше, чем при Y/Y0
, так как оно в основном определяется полем рассеяния, таким же, как и поле рассеяния, созданное токами прямой или обратной последовательности. Значение z
н
при соединении обмоток
— напряжения, приложенные к фазам первичной обмотки: сопротивление Zн
при соединении обмоток Y/Y0
значительно меньше, чем при Y/Y0
, так как оно в основном определяется полем рассеяния, таким же, как и поле рассеяния, созданное токами прямой или обратной последовательности. Значение z
н
при соединении обмоток ![]() /Y0
может быть найдено опытным путем. Используется та же схема, что и на рис. 2-64, но рубильник на вторичной стороне при этом должен быть замкнут. Здесь также
/Y0
может быть найдено опытным путем. Используется та же схема, что и на рис. 2-64, но рубильник на вторичной стороне при этом должен быть замкнут. Здесь также ![]()
Схема замещения для z
н
при соединении обмоток ![]() /Y0
, приведена на рис. 2-67.
/Y0
, приведена на рис. 2-67.
Рис. 2-67. Схема замещения для Z
н
трансформатора при соединении его обмоток ![]() /Y0
.
/Y0
.
Согласно схеме имеем:

так как Z 0 во много раз больше Z 1 .
Смещение потенциала нулевой точки вторичной обмотки (Iа0
z
н
) будет значительно меньше, поэтому, если ожидается большой ток нулевой последовательности, следует соединению обмоток Y/Y0
предпочесть соединение ![]() /Y0
.
/Y0
.
г) Несимметричная нагрузка трансформатора при соединении обмоток
Y/![]() /Y0
.
/Y0
.
Соответствующая схема представлена на рис. 2-68.
Рис. 2-68. Несимметричная нагрузка трехобмоточного трансформатора при соединении обмоток Y/![]() /Y.
/Y.
Мы здесь рассмотрим случай, когда со вторичной стороны нагружена только одна вторичная обмотка, соединенная звездой с выведенной нулевой точкой. Как и в предыдущем случае, в обмотке, соединенной треугольником, мы будем иметь токи нулевой последовательности, в первичной обмотке будут токи прямой и обратной последовательностей. Следовательно, н.с. обмоток каждой фазы взаимно уравновешиваются и потоки нулевой последовательности практически равны нулю.
Если третья обмотка, соединенная треугольником, используется только как компенсационная для компенсации третьей гармоники в кривой потока, то она должна быть рассчитана на наибольший ток нулевой последовательности с учетом длительности его протекания. Поэтому применение третьей обмотки только как компенсационной в большинстве случаев невыгодно.
д) Несимметричная нагрузка трансформаторов при соединении обмоток
Y/Y, Y/![]() ,
, ![]() /Y.
/Y.
Здесь мы не будем иметь во вторичной и в первичной обмотках токи нулевой последовательности, следовательно, не будем иметь для обмотки, соединенной звездой, смещения потенциала нулевой точки относительно центра тяжести треугольника линейных напряжений При данных соединениях обмоток мы можем рассматривать первичную и вторичную, обмотки каждой фазы как независимый однофазный трансформатор. Уравнения напряжений (2-161), (2-163) и (2-164), если в них взять Iа 0 = 0, могут быть использованы при определении вторичных напряжений для заданных первичных напряжений, вторичных токов (при известных параметрах трансформатора Z к = r к + jx к ). При помощи тех же уравнений могут быть определены фазные и линейные токи при двухфазных коротких замыканиях.
2-20. Переходные процессы в трансформаторах
В предыдущих параграфах рассматривались установившиеся режимы работы трансформаторов, когда значения амплитуд токов, напряжений, э.д.с. и потоков длительно остаются неизменными.
Переходные процессы получаются при переходе от одного установившегося режима работы к другому. Такой переход не совершается мгновенно, так как энергия магнитных и электрических полей, связанных с цепями, различна при различных установившихся режимах, а для конечного изменения энергии полей необходимо некоторое время. Изменение энергии полей сопровождается возникновением так называемых свободных полей и соответствующих им токов и напряжений, накладывающихся на токи и напряжения установившегося режима.
При переходных процессах результирующие токи, а, также напряжения на отдельных частях обмоток могут значительно превышать те же величины при установившихся режимах, что необходимо учитывать при проектировании и эксплуатации трансформаторов и электрических машин.
а) Включение трансформатора.
Будем рассматривать переходный процесс при включении ненагруженного трансформатора. Для этого случая можем написать:
где Ф — полный поток сцепляющийся со всеми витками первичной обмотки, а ψ — угол, определяющий мгновенное значение напряжения в момент включения трансформатора (при t = 0). Так как в трансформаторе со стальным сердечником поток Ф и ток i 1 связаны сложной зависимостью, то приходится искать приближенное решение.
Можем заменить:
где L 1 — статическая индуктивность, являющаяся функцией потока Ф. Теперь уравнение (2-169) примет вид:
Второй член левой части количественно в обычных случаях значительно меньше, чем первый член; поэтому примем, что L 1 не зависит от потока и представляет собой постоянную величину. Тогда получаем уравнение с постоянными коэффициентами, которое решается обычным способом. Его решение состоит из двух слагаемых:
где Ф' — мгновенное значение установившегося потока, а Ф'' — мгновенное значение свободного потока.
Установившийся поток
Рис. 2-69. Изменение потока при наихудших условиях включения трансформатора.
Свободный поток определяется из уравнения
интеграл которого имеет вид:
Постоянная интегрирования С находится из начальных условий. Рассмотрим случай, когда в момент включения в сердечнике трансформатора имел место поток остаточного магнетизма ±Фост . Тогда при t = 0 согласно (2-172) и (2-173)
откуда
![]()
и
Подставляя найденные значения Ф' и Ф" в (2-172), получим:
Наиболее благоприятные условия получаются при включении, когда ![]() (при
(при ![]() ) и Фост
= 0. В этом случае имеем:
) и Фост
= 0. В этом случае имеем:
т. е. с первого же момента устанавливается нормальный поток, а следовательно, и ток холостого хода.
Наихудшие условия включения получим при ψ = 0 (при u 1 = 0) и при Фост направленном против Ф'. В этом случае
Поток Ф достигает наибольшего значения, спустя приблизительно полпериода после включения, т. е. при ωt
![]() π. Если принять Фост
=0,5Фм
, то для наибольшего значения потока можем, следовательно, написать (рис. 2-69):
π. Если принять Фост
=0,5Фм
, то для наибольшего значения потока можем, следовательно, написать (рис. 2-69):
Найдя кривую изменения потока, можно при помощи кривой намагничивания трансформатора (рис. 2-70) построить кривую намагничивающего тока.
Рис. 2-70. К определению «броска тока» при включении по кривой намагничивания трансформатора.
Мы видим, что при наиболее неблагоприятном случае ток холостого хода достигает весьма большого значения, в десятки раз превышающего максимальное значение установившегося тока холостого хода. Такой «бросок тока» следует иметь в виду, например, при опыте холостого хода: токовые цепи прецизионных измерительных приборов во избежание поломки стрелок нужно до включения трансформатора шунтировать
Приведенное решение, как отмечалось, является приближенным, так как не были учтены поле рассеяния, действие вихревых токов и непостоянство L 1 . Однако опыт подтверждает, что броски тока при включении трансформатора достигают указанных значений.
б) Внезапное короткое замыкание.
Наибольшие токи в обмотках трансформатора получаются при трехфазном коротком замыкании. Мы ранее нашли, что установившийся ток короткого замыкания равен I
к
=![]()
При U = U н он достигает весьма большого значения. Оно может быть найдено из следующего соотношения:
где ![]() – номинальное напряжение короткого замыкания.
– номинальное напряжение короткого замыкания.
Задача определений тока для переходного процесса достаточно точно решается при пренебрежении током холостого хода. Мы в этом случае в дифференциальных уравнениях напряжений обмоток
приняв w1 = w2 можем положить i 1 = -i 2 .
Тогда, вычитая (2-184) из (2-183) и исключая i2 при помощи равенства i 1 = -i 2 , получим:
Так как ![]()
![]() где L
к
и r
к
— индуктивность и активное сопротивление при коротком замыкании, то (2-185) можем переписать в следующем виде:
где L
к
и r
к
— индуктивность и активное сопротивление при коротком замыкании, то (2-185) можем переписать в следующем виде:
Таким образом, переходный ток здесь определяется так же, как для реактивной катушки, включенной на синусоидальное напряжение.
Он состоит из установившегося тока и свободного, затухающего в соответствии с постоянной времени ![]()
Если пренебречь затуханием свободного, тока, то в самом неблагоприятном случае мгновенное значение тока короткого, замыкания i
м
будет в 2 раза, а с учетом затухания свободного тока — в 1,5![]() 1,8 раза больше амплитуды установившегося тока, т. е.
1,8 раза больше амплитуды установившегося тока, т. е.
Если, например, u
к
= 6%, то ![]()
Такие токи в обмотках трансформатора создают очень большие электромагнитные силы, опасные в отношении механической прочности обмоток. При конструировании обмоток их необходимо принимать во внимание, особенно в случае мощных трансформаторов, где эти силы на единицу длины обмотки иногда получаются настолько большими, что приходится для таких трансформаторов брать повышенные значения u к , чтобы уменьшить ток короткого замыкания. Кроме того, следует по возможности выполнять трансформаторы с обмотками одинаковой высоты. Если высоты обмоток неодинаковы, то возникают большие аксиальные силы, которые могут привести к разрушению изоляции с последующим пробоем ее.
в) Перенапряжения в трансформаторах.
Перенапряжения, возникающие в трансформаторах, могут быть вызваны различными причинами. Из них главнейшие: процессы при включении и выключении трансформатора; короткие замыкания и повторные заземляющие дуги на линии передачи, к которой присоединен трансформатор; грозовые разряды вблизи линии. Наибольшие перенапряжения в обмотках трансформатора получаются при грозовых разрядах. Они называются атмосферными перенапряжениями.
В большинстве случаев грозовые разряды создают в линии апериодические электрические импульсы большой амплитуды и малой продолжительности действия. Примерная форма такого импульса показана на рис. 2-71.
Рис. 2-71. Примерная форма кривой электрического импульса при грозовых разрядах.
Здесь время подъема напряжения от нуля до максимума, достигающего пяти- шестикратного значения амплитуды фазного напряжения, измеряется иногда десятыми долями микросекунды (отрезок![]() ). Соответствующая часть кривой называется фронтом волны. Она может рассматриваться как четверть периода периодического процесса весьма высокой частоты. При такой частоте мы можем считать, что ток будет проходить только по емкостным связям между витками отдельных катушек и между катушками обмотки высшего напряжения, а также между катушками и сталью. Обмотку низшего напряжения при этом приближенно можно принять заземленной, так как она соединена со сталью большими емкостями (т. е. малыми емкостными сопротивлениями). Токами по индуктивным и активным сопротивлениям катушек мы пренебрегаем: при очень высокой частоте они малы по сравнению с емкостными токами.
). Соответствующая часть кривой называется фронтом волны. Она может рассматриваться как четверть периода периодического процесса весьма высокой частоты. При такой частоте мы можем считать, что ток будет проходить только по емкостным связям между витками отдельных катушек и между катушками обмотки высшего напряжения, а также между катушками и сталью. Обмотку низшего напряжения при этом приближенно можно принять заземленной, так как она соединена со сталью большими емкостями (т. е. малыми емкостными сопротивлениями). Токами по индуктивным и активным сопротивлениям катушек мы пренебрегаем: при очень высокой частоте они малы по сравнению с емкостными токами.
В этом случае обмотка высшего напряжения, обычно состоящая из последовательно соединенных катушек, может быть заменена цепочкой емкостей, показанной на рис. 2-72,а , где С 3 — емкости между катушками и землей; С к — емкости между катушками.
Рис. 2-72. Приближенная схема замещения трансформатора при высокочастотных процессах (a ); кривые распределения напряжения вдоль обмотки (б ).
Распределение напряжения вдоль обмотки получается неравномерным (кривая а на рис. 2-72,б ), так как токи, проходящие по емкостям С к , будут неодинаковы. Они больше вблизи линейного конца и меньше вблизи заземленной нейтрали. Показанное распределение напряжения называется емкостным.
После затухания свободных полей получим равномерное распределение напряжения вдоль обмотки (кривая b на рис. 2-72,б ). Теперь оно будет обусловлено только индуктивными и активными сопротивлениями катушек и будет соответствовать установившемуся режиму работы при нормальной частоте тока.
Кривая а на рис. 2-72,б показывает, что при начальном распределении напряжения большая его часть приходится на первые катушки, и, следовательно, их изоляция подвергается наибольшей опасности. Опыт это подтверждает, так как пробои изоляции чаще всего имеют место именно на первых катушках, поэтому их часто выполняют с усиленной изоляцией.
Переход от начального распределения напряжения к установившемуся (от кривой а к кривой b ) сопровождается колебательными процессами и перенапряжениями резонансного характера, так как здесь вступают в действие не только емкостные, но и индуктивные связи между катушками. Опытные исследования этих процессов показывают, что высокие градиенты электрического поля получаются также для средних и нижних катушек, но все же наибольшие значения они имеют для начальных катушек.
В крупных трансформаторах на напряжения 115, 220 кВ и выше применяется так называемая емкостная компенсация. Сущность ее заключается в применении добавочных емкостей, выполненных в виде особой формы экранов, окружающих обмотку высшего напряжения (рис. 2-73,а ).
Рис. 2-73. Частичная емкостная компенсация катушечной обмотки (a ); соответствующая схема замещения (б ).
При этом получается схема замещения, показанная на рис. 2-73,б . Емкости С 'э , С "э , С "'э ,…можно подобрать таким образом, чтобы токи по емкостям С к были приблизительно одинаковы хотя бы на протяжении 40 — 50% длины обмотки. Тогда начальное распределение становится более равномерным и перенапряжения между катушками будут значительно снижены.
Высоковольтные трансформаторы с емкостной компенсацией, конструкция которых разработана на заводах советской электропромышленности, являются достаточно надежными, что подтверждается длительным сроком их эксплуатации на линиях Советского Союза.
2-21. Трансформаторы специального назначения
а) Измерительные трансформаторы.
1. Трансформаторы напряжения.
Трансформаторы напряжения (ТН на рис. 2-74) служат для понижения напряжения (обычно до 100 — 150 В), так как вольтметры и катушки напряжения ваттметров и счетчиков (или реле) не могут быть включены непосредственна на высокое напряжение из-за недостаточной изоляции измерительных приборов и необходимости обеспечить безопасность обслуживающего персонала.
Рис. 2-74. Схема включения трансформаторов напряжения (ТН) и тока (ТТ).
Они выполняются как двухобмоточные трансформаторы и электрически отделяют цепь приборов от цепи высокого напряжения; их вторичная цепь надежно заземляется.
По принципу действия трансформаторы напряжения не отличаются от ранее рассмотренных двухобмоточных трансформаторов. Для их исследования можно применить векторные диаграммы (например, рис. 2-14) или уравнения напряжений и токов (2-41), (2-42) и (2-43). Из этих уравнений следует:
где ![]() — комплексный коэффициент;
— комплексный коэффициент;
 — сопротивление прибора, приведенное к числу витков первичной обмотки.
— сопротивление прибора, приведенное к числу витков первичной обмотки.
При расчете трансформатора напряжения и его выполнении стремятся к тому, чтобы погрешности, вносимые им в измерения, были как можно меньше. Различают следующие погрешности измерения: погрешность напряжения

и угловую погрешность δu
, равную углу между ![]() и
и ![]() (δu
измеряется в минутах и принимается положительным, когда
(δu
измеряется в минутах и принимается положительным, когда ![]() опережает
опережает![]() ).
).
Из (2-187) следует, что обе погрешности fu
и δu
будут тем меньше, чем больше сопротивление прибора ![]() , чем меньше Z
1
, и
, чем меньше Z
1
, и ![]() и чем ближе С
1
к единице.
и чем ближе С
1
к единице.
Трансформаторы напряжения имеют максимальные погрешности в зависимости от класса точности, установленные ГОСТ: класс 0,5 — fu = ±0,5% и δu = ±20' ; класс 1 — fu = ±1%, и δu = ±40' ; класс 3 — fu = ±3% (δu не нормируется). Прецизионные трансформаторы напряжения для точных лабораторных измерений имеют fu » ±0,2% и δu » ±10'.
Номинальные мощности трансформаторов напряжения лежат примерно в пределах 25 — 300 ВА. Они обычно могут быть длительно нагружены по условиям нагрева (без соблюдения точности в отношении fu и δu ) до мощности, в 5 — 8 раз превышающей номинальную.
2. Трансформаторы тока.
Трансформаторы тока (ТT на рис. 2-74) также выполняются в виде двухобмоточных трансформаторов. Их первичная обмотка включается в цепь последователи с потребителями, ток которых надо измерить; во вторичную обмотку включаются амперметр, реле, а при измерении мощности и энергии — токовые катушки ваттметра и счетчика. Все приборы во вторичной цепи соединяются последовательно.
При помощи трансформатора тока цепь приборов электрически отделяется от первичной цепи и вторичная обмотка надежно заземляется, что необходимо, если первичная обмотка включается в цепь высокого напряжения.
Отношение токов трансформатора тока практически равно обратному отношению чисел витков:![]() Последнее обычно подбирается таким образом, чтобы при номинальном первичном токе I
1н
номинальный вторичный ток был равен 5 или 1 А. При больших значениях I
1н
часто выбирается w
1
= l. Получается в этом случае одновитковый трансформатор тока. Здесь первичной обмоткой служит шина (или круглый проводник), которая проходит внутри сердечника; на сердечнике помещается вторичная обмотка с числом витков w
2
.
Последнее обычно подбирается таким образом, чтобы при номинальном первичном токе I
1н
номинальный вторичный ток был равен 5 или 1 А. При больших значениях I
1н
часто выбирается w
1
= l. Получается в этом случае одновитковый трансформатор тока. Здесь первичной обмоткой служит шина (или круглый проводник), которая проходит внутри сердечника; на сердечнике помещается вторичная обмотка с числом витков w
2
.
Исследование трансформатора тока может быть проведено с помощью схемы замещения (рис. 2-17) или уравнений напряжении и токов (2-41), (2-42) и (2-43).
Из этих уравнений следует:
где  — сопротивление нагрузки (всех последовательно соединенных приборов), приведенное к числу витков первичной обмотки.
— сопротивление нагрузки (всех последовательно соединенных приборов), приведенное к числу витков первичной обмотки.
Равенство (2-188) показывает, что отношение токов будет тем ближе к обратному отношению чисел витков, чем меньше ![]() и
и ![]() по сравнению с Z
12
. Поэтому стремятся к уменьшению суммы (
по сравнению с Z
12
. Поэтому стремятся к уменьшению суммы (![]() +
+![]() ) и увеличению Z
12
. Последнее, как известно, зависит от индуктивного сопротивления взаимной индукции x
12
для увеличения которого надо снизить магнитное сопротивление главному по току в сердечника трансформатора, что достигается за счет уменьшения его насыщения.
) и увеличению Z
12
. Последнее, как известно, зависит от индуктивного сопротивления взаимной индукции x
12
для увеличения которого надо снизить магнитное сопротивление главному по току в сердечника трансформатора, что достигается за счет уменьшения его насыщения.
При трансформаторах тока различают следующие погрешности измерения:
токовую погрешность

и угловую погрешность di
, (равную углу сдвига по фазе между ![]() и
и ![]() (di
измеряется в минутах и принимается положительным, когда
(di
измеряется в минутах и принимается положительным, когда ![]() опережает
опережает![]() ). Токовая и угловая погрешности изменяются с изменением тока I
1
и
). Токовая и угловая погрешности изменяются с изменением тока I
1
и ![]() . Поэтому при точных измерениях желательно иметь калибровочные кривые: fi
,
. Поэтому при точных измерениях желательно иметь калибровочные кривые: fi
, 
В зависимости от допускаемых погрешностей согласно ГОСТ различаются пять классов точности трансформаторов тока 0,2; 0,5; 1; 3 и 10.
Приведенные числа указывают допускаемую для данного класса токовую погрешность в процентах при номинальном первичном токе. Угловая погрешность при том же первичном токе не должна быть соответственно больше 10, 40 и 80 минут для первых грех классов; для классов 3 и 10 она не нормируется.
Первичные номинальные токи стандартизованы в пределах 5 ![]() 15000 А. Вторичные номинальные токи имеют два стандартных значения: 5 и 1 А. При токе 5 А общее сопротивление нагрузки колеблется в пределах 0,2
15000 А. Вторичные номинальные токи имеют два стандартных значения: 5 и 1 А. При токе 5 А общее сопротивление нагрузки колеблется в пределах 0,2 ![]() 2 Ом, а при токе I А — 5
2 Ом, а при токе I А — 5![]() 30 Ом.
30 Ом.
Трансформаторы тока должны быть механически достаточно прочными, чтобы выдержать электродинамические воздействия, возникающие при аварийном повышении первичного тока.
Особенностью трансформатора тока в отличие от трансформатора напряжения является то, что его магнитный поток при неизменном токе в первичной обмотке и переменном сопротивлении нагрузки будет изменяться. При большом сопротивлении нагрузки магнитный поток трансформатора тока может возраст до чрезмерного значения. Режим работы при разомкнутой вторичной обмотки следует считать аварийным, так как при этом магнитный поток и индукция в сердечнике будут иметь наибольшие значения, что приведет не только к большому увеличению магнитных потерь и, следовательно, нагреву трансформатора, но и к значительному возрастанию напряжения на разомкнутых зажимах вторичной обмотки. В этом, случае магнитный поток будет создаваться только током I
1
(при отсутствии размагничивающего вторичного тока I
2
) и напряжение вторичной обмотки может достигнуть опасных значений. Следует здесь учитывать, что опасным является максимальное значение напряжения, а оно вследствие уплощения кривой потока [см. кривую Ф = f
(t
) при синусоидальном намагничивающем токе на рис. 2-42] может значительно возрасти: например, у многовитковых трансформаторов тока отношение максимального напряжения к действующему часто получается равным 2![]() 2,5, а не
2,5, а не![]() как при синусоидальной кривой напряжения.
как при синусоидальной кривой напряжения.
Кроме того, намагничивание сердечника трансформатора тока в режиме разомкнутой вторичной обмотки при последующем его использовании из-за остаточного магнетизма может давать большие погрешности в измерениях, не соответствующие его калибровочным кривым.
б) Сварочные трансформаторы.
Для дуговой электросварки применяются трансформаторы с повышенным рассеянием или трансформаторы при последовательном включении с дугой регулируемой реактивной катушки (рис. 2-75).
Рис. 2-75. Схема сварочного трансформатора с регулируемой реактивной катушкой.
Повышение рассеяния в трансформаторе достигается размещением первичной и вторичной обмоток на разных стержнях и применением магнитного шунта между стержнями.
Вторичное напряжение сварочного трансформатора выбирается равным 40![]() 70 В, что соответствует напряжению зажигания дуги при переменном токе. Для устойчивого и непрерывного горения дуги требуется, чтобы внешняя характеристика (зависимость напряжения дуги от тока) была резко падающей (рис. 2-76) и чтобы цепь имела большое индуктивное сопротивление.
70 В, что соответствует напряжению зажигания дуги при переменном токе. Для устойчивого и непрерывного горения дуги требуется, чтобы внешняя характеристика (зависимость напряжения дуги от тока) была резко падающей (рис. 2-76) и чтобы цепь имела большое индуктивное сопротивление.
Рис. 2-76. Внешняя характеристика при дуговой сварке.
На практике более часто применяется схема, показанная на рис. 2-75, при которой путем изменения зазора ![]() в сердечнике реактивной катушки можно изменять номинальный ток дуги. Такая схема применяется при многопостовой сварке; при этом она позволяет от одного трансформатора (обычно трехфазного) одновременно питать несколько постов, имеющих каждый свою реактивную катушку.
в сердечнике реактивной катушки можно изменять номинальный ток дуги. Такая схема применяется при многопостовой сварке; при этом она позволяет от одного трансформатора (обычно трехфазного) одновременно питать несколько постов, имеющих каждый свою реактивную катушку.
в) Регулировочные трансформаторы.
Силовые трансформаторы снабжаются ответвлениями обычно от обмотки высшего напряжения, позволяющими изменять ее число витков на ±5%, или на ±2´2,5%. В мощных трансформаторах ответвления, как правило, делаются в середине обмотки (по высоте), так как в этом случае при внезапном коротком замыкании в меньшей степени возрастают аксиальные электромагнитные силы, действующие на обмотки.
На рис. 2-77 показаны различные способы размещения ответвлений от средней части обмотки (по высоте), и здесь же указаны их обозначения согласно ГОСТ.
Рис. 2-77. Способы размещения ответвлений от средней части обмотки (a 1 , б 1 , в 1 ) и соответствующие им переключатели ответвлений (a 2 , б 2 , в 2 ).
В современных трансформаторах переключения производятся при помощи контактного переключателя, имеющего в обычных случаях систему неподвижных контактов, соединенных с ответвлениями, и систему движущихся контактов, замыкающих разные пары неподвижных контактов.
Переключения ответвлений при помощи переключателя, рукоятка которого выводится наружу на крышку или на боковую сторону бака трансформатора, производятся только после его отключения от первичной и вторичной сетей. В трансформаторах устаревших конструкций, еще встречающихся на практике, ответвления выводились наружу при помощи проходных изоляторов с тремя зажимами; здесь переключения делаются вручную.
Регулировочными трансформаторами обычно называются трансформаторы, позволяющие регулировать вторичное напряжение под нагрузкой. Для этого используется переключатель, при котором осуществляется изменение числа витков обмотки без разрыва цепи. Наиболее часто применяется переключатель с токоограничивающим реактором, принципиальная схема которого показана на рис. 2-78.
Рис. 2 78. Схема переключения обмотки трансформатора под нагрузкой с токоограничиваюшим реактором (ответвления от обмотки соединяются с соответственно пронумерованными пластинами переключателя).
При указанном на рисунке положении, когда переключатели а и b соединены с одной и той же пластиной 1 и когда выключатели В 1 и В 2 включены, токи в обеих половинах обмотки реактора Р направлены противоположно друг другу и поэтому сопротивление его мало. При изменении числа витков в процессе переключений сначала выключается B 1 , затем переключатель а переводится на пластину 2 и B 1 снова включается. Теперь по реактору, кроме рабочего, проходит ток, вызванный напряжением между точками 1 и 2 . Но этот ток будет проходить по обеим половинам обмотки реактора в одном и том же направлении, вследствие чего возрастет его индуктивное сопротивление и ток не будет превышать некоторого допустимого значения. После этого выключается В 2 , переключатель b переводится на пластину 2 и В 2 снова включается. Таким образом, перерод переключателей а и b производится практически без разрыва цепи при очень небольших токах. Все переключающее устройство автоматизируется. Оно обычно помещается в специальном баке, пристраиваемом сбоку к главному баку трансформатора.
г) Трансформаторы для радиоэлектроники.
Широкое применение в различных схемах радиоэлектроники находят трансформаторы малой мощности (от нескольких ВА до тысячных долей ВА). К таким трансформаторам предъявляются особые требования, которые могут быть удовлетворены только при применении специальных ферромагнитных материалов и специального устройства их обмоток и сердечника.
В современной электронной аппаратуре, применяемой в разнообразных отраслях техники, используются трансформаторы, преобразующие ток или напряжение электрических сигналов в широком спектре звуковых и сверхзвуковых частот. Они, как и усилители, рассчитанные на этот диапазон частот, условно называются трансформаторами и усилителями низких частот.
Также широко применяются «импульсные трансформаторы», преобразующие кратковременные импульсные токи, продолжительность которых измеряется микросекундами при числе импульсов в секунду до 1 000.
Указанные трансформаторы должны быть устроены таким образом, чтобы искажения, вносимые ими, были как можно меньше, т. е. форма кривой напряжения (или тока) на вторичной стороне должна повторять возможно точнее форму кривой напряжения (или тока) на первичной стороне. При этом приходится брать малые насыщения сердечника трансформатора и учитывать не только активные и индуктивные сопротивления обмоток, но и их емкостные связи, так как при высокой частоте (преобразуемого тока) токи, протекающие через емкости между обмотками, соизмеримы с токами, непосредственно протекающими по обмоткам. Приходится в этом случае применять специальную укладку витков обмоток и иногда особые системы металлических экранов.
В электронной технике находят себе также применение трансформаторы, которые на выходе дают периодически изменяющееся напряжение резко заостренной (пикообразной) формы. Они получили название пик-трансформаторов. Применяются они, например, при регулировании сеточного напряжения тиратронов.
Рассмотрим здесь два возможных исполнения таких трансформаторов, принцип устройства которых показан на рис. 2-79.

Рис. 2-79. Принцип устройства пик-трансформаторов. a — трансформатор с сильно насыщенным сердечником и большим активным сопротивлением в первичной цепи; б — трансформатор с насыщенным стержнем и магнитным шунтом.
В первом случае (а
) трансформатор включается на синусоидальное напряжение u
1
= U
1м
sinwt
через большое активное сопротивление R
. Его сердечник должен быть сильно насыщенным. При холостом ходе ток i
1
в первичной обмотке будет близок к синусоидальному, так как в основном он будет определяться сопротивлением R
. При этом магнитный поток Ф, как показано на рис. 2-79,а
, будет иметь сильно уплощенную форму. Следовательно, э.д.с. ![]() будет иметь пикообразную форму. Во втором случае (б
) вторичная обмотка располагается на стержне, имеющем относительно малое сечение. Параллельно ему устанавливается магнитный шунт с почти линейной характеристикой. При синусоидальном магнитном потоке Ф = Ф2
+Фш
его составляющие Ф2
и Фш
будут несинусоидальными (рис. 2-79,б
); поток Ф2
из-за быстрого насыщения стержня 2
будет иметь уплощенную форму, при которой э.д.с. е
2
вторичной обмотки получит пикообразную форму.
будет иметь пикообразную форму. Во втором случае (б
) вторичная обмотка располагается на стержне, имеющем относительно малое сечение. Параллельно ему устанавливается магнитный шунт с почти линейной характеристикой. При синусоидальном магнитном потоке Ф = Ф2
+Фш
его составляющие Ф2
и Фш
будут несинусоидальными (рис. 2-79,б
); поток Ф2
из-за быстрого насыщения стержня 2
будет иметь уплощенную форму, при которой э.д.с. е
2
вторичной обмотки получит пикообразную форму.
2-22. Мощность, потери и размеры трансформатора
Мощность, потери и размеры трансформаторов связаны важными практически соотношениями, имеющими общее значение и для всех электрических машин.
Представим себе ряд трансформаторов возрастающей мощности, геометрически подобных друг другу и имеющих одинаковые плотности тока D (A/мм2 ) в обмотках и одинаковые индукции В (Гс) в сердечниках. Под геометрически подобными трансформаторами понимаются трансформаторы, соответственные размеры которых находятся в одном и том же отношении. Два геометрически подобных трансформатора изображены на рис. 2-80.
Рис. 2-80. Геометрически подобные трансформаторы.
Здесь все линейные размеры второго трансформатора в 2 раза больше соответственных линейных размеров первого трансформатора.
Мощность трансформатора пропорциональна произведению э.д.с. и тока, т. е.
При данной частоте тока э.д.с. Е пропорциональна числу витков w обмотки и магнитному потоку Ф:
Заменяя Ф = BS c , где В — индукция в сечении S с , получим:
Ток I = Dsn , где D — плотность тока в проводнике, имеющем сечение sn . Поэтому вместо (2-189) можем написать:
Если обозначить общее сечение меди всех витков обмотки через S м = wsn , то получим:
Площади S c и S м пропорциональны квадрату линейного размера, причем здесь мы можем взять любой линейный размер (рис. 2-80), который обозначим через l ; следовательно,
S c S м º l 2 l 2 = l 4 . (2-194)
Вместо (2-193) мы можем теперь написать (при D = const и В = const):
или
Веса активных материалов (стали и меди) пропорциональны их объему, т. е. кубу линейных размеров:
поэтому
Следовательно, вес трансформатора при увеличении линейных размеров растет медленнее, чем его мощность.
Можно считать, что стоимость С активных материалов и потери SP в них при заданных индукции и плотности тока также пропорциональны весу:
SP º G º l 3 º P 3/4 . (2-200)
Если отнести вес, стоимость трансформатора и его потери к единице мощности, то получим:
Следовательно, вес и стоимость активных материалов на 1 кВА и относительное значение потерь (потерь на единицу мощности) в ряде геометрически подобных трансформаторов изменяются обратно пропорционально корню четвертой степени из их мощности при сохранении постоянными значений D и В .
Этим и объясняется тенденция применять в современных электроустановках (там, где это возможно и целесообразно) трансформаторы большой мощности вместо нескольких малых трансформаторов той же суммарной мощности.
Из равенства (2-200) следует, что потери трансформатора растут пропорционально кубу линейных размеров. Но его поверхность охлаждения возрастает пропорционально только квадрату линейных размеров. Поэтому по мере увеличения мощности трансформаторов приходится повышать интенсивность их охлаждения и отступать от геометрического подобия их форм.
Приведенные соотношения (2-198) ![]() (2-201) дают лишь общую ориентировку при определении зависимости мощности трансформатора и его потерь от размеров, и они правильны лишь приближенно. При проектировании ряда трансформаторов возрастающей мощности приходится в той или иной мере от них отступать по конструктивным, технологическим и прочим соображениям.
(2-201) дают лишь общую ориентировку при определении зависимости мощности трансформатора и его потерь от размеров, и они правильны лишь приближенно. При проектировании ряда трансформаторов возрастающей мощности приходится в той или иной мере от них отступать по конструктивным, технологическим и прочим соображениям.
2-23. Нагревание и охлаждение
Магнитные потери в сердечнике трансформатора и электрические потери в его обмотках обусловливают выделение тепла. В начальный промежуток времени работы трансформатора с нагрузкой имеет место неустановившийся тепловой процесс, в течение которого лишь часть тепла отдается окружающей среде, а другая часть остается в сердечнике и обмотках, повышая их температуру. По мере роста последней увеличивается отдача тепла. При некоторой температуре сердечника и обмоток все тепло, выделяющееся в них, отдается окружающей среде. Эта температура является установившейся, соответствующей установившемуся тепловому режиму. Она не должна превышать определенных пределов.
По ГОСТ 401-41 допускаются следующие температуры (°С):
| Для обмоток |
105 |
| Для сердечника (на поверхности) |
110 |
| Для масла (верхних слоев) |
95 |
При этом температура окружающего воздуха принимается равной 35°С.
Применяемые для трансформаторов изоляционные материалы резко снижают свои изоляционные и механические свойства при длительном повышении температуры. Особенно это относится к бумаге, являющейся одним из основных изоляционных материалов, применяемых в трансформаторостроении. Она в большой степени подвержена так называемому старению. Чем выше выбрана для нее температура, тем меньше срок ее службы.
Нужно отметить, что указанные температуры не должны непрерывно искусственно поддерживаться в трансформаторе путем увеличения его нагрузки, так как в этом случае значительно сократился бы срок службы трансформатора по сравнению с его нормальным сроком в 15![]() 20 лет. Указанные температуры установлены в предположении суточного и годового колебаний температуры окружающей среды, следовательно, в предположении, что в эксплуатационных условиях периоды работы трансформатора с наивысшими указанными температурами чередуются с периодами работы при более низких температурах.
20 лет. Указанные температуры установлены в предположении суточного и годового колебаний температуры окружающей среды, следовательно, в предположении, что в эксплуатационных условиях периоды работы трансформатора с наивысшими указанными температурами чередуются с периодами работы при более низких температурах.
Чтобы при допустимых превышениях температуры нагретых сердечников и обмоток над температурой окружающей среды все тепло отдавалось окружающей среде, необходимо иметь достаточную поверхность охлаждения.
В масляных трансформаторах тепло, образующееся в сердечнике и обмотках, отдается маслу. Масло отводит это тепло к стенкам бака, которые с наружной стороны отдают его окружающему бак воздуху. Движение тепла от одной части трансформатора к другой обусловлено разностью температур. Распределение температур отдельных частей трансформатора показано на рис. 2-81. Здесь же показаны пути движения частиц масла, омывающего сердечник и обмотки, и частиц воздуха, омывающего наружные стенки бака.
Рис. 2-81. Распределение температуры отдельных частей трансформатора по его высоте.
1
— обмотка, 2
— сердечник, 3
— масло, 4
— стенки бака.
Чем больше мощность трансформатора, тем больше в нем потери (по абсолютной величине) и тем больше, следовательно, должна быть его поверхность охлаждения для отвода образующегося тепла. Этим и объясняется главным образом увеличение размеров трансформатора при увеличении его мощности.
При увеличении размеров трансформатора его мощность и потери растут быстрее, чем поверхность охлаждения (§ 2-22). Поэтому при возрастании мощности трансформатора охлаждение его должно быть более интенсивным.
Для трансформаторов небольшой мощности (до 20![]() 30 кВА) применяются баки с гладкими стенками (рис. 2-82). Для трансформаторов средней и большой мощности приходится брать трубчатые баки (рис. 2-83) или баки с радиаторами (рис. 2-84). Для очень мощных трансформаторов применяются баки с радиаторами, которые обдуваются при помощи особых вентиляторов, вследствие чего значительно увеличивается теплоотдача с их поверхности.
30 кВА) применяются баки с гладкими стенками (рис. 2-82). Для трансформаторов средней и большой мощности приходится брать трубчатые баки (рис. 2-83) или баки с радиаторами (рис. 2-84). Для очень мощных трансформаторов применяются баки с радиаторами, которые обдуваются при помощи особых вентиляторов, вследствие чего значительно увеличивается теплоотдача с их поверхности.
Рис. 2-82. Трансформатор с гладким баком.
Рис. 2-83. Трансформатор с трубчатым баком.
Рис. 2-84. Трансформатор с радиаторным баком.
2-24. Конструкции трансформаторов
Наиболее распространенными являются масляные трансформаторы. Они при мощности S
н
![]() 100 кВА (для напряжений свыше 6300 В и при меньшей мощности) снабжаются маслорасширителями. Маслорасширитель представляет собой резервуар, помещенный на крышке бака и соединенный с ним трубой (рис. 2-85), причем труба должна находиться несколько выше дна расширителя. Емкость расширителя выбирается таким образом, чтобы масло в нем находилось все время при всех режимах работы трансформатора и при колебаниях температуры окружающего воздуха от -35 до +35° С. Для контроля за уровнем масла расширитель снабжается маслоуказателем. При наличии расширителя поверхность соприкосновения масла с воздухом значительно сокращается, что уменьшает его загрязнение и увлажнение; кроме того, продукты разложения масла и влага почти не попадают в основной бак на обмотки, а скапливаются на дне расширителя.
100 кВА (для напряжений свыше 6300 В и при меньшей мощности) снабжаются маслорасширителями. Маслорасширитель представляет собой резервуар, помещенный на крышке бака и соединенный с ним трубой (рис. 2-85), причем труба должна находиться несколько выше дна расширителя. Емкость расширителя выбирается таким образом, чтобы масло в нем находилось все время при всех режимах работы трансформатора и при колебаниях температуры окружающего воздуха от -35 до +35° С. Для контроля за уровнем масла расширитель снабжается маслоуказателем. При наличии расширителя поверхность соприкосновения масла с воздухом значительно сокращается, что уменьшает его загрязнение и увлажнение; кроме того, продукты разложения масла и влага почти не попадают в основной бак на обмотки, а скапливаются на дне расширителя.
Рис. 2-85. Маслорасширитель и выхлопная труба.
1
— расширитель; 2
— труба, соединяющая расширитель с главным баком; 3
— маслоуказатель; 4
— отстойник (водоотделитель); 5
— клапан для взятия проб; 6
— выхлопная труба; 7
— стеклянная мембрана.
Мощные трансформаторы при S н ³ 1000 кВА снабжаются также выхлопной трубой (рис. 2-85). Она представляет собой стальную трубу, соединенную одним концом с основным баком и закрытую с другого конца стеклянной пластиной — мембраной толщиной 3—5 мм. При внутренних повреждениях обмоток трансформатора быстро образуется вследствие испарения масла большое количество газов, которые выдавливают мембрану и выходят в атмосферу. В противном случае неизбежна деформация бака.
Согласно ГОСТ 401-41 трансформаторы снабжаются устройством для измерения температуры верхних слоев масла: а) Трансформаторы до 750 кВА снабжаются термометрами обычного типа или с сигнальными контактами. б) Трансформаторы от 1000 кВА и выше имеют термометрический сигнализатор, укрепляемый на боковой части бака на высоте 1,5 м от днища трансформатора. в) Трехфазные трансформаторы мощностью от 7500 кВА и выше и однофазные трансформаторы мощностью 3333 кВА и выше должны иметь дистанционный измеритель температуры масла для передачи результатов измерения на щит управления.
Защита от чрезмерных повышений температуры внутри трансформатора (тепловая защита) осуществляется при помощи газовых реле, устанавливаемых в трубе, соединяющей бак с маслорасширителем.
Принцип действия газового реле основан на следующем.
При всяком чрезмерном перегреве какой-либо части трансформатора начинается разрушение ее изоляции. В результате появляется некоторое количество газообразных продуктов распада, выделяющихся с большей или меньшей скоростью в зависимости от интенсивности теплового процесса. Образующийся газ поднимается вверх и частично задерживается в газовом реле, схематично изображенном на рис. 2-86.
Рис. 2-86. Газовое реле.
В нормальном состоянии все реле заполнено маслом. При быстром выделении газа в трансформаторе он скапливается в верхней части резервуара А и постепенно понижает уровень масла. Вследствие этого поплавок В 1 опускается и замыкает цепь с сигнальным приспособлением. В том случае, когда процесс выделения газа носит более интенсивный характер, частицы газа достигают поплавка В 2 и, наклонив его, замыкают цепь управления масляного выключателя. Таким образом, газовое реле не только предупреждает о грозящей аварии, но и выключает трансформатор, если авария принимает большие размеры.
Надежность работы трансформатора в большой степени зависит от выполнения его. изоляции. Трансформаторы на напряжение 115000 В и выше должны иметь особенно прочную изоляцию. Теоретические и экспериментальные исследования советских ученых и инженеров Московского трансформаторного завода (МТЗ) имени В. В. Куйбышева позволили разработать оригинальные конструкции изоляции трансформаторов с экранирующими емкостями (§ 2-20,в ), что значительно повысило надежность их работы. Такие трансформаторы получили название грозоупорных и нерезонирующих, так как при грозовых разрядах на линию передачи, соединенную с трансформаторами, в них почти не возникают опасные перенапряжения резонансного характера.
Выводы концов обмоток на крышку трансформатора производятся при помощи проходных фарфоровых изоляторов, выполнению которых также уделяется всегда большое внимание.
Масляные трансформаторы взрывоопасны. При большой мощности они устанавливаются на открытых подстанциях, вдали от производственных и жилых строений. Если же необходимо масляный трансформатор установить в помещении, то последнее должно быть специальным образом оборудовано (под трансформатором часто устраивается забетонированная яма, чтобы в случае повреждения бака и воспламенения масла оно стекало в эту яму).
В связи с этим большое значение приобретают безопасные в отношении взрыва сухие трансформаторы для установки их в помещениях. Такие трансформаторы в настоящее время на наших заводах изготовляются и находят себе все более широкое применение.
В Советском Союзе изобретены специальные негорючие масла (совол и совтол) для заполнения баков трансформаторов. Однако вследствие их относительно высокой стоимости они применяются еще редко.
Для прогресса трансформаторостроения большое значение имеет улучшение качества электротехнической стали. В последние годы на отечественных заводах освоено изготовление холоднокатаной электротехнической стали различных марок (Э310 и др.), которая обладает высокими магнитными свойствами в направлении прокатки (большая магнитная проницаемость и малые удельные потери). Применение такой стали позволяет значительно увеличить индукцию в сердечниках трансформаторов, повысить их к.п.д. и снизить расход активных материалов. Широкое внедрение стали Э310 в трансформаторостроение — важнейшая ближайшая задача дальнейшего улучшения советских трансформаторов. Из нее также выполняются небольшие однофазные трансформаторы с оригинальной конструкцией сердечника, который наматывается при помощи особых станков; при этом получаются трансформаторы броневого типа (рис. 2-87). Они обладают высоким к.п.д.
Рис. 2-87. Однофазный трансформатор с намотанным сердечником.












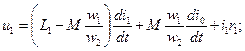 (2-24)
(2-24) (2-25)
(2-25)

 (2-39)
(2-39)
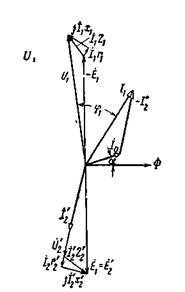

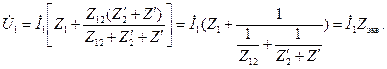 (2-43)
(2-43)






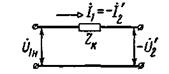







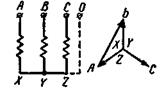












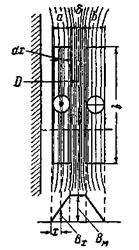
 (2-71)
(2-71)
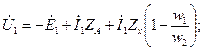 (2-87)
(2-87) (2-88)
(2-88) (2-89)
(2-89) (2-90)
(2-90)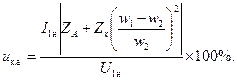 (2-91)
(2-91) (2-92)
(2-92)
 (2-97)
(2-97)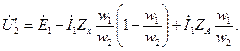 (2-98)
(2-98) (2-99)
(2-99) (2-100)
(2-100) (2-101)
(2-101) (2-102)
(2-102)




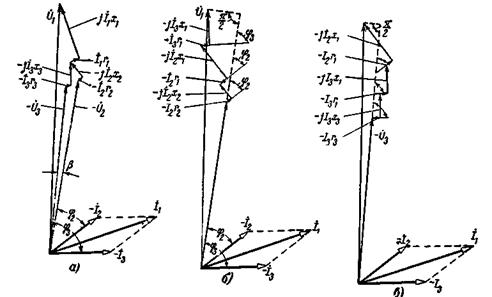
 (2-129)
(2-129) (2-130)
(2-130) (2-131)
(2-131)