Реферат: Використання комп’ютерів у фізиці

Реферат

"Використання комп’ютерів у фізиці"

1. Значення комп’ютерів у фізиці, природа чисельного моделювання.

1.1. Вступ.

Комп’ютер виступає у ролі експериментальної установки для проведення фізичних дослідів, причому потрібно самому проводити дослід і інтерпретувати результат.

Чисельне моделювання наближається до традиційних методів: експериментального і теоретичного.

Згідно з китайським прислів’ям: “Я чую і забуваю, я бачу і запам’ятовую, роблю і осягаю” представлено представлено роботу з пропонованим матеріалом. Розділи містять необхідні фізичні поняття, за якими йдуть тексти програми, задачі і контрольні питання. Тексти програми вводимо із клавіатури.

1.2. Використання комп’ютерів.

а) Чисельний аналіз, наприклад, взяти багатовимірний інтеграл, провести операцію з великою матрицею, розв’язати складне диференціальне рівняння.

б) Символьне перетворення або аналітичне перетворення виразів, наприклад виразу

в) Моделювання наприклад, обміну грошима (енергією) 100 учнів по 10$ і вчитель10$ обмінюються 0.5$ тільки з учителем.

г) Використання комп’ютерів допомогло знайти нові спрощуючі принципи.

д) Керування процесами в реальному часі. Проектування апаратури, керування, збір і аналіз даних.

Важливість чисельного моделювання проявляється в тому, що більшість систем, що аналізуються є нелінійними, а аналітично їх можна розв’язати в окремих лінійних випадках. Більшість систем має велике число ступенів вільності або змінних. Розвиток комп’ютерних технологій привів до нового погляду на фізичні системи. До формування законів у вигляді правил для комп’ютерів.

Для початку моделювання формують ідеалізовану модель фізичної системи. Чисельний експеримент є мостом між лабораторними експериментами і теоретичними розрахунками. Однак чисельне моделювання не усуває розміркування, а є інструментом що використовують для осягнення складних явищ.

Мета досліджень фундаментальних явищ у пошуку пояснень, які можна записати на конверті, або представити на пальцях.

Відмітимо важливість графіки для наочного представлення функцій, наприклад,

Важливим критерієм якості програми є її “читабельність”, бо є аналогія між добре написаною програмою і добре написаним документом.

Потрібно завести журнал де будуть записані програми, результати, видані комп’ютером графіки і аналіз даних. Цим ви виробите навики ведення дослідницьких проектів, приведете у порядок думки зекономите час. Журнал знадобиться для написання лабораторного звіту, або міні дослідження за програмами, результатами, аналізу даних і їх інтерпретації.

2. Метод Ейлера розв’язування диференціального рівняння на прикладі закону теплопровідності Ньютона.

2.1. Основні поняття.

Якщо різниця температур об’єкта і середовища не велика то

де r - коефіцієнт остигання, залежить від механізму теплопередачі, площі поверхні та теплових властивостей тіла.

Зміна температури за законом теплопровідності Ньютона має вигляд диференціального рівняння 1-го порядку

Часто розв’язок у аналітичному виді представити не можливо.

2.2. Алгоритм Ейлера (метод дотичних).

Представимо рівняння у різницевому вигляді в x₀ , y=y₀ , на малому , g(x,y) стала

y₁ = y(x₀ ) + y(x₀ ) + g(x_0, y₀ ) x

Повторюючи знайдемо

y₂ = y(x₁ + x) y(x₁ ) + g(x₁ , y₁ ) x

y_n = y_n-1 + g(x_n-1 ,y_n-1 ) x, (n=0,1,2…)

нахил дотичної визначається початковою точкою інтервалу.

2.3. Програма для комп’ютера.

Алгоритм методу.

1. Вибирається початкова умова, величина кроку і кількість ітерацій (кроків).

2. Визначається y і нахил у початковій точці відрізку.

3. Обчислюється y у кінцевій точці відрізку і друкується результат.

4. Кроки 2 і 3 повторюємо необхідне число раз.

3. Розв’язування задач руху.

3.1. Основні поняття.

1. Об’єкт, що рухається, розглядають, як матеріальну точку , тобто такий, що немає внутрішньої структури.

Розглянемо задачу падіння тіл поблизу поверхні землі.

Одновимірний рух:

y(t) – координата, v(t) – швидкість, a(t) – прискорення.

За означенням:

v(t)=dy(t)/dt, (1)

a(t)=dv(t)/dt. (2)

Це кінематичні величини, бо описують рух безвідносно до причини, що його викликає.

Ньютон вказав, що прискорення пропорційне силі, що діє на тіло:

a(t)= F(y, v, t) /m, (3)

m – інертна маса.

Бачимо, що рух матеріальної точки не залежить від похідних координати по часу вищих ніж друга. Можемо звести рівняння до одного:

d² y(t)/dt² =F(y, v, t)/m. (4)

3.2. Сили, що діють на падаюче тіло.

Якщо опором повітря знехтувати, то розглядаємо вільне падіння g=9,8 м/с² , тому a = g. Розв’язок (4) можна записати:

v(t)=v₀ +gt,

y(t)=y₀ +v₀ t+(1/2)gt² .

Розв’язок буде складнішим, якщо враховувати зміну прискорення в залежності від відстані до центра Землі:

F = GMm/(R+y)² = gm/(1+y/R)² , g = GM/R.

Іншою важливою модифікацією є врахування гальмівної сили, зумовленої опором повітря. Напрямок сили опору середовища протилежний до напряму швидкості. Запишемо силу, що діє на матеріальну точку:

F = F_g - F_d = mg - F_d .

Для знаходження F_d (v) – залежності гальмівної сили від швидкості, можна скористатись експериментальною залежністю y(t).

Для F_d (v) – приймається певний вид залежності від v, і ця формула використовується для знаходження функції y(t). Якщо обчислені значення узгоджуються з експериментальними, то прийнята залежність F_d (v) вважається експериментально підтвердженою.

Найбільш загальні залежності:

F_d (v)=k₁ v, F_d (v)=k₂ v² ,

де k₁ , k₂ – залежать від властивостей середовища і геометрії тіла. Записані залежності - корисні феноменологічні вирази, що наближено описують силу у обмеженому діапазоні швидкостей.

Через те, що сила опору є зростаючою зі швидкістю існує гранична швидкість, така що встановлюється, за умови рівності нулю прискорення або сили:

F_g = F_d ,

v₁ = mg/k₁ , v₂ = (mg/k₂ )^1/2 .

Часто зручно вимірювати швидкість в цих одиницях.

F_d = k₁ v₁ (v/v₁ ), F_d = k₂ v₂ ² (v/v₂ )² .

Отже рівнодійна сили, що діє на тіло

F₁ (v) = mg(1 - v/v₁ ), F₂ (v) = mg(1 - (v/v₂ )² ).

Реальні дані: m = 10^-2 кг, r = 0.01м, k₂ = 10^-4 кг/м. Можна знайти v₂ = 30 м/с, цю швидкість має вільне тіло за 3 с пролетівши 50 м без опору повітря. Отже опір повітря грає суттєву роль.

3.3. Чисельний розв’язок рівняння руху.

Узагальнимо метод Ейлера на рівняння другого порядку. Позначимо через dt – крок по часу, тоді t_n – що відповідає n – кроку

t_n = t₀ + n dt.

Позначимо на n – кроці a_n , v_n , y_n . Пряме узагальнення набуде вигляду

v_n+1 = v_n + a_n dt, y_n+1 = y_n + v_n dt.

Значення у наступній точці визначається через значення у початковій точці. Можна ввести зміну:

v_n+1 = v_n + a_n dt, y_n+1 = y_n + v_n+1 dt.

Це модифікований метод Ейлера, метод Ейлера – Кромера, що виконує наближення за наступною точкою.

4. Задача Кеплера.

4.1 Вступ.

Значний вплив на світогляд людини справили закони руху і всесвітнього тяжіння.

Знання про рух планет об’єднали закони Кеплера.

1. Будь-яка планета рухається за еліптичною орбітою у одному з фокусів якої знаходиться сонце.

2. Швидкість планети зменшується у міру віддалення її від Сонця таким чином, що пряма, що з’єднує Сонце і планету за рівні проміжки часу замітає однакову площу.

3. Для всіх планет, що обертаються навколо Сонця, відношення T² /a³ однакове (T-період обертання планети навколо Сонця, а - велика піввісь еліпса).

4.2. Рівняння руху планет.

Задачу двох тіл зводимо до задачі одного тіла.

Перший спосіб. М_с >>m_з , з Сонцем можна зв’язати початок системи координат.

Другий спосіб. Якщо потенціальна енергія залежить тільки від відстані між тілами M і m, зводимо до руху одного тіла масою

m _з =5.99 10²⁴ кг, M_c =1.99 10³⁰ кг

Отже .

Кілька планет, що взаємодіють між собою і з Сонцем. Чи починаючи з випадкових орбіт прийдуть вони у плоску систему?

Чи газова хмаринка розділиться на планети?

Закон всесвітнього тяжіння.

F= - (1)

Частинка М притягує m з силою F, r напрямлено від M до m.

G = 6.66 10^-11

‘-’ означає, що гравітаційна сила є силою притягання.

Закон відноситься до тіл малих точкових розмірів, або для однорідної кулі, сферичної оболонки, якщо вимірювати від центра маси. Зауважимо, що Ньютон 20 років не публікував цього закону.

Сила тяжіння залежить від відстані між тілами і напрямлена вздовж лінії, що їх сполучає. Це центральна сила. З цього слідує, що орбіта Землі лежить у площині хоу, а момент імпульсу L зберігається і спрямований вздовж OZ, запишемо L_z у виді L_z =[r mv]_z =m(xv_y - yv_x ).

L = [r p] ; p =[mv].

Крім того, рух обмежує закон збереження повної енергії Е:

E = mv² /2 – GmM/r.

З малюнка одержимо:

cos = x/r, sin = y/r.

Пов’яжемо систему з масою М, рівняння руху буде:

m(d² /dt² ) = - (GmM/r³ ).

Запишемо силу у декартових координатах:

F_x = F cos = - (GMm/r² ) cos = - (GMm/r³ ) x,

F_y = F sin= - (GMm/r² ) sin = - (GMm/r³ ) y.

Отже, рівняння руху матиме вигляд:

d² x/dt² = - (GM/r³ ) x,

d² y/dt² = - (GM/r³ ) y,

r² = x² + y² .

Маємо систему диференціальних рівнянь.

4.3. Рух по колу.

Одержимо умову руху тіла за коловою орбітою:

a = v² /r,

зумовлене гравітаційною силою:

mv² /r = GMm/r²

або

v = (MG/r)^1/2 .

Це є умова колової орбіти.

T = 2r/v

залежність періоду від радіуса знайдемо.

(2r)² /T² = MG/r,

T² = (2)² r³ /MG – частинний випадок з закону Кеплера.

4.4. Еліптичні орбіти.

Опишемо властивості еліптичних орбіт:

F₁ і F₂ – фокуси еліпса. Для будь-якої точки Р.

F₁ Р + F₂ Р = const = 2a, остання рівність слідує з P(a, 0),

a – велика піввісь, b – мала піввісь.

В астрономії використовують a і e – ексцентриситет.

Відношення:

e = /2a,

пов’яжемо з b.

Нехай Р(0, b):

(ea)² + b² = a² ,

e = (1 – b² /a² )^1/2 , причому 0<e<1

В частинному випадкуb = a еліпс стає колом і . Для орбіти Землі е =0.016.

4.5. Астрономічні одиниці

Зручно вибрати таку систему одиниць щоб . Для опису руху Землі, у якості просторової одиниці, вибирають велику піввісь земної орбіти. Вона називається астрономічна одиниця (а.о.), яка рівна 1а.о.=1.496 10¹¹ м.

У якості одиниць часу приймають 1рік = 3.15 10¹⁷ с. У цих одиницях

Т=1рік, а=1а.о.

можемо записати

4.6. Зауваження до програмування

Будемо користуватись масивом чисел

^/ Коментар, Основна програма

DECLARE SUB ff(y) – об’явити підпрограму

REM Коментар

REM PROGRAM

CALL ff(x) – викликати підпрограму

END

SUB name [( parameterlist)]

END SUB

FOR I=1 to n,

де I – змінна циклу.

PRINT y,z видає на екран y, z

INPUT x, y - ввід даних

Точність чисельного розв’язку визначають, зменшуючи величину кроку до того часу, поки чисельний розв’язок не перестане залежати від кроку при заданому рівні точності, але це має виконуватись обережно, бо зростає число кроків і похибка округлення.

Найпростіша графіка.

CLS – очистити екран;

SCREEN 12 – графічна сторінка;

LINE (x1,y1) – (x2,y2), color, B – не замальовує рамку, якщо BF – замальовує.

CIRCLE (x1,y1), radius, PSET (x,y) – засвітити точку, PRESET (x,y) – погасити точку.

DO [white: until] condition

LOOP

LOOP [{white: until}]

Оператор друкування по місцю:

LOCATE 5,5

VIEW PRINT 10 TO 15

Зупинка циклу з клавіатури при натисканні на клавішу “h”

DO UNTIL INKEY$ = ”h”

Задати логічні координати екрану

SCREEN 12

WINDOW (x1,y1)-(x2,y2)

Друкувати дані по формату експоненційної форми

PRINT USING “##.###^^^^”;x

4.7. Простий гармонічний осцилятор.

m d² x/dt² =-kx;

F = - kx – повертаюча сила, нехай w₀ ² =k/m. Розв’язок цього рівняння можемо представити у наступному вигляді

x(t)=Acos(w₀ t + ).

A,  - амплітуда і фаза визначаються з початкових умов.

Перевіркою правильності роботи програми може бути умова збереження повної енергії.

E = mv² /2 +kx² /2.

Рівняння руху, що описує затухаючі коливання

d² x/dt² =-₀ ² x – g dx/dt + F(t)/m;

де другий доданок гальмуюча сила, третій – вимушуюча сила

F(t)/m = A₀ cos(wt).

Математичний маятник довжиною L.

Швидкість точки, що рухається по колу v = L dq/dt, тангенціальне прискорення a = L d² q/dt² .

Рівняння руху матиме вигляд

d² x/dt² = - mg sinq.

Повна енергія представиться формулою

E = mL² (dq/dt)² /2 + mgL(1 – cosq).

8. Хвильові явища

Моделюємо лінійний ланцюг зв’язаних осциляторів. Виділимо властивості ланцюга, що відносяться до хвильових явищ. У наближенні неперервного ланцюжка виводиться лінійне хвильове рівняння. Демонструються інтерференція, дифракція, рефракція і поляризація. Розглядаємо ряд Фур’є і принцип Ферма.

8.1. Вступ

Для опису коливального і хвильового руху використовують такі поняття як період, амплітуда і частота. Як пов’язані ці величини. Розглянемо натягнутий шнур.

Імпульс розповсюджується по ньому зі швидкістю, що визначається натягом і інерційними властивостями шнура. Рух ділянки локалізований і здійснюється перпендикулярно руху хвилі.

На макроскопічному рівні спостерігаємо поперечну, хвилю на мікроскопічному рівні дискретні частинки здійснюють коливний рух.

Почнемо з мікроскопічної картини і розглянемо коливний рух лінійного ланцюга частинок сполучених пружинками. Рух моделюється, чисельно розв’язуючи рівняння руху для окремої частинки.

Побачимо, що енергія передається вздовж ланцюга, хоча кожний осцилятор знаходиться поблизу свого положення рівноваги.

Побачимо, що найзагальніший рух системи N часток можна представити як суперпозицію N незалежних простих гармонічних рухів.

8.2. Зв’язані осцилятори.

Розглянемо простішу ніж у попередніх розділах модель.

Нехай u_i -зміщення ії маси вздовж осі системи.

Кінці лівої і правої частинок нерухомі. Нерухомість виразимо U₀ = U_N+1 =0.

Рівняння руху і-ї частинки

, i=2, …, N-1

Це рівняння не тільки для повздовжніх коливань, але і для поперечних рівняння аналогічні.

Частоти нормальних коливань для k_с =k

² _n =,

де N-число частинок, n-номер коливань n=1, …, N.

8.3. Фур’є аналіз.

Зміщення частинок можна представити у вигляді лінійної комбінації нормальних коливань, тобто лінійної суперпозиції синусоїдальних доданків.

Взагалі довільна періодична f(t) з періодом Т може бути записана у вигляді ряду Фур’є по sin i cos

f(t)=1/2 a₀ +,

₀ -основна кругова частота, ₀ =2/Т

Доданки для n = 2, 3… являють другу і третю гармоніки. Коефіцієнти Фур’є виражаються

a_n =2/T,b_n =2/T,

На практиці використовують скінчене число членів n.

8.4. Хвильовий рух.

Ми виявили, що коливання окремих зв’язаних осциляторів призводить до розповсюдження енергії на довільну відстань. Знову запишемо рівняння для зміщення

, i=1, …, N.

Розглянемо перехід N прямує до нескінченості, a прямує до 0 за сталої довжини ланцюга. Це дискретне рівняння можна замінити хвильовим. u_i (t) замінити на u(x, t), де x – неперервна змінна

похідну по часу записати як частинну похідну.

Через те що частинки розподілені неперервно, можна ввести величини M=m/a T=ka

легко показати що

Хвильове рівняння має величезну кількість розв’язків наприклад

Оскільки хвильове рівняння лінійне, то розв’язок можна представити у вигляді ряду Фур’є.

Якщо хвиля при русі зберігає свою форму то кажуть, що вона не диспергує, це зумовлено лінійністю зв’язку i k, інакше кожна гармоніка хвилі рухається з тією ж швидкістю. Якщо ж швидкість хвилі залежить від довжини хвилі (або хвильового числа), то кажуть, що диспергує, і цьому випадку форма хвилі змінюється з часом.

8.5. Інтерференція і дифракція.

Про інтерференцію говорять, коли змішуються хвилі від невеликого числа джерел, а про дифракцію коли від великого.

Дослід Юнга.

Дві щілини, монохроматичне світло. Щілини як точкові джерела

Електричне поле буде рівне сумі

Інтенсивність дорівнює .

8.6. Поляризація.

Розглянемо явище, коли цікавить напрямок коливань. Для поперечної електромагнітної хвилі. Напруженість двовимірна векторна функція вздовж z-розповсюджується хвиля.

E_x (z,t) і E_y (z,t) Для монохроматичної хвилі =const, але компоненти коливаються незалежно.

Щоб сумарне поле знайти треба векторно скласти компоненти.

8.7. Геометрична оптика і принцип найменшого часу.

Геометричною оптикою можна користуватись, коли <<l, l – розмір перепон чи детекторів.

Для променів, що розповсюджуються, виконується принцип Ферма: промінь світла йде по шляху між двома точками, який вимагає найменшого часу.

Аналогічний принцип найменшої дії використовується замість законів Ньютона у якості фундамента всієї класичної механіки. В однорідному середовищі світло поширюється прямолінійно.

Розглянемо дзеркало:

a + b = d

Цікавим є застосування принципа Ферма для задач заломлення, коли світло падає на поверхню розділу двох речовин, у яких швидкість світла різна:

n = c/v,

де n – показник заломлення.

9. Статичні поля зарядів струмів.

Обчислюємо поля, що створюються розподілом зарядів або струмів. Одержуємо за методом релаксації розв’язок рівняння Лапласа і Адассона.

9.1.Вступ.

Дано q, v. Сила Лоренца діє на рухомий заряд, перший доданок сила Кулона.

F = q(E + [vB]), у точці знаходження заряду, можемо розрахувати рух зарядженої частинки.

9.2. Електричне поле і потенціал.

N-зарядів q_i в r_i . E(r) = K((q_i /|r - r_i |³ )(r – r_i )) – згідно принципу суперпозиції.

K = 1/4₀ = 3 *10⁹ (H*м² /Кл² ), ₀ – діелектрична стала вакууму, e = 1.6*10^-19 (Кл).

Кулон є великою одиницею і у розрахунках будемо вибирати різні одиниці.

Наочне представлення Е векторного поля є зображення силових ліній електричного поля:

1. Силова лінія є напрямленою лінією, дотична до якої в кожній точці паралельна полю.

2. Це гладкі і неперервні лінії за виключенням зарядів.

3. Число ліній пропорційне величині заряду.

Побудова ліній.

Беремо точку (x, y) обчислюємо Е_х і Е_у .

В точці будуємо відрізок S в напрямку Е,

х = S(Е_х /|E|), =S(Е_y /|E|)|

Продовжуємо поки лінія не піде до “ – “ заряду.

Починаємо малювати силові лінії поблизу позитивного заряду, так щоб число ліній було пропорційне заряду. Основні особливості програми стосуються графічних інструкцій. Розсіювання  – частинок на Au

a = K (2e79e/m_б )(1/r² ), m_б = 6.65*10^-27 кг, 1фм = 10^-15 (м), с = 3*10⁸ (м/с).

Часто зручніше розглядати енергії, а не сили. Для цього вводять поняття потенціалу:

v(r₂ ) – v(r₁ ) = -.

або - напруженість поля мінус градієнт потенціалу.

v – скалярна величина і зміст має різниця потенціалів:

В одновимірному випадку Е = - dv/dx. Якщо v залежить від , то Е = - dv/dr

Напрямок Е співпадає з напрямком найскорішого зменшення електричного потенціалу.

Для точкового заряду якщо .

Поверхня на якій потенціал приймає однакові значення називається еквіпотенціальною поверхнею. Лінії поля ортогональні до еквіпотенціальних ліній. Компоненти еквіпотенціалів рівні: , .

9.3. Магнетизм і силові лінії магнітного поля.

Поле В визначається законом Біо-Савара і має вигляд:

[I] = A; [B] = Тл; (Тл м)/А – магнітна проникність.

Це для ділянки струму, що знаходиться у початку координат. Для довільної ділянки довжиною , що знаходиться в точці , магнітне поле в точці :

Найважливіші задачі: провідник, петля, котушка.

9.4. Числовий розв’язок рівняння Лапласа.

Часто є відомим електричний потенціал на границях області. Нехай маємо систему провідників і кожний під’єднано до батареї. Легко визначити потенціали провідників. Для металу потенціал одинаковий. Однак, розподіл заряду визначити складно, бо він залежить від форми тіла.

Нехай задано потенціал на границі і потрібно знайти потенціал в точках, де немає заряду. Будемо знати , то знайдемо . Така задача називається краєвою.

Прямий метод базується на рівнянні Лапласа, яке має вигляд:

Для довільної форми провідників аналітичних методів немає. Скористаємося наближеними чисельними методами.

Для двовимірної сітки за відсутності зарядів потенціал визначається:

Тобто, значення у центральній дорівнює середньому за сусідніми комірками. Така властивість є аналог рівняння Лапласа. У правильності цієї формули можна переконатись для точкового заряду.

Метод релаксації базується на наступному алгоритмі:

Розбиваємо область сіткою із заданим потенціалом на границі.

Комірки ділимо на внутрішні і граничні, граничним приписуємо потенціал границі.

Внутрішнім приписуємо довільний потенціал, найкраще розумне початкове значення.

Приписуємо внутрішнім значення, усереднені за 4-ма сусідніми точками.

Повторюємо пункт 4, поки не досягнемо заданої точності.

Якщо область має заряди з об’ємною густиною , то використовуємо рівняння Пуассона:

- густина зарядів.

Для двовимірного випадку:

10. Чисельне інтегрування

Ілюструємо класичні методи і метод Монте-Карло для оцінки чисельних інтегралів.

10.1. Прості одномірні методи чисельного інтегрування.

Ці методи (класичні) мають перевагу для малих розмірностей.

Геометрична інтерпретація інтегралу - площа під графіком у межах x = a до x = b, відрізок ділимо на n відрізків довжиною :

де , і ,

Оцінка площі - сума площ прямокутників. Значення обчислюється у початку відрізків і оцінка інтегралу дається формулою:

10.2. Інший метод трапеції із сторонами у початку і кінці відрізка.

Тобто, f(x) замінюємо прямою, що сполучає значення f(x) в кінцях відрізка. Площа

Повна площа

Більшу точність дає квадратична, або параболічна інтерполяція за трьома точками

Площа під параболою між точками виражається формулою:

Повна площа всіх параболічних сегментів:

де n – має бути парним.

Точність методу прямокутників зростає, як = , трапецій – n^-2 , парабол – n^-4 .

10.3.Чисельне інтегрування багатовимірних інтегралів.

Багато фізичних задач містять усереднення по багатьом змінним. Наприклад, середнє значення енергії системи частинок E(r_i ,p_i ), i =1, ..., n. Якщо розмірність простору N = 6n, а число точок на відрізку одного виміру p, то потрібно обчислити за p^N точками суму.

Ще дуже складно визначати N-1 - межу інтегрування. Стандартні методи використовуються для N = 2 - 5.

Найпростіший метод оцінки багатовимірних інтегралів зводиться до послідовного взяття одновимірних інтегралів:

і .

10.4. Обчислення інтегралів найпростішим методом Монте-Карло.

а) n_S - число точок, для яких , - загальне число точок. Рівномірно розігруємо точки (x_i , y_i ) , оцінка інтегралу є:

б) Ймовірнісна інтерпретація . Інтеграл - середнє значення функції, помножене на відрізок інтегрування. Розігруються, рівномірно, значення х_і і розраховується значення f(x_i ).

10.5. Обчислення багатовимірних інтегралів методом Монте-Карло.

Для прикладу знайдемо центр мас і момент інерції двовимірного тіла:

Межі інтегрування визначаються геометрією тіла. Координати центра мас:

, .

Момент інерції навколо осі z:

Чисельна оцінка:

n - число точок, для яких - незалежні випадкові числа на відрізках

і такі, що попадають у границі фігури.

Якщо для d = 1 - похибка апроксимації спадає, як n^-a , то в d - вимірному випадку ця похибка спадає як n^-a/d .

10.6. Аналіз похибки метода Монте-Карло.

Точність визначається кількістю випробувань в методі Монте-Карло або кількістю відрізків у класичних методах.

Для методу Монте-Карло похибка прямує до нуля, як .

Дисперсія є мірою похибки:

- дисперсія одиничного виміру,

, , ,

, .

Якщо б не залежала від х, то .

- дисперсія середнього.

Похибку можна зробити малою, збільшуючи число випробувань або збільшуючи ефективність випробувань.

10.7. Нерівномірний розподіл ймовірності.

Побачили, як можна рівномірний розподіл використовувати для оцінки інтеграла.

Однак, важливо вибірку підінтегральної функції частіше виконувати, у областях , де велика або швидко змінюється. Для такої вибірки потрібен нерівномірний розподіл ймовірності. Розглянемо метод оберненого перетворення.

Введемо поняття щільності ймовірності p(x), при цьому - ймовірність того, що випадкове число належить відрізку .

нормується так, щоб

Нехай r – випадкове число, рівномірно розподілене на одиничному інтервалі [0,1] з густиною ймовірності:

Наше завдання знайти зв’язок між x i r_, такий, що якщо r рівномірно розподілено, то х за законом p(x). Зв’язок встановлюють через інтегральну функцію розподілу:

де Р(x) – інтегральна функція розподілу, яка рівна ймовірності одержання випадкового числа меншого за х.

Зв’язок має вигляд:

Випадкова величина P(x) розподілена рівномовірно.

Ймовірність знайти x в інтервалі , рівна dP(x).

Співвідношення між dP(x) і dx можна знайти

отже в межах 0r1 маємо dP(x)=P(x) dx=P_u (r) dr

Бачимо, що х розподілено з бажаною густиною імовірності.

Приклади:

Згенеруємо рівномірно розподілені на [a, b] числа. Шукана густина

P(x) = r

x = P^-1 (r), , x= a + (в-a) r.

Змінна розподілена за законом (1), коли r—рівномовірне.

Інший випадок

Однак метод оберненого перетворення може бути не найефективнішим. Для використання методу має виконуватись два співвідношення, має братись інтеграл Р(х) і розв’язуватись співвідношення Р(х)=r відносно х.

Для цього зробити не можна.

Однак можна згенерувати двовимірний гаусів розподіл

перейдемо до полярних координат.

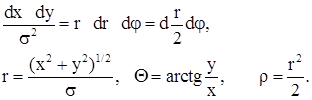
знайдемо імовірність у вигляді:

можемо генерувати розподілами за експоненційним законом, а рівномірно в межах [0,2] то змінні будуть розподілені за нормальним законом з нульовим середнім і дисперсією .

10.8. Вибірка за значимістю (суттєва вибірка).

Похибка методу Монте-Карло пропорційна , познайомимось з методом зменшення . Введемо додатню Р(х) таку, що тоді

можна переписати у такому виді

Обчислимо інтеграл , виконуючи вибірку у відповідності до розподілу Р(х), при рівномірному Р(х)=1/(в-а).

Вибираємо Р(х), що веде себе подібно до f(x) там де f(x) велика, тому підінтегральний вигляд буде функцією, що слабо змінюється і дисперсія буде малою.

10.9 Метод випадкового блукання (метод Метрополіса)

Метод одержання не рівномірного розподілу полягає у тому , що деякі вибірки відкладаються.

Нехай хочемо генерувати змінні з розподілом Р(х).

Випадкове блукання задається імовірністю переходу w(x_i x_j ) від одного x_i до іншого x_j для того, щоб розподіл точок x₀ , x₁ , x₂ ,… сходився до Р(х).