| Скачать .docx |
Реферат: Оптические свойства полупроводниковых пленок в видимой и ИК частях спектра
Министерство образования Украины
Национальный технический университет
“Харьковский политехнический институт”
Кафедра физического материаловедения для электроники и гелиоэнергетики (ФМЭГ)
РЕФЕРАТ
“Оптические свойства полупроводниковых пленок в видимой и ИК частях спектра”
Исполнитель:
студент группы ФТ-18б Карасёв С.Н.
2003
1 . Оптические свойства полупроводников
В опытах по поглощению света полупроводниками часто используются сравнительно слабые световые потоки. При этом электромагнитная волна не изменяет энергетический спектр носителей заряда (или решетки), а лишь создает новые пары электрон—дырка (или новые фононы) или вызывает перераспределение носителей заряда по состояниям. При этом величины, характеризующие оптические свойства среды, не зависят от интенсивности света. В таком случае говорят о линейном приближении: величина световой энергии, поглощаемой в образце, линейно связана с интенсивностью света. Ограничимся здесь этим приближением. Будем считать также, что длина электромагнитной волны значительно превышает постоянную решетки. Последнее условие обычно хорошо выполняется вплоть до энергий фотонов порядка нескольких сот электрон-вольт.
Опыты, нас здесь интересующие, сводятся в конечном счете к измерению интенсивности света, прошедшего через образец или отраженного от него. Для описания экспериментальных результатов, относящихся к кристаллам кубической симметрии (или к изотропным материалам), вводят две величины: коэффициенты преломления п и экстинкции χ. Чтобы связать их с микроскопическими характеристиками вещества, рассмотрим задачу о распространении плоской электромагнитной волны, нормально падающей на поверхность образца. Пусть последняя совпадает с плоскостью х = 0, причем область х > 0 занята полупроводником. Размеры образца во всех направлениях будем считать сколь угодно большими.
Обозначим через E, D и H, B векторы напряженности и индукции электрического и магнитного полей электромагнитной волны. Уравнения Максвелла, описывающие распространение поперечной волны, имеют вид [1]
![]() (1.1)
(1.1)
![]() (1.2)
(1.2)
![]() (1.3)
(1.3)
![]() (1.4)
(1.4)
Ограничиваясь кристаллами кубической симметрии, можем положить
![]() (1.5)
(1.5)
причем, σ = σ1 + i σ2 , ε0 = ε1 + i ε2 , где σ1 σ2 , ε1 , ε2 — вещественные величины, зависящие от частоты падающей волны ω. Магнитную проницаемость μ будем считать вещественной константой, не зависящей от ω; в немагнитных полупроводниках значение μ обычно очень близко к единице.
Возьмем ротор от обеих частей уравнения (1.1). Как известно из векторного анализа,
![]()
Пользуясь этим соотношением и равенствами (1.2), (1.3) и (1.5), мы получаем
![]() (1.6)
(1.6)
Такому же уравнению удовлетворяет и вектор H [1].
В соответствии с постановкой задачи положим (при х ≥ 0)
![]() (1.7)
(1.7)
где Em — амплитуда волны, прошедшей в образец, при х = 0, ξ — единичный вектор в направлении E, k — комплексное волновое число. Из физических соображений ясно, что в поглощающей среде мнимая часть его должна быть положительна: она описывает затухание волны по мере углубления ее в среду. Подставляя (1.7) в (1.6), получим
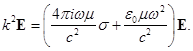 (1.8)
(1.8)
Это уравнение, совместно с условием Em ≠ 0, дает связь между k и ω, т. е. закон дисперсии электромагнитной волны в рассматриваемой среде.
Удобно ввести комплексную проводимость σ' [1], полагая
![]() (1.9)
(1.9)
при этом
![]() (1.9')
(1.9')
Положим
![]() (1.10)
(1.10)
где п и χ — безразмерные вещественные положительные величины. Это и есть соответственно коэффициенты преломления и экстинкции. Смысл названий становится ясным при подстановке выражения (1.10) в (1.7). Мы получаем при этом
![]() (1.7)
(1.7)
При χ = 0, т. е. в отсутствие поглощения, выражение (1.7') описывало бы плоскую волну, распространяющуюся с фазовой скоростью с/п и постоянной амплитудой. Если же χ ≠ 0, то амплитуда волны экспоненциально убывает по мере проникновения ее в образец.
Вместо коэффициента экстинкции часто вводят показатель поглощения α, определяемый равенством [1]
![]() (1.11)
(1.11)
Смысл величины α легко понять, вспоминая, что плотность энергии электромагнитной волны пропорциональна квадрату амплитуды последней. Согласно (1.7') это означает, что плотность энергии (и тем самым число фотонов в единице объема) убывает с ростом координаты х, как
![]()
Таким образом, α-1 есть длина, на которой плотность энергии волны в результате поглощения убывает в е раз.
Обращая равенство (1.11), получим
![]() (1.11)
(1.11)
где ![]() — есть длина световой волны в вакууме.
— есть длина световой волны в вакууме.
Подставим выражение (1.10) в равенство (1.8) и сократим последнее на Em . Получим
![]() (1.12)
(1.12)
Отделяя здесь вещественную часть от мнимой, находим два алгебраических уравнения для определения n и χ. Корни их имеют вид [1]
![]() (1.1За)
(1.1За)
![]() (1.136)
(1.136)
Формулы (1.13а, б) решают поставленную задачу. Иногда их записывают по-другому, вводя вместо комплексной проводимости σ' комплексную диэлектрическую проницаемость
![]() (1.14)
(1.14)
Здесь ε1 ' и ε2 ' — вещественные величины. Очевидно,
![]() (1.15)
(1.15)
и, следовательно,
![]() (1.16а)
(1.16а)
![]() (1.16б)
(1.16б)
Равенства (1.13а, б) и (1.16а, б) эквивалентны, и выбор тех или других есть дело вкуса.
Согласно (1.16а) коэффициент экстинкции оказывается отличным от нуля, если отлична от нуля мнимая часть диэлектрической проницаемости. Последняя может быть обусловлена как носителями заряда, так и решеткой. В первом случае имеет место поглощение электромагнитной волны, связанное с различными электронными переходами, во втором — поглощение, связанное с передачей энергии непосредственно решетке, т. е. с генерацией только фононов.
Отметим два случая [1].
а. Непоглощающая среда. Пусть σ1 = ε2 = 0. Тогда, согласно (1.16а, б),
χ = 0 и
![]() (1.17)
(1.17)
Это есть формула Максвелла для показателя преломления, дополненная лишь учетом возможной частотной зависимости ε1 '.
б. Слабое поглощение волны достаточно большой частоты. Пусть ω больше плазменной частоты, т. е. ε1 ' > 0. Пусть также
![]() (1.18)
(1.18)
Тогда коэффициент преломления по-прежнему дается формулой (1.17), а коэффициент экстинкции есть
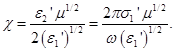 (1.19)
(1.19)
Показатель поглощения равен теперь
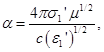 (1.20)
(1.20)
Смысл условия (1.18) можно выяснить, вспоминая, что длина электромагнитной волны в среде есть ![]() . С помощью этого соотношения и равенств (1.17), (1.20) легко привести условие (1.18) к виду
. С помощью этого соотношения и равенств (1.17), (1.20) легко привести условие (1.18) к виду
![]() (1.18')
(1.18')
Иначе говоря, расстояние, на котором волна заметно поглощается, должно быть велико по сравнению с ее длиной.
Условие ε2 ' > 0 и неравенство (1.18') выполняется во многих интересных случаях. При этом вклад свободных носителей заряда в диэлектрическую проницаемость образца обычно невелик, т. е. ε1 ' ≈ ε1 . Небольшим оказывается обычно и решеточное поглощение в рассматриваемой области частот:
ε2 << 1. При этом формулу (1.20) можно переписать в виде (при μ ≈ 1)
![]() (1.20')
(1.20')
На опыте часто измеряют еще коэффициент отражения R. Последний определяется равенством [1]
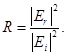 (1.21)
(1.21)
Здесь Ei — амплитуды волны, падающей на образец, Er —амплитуда отраженной волны. Пользуясь граничными условиями для компонент вектора E на поверхности образца, можно выразить R через коэффициенты преломления и экстинкции п и χ. В случае нормального падения мы имеем
![]() (1.22)
(1.22)
2. Механизмы поглощения
Процессы поглощения света следует классифицировать по тому, на что непосредственно расходуется энергия поглощенных фотонов. Можно выделить следующие механизмы [1]:
1) Решеточное поглощение: электромагнитная волна непосредственно возбуждает колебания решетки. Этот механизм поглощения особенно важен в ионных кристаллах, в которых генерация оптических фононов приводит к заметному изменению вектора поляризации; однако такое поглощение наблюдается и в гомеополярных материалах. Его испытывают волны, частоты которых близки к предельной частоте оптических фононов ω0 . (Обычно это соответствует энергии в несколько сотых долей электронвольта.)
2) Поглощение свободными носителями заряда: энергия расходуется на создание тока высокой (оптической) частоты и, в конечном счете, переходит в джоулево тепло.
3) Примесное поглощение: энергия поглощается носителями заряда, локализованными на примесных или иных структурных дефектах решетки. Она расходуется либо на перевод носителей с основного уровня примесного центра на возбужденный, либо на ионизацию примеси. В последнем случае электроны (дырки) попадают в зону проводимости (валентную), т. е. имеет место внутренний примесный фотоэффект. Таким путем можно определять энергии ионизации ряда примесей.
4) Междузонное поглощение: энергия фотона расходуется на создание пары «электрон проводимости + дырка». В отсутствие сильного электрического поля и/или большой концентрации примеси этот тип поглощения опознается по наличию граничной частоты ωm , близкой к Еg /ћ. При ω < ωm поглощение этого типа отсутствует. Следует, однако, заметить, что вид спектра поглощения вблизи частоты ω = ωm в разных материалах оказывается различным. На рисунке 2.1 представлен спектр поглощения арсенида галлия.
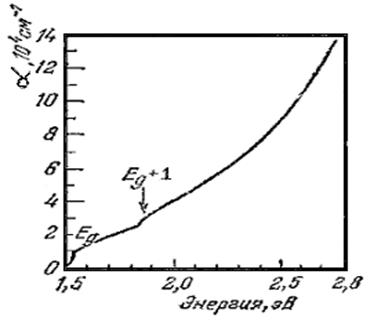
Рисунок 2.1. Спектр поглощения пленки арсенида галлия [1].
Видны два края поглощения. Первый из них приближенно соответствует значению ћωm = Eg (вблизи красной границы коэффициент поглощения очень мал, поэтому поглощение становится заметным при несколько больших частотах), второй отвечает энергии Eg + Δ, где Δ — расстояние между потолком валентной зоны и верхним краем валентной подзоны, отщепленной из-за спин-орбитального взаимодействия.
Примерно такие же (в измененном масштабе частот) кривые получаются и при исследовании многих других материалов — антимонида и арсенида индия, антимонида галлия и др. С другой стороны, у ряда интересных полупроводников частотная зависимость и величина показателя поглощения вблизи красной границы оказываются существенно иными. Так, на рисунке 2.2 изображен ход показатель поглощения света в германии при различных температурах. При ω = ωm (ћωm = Eg = 0,66 эВ при комнатной температуре) показатель поглощения относительно мал; он становится сравнимым с тем, что наблюдается в арсениде галлия, лишь при ћω ~ Eg + 0,1 эВ. Похожая картина (в другом масштабе частот) наблюдается также в кремнии, фосфиде галлия и других материалах. Это различие имеет глубокую физическую природу: оно обусловлено тем, что в материалах первого типа экстремумы зон проводимости и валентной лежат в одной точке зоны Бриллюэна, а в материалах второго типа — в разных.
5) Экситонное поглощение: энергия фотона расходуется на образование экситона.
В материалах первого типа экситонному поглощению отвечают узкие пики α при частотах, несколько меньших ωm ; в материалах второго типа вместо пиков наблюдаются «ступеньки».
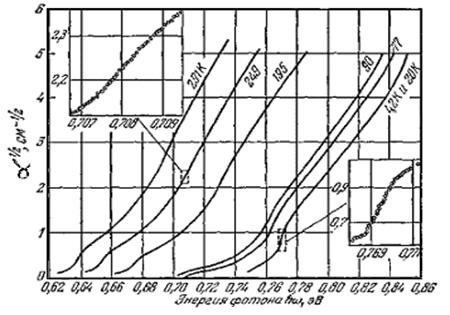
Рисунок 2.2. Край поглощения германия при различных температурах [1].
3. Поглощение свободными носителями
Говоря «свободный носитель», мы имеем в виду носитель, который может свободно двигаться внутри зоны и реагировать на внешние воздействия [2]. Поглощение свободными носителями характеризуется монотонным, часто бесструктурным спектром, описываемым законом lp , где l = c/n— длина волны фотона, а р меняется в пределах от 1,5 до 3,5.
При поглощении фотона электрон совершает переход в состояние с большей энергией в пределах той же долины (рисунок 3.1). Такой переход требует дополнительного взаимодействия для того, чтобы выполнялся закон сохранения квазиимпульса.
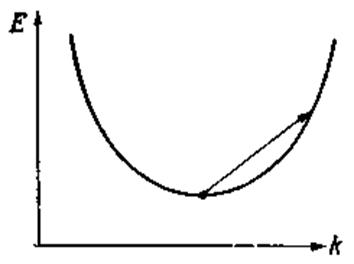
Рисунок 3.1. Переход свободного электрона в зоне проводимости [2].
Изменение квазиимпульса можно обеспечить либо в результате взаимодействия с решеткой (фононы), либо путем рассеяния на ионизованных примесях.
Согласно теории Друде, описывающей колебания электрона в металле под действием периодического электрического поля, затухание должно увеличиваться пропорционально l2 . В полупроводниках рассеяние акустическими фононами приводит к поглощению, меняющемуся как l1.5 . Рассеяние на оптических фононах дает зависимость l2.5 , тогда как рассеяние ионизованными примесями может дать зависимость l3 или l3.5 , что связано с аппроксимациями, использованными при построении теории [2].
В общем случае реализуются все типы рассеяния и результирующий показатель поглощения af свободными носителями представляет собой сумму трех членов
af = Al1.5 + Bl2.5 + Сl3.5 , (3.1)
где А, В и С — константы. В зависимости от концентрации примесей тот или иной механизм рассеяния будет доминирующим. Показатель р в зависимости lp должен возрастать с увеличением легирования или степени компенсации.
В таблице 3.1 приведены значения р и сечения поглощения af /N для различных соединений [2].
Таблица 3.1. Поглощение свободными носителями в соединениях n-типа.
| Соединение | Концентрация носителей, 1017 см-з | af /N * , 10-17 см-2 | р |
| GaAs | 1-5 | 3 | 3 |
| InAs | 0,3-8 | 4,7 | 3 |
| GaSb | 0,5 | 6 | 3,5 |
| InSb | 1-3 | 2,3 | 2 |
| InP | 0,4-4 | 4 | 2,5 |
| GaP | 10 | (32) | (1,8) |
| AlSb | 0,4—4 | 15 | 2 |
| Ge | 0,5—5 | ~ 4 | ~ 2 |
* Отношение показателя поглощения к концентрации свободных носителей af /N приведено для длины волны 9 мкм. Параметр р определяет зависимость поглощения от длины волны в приближении af ~ lр .
Классическая формула для показателя поглощения свободными носителями af имеет вид
![]() (3.2)
(3.2)
где N — концентрация носителей, п — коэффициент преломления, а t — время релаксации. Отметим, что t учитывает влияние рассеяния. Таким образом, следует ожидать, что вероятность рассеяния ионизованными примесями будет зависеть от природы примеси. Такая зависимость показателя поглощения от химической природы примеси была обнаружена в германии n-типа, где при данной длине волны
af (As) > af (P) > af (Sb),
и в GaAs, где также при фиксированной длине волны
af (S) > af (Se) > af (Te).
Далее, время релаксации зависит от концентрации рассеивающих центров. Поэтому при сильном легировании показатель af не должен быть просто пропорциональным N, как записано в формуле (3.2). На рисунке 3.2 видно, что в германии, легированном сурьмой, показатель af пропорционален N3/2 . Поскольку эффективная масса постоянна в этой области концентраций, то из формулы (3.2) следует, что t пропорционально N‑1/2 .
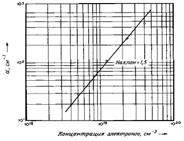
Рисунок 3.2. Поглощение свободными носителями в Ge (Т = 4,2 К) при 2,4 мкм.
Полупроводниковые соединения, состоящие из атомов различного типа, можно рассматривать как набор электрических диполей. Эти диполи могут поглощать энергию электромагнитного поля; наиболее сильное взаимодействие с излучением имеет место, если частота излучения равна частоте колебаний диполя. Это происходит в далекой инфракрасной области спектра. Обычно колебания являются сложными, включающими несколько типов нормальных колебаний (эмиссия многих фононов). Импульс фотона h/l пренебрежимо мал, тогда как фононы могут обладать квазиимпульсом вплоть до величины h/а (а — постоянная решетки).
Поэтому для выполнения закона сохранения квазиимпульса должны быть испущены два или более фононов. В полупроводниках имеются две поперечные оптические (ТО) ветви колебаний, две поперечные акустические (ТА), одна продольная оптическая (LO) и одна продольная акустическая (LA). Иногда две поперечные ветви колебаний обладают сходными кривыми дисперсии Ер (k). Далее, некоторые комбинации фононов запрещены согласно правилам отбора. Тем не менее число возможных комбинаций всех этих типов колебаний чрезвычайно велико, и именно это обусловливает сложность обычно наблюдаемой структуры. На рисунке 4.1 показана часть спектра поглощения GaAsn-типа, связанного с колебаниями решетки [2].
В гомеополярных полупроводниках нет диполей. Однако спектры решеточного поглощения наблюдаются. Очевидно, имеет место процесс второго порядка: излучение индуцирует диполь, который сильно взаимодействует с излучением, и в результате возникают фононы. На рисунке 4.2 показан для примера спектр решеточного поглощения гомеополярного полупроводника Si, соответствующая идентификация фононов приведена в таблице 4.1. Для объяснения поглощения в области больших энергий привлекались процессы еще более высокого порядка, соответствующие одновременному испусканию четырех фононов [2].
Интересно отметить, что введение в гомеополярный полупроводник дефектов (например, путем облучения нейтронами) создает локальные поля, которые делают возможными однофононные переходы (в нормальных условиях запрещенные).
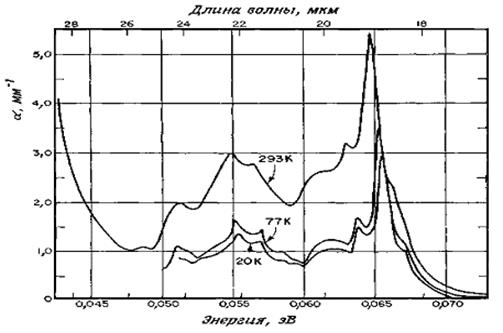
Рисунок 4.1. Спектр поглощения, связанного с колебаниями решетки, высокоомного GaAsn-типа в области энергий 0,04 — 0,07 эВ (нижняя шкала) при 20, 77 и 293 К.
Таблица 4.1. Фононы, участвующие в поглощении в кремнии
| Волновое число, мм-1 | Энергия пика, эВ | Тип фононов * |
| 144,8 | 0,1795 | 3TO |
| 137,8 | 0,1708 | 2TO + LO |
| 130,2 | 0,1614 | 2TO + LO |
| 2TO + LA | ||
| 96,4 | 0,1195 | 2ТО |
| 89,6 | 0,1111 | TO + LO |
| 81,9 | 0,1015 | TO + LA |
| 74,0 | 0,0917 | LO + LA |
| 68,9 | 0,0756 | ТО + ТА |
| 61,0 | 0,0702 | LO + TA |
* ТО = 0, 0598 эВ, LO = 0 0513 эВ, LA = 0, 0414 эВ, ТА = 0, 0158 эВ.
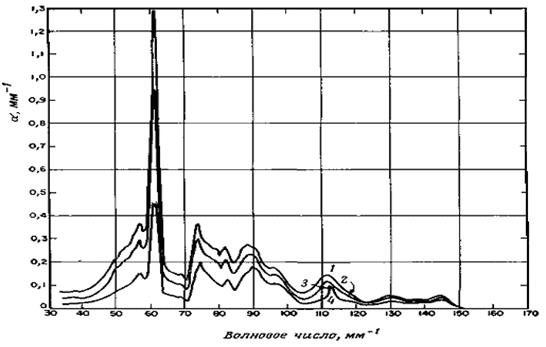
Рисунок 4.2. Решеточное поглощение в Si, выращенном в вакууме.
Кривая 1 — 365 К, кривая 2 — 290 К, кривая 3 — 77 К, кривая 4 — 20 К.
5. Методы определения коэффициента поглощения
Методы определения коэффициента поглощения можно разделить на несколько типов:
1. Измерение коэффициента отражения и/или коэффициента отражения.
· Если пленка не прозрачна (Т = 0), то выполняется равенство:
![]() (5.1)
(5.1)
Следовательно, по данным измерений спектральной зависимости коэффициента отражения рассчитывается спектральная зависимость коэффициента поглощения [3].
· Если пленка прозрачна, то равенство (5.1) преобразится в:
![]() (5.2)
(5.2)
Таким образом из (5.2) следует, что по данным измерений спектральной зависимости коэффициентов отражения и пропускания можно рассчитать спектральную зависимость коэффициента поглощения.
2. Расчеты по известным оптическим константам.
Оптические свойства веществ характеризуют, указывавшимся выше, комплексным показателем преломления. Зная его, можно вычислить коэффициент отражения любого материала. Один из методов рассчета описан Борном и Вольфом в [4].
3. Прямые методы измерения коэффициента поглощения.
Например метод Табора и Стейнбергера [3]. На одной стороне образца находится исследуемая поверхность, а другая покрыта слоем с известным коэффициентом поглощения (например черной краской). Стороны попеременно подвергаются циклам облучения. Очевидно, что если подобрать подходящий температурный цикл, то тепловые потери скомпенсируются и можно будет определить отношение известного коэффициента поглощения к неизвестному.
6. Пример расчета спектральной зависимости коэффициента поглощения селективно поглощающего покрытия в видимой и ИК части спектра
Более полные теоретические выкладки с пояснениями вы можете найти в [4].
Зададим толщину мультипленки и количество пленок входящих в ее состав:
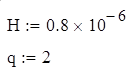
Определим комплексный показатель преломления (в мультипленке две пленки - q):
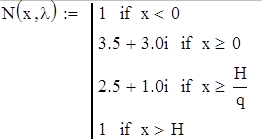
Определим характеристическую матрицу-функцию для одного слоя:
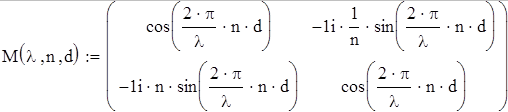
Введем характеристическую матрицу мультипленки, как произведение характеристических матриц пленок входящих в ее состав:
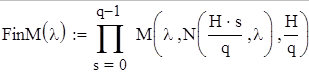
Энергетический коэффициент прозрачности будем вычислять по:
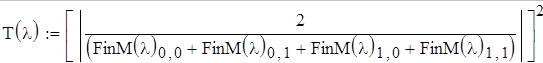
Энергетический коэффициент отражения будем вычислять по:
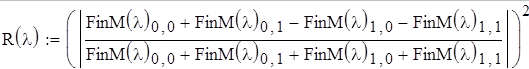
На рисунках 6.1, 6.2, 6.3 приведены рассчитанные программой MathCAD спектральные зависимости энергетических коэффициентов пропускания, отражения и поглощения.
Из этих рисунков видно, что чем тоньше мультиплека, тем более в коротковолновую часть спектра, в силу интерференции, сдвигается пересечение кривых спектральных зависимостей энергетических коэффициентов поглощения и отражения.
Можно заметить, что мультислой, спектральные зависимости энергетических коэффициентов которого представлены на рисунке 6.3, наиболее подходит для применения в качестве покрытий для тепловых коллекторов. При уменьшении толщины мультислоя и увеличении разницы в действительных частях комплексного коэффициента преломления можно достигнуть лучших спектральных зависимостей, т.е. больших значений коэффициента отражения в средней ИК части спектра и коэффициента поглощения в видимой области спектра.
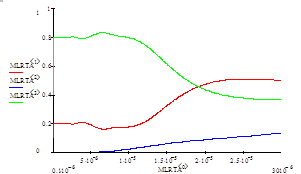
Рисунок 6.1 Рассчитанные спектральные зависимости энергетических коэффициентов поглощения (зеленая), пропускания (синяя) и отражения (красная) при N1 = 2.0 + 1.0iN2 = 4.0 + 1.5idмультипленки = 2 мкм.
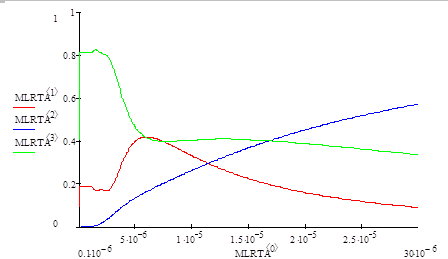
Рисунок 6.2 Рассчитанные спектральные зависимости энергетических коэффициентов поглощения (зеленая), пропускания (синяя) и отражения (красная) при N1 = 1.8 + 1.0iN2 = 3.0 + 1.0idмультипленки = 0.6 мкм.
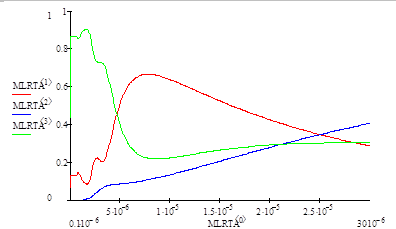
Рисунок 6.3 Рассчитанные спектральные зависимости энергетических коэффициентов поглощения (зеленая), пропускания (синяя) и отражения (красная) при N1 = 1.6 + 0.8iN2 = 5.0 + 1.0idмультипленки = 0.6 мкм.
1. В.Л. Бонч-Бруевич, С.Г. Калашников «Физика полупроводников», М.:«Наука», 1977.
2. Ж. Панков «Оптические процессы в полупроводниках», перевод с англ. под ред. Ж.И. Алферова, М.:«Мир», 1973.
3. Л.Ф. Друмметер, Г. Хасс «Поглощение солнечного излучения и тепловое излучение напыленных покрытий», в книге «Физика тонких пленок», том 2, перевод с англ. под ред. М.И. Елинсона, М.:«Мир», 1967.
4. М. Борн, Э. Вольф «Основы оптики», перевод с англ. под ред. Г.П. Мотулевич, М.:«Наука», 1973.