| Скачать .docx |
Реферат: Аналіз фінансових інвестицій
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ПВНЗ «Європейський університет»
Житомирська філія
Кафедра «Фінанси»
Реферат
На тему
«Аналіз фінансових інвестицій»
Виконала:
студентка V курсу, групи ФБ – 08
факультету економіки та менеджменту
Житомир – 2011
Зміст
1. Поняття та визначення фінансових інвестицій
2. Оцінка майбутньої вартості грошових вкладень
3. Методи оцінки акцій
4. Методи оцінки облігацій
5. Методи оцінки векселів
Список використаної літератури
1. Поняття та визначення фінансових інвестицій
Фінансові інвестиції — це вкладення коштів у фінансові інструменти, серед яких переважають цінні папери, із метою одержання доходу (прибутку) у майбутньому.
Фінансові інструменти поділяють на:
- фінансові активи, які включають у себе: грошові кошти, необмежені для використання, та їх, еквіваленти; дебіторську заборгованість, не призначену для перепродажу; фінансові інвестиції, що утримуються до погашення; фінансові активи, призначені для перепродажу; інші фінансові активи;
- фінансові зобов'язання — включають фінансові зобов'язання, призначені для перепродажу та інші фінансові зобов'язання;
- інструменти власного капіталу — це прості акції, частки та інші види власного капіталу;
- похідні фінансові інструменти — ф'ючерсні контракти, форвардні контракти та інші похідні цінні папери.
2. Оцінка майбутньої вартості грошових вкладень
При розробці оптимальних фінансових рішень у конкретних ситуаціях інвестор має вміти оцінювати майбутню вартість інвестованих грошових коштів.
Оцінка майбутньої вартості грошових вкладень, інвестованих на строк більше одного року (періоду) залежить від того який процент (простий чи складний) буде прийматися в розрахунках. При використанні простого відсотку інвестор буде одержувати доход (нарощувати капітал) тільки з суми початкових інвестицій протягом всього строку реалізації проекту. При використанні складного проценту, одержаний доход періодично додається до суми початкових інвестицій. У результаті чого відсоток нараховується також із накопиченої у попередніх періодах суми відсоткових платежів або будь-якого іншого виду доходу. Знаходження майбутньої вартості грошових коштів через n-період і при відомому значенні темпу їх приросту здійснюється за такою формулою:
FVn = PV(1+r)n = PV*FVIFr,n де
FVn — сума грошових коштів, інвестованих у період 1=0;
r — ставка відсотку, Коеф.;
n — кількість періодів (років)
FVIFr,n — фактор майбутньої вартості грошових вкладень, Коеф..
Якщо нарахування відсотків здійснюється m раз у рік, то формула буде мати такий вигляд:
FVn = PV(1+r/m)n*m
Процес, в якому при заданих значення PV та r необхідно знайти величину майбутньої вартості інвестованих коштів до кінця певного періоду часу (n) називається операцією нарощування.
У фінансових розрахунках часто виникає потреба в оцінці поточної вартості майбутніх грошових потоків (PV). Метою даної процедури є визначення цінностей майбутніх надходжень від реалізації того чи іншого проекту з позицій поточного моменту. Процес конвертування грошових коштів, що планується одержати у майбутніх періодах в їх, поточну вартість називається операцією дисконтування. Процентна ставка, що використовується у розрахунку PV називається дисконтною ставкою. А показник поточної вартості визначається за такою формулою:
PV = FVn * 1/(1+r)n де
1/(1+r)n — називається фактором (множником) поточної вартості (FVIFr,n ).
Якщо нарахування відсотків планується здійснювати більше одного разу у період, то формула буде мати такий вигляд:
PV =FVn *1/(1+r/m)n
Крім номінальної ставки відсотку за депозит r у фінансових розрахунках використовується і ефективна ставка, або дійсна ставка відсотку. Ця ставка визначає той відносний доход, який одержує власник капіталу за рік у цілому. Іншими словами, це річна ставка доходності, яку одержує інвестор при m-раз нарахувань у році за ставкою відсотку г/m. Таким чином, ефективна ставка складних відсотків визначається за формулою:
EAR=(1+r/m)m – 1= FVIFr/m – 1
В інвестиційному аналізі виникає необхідність оцінити грошові потоки, які генеруються інвестиційним проектом у різні періоди часу. Одним із способів оцінки їх є представлення цих потоків у вигляді аннуітету, або фінансової ренти, який представляє собою рівні за величиною грошові потоки за кожний період протягом точно визначеного часу.
Узагальнюючими показниками ренти є нарощена (майбутня) сума ренти та сучасна (поточна, приведена) рента.
Нарощена сума — це сума усіх членів потоку платежів з нарахуванням на них відсотків у кінці строку, тобто на дату останньої виплати. Цей показник показує яку величину буде представляти капітал, який вноситься через рівні проміжки часу протягом усього строку ренти з нарахованими відсотками.
Майбутня вартість звичайного аннуітету (FVA) протягом періоду n визначається за формулою:
FVAn = P*FVIF r, n-1 =P* FVIFAr,n де
P — періодичні надходження рівні за величиною грошові потоки;
FVIFAr,n — фактор майбутньої вартості аннуітету, Коеф..
Показник, який характеризує майбутню вартість однієї грошової одиниці в кінці строку реалізації інвестиційного проекту (Коеф. нарощування ренти або Коеф. накопичення грошової одиниці за період) визначається за формулою:
FVIFAr,n = (1+r)n-t =[(1+r)n – 1) / r]
Сучасна величина ренти (поточна вартість аннуітету) — це сума усіх членів ренти, дисконтова них на момент приведення по вибраній дисконтній ставці.
PVAn = P* FVIFr,n-1 =P FVIFAr,n де
PVAn — поточна вартість звичайного аннуітету з строком інвестування n періодів;
FVIFr,n-1 — фактор поточної вартості аннуітету, Коеф., який визначається за формулою:
FVIFr,n-1 =(1+r)n-1 =[(1-(1+r)-n /r]
3. Методи оцінки акцій
Оціночна система показників доходності акцій:
1. Дохід на акцію = Чистий прибуток - Дивіденди за привілейованими акціями / Загальну кількість звичайних акцій
2. Цінність акцій = Ринкова ціна акції / Дохід на акцію
3. Рентабельність акції = Дивіденди на одну акцію / Ринкова ціна акції
4. Дивідендний дохід = Дивіденди на одну акцію / Дохід на акцію
5. Коеф. котирування акції = Ринкова ціна акції / Облікова ціна акції
Оцінка акцій з постійними дивідендами:
![]() де
де
D — річний дивіденд;
K — ставка доходності акції.
Оцінка акцій з постійним приростом дивідендів (Модель Гордона):
 де
де
D1 — сподівані дивіденди на акцію через рік 0,= 0^ (1+ ^):
g — темп приросту дивідендів.
Оцінка акцій з непостійним приростом дивідендів:
![]() де
де
Dn — сподіваний щорічний дивіденд на акцію.
Для аналізу ефективності вкладені, інвестора акцій можуть використовуватися види доходності: ставка дивіденду, поточна доходність акції для інвестора, поточна ринкова доходність, кінцева та сукупна доходність.
Ставка дивіденду (dc ):
![]() де
де
D — величина річних дивідендів, що виплачуються, грн.;
N —номінальна ціна акції, грн.
На практиці ставка дивіденду використовується для оголошення річних дивідендів.
Поточна доходність акції для інвестора — ренти (dT ):
![]() де
де
Р — ціна придбання акції, грн.
Поточна ринкова доходність (dT ): співвідношенням величини дивідендів, що виплачуються, до поточної ринкової ціни акції:
 де
де
Ро — поточна ринкова ціна акції, грн.
Кінцева доходність акції (dk ):
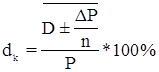 де
де
P — величина дивідендів, виплачених в середньому за рік, грн.;
∆P— приріст або збиток капіталу інвестора, що дорівнює різниці між ціною продажу та ціною придбання акції, грн.;
n—кількість років, протягом яких інвестор володів акціями.
Узагальнюючим показником ефективності вкладень інвестора в покупку акцій є сукупна доходність (dc ):
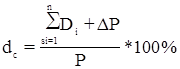 де
де
Di — величина дивідендів, виплачених в i-тому році, грн.
Кінцева та сукупна доходності можуть використовуватися в тому випадку, якщо інвестор продав акцію або планує її продати за ціною, відомою йому.
У випадку, коли інвестор не бажає отримувати поточних доходів у вигляді дивідендів, він отримує доход від приросту курсової вартості акцій. Доходність (річна) буде визначатися:
 де
де
Рі — ціна покупки акції, у процентах до номіналу, або грн.;
Ро — ціна продажу акції, у процентах до номіналу, або грн.;
t — кількість днів із дня покупки до продажу акцій.
4. Методи оцінки облігацій
Ринкова вартість відсоткової облігації (PV):
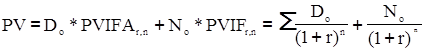 де
де
Do — сума відсотків по облігації за кожен рік;
No — номінальна вартість облігації;
г— середня ставка доходності на ринку або дисконтна ставка;
n — число періодів, які залишилися до погашення облігації.
Ринкова вартість безвідсоткової облігації:
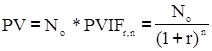 де
де
Для оцінки облігацій використовують такі види доходності:
Купонна доходність (dk ):
![]() де
де
D — річний купонний доход, грн.;
N — номінальна ціна облігації, грн.
Поточна доходність (dp ):
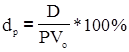 де
де
PVo — ціна, за якою була придбана облігація інвестором, грн.
Кінцева доходність (dk ):
 де
де
∆PV — приріст або збиток капіталу, який дорівнює різниці між ціною реалізації (номіналом) та ціною купівлі облігації інвестором, грн.;
n — кількість років обігу облігації.
Облігації з нульовим купоном доходність (d):
 де
де
PV o — ціна покупки облігацій, у процентах до номіналу, або в грн.;
PV i — ціна продажу облігацій, у процентах до номіналу, або в грн.;
t — кількість днів із дня покупки до продажу облігацій.
Розрахунок очікуваної прибутковості по облігаціям (Ro ):

5. Методи оцінки векселів
Для оцінки ефективності фінансових операцій з векселями використовують такі розрахунки:
Сума процентів — доход (Ів ) нараховується на основі річної процентної ставки та періоду обігу:
![]() де
де
IB — вексельний доход, грн.;
iB — річний відсоток по векселю, Коеф.;
t — число днів обігу векселя;
Pn — номінал векселя, грн.
Дисконтний доход (Id ) — різниця між номіналом векселя та дисконтною ціною (ціною придбання векселя):
Id =Pn - Ppr де
Ppr — ціна придбання векселя.
Доходність векселя (ІD ) за строк позики:
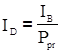
Доходність векселя за рік:
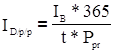 де
де
t — число днів обігу векселя.
При продажі фінансового векселя на ринку цінних паперів до закінчення строку боргового зобов'язання доход ділиться між продавцем та покупцем.
Доход, який одержить покупець (І пок ):
інвестиція облігація вексель акція
Іпок = (ir *Pn *ti )*365 де
Іпок — дохід покупця, грн.;
ir — ринкова ставка на момент угоди за борговими зобов'язаннями такої строковості, яка залишилася до погашення векселя, грн.;
Pn — номінальна ціна векселя, грн.;
ti — число днів до погашення векселя.
З однієї сторони, доход покупця не повинен бути менше тої суми, що він отримав би при ринковій ставці за борговими зобов'язаннями такої строковості, яка залишилася до погашення векселя. З іншої - його реальний прибуток визначається як різниця ціни погашення (номіналу) та ціна покупки (Рr ):
Pr =Pn - (ir *Pn *ti )*365;
Доход продавця — першого векселедержателя — визначається як різниця між ринковою ціною векселя та ціною його розміщення:
Ipr = Рr — Рpr
Доход покупця — другого векселедержателя — визначається як різниця між номінальною ціною векселя та його ринковою ціною за формулою:
Iпот =Pn - Pr
Загальний доход по векселю (ІB ) визначається як сума доходу продавця (Ipr ) та покупця (Іпок ).
В банківській практиці при врахуванні простих векселів використовуються такі розрахунки: сума, яку банк віднімає з вексельної суми як премію за дострокове погашення кредиту, називається дисконтом (D). Величина дисконту визначається як різниця вексельної суми та її приведеної величини на момент врахування векселя комерційним. Приведена величина вартості векселя залежить від строку, який залишився до дати погашення боргового зобов'язання, та визначається шляхом комерційного обліку на основі облікової ставки, визначеної самим банком.
Визначення приведеної величини вексельної суми:
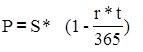 ; де
; де
P — приведена величина вексельної суми на момент врахування банком, грн.;
S — вексельна сума, грн.
г — облікова ставка банку, Коеф.;
t — число днів від дати врахування до дати погашення векселя.
Дисконт на користь банку:
![]() або
або ![]()
Аналогічні розрахунки проводяться з переказним векселем.
Список використаної літератури
1. Бутинець «Бухгалтерський фінансовий облік»: підручник – Житомир: ЖИТІ, 2001 – 672 с
2. Гриньова В.М., Коюда В.О. «Фінанси підприємства»: навчальний посібник – 3-тє видання, – К.: Знання-Прес, 2006, - 423 с. – (Вища освіта ХХІ століття).
3. Загородній А.Г., Вознюк Г.Л. «Фінансово-економічний словник» – К.: Знання, 2007. – 1072 с.
4. Кірейцева Г.Г. «Фінанси підприємств»: навчальний посібник: Курс лекцій – К.: ЦУЛ, 2002 – 268 с.