| Скачать .docx |
Реферат: Интервальная группировка
2.ИНТЕРВАЛЬНАЯ ГРУППИРОВКА
Практически каждый исследовательский проект начинается с построения таблиц частот. Например, в социологических опросах ответы, измеренные в определенной шкале (в номинальной шкале, в порядковой шкале, в количественной шкале) можно свести в таблицу частот, например результаты голосования за кандидатов той или иной партии в зависимости от социального положения и среднедушевого дохода. В медицинских исследованиях табулируют пациентов с определенными симптомами. В маркетинговых исследованиях - покупательский спрос на товары разного типа у разных категорий населения. В промышленности - частота выхода из строя элементов устройства, приведших к авариям или отказам всего устройства при испытаниях на прочность (например, для определения какие детали телевизора действительно надежны после эксплуатации в аварийном режиме при большой температуре, а какие нет). Обычно, если в данных имеются группирующие переменные, то для них всегда вычисляются таблицы частот.
Переменные из файла данных могут быть проанализированы и представлены в виде таблиц частот. Таблица показывает частоты, кумулятивные (накопленные) частоты, процент, кумулятивный процент респондентов. STATISTICA позволяет ввести коды , задать интервалы группировки (для переменных, принимающих числовые значения), определить логические условия , позволяющие отнести наблюдения к определенной группе. Технически это делается несколькими щелчками мыши. Переменные, представленные в виде частот наблюдений, попавших в определенные категории (классы), называются категоризованными. Категоризованная переменная может представлять собой классификацию обычной числовой переменной по группам. Однако часто она может вовсе не иметь числового выражения (например, если переменная измерена в порядковой или номинальной шкале).
Одновходовые таблицы представляют собой простейший метод анализа категориальных (номинальных) переменных (см. Элементарные понятия статистики ). Часто их используют как одну из процедур разведочного анализа , чтобы просмотреть, каким образом различные группы данных распределены в выборке. При этом исходные данные (измеренные в любой подходящей шкале) представляются в виде частот наблюдений, попавших в некоторые определенные исследователем категории или классы. Например, изучая зрительский интерес к разным видам спорта (с целью рекламы какого-либо продукта на ТВ), вы могли бы представить ответы респондентов таблицей
Технология выполнения интервальной группировки состоит из решения следующих задач:
- построение интервального ряда;
- расчет статистических характеристик интервального ряда;
- проверка гипотезы о нормальном распределении интервального ряда;
- графическое изображение интервального ряда.
2.1. ПОСТАНОВКА ЗАДАЧИ
2.1.1. Построение интервального ряда.
Один из методов группировки в статистике является разбивка единиц совокупности на отдельные группы по количественному группировочному признаку. Множество значений группировочного признака разбивается на несколько интервалов. Интервал это значения варьирующего признака, лежащие в определенных границах - нижней и верхней границах. Далее каждое отдельное значение признака X условимся обозначать x1 , x2 , ,xn .
Построение интервального вариационного ряда распределения включает следующие этапы:
- определение количества групп по формуле Стерджесса:
![]() ; (2.1).
; (2.1).
Данная формула имеет ориентировочный характер. Значение k округляется до большего целого значения.
- определение среди имеющихся наблюдений минимального xmin и максимального xmax значений признака;
- определение размаха варьирования признака:
![]() ; (2.2).
; (2.2).
- определение длины интервала по формуле;
![]() . (2.3).
. (2.3).
За нижнюю границу первого интервала принимается величина равная
![]() . (2.4).
. (2.4).
За верхнюю границу последнего интервала принимается величина равная
![]() . (2.5).
. (2.5).
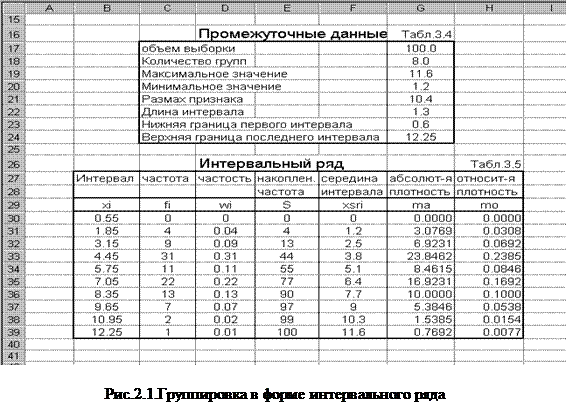
Результаты группировки оформляются в виде таблицы распределения значений совокупности по интервалам (табл. 2.1).
Табл. 2.1.
Результаты группировки
Группировка данных |
||||||
| Интервал Xi |
Частота fi |
Частость wi |
Накопленная частота si |
Середина интервала xSRi |
Абсолютная плотность ma |
Относительная плотность Mo |
| … |
… |
… |
… |
… |
… |
… |
2.1.2. Расчет статистических показателей интервального ряда .
В этом задании лабораторной работы рассчитываются следующие характеристики интервального ряда:
- средняя арифметическая: ![]() ; (2.6).
; (2.6).
- выборочная дисперсия: 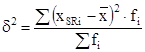 , (2.7)
, (2.7)
где xSRi - среднее значение i - ого интервала;
- выборочное среднее квадратическое отклонение ![]() ; (2.8)
; (2.8)
- выборочные коэффициенты асимметрии и эксцесса
![]() ,
, ![]() ; (2.9)
; (2.9)
где M3 и M4 - выборочные центральные моменты соответственно 3-го и 4-го порядков:
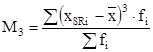 ;
; 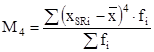 (2.10)
(2.10)
-Медиана: ![]() ; (2.11)
; (2.11)
где: me-1 - номер интервала, предшествующего медианному;
xme - начало медианного интервала;
S(me-1) - накопленная частота интервала, предшествующего медианному.
В качестве медианного интервала берется интервал, в котором накопленная частота впервые превышает половину объема выборки - n/2.
- Мода: ![]() ; (2.12).
; (2.12).
где индексы mo, mo-1, mo+1 означают соответственно модальный интервал; интервал, предшествующий модальному и интервал, следуемый за модальным;
f( mo ) , f( mo -1) , f( mo +1) - частоты соответствующих интервалов;
xmo - начало модального интервала.
Интервал с наибольшей частотой принимается за модальный.
Для расчета статистических характер составляется таблица промежуточных результатов табл.2.2 (символом "?" обозначена сумма данных в столбце).
Табл. 2.2.
Промежуточные результаты
| Расчет статистических показателей (промежуточные данные) |
|||||
| xSRi |
fi |
|
|
|
|
| ... |
... |
... |
... |
... |
... |
| ? |
? |
? |
? |
? |
? |
Результаты расчета характеристик представить в виде результирующей таблицы (табл. 2.3).
Табл. 2.3.
Результаты расчета
| Статистические характеристики ряда |
Условное обозначение |
Значение |
| Среднее значение Дисперсия … … |
d 2 ... ... |
<значение> <значение> ... ... |
Коэффициенты асимметрии и эксцесса позволяют сделать предварительный вывод о близости изучаемого распределения к нормальному. Распределение принято считать нормальным, если выполняются условия AS <=3SA и E<=5SE .
2.1.3. Проверка гипотезы о нормальном распределении
интервального ряда
Предварительное заключение о близости изучаемого распределения к нормальному можно выполнить по алгоритму, приведенному в предыдущем пункте - по значениям коэффициента асимметрии AS и показателя эксцесса Е и их среднеквадратическим отклонениям SA , SE .
Для формулировки окончательного вывода необходимо рассчитать критерии c-квадрат - критерий согласия Пирсона.
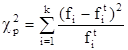 ; (2.13).
; (2.13).
где: k - количество интервалов;
fi - эмпирическая частота j-го интервала;
fi t - теоретическая частота j-го интервала.
Tеоретические частоты определяются по формуле:
![]() ; (2.14).
; (2.14).
где ti - центрированные и нормированные значения:
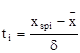 ; (2.15).
; (2.15).
d- среднеквадратическое отклонение.
Правило проверки заключается в следующем. Определяем по таблице распределения c - квадрат критическое значение ![]() для числа степеней свободы m=k-2 и заданного уровня значимости a=0.05. Затем сравниваем расчетное и критическое значения критерия Пирсона. Если
для числа степеней свободы m=k-2 и заданного уровня значимости a=0.05. Затем сравниваем расчетное и критическое значения критерия Пирсона. Если![]() , то выдвинутая гипотеза о нормальном распределении интервального ряда не отвергается (не противоречит опытным данным) с вероятностью ошибки a=0.05.
, то выдвинутая гипотеза о нормальном распределении интервального ряда не отвергается (не противоречит опытным данным) с вероятностью ошибки a=0.05.
2.1.4. Графическое изображение интервального ряда
Для визуального наблюдения характера распределения частот, определения положения среднего значения ![]() , моды MO
, медианы ME
и характера рассеивания значений дисперсии d2
и среднеквадратичного отклонения d интервальные ряды изображают графически. Для этого строятся следующие диаграммы - гистограмма, полигон частот и кумулятивная кривая.
, моды MO
, медианы ME
и характера рассеивания значений дисперсии d2
и среднеквадратичного отклонения d интервальные ряды изображают графически. Для этого строятся следующие диаграммы - гистограмма, полигон частот и кумулятивная кривая.
При построении гистограммы по оси абсцисс прямоугольной системы координат откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах. Высота столбиков в случае равных интервалов пропорциональна частотам. В случае неравных интервалов высота столбиков пропорциональна относительным частотам (частостям).
При построении полигона частот по оси абсцисс прямоугольной системы координат откладываются средние значения интервалов, по оси ординат наносится шкала для выражения величины частот. Полученные на пересечении абсцисс и ординат точки соединяют прямыми линиями, в результате получают ломанную, называемую полигоном частот.
При построении кумулятивной кривой по оси абсцисс откладываются величины интервалов, по оси ординат накопленные частоты, которые наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Эти перпендикуляры соединяют и получают ломанную линию - кумулятивную кривую.
2.2.ТЕХНОЛОГИЯ ВЫПОЛНЕНИЯ РАБОТЫ
Алгоритм выполнения лабораторной работы покажем на примере данных, представленных на рис 6.1.
2.2.1.С использованием табличного процессора Excel .
2.2.1.1. Построение интервального ряда.
1.Открываем новый рабочий лист электронной таблицы. В блок ячеек A5:J14 заполняем значения исходного ряда (см. рис.6.1). Расположение блоков с промежуточными данными и результатами вычислений представлено на рис.2.1.
2. Определяется количество групп К. Значение К округляется до большего нечетного целого. Для определения большего целого от вещественного числа используется встроенная функция ОКРВВЕРХ(). Для вычисления логарифма от объема выборки используется функция LOG10(). Для вычисления К в ячейку G18 (см. рис.2.3) записывается следующая формула:
ОКРВВЕРХ(1+3,3222*LOG10(G17);1).
 |
Примечание : Здесь далее е сли в тексте приведены расчетные формулы и функции в интерпретации Excel, то адреса ячеек и блоков ячеек в этих формулах соответствуют рассматриваемому примеру, т.е. такому расположению данных, как на представленных рисунках. При другом расположении эти адреса будут другими.
3. Определение минимального и максимального значений xmin , xmax осуществляется с использованием встроенных функций МАКС(A5:J14) и МИН(A5:J14), записываемые в ячейки G19 и G20;
4. Определение размаха варьирования признака R, в ячейку G21 вводится формула =G19-G20;
5. Вычисляется длина интервала h, в ячейку G22 вводится формула =G21/G18;
6. Вычисляются начальное и конечное значения соответственно первого и последнего интервалов xo , xk . В ячейку G23 вводится формула =G20-G22/2. В ячейку G24 вводится формула =G19+G22/2.
Значения ![]() представить в расчетном блоке в виде таблицы (табл.3.4 рис.2.1)
представить в расчетном блоке в виде таблицы (табл.3.4 рис.2.1)
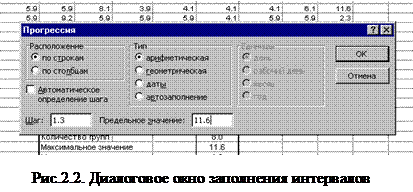
7. Далее приступаем к построению интервального ряда, который на рис.2.1 представлен в виде результирующей таблицы (табл.3.5). Колонка "интервал" результирующей таблицы содержит верхние граничные значения интервалов. Определение их выполняется следующим образом. В первую ячейку колонки "интервал" (в ячейку B31) ввести значение x0 , выделить блок для заполнения значений интервалов, т.е. колонку, содержащую к+2 ячеек (блок B30:B39), выполнить команду /Правка/заполнить/прогрессия/арифметическая . По этой команде раскрывается диалог рис.2.2, в котором устанавливаются следующие опции: Расположение - по столбцам , Тип - арифметическая . В строке ввода Шаг ввести значение h, в строке ввода Предельное значение ввести значение xk , затем нажать кнопку ОК .
 8. Определение частот. Выделить массив ячеек (колонку "частота"). Размер выделенного блока должен быть равен размеру заполненной колонки "интервал". Выполнить команду /Встроить/функцию
или нажать кнопку Мастер функции
fx
. Открывается диалоговое окно Мастер функций
в положении “шаг 1 из 2”, в котором выбрать функцию /Статистические/частота
. После этого раскрывается диалоговое окно для установки параметров рис. 2.3.
8. Определение частот. Выделить массив ячеек (колонку "частота"). Размер выделенного блока должен быть равен размеру заполненной колонки "интервал". Выполнить команду /Встроить/функцию
или нажать кнопку Мастер функции
fx
. Открывается диалоговое окно Мастер функций
в положении “шаг 1 из 2”, в котором выбрать функцию /Статистические/частота
. После этого раскрывается диалоговое окно для установки параметров рис. 2.3.
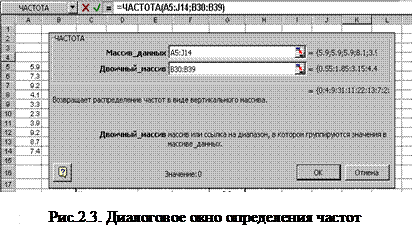 В строку ввода Массив данных
ввести координаты блока ячеек (в рассматриваемом примере блок [A5:J14]), содержащего исходный массив данных). В строку ввода Двоичный массив
ввести координаты блока ячеек со значениями интервалов (в примере блок [B30:B39]). Нажать кнопку ОК
. После этого нажать клавишу [F
2
] (редактирование) и затем нажать комбинацию клавиш Ctrl
+
Shift
+
Enter
. Частота в i-ой строке fi
соответствует интервалу [xi
-1
;xi
].
В строку ввода Массив данных
ввести координаты блока ячеек (в рассматриваемом примере блок [A5:J14]), содержащего исходный массив данных). В строку ввода Двоичный массив
ввести координаты блока ячеек со значениями интервалов (в примере блок [B30:B39]). Нажать кнопку ОК
. После этого нажать клавишу [F
2
] (редактирование) и затем нажать комбинацию клавиш Ctrl
+
Shift
+
Enter
. Частота в i-ой строке fi
соответствует интервалу [xi
-1
;xi
].
9. Для расчета относительной частоты wi , накопленной частоты Si , середины интервалов xSRi , абсолютной плотности mai , относительной плотности moi во вторые ячейки каждой колонки вводится соответствующая формула (первая строка таблицы частот имеет нулевую частоту, т.е. является не информативной). Затем производится копирование формул на всю колонку командой /Правка/копировать .
Замечания по вводу формул:
- формула для частости wi =fi /n должна иметь абсолютную ссылку на ячейку, содержащую значения n. При расположении блоков данных так как на рис.2.1 в ячейку D31 вводится следующая формула =C31/$G$17;
- для определения накопленной частоты используется встроенная функция СУММ(). Установить курсор в ячейку E31 и вызвать функция СУММ() с помощью команды меню /Вставка
или кнопки Мастера функций
. Аргументом функции является блок ячеек, состоящий из одной ячейки, в качестве которой будет вторая ячейка колонки 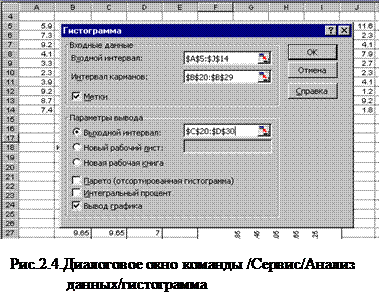 "частота". Первая координата блока должна быть абсолютной (фиксированной), вторая - относительной. Поэтому при копировании формулы в последующие ячейки происходит вычисление суммы с накоплением. В рассматриваемом примере формула во второй ячейке колонки "накопленная частота" E31 имеет вид СУММ($C$31:C31).
"частота". Первая координата блока должна быть абсолютной (фиксированной), вторая - относительной. Поэтому при копировании формулы в последующие ячейки происходит вычисление суммы с накоплением. В рассматриваемом примере формула во второй ячейке колонки "накопленная частота" E31 имеет вид СУММ($C$31:C31).
- при вычислении середины интервала xSRi =(xi -1 +xi )/2 во вторую ячейку этой колонки (ячейку F31) вводится формула =(B30+B31)/2.
- формулы для абсолютной плотности mai =fi /h и для относительной плотности moi =wi /h должны иметь абсолютную ссылку на ячейку, содержащую значение интервала h. Соответственно в ячейки G31 и H31 вводятся следующие формулы =C31/$G$22 и =D31/$G$22.
10. В Excel группировку можно выполнить с помощью команды / C ервис/анализ данных/гистограмма . При этом раскрывается диалоговое окно рис.2.4. В строке ввода Входной диапазон указываются координаты блока исходного ряда [A5:J14]; в строке Интервал карманов - координаты блока значений интервалов [B30:B39]; в строке Выходной диапазон – координаты блока результатов J28, которые также показаны на рис. 2.4. Установить флажок в строке Вывод графика для вывода гистограммы.
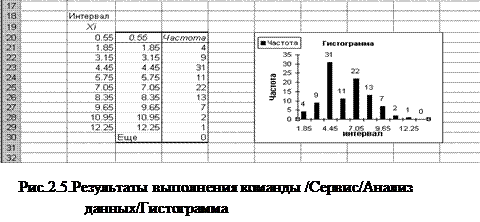
Результаты выполнения команды / C ервис/анализ данных/гистограмма приведены на рис. 2.5.
 |
2.2.1.2. Статистические характеристики интервального ряда
1. Исходными данными для расчета статистических характеристик интервального ряда является интервальный ряд, полученный в предыдущей пункте.
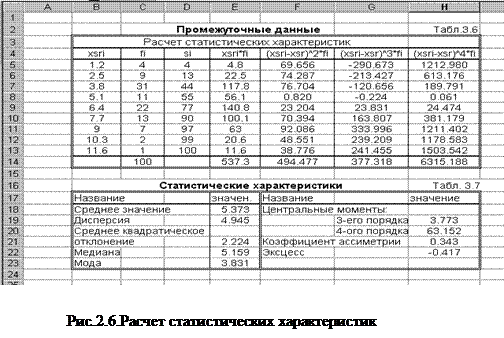
2. Для удобства вычислений составим вспомогательную таблицу, содержащую промежуточные данные. Ее можно расположить на новом рабочем листе (см. табл.3.6 рис.2.6). Данные колонок xSRi , fi , si копируются в новый рабочий лист из предыдущего листа (табл.3.5 рис. 2.1). Для этого необходимо выполнить следующие действия: выделить копируемый блок ячеек из табл.3.5 рис.2.1, выполнить команду /Правка/копировать , перейти на новый лист, указать блок-получатель (левую верхнюю ячейку), выполнить команду /Правка/специальная вставка/значения.
3.
 |
Выполнить расчет в колонке xSri * fi . Для этого в первую ячейку колонки E5 ввести формулу [=B5*C5], затем выполнить копирование ее в остальные ячейки колонки.
4. Используя функцию СУММ() или нажать кнопку Автосуммирование , определить итоговые суммы в колонках fi и xSRi ×fi (ячейки C14, E14).
5. Рассчитать среднее значение ![]() . Для этого в ячейку E18 ввести формулу [=E14/C14].
. Для этого в ячейку E18 ввести формулу [=E14/C14].
6. В следующих колонках выполнить вычисления: (xsri -`x )2 ×fi , (xsri -`x)3 ×fi , (xsri -`x)4 ×fi . Необходимо помнить, что `x - средняя арифметическая является скалярной величиной, поэтому ссылка на ячейку, содержащую значения `x должна быть абсолютной. Формулы в ячейках F5, G5, H5 будут такими: [=(B5-$F$18)^2*C5], [=(B5-$F$18)^3*C5], [=(B5-$F$18)^4*C5]. Выполнить копирование формул в остальные ячейки колонок таблицы.
7. Вычислить итоговые суммы в колонках "(xsri -`x )2 ×fi ", "(xsri -`x)3 ×fi ", "(xsri -`x)4 ×fi ". Для этого используется встроенная функция СУММ() или нажать кнопку Автосуммирования .
8. Рассчитать значения дисперсии d2 , среднего квадратического отклонения d, центральных моментов М3 , М4 , коэффициента асимметрии AS , показателя эксцесса Е. (2.7, 2.8, 2.9, 2.10). Результаты расчета оформляются в виде табл.3.7 рис.2.6. В соответствующие ячейки колонок "значения" записываются следующие формулы: в E19 – [=F14/C14], в E21 – [=КОРЕНЬ(Е19)], в H19 – [=G14/C14], в H20 – [= H14/C14], в H21 – [=H19/E21^3], в H22 – [=H20/E21^4-3].
9. Рассчитываются значения медианы Ме и моды Мо . (2.11, 2.12). Т.к. значение частоты fi в i-ой строке таблицы соответствует интервалу [xi -1 ;xi ], то в качестве начала медианного интервала xme и модального интервала xmo берутся значения интервала из предшествующих строк таблицы. В расчетных формулах используются данные xme , xmo из табл. 3.5, расположенной на другом рабочем листе (например ЛИСТ1), то для правильной адресации в расчетных формулах используются консолидированные ссылки. Формулы в ячейках для xme и xmo будут соответственно выглядеть так: в ячейке E22 – [=Лист1!В33+Лист1!G22*(Лист1!G17/2-D7)/C8], в ячейке E23 – [=ЛИСТ1!В32+ЛИСТ1!G22*(C7-C6)/(2*C7-C6-C8)].
2.2.1.3. Проверка гипотезы о нормальном распределении
интервального ряда
1. Исходными данными для проверки гипотезы являются интервальный ряд (табл.3.5, рис.2.1.) и статистические характеристики интервального ряда (табл.3.7, рис.2.6).
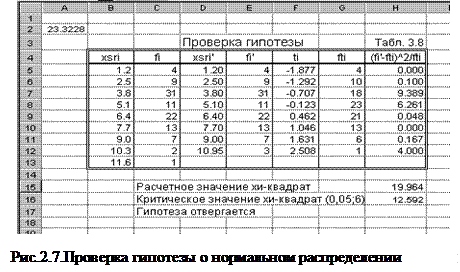
2. Для удобства вычислений составляется вспомогательная таблица (табл. 3.8), которую можно создать на новом рабочем листе (рис.2.7).
Значения колонок xSRi и fi копируются из табл.3.5 (команды: /Правка/копировать и /Правка/специальная вставка/значения).
3. При малых значениях частот (менее 3) рекомендуется объединять интервалы. При объединении интервалов частоты складываются и пересчитывается среднее значение переменной в объединенном интервале. В рассматриваемом примере это касается последнего и предпоследнего интервалов. Полученные при объединении средние значения интервалов и частоты представлены в колонках x' SRi и fi ' . При объединении в ячейках D12 и E12 записываются следующие формулы [=(B12+B13)/2] и [=C12+C13].
4. Выполнить расчеты в колонках ti
, fi
t
, (fi
'
- fi
t
)2
/fi
t
(2.13, 2.14, 2.15].
При расчете fi
t
по формуле (2.13) предварительно в любой свободной ячейке (например в ячейке А2) рассчитаем промежуточную скалярную величину ![]() . Формула в ячейке А2 будет иметь вид:
. Формула в ячейке А2 будет иметь вид:
=Лист1!G22*Лист1!G17/Лист2!E21/КОРЕНЬ(2*ПИ())
После этого в ячейки F5, G5, H5 вводим следующие формулы:
в ячейке F5 - =[(D5-Лист1!$E$18)/Лист1!$E$21],
в ячейке G5 - =ОКРУГЛ($A$2*EXP(-0.5*F5^2);0),
в ячейке H5 - =[(E5-G5)^2/G5].
Пояснение: на Лист1 расположены параметры интервального ряда; на Лист2 – статистические характеристики интервального ряда. Теоретическая частота, рассчитываемая по формуле (2.15), является дробной величиной. Она округляется до ближайшего целого с помощью функции ОКРУГЛ().
5. Значение суммы в колонке ![]() есть искомое значение критерия
есть искомое значение критерия ![]() Пирсона. Для вычисления суммы используется встроенная функция СУММ() или кнопка "Автосуммирования".
Пирсона. Для вычисления суммы используется встроенная функция СУММ() или кнопка "Автосуммирования".
6. Для определения критического значения c2 кр можно воспользоваться встроенной функцией ХИ2ОБР(a,m) при уровне значимости a=0,05 и числе степеней свободы m=k-2. Для данных примера расчетное значение c2 p =19,964, критическое значение c2 kr =12,592. Т.к. c2 p >c2 kr , то гипотеза о нормальном распределении отвергается.
2.2.1.4. Построение графиков
1. Исходными данными для построения графиков является интервальный ряд (табл.3.5 рис.2.1).
2. Выполнить команду /Вставка/Диаграмма/ либо нажать кнопку Мастера диаграмм . Это действие раскрывает диалоговое окно Мастер диаграмм . Мастер диаграмм представляет собой серию диалоговых окон для управления режимом построения диаграмм и установки параметров диаграмм. Построение диаграмм осуществляется по шагам - 4 шага. На каждом шаге раскрывается соответствующее диалоговое окно Мастера диаграмм . Диалоговые окна имеют несколько вкладок, которые открываются кнопками, расположенными в верхней части диалоговых окон. В нижней части окон Мастера диаграмм изображены кнопки Отмена , <Назад , Далее>, Готово . Кнопка Отмена прекращает построение диаграмм и закрывает окно Мастера диаграмм . Кнопка Далее> осуществляет переход к следующему шагу построения диаграмм. Кнопка <Назад позволяет вернуться к предыдущему шагу при необходимости исправить установки на предыдущих шагах. Окна имеют одно или несколько строк ввода для установки значений параметров диаграмм.
3. Окно шаг 1 из 4 Мастера диаграмм предлагает выбрать тип диаграммы. Excel имеет возможность выбора 14 различных типов стандартных диаграмм. Каждый тип в свою очередь имеет насколько форматов. Окно имеет две вкладки - стандартные и нестандартные. Открываем вкладку стандартные и выбираем следующие типы диаграмм: для гистограммы - "гистограмма", для полигона частот и кумулятивной кривой - "график".
4. Окно Шаг 2 из 4 Мастера диаграмм предлагает выбрать данные для построения диаграммы, положение данных в таблице (по строкам или столбцам), данные для разметки оси Х. Для выбора данных раскрываем вкладку Диапазон данных , активизируем строку ввода диапазон , открываем лист, содержащий интервальный ряд. Далее выделяем соответствующий блок ячеек: построение гистограммы и полигона частот осуществляется по данным колонки fi табл.3.5 рис.2.3, кумулятивная кривая строится по данным колонки si . Вкладка Ряды позволяет выбрать данные для разметки оси Х. Активизируем в ней строку ввода Подписи оси Х и в табл.3.5 выделяем данные для разметки оси Х: для гистограммы и кумулятивной кривой это будут данные столбца xi , для полигона - данные столбца xSRi .
5. Окно Шаг 3 из 4 Мастера диаграмм предлагает установить следующие параметры диаграмм: название диаграммы, названия оси Х и оси У, надписи на осях, установить координатную сетку или ее отменить, изменить размещение легенд. Открываем вкладку Заголовки и поочередно активизируя соответствующие строки ввода, вводим название диаграммы и название осей. Вкладка Оси позволяет установить или убрать разметку осей. Вкладка Подписи данных позволяет установить или убрать подписи значений данных на диаграмме. Вкладка Линии сетки позволяет изменить координатную сетку или убрать ее совсем. Вкладка Таблица данных позволяет поместить таблицу значений признака под диаграммой.
6. Окно Шаг 4 из 4 Мастера диаграмм предлагает поместить диаграмму на отдельном листе или на существующем. Выбираем на существующем. После этого нажать кнопку Готово .
7. При неудовлетворительном выборе параметров диаграмм и графиков можно выполнить редактирование соответствующих элементов (см.п.1.9).
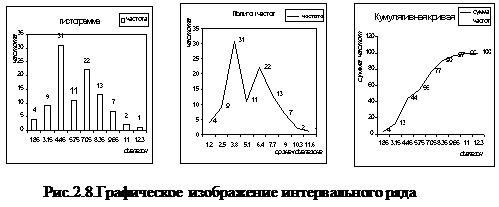 |
8. Гистограмма, полигон частот и кумулятивная кривая изображены на рис.2.8.
3.2. Технология выполнения интервальной группировки в Statistica
Для выполнения группировки в системе Statistica из стартовой панели модуля Описательные статистики и таблицы выбирается процедура Таблицы частот По этой команде открывается одноименный диалог рис.3.1. Это окно содержит пять вкладок: Быстрый, Дополнительно, Опции, Описательные, Нормальность и кнопки управления: Переменные, Ок, Отмена, Опции .
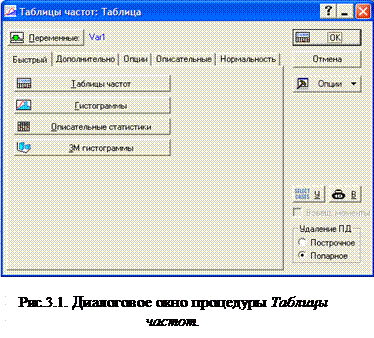 Этот диалог предлагает множество настроек, позволяющие изменять вид и группировку в таблицах частот, проверять нормальность распределения, в том числе и графическим способом. Диалог в режиме вкладки Быстрый
содержит несколько управляющих кнопок.
Этот диалог предлагает множество настроек, позволяющие изменять вид и группировку в таблицах частот, проверять нормальность распределения, в том числе и графическим способом. Диалог в режиме вкладки Быстрый
содержит несколько управляющих кнопок.
Кнопка Переменные открывает стандартное окно выбора списка переменных для анализа.
После нажатия этой кнопки ОК программа вычислит описательные статистики для всех выбранных переменных и разместит их в таблице.
Отмена . При нажатии кнопки Отмена закрывается текущий диалог и появляется стартовая панель модуля Основные статистики и таблицы .
Опции . При нажатии этой кнопки вызывается меню Опции в котором устанавливаются режим вычисления с повышенной точностью и некоторые параметры отображения таблиц и графиков.
Ниже кнопки Опции находятся две кнопки: Кнопка SELEKT CASES (Выбор наблюдений) . При нажатии этой кнопки появляется диалоговое окно Условия выбора наблюдений Анализа/Графика . Эта функция используется для того, чтобы включить в анализ только подмножество наблюдений.
При нажатии кнопки В (Вес) появляется диалоговое окно Веса наблюдений Анализа/Графика . Эта функция позволяет "изменять" вклад отдельных наблюдений, пропорциональных значениям выбранной переменной.
Правила установки Условий выбора наблюдений и установка весов наблюдений описаны в гл.1.
В правом нижнем углу диалогового окна находится группа опций Удаление ПД . Если выбрано Построчное удаление пропусков , то STATISTICA игнорирует все наблюдения, имеющие пропуски хотя бы для одной переменной в списке. Если выбрано Попарное удаление пропусков , то наблюдения будут удаляться из вычислений вместе с переменными, для которых в них содержатся пропущенные данные.
Вкладка Быстрый
Вкладка Быстрый содержит доступ к опциям, представленным на рис.3.1.
Кнопка Таблицы частот строит последовательность таблиц частот для выбранных переменных по одной для каждой переменной. Способ, которым переменные группируются в таблицах частот определяется опцией из набора опций M етод категоризации для таблиц и графиков ( см. вкладку Дополнительно ). Опции из раздела Опции отображения (см. вкладку Опции ) определяют различные обобщающие статистики, которые будут включены в таблицу частот. Если выбран какой-либо Критерий нормальности (например, если выбрана любая опция из раздела, см. вкладку Нормальность ), тогда для каждой переменной появится дополнительная таблица с результатами вычисления соответствующего критерия.
Кнопка Гистограммы строит последовательность гистограмм по одной для каждой выбранной переменной. Способ группировки переменных при построении гистограмм определяется теми же настройками, что и при построении Таблиц частот .
Кнопка Описательные статистики строит таблицы с описательными статистиками для каждой переменной. Способ обработки данных при вычислении описательных статистик зависит от установки опции в наборе M етод категоризации для таблиц и графиков ( см. вкладку Дополнительно ):
В частности:
1. Если выбрана опция Размер шага и пользователем задано минимальное значение, тогда все наблюдения, которые не превышают это заданное значение, будут проигнорированы;
2. Если выбрана опция Целые категории , то все нецелые значения будут проигнорированы;
3. Если выбрана опция Заданные группирующие коды (значения ), то все значения, которые не совпадают ни с одним из выбранных целых кодов, будут проигнорированы;
4. Если выбрана опция Определенные пользователем категории , то кнопки Описательные статистики будут неактивными (потому что сложные правила разбиения на группы могут привести к тому, что одно наблюдение может быть приписано более чем к одной категории). Наблюдение будет приписано первому Определенному пользователем интервалу , которому оно "удовлетворяет" и Описательные статистики для этих интервалов вычисляться не будут.
Во всех случаях пропущенные данные будут построчно или попарно , удаляться в зависимости от выбора в разделе У даление ПД .
3М гистограммы . Эта опция строит последовательность 3М гистограмм для выбранных переменных, по одному на каждую выбранную переменную. После нажатия этой кнопки программа попросит пользователя выбрать два набора переменных (из выбранных ранее с помощью кнопки Переменные ). 3М гистограммы будут построены для каждой пары переменных, включающей переменные из разных списков.
Вкладка Дополнительно
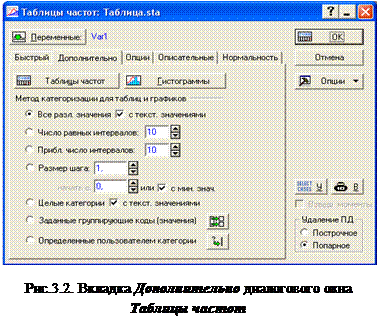 Вкладка Дополнительно
содержит доступ опциям, представленным на рис.2.3. Данные опции служат для управления способом группировки в таблицах частот, в графиках и при расчете описательных статистик.
Вкладка Дополнительно
содержит доступ опциям, представленным на рис.2.3. Данные опции служат для управления способом группировки в таблицах частот, в графиках и при расчете описательных статистик.
Кнопки Таблицы частот и Гистограммы имеют такое же назначение, что и во вкладке Быстрый .
Опции в наборе M етод категоризации для таблиц и графиков определяют, как будут сгруппированы или табулированы выбранные переменные в таблицах частот и в гистограммах, а также как обрабатываются наблюдения при расчете описательных статистик.
Все различные значения – частоты строятся с учетом всех различных значений анализируемых переменных.
С текстовыми значениями – частоты строятся с учетом всех текстовых значений выбранных переменных.
Число равных интервалов – диапазон значений каждой переменной делится на указанное число интервалов:
Приблизительное число интервалов : – построит приближенные интервалы и выберет приближенный шаг так, что последняя десятичная цифра в значениях границ интервалов будет равна 1, 2 или 5 (например, 10.5, 11.0, 11.5, и т.д.). Такие интервалы легче интерпретировать, чем интервалы с большим числом десятичных разрядов.
Размер шага – Опция задает ширину интервала категоризации в таблицах частот (и гистограммах). Если выбрана опция с мин. значения , то группировка начинается с минимального значения переменной (первый интервал группировки включает это значение). Если опция не выбрана, то левая граница первого интервала группировки задается пользователем в соответствующем поле.
Целые значения – Если опция выбрана, то границами интервалов категоризации в таблицах частот (и гистограммах) будут целые числа, а размер шага равен наименьшему целому значению. Все нецелые значения переменных будут проигнорированы программой в процедурах Таблицы частот - Гистограммы и Описательные статистики . Если выбрана опция с текст. значениями , тогда категории при выборе таблиц частот и гистограмм будут помечены текстовыми значениями (например, мужчины, женщины) а не целыми значениями (например, 1, 2), которые доступны в текущем файле данных границами интервалов группировки будут целые значения, а размер шага будет равен наименьшему целому значению. Все нецелые значения переменных будут игнорированы программой.
Заданные группирующие коды (значения ) – таблицы частот и гистограммы будут построены с помощью целых кодов, определенных пользователем и задаваемых с помощью отдельной группирующей переменной (см рис.2.5). Все нецелые значения переменных будут проигнорированы программой
Определенные пользователем категории – позволяет определить до 16 логических условий, позволяющих отнести наблюдения к определенной категории в таблице частот.
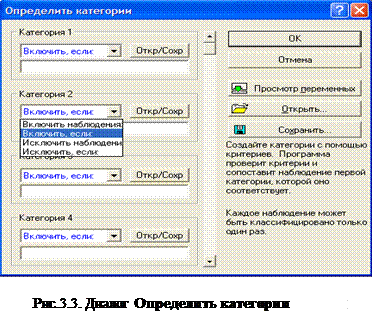 При нажатии кнопки Определенные пользователем категории
вызовается диалоговое окно Определить категории
рис.3.3. Диалоговое окно позволяет вам задать до 16 условий выбора наблюдений для использования их в вычислениях таблиц частот (разбиения наблюдений на категории). Заданные здесь условия выбора будут проверены последовательно; т.е. наблюдение попадет в первую категорию, к которой он "подходит".
При нажатии кнопки Определенные пользователем категории
вызовается диалоговое окно Определить категории
рис.3.3. Диалоговое окно позволяет вам задать до 16 условий выбора наблюдений для использования их в вычислениях таблиц частот (разбиения наблюдений на категории). Заданные здесь условия выбора будут проверены последовательно; т.е. наблюдение попадет в первую категорию, к которой он "подходит".
Заметим, что в файле данных вы так же можете создать новую (группирующую) переменную и задать в ней необходимые значения. Например, это бывает удобным, когда вам требуется перекодировать данные так, что значения целевой переменной не фиксированы, а рассчитываются по специальному закону (например как среднее набора других значений). Для этого воспользуйтесь формулами в таблице исходных данных, или для более сложных вычислений, средой разработки STATISTICA Visual Basic.
Пример. Этот набор (двух) условий выбора приведет к образованию двух групп в таблице частот. Первая группа будет содержать все наблюдения со значениями переменной 1, которые больше нуля или равны нулю, вторая группа будет содержать все наблюдения со значениями переменной 1, которые меньше нуля.
Категория 1: Включ., если: v1>=0
Категория 2: Включ., если: v1<0
Задание категорий в полях Категория 1, 2, 3, …. Прокручивая этот список, можно определить до 252 категорий, разбивающих наблюдения на подгруппы. Заданные здесь условия выбора будут проверены последовательно; т.е. наблюдение попадет в первую категорию, к которой он "подходит"
· Включить/Исключить, если : Если выбрана команда Включ., если то значения выделенной переменной для наблюдений, которые удовлетворяют условию, будут помещены в соответствующую группу. Если выбрана команда Искл., если то значения выделенной переменной для наблюдений, которые удовлетворяет заданному условию, будут исключены из группы.
· Условия выбора наблюдений задаются в полях ввода Категория 1, 2, 3, … согласно стандартным Условиям выбора наблюдений системы STATISTICA.
· Операторы. При задании условия используются операторы: =, <>, <, >, <=, >=, NOT, AND, OR
· Имена переменных . В условиях необходимо указать имена переменных (например, v1, v2, v3, . . . ) или их имена (например, Пол, Дата, Время, . . .).
· Номер наблюдения . Обозначение v0 задает номера наблюдений
Примеры : v1=0 OR v2>=0;
(v1<1 OR v9='YES' ) AND v4<>0
Замечание : При использовании текстовых значений нужно заключать их в апострофы, например, 'Yes'.
Кнопка Откр/Сохр используется для открытия файла системы STATISTICA со стандартными Условиями выбора наблюдений (которые могут использоваться в программе для выбора или фильтрации наблюдений для всех видов анализа), а также для сохранения текущего условия для каждой Категории. При нажатии кнопки Откр/Сохр открывается диалоговое окно Условия выбора наблюдений , в котором можно отредактировать, сохранить или открыть условия выбора наблюдений (это те же самые условия, которые используются для обработки подгрупп наблюдений во всей программе). Условия выбора наблюдений из этого диалогового окна сохраняются в файле с расширением *.sel . При нажатии кнопки OK в диалоговом окне Условия выбора наблюдений , введенные условия будут использованы для разбиения на подгруппы.
Кнопка Просмотр переменных открывает диалоговое окно Выбрать переменную , в котором можно посмотреть переменные текущего файла данных.
Кнопка Открыть ... открывает диалоговое окно Открыть условия , в котором можно выбрать файл (содержащий все условия выбора подгрупп), который нужно открыть в диалоговом окне Определить категории . В этом диалоговом окне открываются стандартные текстовые файлы с расширением *.txt.
Кнопка Сохранить ... открывает диалоговое окно Сохранить условия , где можно указать имя файла, в котором будут сохранены все условия выбора. Это файл будет сохранен в текстовом виде с расширением *.txt.
Вкладка Опции
Установки опций этой вкладки определяют способы отображения результатов и то, как будут удаляться пропущенные данные рис.3.4.
Группа Опции отображения в таблицах частот определяет статистики, которые вычисляются для каждой категории в Таблицах частот . В зависимости от выбора в поле Удаление ПД STATISTICA включает ПД в обработку, или исключает их из нее.

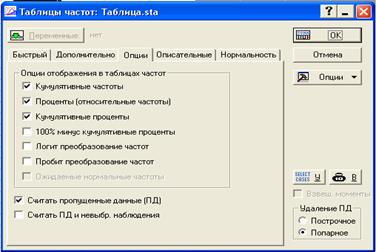 Кумулятивные частоты
– Опция вычисляет кумулятивные или накопленные частоты. Это сумма частот по последовательным интервалам группировки.
Кумулятивные частоты
– Опция вычисляет кумулятивные или накопленные частоты. Это сумма частот по последовательным интервалам группировки.
Проценты (относительные частоты)) – вычисляются относительные частоты.
Кумулятивные проценты - вычисляются кумулятивные или накопленные проценты.
100% минус кумулятивные проценты – вычисляются 100 минус кумулятивные проценты.
Логит преобразования частот – для частот каждого интервала производится преобразование логит. В частности, логиты для категории i вычисляются из соответствующей кумулятивной пропорции pi как:
![]() .
.
Пробит преобразования частот – для кумулятивных частот каждого интервала производится преобразование пробит – вычисляются z-значения, связанные с вероятностью в соответствующей ячейке.
Ожидаемые нормальные частот – вычисляется нормальное приближение для наблюдаемых частот.
В нижней части окна указаны опции, назначение которых опций следующее:
Считать пропущенные данные (ПД) – Опция вычисляет группу специально для пропущенных данных. Проценты и кумулятивные (накопленные) проценты также вычисляются для пропущенных данных.
Считать ПД и невыбранные переменные – опция вычисляет дополнительно группы невыбранных (и не пропущенных) наблюдений в таблице частот. Вычисляются проценты и кумулятивные проценты относительно общего числа наблюдений.
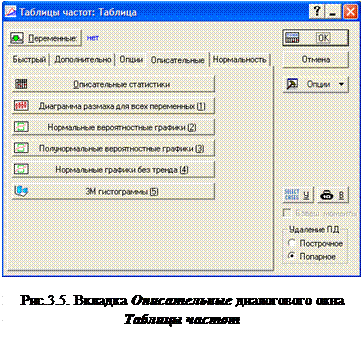
Вкладка Описательные
Опции этой вкладки рис.3.5 служат для просмотра набора статистик и графиков распределений для каждой из выбранных переменных.
 Описательные статистики
.
Опция строит таблицы с описательными статистиками для выбранных переменных аналогично одноименной опции во вкладке Быстрые
.
Описательные статистики
.
Опция строит таблицы с описательными статистиками для выбранных переменных аналогично одноименной опции во вкладке Быстрые
.
Имеется несколько кнопок для графического представления результатов наблюдений:
Диаграмма размаха для всех переменных . Процедура строит каскад диаграмм размаха для зависимых переменных; один график для каждой переменной. Каждая группа представлена одним графиком, который состоит из трех компонент:
1. Центральная точка, показывающая главную тенденцию или положение;
2. Прямоугольник, показывающий разброс значений относительно главной тенденции;
3. Отрезки вокруг прямоугольника, показывающие диапазон значений переменной.
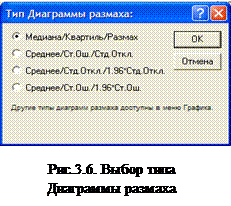 При нажатии этой кнопки появляется диалоговое окно Диаграмма размаха
рис.3.6 , в котором необходимо выбрать тип диаграммы для построения.
При нажатии этой кнопки появляется диалоговое окно Диаграмма размаха
рис.3.6 , в котором необходимо выбрать тип диаграммы для построения.
Нормальные вероятностные графики . Процедура строит последовательность нормальных вероятностных графиков - один график для каждой выбранной переменной.
Полунормальные вероятностные графики . Процедура строит последовательность полунормальных вероятностных графиков - один график для каждой выбранной переменной.
Нормальные вероятностные графики без тренда . Процедура строит последовательность нормальных вероятностных графиков без тренда - один график для каждой выбранной переменной.
Правила построения вероятностных графиков описаны в гл. 2.
3М гистограммы . Эта опция строит каскад 3М гистограмм для выбранных переменных, по одному на каждую выбранную переменную. После нажатия этой кнопки программа попросит пользователя выбрать два набора переменных (из выбранных ранее с помощью кнопки Переменные). 3М гистограммы будут построены для каждой пары переменных, включающей переменные из разных списков.
Вкладка Нормальность
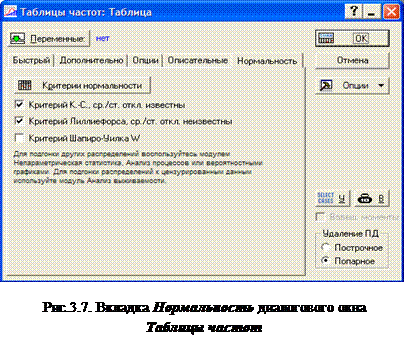 Вкладку Нормальность
обеспечивает доступ к представленным опциям рис.3.7. Эти опции служат для проверки нормальности выбранных переменных. Если выбрана любая из представленных здесь опций, то при построении таблицы частот (посредством кнопки ОК
) для выбранной переменной, будет построена еще одна таблица, содержащая результаты выбранных критериев нормальности
(одна таблица на критерий).
Вкладку Нормальность
обеспечивает доступ к представленным опциям рис.3.7. Эти опции служат для проверки нормальности выбранных переменных. Если выбрана любая из представленных здесь опций, то при построении таблицы частот (посредством кнопки ОК
) для выбранной переменной, будет построена еще одна таблица, содержащая результаты выбранных критериев нормальности
(одна таблица на критерий).
Критерии нормальности . Кнопка выведет таблицы результатов с запрошенными критериями нормальности для выбранных переменных.
Критерий Колмогорова-Смирнова , ср./ст.откл. известны . Опция вычисляет одновыборочный критерий Кoлмогорова-Смирнова. Если D статистика значима, то гипотеза нормальности распределения значений переменной отвергается. Вычисляются два значения вероятности для каждого критерия: первое, табулировано Massey (1951), относится к случаю, когда параметры распределения - среднее и стандартное отклонение известны заранее и не оцениваются. Однако обычно эти параметры не известны и оцениваются по наблюдениям. Тогда проверяется сложная гипотеза (с неизвестными заранее параметрами распределения и вычисляются вероятности Лиллиефорса.
Критерий Лиллиефорса, ср./ст.откл. неизвестны . Если эта опция выбрана, то программа вычислит одновыборочную D статистику Колмогорова-Смирнова, а также вероятности Лиллиефорса (см. предыдущий абзац).
Критерий Шапиро-Уилка W . Опция вычисляет W статистику Шапиро-Уилка для каждой выбранной переменной. Если W-статистика значима , то гипотеза нормальности отвергается. Заметим, что в STATISTICA используется улучшенная версия алгоритма, которая применима к выборкам, содержащим до 2000 наблюдений; если число наблюдений больше 2000, этот критерий неприменим.
Пример: Технологию расчета описательных характеристик вариационного ряда в программе Statistica покажем на примере данных, представленных в табл.2.1.
Расположение исходных данных в таблице данных представлено на рис.2.9.
Для выполнения группировки в системе Statistica из стартовой панели Описательные статистики и таблицы выбирается процедура Таблица частот . По этой команде открывается одноименный диалог рис.3.1, в котором произведем следующие установки:
· Переменные - выбираем список переменных для анализа, в данном случае переменную Var1.
· Активизируем вставку Дополнительно и в группе опций M етод категоризации для таблиц и графиков у станавливаем флажок перед опцией Число равных интервалов равным 9 интервалов
· Активизируем вставку Опции и в группе опций Опции отображения устанавливаем флажки перед опциями:
- Кумулятивные частоты – вычисляем кумулятивные или накопленные частоты.
- Проценты (относительные частоты ) – вычисляем относительные частоты.
- Кумулятивные проценты - вычисляем кумулятивные или накопленные проценты.
- 100% минус кумулятивные проценты – вычисляем 100 минус кумулятивные проценты.
- Логит преобразования частот – для частот каждого интервала производим преобразование логит:
- Ожидаемые нормальные частоты – вычисляем нормальное приближение для наблюдаемых частот.
· Активизируем вставку Нормальность и выделяем флажками следующие опции:
- Критерий Колмогорова-Смирнова, ср./ст. откл. известны – вычисляем одновыборочный критерий Колмогорова-Смирнова
- Критерий Лиллиефорса, ср./ст. откл. неизвестны –вычисляем вероятности Лиллиефорса, на основе которых вычисляем одновыборочную D статистику Колмогорова-Смирнова.
- W критерий Шапиро-Уилка – вычисляем W статистику Шапиро-Уилка.
При нажатии на кнопку Таблицы частот получаем результирующую таблицу частот, представленную на рис.3.8,а).
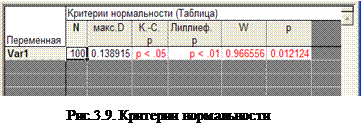
 При нажатии на кнопку Гистограммы
получаем гистограмму распределения частот рис.3.8,б).
При нажатии на кнопку Гистограммы
получаем гистограмму распределения частот рис.3.8,б).
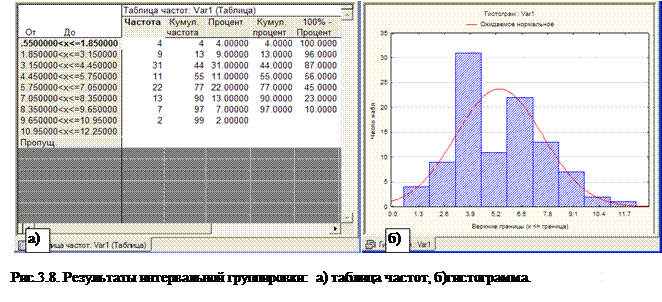
При нажатии на Критерий нормальности вкладки Нормальность – на экран выводятся таблицы результатов со значениями критериев нормальности рис.3.9.
На рис.2.14 представлена распечатка таблицы частот.
STAT. VAR1 (new.sta)
Cumul. Cumul. 100% -
Category Count Count Percent Percent Percent
,457143<x<=1,94285 4 4 4,00 4,00 100,00
1,94286<x<=3,42857 12 16 12,00 16,00 96,00
3,42857<x<=4,91428 35 51 35,00 51,00 84,00
4,91429<x<=6,40000 22 73 22,00 73,00 49,00
6,40000<x<=7,88571 11 84 11,00 84,00 27,00
7,88571<x<=9,37142 13 97 13,00 97,00 16,00
9,37143<x<=10,8571 2 99 2,00 99,00 3,00
10,8571<x<=12,3428 1 100 1,00 100,00 1,00
Missing 0 100 0,00 100,00 0,00
STAT. VAR1 (new.sta)
Category Logits
,457143<x<=1,94285 -3,17
1,94286<x<=3,42857 -1,65
3,42857<x<=4,91428 ,04
4,91429<x<=6,40000 ,99
6,40000<x<=7,88571 1,65
7,88571<x<=9,37142 3,47
9,37143<x<=10,8571 4,59
10,8571<x<=12,3428 --
Missing
Рис.2.14. Распечатка таблицы частот