Книга: Устойчивость дисперсных систем седиментация и диффузия

Виды устойчивости дисперсных систем. Лиофобные и лиофильные золи

Устойчивость дисперсных систем – это возможность их нахождения в исходном состоянии неопределенно долгое время.

Устойчивость дисперсных систем может быть:

1. К осаждению дисперсной фазы - характеризует способность дисперсной системы сохранять равновесное распределение фазы по объему дисперсионной среды или ее устойчивость к разделению фаз. Это свойство называется седиментационная (кинетическая) устойчивость.

2. К агрегации ее частиц.

Агрегативная устойчивость – это способность дисперсной системы сохранять неизменной во времени степень дисперсности, т.е. размеры частиц и их индивидуальность.

Она обусловлена способностью дисперсных систем образовывать агрегаты (т.е. укрупняться). По отношению к агрегации дисперсные системы могут быть устойчивыми кинетически и термодинамически . Термодинамически устойчивые системы образуются в результате самопроизвольного диспергирования одной из фаз, т.е. самопроизвольного образования гетерогенной свободнодисперсной системы. Дисперсные системы также делят на:

· лиофильные, обладающие термодинамической устойчивостью;

· лиофобные, которые термодинамически неустойчивы к агрегации, но могут быть устойчивы кинетически, т.е. обладать значительным временем жизни.

Особенности этих двух видов устойчивости показаны на схеме:

Термодинамическая устойчивость лиофильных систем означает, что они равновесны (энергия Гиббса DG ® min), обратимы и образуются самопроизвольно, как из макрофаз, так и из истинных растворов. Поскольку образуются гетерогенные системы, то поверхностная энергия должна быть скомпенсирована энтропийной составляющей, т.е. частицы дисперсной системы должны участвовать в молекулярно кинетическом (тепловом) движении. Отсюда следует, что лиофильные системы могут быть только ультромикрогетерогенными, а поверхностное натяжение на границе «частица – среда» должно быть очень малым. Значение поверхностного натяжения, при котором обеспечивается термодинамическая устойчивость дисперсных систем, определяется соотношением Ребиндера – Щукина :

где безразмерный коэффициент;

K – постоянная Больцмана;

а – средний размер частицы.

Расчеты показывают, что межфазное поверхностное натяжение в лиофильных дисперсных системах в зависимости от размеров частиц может иметь значение от 1,4×10^-7 до 1,4×10^-3 Дж/м² . Типичными представителями лиофильных дисперсных систем являются растворы коллоидных поверхностно активных веществ (ПАВ) (ассоциативные коллоиды) и растворы полимеров (молекулярные коллоиды).

Лиофобные системы термодинамически неустойчивы, т.к. частицы дисперсной фазы склонны к агрегации. Их агрегативная термодинамическая неустойчивость обусловлена избытком поверхностной энергии. Межфазное натяжение в них больше рассчитанного по соотношению Ребиндера – Щукина, поэтому они не могут быть получены самопроизвольным диспергированием. Для их образования должна быть затрачена внешняя энергия. Укрупнение частиц дисперсной фазы при потере агрегативной устойчивости достигается двумя путями:

1. Изотермическая перегонка, т.е. растворение мелких и рост крупных частиц в соответствии с уравнением Кельвина;

2. За счет слипания частиц, т.е. коагуляцией.

В зависимости от природы среды и концентрации дисперсной фазы эти процессы могут заканчиваться или осаждением, или структурообразованием.

При нарушении агрегативной устойчивости происходит коагуляция .

Седиментация и диффузия. Гипсометрический закон. Седиментационно-диффузионное равновесие. Скорость седиментации

Грубодисперсные системы под действием гравитационных сил будут оседать (седиментировать). В результате в системе устанавливается определенное равновесие распределения частиц по высоте. Коллоидные системы по устойчивости занимают промежуточное положение между истинными растворами (max ) и грубодисперсными растворами (min ). На каждую частицу дисперсной фазы действует 3 силы:

1. Сила тяжести F _т .

2. Архимедова сила F _A .

3. Сила трения F _тр .

Сила седиментации будет результирующей между первой и второй силой

Если , F _сед > 0 – происходит оседание частиц. Если F _сед < 0 – то частицы всплывают. Результирующая сила, действующая на частицу:

где B – коэффициент трения; U – скорость седиментации.

при равновесии F_сед = F_тр

Сила трения, согласно закону Стокса

для сферических частиц

Отсюда уравнение скорости оседания и радиуса частиц

Результатами седиментационного анализа может служить интервал радиусов частиц в данной системе, просто радиус частиц или доля фракций определенного радиуса.

Способность к седиментации принято выражать через константу седиментации S , которая определяется скоростью седиментации:

Для сферических частиц эта константа равна

Из уравнения следует, что S зависит как от размеров частиц, так и от природы среды. За единицу измерения S принят сведберг (сб), равный 10¹³ с.

Часто для характеристики процесса седиментации используют удельный поток седиментации I _сед.

Удельный поток седиментации – это число частиц, оседающих в единицу времени через сечение единичной площади, нормальное к направлению седиментации.

Размерность: [i _сед ] = част/см² * с.

Из определения i _сед следует: i _сед = U_сед * v , где v – частичная концентрация частиц в дисперсной системе.

Подставив в это уравнение U _сед , получим:

Таким образом, удельный поток прямо пропорционален V , v , (ρ – ρ_о ) и обратно пропорционален S . Подставив эти выражения в уравнение, получим

Значит, в случае сферических частиц удельный поток прямо пропорционален квадрату радиуса и обратно пропорционален вязкости среды.

Рассматривая процесс седиментации, мы не учитываем броуновского движения, в котором участвуют частицы. Следствием броуновского движения, является диффузия, которая стремится выровнять концентрацию частиц по всему объёму, в то время как седиментация приводит к увеличению концентрации в нижних слоях.

Таким образом, наблюдается два противоположных потока: поток седиментации i _сед и поток диффузии i _диф.

, где

В результате конкуренции этих потоков возможны три варианта:

1. , т.е., т.е.

Чтобы выполнилось это неравенство, значения Т и должны быть малы, а (ρ – ρ_о ) и v – велики. В реальных условиях эти параметры заметно изменить сложно, а радиус частиц в дисперсных системах изменяется в широком интервале: от 10^-7 до 10^-2 см и именно радиус частиц является определяющим. Установлено, что данное неравенство соблюдается, когда r 10^-3 см. В этих случаях диффузией можно пренебречь, идёт быстрая седиментация – система является седиментационно неустойчивой.

2. , т.е. ,

т.е.

Это условие должно выполняться, когда Т и велики, а (ρ – ρ_о ) и v – малы. Но и здесь решающую роль играет радиус частиц. Установлено, что это неравенство выполняется при r 10^-5 см. В этом случае можно пренебречь седиментацией, диффузия приведёт к равномерному распределению частиц по всему объёму сосуда. Дисперсная система является седиментационно устойчивой.

3. , т.е. ,

т.е.

В системе имеет место седиментационно-диффузионное равновесие.

Проинтегрируем это уравнение, разделив переменные:

;

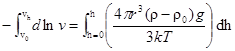Примем ,

где v _o – концентрация частиц на дне сосуда;

v_h – концентрация частиц на высоте h от дна.

Отсюда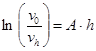

- гипсометрический закон Лапласа-Перрена .

В этом случае система является седиментационно-устойчивой , но распределение частиц в ней не равномерное, а равновесное . Это распределение наблюдается, когда 10^-5 < r < 10^-3 см.

Если сравнить седиментацию с учетом диффузии и без нее, то видно различие факторов обусловливающих кинетическую устойчивость. Эти факторы позволяют различать кинетическую седиментационную устойчивость (КСУ) и термодинамическое равновесие, которого не может быть при КСУ. Мерой КСУ является величина, обратная константе седиментации.

Эта устойчивость обеспечивается гидродинамическими факторами: вязкостью и плотностью среды, плотностью и размерами частиц. КСУ измеряется в обратных сведбергах: обр. св. = 10¹³ с^{– 1} .

ТСУ обусловлена статистическими законами диффузии и непосредственно связана с диффузионно–седиментазионным равновесием. Мерой ТСУ является гипсометрическая высота. Ее удобнее определять как высоту h _е , на протяжении которой концентрация дисперсной фазы изменяется в e раз.

Из формулы следует, что h _е и ТСУ тем больше, чем меньше размер частиц и разность между плотностями. Вязкость не влияет на ТСУ, а увеличение Т способствует повышению устойчивости, т.к. увеличивается тепловое движение. КСУ с увеличением Т убывает, за счет снижения вязкости среды.

Итак, седиментационная устойчивость дисперсных систем определяется, главным образом, размерами частиц дисперсной фазы:

· лиофобные золи (10^{– 7} – 10^{– 5} см) – седиментационно устойчивые системы, характерна диффузия, обеспечивающая равномерное распределение частиц по объему системы;

· микрогетерогенные системы (10^{– 5} 10^{– 3} см) – устанавливается седиментационно – диффузионное равновесие, для которого характерно гипсометрическое распределение частиц по объему системы;

· грубодисперсные (более 10^{– 3} см) - седиментационно неустойчивые системы, происходит быстрая седиментация.

Зависимость распределения частиц по высоте в равновесном состоянии аналогична барометрической формуле Ла-Пласса для газов в атмосфере:

где m – масса частицы;

h₁ , h ₂ – высоты уровней замера;

с ₁ , с ₂ – концентрации на уровнях h ₁ и h ₂ соответственно;

 - плотность частицы;

₀ - плотность среды.

При коагуляции золя смесью двух и более электролитов возможны три случая (рис. 3.1.2.3). По оси абсцисс отложена концентрация первого электролита С ₁ , а C _к1 – его порог коагуляции. Аналогично по оси ординат отложена концентрация второго электролита С ₂ , а С _к2 – его порог коагуляции.

1. Аддитивное действие электролитов (линия 1 рис. 3.1.2.3). Электролиты действуют как бы независимо один от другого, их суммарное действие складывается из воздействий каждого из электролитов. Если с₁ ^´ - концентрация первого электролита, то для коагуляции золя концентрация второго электролита должна быть равной с₂ ^´ . Аддитивность наблюдается обычно при сходстве коагулирующей способности обоих электролитов.

2. Синергизм действия (линия 2 рис. 3.1.2.3). Электролиты как бы способствуют друг другу – для коагуляции их требуется меньше, чем нужно по правилу аддитивности (с₂ ^″ < c₂ ^′ ). Условия, при которых наблюдается синергизм, сформулировать трудно.

3. Антагонизм действия (линия 3 рис. 3.1.2.3). Электролиты как бы противодействуют друг другу и для коагуляции их следует добавить больше, чем требуется по правилу аддитивности. Антагонизм наблюдается при большом различии в коагулирующем действии электролитов.

Существует несколько теорий, объясняющих явление антагонизма. Одной из его причин может служить химическое взаимодействие между ионами.

Например, для золя AgCl, стабилизированного хлоридом калия, коагулирующем действием обладают катионы. Например, большой коагулирующей способностью обладает четырёхзарядный ион тория Th⁴⁺ . Однако если взять для коагуляции смесь Th(NO₃ )₄ и K₂ SO₄ , то коагулирующая способность этой смеси значительно меньше, чем отдельно взятого Th(NO₃ )₄ . Связано это с тем, что в результате химической реакции образуется комплекс:

и вместо четырёхзарядных ионов Th ⁴⁺ в золе будут находиться однозарядные катионы K ⁺ , коагулирующее действие которых значительно слабее (правило Шульце-Гарди).

Гетероадагуляция - прилипание частиц дисперсной фазы к вводимой в систему чужеродной поверхности.

Одной из причин этого явления является адсорбция стабилизатора на этой поверхности. Например: отложение коллоидных частиц на волокнах при крашении и дроблении.

Для гидрофобных золей в качестве ВМС обычно используют белки, углеводы, пектины; для неводных золей – каучуки.

При введении в коллоидный раствор электролитов, содержащих многовалентные ионы с зарядом противоположные заряду частиц, наблюдается явление «неправильные ряды» . Оно состоит в том, что при добавлении к отдельным порциям золя все возрастающего его количества электролита золь сначала остается устойчивым, затем в определенном интервале концентраций происходит коагуляция; далее золь снова становится устойчивым и, наконец, при повышении концентрации электролита опять наступает коагуляция уже окончательная. Подобные явления могут вызывать и большие органические ионы. Объясняется это тем, что при весьма малых количествах введенного электролита ионов недостаточно, чтобы коагулировать золь, т. е. значение x- потенциала остается выше привычного (рис. 3.1.2.4). При больших количествах электролита его ионы проявляют коагулирующее действие. Этот интервал концентраций отвечает значениям x- потенциала частиц от x критического первого знака до x критического другого знака.

При еще больших концентрациях многовалентные ионы перезаряжают коллоидную частицу и золь опять устойчивый. В этой зоне x-потенциал опять выше критического значения, но обратен по знаку частицам исходного золя. Наконец, при высоком содержании исходного электролита многовалентные ионы снова снижают значение x-потенциала ниже критического и снова происходит окончательная коагуляция.

Повышение агрегативной устойчивости золя путём введения в него высокомолекулярного соединения (ВМС) называется коллоидной защитой. Происходит образование защитной пленки на поверхности золя (гидратной или ВМС), препятствующей взаимодействию частиц электролита.

В качестве количественной характеристики коагуляции Зигмонди предложил использовать скорость коагуляции .

Скорость коагуляции u - это изменение концентрации коллоидных частиц в единицу времени при постоянном объеме системы .

где n - концентрация частиц;

t - время.

Знак «-» стоит потому, что концентрация частиц со временем уменьшается, а скорость всегда положительна.

Степень коагуляции a:

где Z - общее число столкновений частиц в единицу времени; Z _эф - число эффективных столкновений (т.е. столкновений, приводящих к коагуляции) в единицу времени.

Если a = 0, коагуляция не происходит, коллоидный раствор агрегативно устойчив.

Если a = 1, происходит быстрая коагуляция, т.е. каждое столкновение частиц приводит к их слипанию.

Если 0 < a < 1, наблюдается медленная коагуляция, т.е. только некоторые столкновения частиц приводят к их слипанию.

Чтобы частицы при столкновении слиплись, а не разлетелись как упругие шары, должен быть преодолен потенциальный барьер коагуляции Δ U _к . Следовательно, коагуляция произойдет только в том случае, когда коллоидные частицы будут обладать кинетической энергией, достаточной дл преодоления этого барьера. Для увеличения степени коагуляции необходимо снижать потенциальный барьер. Это может быть достигнуто добавлением к золю электролита – коагулянта.

Зависимость скорости коагуляции от концентрации электролита представлена на рис. 3.1.2.5.

На графике видны три участка:

I. .

Следовательно, кинетическая энергия kТ << Δ U _к , (k – постоянная Больцмана) – лиофобный золь агрегативно устойчив.

II. , т.е. потенциальный барьер коагуляции больше, но соизмерим с кинетической энергией коллоидных частиц, причем с увеличением концентрации электролита – коагулянта он уменьшается, а скорость коагуляции возрастает. С_км – порог медленной коагуляции, С_кб – порог быстрой коагуляции. Этот участок кривой выражает зависимость: