Реферат: Постулаты квантовой механики

Каждый из постулатов квантовой механики, конечно, можно сформулировать в виде лаконичного математического утверждения, но, как всякое исходное допущение, любой из них построен на целой совокупности понятий и образов, которые, в свою очередь, требуют подробного разъяснения.

2.1. Постулат 1. Волновая функция.

2.1.1. Всякое физическое состояние квантово-механической системы изображается волновой функцией . Ее аргументами являются все координаты всех частиц системы и время.

2.1.2. Совокупность всех пространственных переменных всех частиц называется конфигурационным пространством системы K. Так, для n частиц

Конфигурационное пространство имеет наглядный геометрический образ только для систем, содержащих не более одной частицы. В остальных случаях – это абстрактное понятие. Каждая переменная задана в пределах своей области определения, которая зависит от характера этой переменной. Очень часто используют не декартовы, а полярные, либо другие, координаты.

2.1.3. Математические свойства волновой функции определяются ее назначением. Являясь функцией состояния, она должна быть:

однозначна

неразрывна

конечна.

Этими свойствами обладают так называемые регулярные функции. Поясним графически смысл этих функций, для чего представим свойства, недопустимые для регулярной функции.

a< х < b

На этом интервале Функция разрывна Функция неограниченна

функция неоднозначна при х = а возрастает при х => а

Рис. 1. Функции, которые по своим свойствам не могут быть использованы в качестве волновых функций состояния квантово-механической системы.

2.1.4. Далее встанет проблема сопоставления физических параметров для состояний как одной системы, так и состояний разных систем. Для этот потребуется стандартизация волновых функций, а, следовательно, их численная калибровка. Это достигается введением условия нормировки волновой функции. Оно имеет истоки в векторной алгебре и в теории вероятностей.

Норма – это одно из названий длины вектора в алгебре. Нормированный вектор имеет единичную норму, то есть его скалярное произведение самого на себя равно единице:

или , (2)

где |а| - модуль вектора. Любой вектор произвольной длины b можно нормировать, умножая на нормировочный множитель

, (2.1)

в результате получим нормированный вектор а, отвечающий условию нормировки (2.1).

Волновая функция, рассматриваемая как абстрактный вектор состояния, должна быть нормирована, т.е. ее скалярное произведение самой на себя равно 1:

Эквивалентная запись условия нормировки имеет вид

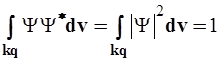(2.2)

2.1.5. Понятию волновой функции до сих пор мы не придавали конкретного физического содержания, принимая ее просто как абстрактный образ состояния. Физическое истолкование волновой функции предложил Макс Борн. Согласно Борну, величину следует рассматривать как вероятность пребывания системы, находящейся в состоянии , в элементе объема конфигурационного пространства , который охватывает точку этого пространства с координатами , т.е.

,

где

И в таком случае условие нормировки приобретает ясный вероятностный смысл, а именно, формула

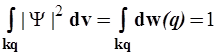(2.3)

оказывается просто условием достоверности существования системы в конфигурационном пространстве, если она находится в состоянии . Квадрат модуля волновой функции приобретает смысл плотности вероятности. Таким образом, волновые функции должны быть

однозначными

непрерывными

конечными

нормированными.

2.1.6. Из формулы нормировки (2.3) следует размерность волновой функции стационарной системы в рассматриваемой задаче, а именно:

,

где размерность объема конфигурационного пространства равна произведению размерностей всех пространственных переменных, образующих его:

2.1.7. Выше говорилось об ортогональных наборах собственных функций эрмитовых операторов. Накладывая на каждую из них условие нормировки, приходим к чрезвычайно удобным ортонормированным наборам функций, например:

,

где

Эти два качества можно объединить в одно условие:

(2.4)

где – символ Кронекера, который может принимать два значения:

при и при .

Читатель, вероятно, догадался, что в нашем распоряжении появился мощный аппарат, подобный векторному.

2.2. Постулат 2. Операторы динамических переменных

2.2.1. Возможные значения физически наблюдаемых величин являются собственными значениями операторных уравнений вида

Каждой динамической переменной ставится в соответствие свой линейный самосопряженный оператор.

2.2.2. Важнейшими динамическими характеристиками одной частицы являются:

- радиус-вектор , где координаты могут быть:

декартовыми или полярными ( - углы, а – длина вектора);

- вектор импульса и его координаты – проекции;

- вектор момента импульса , являющийся векторным произведением радиуса-вектора на импульс

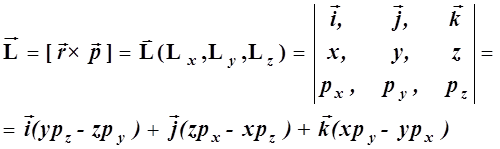(2.5)

и, соответственно, его проекции равны

(2.6)

(2.7)

(2.8

- кинетическая энергия Т, скалярная величина, которая в поступательном движении связана и с массой и импульсом

;

для одномерного вращения вокруг оси (например, z ) справедлива подобная же формула, где масса заменена моментом инерции I_z , а импульс – его моментом :

- потенциальная энергия, т.е. скалярное силовое поле, задаваемое функци-ей координат , в котором движется частица;

- полная энергия Е, равная сумме кинетической и потенциальной энергий

2.2.3. С учетом общих требований, предъявляемых к операторам квинтовой механики, постулируются простейшие операторы, а именно: операторы координат, определяющие положение частицы, и импульса ее,

- оператор координаты совпадает с умножением на саму координату q, т.е.: , или угол,

или, в общем виде ;

- оператор импульса имеет дифференциальную форму

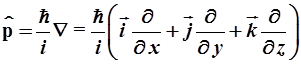(2.9)

где постоянная Планка Дж·с, и операторы координат импульса соответственно равны:

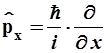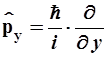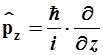, , (2.10)

Введение в оператор, мнимой единицы превращает его в самосопряженный т.е. отвечающий условию (1.5).

2.2.4. Остальные операторы строятся по формулам классической механики, где вместо координат и импульсов используются их операторы, Это утверждение можно считать следствием макроскопического устройства приборов по законам классической физики. Построим операторы и для одной частицы:

- операторы момента импульса и его проекций:

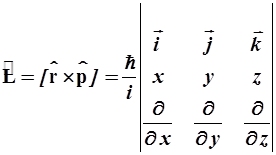, (2.11)

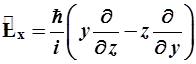, (2.12)

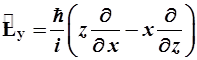, (2.13)

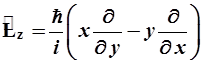(2.14)

В полярных координатах (например, сферических) соответствующие производные декартовых координат следует заменить их выражениями через полярные переменные;

- оператор кинетической энергии в декартовых координатах:

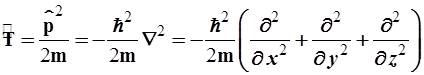(2.15)

Переходя к полярным координатам, лапласиан преобразуют к ним. Для случая вращения по поверхности без радиальной компоненты движения, как это имеет место при вращении двухатомной молекулы вокруг центра масс, можно записать:

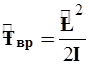(2.16)

оператор потенциальной энергии, подобно координате, дается просто умножением на функцию потенциальной энергии, т.е.

, или (2.17)

оператор полной энергии называют гамильтонианом, в честь английского ученого Гамильтона, оставившего фундаментальные труды в механике, астрономии и математике, и обозначают его

(2.18)

2.3. Постулат 3. Уравнение Шрёдингера

2.3.1. Эволюция системы определяется, с одной стороны, ее мгновенным состоянием и, следовательно, волновой функцией. С другой стороны, изменение состояния во времени зависит от "скорости" эволюции, т.е. от производной волновой функции по времени. Вместе с тем такое изменение связано с каким-либо взаимодействием с окружающими систему объектами и, следовательно, с обменом энергией. Это означает, что при описании эволюции необходимо связать саму волновую функцию, ее производную по времени и гамильтониан, в общем случае зависящий от координат и времени.

2.3.2. Такая связь вводится в виде временнớго уравнения Шрёдингера, которое является одним из постулатов квантовой механики и записывается в форме:

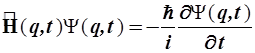(2.19)

Возможные функции состояния системы удовлетворяют уравнению (2.19)

2.3.3. В том случае, когда гамильтониан Н, а, следовательно, и энергия системы не зависят от времени, временное уравнение Шредингера легко преобразуется в стационарное уравнение Шредингера, имеющее структуру операторного уравнения (1.1).

Произведем соответствующие преобразования. Для этого положим, что гамильтониан не включает времени в явном виде и зависит только от координат

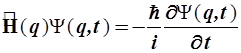(2.20.)

Это позволяет нам использовать метод Фурье для разделения переменных и представить волновую функцию в виде двух сомножителей, одного покоординатного и другого временного:

(2.21)

Подставим результат в (2.20) и перенесем влево от , а влево от оператора дифференцирования по времени, так как по отношению к этим операторам выносимые множители условно постоянны и не преобразуются:

,

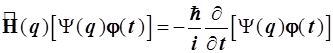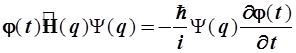(2.22)

Теперь разделим переменные в уравнении (2.22)

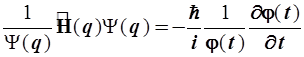(2.23)

С учетом независимости пространственных и временных переменных следует обе части полученного равенства (2.23) приравнять одной и той же постоянной величине, в результате получим систему из двух уравнений:

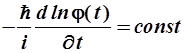(2.24)

(2.25)

Легко видеть, что выражение (2.25) имеет вид операторного уравнения (1.1) и, следовательно, постоянная const есть собственное значение гамильтониана, то есть энергия системы:.

Временная часть волновой функции φ(t), получаемая как решение уравнения (2.24), имеет вид строго периодического процесса, совершающеюся с круговой частотой, а именно:

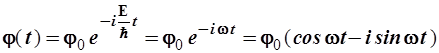(2.26)

Как уже говорилось ранее, временная периодичность функций состояния является неотъемлемой чертой стационарного движения. Операция комплексного сопря­жения уравнения (2.19) означает замену t на -t, т.е. время как бы обраща­ется вспять. Временная часть волновой функции в (2.26) обратится в физически эквивалентную , но любая наблюдаемая величина останется той же самой согласно (1.5). Уравнение Шрёдингера описывает, таким образом, процессы, обратимые во времени.

2.3.5. Наконец, из уравнения (1.25) для стационарных систем получаем операторное выражение закона сохранения энергии:

(2.27)

Это выражение называется стационарным уравнением Шрёдингера. Оно не содержит времени в явном виде. Стационарное уравнение Шрёдингера является основным инструментом для решения теоретических задач об электронном строении атомно-молекулярных систем. В процессе точного или приближенного решения уравнения (2.27) находится вид волновой функции, а также энергия исследуемых состояний.

2.3.6. Всякая система характеризуется своим гамильтонианом, и он является тем исходным общим условием, которое управляет и характером движения, и предписывает возможный вид состояний и уровней системы

2.4. Постулат 4. Принцип суперпозиции состояний

2.4.1. Если возможными волновыми функциями являются и то возможно такое состояние системы, которому отвечает волновая функция

(2.28)

2.4.2. Этот постулат математически оформляет связь между чистыми и смешанными состояниями квантово-механической системы, о которых говорилось в разделе 1. Образ смешанного состояния, согласно сформулированному утверждению, оказывается суперпозицией – наложением волновых функций чистых состояний, Отсюда данный постулат называется принципом суперпозиций.

Если и принадлежат некоторому ортонормированному набору, т.е.

и ,

то формулу нормировки смешанного состояния (2.29) можно считать условием, определяющим вклады отдельных чистых состояний в смешанное:

(2.29)

Отсюда следует, что вероятность обнаружить систему в каком-либо из чистых состояний (1 или 2) в составе смешанного равна квадрату коэффициента ( или соответственно).

2.5. Постулат 5. Средние значения динамических переменных

2.5.1. Среднее значение динамической переменной , получаемое из множества измерений, равно математическому ожиданию этой величины:

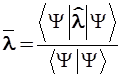(2.30)

Если волновая функция нормирована, то знаменатель единичен, и получаем более простое выражение;

(2.31)

2.5.2. Покажем, что у чистых состояний квантово-механической системы средние значения наблюдаемых переменных совпадают с собственными значениями соответствующих эрмитовых операторов. В этом случае формулы (2.30) и (2.31) непосредственно следуют из фундаментального операторного уравнения (1.1).

Чтобы показать это, запишем уравнение (1.1) с помощью символики Дирака, далее слева скалярно домножим каждую его часть на бра-вектор | и выделим в правой части равенства собственное число . В итоге приходим к формулам (2.30) и (2.31). Цепочка простейших преобразований имеет вид:

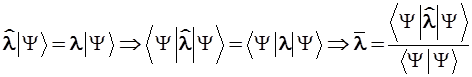
Для общего случая смешанных состояний подобного обоснования нет, и формулы (2.30) и (2.31) постулируются. Этот постулат приобретает уже универсальное содержание. С его помощью можно рассчитывать средние значения даже тех динамических переменных, операторы которых не обладают дискретными спектрами волновых функций и собственных значений, например, координаты и потенциальной энергии.