Реферат: Применение сингулярной матрицы в химии

(Реферат)

О Г Л А В Л Е Н И Е

Введение. 3

Глава 1. Общие сведения о сингулярном разложении и сингулярных матрицах 4

1.1. Ортогональное разложение посредством сингулярного разложения. 4

1.2. Вычисление сингулярного разложения. 5

Глава 2. Применение сингулярных матриц при многомерном анализе химических данных факторными методами. 7

2.1. Общие сведения о факторных методах. 7

2.2. Операции с матрицами и многомерный анализ данных. 9

2.3. Свойства сингулярной матрицы.. 10

Заключение. 12

Список используемой литературы.. 16

Введение

Как известно, химия часто оказывается на перекрестке разных дисциплин. Для химика всегда есть большой соблазн в том, чтобы заняться какой-то чрезвычайно узкой областью, где он останется защищенным от всех превратностей, наслаждаясь удобством положения единст­венного в своем роде специалиста. Чтобы постоянно быть в курсе дела и в готовности встретить любую новую ситуацию, химику требуется быть знако­мым с огромным объемом информации, необходимой не только для движения вперед, но и просто для сохранения своего положения.

При написании данного реферата была использована следующая литература, содержащая информацию о сингулярных матрицах и применении их в химии:

· книга «ЭВМ помогает химии» (пер. с англ) под ред. Г. Вернена, М. Шанона, в которой рассмотрено применение ЭВМ в различных областях химии: синтез органических соединений, кристаллография, масс-спектрометрия и т. д.

· книга Ч.Лоусона и Р.Хенсона «Численное решение задач метода наименьших квадратов» (пер. с англ), посвященная изложению численных решений линейных задач метода наимень­ших квадратов.

Глава 1. Общие сведения о сингулярном разложении и сингулярных матрицах

1.1. Ортогональное разложение посредством сингулярного разложения

В этом пункте данного реферата будет описано одно практически полезное ортогональ­ное разложение т xn - матрицы А. Мы покажем здесь, что невырожденную под­матрицу R матрицы A можно еще более упростить так, чтобы она стала невырожден­ной диагональной матрицей. Получаемое в результате разложение особенно полезно при анализе влияния ошибок входной информации на решение задачи НК.

Это разложение тесно связано со спектральным разложением симметрич­ных неотрицательно определенных матриц A^T A иAA^T .

Теорема (сингулярное разложение). Пусть А - m xn -матрица ранга k. Тогда существуют ортогональная m xm матрица U, ортогональ­ная n xn -матрица V и диагональная m xn -матрица S) такие, что

Матрицу S можно выбрать так, чтобы ее диагональные элементы составля­ли невозрастающую последовательность; все эти элементы неотрицательны и ровно k из них строго положительны.

Диагональные элементы S называются сингулярными числами А.

Доказательства данной теоремы приводить не имеет смысла во избежание нагромождения множества сложных математических выкладок, прямого отношения к теме, рассматриваемой в данном реферате, не имеющих. Ограничимся следующим численным примером, в котором дано сингулярное разложение матри­цы А вида:

1.2. Вычисление сингулярного разложения

Рассмотрим теперь построение сингулярного разложения т Х n - матрицы в предположении, что т > п. Сингулярное разложение будет вычислено в два этапа.

На первом этапе А преобразуется к верхней двухдиагональной матрице посредством последовательности (не более чем из n — 1) преобразований Хаусхолдера

где

Трансформирующая матрица выбирается так, чтобы аннулировать элементы i + 1, ..., т столбца i; матрица Hi — так, чтобы аннулировав элементы i + 1,.... п строки / - 1.

Заметим, что Q_n - это попросту единичная матрица. Она включена, чтобы упростить обозначения; Q_n также будет единичной матрицей при от = я, но при т > п она, вообще говоря, отличается от единичной.

Второй этап процесса состоит в применении специальным образом адап­тированного QR-алгоритма к вычислению сингулярного разложения матрицы

Здесь - ортогональные матрицы, aS диагональная.

Можно получить сингулярное разложение А:

Сингулярное разложение матрицы В будет получено посредством следующего итерационного процесса:

Здесь - ортогональные матрицы, а B_k - верхняя двухдиагональ­ная матрица для всех k.

Заметим, что диагональные элементы матрицы полученной непосред­ственно из этой итерационной процедуры, не являются в общем случае ни положительными, ни упорядоченными. Эти свойства обеспечиваются специальной последующей обработкой.

Сама итерационная процедура представляет собой (QR-алгоритм Фрэнсиса, адаптированный Голубом и Райншем к задаче вычисления сингулярных чисел.

Глава 2. Применение сингулярных матриц при многомерном анализе химических данных факторными методами

2.1. Общие сведения о факторных методах

Многомерный анализ данных играет все возрастающую роль во многих научных дисциплинах, включая науки о земле, жизнеобес­печении, в социологии, а также менеджменте. Однако в химии эти методы развивались не так быстро. Хотя основы методов были созданы в начале века, а области их применения были опре­делены в тридцатых годах , первые случаи их использова­ния отмечены только в шестидесятых годах. Действительно, наи­более часто применяемыми в хемометрике методами стали фактор­ный анализ (ФА), анализ (метод) главных компонент (МГК) и факторный дискриминантный анализ (ФДА).

Хемометрика преследует две цели :

· извлечение максимума информации за счет анализа химиче­ских данных;

· оптимальное планирование измерительных процедур и экспе­риментов.

Первая цель может быть подразделена на две:

1) описание, классификация и интерпретация химических данных;

2) моделирование химических экспериментов, процессов и их последующая оптимизация.

Из всего многообразия видов обработки наборов химических данных можно выделить некоторые наиболее характерные области применения:

· многокомпонентный анализ спектрометрических или хромато-графических данных различных смесей. Цель анализа — опреде­ление числа компонентов и иногда также их идентификация. Для решения задач, связанных с равновесиями в растворе и сложной кинетикой, используется факторный анализ;

· поиск неизмеряемых факторов, отражающих те физико-хими­ческие свойства, которые оказываются слишком сложными для точного моделирования, например, таких, как:

а) времена задержки для хроматографии;

б) данные по химическому сдвигу;

в) константы равновесия и кинетические константы;

г) данные по степени превращения и селективности.

Интерпретация этих факторов может высветить новые явле­ния или подчеркнуть те физические свойства, которые помогут объяснить исходные наблюдения:

· сведение наборов химических данных с большим числом пере­менных (которые часто коррелируют, а иногда и избыточны) к на­борам с меньшим числом независимых переменных. Каждая точ­ка будет характеризоваться меньшим числом новых переменных, которые затем могут быть использованы для модельных исследо­ваний. Этот метод можно применять для многокомпонентных природных продуктов со сложными физико-химическими свойства­ми (эфирные масла, продукты из сырой нефти и т. д.), а также для замеренных в ходе процесса наборов данных;

· анализ многомерных наборов химических данных посредством графического представления объектов и переменных в векторном подпространстве с меньшим числом измерений. Подобное пред­ставление позволяет осуществить обзор всего набора данных для классификации объектов и объяснения их положения.

Цель данного пункта моего реферата — введение в методы факторного анализа с рассмотрением его теоретических основ и практических приложений.

Факторный анализ (ФА), анализ главных компонент (МГК) и факторный дискриминантный анализ (ФДА) будут представлены на различных специально подобранных примерах, иллюстрирую­щих множество областей их применения.

2.2. Операции с матрицами и многомерный анализ данных

Применение линейной алгебры в анализе данных будет проил­люстрировано на примере УФ-спектроскопии сложной смеси. В соответствии с законом Ламберта — Бера при данной частоте v полное поглощение образца, состоящего из l поглощающих компо­нентов, определяется как

, где – молярный коэффициент поглощения компонента j, а – молярная концентрация компонента j.

Если измерение проводится при п различных частотах, тогда единственное уравнение заменяется системой линейных уравнений

С использованием матриц следующую систему линейных урав­нений можно записать в виде:

Для дальнейшего упрощения выражения запишем матрицу поглощения (А) как произведение матриц коэффициентов экстинкции () и концентрации (С):

(A) = () (C)

Следует отметить, что матричные расчеты и их компьютерное применение дали тол­чок быстрому развитию многомерного анализа данных.

2.3. Свойства сингулярной матрицы

Матрица (X— Х)'(Х—) — квадратная, симметричная и положи­тельно определенная. Такие матрицы проявляют некоторые свой­ства, особенно полезные при анализе данных:

· собственные значения, действительные, а также положитель­ные или равные нулю;

· число ненулевых собственных значений равняется рангу мат­рицы;

· два собственных вектора, связанные с двумя различными соб­ственными значениями ортогональны.

В качестве иллюстрации этих свойств, а также чтобы пока­зать их важность при анализе данных можно взять матрицу дисперсий-ковариаций и определим собственные значения матрицы методом наименьших квадратов.

Решая уравнение, получаем два собственных значения:

= 0 ,

что дает =1 и =0,6.

Как , так и действительны и положительны. Ранг матрицы должен равняться 2, поскольку в системе существуют два ненуле­вых собственных значения. Компоненты собственных векторов, связанные с каждым из собственных значений, получаем из опре­деления собственных векторов следующим образом:

для первого собственного значения

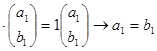
для второго собственного значения

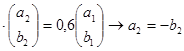
Отметим, что два связанных с каждым из собственных зна­чений вектора действительно ортогональны (т. е. их скалярное произведение равно нулю). В этих двух наборах векторов мы можем выбрать два нормированных вектора, которые соответствен­но составляют ортогональный базис:

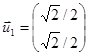
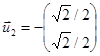
Векторы и действительно аналогичны тем, которые опре­делены в разделе 5.2.1, а координаты матрицы данных относитель­но этой точки отклика уже вычислены:

( Y) = ( X-) ( U)

Заключение

Факторные методы (в том числе связанные с использованием сингулярных матриц) ныне широко применяются для анализа дан­ных в химии. Они в основном носят описательный характер и позволяют существенно сократить размерность массива данных при минимальной потере информации и возможности их графи­ческого представления.

Хотя эти методы и не обладают возможностями моделирования, как регрессионный анализ, их можно применять для идентифи­кации:

· компонентов в многокомпонентных смесях, проанализирован­ных посредством ультрафиолетового, инфракрасного и видимого излучения, флюоресценции, масс-спектрометрии, хроматографии (ФА);

· реальных физических факторов, управляющих эксперименталь­ными данными (целевой факторный анализ):

· группы, к которой можно отнести новый объект в системе ис­ходных групп, на которые был классифицирован первоначальный набор данных (ФДА).

Известная мысль А.Пуанкере о том, что в конечном счёте главной задачей науки является экономия мысли и труда, со всей очевидностью проявилась в разработке в 80-90-х годах ХХ века компьютерных программ для упрощения расчетов, связанных с сингулярными матрицами.

Действительно, в настоящее время химик, желающий применить эти методы к соб­ственным массивам данных, имеет возможность широкого выбора имеющихся в продаже программ для компьютеров. Множество программ было написано для больших, мини- и в последнее время — микрокомпьютеров.

Однако нельзя упустить из виду, что хорошая интерпретация результатов невозможна без знания физико-химических моделей, которые позволяют правильно поставить эксперимент и получить необходимые данные. Следовательно, участие человека будет все еще незаменимо в извлечении полезной информации из распечаток (листингов) с численными результатами и графиками.

Вмешательство химика происходит на различных стадиях:

· при выборе исходных наборов данных, которые корректно представляют все множество исследуемых объектов;

· выборе удовлетворительных методов преобразования данных;

· поиске физического смысла абстрактных факторов;

· интерпретации относительных положений объектов;

· классификации.

Применительно к ближайшему будущему можно выделить два основных параллельных направления развития приложений факторных методов в химии: первое, связано с развитием области применения; второе — с развитием программных средств и совер­шенствованием методик.

Факторный анализ можно применять:

· для завершения многокомпонентного анализа в частотной области, сравнения спектров и библиотечного поиска, улучшения методик хроматографического определения и т. д.;

· анализа сложных промышленных процессов с большим коли­чеством данных, для которых нельзя создать чистой фундамен­тальной модели. Факторный анализ этих наборов данных будет первой ступенью в моделировании указанных процессов;

· изучения взаимосвязи структуры с физико-химическими свой­ствами, такими, как реакционная способность, биологическая активность органических, неорганических и биоорганических соединений;

· рассмотрения химических процессов в окружающей среде с учетом географических и климатических особенностей регионов.

С развитием программных средств и совершенствованием методик факторные методы будут становиться все проще для использования неспециалистами. Отметим здесь только некоторые тенденции:

· интеграция доступных программных средств со множеством вспомогательных программ представления данных, предваритель­ной их обработки, факторного анализа, моделирования, решения задач оптимизации и распознавания образов. Эти средства будут поставлены на персональных компьютерах, что удобно для хими­ков. Более того, они станут частью автоматизированных систем сбора и обработки данных физико-химического анализа;

· включение в программные средства модулей для проверки предположения о линейности при выборе исходных переменных как непосредственно по экспериментальным результатам, так и по выбранным соотношениям между переменными;

· включение в программные средства модулей оценки погреш­ности факторных нагрузок, что поможет аналитику оценить реальность выявленных факторов. Целесообразна разработка ста­тистических тестов для использования при решении об отнесении нового объекта к одной из групп;

· использование одновременной обработки многопараметриче­ских наборов данных, что позволит сопоставить методы много­компонентного анализа, а при обработке массивов данных, завися­щих от времени,— исследовать эволюцию химических процессов;

· введение в программное обеспечение концепции искусственно­го интеллекта. Это поможет аналитику в интерпретации резуль­татов, анализе геометрического представления объектов, а в даль­нейшем — в автоматическом моделировании групп и кластеров объектов.

Список используемой литературы

1. ЭВМ помогает химии: Пер. с англ. /Под ред. Г. Вернена, М. Шанона.— Л.: Химия, 1990.— Пер. изд.: Вели­кобритания, 1986. - 384 с.

2. Лоусон Ч., Хенсон Р. Численное решение задач метода наименьших квадратов/Пер, с англ. - М.: Наука. Гл. ред. физ.-мат. лит., 1986. - 232 с.