| Скачать .docx |
Курсовая работа: Определение термодинамических параметров реакции полимеризации тетрафторэтилена
Курсовая работа
по основам термодинамики и кинетики синтеза полимеров
Определение термодинамических параметров реакции полимеризации тетрафторэтилена
Реакция полимеризации имеет вид:
![]()
В качестве инициатора процесса применяется персульфат аммония ![]() . Примесь в исходном мономере – триэтиламин.
. Примесь в исходном мономере – триэтиламин.
Рассчитаем теплоемкость и некоторые другие термодинамические параметры реагентов и продукта реакции:
1. Тетрафторэтилен:
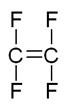
Проведем расчет теплоемкости тетрафторэтилена по методу Добратца. Согласно этому методу, теплоемкость вещества определяется следующим выражением:
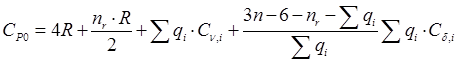 ,
,
где: CP 0 – теплоемкость при низком давлении, [кал/(моль·К) ];
![]() кал/(моль·К)
– универсальная газовая постоянная;
кал/(моль·К)
– универсальная газовая постоянная;
![]() – число атомов в молекуле CF
2
=
CF
2
;
– число атомов в молекуле CF
2
=
CF
2
;
![]() – число простых связей, относительно которых может иметь место внутреннее вращение групп;
– число простых связей, относительно которых может иметь место внутреннее вращение групп;
![]() – число связей типа
– число связей типа ![]() , то есть:
, то есть:
для связей ![]()
![]() ;
;
для связей ![]()
![]() .
.
Общее число связей равно 5.
Тогда получим:
![]()
![]()
![]()
![]()
Подставляя полученные выражения в исходную формулу Добратца, получим:
![]()
![]()
![]()
Переходя от калорий к джоулям, получаем:
![]() [Дж/(моль·К)
].
[Дж/(моль·К)
].
Таким образом, теплоемкость тетрафторэтилена при двух температурах – на входе и выходе из реактора (275 К и 333 К), равна:
![]() 44,814 Дж/(моль·К)
=10,695 кал/(моль·К)
и
44,814 Дж/(моль·К)
=10,695 кал/(моль·К)
и
![]() 53,845 Дж/(моль·К)
=12,851 кал/(моль·К)
.
53,845 Дж/(моль·К)
=12,851 кал/(моль·К)
.
2. Расчет мольной теплоемкости политетрафторэтилена:
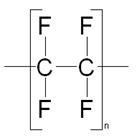
Расчет мольной теплоемкости полимера по методу Сато и Шоу (при степени кристалличности 80%):
| Группы |
Кол-во |
|
|
|
|
|||
| 2 |
1,47 |
1,76 |
|
|
|
4 |
5,1 |
5 |
Тогда (при 298 К):
![]() кал/(моль·К)
= 97,80 Дж/(моль·К)
;
кал/(моль·К)
= 97,80 Дж/(моль·К)
;
![]() кал/(моль·К)
= 98,55 Дж/(моль·К)
.
кал/(моль·К)
= 98,55 Дж/(моль·К)
.
Учитывая степень кристалличности ПТФЭ, равную 80%, получим теплоемкость при 298 К:
![]() кал/(моль·К)
= 97,95 Дж/(моль·К)
.
кал/(моль·К)
= 97,95 Дж/(моль·К)
.
Зная температурную зависимость значений ![]() и
и ![]() , получим значения мольной теплоемкости полимера при 275 К и 333 К:
, получим значения мольной теплоемкости полимера при 275 К и 333 К:
· ![]() кал/(моль·К)
;
кал/(моль·К)
;
![]() кал/(моль·К)
;
кал/(моль·К)
;
· ![]() кал/(моль·К)
;
кал/(моль·К)
;
![]() кал/(моль·К)
;
кал/(моль·К)
;
С учетом степени кристалличности находим:
![]() кал/(моль·К)
= 91,956 Дж/(моль·К)
.
кал/(моль·К)
= 91,956 Дж/(моль·К)
.
![]() кал/(моль·К)
= 106,941 Дж/(моль·К)
.
кал/(моль·К)
= 106,941 Дж/(моль·К)
.
Температурная зависимость теплоемкости политетрафторэтилена имеет вид:
Сp (Т)=(0,106+0,003·T)·97,80·0,8+(0,64+0,0012·T)·98,55·0,2=
= 20,91+0,26·T [Дж/моль·К ].
То есть, коэффициенты уравнения С = f (T) равны: а = 20,91; b = 0,26.
3. Расчет мольной теплоемкости триэтиламина (примеси) по методу Добратца:
С р ,0 = 4R + nr R/2 +Σqi Cν i +((3n-6-nr -Σqi )·Σqi Cδ,i ) / Σqi
R=1,987 кал/моль·К;
nr =3, число простых связей, относительно которых может иметь место внутреннее вращение групп;
q i -число связей типа i :
q N - C =3;
q C - C =3;
qC - H =15;
n=22 - число атомов в молекуле;
Σqi =21 - общее число связей в молекуле;
Cν i , Cδ , j - функции Эйнштейна для связей типа i .
Σqi Cδ i = 3(1,016+1,663·10-3 T-0,723·10-6 ·T2 )+3(0,503 +2,472 ·10-3 ·T-1,058·10-6 ·T2 )+ +15(-0,579+3,741·10-3 ·T - 1,471·10-6 ·T2 ) = (-2,619 +75,94·10-3 ·T- 30,582·10-6 ·T2 );
Σqi Cν i = 3(-0,501+3,695·10-3 T-1,471·10-6 ·T2 )+3(-0,836 +3,208 ·10-3 ·T-1,087·10-6 ·T2 )+ +15(-0,139+0,168·10-3 ·T+0,447·10-6 ·T2 ) = (-8,604 +32,85·10-3 ·T- 4,23·10-6 ·T2 );
Тогда:
С р,0
=4·1,987 + ![]() + (-8,604 + 32,85·10-3
·T - 4,23·10-6
·T2
) +
+ (-8,604 + 32,85·10-3
·T - 4,23·10-6
·T2
) +![]() (-2,619 + + 75,94·10-3
·T - 30,582·10-6
·T2
)= -0,259 + 123,17·10-3
T - 41,601·10-6
T2
[кал/моль·К
].
(-2,619 + + 75,94·10-3
·T - 30,582·10-6
·T2
)= -0,259 + 123,17·10-3
T - 41,601·10-6
T2
[кал/моль·К
].
При T=298 K: С р,0 = 32,75 кал/(моль·К) = 137,26 Дж/(моль·К) ;
При Т=275 К: С р,0 = 30,42 кал/(моль·К ) = 127,68 Дж/(моль·К) ;
При T=333 K: С р,0 = 36,08 кал/(моль·К) = 151,45 Дж/(моль·К) .
Коэффициенты: а = -0,259; b = 123,17; c = -41,601.
4. Пользуясь методом введения поправок на замещение водорода группами –СН3 и другими (метод Андерсена, Байера и Ватсона), рассчитаем теплоемкость мономера – тетрафторэтилена.
В качестве основного вещества примем метан, для которого ![]() ккал/моль. Схема построения самой длинной углеродной цепи и замещения групп:
ккал/моль. Схема построения самой длинной углеродной цепи и замещения групп:
![]()
![]()
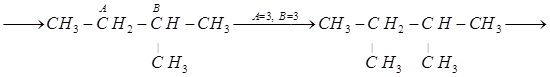
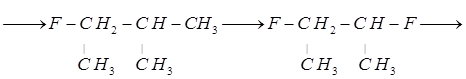
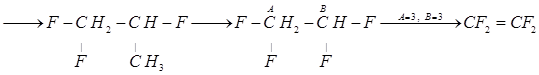
Результат расчета термодинамических характеристик тетрафторэтилена находим суммированием свойств исходного вещества (метана) и всех поправок, полученных при построении углеродного скелета молекулы замещением группами![]() ,
, ![]() и кратной связью. Составим сводную таблицу поправок с этапами расчета и полученными термодинамическими параметрами:
и кратной связью. Составим сводную таблицу поправок с этапами расчета и полученными термодинамическими параметрами:
Сводная таблица поправок
| № |
Этапы расчета |
ккал/моль |
|
а |
b·103 |
c ·106 |
|
| 1 |
Метан |
-17,89 |
44,50 |
3,79 |
16,62 |
-3,24 |
|
| 2 |
Первичные замещения -Н на –СH3 в цепи (3 замещения) |
-7,50 |
31,05 |
-6,0 |
69,60 |
-27,4 |
|
| 3 |
Вторичные замещения -Н на –СН3 (тип А=3, В=3) (2 заме- щения) |
-10,38 |
7,98 |
-6,54 |
61,92 |
-28,12 |
|
| 4 |
Замещение группы –СН3 на -F (4 замещения) |
-140,0 |
-4,00 |
8,96 |
-94,44 |
47,16 |
|
| 5 |
Замена ординарной связи на двойную (тип 3=3) |
25,70 |
-0,66 |
-0,41 |
-15,14 |
6,39 |
|
| ИТОГО: |
в системе СГС |
-150,07 |
78,87 |
-0,2 |
38,56 |
-5,21 |
|
| в системе СИ |
-628,79 |
330,47 |
-0,838 |
161,57 |
-21,83 |
||
Таким образом, величина ![]() для тетрафторэтилена составляет 45,37 Дж/моль·К,
для тетрафторэтилена составляет 45,37 Дж/моль·К, ![]() кДж/моль,
кДж/моль, ![]() Дж/моль·К.
Дж/моль·К.
Коэффициенты уравнения температурной зависимости:
а = -0,838; b = 161,57·10-3 ; c = -21,83·10-6 .
5. Расчет изобарно-изотермического потенциала тетрафторэтилена по методу Ван Кревелена и Чермина:
| 2 группы |
20000 + 28,0·Т |
| 4 группы |
-184000 - 8,8·Т |
| RTlnσ (σ=1) |
0 |
| сопряжение |
0 |
| ∑ |
-164000+19,2·Т |
Таким образом, ![]() кал/моль = -687,16 кДж/моль;
кал/моль = -687,16 кДж/моль;
![]() кал/моль = 80,448 Дж/моль·К;
кал/моль = 80,448 Дж/моль·К;
![]() Дж/моль.
Дж/моль.
6. Расчет изобарно-изотермического потенциала газообразного (условно) политетрафторэтилена по методу Ван Кревелена и Чермина:
| 2 группы |
6000 + 73,0·Т |
| 4 группы |
-184000 - 8,8·Т |
| RTlnσ (σ=1) |
0 |
| сопряжение |
0 |
| ∑ |
-178000+64,2·Т |
Таким образом, ![]() кал/моль = -745,82 кДж/моль;
кал/моль = -745,82 кДж/моль;
![]() кал/моль = 268,99 Дж/моль·К;
кал/моль = 268,99 Дж/моль·К;
![]() Дж/моль.
Дж/моль.
7. Мольный изобарно-изотермический потенциал реакции полиме- ризации:
![]() гг
= -178000+64,2·Т – (-164000+19,2·Т) = -14000 + 45·Т,
гг
= -178000+64,2·Т – (-164000+19,2·Т) = -14000 + 45·Т,
а с учетом эмпирической поправки для перехода мономера из газообразного состояния в кристаллический полимер:
![]() гк
= -14000 + 45·Т – 4000 + 7,5·Т = -18000 + 52,5·Т [кал/(моль·К)].
гк
= -14000 + 45·Т – 4000 + 7,5·Т = -18000 + 52,5·Т [кал/(моль·К)].
При 298 К:
![]() гк
(298)= -18000 + 52,5·298 = -2355 кал/моль = -9867,45 Дж/моль;
гк
(298)= -18000 + 52,5·298 = -2355 кал/моль = -9867,45 Дж/моль;
Тепловой эффект реакции:
Qр-ии = -∆Н 0 = 18000 кал/моль = 75,42 кДж/моль.
∆S0 гк = 52,5 кал/моль·К= 219,98 Дж/моль·К.
Таким образом, реакция является экзотермической.
![]() .
.
Предельная температура полимеризации:
ТПР
= ![]() .
.
8. Выберем температурный интервал и рассчитаем изменение энергии Гиббса, логарифм константы равновесия реакции полимеризации для построения графиков зависимости этих величин от температуры:
Изменение теплоемкости в реакции полимеризации определим как разность между теплоемкостью полимера и теплоемкостью мономера:
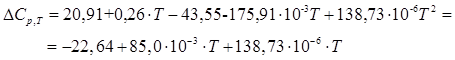
Энтальпию реакции полимеризации можно определить из уравнения Кирхгофа:
![]() .
.
Тогда, после интегрирования:
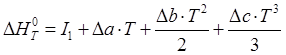 ,
,
где постоянную интегрирования![]() можно определить, подставив в приведенное выше уравнение Т = 298 К,
можно определить, подставив в приведенное выше уравнение Т = 298 К, ![]() Дж/моль:
Дж/моль:
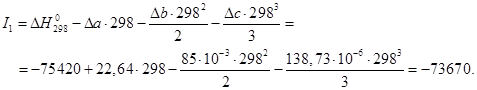
Тогда получим зависимость:
![]() .
.
Поскольку зависимость энергии Гиббса от температуры определяется следующим образом:
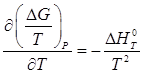 ,
,
то после интегрирования можно записать:
![]() ,
,
откуда постоянную интегрирова- ния I
2
можно определить, подставив ![]() ,
, ![]() Дж/моль:
Дж/моль:
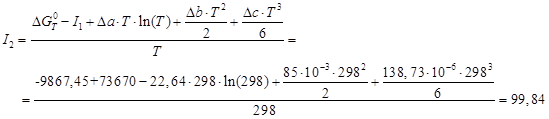
Тогда температурная зависимость энергии Гиббса:
![]()
Значение ![]() может быть вычислено по уравнению:
может быть вычислено по уравнению:
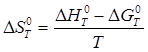 .
.
Логарифм константы скорости равен:
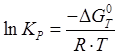 .
.
Рассчитаем ∆Н0 , ∆S0 , ∆G0 , и lnKp для разных температур. Полученные значения сведем в нижеследующую таблицу:
| Температура, К |
∆Н0 , кДж/моль |
∆S0 , Дж/моль·К |
∆G0 , кДж/моль |
lnKp |
Kp |
| 270 |
-75774,34 |
-221,22 |
-16044,52 |
7,15 |
1270,90 |
| 280 |
-75662,07 |
-220,81 |
-13834,31 |
5,94 |
380,99 |
| 290 |
-75533,52 |
-220,36 |
-11628,39 |
4,82 |
124,33 |
| 300 |
-75388,43 |
-219,87 |
-9427,19 |
3,78 |
43,80 |
| 310 |
-75226,51 |
-219,34 |
-7231,11 |
2,81 |
16,54 |
| 320 |
-75047,50 |
-218,77 |
-5040,52 |
1,89 |
6,65 |
| 330 |
-74851,10 |
-218,17 |
-2855,79 |
1,04 |
2,83 |
| 380 |
-73598,74 |
-214,65 |
7967,95 |
-2,52 |
8,03·10-2 |
| 480 |
-69631,06 |
-205,47 |
28995,90 |
-7,27 |
6,99·10-4 |
| 580 |
-63481,57 |
-193,90 |
48983,08 |
-10,16 |
3,88·10-5 |
| 680 |
-54872,82 |
-180,27 |
67707,93 |
-11,98 |
6,29·10-6 |
По полученным данным построим графики зависимости термодинамических величин от температуры (рис. 1-4).
Исходя из расчетов, можно сделать вывод о том, что с ростом температуры, энтальпия реакции полимеризации стремится в положительную область, а это означает уменьшение теплового эффекта при увеличении температуры проведения процесса. Так же видно, то, что энтропия системы отрицательна, и с возрастанием температуры стремится к нулевому значению. Увеличение абсолютного значения энергии Гиббса также можно определить из графика. В виду того, что энергия Гиббса не на всем интервале температур принимает отрицательные значения, протекание реакции термодинамически вероятно лишь в интервале Т ≈ 340 К.
Из графика зависимости константы равновесия от температуры можно сделать вывод о том, что целесообразно проводить реакцию при низких температурах, поскольку при температуре 270 К константа равновесия принимает наибольшее значение, что говорит о сильном смещении равновесия в сторону образования продукта реакции (полимера).
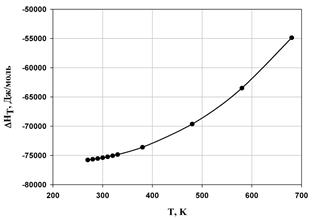
Рис. 1. Зависимость энтальпии реакции от температуры
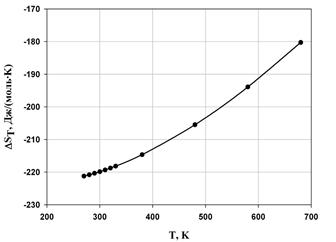
Рис. 2. Температурная зависимость энтропии реакции
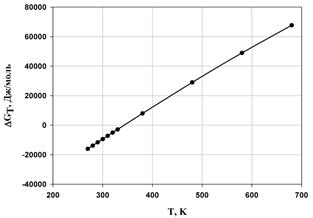
Рис. 3. Зависимость энергии Гиббса от температуры.
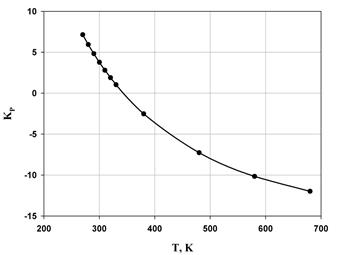
Рис. 4. Температурная зависимость константы равновесия.
9. Рассчитаем предельную температуру проведения полимеризации тетрафторэтилена:
Тпр
= 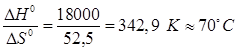
10. Проведем расчет реакционных способностей для случая сополимеризации тетрафторэтилена и этилена:
Эти мономеры имеют следующие значения реакционной способности и полярности (константы Алфрея – Прайса):
е Q
Тетрафторэтилен 1,22 0,0049
Этилен -0,20 0,015
Тогда:
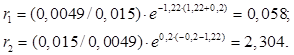
Получим, что ![]() . Это свидетельствует о том, что сополимеризация не является статистической.
. Это свидетельствует о том, что сополимеризация не является статистической.
В сополимере присутствует больше этилена, чем тетрафторэтилена, поскольку ![]() .
.
Рассчитаем состав сополимера:
Пусть f1 – доля тетрафторэтилена, f2 – этилена в смеси мономеров. Зададим: f1 = 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9 и, соответственно, f2 = 0,9; 0,8; 0,7; 0,6; 0,5; 0,4; 0,3; 0,2; 0,1.
Тогда пользуясь уравнением для расчета состава полимера:
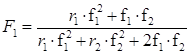 ,
,
рассчитаем состав сополимера.
Результаты расчетов представлены в таблице:
| f 1 |
f 2 |
F1 |
F2 |
| 0,1 |
0,9 |
0,027 |
0,973 |
| 0,2 |
0,8 |
0,030 |
0,970 |
| 0,3 |
0,7 |
0,034 |
0,966 |
| 0,4 |
0,6 |
0,039 |
0,961 |
| 0,5 |
0,5 |
0,047 |
0,953 |
| 0,6 |
0,4 |
0,059 |
0,941 |
| 0,7 |
0,3 |
0,079 |
0,921 |
| 0,8 |
0,2 |
0,120 |
0,880 |
| 0,9 |
0,1 |
0,238 |
0,762 |
По полученным данным построим график зависимости состава полимера от состава мономера:
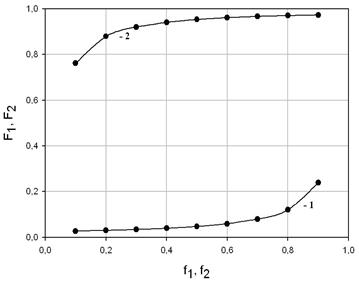
Рис. 5. Зависимость состава полимера от состава мономера
1 – зависимость F1 от f1 ;
2 – зависимость F2 от f2 .
11. Оценка термической устойчивости политетрафторэтилена по температуре полураспада:
Согласно имеющейся зависимости энергии диссоциации связей от температуры полураспада, выбираем связь в политетрафторэтилене  с наименьшей энергией диссоциации, то есть, ту связь, которая разрывается легче всего. Такой связью является связь С-С, которая имеет Едисс
= 98 кал/моль, и
с наименьшей энергией диссоциации, то есть, ту связь, которая разрывается легче всего. Такой связью является связь С-С, которая имеет Едисс
= 98 кал/моль, и ![]() .
.
12. Определение термодинамической вероятности реакций между радикалами: диспропорционирования и рекомбинации:
Диспропорционирование:
![]()
Рекомбинация:
![]()
Рассчитаем с помощью метода групповых вкладов энергию Гиббса каждой реакции:
Диспропорционирование:
| Группы |
Количество |
Δ G0 , кал/моль |
| F- |
6 |
6·(-46000-2,2·T) |
| >C< |
3 |
3·(3000+36,5·T) |
|
|
2 |
2·(38000+15·T) |
| F- |
6 |
6·(-46000-2,2·T) |
| >C< |
1 |
3000+36,5·T |
| ИТОГО: |
-70000+43 ·T |
Рекомбинация:
| Группы |
Количество |
Δ G0 , кал/моль |
| F- |
6 |
6·(-46000-2,2·T) |
| >C< |
1 |
3000+36,5·T |
| =С< |
2 |
2·(10000+14·T) |
|
|
2 |
2·(38000+15·T) |
| F- |
6 |
6·(-46000-2,2·T) |
| >C< |
1 |
3000+36,5·T |
| ИТОГО: |
-56000-2·T |
Разность изобарно-изотермических потенциалов этих реакций составляет:
![]() при Т = 311,1 К ≈ 38 °С.
при Т = 311,1 К ≈ 38 °С.
Таким образом, при температурах выше 38 °С преобладает диспропорционирование, а при Т<38 °С – рекомбинация.
Выводы
Таким образом, в результате проведенных расчетов термодинамических параметров полимеризации тетрафторэтилена, можно сделать выводы о том, что реакция экзотермическая, термодинамически возможно проводить ее при температурах до ≈340 К.
При проведении сополимеризации тетрафторэтилена с этиленом, в сополимере присутствует больше этилена, чем тетрафторэтилена.
При температурах выше 38 °С преобладает реакция диспропор- ционирования, ниже 38 °С – рекомбинация.
Определена температура полураспада политетрафторэтилена, она составляет около 400 °С.
Сопоставляя рассчитанные термодинамические параметры процесса с некоторыми литературными, представленными в нижеследующей таблице:
| c` |
|
|
|
||||
| a |
b |
c |
d |
ΔH 0 f 298 кДж/моль |
S 0 298 Дж/моль·K |
ΔG 0 298 кДж/моль |
|
| ТФЭ |
43,55 |
175,91 |
-138,73 |
40,36 |
-658,56 |
299,99 |
-615,33 |
| (NH 4 ) 2 S 2 O 8 |
33,3 |
0,15 |
-3,92·10-5 |
- |
-1648,5 |
181,20 |
-55646,1 |
| Триэтиламин |
-8,67 |
0,5675 |
-1,96·10-4 |
- |
-77,096 |
173,5 |
-51770 |
приходим к выводу, подтверждающему то, что метод Добратца неприменим для расчета термодинамических параметров для неорганических веществ.
Кроме этого, рассчитанные значения для тетрафторэтилена и триэтил- амина отличаются от приведенных в литературе.
Так, например, рассчитанное по методу Андерсена-Байера-Ватсона значение ![]() Дж/моль·К отличается от табличного
Дж/моль·К отличается от табличного ![]() Дж/моль·К, то есть на 30,5 Дж/моль·К (или 10%).
Дж/моль·К, то есть на 30,5 Дж/моль·К (или 10%).