| Скачать .docx |
Курсовая работа: Кинетика химических реакций
РАСЧЕТНО-ГРАФИЧЕСКАЯ КУРСОВАЯ РАБОТА
ПО КУРСУ "ФИЗИЧЕСКАЯ ХИМИЯ"
ч. II
Содержание
1. Формулировка заданий
1.2 Работа 2 - Кинетика химических реакций
1.3 Работа 3 - Поверхностные явления
2. Решение задания 9 первого варианта
2.1 Работа 1
2.2 Работа 2
2.3 Работа 3
3. Исходные данные
1. Формулировка заданий
1.1 Работа 1 - Растворы электролитов
1. Растворы электролитов.
2. Кинетика химических реакций.
3. Поверхностные явления.
Рассчитать температуру замерзания водного раствора дихлоруксусной кислоты при ее концентрации Cm = 1,300, моль / кг если известно, что при ее концентрации С’ m = 0,331, моль / кг величина электродного потенциала водородного электрода при 00 C и давлении водорода 101,3 кПа составляет E0 = - 0,066 B при расчете принять, что активности кислоты и ионов совпадают с их концентрациями, т.е. Cmi = ai .
Исходные данные находятся в колонках табл.3.1
1.2 Работа 2 - Кинетика химических реакций
Для реакции A + B → D начальные концентрации веществ A и B равны и составляют
С0 ( A) = С0 ( B) = 1,00, моль / л (табл.3.2). Изменение концентрации веществ (Ci ) во времени при различных температурах (Ti ) находятся в стороне, соответствующе номеру задания.
Определить энергию активации (E ), предэкспоненциальный множитель (K0 ) и время, за которое 60% веществ A и B (табл.3.2) при температуре T5 = 395 K (табл.3.2) превратится в продукты реакции D .
1.3 Работа 3 - Поверхностные явления
При адсорбции некоторой кислоты из 200 мл водного раствора этой кислоты различных исходных концентраций C0,, i ( табл.3.3) на 4 г активированного угля концентрация кислоты уменьшается до значений Ci (табл.3.3).
Установить, каким из уравнений (Лангмюра или Фрейндлиха-Зельдовича) описывается процесс адсорбции в данном случае. Найти постоянные в соответствующем уравнении, а также равновесную концентрацию раствора (C5 ) при такой же температуре, если исходная концентрация кислоты равна С0,5 = 0,56 моль / л ( табл.3.3), а масса адсорбента - 4 г .
2. Решение задания 9 первого варианта
2.1 Работа 1
Рассчитать температуру замерзания водного раствора дихлоруксусной кислоты при ее концентрации С m = 1,300, моль / кг, если известно, что при ее концентрации
С’ m = 0,331, моль / кг величина электродного потенциала водородного электрода при 00 С и давлении водорода 101,3 кПа составляет Е0 = - 0,066 В (при расчете полагать, что активности совпадают с концентрациями).
Решение
Дихлоруксусная кислота диссоциирует по уравнению:
CCl2 COOH = Н+ + CCl2 COO- (1)
Обозначив молекулу кислоты AH , запишем уравнение (1 ) в форме:
AH = H+ + A- (1’)
Понижение температуры замерзания раствора электролита определяется соотношением:
ΔT3 = i * Kk * Cm , (2)
где i - изотонический коэффициент; Kk - криоскопическая постоянная (для воды равна 1,86 кг * K / моль ); С m - концентрация электролита, моль / кг,
Таким образом, задача сводится к нахождению изотонического коэффициента для раствора кислоты моляльной концентрации С m = 1,300 моль / кг.
Изотонический коэффициент связан со степенью диссоциации α уравнением:
i = 1 + α ( K - 1) ( 3)
K - число ионов, на которое распадается молекула электролита (для нашей задачи K = 2) .
Для раствора слабого электролита "AH " степень диссоциации определяет величину константы диссоциации Kd :
Kd = CH+ * CA - / CAH = Cm * α2/ 1 - α (4)
где CAH , CH + , CA - равновесные концентрации молекул кислоты и соответствующих ионов. Если известна концентрация ионов водорода С H+ и концентрация кислоты С’m , то по уравнению (4 ) рассчитываются величины Kd и α.
Концентрация ионов водорода в растворе (CH + ) определяет величину электродного потенциала нестандартного водородного электрода.
При PH = 101,3 кПа
Е = ( RT / F) lnCH + , (5)
где R - универсальная газовая постоянная, равная 8,31 Дж / моль * К; F - число Фарадея (96487 кул / г - экв ). По уравнению (5 ) рассчитываем концентрацию водорода С H+ в 0,331 моляльном растворе дихлоруксусной кислоты при 00 С :
lnС H+ = EF / RT = - 0,066 * 96487/8,31 * 273 = - 6368,142/2268,63 = - 2,807, CH + = 0,060 г - ион / кг
В соответствии с уравнением (1’ ) концентрация ионов водорода С H+ равна концентрации анионов С A - ; концентрация молекул кислоты САН определяется как разность между исходной концентрацией кислоты С’ m и концентрацией ионов водорода:
С H+ = С A - = 0,060 г - ион / кг
CAH =С’ m - CH \+ = 0,331 - 0,060 = 0,271 моль / кг .
По уравнению (4 ) рассчитываем Kd
Kd = CH + * С A - / С AH = 0,060 * 0,060/0,271 = 1,33 * 10-2 .
Полученное значение константы диссоциации слабой кислоты соответствует температуре замерзания чистой воды - 273,15 K ; при незначительных изменениях температуры (несколько градусов) можно полагать Kd постоянной.
Рассчитаем по уравнению (4 ) степень диссоциации для раствора кислоты с концентрацией Сm = 1,300 моль / кг . Для этого решим уравнение (4 ) относительно α:
![]()
![]()
Cm * α2 + Kd * α - Kd = 0
1,3 * α2 + 1,33 * 10-2 * α - 1,33 * 10-2 = 0
D = b2 - 4ac = (1,33 * 10-2 ) 2 + 4 * 1,3 * 1,33 * 10-2 = 0,0693
![]()
![]()
α = 0,0962 (отрицательный корень, как не имеющий физического смысла выбрасываем).
В соответствии с уравнением (3 ) изотонический коэффициент
i = 1 + 0,0962 * (2 - 1) = 1,0962
Понижение температуры замерзания по уравнению (2 ) составит:
ΔТ3 = 1,0962 * 1,86 * 1,3 = 2,651 К.
Итак, температура замерзания 1,300 мольного раствора дихлоруксусной кислоты понизится на 2,651 K по сравнению с чистой водой и составит
Т3 = 273,150 - 2,651 = 270,499 К.
2.2 Работа 2
Для реакции A + B → D начальные концентрации веществ А и В равны и составляют
С0 ( A) = C0 ( B) = 1,00 моль /л . Изменение концентрации вещества A во времени при различных температурах представлено в табл.2.1
Определить энергию активации и время, за которое 60% вещества A при температуре
Т5 =395 К превратится в продукты реакции D .
Решение
Представим исходные данные в виде таблицы 2.1
Таблица 2.1. Изменение концентрации вещества A во времени при различных температурах
| Время, с | Текущая концентрация С A , моль / л | ||||
| 0 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 |
| 70 | 0,50 | 0,42 | 0,35 | 0,24 | ----- |
| 136 | 0,30 | ----- | ----- | ----- | ----- |
| 285 | 0,15 | ----- | ----- | ----- | ----- |
| Температура, K | 403 T1 | 406 T2 | 410 T3 | 417 T4 | 395 T5 |
Чтобы решить задачу, необходимо определить вид кинетического уравнения реакции, т.е. найти значения константы скорости реакции Ki для различных температур и порядок реакции "n ".
Для случая, когда С0 ( A) = C0 ( B) кинетическое уравнение в дифференциальной форме имеет вид:
V = - dc / dτ = K * Cn , (6)
где V - скорость химической реакции; K - константа скорости;
С - текущая концентрация.
Интегрирование этого уравнения дает выражение:
Kτ = ( 1/n-1) (1/Сn-1 -1/С0 n-1 ) (7)
Зная порядок реакции "n ", константу скорости "K " и исходную концентрацию С0 , можно решить поставленную задачу.
Порядок реакции удобно определить графически (рис.1). Для этого по данным табл.2.1 построим кривую изменения концентрации исходного вещества во времени при T1 = 403 K .
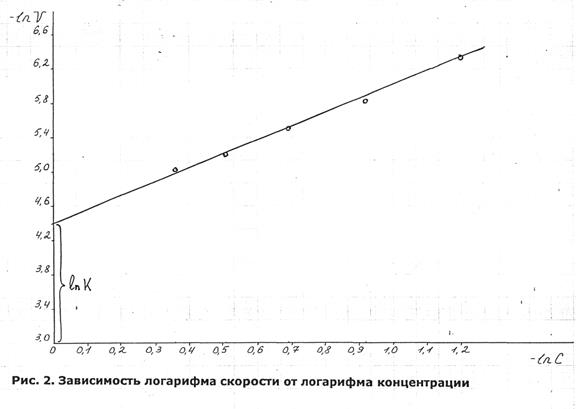
Графически скорость реакции определяется как тангенс угла наклона касательной к кривой в выбранной точке. Логарифмируя уравнение V = K * Cn , получим выражение
LnV = lnK + n lnC , (8)
т.е. в координатах "lnV - lnC " график представляет собой прямую, тангенс угла которой определяет порядок реакции (рис.2). Для построения этого графика найдем пять значений скорости при произвольно выбранных концентрациях, моль / л :
C1 = 0,7; С2 = 0,6; С3 = 0,5; С4 = 0,4; С5 = 0,3.
В качестве примера на рис.1 проведена касательная к точке при С4 = 0,4 моль / л , тангенс угла наклона ее к оси абсцисс равен 0,7/236 = 2,97 * 10-3 моль / л * с .
Аналогично определяем скорость и в других выбранных точках.
C1 = 0,7 моль / л0,9/136 = 6,62 * 10-3 моль / л * с
С2 = 0,6 моль / л0,9/159 = 5,66 * 10-3 моль / л * с
С3 = 0,5 моль / л0,8/197 = 4,06 * 10-3 моль / л * с
С5 = 0,3 моль / л0,5/285 = 1,75 * 10-3 моль / л * с
Полученные данные сведем в табл.2.2
Таблица 2.2. Скорость реакции Vi при концентрациях Ci
| Ci , моль / дм3 | 0,7 | 0,6 | 0,5 | 0,4 | 0,3 |
Vi * 103 моль / л * с |
6,62 | 5,66 | 4,06 | 2,97 | 1,75 |
| lnCi | -0,357 | -0,511 | -0,693 | -0,916 | -1, 204 |
| lnVi | -5,02 | -5,17 | -5,51 | -5,82 | -6,35 |
По данным табл.2.2 строим график в координатах "lnV - lnC " (рис.2), представляющей прямую. Значение "n ", равное тангенсу угла наклона этой прямой к оси абсцисс tgα , казалось равным - 0,65/0,4 = 1,625 ≈ 2.
Итак, порядок реакции второй.
Отрезок, который эта прямая отсекает на оси ординат, равен логарифму константы скорости при T1 = 403 K ( lnK). Из графика на рис.2 lnK ≈ 4,4.
Данный метод определения порядка реакции может дать неверные результаты, т.к зависит от точности проведения касательной к кривой (рис.1). Поэтому для проверки определим порядок реакции по периоду полупревращения τ0,5 , т.е. времени, в течение которого претерпевает превращение половина исходного вещества
С = С0/ 2.
Период полупревращения (полураспада) связан с порядком реакции соотношением:
τ0,5 = (2 n-1 -1) * С0 1- n / К ( n-1) ( 9)
Логарифмируя выражение (9 ) и обозначив (2 n-1 -1) / К ( n-1) = B , получим
ln τ 0,5 = lnB - (n - 1) * lnC0 (10)
Уравнение (10 ) имеет вид прямой в координатах "l n τ0,5 - lnC0 ". Тангенс угла наклона этой прямой есть "n - 1 " или n = tgα + 1 . Определить период полупревращения при различных исходных концентрациях можно на рис.1. Например, при исходной концентрации C0 (1) = 1 моль / л концентрация вещества A уменьшается до значения 0,5 моль / л за 70 с , т.е. τ0,5 (1) = 70 с .
Если за исходную концентрацию взять С0 (3) = 0,8 моль / л , то уменьшение концентрации в 2 раза происходит за 82 с и т.д. Аналогичным образом определим τ0,5 (i) при концентрациях
С0 (2) = 0,9 моль / л, С0 (4) = 0,7 моль / л, C0 (5) = 0,6 моль / л.
Данные сведем в табл.2.3
Таблица 2.3. Период полупревращения τ0,5 ( i) при различных исходных концентрациях С0 (i)
| C0 (i), моль / л | 1,0 | 0,9 | 0,8 | 0,7 | 0,6 |
| τ0,5 (i), с | 70 | 77 | 82 | 85 | 86 |
| lnC0 (i) | 0 | -0,105 | -0,223 | -0,357 | -0,511 |
| lnV0 ( i) | 4,25 | 4,34 | 4,41 | 4,44 | 4,45 |
По данным табл.2.3 строим график в координатах "l n τ0,5 - lnC0 " (рис.3). Он представляет прямую линию, значение
tgα = 0,41/0,50 = 0,82 . Отсюда n = tgα + 1 ≈ 2.
Оба способа дали одинаковое значение порядка реакции. Подставив значение n = 2 в уравнение (7 ) получим кинетическое уравнение для рассматриваемой реакции:
Kτ = (1/С) - (1/С0 ) ( 11)
Зная исходные С0 ( i) и текущие С i концентрации по уравнению (11 ) можно рассчитать константы скорости при различных температурах. Значения исходных и текущих концентраций через 70 с от начала реакции возьмем из табл.2.1
ри T1 = 403 К
K1 = (1/70) [ (1/0,50) - (1/1)] = 14,29 * 10-3
При T2 = 406 К
K2 = (1/70) [ (1/0,42) - (1/1)] = 19,73 * 10-3
При T3 = 410 К
K3 = (1/70) [ (1/0,35) - (1/1)] = 26,53 * 10-3
При T4 = 417 К
K4 = (1/70) [ (1/0,24) - (1/1)] = 45,24 * 10-3
Зависимость константы скорости от температуры описывается уравнением Аррениуса:
K = K0 * e- E / ( RT) ( 12)
K0 - предэкспоненциальный множитель;
e- основание натурального логарифма;
E- энергия активации;
R- универсальная газовая постоянная;
T- температура.
В нешироком интервале температур (до 200 градусов) величины K0 и E изменяются незначительно и их можно считать постоянными. Таким образом, чтобы определить константу скорости при любой температуре необходимо знать величины K0 и E, которые можно определить графически. Прологарифмируем уравнение (12 ).
LnK = LnK0 - E / RT (13)
В координатах "LnK- 1/ T " график этой функции представляет собой прямую линию.
Для построения графика все данные сведем в табл.2.4
| K * 103 , л / моль * с | 14,29 | 19,73 | 26,53 | 45,24 |
| T, K | 403 | 406 | 410 | 417 |
| (1/T) * 10-3 , K-1 | 2,481 | 2,463 | 2,439 | 2,398 |
| LnK | -4,25 | -3,93 | -3,63 | -3,10 |
По данным табл.2,4. строим график в координатах "LnK- 1/ T" (рис.4). Тангенс угла наклона полученной прямой к оси абсцисс определяет E :
tgα = - Е / R (14), E = - R * tgα = - 8,31 * (-13750) = 114263 Дж / моль
Значение множителя K0 найдем из уравнения (13 ), подставив в него любую пару значений LnK и 1/Т из табл.2.4 Например, при Т = 403 К .
LnК0 = LnК + Е / RT1 = - 4,25 + (114263/8,31) * 2,481 * 10-3 = 29,864 .
Откуда К0 = 9,33 * 1012 л / моль * с .
Итак, все постоянные в уравнении (12) известны. Находим K5 при
Т = 395 К.
K5 = 9,33 * 1012 * е-114263/ (8.31 * 395) = 9,33 * 1012 * 7,63 * 10-16 = 7,12 * 10-3 л / моль * с
Используя формулу (11 ), рассчитываем время, за которое 60% вещества превратятся в продукты реакции при 395 K . Так как исходная концентрация вещества равна 1,0 моль / л , тo в искомый момент времени τ x текущая концентрация будет
Cx = 0,40 * С0 = 0,40 * 1,0 = 0,40 моль / л.
Отсюда по уравнению (11):
τ = ( (l / C) - (l / C0 )) / K5 = ( (l / 0,40) - (l / l)) / 7,12 * 10-3 = 211 с
Итак, при температуре 395 K 60% исходного вещества превратится в продукты реакции за 211 с .
2.3 Работа 3
При адсорбции уксусной кислоты из 200 мл водного раствора на 4 г активированного угля при 200 C получены следующие данные (табл.2.5).
Установить, каким из адсорбционных уравнений (Фрейндлиха-Зельдовича или Лангмюра) описывается данный случай. Найти постоянные в соответствующем уравнении, а также равновесную концентрацию раствора (C5 ), если исходная концентрация была равна
C0,5 = 0,56 моль / л (температура раствора 200 С , масса адсорбента 4 г ).


Решение
Представим данные задачи в виде табл.2.5

Таблица 2.5. Исходные и равновесные концентрации раствора уксусной кислоты при адсорбции на угле
Исходная концентрация раствора C0 i , моль / л |
Равновесная концентрация раствора Ci , моль / л |
||||||||
| С0,1 | С0,2 | С0,3 | С0 ,4 | С0 ,5 | С1 | С2 | С3 | С4 | С5 |
| 0,080 | 0,130 | 0,270 | 0,520 | 0,560 | 0,058 | 0,098 | 0,218 | 0,447 | |
Уравнение Фрейндлиха для адсорбции из раствора на твердом адсорбенте имеет вид:
Г = К * С n , (15)
Зельдовича
Г = К * С1/ n , (15’)
где Г - адсорбция, т.е. масса адсорбированного вещества на ед. массы адсорбента,
моль / г ; С - равновесная концентрация раствора, моль / л ; К и n - постоянные при данной температуре. Прологарифмируем уравнение (15).
![]() (16)
(16)
Если адсорбция описывается уравнениями Фрейндлиха-Зельдовича, то в координатах "LnГ - lnC" график функции должен представлять прямую линию. Для проверки высказанного предположения рассчитаем величину адсорбции при различных концентрациях раствора:
Г i = ( C0 i - Ci ) * V / m, (17)
где Г - число молей вещества, адсорбированного из V литров раствора на m граммах адсорбента при исходной и равновесной концентрациях C0 i и Ci соответственно.
После подстановки данных задачи (m = 4 г , V = 0,2 л ) выражение (17 ) примет вид:
Г i = ( C0 i - Ci ) / 20.
Найденные по уравнению (18 ) значения Г i , - вместе с величинами lnCi , lnГ i , Ci / Г i сведем в табл.2.6
Таблица 2.6. Данные для построения изотерм адсорбции
Исходная концентрация раствора C0 i , моль / л |
Равновесная концентрация раствора Ci , моль / л |
Величина адсорбции, Г i * 103, моль / г |
- lnCi | - lnГ i | |
| 0,080 | 0,058 | 1,10 | 2,847 | 6,81 | 52,7 |
| 0,130 | 0,098 | 1,60 | 2^323 | 6,44 | 61,3 |
| 0,270 | 0,218 | 2,60 | 1,523 | 5,95 | 83,8 |
| 0,520 | 0,447 | 3,65 | 0,805 | 5,61 | 122,5 |
| 0,560 | ----- | ----- | ----- | ----- | ----- |
График в координатах "LnГ - lnC" представленный на рис.5 отличается от прямой, т.е. наш случай не описывается изотермой адсорбции Фрейндлиха-Зельдовича. Изотерма адсорбции Лангмюра имеет вид
Г = Z * вс / ( l + вс), (19)
где Z - число мест на адсорбенте; в - постоянная, зависящая от температуры.
При полном заполнении поверхности адсорбента молекулами
адсорбата Z = Г0 предельной адсорбции. После подстановки в уравнение (19) и последующих преобразований его можно представить в линейной, удобной для графического представления, форме:
С / Г = (1/вГ0 ) + (С / Г0 ). ( 20)
Если наш случай описывается изотермой Лангмюра, то в координатах С / Г = f ( c) график должен представлять прямую. По данным табл.2.6 строим график (Рис.6).
Вид графика подтверждает наше предположение. Из графика определим постоянные:
Г0 = ctga = 5,8 * 10-3 , моль / г; 1/Г0 В = 45, B = 1/ (45 * 5,8 * 10-3 ) = 3,83
Таким образом, изотерма адсорбции Лангмюра для рассматриваемого случая при 200 С имеет вид:
Г = 5,8 * 10-3 * 3,83С / (1 + 3,83С) ( 21)

Перейдем к определению равновесной концентрации C5 при исходной концентрации раствора C05 = 0,56 моль / л .,
В соответствии с уравнениями (18 ) и (21 ) можно записать:
Г5 = ( C05 - C5 ) / 20 = (0,56 - C5 ) / 20

Приравняв правые части, решим полученное уравнение относительно C5:
(0,56 - С5 ) / 20 = 5,8 * 10-3 * 3,83С / (1 + 3,83С)
![]()
(0,56 - С5 ) (1 + 3,83С) = 5,8 * 10-3 * 3,83С * 20
3,83С5 2 - 0,71С5 - 0,56 = 0
Равновесная концентрация C5 = 0,484 моль / л .
3. Исходные данные
Вариант и номер задания расчетно-графической работы.
Работа №1
Таблица 3.1
| Вариант | 1 | ||
| Номер задания | 9 | ||
| Кислота | Дихлороуксусная (CCl2 COOH ) | ||
Исходные данные |
C'm , моль / кг |
-E0, B | Cm , моль / кг |
| 0,331 | 0,066 | 1,3 | |
Работа №2
Таблица 3.2
| Вариант | 1 | ||
| Номер задания | 9 | ||
Время (τ), c |
0 | 0 | |
| 1 | 70 | ||
| 2 | 136 | ||
| 3 | 285 | ||
Изменение концентрации (С) во времени при температуре |
T1 | C0 | 1,00 |
| C1 | 0,50 | ||
| C2 | 0,30 | ||
| C3 | 0,15 | ||
| T2 | C0 | 1,00 | |
| C1 | 0,42 | ||
| T3 | C0 | 1,00 | |
| C1 | 0,35 | ||
| T4 | C0 | 1,00 | |
| C1 | 0,24 | ||
| T1 | 403 | ||
| T2 | 406 | ||
| T3 | 410 | ||
| T4 | 417 | ||
| T5 | 395 | ||
| % прореагировавшего вещества | 60 | ||
Работа №3
Таблица 3.3
| Вариант | 1 | |
| Номер задания | 9 | |
Исходная концентрация C0 i , моль / л |
C0,1 | 0,08 |
| C0,2 | 0,13 | |
| C0,3 | 0,27 | |
| C0,4 | 0,52 | |
Концентрация после адсорбции Ci , моль / л |
C1 | 0,058 |
| C2 | 0,098 | |
| C3 | 0,218 | |
| C4 | 0,447 | |
| C0,5 , моль / л | 0,56 | |