| Скачать .docx |
Реферат: Методы исследования биологически активных соединений
методы исследования, применяемые для анализа, установления структуры и количественного определения биологически активных соединений являются обычными химическими, физическими или физико-химическими методами. Специфика состоит только в том, что эти обычные методы применяются для анализа определенных объектов, таких, что требования к результатам анализа могут отличаться (и часто действительно отличаются) от методов, применяемых в других случаях. В частности, это относится к исследованию и анализу соединений, являющихся лекарственными средствами – как субстанций, так и входящих в лекарственную форму.
![]() Методы исследования биологически активных соединений можно условно разделить на три группы:
химические методы, физические методы и физико-химические методы. Это деление во многих случаях является условным, потому что очень часто использование одного метода приводит к изменениям характеристик, определяемых другим методом. Например, проведение химических реакций часто сопровождается изменением окраски или выпадением осадка, что является изменением характеристик физического состояния анализируемой системы.
Методы исследования биологически активных соединений можно условно разделить на три группы:
химические методы, физические методы и физико-химические методы. Это деление во многих случаях является условным, потому что очень часто использование одного метода приводит к изменениям характеристик, определяемых другим методом. Например, проведение химических реакций часто сопровождается изменением окраски или выпадением осадка, что является изменением характеристик физического состояния анализируемой системы.
Для установления структуры и анализа биологически активных соединений, в основном, используются физико-химические методы, рассмотрением которых мы и займемся.
ФИЗИКО-ХИМИЧЕСКИЕ МЕТОДЫ
К физико-химическим методам можно отнести следующие методы:
1. Оптические методы:
Электронная спектроскопия (спектроскопия в УФ и видимой областях спектра).
Спектрофлуориметрия.
Колебательная спектроскопия: ИК-спектроскопия и спектроскопия комбинационного рассеяния.
поляриметрия, в том числе оптический круговой дихроизм и дисперсия оптического вращения.
рефрактометрия.
2. Масс-спектрометрия.
3. Спектрометрия ядерного магнитного резонанса.
4. Хроматография :
планарная – хроматография на бумаге, тонкослойная (ТСХ).
газовая (ГХ) и газо-жидкостная (ГЖХ) .
высокоэффективная жидкостная хроматография (ВЭЖХ).
Применение физико-химических методов основано на использования соответствующего оборудования, с помощью которого исследователь получает искомую информацию. Эта информация всегда получается в результате обработки сигналов.
ОБРАБОТКА СИГНАЛОВ
Сигналом называются первичные данные, получаемые в ходе анализа. Это могут быть спектры, хроматограммы, какие-либо временные зависимости, например, зависимости от времени рН или оптической плотности и многое другое. Подобные данные представляют собой зависимости некоторой величины от времени, длины волны, расстояния (для данных по пространственному распределению) или иного параметра. Они включают в себя не только полезную, но и ненужную, мешающую информацию.
Аналитический сигнал, получаемый от любого прибора, всегда включает в себя полезную информацию, шум и сигнал фона. Составляющая, несущая полезную информацию, часто может быть представлена графически в форме пика. при этом, в зависимости от частоты составляющие суммарного сигнала могут быть разделены следующим образом (F 1).
Таблица 1.
| ЧАСТОТА | КОМПОНЕНТА СИГНАЛА |
| Промежуточная | Полезная информация (пик) |
| Низкая | Фон, дрейф базовой линии |
| Высокая | ШУМ |
Это легко видеть, например, на хроматограмме (F 2), где имеются как пики отдельных веществ (их площади связаны с содержаниями), так и участки базовой линии (прямой или искривленной) между ними. В общем случае при регистрации сигнала как на пики, так и на базовую линию накладывается шум (F 3). Шум может настолько перекрывать полезный сигнал, что последний становится трудно различим. Качество такого рода данных обычно характеризуют отноше нием (полезный сигнал/шум).
Одна из важнейших задач обработки сигналов состоит в том, чтобы отличить полезный сигнал от шума, подавить шум и таким образом извлечь из исходных данных «чистый> сигнал, увеличив количество полезной информации. При графическом представлении полезный сигнал, соответствующий индивидуальному веществу, обычно имеет форму пика, реже ступени.
Для усиления полезного сигнала используют те или иные различия между ним и шумом, в первую очередь различия в их частотах. Частота электронного шума прибора обычно гораздо выше частоты полезного сигнала. В то же время, компонента, имеющая частоту значительно более низкую, чем сигнал, также является помехой и соответствует сдвигу или дрейфу базовой линии (F 3).
Наиболее эффективные методы усиления сигнала основаны на различиях в частотах или фазах между полезным сигналом и помехами. Желательно, чтобы используемый для получения информации прибор обладал как можно меньшим уровнем шумов, поскольку в этом случае задача выделения полезного сигнала облегчается.
Наиболее распространенными методами извлечения полезной информации являются различные алгебраические преобразования, сглаживание, корреляционный анализ, свертка, дифференцирование и интегрирование. Предварительно информацию, поступающую с прибора в непрерывном аналоговом виде (например, на самописец), подвергают оцифровке для обработки и хранения ее в памяти компьютера. Устройства, применяемые для оцифровки аналоговых сигналов, называются аналого-цифровыми преобразователями (АЦП). В этом случае выделение полезного сигнала осуществляют численными методами.
Для экспериментатора, анализирующего данные, полученные на каком-либо приборе, наиболее важным является решение следующих задач:
1. Увеличение отношения сигнал/шум, сглаживание данных.
2. Улучшение разрешения перекрывающихся пиков и устранение сигнала фона.
3. Интегрирование сигналов для получения количественных данных.
Одним из наиболее распространенных методов обработки сигналов является цифровая фильтрация данных. Эту операцию сейчас осуществляют большинство современных приборов. Для такой популярности метода цифровой фильтрации есть много причин:
- соответствующее программное обеспечение можно реализовать практически на любом компьютере;
- в методе используются только простейшие арифметические операции (сложение и умножение);
- цифровые фильтры легко адаптировать к любой конкретной ситуации;
- действия, выполняемые цифровыми фильтрами, легко поддаются интерпретации.
Конечно, никакая фильтрация не может увеличить количество информации, содержащееся в данных, но она позволяет извлечь имеющуюся информацию, сделать ее более наглядной.
В основе простейшего цифрового фильтра лежит операция усреднения: серия последовательных значений заменяется их средним арифметическим. Как известно из математической статистики, среднее характеризуется меньшим уровнем шумов (стандартным отклонением), чем исходные данные.
общая для всех методов фильтрации проблема заключается в следующем. Нестационарные (т. е. изменяющиеся в пространстве и времени) данные не могут быть адекватно описаны средним. Структура данных, имеющих форму пика, при усреднении искажается.
Возможное решение проблемы состоит в таком выборе ширины диапазона (числа точек) для усреднения, чтобы сигнал усиливался, а шум подавлялся. Эта величина, называемая шириной фильтра, является одной из самых важных его характеристик. Слишком широкий фильтр подавляет структуру данных, слишком узкий — недостаточно эффективно устраняет шумы. Простейший тип цифрового фильтра называется оконным фильтром (или дви жущимся средним). Пример его использования приведен на рисунке (F 4). После фильтрации (F 4) структура данных выражена четче, а уровень шума ниже по сравнению с исходным спектром.
На врезке (F 4) показана конкретная форма цифрового фильтра, использованного в этом примере. В простейшем случае, когда усреднение проводится по п соседним точкам, каждая точка входит в общую сумму с коэффициентом 1/n. Например, при усреднении по 8 точкам каждая точка входит с коэффициентом 1/8.
Более сложным и более эффективным является способ фильтрации, основанный на методе наименьших квадратов. В пределах окна экспериментальные данные аппроксимируют каким-либо полиномом (например, квадратичной или кубической функцией). Широко распространен метод, который предложили Савицки и Голэй. Метод так и называется «Savizky-Golaysmoothing» - сглаживание методом Савицки-Голэя.. В этом методе задается определенное число экспериментальных точек n (ширина окна), методом полиномиальной регрессии определяется сглаженное значение для каждой точки и окно передвигается дальше, проходя таким образом всю кривую. Эффективность фильтрации этим методом иллюстрирует рис. 4.
Мы начнем с изучения оптических методов. Это связано как с универсальностью этих методов, так и с тем, что оптические методы используются для детектирования в ряде других физико-химических методов, например, хроматографии.
Несомненно, наиболее простым и наиболее распространенным из оптических методов (в смысле его применения на практике) можно считать метод электронной спектроскопии. Этот метод часто называют либо УФ-спектроскопией, либо просто спектроскопией. Если химик говорит, что нужно снять спектр, определенно имеется в виду спектр в видимой или ультрафиолетовой (или в обеих) областях спектра, т.е. электронный спектр.
Видимый спектр. Спектроскопия как наука возникла после открытия Ньютона (около 1672 г.), показавшего, что величина преломления света при прохождении его через призму меняется в зависимости от цвета. Этот вывод был сделан после того, как было обнаружено, что изображения окрашенных тел при наблюдении их через призму в большей или меньшей мере смещаются в соответствии с различиями в окраске. Было установлено также, что изображение синего тела смещается больше, чем изображение красного.
В одном из последующих опытов Ньютон, используя в качестве источника света отверстие в оконной шторе, пропустил солнечный луч через стеклянную призму и таким образом получил спектр. Было известно и ранее, что сквозь призму можно наблюдать окрашенное изображение, но тогда предполагали, что эту окраску дает сама призма. Ньютон же на основании этого и других своих опытов сделал вывод, что белый свет является сложным, и в настоящее время известно, что семь первичных цветов — красный, оранжевый, желтый, зеленый, голубой, синий и фиолетовый — дают вместе белый свет.
Окраска раствора позволяет характеризовать испытуемый образец. Одновременно эта окраска характеризует и ту область спектра, в которой поглощает этот образец. Соответствующие данные приведены в следующих таблицах (F 5 и 6).
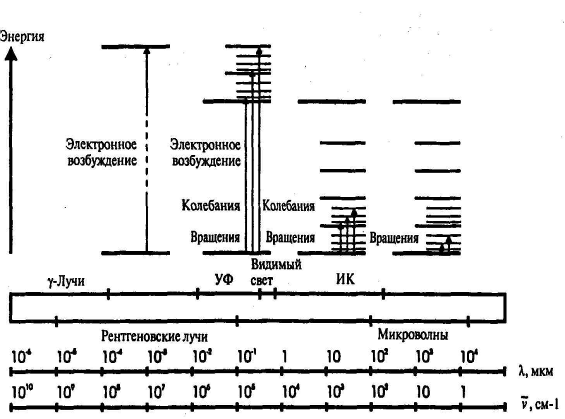
Последующими открытиями было установлено, что видимая иприлегающие к ней инфракрасная и ультрафиолетовая области спектра представляют лишь очень небольшие участки всего спектра излучения, известного теперь под названием электромагнитного спектра.
Уже давно установлено, что свет представляет собой электромагнитное излучение с длиной волны, изменяющейся в определенном интервале (Рис. F 7 и 8).
При попадании на тот или иной предмет свет может отражаться, поглощаться или рассеиваться (Рис. F 9). Обычно эти три явления протекают одновременно, но доля каждого из них различна в каждом конкретном случае.
Очень важно, что поглощение света веществом происходит избирательно, в зависимости от свойств вещества. На избирательном поглощении света основаны спектральные методы анализа. Эти методы применяются для установления строения соединений, их идентификации и количественного определения.
Приборы, применяемые для таких исследований, называются спектрофотометрами, и в них используется монохроматическое излучение, т.е. излучение с определенной длиной волны.
![]() в спектральных исследованиях помимо длины волны обычно используются следующие ее функции (рис. F 10):
в спектральных исследованиях помимо длины волны обычно используются следующие ее функции (рис. F 10):
![]() волновое число
волновое число ![]() - число волн на сантиметр = 1/l см-1
;
- число волн на сантиметр = 1/l см-1
;
частота колебаний n (с-1 ) – число полных колебаний в секунду.
v = Скорость света (см/сек)/ Длина волны (см) = 3´1010 / l.
Все эти единицы связаны между собой:
|
|
|
|
Длина волны Скорость света
Единицы длины волны и частоты приведены в таблице (Рис. F 11).
ЗАКОНЫ ПОГЛОЩЕНИЯ СВЕТА
Количественные измерения поглощения света любой длины волны основаны на двух законах, установленных эмпирически в 18-м и 19-м веках, которые теперь связывают с именами Бугера, Ламберта и Бера. Так, в некоторых руководствах утверждается, что независимо Бугером в 1729 г. и Ламбертом в 1760 г. был сформулирован следующий закон:
«Каждый тонкий слой постоянной толщины внутри однородной окрашенной среды поглощает определенную долю входящего в него потока излучения независимо от интенсивности этого излучения»
На самом деле, Бугер сформулировал свои выводы так: «При возрастании толщины на равные величины свет уменьшается подобно членам геометрической прогрессии». И далее: «Надлежит сделать вывод, что пропорциональными поглощению света являются не толщины, а массы вещества, содержащиеся в этих толщинах».
В 1760 г. Ламберт со ссылкой на Бугера выразил зависимость интенсивности прошедшего света от толщины слоя математической формулой. Практически во всех современных учебниках и монографиях основной закон поглощения света называют законом Бера (его фамилии на самом деле Беер) и формулируют так:
«Поглощение данным тонким слоем пропорционально числу содержащихся в нем поглощающих молекул, т.е. концентрации поглощающего вещества» и датируют 1852 годом. Это выражение и приписывание авторства Беру теперь являются общепринятыми, хотя на самом деле этот закон открыл Бугер.
Согласно этому закону, доля света, поглощенного в слое вещества, не зависит от интенсивности падающего излучения.
Зависимости, устанавливаемые этими законами, обычно выражаются одной формулой, которая связывает отношение интенсивностей падающего на образец (I0 ) и прошедшего через него (I) света с концентрацией (с) поглощающего вещества, содержащегося в образце толщиной ℓ (F 12):
log(I0 /I) = D = ccℓ , (2)
где
ℓ - толщина образца,
D – оптическая плотность,
c - коэффициент экстинкции или показатель поглощения.
закон поглощения излучения может быть выведен без каких-либо предположений о природе этого излучения. Следовательно, этот закон применим к любому излучению независимо от длины волны.
Электронная абсорбционная спектроскопия (или спектроскопия в ультрафиолетовой и видимой областях спектра) относится к старейшим физическим методам, используемым химиками для качественного и количественного анализа. Это в полной мере относится и к исследованию биологически активных соединений несмотря на широкое применение и других методов, как химических, так и физических.
Рассмотрим закон поглощения света подробнее (рис. 8 и 9).
Отношение интенсивности прошедшего через образец света (I) к интенсивности подающего на него света (I0 ) называется пропусканием обозначается Т, и выражается обычно в %, т.е.
T = (I/I0 )´100 %.
Согласно закону поглощения, десятичный логарифм величины, обратной пропусканию, пропорционален концентрации анализируемого вещества. Эта величина называется оптической плотностью и обозначается заглавной латинской буквой D, т.е.
D = cсℓ,
где c - показатель поглощения или экстинкция раствора, концентрация которого равна единице, с – концентрация анализируемого вещества в образце и ℓ – толщина образца в сантиметрах, т.е. длина пути луча света в образце.
Величина c является специфической физической константой для каждого вещества и может быть использована для целей его идентификации. Знание этой величины позволяет определять содержание данного вещества в растворах неизвестной концентрации по измеренным значениям оптической плотности D.
Обычно используют два типа показателя поглощения c в зависимости от того, в каких единицах выражена концентрация анализируемого раствора.
Если концентрация выражена в молях на литр, то используется молярный коэффициент экстинкции e. Его размерность – л/моль см.
При проведении анализов лекарственных средств значительно чаще используется так называемый удельный показатель поглощения. В этом случае концентрация раствора выражается в г/100 мл раствора. Его обозначение Е1% 1см или А1% 1см . Следует помнить, что при стандартных измерениях толщина образца, т.е. толщина кюветы, всегда равна 1 см. Таким образом, молярный коэффициент экстинкции – это коэффициент экстинкции раствора с концентрацией 1 моль/л, а удельный показатель поглощения Е1% 1см – это показатель поглощения раствора с концентрацией 1 г/100 мл.
Если при измерении используется слой другой толщины, в расчеты необходимо ввести соответствующий коэффициент.
Таким образом, если концентрация раствора выражена в моль/л, то закон Ламберта-Бера имеет вид:
D = eсℓ.
Если же используется процентная концентрация (вес/объем), то
D = Е1% 1см сℓ.
Соотношения между показателями поглощения и примеры приведены в таблице (F 13).
|
||
|
||
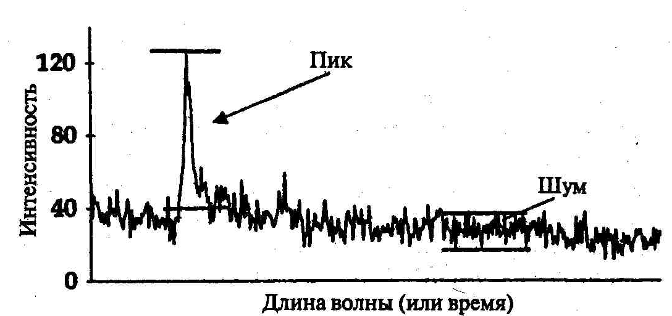

Рис. 2. Полезный сигнал (пик), шум и базовая линия (с небольшим наклоном). Для изображенного пика отношение сигнал/шум равно примерно 5.

|
|
|
![]() волновое число n - число волн на сантиметр = 1/l см-1
;
волновое число n - число волн на сантиметр = 1/l см-1
;
частота колебаний n (с-1 ) – число полных колебаний в секунду.
v = Скорость света / Длина волны (см) = 3´1010 / l (см).
Все эти единицы связаны между собой:
|
Длина волны. Скорость света
Таблица 1
![]() Единицы длины волны (l) и частоты (n )
Единицы длины волны (l) и частоты (n )
ЕДИНИЦА |
ОБОЗНАЧЕНИЕ |
ОПРЕДЕЛЕНИЕ |
ДЛИНА ВОЛНЫ |
||
Микрометр (микрон) Нанометр (миллимикрон) Ангстрем |
мкм (m) нм Å |
10-4 см 10-9 м (10-7 см) 10-8 см |
|
||
| Волновое число | 1/l, см-1 | |
Частота |
n | 3´1010 / l (с-1 ) |
|
||
|
РАСПРЕДЕЛЕНИЕ КОМПОНЕНТ СИГНАЛА ПО ЧАСТОТЕ
| ЧАСТОТА | КОМПОНЕНТА СИГНАЛА |
| Промежуточная | Полезная информация (пик) |
| Низкая | Фон, дрейф базовой линии |
| Высокая | ШУМ |
СООТНОШЕНИЯ МЕЖДУ ПОКАЗАТЕЛЯМИ ПОГЛОЩЕНИЯ
ПОКАЗАТЕЛЬ ПОГЛОЩЕНИЯ |
ОБОЗНАЧЕНИЕ |
РАЗМЕРНОСТЬ |
СООТНОШЕНИЕ |
МОЛЯРНЫЙ КОЭФФИЦИЕНТ ЭКСТИНКЦИИ |
e |
л/моль см |
e = Е1% 1см ´ М.м./10 |
УДЕЛЬНЫЙ ПОКАЗАТЕЛЬ ПОГЛОЩЕНИЯ (ИЛИ УДЕЛЬНЫЙ КОЭФФИЦИЕНТ ЭКСТИНКЦИИ) |
Е1% 1см (А1% 1см ) |
100 мл/г см |
Е1% 1см = 10e/ М.м. |