| Скачать .docx |
Дипломная работа: Теория симметрии молекул
Министерство общего и профессионального образования РФ
Дипломная работа
«Теория симметрии молекул»
Содержание
Введение
Глава 1 Элементы теории групп симметрии молекул
1.1 Операции симметрии молекул
1.2 Групповые постулаты
1.3 Классы смежности и классы сопряженных элементов
1.4 Факторизация групп
Глава 2 Введение в теорию представлений групп симметрии молекул
2.1 Векторные (линейные) пространства
2.2 Эвклидовы и унитарные пространства
2.3 Матрицы
2.4 Представления групп
2.5 Характеры представлений
2.6 Операторы проектирования
Заключение
Список использованной литературы
Введение
Понятие симметрии играет важную роль во всех естественных науках. Свойствами симметрии обладают структуры многих молекул, ионов, образуемых ими реагирующих систем.
Математической основой теории симметрии является теория групп. Понятие группы – предмет теории групп.
Множество G с бинарной операцией называется группой , если:
1. Операция ассоциативна, т. е. ![]() для любых a, b, c из G.
для любых a, b, c из G.
2. Операция гарантирует единицу, т. е. в G существует такой элемент е – он называется единицей, - что ![]() для любого а из G.
для любого а из G.
3. Операция гарантирует обратные элементы, т. е. для любого а из G существует в G такой элемент а-1
– он называется обратным к а, - что ![]() .
.
В теории молекулярной симметрии понятие представления группы играет центральную роль. Учитывая это, дадим определение представления группы, используя различные математические объекты, представляющие группу.
Представлением группы, действующим в n-мерном векторном пространстве V, называется гомоморфизм этой группы в группу невырожденных линейных операторов пространства V.
Задача настоящей работы состояла в самостоятельном изучении основных понятий и методов данной области и рассмотрении примеров по изучаемым темам.
В процессе написания были проработаны следующие разделы: операции симметрии молекул; классы смежности и факторизация групп; векторные, эвклидовы и унитарные пространства; представления групп и характеры представлений; операторы проектирования. Материал разбит на две главы, которые в свою очередь разбиваются на параграфы. На протяжении всего теоретического материала рассматриваются примеры, которые иллюстрируют применение изучаемых вопросов. Так большинство примеров показаны на множестве операций симметрии молекул аммиака NH3 – группе C3 V .
Глава 1 Элементы теории групп симметрии молекул
1.1 Операции симметрии молекулы
1. Элементы и операции симметрии молекулы
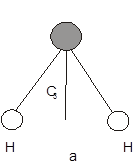
Под геометрической конфигурацией молекулы или иона будем понимать пространственное расположение ядер атомов в молекуле или ионе относительно друг друга. Геометрическую конфигурация молекулы можно охарактеризовать, построив модель молекулы. Впервые модели молекул из шаров и стержней были построены в 1810 г. Джоном Дальтоном. Современные представления о структуре молекулы являются более точными благодаря применению точных экспериментальных методов определения этой структуры (оптические и дифракционные методы). Использовав эти методы, мы можем построить геометрическую модель молекулы в виде конечной фигуры.
Важной особенностью современных представлений о строении молекул является наличие симметрии молекул.
Определение 1. Отображением множества M на множество N называется правило f, которое каждому элементу m из множества M ставит в соответствие элемент n из множества N, называемый образом элемента m, при этом каждый элемент множества N является образом хотя бы одного элемента из множества M.
Если M=N, то говорят об отображении множества М на себя.
Определение 2. Операцией симметрии конечной фигуры называется ее изомерическое (т. е. сохраняющее расстояние между точками фигуры) отображение на себя.
Рассматривая эти примеры, приходим к заключению, что помимо геометрической модели, с молекулой аммиака необходимо связать геометрические образы – прямую C3
и плоскость ![]() , которые не принадлежат модели хотя бы потому, что они бесконечны
, которые не принадлежат модели хотя бы потому, что они бесконечны
Операции симметрии пространственной фигуры, соответствующей молекуле, называются операциями симметрии молекулы.

|
|
|
|
|
|
|
 |
В качестве примера рассмотрим молекулу аммиака NH3 . Ее геометрическая конфигурация имеет форму правильной треугольной
|
К числу операций симметрии правильной треугольной пирамиды относятся повороты, совмещающие ее с собой. Точки N и O определяют ось поворота, которую обозначим через С3
. Повернем пирамиду вокруг этой оси на 120о
против часовой стрелки. Указанный поворот обозначим через ![]() . На рис. 1, б изображена фигура (результат поворота), которая совмещается с исходной (рис. 1, а) при наложении. Рассмотрим отражение в плоскости
. На рис. 1, б изображена фигура (результат поворота), которая совмещается с исходной (рис. 1, а) при наложении. Рассмотрим отражение в плоскости ![]() , совмещающее фигуру с собой, и обозначим его
, совмещающее фигуру с собой, и обозначим его ![]() . Очевидно, что
. Очевидно, что ![]() , как и
, как и ![]() , является операцией симметрии молекулы аммиака, так как операции
, является операцией симметрии молекулы аммиака, так как операции ![]() и
и ![]() не изменяют расстояний между точками фигуры NH3
.
не изменяют расстояний между точками фигуры NH3
.
Рассматривая эти примеры, приходим к заключению, что помимо геометрической модели, с молекулой аммиака необходимо связать геометрические образы – прямую C3
и плоскость ![]() , которые не принадлежат модели хотя бы потому, что они бесконечны.
, которые не принадлежат модели хотя бы потому, что они бесконечны.
Определение 3. Элементом симметрии молекулы называется вспомогательный геометрический образ (точка, прямая, плоскость), характеризующий некоторое множество операций симметрии фигуры, изображающей молекулу.
Например, ось C3
характеризует множество операций симметрии, состоящее из рассмотренного нами поворота ![]() , а также поворотов
, а также поворотов ![]() на 240о
и
на 240о
и ![]() на 360о
против часовой стрелки молекулы аммиака. Поворот
на 360о
против часовой стрелки молекулы аммиака. Поворот ![]() называется тождественной операцией симметрии. При этой операции симметрии все точки геометрической модели молекулы отображаются в себя. Плоскость
называется тождественной операцией симметрии. При этой операции симметрии все точки геометрической модели молекулы отображаются в себя. Плоскость ![]() характеризует множество операций симметрии, состоящее из
характеризует множество операций симметрии, состоящее из ![]() и
и ![]() .
.
Элементы симметрии не следует путать с операциями симметрии. Элементы симметрии будем обозначать буквами, а операции симметрии – буквами «со шляпками» над ними.
Рассмотрим множество, элементами которого являются всевозможные операции симметрии молекулы, для случая молекулы аммиака. Четыре элемента ![]() ,
, ![]() ,
, ![]() ,
, ![]() этого множества мы уже нашли. Кроме плоскости
этого множества мы уже нашли. Кроме плоскости ![]() (рис. 1, а), молекула аммиака имеет еще две плоскости симметрии
(рис. 1, а), молекула аммиака имеет еще две плоскости симметрии ![]() и
и ![]() , содержащие прямые NH(2)
и NH(3)
соответственно. С плоскостями
, содержащие прямые NH(2)
и NH(3)
соответственно. С плоскостями ![]() и
и ![]() связаны операции симметрии
связаны операции симметрии ![]() и
и ![]() . Множество операций симметрии молекулы аммиака может быть обозначено следующим образом:
. Множество операций симметрии молекулы аммиака может быть обозначено следующим образом:
![]() .
.
2. Классификация элементов симметрии молекулы
1. Поворотная ось Cn порядка n. Поворотной осью симметрии n-го порядка называется ось Cn , при повороте вокруг которой на угол a=2p/n молекула совмещается сама с собой. Примеры: C3 – для случая молекулы аммиака; C2 (рис. 2, а) – для случая молекулы воды; C6 – для случая молекулы бензола (рис. 2, б).
|
|
|
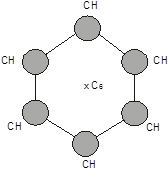
2. Поворотная ось бесконечного порядка C ¥ . Это поворотная ось, при повороте вокруг которой на любой угол молекула совмещается с собой. Примером может служить любая линейная молекула, например, молекула ацетилена C2 H2 (рис. 3).

Рис. 2
|
|
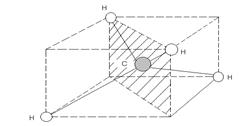
Рис. 3
3. Плоскость симметрии. Плоскостью симметрии молекулы называется плоскость, при отражении в которой молекула совмещается сама с собой. Пример молекулы с вертикальной плоскостью симметрии уже приведен (молекула аммиака). У бензола C6 H6 (рис. 2, б) есть плоскость симметрииДиагональную плоскость симметрии имеет молекула метана (рис. 4). Геометрической моделью CH4 является тетраэдр, в вершине которого расположены атомы водорода. Диагональная плоскость симметрии sd заштрихована. При отражении в плоскости sd атомы водорода, находящиеся в плоскости, переходят в себя, а атомы, расположенные симметрично этой плоскости, переходят друг в друга.
4. Центр симметрии. Это точка i, при отражении в которой молекула совмещается сама с собой, например, молекула трансдихлорэтилена C2 Cl2 H2 (рис. 5).

Рис. 5
5. Зеркально-поворотная ось n-го порядка Sn . Зеркально-поворотной осью n-го порядка называется ось, при повороте вокруг которой на угол a=2p/n с последующим
|
|
|
|
|
Рис. 6
|
|
|
|
1.2 Групповые постулаты
1. Алгебраические операции
Определение 1. Бинарной алгебраической операцией, определенной на множестве М, называется правило, согласно которому каждые два элемента a и b множества М, взятые в определенном порядке, однозначно сопоставляются с элементом с из этого множества, называемым результатом выполнения операции.
Рассмотрим в качестве общего примера множество операций симметрии молекулы. Под произведением операций симметрии ![]() и
и ![]() будем понимать их последовательное выполнение. Первые два требования к алгебраической операции, очевидно, выполняются. Проверим выполнение третьего условия из определения алгебраической операции.
будем понимать их последовательное выполнение. Первые два требования к алгебраической операции, очевидно, выполняются. Проверим выполнение третьего условия из определения алгебраической операции.
Операция симметрии ![]() совмещает геометрическую модель с собой, и если после выполнения операции
совмещает геометрическую модель с собой, и если после выполнения операции ![]() мы выполнили операцию
мы выполнили операцию ![]() , модель снова совместится сама с собой. Проверим изометричность произведения
, модель снова совместится сама с собой. Проверим изометричность произведения ![]() . Пусть геометрическая модель молекулы изображена на рисунке в виде фигуры F. Операции симметрии этой фигуры являются операциями симметрии молекулы. Пусть x и y – любые две точки фигуры F и пусть при операции
. Пусть геометрическая модель молекулы изображена на рисунке в виде фигуры F. Операции симметрии этой фигуры являются операциями симметрии молекулы. Пусть x и y – любые две точки фигуры F и пусть при операции ![]() точки x и y переходят в точки x¢ и y¢ соответственно, что запишем в виде x¢=x
точки x и y переходят в точки x¢ и y¢ соответственно, что запишем в виде x¢=x![]() , y¢=y
, y¢=y![]() . Аналогично, пусть x¢¢=x¢
. Аналогично, пусть x¢¢=x¢![]() , y¢¢=y¢
, y¢¢=y¢![]() . Тогда при последовательном выполнении операций
. Тогда при последовательном выполнении операций ![]() и
и ![]() , т. е. в результате выполнения операции
, т. е. в результате выполнения операции ![]() , получаем x¢¢=x
, получаем x¢¢=x![]() , y¢¢=y
, y¢¢=y![]() . Так как
. Так как ![]() изометрично, то r(x, y)=r(x¢, y¢), где r(x, y) обозначает расстояние между точками x и y, а r(x¢, y¢) – расстояние между точками x¢, y¢. Поскольку
изометрично, то r(x, y)=r(x¢, y¢), где r(x, y) обозначает расстояние между точками x и y, а r(x¢, y¢) – расстояние между точками x¢, y¢. Поскольку ![]() тоже изметрично, то r(x¢, y¢)=r(x¢¢, y¢¢). Из полученных равенств следует, что r(x, y) =r(x¢¢, y¢¢), т. е.
тоже изметрично, то r(x¢, y¢)=r(x¢¢, y¢¢). Из полученных равенств следует, что r(x, y) =r(x¢¢, y¢¢), т. е. ![]() изометрично. Так как самосовмещение фигуры есть ее отображение на себя, то
изометрично. Так как самосовмещение фигуры есть ее отображение на себя, то ![]() есть изометрическое отображение фигуры F на себя, т. е. операция симметрии фигуры. Поскольку
есть изометрическое отображение фигуры F на себя, т. е. операция симметрии фигуры. Поскольку ![]() и
и ![]() можно считать любыми элементами множества операций симметрии молекулы, третье условие из определения алгебраической операции выполнено.
можно считать любыми элементами множества операций симметрии молекулы, третье условие из определения алгебраической операции выполнено.
2. Таблица Кэли
Подобно тому, как существует таблица умножения натуральных чисел, можно составить таблицу умножения в множестве операций симметрии молекулы. Эта таблица называется таблицей Кэли (или квадратом Кэли). Для того, чтобы понять общий принцип составления таких таблиц, запишем таблицу Кэли для случая множества операций симметрии молекулы аммиака NH3 (табл. 1).
Таблица 1
Квадрат Кэли группы C3 V
3. Определение группы
Определение 2. Множество G называется группой, если в этом множестве определена бинарная алгебраическая операция, удовлетворяющая следующим аксиомам (в мультипликативной записи операций):
1. Для всех элементов a, b, c из множества G![]() (аксиома ассоциативности).
(аксиома ассоциативности).
2. Для всех элементов а из множества G существует элемент e из этого множества, такой, что ![]() (е называется единичным элементом группы).
(е называется единичным элементом группы).
3. Для каждого элемента а для множества G существует элемент а-1
из этого из этого множества, такой, что ![]() (а-1
называется обратным элементом к элементу а).
(а-1
называется обратным элементом к элементу а).
Рассмотрев таблицу Кэли для множества C3 V , можно убедиться, что множество операций симметрии молекулы аммиака является группой относительно введенной нами операции умножения в этом множестве.
Определение 3. Подмножество H группы G называется подгруппой группы G, если H само является группой относительно операции, введенной в группе G.
Для проверки того, что H является подгруппой группы G, надо проверить два условия: произведение двух элементов из Н снова принадлежит Н и вместе с элементом h обратный к нему элемент из группы G (он должен существовать) также принадлежит Н. В самом деле, тогда ![]() ; ассоциативность же умножения, будучи верной во всей группе G, будет иметь место и в подгруппе Н.
; ассоциативность же умножения, будучи верной во всей группе G, будет иметь место и в подгруппе Н.
Теорема 1. Множество всех операций симметрии молекулы является группой. Эта группа является подгруппой симметрической группы перестановок фигуры, изображающей геометрическую модель молекулы.
Определение 4. Группой симметрии молекулы называется множество S всех операций симметрии молекулы, на котором введена структура группы относительно умножения операций симметрии молекулы.
4. Гомоморфизмы и изоморфизмы
Определение 5. Отображение множества М в множество N – это правило f, по которому каждому элементу m из множества M ставится в соответствие однозначно определенный элемент mf=n из множества N.
Определение 6. Гомоморфизмом группы G в группу G¢ называется отображение j множества G в множество G¢ такое, что
![]() (1)
(1)
В качестве примера рассмотрим группу C3 V и группу {-1}2 , состоящую всего из двух элементов {-1}2 ={-1, 1}.
Построим отображение j группы C3
V
в группу {-1}2
(записываем это в виде j: C3
V
®{-1}2
) по следующему правилу: элементам ![]() ,
, ![]() ,
, ![]() сопоставим 1, а элементам
сопоставим 1, а элементам ![]() ,
,![]() ,
, ![]() сопоставим -1. Отображение j построено, причем, как видим, у элемента 1 группы {-1}2
есть три прообраза, т. е. три элемента группы C3
V
, образом каждого из которых является 1: у элемента –1 также три прообраза – это не запрещено определением отображения.
сопоставим -1. Отображение j построено, причем, как видим, у элемента 1 группы {-1}2
есть три прообраза, т. е. три элемента группы C3
V
, образом каждого из которых является 1: у элемента –1 также три прообраза – это не запрещено определением отображения.
Покажем теперь, что j есть гомоморфизм. Из таблицы Кэли группы C3
V
видно, что произведение любых двух элементов множества C3
={![]() ,
, ![]() ,
, ![]() } принадлежит этому же множеству, в то же время
} принадлежит этому же множеству, в то же время ![]() . Из этой таблицы видно, что
. Из этой таблицы видно, что ![]() , i, j=1, 2, 3 принадлежит множеству C3
, но с другой стороны,
, i, j=1, 2, 3 принадлежит множеству C3
, но с другой стороны, ![]() . Наконец, произведения
. Наконец, произведения ![]() и
и ![]() , i, j=1, 2, 3 принадлежат множеству
, i, j=1, 2, 3 принадлежат множеству ![]() , с другой стороны
, с другой стороны ![]() ,
, ![]() . Таким образом для любых двух операций симметрии
. Таким образом для любых двух операций симметрии ![]() и
и ![]() из множества C3
V
получаем, что
из множества C3
V
получаем, что ![]() , где
, где ![]() ,
, ![]() ,
, ![]() есть 1 или –1, т. е. отображение j, действительно есть гомоморфизм.
есть 1 или –1, т. е. отображение j, действительно есть гомоморфизм.
Определение 7. Отображение f множества М в множество N называется взаимно однозначным отображением множества М на множество N, если каждый элемент множества N является образом в точности одного элемента множества M.
Определение 8. Две группы G и G¢ называются изоморфными (обозначение G@G¢), если существует взаимно однозначное отображение q группы G на группу G¢ такое, что
![]() (2)
(2)
Свойства группы или других математических объектов, сохраняющиеся при изоморфизме, называются структурными свойствами. Приведем два примера структурных свойств групп, которым предшествуют два важных определения.
Определение 9. Если группа G содержит конечное число элементов, то число n элементов группы называется порядком группы и обозначается n=|G|.
Например, |C3 V |=6; |{-1}2 |=2.
Определение 10. Группа называется абелевой или коммутативной, если для всех элементов a и b этой группы выполняется равенство ab=ba.
Так, группа {-1}2 является абелевой, а группа C3 V не абелева.
Теорема 2. Если две конечные группы G и G¢ изоморфны, то их порядки равны.
Теорема 3. Если G – абелева группа и G@G¢, то и G¢ - абелева группа.
Теорема 4. Каждая конечная группа изоморфна некоторой группе перестановок и некоторой группе матриц.
Приведем пример. Пронумеруем элементы группы C3
V
в виде ![]() =1;
=1; ![]() =2;
=2; ![]() =3;
=3; ![]() =4;
=4; ![]() =5;
=5; ![]() =6. Используя таблицу Кэли группы C3
V
, запишем
=6. Используя таблицу Кэли группы C3
V
, запишем
 .
.
Далее, ![]() получим, используя правило умножения перестановок. Ясно, что
получим, используя правило умножения перестановок. Ясно, что
 .
.
Аналогично получаем остальные четыре перестановки искомой группы: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Мы получили другое выражение группы C3
V
: ее представление в виде группы перестановок.
. Мы получили другое выражение группы C3
V
: ее представление в виде группы перестановок.
1.3 Классы смежности и классы сопряженных элементов
Пусть G – группа, H – ее подгруппа.
Определение 1. Всякое множество Hg (т. е. совокупность всех элементов hg, где h пробегает H, g – фиксированный элемент группы G) называется правым смежным классом группы G по подгруппе H. Аналогично определение левого смежного класса gH.
Каждый элемент смежного класса называется его представлением. Так, элемент g – представитель класса Hg, поскольку из-за наличия в группе Н единицы е группы G элемент g=egÎHg.
Будем считать подгруппу H первым правым смежным классом. В результате группу G можно представить в виде объединения правых смежных классов:
Hg1 +Hg2 +…+Hgm =G(3)
Выражение (3) называется правосторонним разложением группы G по подгруппе H.
Рассмотрим пример. В группе C3
V
выберем подгруппу {![]() ,
, ![]() }={
}={![]() }2
, считая ее первым правым смежным классом. Возьмем элемент
}2
, считая ее первым правым смежным классом. Возьмем элемент ![]() и по таблице Кэли группы C3
V
найдем второй правый смежный класс {
и по таблице Кэли группы C3
V
найдем второй правый смежный класс {![]() ,
, ![]() }
}![]() ={
={![]() ,
, ![]() }. Элемент
}. Элемент ![]() не входит в оба класса, и с помощью его получаем третий правый смежный класс {
не входит в оба класса, и с помощью его получаем третий правый смежный класс {![]() ,
, ![]() }
}![]() ={
={![]() ,
, ![]() }. Таким образом, правостороннее разложение группы C3
V
по подгруппе {
}. Таким образом, правостороннее разложение группы C3
V
по подгруппе {![]() }2
имеет вид
}2
имеет вид
C3
V
={![]() ,
, ![]() }+{
}+{![]() ,
, ![]() }+{
}+{![]() ,
, ![]() }. (4)
}. (4)
Аналогично левостороннее разложение группы C3
V
по подгруппе {![]() }2
имеет вид
}2
имеет вид
C3
V
={![]() ,
, ![]() }+{
}+{![]() ,
, ![]() }+{
}+{![]() ,
,![]() }. (5)
}. (5)
Существенно, что левостороннее разложение (5) не совпадает с правосторонним разложением (4).
Теорема Лагранжа. Порядок подгруппы H конечной группы G является делителем порядка группы G.
Теорема Лагранжа облегчает нахождение подгруппы группы G. Надо искать подгруппы группы G не любых порядков, а порядков, равных делителям порядка группы G. Например, группа C3
V
имеет порядок 6, а у числа 6 делителями являются числа 1, 2, 3, 6. Мы уже нашли подгруппы группы C3
V
, имеющие приведенные порядки – это подгруппы {![]() }, {
}, {![]() }, {
}, {![]() }3
={
}3
={![]() ,
, ![]() ,
, ![]() } и сама C3
V
. Подчеркнем, что если число m является делителем порядка группы G, то отсюда не следует, что в группе G есть подгруппа порядка m, т. е. теорема, обратная теореме Лагранжа, не имеет места.
} и сама C3
V
. Подчеркнем, что если число m является делителем порядка группы G, то отсюда не следует, что в группе G есть подгруппа порядка m, т. е. теорема, обратная теореме Лагранжа, не имеет места.
Определение 2. Элементы а и b группы G называются сопряженными, если существует элемент х из группы G такой, что выполняется равенство
a=x-1 bx(6)
Например, в группе C3
V
согласно таблице Кэли этой группы, имеем ![]()
![]()
![]() =
=![]() -1
-1
![]()
![]() =
=![]() , поэтом элементы
, поэтом элементы ![]() и
и ![]() сопряжены с помощью элемента
сопряжены с помощью элемента ![]() .
.
С помощью понятия сопряженности можно дать классификацию элементов группы G. Обозначим через Kg1 , Kg2 , …, Kgt все классы сопряженных элементов. Всю группу G можно представить в виде
Kg1 + Kg2 + …+ Kgt =K1 +K2 +…+Kt =G, (7)
где Kgi =Ki ; i=1, 2, …, t – непересекающиеся классы сопряженных элементов.
Найдем эти классы для группы C3
V
. Очевидно, что единица ![]() сама является классом сопряженных элементов, ибо всегда
сама является классом сопряженных элементов, ибо всегда ![]()
![]()
![]() =
=![]() . Обозначим этот класс R1
. Второй класс сопряженных элементов – это {
. Обозначим этот класс R1
. Второй класс сопряженных элементов – это {![]() ,
, ![]() }, поскольку
}, поскольку ![]() не сопряжено с
не сопряжено с ![]() и
и ![]() , а других возможностей нет. С помощью таблицы Кэли проверяется, что третий класс сопряженных элементов есть {
, а других возможностей нет. С помощью таблицы Кэли проверяется, что третий класс сопряженных элементов есть {![]() ,
, ![]() ,
, ![]() }, в итоге
}, в итоге
C3
V
= K1
+K2
+K3
={![]() }+{
}+{![]() ,
, ![]() }+{
}+{![]() ,
, ![]() ,
, ![]() } (8)
} (8)
1.4 Факторизация групп
Пусть дана группа G и два подмножества M и N множества G.
Определение 1. Произведением подмножеств М и N группы G называется множество MN, состоящее из всевозможных произведений mn, где m пробегает множество M, а n – множество N.
Теорема 1. Произведение АВ двух подгрупп А и В группы G будет подгруппой группы G, если А и В перестановочны, т. е. если АВ=ВА.
Рассмотрим примеры. В группе C3
V
перемножим подгруппы {![]() }3
и {
}3
и {![]() }2
. Используя таблицу Кэли для C3
V
, получаем, что C3
V
факторизуема: C3
V
={
}2
. Используя таблицу Кэли для C3
V
, получаем, что C3
V
факторизуема: C3
V
={![]() }3
{
}3
{![]() }2
. По таблице Кэли группы C3
V
находим {
}2
. По таблице Кэли группы C3
V
находим {![]() }2
{
}2
{![]() }2
={
}2
={![]() ,
, ![]() ,
, ![]() ,
, ![]() }. Но это не подгруппа группы C3
V
. Следовательно, согласно теореме должно выполняться неравенство {
}. Но это не подгруппа группы C3
V
. Следовательно, согласно теореме должно выполняться неравенство {![]() }2
{
}2
{![]() }2
¹{
}2
¹{![]() }2
{
}2
{![]() }2
. Действительно, перемножая, получим
}2
. Действительно, перемножая, получим
{![]() }2
{
}2
{![]() }2
={
}2
={![]() ,
, ![]() ,
, ![]() ,
, ![]() }.
}.
Определение 2. Группа G называется прямым произведением подгруппы А и В, если элементы подгрупп А и В перестановочны: ab=ba, "aÎA, "bÎB и каждый элемент gÎАВ однозначно представляется в виде произведения g=ab. Обозначается прямое произведение подгруппы как G=A´B.
Определение 3. Подгруппа Н группы G называется циклической, порожденной элементом h, если все ее элементы являются степенями элемента h. Если же сама группа G совпадает со своей циклической подгруппой, то она называется циклической группой.
Элементом симметрии называется вспомогательный геометрический образ, характеризующий циклическую группу преобразования симметрии.
Теорема 2. Каждая конечная абелева группа G является прямым произведением конечных циклических групп, порядки которых являются степенями простых чисел.
Определение 4. Множество элементов a, b, c… группы G называется системой образующих групп G, если каждый элемент группы может быть представлен в виде произведения степеней элементов указанного множества
ak bl cm …=g.
Например, для циклической группы {![]() }3
образующим элементом или генератором группы является элемент
}3
образующим элементом или генератором группы является элемент ![]() . У группы C3
V
два образующих элемента:
. У группы C3
V
два образующих элемента: ![]() и
и ![]() , в чем можно убедиться, рассматривая факторизацию C3
V
={
, в чем можно убедиться, рассматривая факторизацию C3
V
={![]() }3
´{
}3
´{![]() }2
.
}2
.
Определение 5. Соотношения вида
ap bq cr …=e,
связывающие образующие элементы группы G, называются ее определяющими соотношениями.
Совокупность всех образующих элементов и определяющих соотношений, полностью описывающих группу, называется генетическим кодом группы.
Например, группа {![]() }3
задается одним образующим элементом
}3
задается одним образующим элементом ![]() и одним определяющим соотношением
и одним определяющим соотношением ![]() =
=![]() . Группа C3
V
задается двумя образующими
. Группа C3
V
задается двумя образующими ![]() и
и ![]() и определяющими соотношениями между ними вида
и определяющими соотношениями между ними вида
![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]()
![]()
![]() =
=![]() (9)
(9)
Последнее соотношение после умножения его на ![]() можно записать в стандартном виде
можно записать в стандартном виде ![]()
![]()
![]()
![]() =
=![]() . Именно способом задания группы объясняется обозначение группы C3
V
, так как операции симметрии
. Именно способом задания группы объясняется обозначение группы C3
V
, так как операции симметрии ![]() и
и ![]() при определенных соотношениях между ними определяют группу C3
V
. Чтобы получить таблицу Кэли группы C3
V
, надо было пользоваться геометрической моделью молекулы NH3
. Зная же систему (9) определяющих соотношений, можно, например, найти, чему равно
при определенных соотношениях между ними определяют группу C3
V
. Чтобы получить таблицу Кэли группы C3
V
, надо было пользоваться геометрической моделью молекулы NH3
. Зная же систему (9) определяющих соотношений, можно, например, найти, чему равно ![]()
![]() , если известно произведение
, если известно произведение ![]()
![]() . В самом деле, так как
. В самом деле, так как ![]()
![]()
![]() =
=![]() , то умножая справа на
, то умножая справа на ![]() , имеем
, имеем ![]()
![]() =
=![]()
![]() . Факторизация группы также значительно облегчается при задании группы с помощью генетического кода. Например, в полупрямом произведении C3
V
={
. Факторизация группы также значительно облегчается при задании группы с помощью генетического кода. Например, в полупрямом произведении C3
V
={![]() }3
´{
}3
´{![]() }2
соотношение
}2
соотношение ![]()
![]()
![]() =
=![]() задает автоморфизм группы {
задает автоморфизм группы {![]() }3
, так как
}3
, так как ![]() является ее образующим элементом. Поэтому, пользуясь тем, что автоморфизм переводит произведение элементов в произведение их образов, получаем уже автоматически
является ее образующим элементом. Поэтому, пользуясь тем, что автоморфизм переводит произведение элементов в произведение их образов, получаем уже автоматически
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]()
![]() =
=![]()
![]() =
=![]()
![]() =
=![]()
![]() =
=![]() .
.
Знание автоморфизма нормального делителя и элементов групп H и F определяет полупрямое произведение, т. е. факторизацию группы.
Глава 2 Введение в теорию представлений групп симметрии молекул
2.1 Векторные (линейные) пространства
1. Модуль и векторное пространство
Определение 1. Кольцом называется множество K, в котором определены операции сложения и умножения и выполняются аксиомы:
1. Относительно сложения кольцо является абелевой группой, т. е. в аддитивной записи операций имеют место условия (для всех a, b, cÎK):
a+b=b+a – коммутативность (абелевость) сложения;
(a+b)+c=a+(b+c) – ассоциативность сложения;
a+0=0+a=a – существование нулевого элемента;
a+(-a)=(-a)+a=0 – существование противоположного элемента.
2. Умножение связано со сложением аксиомами дистрибутивности:
(a+b)c=ac+bc; c(a+b)=ca+cb.
3. Умножение ассоциативно:
(ab)c=a(bc).
Определение 2.
Полем называем коммутативное по умножению кольцо, в котором каждый ненулевой элемент а имеет обратный элемент, т. е. такой элемент a-1
, что ![]() , где е – единица кольца.
, где е – единица кольца.
Определение 3. Левым модулем над кольцом K называется абелева группа по сложению М, для которой определены произведения kmÎM для всех kÎK и mÎM, причем выполняются аксиомы:
1) k(m1 +m2 )=km1 +km2 ;
2) (k1 +k2 )m=k1 m+k2 m;
3) (k1 k2 )m=k1 (k2 m)
для любых m, m1 , m2 ÎM и k, k1 , k2 ÎK.
Если в кольце K есть единицы (что мы предполагаем), то выполняется еще аксиома
4) em=m
для любого mÎM.
Аналогично определяются правые модули, в которых произведение записывается в виде mk. Модуль одновременно левый и правый называется двусторонним модулем, будем называть его просто «модулем».
Определение 4. Модуль над полем P называется векторным, или линейным пространством над полем Р.
Определение 5. Подмножество M1 левого модуля М над кольцом K называется подмодулем модуля М, если (m1 +m2 )ÎM1 для всех m1 , m2 ÎM1 и kmÎM1 для всех kÎK и mÎM1 .
Определение 6. Подмодуль векторного пространства называется подпространством векторного пространства.
2. База (базис) и размерность векторного пространства
Пусть М – левый модуль над кольцом K. Выражение вида k1 v1 +k2 v2 +…+kn vn , где ki ÎK, vi ÎM, называется линейной комбинацией векторов v1 , v2 , …, vn . Если все ki =0, то линейная комбинация называется тривиальной. Если вектор v является линейной комбинацией векторов v1 , v2 , …, vn , то говорят, что он выражается через систему S=<v1 , v2 , …, vn >.
Определение 7. Конечная система векторов v1 , v2 , …, vn векторного пространства называется линейно зависимой, если существует нетривиальная линейная комбинация этих векторов равная нулю. Система, не являющаяся линейно зависимой, называется линейно независимой.
Бесконечная система векторов векторного пространства называется линейно независимой, если любая ее конечная подсистема линейно независима.
Определение 8. Векторное пространство V называется конечномерным, имеющим разность n, если в нем найдется n линейно независимых векторов, а любые n+1 векторов линейно зависимы. Если в векторном пространстве можно указать систему из n линейно независимых векторов для любого конечного числа n, то это пространство называется бесконечномерным.
Размерность пространства обозначается в виде dimV.
Определение 9. Базисом или базой, в n-мерном векторном пространстве V называется любая ее система из n линейно независимых векторов.
Если e1 , e2 , …, en – база пространства V и v=x1 e1 +x2 e2 +…+xn en , то числа x1 , x2 , …, xn определяются однозначно и называются координатами вектора v в базе e1 , e2 , …, en . Вектор v в этом случае можно записать в виде v=( x1 , x2 , …, xn ).
2.2 Эвклидовы и унитарные пространства
1. Билинейные и квадратичные формы
Определение 1. Линейной функцией, или линейной формой, в векторном пространстве V над полем вещественных (комплексных) чисел Р называется отображение f векторного пространства V в поле Р, ставящее в соответствие каждому вектору вещественное (комплексное) число, если это отображение удовлетворяет следующим условиям:
1) f(x+y)=f(x)+f(y);
2) f(ax)=af(x),
где x, y- произвольные векторы из пространства V, а aÎP.
Если dimV=n, e1 , e2 , …, en – базис пространства V и x= x1 e1 +x2 e2 +…+xn en – произвольный вектор из этого пространства, то
f(x)=f(x1 e1 +x2 e2 +…+xn en )= x1 f(e1 )+x2 f(e2 )+…+xn f(en ) или
f(x)= a1 x1 +a2 x2 +…+an xn , где ai =f(ei ), i=1, 2, …, n.
Таким образом, при фиксированном базисе линейная функция представляется линейной формой (формой называется однородный многочлен).
Определение 2. Полулинейной формой или линейной функцией второго рода называется функция f, удовлетворяющая следующим условиям:
1) f(x+y)=f(x)+f(y)
2) ![]()
где ![]() - число, комплексно-сопряженное с l.
- число, комплексно-сопряженное с l.
Определение 3. Функция A(x, y) векторов x и y векторного пространства V над полем вещественных чисел называется билинейной функцией или билинейной формой, если при фиксированном x она является линейной функцией от y, а при фиксированном y – линейной функцией от x.
По аналогии с линейной функцией можно показать, что билинейная функция представляется билинейной формой, т. е. выражением вида
 , где aik
=A(ei
, ek
).
, где aik
=A(ei
, ek
).
Поэтому билинейную функцию часто тоже называют билинейной формой.
Если A(x, y)=A(y, x) при любых x и y, билинейная форма A(x, y) называется симметрической.
Определение 4. Функция A(x, x), которая получена из симметрической билинейной формы, если наложить y=x, называется квадратичной формой.
Определение 5. Функция A(x, y) называется полуторалинейной формой векторов x и y комплексного пространства или билинейной формой в комплексном векторном пространстве, если при фиксированном y форма A(x, y) есть линейная форма от x, а при фиксированном x форма A(x, y) есть полученная форма от y.
В комплексном векторном пространстве полуторалинейную функцию можно представить в виде билинейной формы  , где aik
=A(ei
, ek
).
, где aik
=A(ei
, ek
).
Определение 6.
Билинейная форма в комплексном пространстве называется эрмитово-симметрической или эрмитовой, если A(x, y)=![]() для всех векторов x и y из этого пространства.
для всех векторов x и y из этого пространства.
Определение 7.
Эрмитовой квадратичной формой называется функция, полученная из эрмитово-симметрической формы A(x, y), если положить в ней y=x. Так как A(x, x)=![]() , то эрмитова квадратичная форма принимает только вещественные значения.
, то эрмитова квадратичная форма принимает только вещественные значения.
Определение 8.
Квадратичной формой на пространстве V (вещественном или комплексном) называется такое отображение ![]() (Р – поле вещественных или комплексных чисел), для которого существует билинейная (полуторалинейная в случае Р=С) форма В(x, y) со свойством A(x)=B(x, x) для любого вектора xÎV.
(Р – поле вещественных или комплексных чисел), для которого существует билинейная (полуторалинейная в случае Р=С) форма В(x, y) со свойством A(x)=B(x, x) для любого вектора xÎV.
2. Эвклидовы и унитарные пространства
Определение 9. Симметрическая билинейная форма A(x, y) на вещественном пространстве (эрмитово-симметрическая форма на комплексном пространстве) называется положительно определенной, если A(x, x)>0 для любого, отличного от нуля вектора x из рассматриваемого пространства.
Определение 9 ¢. Квадратичная форма (эрмитова квадратичная форма) называется положительно определенной, если для любого вектора x¹0 она принимает положительное значение.
Определение 10. n-мерным эвклидовым (унитарным) пространством называется n-мерное вещественное (комплексное) векторное пространство с положительно определенным симметрическим (эрмитовым) скалярным произведением.
Все вводимые далее понятия пригодны как для эвклидовых, так и для унитарных пространств.
Определение 11. База e1 , e2 , …, en эвклидова (унитарного) пространства называется ортогональной, если (ei , ej )=0, i¹j, i, j=1, 2, …, n, и ортонормированной, если она ортогональна и длина всех векторов равны единице.
3. Изометрия эвклидовых и унитарных пространств
Определение 12. Взаимно однозначное отображение f модуля М на модуль М¢ над одним и тем же кольцом K называется изоморфизмом, если выполняются следующие условия:
1. f(x, y)=f(x)+f(y)=x¢+y¢; x¢=f(x); y¢=f(y);
"x, yÎM;
2. f(ax)=af(x)=ax¢; "xÎK; "xÎM; x¢=f(x)ÎM¢.
Определение 13. Два векторных пространства W и W¢ над полем Р называются изоморфными, если они изморфны как модули над кольцом, которым является поле Р.
Пусть теперь даны два векторных пространства W и W¢ со скалярными произведениями A(x, y) и A¢(x¢, y¢) над полем Р.
Определение 14. Изометрией векторных пространств W и W¢ называется любой их изморфизм, который сохраняет значения всех скалярных произведений, т. е.
A(x, y)= A¢(f(x), f(y))= A¢(x¢, y¢); "x, yÎW;
f(x)=x¢; f(y)=y¢.
В эвклидовом пространстве из определения длины вектора и угла между двумя векторами следует, что при изометрии сохраняются длины векторов и углы между ними, т. е. сохраняются метрические соотношения, чем и объясняется название «изометрия». В унитарном пространстве при изометрии сохраняются длины векторов, ортогональные векторы переходят в ортогональные векторы.
2.3 Матрицы
1. Линейные отображения, операторы и матрицы
Определение 1. Отображение f: V®W векторного пространства Vв векторное пространство W над полем Р называется линейное отображение, если для всех v, v1 , v2 ÎV, aÎP выполняются условия:
1) f(v1 +v2 )=f(v1 )+f(v2 );
2) f(av)=af(v).
Если V=W, то линейное отображение называется линейным оператором или линейным преобразованием пространства V.
Пусть e1 , e2 , …, en – базис пространства V, а e1 ¢, e2 ¢, …, en ¢ - базис пространства W. Образы базисных векторов пространства V в базисе пространства W можно записать в виде
 (i=1, 2, …, m) (1)
(i=1, 2, …, m) (1)
Коэффициенты в выражении (1) запишем в виде матрицы, которая называется матрицей линейного отображения f.
 .
.
В случае линейных операторов, т. е. линейных отображений векторного пространства в себя, операторы удобно обозначать ![]() , а матрицу оператора
, а матрицу оператора ![]() в фиксированном базисе – в виде А.
в фиксированном базисе – в виде А.
2. Унитарные, ортогональные, эрмитовы операторы и матрицы
Определение 2. Линейные операторы эвклидова (унитарного) пространства, которые сохраняют скалярное произведение векторов этого пространства, называется ортогональными (унитарными) операторами.
Пусть e1
, e2
, …, en
– ортонормированная база унитарного (эвклидова) пространства. Если ![]() - унитарный (ортогональный) оператор, то согласно его определению
- унитарный (ортогональный) оператор, то согласно его определению
(ei
, ej
)= (![]() ei
,
ei
, ![]() ei
)=1, i=1, 2, …, n;
ei
)=1, i=1, 2, …, n;
(ei
, ej
)= (![]() ei
,
ei
, ![]() ej
)=0, i¹y. (2)
ej
)=0, i¹y. (2)
Это означает, что система векторов ![]() e1
,
e1
, ![]() e2
, …,
e2
, …, ![]() en
сама составляет ортонормированную базу в соответствующем пространстве.
en
сама составляет ортонормированную базу в соответствующем пространстве.
Пусть А – матрица унитарного (ортогонального) оператора. Тогда можно записать  . Из выражения (2) следует, что в матрице А скалярные произведения векторов-столбцов на себя равны единице, а скалярное произведение различных векторов-стобцов равно нулю. Такая матрица называется унитарной (ортогональной). Унитарность (ортогональность) матрицы А означает, что сумма произведений элементов, стоящих в любом столбце этой матрицы, на сопряженные (на те же самые) к ним элементы равны единице, а сумма произведений элементов любого столбца на сопряженные к ним (на соответственные к ним) элементы другого столбца равна нулю.
. Из выражения (2) следует, что в матрице А скалярные произведения векторов-столбцов на себя равны единице, а скалярное произведение различных векторов-стобцов равно нулю. Такая матрица называется унитарной (ортогональной). Унитарность (ортогональность) матрицы А означает, что сумма произведений элементов, стоящих в любом столбце этой матрицы, на сопряженные (на те же самые) к ним элементы равны единице, а сумма произведений элементов любого столбца на сопряженные к ним (на соответственные к ним) элементы другого столбца равна нулю.
Определение 3.
Матрица А*
называется эрмитово сопряженной (или просто сопряженной) по отношению к матрице А, если А*
=![]() , т. е. для того, чтобы из матрицы А получить эрмитово сопряженную матрицу, ее надо транспонировать и заменить элементы транспонированной матрицы комплексно-сопряженными элементами.
, т. е. для того, чтобы из матрицы А получить эрмитово сопряженную матрицу, ее надо транспонировать и заменить элементы транспонированной матрицы комплексно-сопряженными элементами.
Определение 4. Матрица А называется самосопряженной или эрмитовой матрицей, если A=A* ; в том же случае, если элементы матрицы вещественны, A* =At =A и матрица А называется симметрической матрицей.
Определение 5. Матрица А называется унитарной (ортогональной) матрицей, если A* =A-1 (если At =A-1 ). Операторы, соответствующие эрмитовым матрицам, будем называть эрмитовыми.
2.4 Представления групп
1. Определение представлений
Определение 1. Представлением группы, действующим в n-мерном векторном пространстве V, называется гомоморфизм этой группы в группу невырожденных линейных операторов пространства V.
Невырожденным называется такой оператор ![]() , который имеет обратный оператор
, который имеет обратный оператор ![]() , дающий по определению в произведении с
, дающий по определению в произведении с ![]() единичный оператор
единичный оператор ![]() :
: ![]()
![]() =
=![]()
![]() =
=![]() .
.
Определение 2. Матричным представлением группы G называется гомоморфизм этой группы в группу невырожденных комплексных или действительных матриц размера n´n.
Определение 3. Подстановочным представлением группы G называется гомоморфизм этой группы в группу подстановок порядка n. Если гомоморфизм группы G в группу операторов, матриц или подстановок является изморфизмом, то он называется точным представлением.
Представление группы будем обозначать буквой Т. Пусть g1 и g2 – любые элементы группы G, а Т(g1 ) и Т(g2 ) – соответствующие этим элементам матрицы представления. Тогда согласно определению гомоморфизма группы
Т(g1 , g2 )= Т(g1 ) Т(g2 ). (4)
Определение 4. Два матричных представления Т1 и Т2 группы G в некоторую группу матриц называется эквивалентным, если существует невырожденная матрица F такая, что для всех матриц Т1 (g), Т2 (g) представления будет иметь место равенство
Т2 (g)=Ф-1 Т1 (g)Ф, "gÎG(5)
Эквивалентные представления не различаются.
2. Приводимые и неприводимые представления
Воспользуемся языком линейных операторов. Пусть дано некоторое представление Т группы G, действующее в векторном пространстве V. Каждому вектору vÎV оператор ![]() (g)º
(g)º![]() сопоставляет вектор
сопоставляет вектор ![]() (v)=v1
этого же пространства. Пусть W – подпространство пространства V.
(v)=v1
этого же пространства. Пусть W – подпространство пространства V.
Определение 5.
Подпространство W пространства V называется инвариантным подпространством действия ![]() , если, каковы бы ни были элементы gÎG и векторы wÎW, T(w)=w1
, где w1
ÎW.
, если, каковы бы ни были элементы gÎG и векторы wÎW, T(w)=w1
, где w1
ÎW.
Определение 6. Представление T группы G, действующее в векторном пространстве V над полем Р, называется приводимым представлением, если в этом пространстве существуют неприводимые инвариантные относительно этого действия подпространства. Представление Т называется неприводимым, если единственные его инвариантные подпространства – О и само пространство V.
Интерпретируем это определение на языке матриц. Пусть представление Т группы G приводимо. Значит, в пространстве V представления может быть найдено нетривиальное инвариантное подпространство W. Пусть e1
, e2
, …, ek
– базис пространства W. Дополним его до базиса е1
, е2
, …, еk
, ek
+1
, …, en
всего пространства V. Так как W инвариантно, то ![]() (еi
), где i=1, 2, …, k лежат в W. Поэтому
(еi
), где i=1, 2, …, k лежат в W. Поэтому
![]() (еi
)=a1i
e1
+a2i
e2
+…+aki
ek
, i=1, 2, …, k.
(еi
)=a1i
e1
+a2i
e2
+…+aki
ek
, i=1, 2, …, k.
Но так как эти векторы лежат и в пространстве V, то можно также написать
![]() (еi
)=a1i
e1
+a2i
e2
+…+aki
ek
+0ek+1
+…+0en
, i=1, 2, …, k.
(еi
)=a1i
e1
+a2i
e2
+…+aki
ek
+0ek+1
+…+0en
, i=1, 2, …, k.
Что же касается отдельных базисных векторов ek +1 , ek +2 , …, en , то, поскольку они не принадлежат W, их образы выражаются через базис наиболее общим способом и получаем следующую картину:
![]() (е1
)=a11
e1
+a21
e2
+…+ak1
ek
+0ek+1
+…+0en
(е1
)=a11
e1
+a21
e2
+…+ak1
ek
+0ek+1
+…+0en
![]() (е2
)=a12
e1
+a22
e2
+…+ak2
ek
+0ek+1
+…+0en
(е2
)=a12
e1
+a22
e2
+…+ak2
ek
+0ek+1
+…+0en
![]() (еk
)=a1k
e1
+a2k
e2
+…+akk
ek
+0ek+1
+…+0en
(еk
)=a1k
e1
+a2k
e2
+…+akk
ek
+0ek+1
+…+0en
![]() (еk+1
)=a1,k+1
e1
+a2,k+1
e2
+…+ak,k+1
ek
+ ak+1,k+1
ek+1
+…+an,k+1
en
(еk+1
)=a1,k+1
e1
+a2,k+1
e2
+…+ak,k+1
ek
+ ak+1,k+1
ek+1
+…+an,k+1
en
![]() (еn
)=a1n
e1
+a2n
e2
+…+akn
ek
+ ak+1,n
ek+1
+…+ann
en
.
(еn
)=a1n
e1
+a2n
e2
+…+akn
ek
+ ak+1,n
ek+1
+…+ann
en
.
Отсюда видно, что матрицы всех элементов группы G в предствлении Т будут одновременно иметь следующий вид:
 (6)
(6)
Поэтому на языке матриц матричное представление называется приводимым, если все матрицы его могут быть записаны при определенном выборе базиса в виде (6). Если же ни при каком выборе базиса матрицы представления нельзя записать в указанном виде, представления называются неприводимыми.
3. Представления групп и модули
Рассмотрим конструкцию, позволяющую, зная представления групп, построить модуль М над кольцом K, связанный с этим представлением. Пусть теория представлений групп сформулирована на языке матриц и линейных операторов. Все матрицы данного порядка (линейные операторы в n-мерном пространстве) образуют относительно операций сложения и умножения матриц (линейных операторов) кольцо. Матрицы (линейные операторы) образуют алгебру в смысле следующего определения.
Определение 7. Алгеброй А над полем Р называется множество, в котором введены операции сложения и умножения элементов, а также операция умножения lаÎА, lÎР, аÎА элементов поля Р на элементы из А, причем: 1) относительно операций сложения и умножения А является кольцом; 2) относительно операций сложения и умножения на элементы поля Р алгебра является векторным пространством; 3) операции умножения элементов кольца и умножения на элементы из поля связаны аксиомой
l(ab)=(la)b=a(lb); lÎP; a, bÎA (7)
Матрицы, которые сопоставляются элементами группы в представлении Т, составляют лишь часть из множества всех матриц Мn , что следует хотя бы из того, что они невырождены. Однако, если Т(g1 ), Т(g2 ), …, T(gs ), s=|G| - все матрицы представления группы G, то с ними можем связать алгебру, состоящую из всевозможных линейных комбинаций этих матриц вида
K=a1 Т(g1 )+a2 Т(g2 )+..+as T(gs ); ai ÎR или С (8)
Пусть Р – поле комплексных или вещественных чисел. Рассмотрим формальные суммы вида
a=a1 g1 +a2 g2 +…+an gn ; ai ÎP; gi ÎG; i=1, 2, …, n; n=|G| (9)
Подчеркнем, что так как в группе G есть только одна операция – умножение, левую часть нельзя рассчитывать как результат сложения элементов правой части. Назовем две суммы  и
и  равными, если ai
=bi
. Введем операцию сложения формальных сумм по правилу:
равными, если ai
=bi
. Введем операцию сложения формальных сумм по правилу:
a+b=(a1
+b1
)g1
+(a2
+b2
)g2
+…+(an
+bn
)gn
= ; gi
=ai
+bi
.
; gi
=ai
+bi
.
Видим, что на множестве формальных сумм определена операция сложения, так как в результате операции снова получилась формальная сумма вида (9). Введем далее операцию умножения формальных сумм. Получим кольцо, которое называется групповым кольцом группы G над полем Р и обозначается в виде PG. Это кольцо можно превратить в алгебру. Для этого надо определить умножение lÎP на aÎPG. Умножение задается по формуле
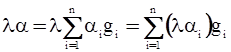 . (10)
. (10)
Относительно сложения и умножения по этой формуле PG представляет собой векторное пространство (аксиома (7)). Построенная алгебра называется групповой алгеброй группы G и обозначается, как и групповое кольцо, в виде PG.
Если сопоставить каждому элементу gi
в выражении (9) матрицу T(gi
) этого элемента в представлении Т, то получим матрицу (8), которую обозначим буквой K, так как она является элементом группового кольца матриц K. Как следует из определения модуля, главное при построении модуля – ввести умножение векторов на элементы группового кольца. Пусть V – пространство представления Т группы G. Произвольный вектор v этого пространства зададим координатами. Если А – матрица линейного оператора ![]() , действующего в векторном пространстве, то можно получить вектор v1
, в который переходит вектор v под действием оператора
, действующего в векторном пространстве, то можно получить вектор v1
, в который переходит вектор v под действием оператора ![]() . Для этого надо просто умножить по правилу умножения матриц вектор v на матрицу А. Аналогично выполняется умножение вектора v на элемент a группового кольца (и алгебры) PG:
. Для этого надо просто умножить по правилу умножения матриц вектор v на матрицу А. Аналогично выполняется умножение вектора v на элемент a группового кольца (и алгебры) PG:
va=vk=v1 , aÎPG, v1 ÎV, kÎK. (11)
Теперь, используя правило умножения (11) легко проверить условия определения модуля. Полученный модуль М называется модулем представления Т.
Если известен модуль М над групповой алгеброй PG, то можно получить представление, связанное с этим модулем. Так как группе G принадлежит единица I, то каждый элемент pÎP можно записать в виде p=pI. Отсюда следует, что модуль М является векторным пространством над полем Р. Поэтому каждому элементу aÎPG можно сопоставить оператор ![]() (a), действующий в векторном пространстве М по правилу
(a), действующий в векторном пространстве М по правилу
![]() (a)(m)=ma(12)
(a)(m)=ma(12)
В частности, любому элементу gÎG можно сопоставить оператор ![]() (g), действующий по правилу
(g), действующий по правилу ![]() (g)(m)=mg. Сопоставляя всем элементам группы G операторы (12), и получим представление Т, связанное с модулем М.
(g)(m)=mg. Сопоставляя всем элементам группы G операторы (12), и получим представление Т, связанное с модулем М.
Учитывая отмеченное соответствие между модулями и представлениями, можно перевести на язык модулей основную терминологию теории представлений. Так, подмодулю М1 модуля М соответствует представление Т1 , которое называется подпредставлением представления Т. Тривиальные подмодули модуля М – это сам модуль М и нулевой модмодуль О. Если все подмодули модуля М тривиальны, он называется неприводимым модулем, а соответствующее ему представление – неприводимым представлением. Если же модуль М имеет нетривиальный модмодуль, он называется приводимым модулем, ему соответствует приводимое представление.
4. Представление алгебр и модули
Обозначим через Endp V алгебру линейных операторов векторного пространства V над полем Р и пусть А – произвольная алгебра.
Определение 8.
Представлением алгебры А называется сопоставление каждому элементу aÎA линейного оператора ![]() ÎEndp
V, причем должны выполняться следующие условия:
ÎEndp
V, причем должны выполняться следующие условия:
1) 1®![]() , где
, где ![]() - единичный оператор;
- единичный оператор;
2) pa®p![]() ; pÎP; aÎA;
; pÎP; aÎA;
3) a+b®![]() +
+![]() ; a, bÎA;
; a, bÎA; ![]() ,
, ![]() Î Endp
V;
Î Endp
V;
4) ab®![]()
![]() ; a, bÎA.
; a, bÎA.
Определение 8 является иной формулировкой определения модуля над кольцом А, если кольцо является алгеброй над полем Р.
Определение 9. Модулем над алгеброй А называется абелева группа по сложению М, для которой определена операция умножения элементов из А на элементы из М: amÎM, aÎA, mÎM и при этом выполняются следующие условия:
1) (a+a¢)m=am+a¢m;
2) (aa¢)m=a(a¢m);
3) em=m;
4) a(m+m¢)=am+am¢;
5) (aa)m=a(am)=a(am), aÎP.
Здесь дано определение левого модуля.
Теорема 1. Всякий левый (правый) модуль М над кольцом А, которым является алгебра, представляет собой также векторное пространство над полем Р, причем для всех aÎA, mÎM, lÎP справедливы равенства
l(ma)=(lm)a=m(la); l(am)=a(lm)=(la)m.
2.5 Характеры представлений
1. Определение и свойства характеров
Определение 1. След матрицы А=(аij ) размера n´n есть сумма ее элементов, стоящих по главной диагонали:
TrA=a11 +a22 +…+ann (14)
Определение 2. След матрицы Т(g), представляющий элемент g в матричном представлении Т группы G, называется характеристикой элемента g в представлении Т и обозначается cT (g).
Определение 3. Совокупность характеристик всех элементов g группы G, составленных для данного представления Т, называется характером представления Т и записывается как cT . Если Т – матричное представление группы G над полем вещественных или комплексных чисел Р, то характеристика каждого элемента группы является вещественным или комплексным числом и, следовательно, характер есть отображение cT группы G в поле Р, определяемое следующим образом:
cT : G®P: cT (g)=TrT(g).
Свойство 1. Характеры эквивалентных представлений совпадают.
Свойство 2. Характер представления Т группы G постоянен на каждом классе сопряженных элементов: cT (g-1 hg)= cT (h), g, hÎG.
Определение 4.
Вектор x¹0 из векторного пространства V над числовым полем Р называется собственным вектором линейного оператора ![]() , действующего в этом пространстве, если он удовлетворяет соотношению
, действующего в этом пространстве, если он удовлетворяет соотношению ![]() x=lx, где l - число, которое называется собственным значением (характеристическим числом) линейного оператора.
x=lx, где l - число, которое называется собственным значением (характеристическим числом) линейного оператора.
Условие того, что вектор х – собственный вектор записывается в виде матричного уравнения
(А - lI)х = 0, (15)
где х – вектор-столбец с неизвестными координатами x1 , x2 , …, xn . Условием существования ненулевого решения системы (15) является равенство нулю его определителя:
|A - lI| = 0. (16)
Это уравнение степени n относительно l называется характеристическим или вековым уравнением матрицы А линейного оператора, а его корни называются собственными значениями матрицы А, они являются собственными значениями оператора ![]() .
.
Свойство 3.
Если l1
, l2
, …, ln
– собственные значения линейного оператора ![]() , то cT
(g)=Tr
T(g)= l1
+l2
+ …+ln
.
, то cT
(g)=Tr
T(g)= l1
+l2
+ …+ln
.
Так как здесь рассматриваем конечные группы, то имеет место следующее свойство.
Свойство 4. Если Т – представление группы G над полем Р, то для каждого элемента gÎG значение cT (g) равно сумме корней из единицы степени, равной порядку элемента g.
Свойство 5. Если Т – представление группы G, то для каждого gÎG справедливо равенство cT (g-1 )= cT (g).
Свойство 6.
Если ![]() и
и ![]() - характеры неприводимых представлений группы G, то
- характеры неприводимых представлений группы G, то
 (17)
(17)
Равенство (17) называется соотношением ортогональности, для характеров, неприводимых представлений группы G.
Свойство 7. (второе соотношение ортогональности) Пусть T1 , T2 , …, Tm – все неэквивалентные представления группы G, K(a), K(b) – классы элементов группы G, сопряженных соответственно с a и b. Тогда
 (18)
(18)
где |G| - число элементов в группе G; |K(b)| - число элементов в классе сопряженных элементов K(b); ![]() - характеры неприводимых представлений Ti
, i=1, 2, …, m.
- характеры неприводимых представлений Ti
, i=1, 2, …, m.
2. Таблицы характеров неприводимых представлений
Приведенные свойства характеров позволяют описать построение таблиц характеров неприводимых представлений. Строки таблицы будем нумеровать, как принято в теории представлений групп характерами, но одновременно будем указывать обозначения, принятые в молекулярной спектроскопии и кристаллографии: одномерные представления обозначаются A1 , B1 , A2 , B2 , …, двумерные – E1 , E2 , … и, наконец, трехмерные – F1 , F2 , … .
Так как по свойству 2 характеры постоянны на каждом классе сопряженных элементов, то столбцы таблицы нумеруются классами сопряженных элементов. Под обозначением класса сопряженных элементов указывается число элементов в классе – порядок класса. Рассмотрим в качестве примера группу C3
V
. Классы сопряженных элементов группы C3
V
имеют вид K1
={I}, K2
={C3
, C3
2
}, K3
={![]() ,
, ![]() ,
, ![]() }. Известно, что группа C3
V
имеет три неприводимых представления, характеры которых приведены в табл. 2.
}. Известно, что группа C3
V
имеет три неприводимых представления, характеры которых приведены в табл. 2.
Таблица 2.
| Классы | K1 ={I} | K2 ={C3 , C3 2 } | K3
={ |
| Порядок класса | 1 | 2 | 3 |
A1 A2 E |
1 1 2 |
1 1 -1 |
1 -1 0 |
3. Разложение характеров по неприводимым представлениям
В соответствии с рассмотренными свойствами характер приводимого представления cT
можно представить в виде разложения по характерам неприводимых представлений ![]() :
:
![]() ,
,
где ni – число, показывающее, сколько раз характер неприводимого представления Ti содержится в характере приводимого представления Т. На основании свойств ортогональности это число легко определяется, а именно:
 . (19)
. (19)
Формула (19) имеет важные применения в теории молекулярных спектров для определения числа состояний данного типа симметрии.
4. Определение характеров неприводимых представлений при применении групповых алгебр групп
Для достаточно широкого класса групп желательно иметь общий метод нахождения характеров неприводимых представлений.
Пусть дана группа G. Найдем классы сопряженных элементов Ki
группы и обозначим ![]() сумму элементов группы, принадлежащих классу Ki
. Здесь Сi
являются элементами групповой алгебры PG группы G над полем Р. Проверим, перестановочны ли элементы Сi
со всеми элементами алгебры PG. Для этого достаточно проверить, что для всех gÎG справедливы равенства gСi
=Сi
gили Сi
=g-1
Сi
g.
сумму элементов группы, принадлежащих классу Ki
. Здесь Сi
являются элементами групповой алгебры PG группы G над полем Р. Проверим, перестановочны ли элементы Сi
со всеми элементами алгебры PG. Для этого достаточно проверить, что для всех gÎG справедливы равенства gСi
=Сi
gили Сi
=g-1
Сi
g.
Действительно,
g-1 Сi g=g-1 (k1 +k2 +…)g=g-1 k1 g+g-1 k2 g+…
Так как в групповой алгебре выполним дистрибутивный закон, то очевидно, что правая часть содержит все элементы Сi и, следовательно, равна Сi .
Определение 5. Множество элементов алгебры, перестановочных со всеми элементами алгебры, называется центром алгебры.
Определение 6.
Подмножество В алгебры называется подалгеброй алгебры А, если оно является подпространством векторного пространства А, и из того, что b1
, b2
ÎB, следует, что ![]() .
.
Можно доказать, что элементы Ci образуют базис центра Z групповой алгебры PG:
Алгебру можно записать, задав таблицу умножения базисных элементов
 . (20)
. (20)
Элементы Cijk называются структурными константами алгебры. Для элементов Сi , образующих базис центра групповой алгебры, формула (20) принимает вид
 . (21)
. (21)
Теперь, на основании выражения (21), фиксируя индекс i (что обозначим, взяв этот индекс в скобки), получим матрицу C(i) коэффициентов Cijk
. Эту матрицу можно рассматривать как матрицу линейного оператора ![]() , действующего в векторном пространстве, которым является центр алгебры Z. Действие его на базисные элементы Cj
состоит в умножении Ci
на Cj
. Для того, чтобы записать матрицу C(i), надо рассмотреть столбец, в котором записаны произведения Ci
на Cj
. В результате получим матричное представление центра групповой алгебры. Матричное представление центра будет центром матричного представления всей алгебры. Иначе говоря, все матрицы C(i) коммутируют со всеми элементами матричного представления алгебры и между собой.
, действующего в векторном пространстве, которым является центр алгебры Z. Действие его на базисные элементы Cj
состоит в умножении Ci
на Cj
. Для того, чтобы записать матрицу C(i), надо рассмотреть столбец, в котором записаны произведения Ci
на Cj
. В результате получим матричное представление центра групповой алгебры. Матричное представление центра будет центром матричного представления всей алгебры. Иначе говоря, все матрицы C(i) коммутируют со всеми элементами матричного представления алгебры и между собой.
Мы приходим к задаче, аналогичной известной квантово-механической задаче: дана система коммутирующих между собой операторов, найти собственные значения и собственные векторы этих операторов. Оказывается, решение такой задачи имеет важное значение и для нахождения характеров неприводимых представлений.
Полученные выше матрицы Ci являются образующими элементами алгебры матриц, изоморфной алгебре Бозуа–Меснера, которая определяется следующим образом.
Назовем i-ой матрицей смежности Ai матрицу порядка, равного порядку группы G, строки и столбцы которой занумерованы элементами группы G, причем элементы матрицы Ai с номером (g, h), g, hÎG определяются как

Матрицы Ai состоят из нулей и единиц, поэтому их называют (0, 1) – матрицами.
Определение 7. Алгеброй Боуза – Меснера называется подалгебра алгебры матриц Mn (C), порожденная (0, 1) – матрицами Ai , i=1, 2, …, d, удовлетворяющими следующим условиям:
1) A1 =E, где Е – единичная матрица;
2) A1 +A2 +…+Ad =J, где J – матрица, все элементы которой равны единице;
3) ![]() , i¢Î[1, 2, …, d], где
, i¢Î[1, 2, …, d], где ![]() - матрица, транспонированная с матрицей Ai
;
- матрица, транспонированная с матрицей Ai
;
4)  ;
;
5) ![]() .
.
Если построить матрицы смежности для группы G по указанному выше правилу, то они образуют базис алгебры Боуза–Меснера в соответствии с определением 7.
Если А – алгебра Боуза–Меснера, то из коэффициентов в соотношении  можно образовать матрицы
можно образовать матрицы ![]() порядка d. Рассмотрим алгебру В, порожденную матрицами C1
, C2
, …, Cd
, являющуюся подалгеброй алгебры d´d матриц Md
(C). Эта алгебра изоморфна алгебре А Боуза–Меснера. В силу того, что в алгебре изоморфные объекты не различаются, будем называть ее также алгеброй Боуза–Меснера.
порядка d. Рассмотрим алгебру В, порожденную матрицами C1
, C2
, …, Cd
, являющуюся подалгеброй алгебры d´d матриц Md
(C). Эта алгебра изоморфна алгебре А Боуза–Меснера. В силу того, что в алгебре изоморфные объекты не различаются, будем называть ее также алгеброй Боуза–Меснера.
Если рассматривать А как векторное пространство, то в А имеется естественный базис, состоящий из матриц Ai
, которые по условию 5 определения 7 попарно коммутируют. Кроме того, эти матрицы нормальны (т. е. ![]() , где
, где ![]() - комплексно-сопряженная и транспонированная с А матрица). Все матрицы Ai
можно одновременно диагонализировать с помощью унитарной матрицы S. Столбцы являются общими собственными векторами матриц Ai
, образующими базис общих собственных подпространств, а ее диагональные элементы являются собственными значениями матриц Ai
, соответствующими общим собственным векторам. Если
- комплексно-сопряженная и транспонированная с А матрица). Все матрицы Ai
можно одновременно диагонализировать с помощью унитарной матрицы S. Столбцы являются общими собственными векторами матриц Ai
, образующими базис общих собственных подпространств, а ее диагональные элементы являются собственными значениями матриц Ai
, соответствующими общим собственным векторам. Если
![]() , (22)
, (22)
где diag – диагональная матрица, вне главной диагонали которой стоят нули, то pi (1), pi (2), …, pi (d) – указанные собственные значения. Тогда можно записать
 k, i=1, 2, …, d,
k, i=1, 2, …, d,
где E1 +E2 +…+Ed =E, Ei 2 =Ei , Ei Ej =Ej Ei =0, i¹j.
Итак, в А появился второй базис, состоящий из идемпотентов Ei , i=1, 2, …, d, который связан с общими собственными векторами матриц Ai , из которых состоят линейно независимые столбцы матриц S.
Определение 8. Квадратная матрица Р порядка d, (j, i)-м элементом которой является pi (j), называется первой собственной матрицей алгебры Боуза–Меснера А. Матрица Q=(gi (j)) такая, что PQ=QP=|G|E, называется второй собственной матрицей Боуза–Меснера.
Возвращаясь к задаче определения характеров неприводимых представлений, сформулируем в приспособленном для наших целей виде теорему, позволяющую обосновать приводимый ниже алгоритм нахождения неприводимых характеров.
Теорема 1. Если G – конечная группа, а Т – ее таблица характеров, А – алгебра Боуза–Меснера классов сопряженных элементов, изоморфная алгебре пересечений В, P=(pi (j)) и Q=(qi (j)) – соответственно первая и вторая собственная матрицы этих алгебр, то таблица характеров определяется как произведение матриц в виде

где k1 , k2 , …, kd – мощности классов сопряженных элементов, mi определяются по формуле mi =fi 2 , где fi – степени неприводимых представлений.
Теорема 2. Каждый столбец таблицы характеров является общим левым собственным вектором матрицы Ci , Cj , …, Cd , а каждая строка является общим правым собственным вектором этих матриц. И наоборот, каждый стандартный общий левый собственный вектор матриц Ci и, каждый стандартный общий правый собственный вектор этих матриц с точностью до расположения строк и столбцов является строкой и соответственно столбцом матрицы характеров.
Замечание. Собственный вектор матрицы называется стандартным, если его правая координата равна единице.
5. Алгоритм нахождения характеров неприводимых представлений
Алгоритм. Для нахождения характеров неприводимых представлений группы G, надо:
1. Найти классы сопряженных элементов группы G, т. е. классы K1 , K2 , …, Kd .
2. Построить групповую алгебру CG группы G над полем С и алгебру классов сопряженных элементов Ci , i=1, 2, …, d необходимо определить структурные константы Cijk алгебры классов сопряженных элементов.
3. Построить алгебру Боуза–Меснера, для чего необходимо найти матрицы Ci
=![]() .
.
4. Найти собственные числа матриц Ci и соответствующие им правые собственные векторы.
5. Найти всевозможные линейно независимые общие правые собственные векторы.
6. Построить первую и вторую собственные матрицы Р и Q алгебры Боуза–Меснера В.
7. Исходя из выражения для матрицы Q по формуле из теоремы 1 определить таблицу характеров неприводимых представлений группы G. Для этого необходимо найти числа ![]() , где f1
2
+f2
2
+…+fd
2
=|G|=m1
+m2
+…+md
. Числа m1
, m2
, …, md
можно также найти по формуле Биггса
, где f1
2
+f2
2
+…+fd
2
=|G|=m1
+m2
+…+md
. Числа m1
, m2
, …, md
можно также найти по формуле Биггса
 ,
,
где ui =(p1 (i)/k1 , p2 (i)/k2 , …, pd (i)/kd ); vi =( p1 (i), p2 (i), …, pd (i)).
Эти векторы получаются стандартизацией i-го столбца матрицы, причем 1=k1 , k2 , …, kd – числа элементов в классах сопряженных элементов группы G порядка |G|.
Примеры
1. На примере группы C3 V покажем некоторые приемы и соображения, с помощью которых можно составить таблицу характеров неприводимых представлений. Характер тождественного представления c1 (А1 ) записывается сразу.
Для составления характера c2
(А2
) воспользуемся перестановочным представлением S3
группы C3
V
. Подстановки, соответствующие элементам ![]() ,
, ![]() ,
, ![]() =1 – четные, остальные подстановки – нечетные. Так как произведение четных подстановок – четная подстановка, причем четные подстановки образуют подгруппу А3
группы S3
, то четным подстановкам сопоставим число 1, а нечетным – число –1. Произведение нечетных подстановок – четная подстановка и (-1)(-1)=1, а произведение подстановок разной четности – нечетная подстановка и (-1)1=1(-1)=-1. Следовательно, мы получили одномерное представление группы C3
V
, в котором элементам 1,
=1 – четные, остальные подстановки – нечетные. Так как произведение четных подстановок – четная подстановка, причем четные подстановки образуют подгруппу А3
группы S3
, то четным подстановкам сопоставим число 1, а нечетным – число –1. Произведение нечетных подстановок – четная подстановка и (-1)(-1)=1, а произведение подстановок разной четности – нечетная подстановка и (-1)1=1(-1)=-1. Следовательно, мы получили одномерное представление группы C3
V
, в котором элементам 1, ![]() ,
, ![]() сопоставляется 1 (эти элементы представляются четными подстановками), а остальным элементам
сопоставляется 1 (эти элементы представляются четными подстановками), а остальным элементам ![]() ,
, ![]() ,
, ![]() сопоставляется –1 (или соответствуют нечетные подстановки). Так как одномерные представления совпадают с характерами, то получаем вторую строку таблицы. Третья строка таблицы получается из следующих соображений. В теории представлений группы известно, что число неприводимых представлений группы равно числу классов сопряженных элементов. Поэтому группа C3
V
имеет три неприводимых представления. Известно также, что сумма квадратов размерностей неприводимых представлений равна порядку группы. В рассматриваемом случае 12
+12
+Z2
=6, т. е. Z=2. Следовательно, группа C3
V
имеет двумерное неприводимое представление, в котором
сопоставляется –1 (или соответствуют нечетные подстановки). Так как одномерные представления совпадают с характерами, то получаем вторую строку таблицы. Третья строка таблицы получается из следующих соображений. В теории представлений группы известно, что число неприводимых представлений группы равно числу классов сопряженных элементов. Поэтому группа C3
V
имеет три неприводимых представления. Известно также, что сумма квадратов размерностей неприводимых представлений равна порядку группы. В рассматриваемом случае 12
+12
+Z2
=6, т. е. Z=2. Следовательно, группа C3
V
имеет двумерное неприводимое представление, в котором
 , т. е. c(1)=2 (см. табл. 2).
, т. е. c(1)=2 (см. табл. 2).
Остальные элементы строки c3
получаются из соотношений ортогональности для неприводимых представлений: ![]() и
и ![]() , где x, y – неизвестные числа из строки c3
. Отсюда 2х+3y=-2, 2x-3y=-2, т. е. х=-1, y=0. Мы построили таблицу характеров неприводимых представлений, не зная двумерного неприводимого представления группы C3
V
.
, где x, y – неизвестные числа из строки c3
. Отсюда 2х+3y=-2, 2x-3y=-2, т. е. х=-1, y=0. Мы построили таблицу характеров неприводимых представлений, не зная двумерного неприводимого представления группы C3
V
.
2. Нахождение характеров неприводимых представлений группы S3 .
Проиллюстрируем алгоритм нахождения характеров на примере групп S3 .
Необходимо разложить все перестановки группы в произведении циклов. Элементы одинакового циклического строения образуют классы. Выпишем все перестановки группы S3 :
 ;
;  ;
;  ;
;  ;
;
 ;
;  .
.
При записи перестановок в циклах, если элемент i переходит в k, то k стоит не под i, а рядом с i; при этом цикле длины 1, кроме e=(1), не пишутся. Таким образом, в циклах e=(1); a=(1 2 3); a2 =(1 3 2); b=(2 3); c=(1 3); d=(1 2).
В такой записи наглядно видно циклическое строение группы. Поэтому сразу находим все три класса сопряженных элементов группы S3 :
K1 ={(1)}; K2 ={(1 2 3), (1 3 2)}; K3 ={(2 3), (1 2), (1 3)}.
Групповая алгебра CS3 группы S3 состоит из элементов
a=a1 e+a2 a+a3 a2 +a4 b+a5 c+a6 d, (23)
где ai ÎC; e, a, a2 , b, c, d – шесть перестановок, образующих группу S3 . Учитывая обозначения перестановок, запишем элементы групповой алгебры, являющиеся суммами элементов классов:
C1 =e1 ; C2 =a+a2 ; C3 =b+c+d.
При построении таблицы Кэли группы S3 воспользуемся таблицей группового умножения группы C3 V и запишем
![]() =е;
=е; ![]() =а;
=а; ![]() =a2
;
=a2
; ![]() =b;
=b; ![]() =c;
=c; ![]() =d.
=d.
Тогда таблица примет следующий вид.
Таблица 3
Квадрат Кэли группы S3
| S3 | e | a | a2 | b | c | d |
| e | e | a | a2 | b | c | d |
| a | a | a2 | e | d | b | c |
| a2 | a2 | e | a | c | d | b |
| b | b | c | d | e | a2 | e |
| c | c | d | b | a | e | a2 |
| d | d | b | c | a2 | a | e |
Таблица Кэли группы S3 определяет групповую алгебру CS3 , в частности, позволяет умножать элементы a из выражения (23).
Переходя к составлению таблицы умножения базисных элементов центра Z групповой алгебры CS3
, заметим, что элемент C1
является ее единицей, так что ![]() , i=1, 2, 3.
, i=1, 2, 3.
Найдем элемент ![]() :
:
![]() =(а+а2
)(а+а2
)=а2
+а3
+а4
=а2
+2е+а=2е+а+а2
=2С1
+С2
.
=(а+а2
)(а+а2
)=а2
+а3
+а4
=а2
+2е+а=2е+а+а2
=2С1
+С2
.
Далее находим ![]() :
:
![]() =(b+c+d)(b+c+d)=b2
+c2
+d2
+bc+bd+cb+cd+db+dc=3e+3a+3a2
=3C1
+3C2
.
=(b+c+d)(b+c+d)=b2
+c2
+d2
+bc+bd+cb+cd+db+dc=3e+3a+3a2
=3C1
+3C2
.
При этом мы воспользовались табл. 3. Заметим, что в силу принадлежности Ci
центру алгебры ![]() , так что таблица будет симметричной относительно главной диагонали. Поэтому нам осталось найти C2
C3
:
, так что таблица будет симметричной относительно главной диагонали. Поэтому нам осталось найти C2
C3
:
C2 C3 =(a+a2 )(b+c+d)=ab+a2 b+ac+a2 c+ad+a2 d=d+c+b+d+c+b=2C3 .
Используя полученные результаты, запишем таблицу умножения базисных элементов центра групповой алгебры группы S3 (см. табл. 4).
Таблица 4
Таблица умножения базисных элементов центра алгебры CS3 .
| Z | C1 | C2 | C3 |
| C1 | C1 | C2 | C3 |
| C2 | C2 | 2C1 + C2 | 2C3 |
| C3 | C3 | 2 C3 | 3 C1 +3C2 |
Запишем матрицы C(i):
 ;
;  ;
;  . (24)
. (24)
Эти матрицы получаются так. Например, действие элемента С(2) на остальные элементы можно представить следующим образом:
![]() ;
;
![]() ;
;
![]() .
.
Записывая коэффициенты правой части в столбец, получаем С(2).
Мы построили матричное представление базисных элементов центра Z алгебры CS3 , что позволяет получить и матричное представление центра этой алгебры.
Запишем характеристические уравнения для определения собственных чисел и собственных векторов матриц Ci в следующем виде (рассматриваем сначала общий случай d матриц Ci ):
 . (25)
. (25)
Возвращаясь к случаю группы S3
получаем d=3, а коэффициенты ![]() можно найти из табл. 4 на основании выражения (24). При этом сначала зафиксируем индекс j, а индексы i и k будем менять, что позволяет разбить систему (25) на три подсистемы, соответствующие значениям j=1, 2, 3. Выпишем сначала 27 значений Cijk
, разбитых на три группы, по 9 значений в каждой:
можно найти из табл. 4 на основании выражения (24). При этом сначала зафиксируем индекс j, а индексы i и k будем менять, что позволяет разбить систему (25) на три подсистемы, соответствующие значениям j=1, 2, 3. Выпишем сначала 27 значений Cijk
, разбитых на три группы, по 9 значений в каждой:
С111 =1; С112 =0; С113 =0;
С211 =0; С212 =1; С213 =0;
С311 =0; С312 =0; С313 =1;
С121 =0; С122 =1; С123 =0;
С221 =2; С222 =1; С223 =0; (26)
С321 =0; С322 =0; С323 =2;
С131 =0; С132 =0; С133 =1;
С231 =0; С232 =0; С233 =2;
С331 =3; С332 =3; С333 =0;
Тогда находим следующие системы уравнений:

 (27)
(27)

Подставляя в найденные системы уравнений (27) значения из выражений (26), получим
(1-х1 ) х1 =0; - х2 х1 + х2 =0; - х3 х1 + х3 =0;
(1-х1 ) х2 =0; (I) 2х1 +(1-х2 ) х2 =0; (II) - х2 х3 +2х3 =0; (III) (28)
(1-х1 ) х3 =0; (1-х2 ) х3 =0; 3х1 +3х2 -x3 2 =0.
Обратим внимание на два обстоятельства.
1. Во всех трех системах находятся одни и те же неизвестные, стоящие вторыми сомножителями, т. е. вектор x=(x1 , x2 , x3 ) является общим собственным вектором всех матриц С(1), С(2), С(3).
2. Указанные системы можно получить, взяв матрицы (24), транспонировать их, рассмотреть разности C(1)-X1 E, C(2)-X2 E, C(3)-X3 E и затем умножить полученные матрицы на столбец (x1 , x2 , x3 )Т (знак Т обозначает транспонирование).
Заметим, что выше уже записаны уравнения для нахождения собственных векторов матриц C(i), однако в этих уравнениях фигурируют собственные значения этих матриц, которые необходимо найти. Для матрицы С(1) получаем трехкратное собственное значение, равное единице, поэтому находим собственные значения матриц С(2) и С(3). Запишем для них вековые уравнения:
 ;
;  . (29)
. (29)
Раскрывая определить третьего порядка, получаем
(l2 -l-2)(2-l)=0; l1 =l2 =2; l3 =-1; -l3 -9l=0; l1 =0; l2 =3; l3 =-3.
4. Находим теперь собственные векторы для рассматриваемых матриц. Для матрицы С(1) – это произвольный вектор x1 (1) = (x1 , x2 , x3 ). Для собственного значения l=2 матрицы С(2) имеем
 ,
,
где x3 – любое. Сам вектор можно записать в виде x2 (2) = (x1 , x2 , x3 ). Поскольку l=2 – двукратное собственное значение, то матрица С(2) имеет два линейно независимых собственных вектора с собственными значениями, равными 2, например, (1 1 0) и (0 0 1) (фундаментальная система решений соответствующей однородной системы уравнений).
Для l=-1 в случае той же матрицы находим
x2 (-1) =(-2x2 , x2 , 0)=(2x2 ¢, -x2 ¢, 0); x2 ¢=-x2 .
Для собственного значения l=0 матрицы С(3) получаем х3 (0) =х2 (-1) , т. е. мы уже нашли общий собственный вектор матриц С(1), С(2), С(3).
Для l=3 в случае матрицы С(3) запишем x3 (3) = (x1 , x1 , x1 ).
Для l=-3 той же матрицы С(3) получим x3 (-3) = (x1 , x1 , -x1 ).
Таким образом, выполнили пункт 4 алгоритма для нахождения характеров неприводимых представлений конечных групп. Чтобы выполнить пункт 5, необходимо найти общие собственные векторы для всех матриц C(i), i=1, 2, 3. Один из них уже найден – это вектор x3 (3) =(x1 , x1 , x1 ) приравнивается вектору x2 (2) = (x1 , x1 , x3 ), откуда следует, что x3 =x1 . Получим второй общий собственный вектор. Соответствующие собственные значения для этого вектора запишем в виде (1, 2, 3).
Приравняем теперь векторы x3 (-3) = (x1 , x1 , -x1 ) и x2 (2) = (x1 , x1 , x3 ). Это дает x3 =-x1 , т. е. третьим общим собственным вектором рассматриваемых матриц будет вектор (x1 , x1 , -x1 ). Поскольку матрица С(3) имеет все различные собственные значения, то соответствующие собственные подпространства одномерны. Но так как у матриц С(2) и С(3) должны быть общие собственные векторы, это накладывает ограничения x3 =-x1 для собственных векторов матриц С(2) вида x2 (2) , которые образуют двумерное собственное подпространство. Чтобы получить характеры неприводимых представлений, необходимо нормировать полученные общие собственные векторы, учитывая, что порядок группы S3 равен 6 и что числа элементов в классах сопряженных элементов образуют вектор (1, 2, 3). Умножив скалярно вектор x3 (3) = (x1 , x1 , x1 ) на вектор (1, 2, 3) и разделив на 6, получим
![]() ; x1
+2x1
+3x1
=6,
; x1
+2x1
+3x1
=6,
т. е. х1 =1.
Таким образом, получаем первый характер х1 =(1, 1, 1). Для вектора (x1 , x1 , -x1 ), умножая его скалярно на (1, 2, -3) и деля на 6, также получаем x1 =1, что дает характер х2 =(1, 1, -1). Наконец, для вектора (2х2 ¢, -х2 ¢, 0) получаем
![]() , (30)
, (30)
откуда х2 ¢=1.
Заметим, что скалярный квадрат вектора (2х2 ¢, -х2 ¢, 0) равен 4x2 ¢2 +2x2 ¢2 =6x2 ¢2 , так как имеется два элемента в классе сопряженных
элементов K2 ={(1 2 3), (1 3 2)} – этим и вызвано появление множителя 2 в выражении (30). С другой стороны, этот множитель равен размерности неприводимого представления группы S3 , так что x3 =(2, -1, 0) есть характер двумерного неприводимого представления группы S3 . Полученные результаты удобно записать в виде следующей таблицы.
Таблица 5
Характеры неприводимых представлений группы S3 =C3 V
| 1 | 2 (1 2 3) | 3 (1 2) | |
c1 c2 c3 |
1 1 2 |
1 1 -1 |
1 -1 0 |
l(1) l(2) l(3) |
1 1 1 |
2 2 -1 |
3 -3 0 |
Таблица 5 – это известная таблица характеров неприводимых представлений группы S3 (см. табл. 2), только в нижней части ее указаны собственные значения матриц C(1), C(2), C(3), которые дают общие собственные векторы этих матриц.
Составив табл. 5, одновременно нашли первую и вторую собственную матрицу P и Q. Матрица, стоящая внизу в таблице, - это первая собственная матрица. Вторую собственную матрицу Q можно получить из соотношения PQ=QP=|G|E или найти с использованием общих правых собственных векторов-матриц Ci . Матрица Q имеет вид (рядом указана транспонированная матрица)
 ;
;  .
.
В соответствии с теоремой 1 таблица характеров неприводимых представлений группы S3 находится по формуле
 .
.
Здесь m1 =1; m2 =1; m3 =4, поэтому
 ,
,
где в правой части находится таблица неприводимых характеров группы S3 , приведенная в верхней части табл. 5.
2.6 Операторы проектирования
1. Операторы проектирования и идемпотенты кольца
Пусть векторное пространство V равно прямой сумме подпространств W и L: ![]() . По определению прямой суммы это означает, что каждый вектор vÎV однозначно представим в виде v=w+l, wÎW. lÎL.
. По определению прямой суммы это означает, что каждый вектор vÎV однозначно представим в виде v=w+l, wÎW. lÎL.
Определение 1.
Если ![]() , так что v=w+l, то отображение
, так что v=w+l, то отображение ![]() , сопоставляющая каждому вектору vÎV его компоненту (проекцию) wÎW, называется проектором пространства V на пространство W.
, сопоставляющая каждому вектору vÎV его компоненту (проекцию) wÎW, называется проектором пространства V на пространство W. ![]() называют также оператором проектирования, или проекционным оператором.
называют также оператором проектирования, или проекционным оператором.
Очевидно, если wÎW, то ![]() (w)=w. Отсюда следует, что
(w)=w. Отсюда следует, что ![]() обладает следующим замечательным свойством
обладает следующим замечательным свойством ![]() 2
=Р.
2
=Р.
Определение 2. Элемент е кольца K называется идемпотентом (т. е. подобным единице), если е2 =е.
В кольце целых чисел есть всего два идемпотента: 1 и 0. Иное дело в кольце матриц. Например, матрицы  ,
,  ,
,  ,
, - идемпотенты. Матрицы операторов проектирования также идемпотенты. Соответствующие им операторы называются идемпотентными операторами.
- идемпотенты. Матрицы операторов проектирования также идемпотенты. Соответствующие им операторы называются идемпотентными операторами.
Рассмотрим теперь прямую сумму n подпространств пространства V:
![]() .
.
Тогда аналогично случаю прямой суммы двух подпространств можем получить n операторов проектирования ![]() ,
, ![]() , …,
, …, ![]() . Они обладают свойством
. Они обладают свойством ![]()
![]() =
=![]()
![]() =0 при i¹j.
=0 при i¹j.
Определение 3.
Идемпотенты ei
и ej
(i¹j) называются ортогональными, если ei
ej
= ej
ei
=0. Следовательно, ![]() и
и ![]() - ортогональные идемпотенты.
- ортогональные идемпотенты.
Из того, что IV=V, и из правила сложения линейных операторов следует, что
![]() .
.
Это разложение называется разложением единицы в сумму идемпотентов.
Определение 4. Идемпотент е называется минимальным, если его нельзя представить в виде суммы идемпотентов, отличных от е и 0.
2. Каноническое разложение представления
Определение 5. Каноническим разложением представления Т(g) называется его разложение вида Т(g)=n1 T1 (g)+ n2 T2 (g)+…+ nt Tt (g), в котором эквивалентные неприводимые представления Тi (g) объединены вместе, причем ni – кратность вхождения неприводимого представления Ti (g) в разложение T(g).
Теорема 1. Каноническое разложение представления определяется с помощью проекционного оператора вида
 , i=1, 2, …, t, (31)
, i=1, 2, …, t, (31)
где |G| - порядок группы G; mi – степени представлений Ti (g), где i=1, 2, …, t; ci (g), i=1, 2, …, t – характеры неприводимых представлений Ti (g). При этом mi определяется по формуле
![]() . (32)
. (32)
3. Проекционные операторы, связанные с матрицами неприводимых представлений групп
С помощью формул (31) можно получить только каноническое разложение представления. В общем случае, надо воспользоваться матрицами неприводимых представлений, которые позволяют построить соответствующие операторы проектирования.
Теорема 2.
Пусть ![]() - матричные элементы неприводимого представления Tr
(g) группы G. Оператор вида
- матричные элементы неприводимого представления Tr
(g) группы G. Оператор вида
 (33)
(33)
является оператором проектирования и называется оператором Вигнера. В выражении (33) mr – размерность представления Tr (g).
4. Разложение представления в прямую сумму неприводимых представлений с помощью оператора Вигнера
Обозначим через М модуль, связанный с представлением Т. Пусть неприводимым представлениям Т1 , Т2 , …, Тt из канонического разложения представления согласно методу, описанному ранее (см. § 4), соответствуют неприводимые подмодули М1 , М2 , …, Мt . Разложение модуля М вида
![]() (34)
(34)
называется каноническим разложением модуля М. Обозначим ni Mi =Li , так, что
![]() . (35)
. (35)
Неприводимые подмодули модулей Li обозначим
![]() ; i=1, 2, …, t. (36)
; i=1, 2, …, t. (36)
Эти модули нам необходимо найти.
Предположим, что задача решена. Следовательно, в каждом из модмодулей Mi
(
s)
(s=1, 2, …, ni
) найдена ортонормированная база ![]() , в которой оператор
, в которой оператор ![]() представлен матрицей Тi
(g) неприводимого представления Т, полученного в результате действия (по правилу из § 3) оператора
представлен матрицей Тi
(g) неприводимого представления Т, полученного в результате действия (по правилу из § 3) оператора ![]() на базу по формуле
на базу по формуле
 , j=1, 2, …, mi
. (37)
, j=1, 2, …, mi
. (37)
В этом выражении можно считать, что mi
– размерность неприводимого представления Ti
(i=1, 2, …, t), причем ![]() - элементы базы с номером g из неприводимого подмодуля Mi
. Разместим теперь элементы базы Li
при фиксированном i следующим образом:
- элементы базы с номером g из неприводимого подмодуля Mi
. Разместим теперь элементы базы Li
при фиксированном i следующим образом:
 (38)
(38)
Справа в выражении (38) расположены базы модулей Mi
(1)
, Mi
(2)
, …, ![]() . Если же i изменять от 1 до t, то получим искомую базу всего модуля М, состоящего из m1
n1
+ m2
n2
+…+ mt
nt
элементов.
. Если же i изменять от 1 до t, то получим искомую базу всего модуля М, состоящего из m1
n1
+ m2
n2
+…+ mt
nt
элементов.
Рассмотрим теперь оператор
 , (39)
, (39)
действующий в модуле М (j фиксировано). Согласно теореме 2, ![]() - оператор проектирования. Поэтому этот оператор оставляет без изменения все базисные элементы
- оператор проектирования. Поэтому этот оператор оставляет без изменения все базисные элементы ![]() (s=1, 2, …, ni
), расположенные в j-м столбце выражения (38), и обращает в нуль все остальные векторы базы. Обозначим через Mij
векторное пространство, натянутое на ортогональную систему векторов
(s=1, 2, …, ni
), расположенные в j-м столбце выражения (38), и обращает в нуль все остальные векторы базы. Обозначим через Mij
векторное пространство, натянутое на ортогональную систему векторов ![]() , стоящие в j-м столбце выражения (38). Тогда можно сказать, что
, стоящие в j-м столбце выражения (38). Тогда можно сказать, что ![]() является оператором проектирования на пространство Mij
. Оператор
является оператором проектирования на пространство Mij
. Оператор ![]() известен, так как известны диагональные элементы матриц неприводимых представлений групп, а также оператор T(g).
известен, так как известны диагональные элементы матриц неприводимых представлений групп, а также оператор T(g).
Теперь можно решить нашу задачу.
Выберем ni
произвольных базисных векторов в M: ![]() и подействуем на них оператором проектирования
и подействуем на них оператором проектирования ![]() . Полученные векторы лежат в пространстве Mij
и являются линейно независимыми. Они не обязательно ортогональны и нормированы. Ортонормируем полученную систему векторов согласно правилу из § 2. Полученную систему векторов обозначим eij
(
s)
в соответствии с обозначениями, принятыми в предположении, что задача решена. Как уже обозначалось, здесь j фиксировано, а s=1, 2, …, ni
. Обозначим eif
(
s)
(f=1, 2, …, j-1, j+1, …, mi
), остальные элементы базы модуля Mi
размерности ni
mi
. Обозначим через
. Полученные векторы лежат в пространстве Mij
и являются линейно независимыми. Они не обязательно ортогональны и нормированы. Ортонормируем полученную систему векторов согласно правилу из § 2. Полученную систему векторов обозначим eij
(
s)
в соответствии с обозначениями, принятыми в предположении, что задача решена. Как уже обозначалось, здесь j фиксировано, а s=1, 2, …, ni
. Обозначим eif
(
s)
(f=1, 2, …, j-1, j+1, …, mi
), остальные элементы базы модуля Mi
размерности ni
mi
. Обозначим через ![]() следующий оператор:
следующий оператор:
 . (40)
. (40)
Из соотношений ортогональности для матриц неприводимых представлений следует, что этот оператор дает возможность получить eig s по формуле
![]() , i=1, 2, …, t. (41)
, i=1, 2, …, t. (41)
Все сказанное можно выразить в виде следующего алгоритма.
Для того, чтобы найти базу модуля М из элементов, преобразующихся по неприводимым представлениям Тi , содержащихся в представлении Т, связанном с модулем М, необходимо:
1.По формуле (32) найти размерности подпространств Мij , соответствующих j-компоненте неприводимого представления Ti .
2.Найти с помощью оператора проектирования (39) все подпространства Mij .
3.В каждом подпространстве Mij выбрать произвольную ортонормированную базу.
4.Используя формулу (41), найти все элементы базы, преобразующихся по остальным компонентам неприводимого представления Тi .
Заключение
Группы – один из основных типов алгебраических систем, а теория групп – один из основных разделов современной алгебры. Понадобилась работа нескольких поколений математиков прежде чем идея групп выкристаллизовалась с ее сегодняшней ясностью. От Лагранжа через работы Руффини и Абеля к Эваристу Галуа, в работах которого уже достаточно сознательно используется идея группы (им же впервые введен и сам термин), - вот путь, по которому развивалась эта идея в рамках теории алгебраических уравнений. В настоящее время теория групп является одной из самых развитых областей алгебры, имеющей многочисленные применения в как в самой математике, так и за ее пределами – в топологии, теории функций, кристаллографии, квантовой механике и других областях математики и естествознания. Конечной целью собственно теории групп является описание всех групповых композиций.
Понятие группы позволяет в точных терминах охарактеризовать симметричность той или иной геометрической фигуры. Именно с таких позиций Е.С. Федоров решил задачу классификации правильных пространственных систем точек, являющуюся одной из основных задач кристаллографии.
Независимо и по другим причинам идея группы возникла в геометрии, когда в середине XIX в. на смену единой античной геометрии пришли многочисленные «геометрии» и остро встал вопрос об установлении связей и родства между ними. Выход был указан «Эрлангенской программой» Клейна, положившей в основу классификации геометрий понятие группы преобразований.
Лежащее в фундаменте современной математики понятие группы является весьма разносторонним орудием самой математики. Вместе с тем группы – это мощный инструмент познания одной из наиболее глубоких закономерностей реального мира – симметрии.
Список использованной литературы
1. Морозов В.П., Дышлис А.А. Лекции по теории симметрии молекулы: Учеб. пособие. – Днепропетровск: Изд-во ДГУ, 1991. – 180 с.
2. Александров П.С. Введение в теорию групп. – М.: Наука. Главная редакция физико-математической лит-ры, 1980 – 144 с.
3. Каргаполов М.И., Мерзляков Ю.И. Основы теории групп – 4-е изд., перераб. – М.: Наука. Физматлит, 1996 – 288 с.
4. Минкин В.И., Симкин Б.Я., Миняев Р.М. Теория строения молекул./ Серия «Учебники и учебные пособия». Ростов-на-Дону: «Феникс», 1997 – 560 с.
5. Дей К., Селби Д. Теоретическая неорганическая химия. Пер. с англ.; под ред. д-ра хим. наук К.В. Астахова. Изд. 3-е, испр. и доп. М., «Химия», 1976 – 568 с.
6. Виленкин Н.Я. Специальные функции и теория представлений групп. – М.: Наука, 1965 – 588 с.
7. Глинка Н.Л. Общая химия: Учеб. пособие для ВУЗов, - 23-е изд., испр./ Под ред. В.А. Рабиновича. – Л.: Химия, 1983 – 704 с.
8. Курош А.Г. Курс высшей алгебры – М.: Наука, 1971 – 432 с.