| Скачать .docx |
Реферат: Термодинамика поверхностного слоя
Термодинамическая характеристика дисперсных систем. Термодинамический метод избыточных величин Гиббса и метод «слоя конечной толщины.
Дисперсной называют систему, в которой одно вещество распределено в среде другого, причем между частицами и дисперсионной средой есть граница раздела фаз. Дисперсные системы состоят из дисперсной фазы и дисперсионной среды.
Дисперсная фаза - это частицы, распределенные в среде. Ее признаки: дисперсность и прерывистость (рис. 1.1.1.1).
Дисперсионная среда - материальная среда, в которой находится дисперсная фаза. Ее признак - непрерывность .
Поверхность раздела фаз характеризуется раздробленностью и гетерогенностью. Раздробленность характеризуется:
1) степенью дисперсности
: 
, [см-1
; м-1
], где S
- суммарная межфазная поверхность или поверхность всех частиц дисперсной фазы; V
- объем частиц дисперсной фазы.
2) дисперсностью - величиной, обратной минимальному размеру:
[
;
];
3)удельной поверхностью
: 
, [м2
/кг; см2
/г]; 
где m
- масса частиц дисперсной фазы.
4) кривизной поверхности
: 
. Для частицы неправильной формы 
,
где r 1 и r 2 - радиусы окружностей при прохождении через поверхность и нормаль к ней в данной точке двух перпендикулярных плоскостей.
5) размером тела по трем осям , причем определяющим является размер по той оси, где он минимальный. В зависимости от размеров частиц они имеют свои исторические названия (см. рис. 1.1.1.1).
Лиофильные системы – в них дисперсная фаза взаимодействует с дисперсионной средой и при определенных условиях способна в ней растворяться – растворы коллоидных ПАВ, растворы ВМС. Свободная энергия системы DF < 0.
DF = DU – TdS ; DS смешения > 0;
DU = W ког - W сольв ,
где W ког - работа когезии;
W сольв - работа сольватации.
При DU > 0, DU < 0 ÞTdS >DU . Эта группа характеризуется малым значением поверхностного натяжения на границе раздела фаз.
Лиофобные системы – в них дисперсная фаза не способна взаимодействовать с дисперсионной средой и растворяться в ней. Для них DF > 0. Диспергирование в этом случае совершается либо за счет внешней работы, либо за счет других процессов, идущих в системе спонтанно (химическая реакция) и характеризуется высоким значением поверхностного натяжения на границе раздела фаз, что соответствует малому значению энергии сольватации.
Существует две группы способов получения дисперсных систем:
1. Способы диспергирования заключаются в раздроблении тела до коллоидного состояния (мукомольное производство).
2. Способы конденсации заключаются в укрупнении частиц, атомов, молекул до частиц коллоидных размеров (химическая реакция с образованием осадка).
Как уже отмечалось, на границе раздела фаз существует избыток свободной энергии. Процесс увеличения площади поверхности при постоянном объеме выводит молекулы из глубины фазы на поверхностный слой, совершая при этом работу против межмолекулярных сил. Эта работа в изотермических условиях равна увеличению свободной поверхностной энергии. Для описания термодинамики поверхностных явлений используют два метода:
1. Метод избыточных величин Гиббса .
2. Метод слоя конечной толщины .
За толщину поверхностного слоя принимаем расстояние по обе стороны границы раздела фаз, за пределами которого свойства слоя перестают отличаться от свойств фазы в объеме.
Определение границы поверхностного слоя задача очень сложная, поэтому Гиббсом предложено относить все изменения термодинамических параметров слоя разделяющей поверхности, не имеющей объема и толщины. При таком рассмотрении поверхность будет обладать избыточными термодинамическими параметрами, непосредственно отражающими проявление поверхностной энергии. В соответствии метода Гиббса позиция 1 на рис. 2.1.1.1 – энергия системы равна сумме энергий Гиббса объемных фаз DG
1
и 
G
2
и поверхностной энергии Гиббса 
×S
, которая является избыточной.
В методе слоя конечной толщины рассматривается поверхностный слой, имеющий определенные размеры (позиция II на рис. 2.1.1.1). Его термодинамические параметры включают как поверхностную энергию, так и энергию объема слоя, имеющего те же свойства, что и объемная фаза. Этот метод не рассматриваем. В методе Гиббса все экстенсивные величины выражаются в виде избытков по сравнению со значением этих величин в реальных объемных фазах.
Тема 2.1.2. Поверхностное натяжение. Методы измерения поверхностного натяжения. Зависимость поверхностного натяжения от температуры и концентрации. Уравнение Шишковского
На образование коллоидной системы затрачивается работа А= × S , где коэффициент пропорциональности; S - новая поверхность.
Поверхностное натяжение есть частная производная от любого термодинамического потенциала по площади межфазной поверхности при постоянстве соответствующих параметров.
Если проводить процесс образования новой поверхности изотермически и обратимо, то вся работа перейдет в запас свободной энергии поверхности: A
=
Fs
, Fs
=
s×S
; 
, [Дж/м2
или Н/м].
Коэффициент s - поверхностное натяжение; - это работа, совершаемая для образования единицы новой поверхности.
Поверхностное натяжение - это сила, действующая на единицу длины контура, ограниченного единицей поверхности и направленная в сторону сокращения поверхности, перпендикулярно к контуру вовнутрь его.
Наиболее часто используются 4 метода определения поверхностного натяжения.
1. Метод максимального давления в пузырьке газа (метод Ребиндера) (рис. 2.1.2.1, а).
Основан на продавливании пузырька газа (воздуха) под воздействием внешнего давления р через калиброванный капилляр радиусом r 0 . С увеличением давления пузырек растет, а радиус кривизны его поверхности R превышает радиус капилляра (положение 1 рис. 2.1.2.1, а : R > r 0 ). Дальнейшее увеличение объема пузырька будет происходить до тех пор, пока внутреннее давление достигнет своего максимального значения; радиус кривизны при этом будет минимальным, т.е. R = r 0 (положение 2). В этот момент пузырек теряет устойчивость: при увеличении его объема он отрывается от капилляра. Если в момент отрыва пузырька измерить давление р , то поверхностное натяжение можно представить
; 
. (1)
Чтобы не измерять радиус капилляра, можно определить р для жидкости, поверхностное натяжение которой известно (эталон, часто, вода). Отсюда
. (2)
Исключив в уравнениях (1) и (2) радиус капилляра, получим выражение для определения поверхностного натяжения
или 
где 
- поверхностное натяжение на границе «жидкость – газ»;
- поверхностное натяжение жидкости, принятой за стандарт (чаще – вода);
- перепад давления в пузырьке стандартной жидкости;
- перепад давления в пузырьке исследуемой жидкости.
2. Сталагмометрический метод (рис. 2.1.2.1, б).
Определяют вес капли, которая отрывается от капилляра под действием силы тяжести. Считают, что при отрыве вес капли Р к уравновешивается силой, равной произведению поверхностного натяжения и длины окружности капилляра радиусом r 0 :
, (3)
где k – поправочный коэффициент, учитывающий, что отрыв капель происходит по радиусу шейки капли, который меньше радиуса самой капли.
Определяют экспериментально вес капель и при помощи разработанных таблиц с учетом (3) находят s. Рекомендуется увеличивать время формирования капли до тех пор, пока число капель станет постоянным.
,
где r - плотность исследуемой жидкости;
n – число капель исследуемой жидкости;
sст , rст , n ст – значения s, r и n для стандартной жидкости.
3. Метод отрыва кольца (рис. 2.1.2.1, в).
Измеряют силу F , которой противодействует поверхностное натяжение жидкости, смачивающей периметр поверхности кольца.
,
где k – поправочный коэффициент, учитывает, что поднимающийся при отрыве кольца столб жидкости не имеет формы правильного полого цилиндра.
Метод капиллярного поднятия (рис. 2.1.2.1, г).
В капилляре за счет смачивания образуется вогнутый мениск с радиусом кривизны r , поверхностное натяжениеsжг вызывает капиллярное давление Dр . Оно уравновешивается весом Р н столба жидкости высотой Н :
, (4)
где q - краевой угол смачивания.
Капиллярное давление уравновешивается весом столба РН жидкости высотой Н , т.е. Dр = РН . С учетом (4) и веса столба жидкости можно записать:
, (5)
где r, r0 – плотность жидкости и газа (воздуха).
В связи с тем, что r >> r0 , плотностью газа можно пренебречь, тогда высота подъема жидкости в капилляре определяется по формуле
.
|
При полном смачивании, когда q = 0 и cosq = 1, имеем
.
- уравнение Жюрена,
гдеD r – разность плотностей жидкости и газовой фазы;
g – ускорение свободного падения;
а – капиллярная постоянная.
Поверхностное натяжение индивидуальных веществ (жидкостей) монотонно убывает с возрастанием температуры.
т
=
0
-
aT
,
где т
- поверхностное натяжение при данной температуре;
0
- поверхностное натяжение при стандартной температуре;
D Т - разность температур;
а
- температурный коэффициент; 
.
Если вещество поверхностно активно, то с увеличением концентрации изотерма резко уменьшается (кривая 1 рис. 2.1.2.2).
Это объясняется тем, что вначале вся поверхность раздела жидкой фазы свободна от поверхностно-активных веществ (ПАВ) и небольшое его количество, присутствующее в растворе, почти целиком уходит на поверхность. Затем следует криволинейный участок, отвечающий средней концентрации. В этих условиях значительная часть поверхности занята молекулами поверхностно-активных веществ (ПАВ), что снижает скорость повышения концентрации на границе раздела. Большим концентрациям на изотерме отвечает почти горизонтальный участок (кривая 3), показывающий, что поверхностное натяжение мало зависит от концентрации. При этих условиях на границе «жидкость – воздух» образуется сплошной монослой поверхностно-активного вещества (ПАВ), и увеличение его концентрации на границе невозможно в дальнейшем. При увеличении концентрации поверхностного инактивного вещества в растворе изотерма полого поднимается (кривая 2). Это объясняется тем, что поверхностные инактивные вещества благодаря высокому поверхностному натяжению и активности уходят в объем, а на границе раздела «жидкость – воздух» имеются лишь сравнительно небольшие концентрации вещества, попадающего туда за счет диффузии из объема раствора. При увеличении концентрации веществ, не влияющих на поверхностное натяжение, изотерма представляет собой прямую, параллельную оси концентрации. Следует отметить, что отнесение веществ к той или иной группе зависит от природы растворителя. Одно и тоже вещество для разных растворителей может быть и поверхностно-активным веществом (ПАВ), и не влиять на поверхностное натяжение.
Для малых и средних концентраций поверхностно-активных веществ (ПАВ) при описании зависимости
=
f
(
c
)
используется уравнение Шишковского
:
,
где s 0 – поверхностное натяжение растворителя (Н/м);
c – концентрация поверхностно-активного вещества (ПАВ);
А, b – константы, данные в справочнике.
Уравнение Гиббса-Гельмгольца для поверхностной энергии. Полная поверхностная энергия
Запишем известное из термодинамики выражение внутренней энергии для поверхности.
Us
=
Gs
+
TSS
- уравнение полной поверхностной энергии.
В этом уравнении qs = T D S - теплота образования единицы поверхности в обратимом процессе. Она равна количеству теплоты, которую необходимо подвести к системе, чтобы увеличить ее поверхность на единицу при T = const . Из уравнений фазы при постоянстве всех параметров, кроме температуры, имеем:
dGs
= -
Ss
dT
,
.
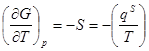Подставляя эти значения в уравнение полной поверхностной энергии, получаем:
- уравнение Гиббса - Гельмгольца для поверхности.
Оно связывает полную поверхностную энергию с энергией Гиббса (поверхностное натяжение).
Для гетерогенной системы изменение внутренней энергии, исходя из I и II начал термодинамики:
dU =TdS – pdV +dS +
i
dni
+
j
dq
,
гдеdU - изменение внутренней энергии;
dS - изменение энтропии;
dV - изменение объема;
Т – температура;
Р – давление;
- поверхностное натяжение;
n - число молей компонента;
dq - изменение электрического заряда;
- химический потенциал компонентов;
- электрический потенциал компонентов;
S - межфазная поверхность.
При S
,
V
,
n
,
q
=const уравнение примет вид: dU
=
dS
,
т.е. - это изменение энтропии на единицу площади.
Из уравнений видно 
, т.е. подтверждается, что при увеличении температуры поверхностное натяжение снижается. Если сопоставить изменение ,
qs
,
Us
от температуры, получим рис. 2.1.2.3. Из графика видно, что величина D
Us
для индивидуального вещества величина практически постоянная т.е. D
Us
не зависит от температуры. Для расчета зависимости =
f
(
T
)
используются эмпирические и полуэмпирические зависимости - метод парохор, формула Этвеша.
В случае твердых фаз процесс образования новой поверхности носит необратимый характер и (поверхностное натяжение) можно изменить только косвенным путем, например, путем расчета. Мерой количественного выражения свободной энергии является f
или G
. В соответствии со вторым законом термодинамики для самопроизвольных процессов,
Возможны два варианта:
1.
2.
Отсюда следует, что в дисперсных системах в самопроизвольных процессах поверхность (а, следовательно, и поверхностное натяжение) уменьшается.