| Скачать .docx |
Реферат: Термодинамический расчет смеси
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Самарский государственный технический университет
Кафедра: «Технология органического и нефтехимического синтеза»
КУРСОВАЯ РАБОТА ПО КУРСУ:
«Физико-химические свойства растворов»
Cамара, 2005 г.
Исходные данные:
| Tb, К |
Tc(эксп) К |
Pc(эксп) ,bar |
Vc(эксп) , см3 /моль |
W(эксп) |
Zc |
yi |
|
| 2.3-диметилбутан |
331.13 |
499.98 |
31.27 |
358 |
0.247 |
0.270 |
0.37 |
| цис-1,2-диметилциклогексан |
402.90 |
606.00 |
29.3 |
461,73 |
0.22 |
||
| метил-третбутиловый эфир |
328.30 |
497.10 |
34.3 |
334 |
0.1 |
||
| индан |
451.10 |
684.90 |
39.5 |
389 |
0.31 |
Задание:
1. Для четырехкомпонентной смеси заданного состава рассчитать энтальпию, энтропию, теплоемкость в стандартном состоянии при заданной температуре.
2. Псевдокритические свойства: температуру, давление, объем, ацентрический фактор и коэффициент сжимаемости.
3. Плотность:
3.1. Ненасыщенной газовой и жидкой смеси при температуре, соответствующей приведенной температуре 0,95 в диапазоне приведенных давлений от 0,01 до 1. Построить график зависимости.
3.2. Плотность жидкой смеси на линии насыщения в диапазоне температур от 298К до критической с шагом 25К. Построить график зависимости.
4. Энтальпию, энтропию, теплоемкость смеси при заданной температуре в диапазоне приведенных давлений от 0,01 до 10. Построить график зависимости соответствующего свойства от давления.
5. Энтальпию испарения в стандартном состоянии при давлении отличном от 1 атм для диапазона температур для диапазона температур от 298К до критической с шагом 25К.
6. «Кажущуюся» стандартную энтальпию образования смеси в жидком состоянии ![]() .
.
7. Вязкость смеси при температуре 730 К и приведенном давлении 10.
8. Теплопроводность смеси при температуре 730К и приведенном давлении 10.
Решение:
1. Для расчета т/д характеристик смеси нужно знать параметры компонентов этой смеси.
Для 2,3-диметилбутана при вычислении ![]() используем следующую формулу:
используем следующую формулу:
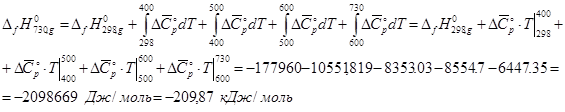
где для диапазона температур ![]() :
:
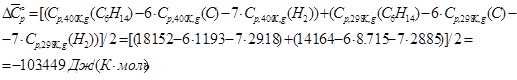
и т.д.
Значения ![]() ,
, ![]() и
и ![]() рассчитаны по табличным данным методом Бенсона.
рассчитаны по табличным данным методом Бенсона.
При расчете ![]() используем уже найденные значения
используем уже найденные значения ![]() для диапазонов температур:
для диапазонов температур:
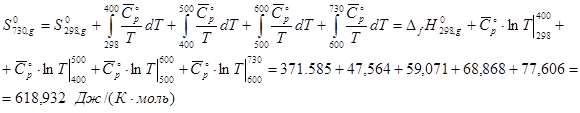
![]()
При расчете ![]() получаем:
получаем: ![]() .
.
Для цис-1,2-диметилциклогексана при вычислении ![]() используем следующую формулу:
используем следующую формулу:
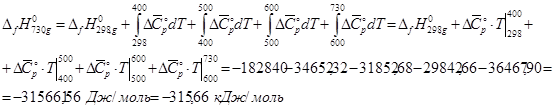
где для диапазона температур ![]() :
:
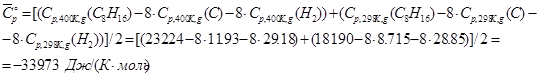
и т.д.
Значения ![]() ,
, ![]() и
и ![]() рассчитаны по табличным данным методом Бенсона.
рассчитаны по табличным данным методом Бенсона.
При расчете ![]() цис-1,2-диметилциклогексана используем уже найденные значения
цис-1,2-диметилциклогексана используем уже найденные значения ![]() для диапазонов температур:
для диапазонов температур:
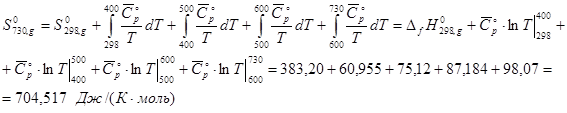
![]()
При расчете ![]() цис-1,2-диметилциклогексана получаем:
цис-1,2-диметилциклогексана получаем: ![]() .
.
Для метил-третбутилового эфира при вычислении ![]() используем следующую формулу:
используем следующую формулу:
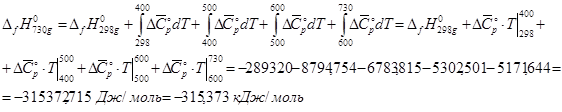
где для диапазона температур ![]() :
:
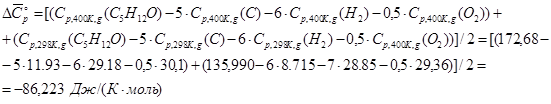
и т.д.
Значения ![]() ,
, ![]() и
и ![]() рассчитаны по табличным данным методом Бенсона.
рассчитаны по табличным данным методом Бенсона.
При расчете ![]() используем уже найденные значения
используем уже найденные значения ![]() для диапазонов температур:
для диапазонов температур:
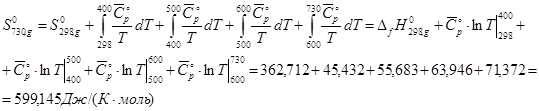
![]()
При расчете ![]() получаем:
получаем: ![]() .
.
Для индана при вычислении ![]() используем следующую формулу:
используем следующую формулу:
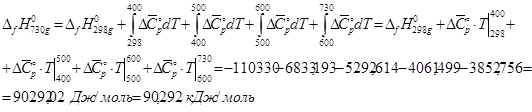 где для диапазона температур
где для диапазона температур ![]() :
:
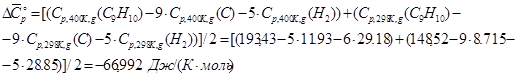
и т.д.
Значения ![]() ,
, ![]() и
и ![]() рассчитаны по табличным данным методом Бенсона.
рассчитаны по табличным данным методом Бенсона.
При расчете ![]() используем уже найденные значения
используем уже найденные значения ![]() для диапазонов температур:
для диапазонов температур:
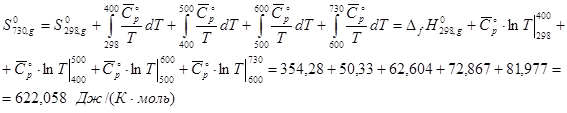
![]() .
.
При расчете ![]() получаем:
получаем: ![]() .
.
Для смесей в состоянии идеального газа энтальпия, энтропия и теплоемкость рассчитываются аддитивно с учетом переменной состава:
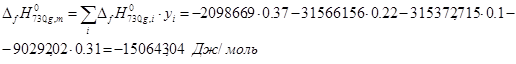 ;
;
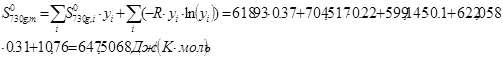 ;
;
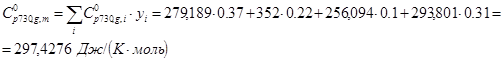 .
.
2. Псевдокритический объем смеси определяется, как функция от состава смеси и критических объемов чистых компонентов смеси: 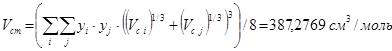 , при этом получена матрица:
, при этом получена матрица:
| 1 |
2 |
3 |
4 |
|
| 1 |
392.0816 |
265.4731 |
102.3749 |
342.5268 |
| 2 |
265.4731 |
178.7814 |
69.4187 |
231.5124 |
| 3 |
102.3749 |
69.4187 |
26.7200 |
89.4788 |
| 4 |
342.5268 |
231.5124 |
89.4788 |
299.0632 |
Псевдокритическая температура рассчитывается, как функция от критической температуры, критического объема и состава смеси:
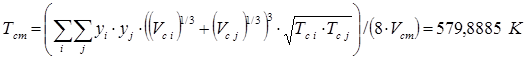
При этом получена следующая матрица:
| 1 |
2 |
3 |
4 |
|
| 1 |
196032.9584 |
146127.9295 |
51037.78151 |
200440 |
| 2 |
146127.9295 |
108341.532 |
38100.82371 |
149150.3 |
| 3 |
51037.78151 |
38100.82371 |
13282.512 |
52210.23 |
| 4 |
200440.0092 |
149150.2849 |
52210.23284 |
204828.4 |
Ацентрический фактор смеси рассчитывается аддитивно: ![]() .
.
Ацентрические факторы чистых компонентов смеси рассчитываются по уравнению:
![]() ,
,
![]()
![]() ,
,
где: ![]() , Рс
– критическое давление, атм.
, Рс
– критическое давление, атм.
Псевдокритическое давление смеси рассчитывается через уравнение: ![]() , где:
, где: ![]() – псевдокритический коэффициент сжимаемости, определяемый с помощью таблиц Ли-Кесслера и разложения Питцера.
– псевдокритический коэффициент сжимаемости, определяемый с помощью таблиц Ли-Кесслера и разложения Питцера.
2.1.
Плотность ненасыщенной газовой и жидкой смеси определяем по формуле:![]() , где:
, где:
![]() - молекулярная масса смеси, определяемая по правилу аддитивности.
- молекулярная масса смеси, определяемая по правилу аддитивности.
![]() - объем смеси, определяемый по уравнению Менделеева-Клапейрона:
- объем смеси, определяемый по уравнению Менделеева-Клапейрона:
![]() ,
,
![]() - фактор сжимаемости смеси, определяемый с помощью разложения Питцера и таблиц Ли-Кесслера.
- фактор сжимаемости смеси, определяемый с помощью разложения Питцера и таблиц Ли-Кесслера.
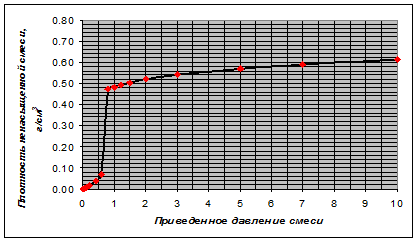
Для диапазона приведенных давлений от 0,01 до 1 имеем:
| Pr |
P, атм |
z(0) |
z(1) |
z |
Vm , см3 /моль |
ρm , г/см3 |
| 0.01 |
0.3316 |
0.9961 |
-0.0012 |
0.9958 |
135736.7088 |
0.00075 |
| 0.05 |
1.6578 |
0.9803 |
-0.0062 |
0.9787 |
26680.6560 |
0.00382 |
| 0.10 |
3.3156 |
0.96 |
-0.0126 |
0.9567 |
13040.6132 |
0.00782 |
| 0.20 |
6.6312 |
0.9174 |
-0.0262 |
0.9105 |
6205.5229 |
0.01644 |
| 0.40 |
13.2624 |
0.8206 |
-0.0589 |
0.8051 |
2743.5055 |
0.03719 |
| 0.60 |
19.8936 |
0.6967 |
-0.1110 |
0.6674 |
1516.3113 |
0.06728 |
| 0.80 |
26.5248 |
0.141 |
-0.0540 |
0.1268 |
215.9884 |
0.47236 |
| 1.00 |
33.1559 |
0.1705 |
-0.0607 |
0.1545 |
210.5945 |
0.48446 |
| 1.20 |
39.7871 |
0.1998 |
-0.0678 |
0.1819 |
206.6516 |
0.49370 |
| 1.50 |
49.7339 |
0.2432 |
-0.0788 |
0.2224 |
202.1250 |
0.50476 |
| 2.00 |
66.3119 |
0.3138 |
-0.0967 |
0.2883 |
196.4949 |
0.51922 |
| 3.00 |
99.4678 |
0.4501 |
-0.1310 |
0.4156 |
188.8181 |
0.54033 |
| 5.00 |
165.7797 |
0.7092 |
-0.1943 |
0.6580 |
179.3773 |
0.56877 |
| 7.00 |
232.0916 |
0.9561 |
-0.2526 |
0.8895 |
173.2122 |
0.58902 |
| 10.00 |
331.5594 |
1.3108 |
-0.3339 |
1.2228 |
166.6762 |
0.61211 |
Зависимость ![]() имеет вид:
имеет вид:
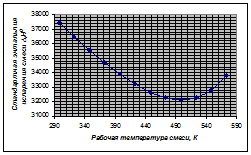
2.2.
Плотность жидкой смеси на линии насыщения определяется по формуле: ![]() , где:
, где:
![]() определяется по уравнению Ганна и Ямады:
определяется по уравнению Ганна и Ямады: ![]() , где:
, где:
![]() ,
,
![]() и Г – функции приведенной температуры.
и Г – функции приведенной температуры.
Для диапазона температур ![]() :
:
![]() ;
;
![]() Для диапазона
Для диапазона ![]() :
:
![]() ;
;
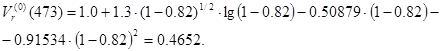
Для диапазона ![]() :
:
![]() ;
; ![]() .
.
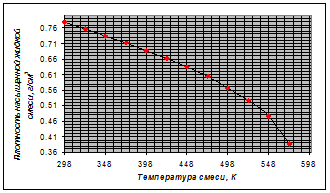
Для диапазона температур от 298К до 573К имеем:
| Т,К |
Тr |
Г |
Vr 0 |
Vs c |
Vm |
ρm , г/см3 |
| 298 |
0.5139 |
0.2368 |
0.3656 |
382.393653 |
131.0658 |
0.7784 |
| 323 |
0.5570 |
0.2307 |
0.3755 |
134.8551 |
0.7565 |
|
| 348 |
0.6001 |
0.2244 |
0.3862 |
138.9467 |
0.7343 |
|
| 373 |
0.6432 |
0.2179 |
0.3980 |
143.4386 |
0.7113 |
|
| 398 |
0.6863 |
0.2112 |
0.4111 |
148.4628 |
0.6872 |
|
| 423 |
0.7295 |
0.2043 |
0.4262 |
154.1862 |
0.6617 |
|
| 448 |
0.7726 |
0.1973 |
0.4436 |
160.8103 |
0.6344 |
|
| 473 |
0.8157 |
0.1901 |
0.4652 |
168.9805 |
0.6038 |
|
| 498 |
0.8588 |
0.1827 |
0.4946 |
180.0206 |
0.5667 |
|
| 523 |
0.9019 |
0.1751 |
0.5307 |
193.5710 |
0.5271 |
|
| 548 |
0.9450 |
0.1674 |
0.5852 |
213.9129 |
0.4769 |
|
| 573 |
0.9881 |
0.1594 |
0.7210 |
264.1337 |
0.3863 |
Зависимость ![]() имеет вид:
имеет вид:
3. Энтальпию, энтропию, теплоемкость смеси при заданной температуре 730К в диапазоне приведенных давлений от 0,01 до 10 определяем с помощью таблиц Ли-Кесслера и разложения Питцера:
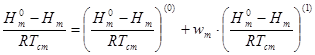 ,
,
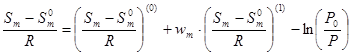 ,
,
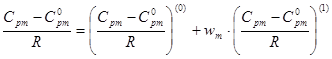 .
.
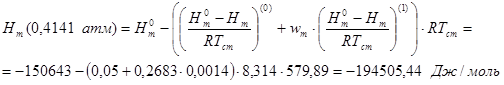
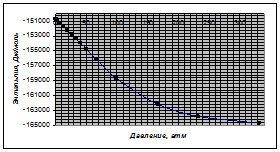
Для энтропии в диапазоне приведенных давлений от 0,01 до 10 получаем:
| Pr |
P, атм |
Н(0) |
Н(1) |
Н, Дж/моль |
| 0.01 |
0.3316 |
0.005 |
0.0014 |
-150668.93 |
| 0.05 |
1.6578 |
0.0252 |
0.0062 |
-150772.42 |
| 0.10 |
3.3156 |
0.0508 |
0.0118 |
-150902.96 |
| 0.20 |
6.6312 |
0.1022 |
0.0236 |
-151165.77 |
| 0.40 |
13.2624 |
0.2072 |
0.0432 |
-151696.91 |
| 0.60 |
19.8936 |
0.3146 |
0.0584 |
-152234.03 |
| 0.80 |
26.5248 |
0.4252 |
0.0688 |
-152780.47 |
| 1.00 |
33.1559 |
0.5382 |
0.0738 |
-153331.62 |
| 1.20 |
39.7871 |
0.653 |
0.0736 |
-153884.84 |
| 1.50 |
49.7339 |
0.8304 |
0.0624 |
-154725.88 |
| 2.00 |
66.3119 |
1.1288 |
0.0232 |
-156114.70 |
| 3.00 |
99.4678 |
1.6722 |
-0.0292 |
-158667.92 |
| 5.00 |
165.7797 |
2.2994 |
0.2868 |
-162093.48 |
| 7.00 |
232.0916 |
2.5242 |
0.7384 |
-163751.36 |
| 10.00 |
331.5594 |
2.5684 |
1.2668 |
-164636.17 |
График зависимости ![]() имеет вид:
имеет вид:
Для энтропии расчет ведем по формуле:
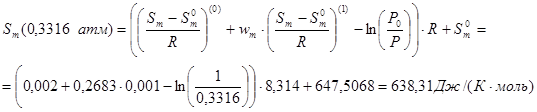
Для энтропий в диапазоне приведенных давлений от 0,01 до 10 получаем:
| Pr |
P, атм |
S(0) |
S(1) |
S,Дж/(Кмоль) |
| 0.01 |
0.3316 |
0.0024 |
0.0014 |
638.31 |
| 0.05 |
1.6578 |
0.0122 |
0.0082 |
651.59 |
| 0.10 |
3.3156 |
0.0246 |
0.0160 |
657.23 |
| 0.20 |
6.6312 |
0.0500 |
0.0310 |
662.75 |
| 0.40 |
13.2624 |
0.1020 |
0.0606 |
668.02 |
| 0.60 |
19.8936 |
0.1554 |
0.0872 |
670.89 |
| 0.80 |
26.5248 |
0.2112 |
0.1114 |
672.76 |
| 1.00 |
33.1559 |
0.2688 |
0.1322 |
674.09 |
| 1.20 |
39.7871 |
0.3282 |
0.1492 |
675.08 |
| 1.50 |
49.7339 |
0.4198 |
0.1682 |
676.13 |
| 2.00 |
66.3119 |
0.5772 |
0.1876 |
677.17 |
| 3.00 |
99.4678 |
0.8622 |
0.2396 |
678.06 |
| 5.00 |
165.7797 |
1.1740 |
0.5794 |
678.97 |
| 7.00 |
232.0916 |
1.2792 |
0.9490 |
680.08 |
| 10.00 |
331.5594 |
1.3168 |
1.3508 |
681.85 |
График зависимости ![]() имеет вид:
имеет вид:
Расчет теплоемкости ведем по формуле:
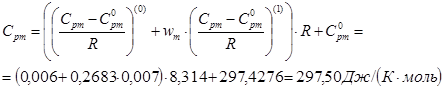
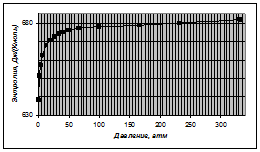
Для теплоемкости в диапазоне приведенных давлений от 0,01 до 10 получаем:
| Pr |
P, атм |
C(0) |
C(1) |
Cp , Дж/(К∙моль) |
| 0.01 |
0.3316 |
0.0064 |
0.0068 |
297.50 |
| 0.05 |
1.6578 |
0.0318 |
0.0348 |
297.77 |
| 0.10 |
3.3156 |
0.0648 |
0.0698 |
298.12 |
| 0.20 |
6.6312 |
0.1328 |
0.1384 |
298.84 |
| 0.40 |
13.2624 |
0.2790 |
0.2726 |
300.34 |
| 0.60 |
19.8936 |
0.4402 |
0.3988 |
301.96 |
| 0.80 |
26.5248 |
0.6186 |
0.5118 |
303.69 |
| 1.00 |
33.1559 |
0.8152 |
0.6074 |
305.54 |
| 1.20 |
39.7871 |
1.0304 |
0.6812 |
307.49 |
| 1.50 |
49.7339 |
1.3866 |
0.7450 |
310.59 |
| 2.00 |
66.3119 |
2.0330 |
0.7616 |
316.00 |
| 3.00 |
99.4678 |
3.0174 |
1.2050 |
325.16 |
| 5.00 |
165.7797 |
3.0630 |
3.5034 |
330.57 |
| 7.00 |
232.0916 |
2.5654 |
4.4436 |
328.50 |
| 10.00 |
331.5594 |
2.0500 |
4.5874 |
324.53 |
График зависимости ![]() имеет вид:
имеет вид:
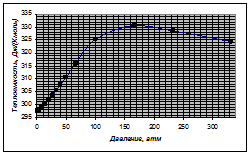
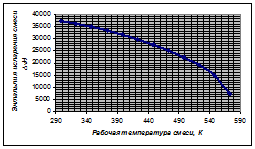
4. Энтальпию испарения смеси в стандартном состоянии и при давлении, отличном от 1атм рассчитываем по уравнению Менделеева-Клапейрона:
![]() , где:
, где:
при стандартном состоянии ![]() =1, при давлении, отличном от 1атм для определения
=1, при давлении, отличном от 1атм для определения ![]() используется выражение:
используется выражение:
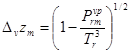 ;
;
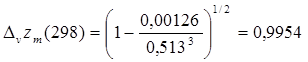 ;
;
![]() ;
;
![]() ,
,
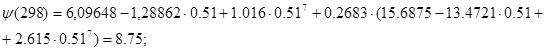
давление насыщенных паров определяется по корреляции Ли-Кесслера:
![]() , где:
, где:
![]() ,
,![]() .
. ![]() .
.
![]() ,
,
![]() ,
,![]() .
.
Для диапазона температур от 298 до 573К:
| Т, К |
Тr |
f(0) |
f(1) |
Pvpr |
∆Zv |
∆v H, Дж/моль |
∆v H0 , Дж/моль |
| 298 |
0.5139 |
-5.0752 |
-6.2981 |
0.00119 |
0.9956 |
37254.7001 |
37418.78 |
| 323 |
0.5570 |
-4.2589 |
-5.0156 |
0.00377 |
0.9890 |
36071.81517 |
36471.57 |
| 348 |
0.6001 |
-3.5658 |
-3.9893 |
0.00988 |
0.9769 |
34737.17427 |
35559.11 |
| 373 |
0.6432 |
-2.9702 |
-3.1614 |
0.02229 |
0.9572 |
33212.48933 |
34697.05 |
| 398 |
0.6863 |
-2.4528 |
-2.4888 |
0.04465 |
0.9284 |
31478.11583 |
33906.18 |
| 423 |
0.7295 |
-1.9985 |
-1.9385 |
0.08130 |
0.8891 |
29531.02569 |
33213.72 |
| 448 |
0.7726 |
-1.5956 |
-1.4850 |
0.13709 |
0.8383 |
27373.36201 |
32654.6 |
| 473 |
0.8157 |
-1.2346 |
-1.1076 |
0.21726 |
0.7744 |
24991.39522 |
32273.04 |
| 498 |
0.8588 |
-0.9077 |
-0.7895 |
0.32763 |
0.6948 |
22319.37859 |
32124.32 |
| 523 |
0.9019 |
-0.6083 |
-0.5165 |
0.47499 |
0.5938 |
19164.33515 |
32276.68 |
| 548 |
0.9450 |
-0.3306 |
-0.2762 |
0.66803 |
0.4566 |
14981.04654 |
32813.54 |
| 573 |
0.9881 |
-0.0696 |
-0.0577 |
0.91869 |
0.2186 |
7396.108869 |
33835.83 |
Зависимость ![]() имеет вид:
имеет вид:
5. «Кажущаяся» стандартная энтальпия образования смеси в жидком состоянии ![]() определяется по уравнению:
определяется по уравнению: ![]() , где:
, где:
![]() - энтальпия парообразования смеси при стандартном давлении и температуре 298К,
- энтальпия парообразования смеси при стандартном давлении и температуре 298К,
![]() - энтальпия образования газовой смеси при стандартном давлении и температуре 298К, определена по правилу аддитивности. Энтальпии образования чистых компонентов смеси определены методом Бенсона.
- энтальпия образования газовой смеси при стандартном давлении и температуре 298К, определена по правилу аддитивности. Энтальпии образования чистых компонентов смеси определены методом Бенсона.
6. Вязкость смеси при атмосферном давлении рассчитываем методом Голубева:
т.к. ![]() , то:
, то:
![]() ,
,
где 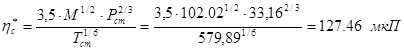
При расчете вязкости для высоких давлений используем корреляцию для смесей неполярных газов, т.к. большинство газов в смеси – неполярные:
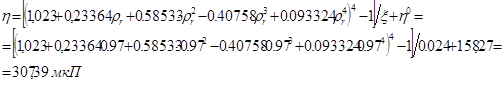
где: 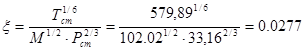 , приведенную плотность смеси определяем по формуле:
, приведенную плотность смеси определяем по формуле: ![]() , где V рассчитывается по уравнению Менделеева-Клапейрона:
, где V рассчитывается по уравнению Менделеева-Клапейрона: ![]() , а псевдокритический коэф. сжимаемости определяется из разложения Питцера с помощью таблиц Ли-Кесслера:
, а псевдокритический коэф. сжимаемости определяется из разложения Питцера с помощью таблиц Ли-Кесслера: ![]() . Условие применимости для
. Условие применимости для ![]() :
: ![]() удовлетворяется.
удовлетворяется.
8. Теплопроводность смеси при стандартном давлении рассчитаем с помощью корреляции Мисика-Тодоса:
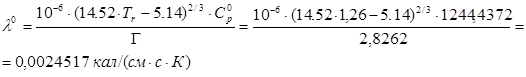
где: ![]() - теплоемкость смеси в стандартном состоянии при температуре 730К,
- теплоемкость смеси в стандартном состоянии при температуре 730К,
 .
.
Теплопроводность при высоком давлении и ![]() определяется по формуле:
определяется по формуле: ![]()