| Скачать .docx |
Реферат: Коллоидная химия и поверхностные явления
Министерство образования и науки РФ
Государственное образовательное учреждение
Высшего профессионального образования
Воронежский государственный университет
Кафедра физической химии
Реферат
Тема: «Поверхностные явления и коллоидная химия»
Выполнил
Студент 2-го курса 2-й группы
Биолого-почвенного факультета
Ларченков Владимир Михайлович
Проверил: проф. Калужина Светлана Анатольевна
Воронеж, 2010 год
Содержание
Поверхностные явления
Свойства межфазовой границы. Поверхностное натяжение
Адгезия и когезия
Смачвание
Адсорбция
Адсорбция на однородной плоской поверхности раздела фаз – в поверхностном слое жидкостей
Поверхностно-активные вещества. Правило Дюкло-Траубе
Адсорбция на твёрдой поверхности
Мономолекулярная адсорбция на твёрдой поверхности. Уравнение изотермы Ленгмюра
Полимолекулярная адсорбция. Уравнение БЭТ
Уравнение изотермы адсорбции Фрейндлиха
Вид изотерм адсорбции по классификации БДДТ
Ионная адсорбция. Иониты. Двойной электрический слой
Хроматография
Коллоидная химия. Дисперсные системы
Лиофильные и лиофобные золи. Получение лиофобных золей
Мицеллярная теория коллоидов
Устойчивость и коагуляция лиофобных золей
Седиментация. Коэффициент Сведберга
Оптические свойства коллоидов
Молекулярно-кинетические свойства коллоидов. Броуновское движение
Поверхностные явления
Фаза – это часть гетерогенной системы, однородная по химическому составу и физическим свойствам и ограниченная от остальной системы границей раздела. Явления, происходящие на границе раздела двух фаз, называются поверхностными явлениями.
Свойства межфазовой границы. Поверхностное натяжение
На границе раздела фаз каждая из граничащих фаз имеет избыток потенциальной энергии, который называется поверхностная энергия. Стремление вещества уменьшить поверхностную энергию – поверхностное натяжение у. Существует оно потому, что состояние молекулы внутри фазы и на её границе различно:
1. Внутри фазы молекула окружена другими такими же молекулами. Силовые поля этих молекул полностью компенсированы друг другом, молекулы связаны между собой одинаково
2. На границе раздела фаз молекулы рассматриваемой фазы одновременно взаимодействуют с молекулами как своей, так и другой фазы, причём характер взаимодействия между молекулами разных фаз другой, нежели между молекулами одной фазы. Это приводит к тому, что молекулы рассматриваемой фазы «выталкиваются» из своей фазы в другую или сильнее притягиваются к молекулам другой фазы, чем к «своим» молекулам
3. Поверхностное натяжение – это величина свободной энергии Гиббса на единицу поверхности вещества. Стремление вещества уменьшить эту величину приводит к самопроизвольному сокращению границы раздела фаз. Примеры: круглая форма капли жидкости при отсутствии воздействий со стороны (в невесомости, при достаточно малом объёме жидкости (поверхностное натяжение сильнее силы тяжести)), коагуляция, коалесценция и др.
4. Если площадь поверхности равна Щ, то при Р, Т=const
у = (dG/dЩ)P , T , nj (1)
Щ = Щуд V (2),
где Щуд – удельная поверхность фазы. Для сферических частиц
Щуд = 6/d (3),
d – диаметр частиц
5. Экспериментально можно определить лишь величину поверхностного натяжения. Существуют статические и полустатические (метод отрыва кольца) методы
Адгезия и когезия
1. Адгезия – это сцепление друг с другом поверхностей разнородных тел. Когезия – это сцепление друг с другом поверхностей одного тела. Обусловлены данные явления межмолекулярными взаимодействиями
2. Работа когезии Wc – это работа, затрачиваемая на преодоление сил сцепления между молекулами однородной жидкости и приводящая к возникновению двух новых поверхностей раздела фаз газ-жидкость. Wc = 2у. Работа адгезии Wа – это работа, затрачиваемая на преодоление сил сцепления между молекулами двух разных жидкостей на площади контакта 1 м2 . Для жидкостей А и В:
Wа = уА + уВ - уАВ (4)
3. Растекание жидкости А по поверхности жидкости В возможно в тех случаях, когда энергия взаимодействия молекул жидкости А друг с другом меньше энергии взаимодействия молекул жидкости А с молекулами жидкости В. Высокая работа адгезии наблюдается у клеев, по адгезионным свойствам различаются нормальные и раковые клетки
Смачивание
1. Смачивание – это явление на границе раздела жидкой и твёрдой фаз, заключающееся в растекании жидкости по поверхности твёрдого тела, пропитывании пористых тел и порошков с образованием мениска за счёт взаимодействий молекул жидкой и твёрдой фаз
2. Если поверхностное натяжение на границе газ-жидкость равна уж-г , поверхностная энергия на границе твёрдое вещество-жидкость утв-г , поверхностная энергия твёрдой поверхности утв , то существует такой угол и, что
утв - утв-г + уж-г cosи=0 (5)
Это – краевой угол смачивания (угол между направлением силы поверхностного натяжения на границе газ-жидкость и твёрдой поверхностью)
3. Критерий смачивания
В=cosи (6)
4. Из формулы
B = (2 Wа - Wc )/ Wc (7)
следует, что чем больше разница между работой адгезии и работой когезии данной жидкости в отношении данного вещества, тем лучше данная жидкость смачивает данное вещество. Это означает, что жидкость будет хорошо смачивать вещество, если энергия взаимодействия молекул жидкости между собой меньше энергии взаимодействия молекул жидкости и твёрдой поверхности
Адсорбция
1. Адсорбция – это концентрирование вещества на границе раздела фаз в результате его самопроизвольного перехода данного вещества из объёма фазы. Адсорбционное равновесие определяется притяжением молекул к поверхности другой фазы и тепловым движением, стремящимся восстановить равенство концентраций в поверхностном слое и объёме фазы
2. Наблюдается адсорбция на поверхностях раздела следующих фаз: твёрдое вещество-жидкость, твёрдое вещество-газ, жидкость-жидкость, жидкость-газ. Адсорбент – твёрдое вещество, на поверхности которого происходит адсорбция. Адсорбтив (адсорбат) – вещество, концентрирующееся на границе раздела фаз
3. Адсорбция – частный случай сорбции. Если на границе раздела фаз вещество поглощается в результате образования химических соединений, это хемосорбция. Если вещество поглощается объёмом другой фазы, это абсорбция
4. Различают два случая адсорбции: адсорбция на твёрдой поверхности и адсорбция в поверхностном слое жидкости.
Адсорбция на однородной плоской поверхности раздела
фаз – в поверхностном слое жидкостей.
1. Данный процесс описывается уравнением изотермы адсорбции Гиббса
2. При контакте двух жидких фаз образуется межфазная область, толщина которой соответствует молекулярным размерам. Та как её измерить невозможно, для устранения неопределённости вводится условная разделяющая поверхность с площадью O
3. Тогда поверхностная энергия системы равна
G( s ) = уO + ∑мi ni ( s ) (8)
4. Путём расчётов получаем
dу = -еdT - ∑Гi dмi (9)
5. При дальнейших расчётах исходить из предположения, что адсорбция растворителя отсутствует
6. Уравнение изотермы адсорбции Гиббса Гi = -(ai /RT)(dу/dai ), Гi – избыточное количество вещества i, отнесённое к единичной поверхности, ai – его активность
7. Экспериментальные данные дают хорошее качественное согласие с уравнением изотермы адсорбции Гиббса, повышение точности измерений подтверждает справедливость данного уравнения

(рис.1, 2)
8. На рисунке справа изображена изотерма адсорбции поверхностно-активного вещества на границе раствор-пар, Г – число молей поверхностно-активного вещества в поверхностном слое, Г0 – максимально возможная концентрация поверхностно-активного вещества в поверхностном слое, на рисунке слева изображены изотермы поверхностного натяжения ПАВ (1, 2) и поверхностно-инактивного вещества/
Поверхностно-активные вещества. Правило Дюкло-Траубе
Поверхностно-активные вещества ПАВ – это вещества, способные концентрироваться на поверхности раздела фаз и понижать поверхностное натяжение жидкости. Направление процесса (концентрирования вещества в поверхностном слое фазы или выход его оттуда) определяется знаком dу/dc. Если c~a, то значению >0 соответствует отрицательная адсорбция, dу/dc<0 – положительная адсорбция. Поверхностная активность
G = - dу/dc (10)
при с→0 – адсорбция поверхностно-активных веществ положительна, адсорбция жидкостей – адсорбатов, имеющих большее поверхностное натяжение, чем у адсорбента, отрицательна.
Большинство поверхностно-активных веществ, меняющих поверхностное натяжение воды, имеет общую структуру: в молекуле содержатся гидрофильная головка и гидрофобный хвост.

(рис.3)
При взаимодействии с водой гидрофильная головка оказывается сильно гидратированной, а гидрофобный хвост выталкивается наружу. Образуется мономолекулярный слой поверхностно-активного вещества на поверхности воды.
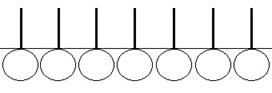
(рис.4)
Правило Дюкло-Траубе: при увеличении числа углеродных атомов в гомологическом ряду в арифметической прогрессии поверхностная активность вещества возрастает в геометрической прогрессии.
Адсорбция на твёрдой поверхности
Мономолекулярная адсорбция на твёрдой поверхности
Уравнение изотермы Ленгмюра
Основные положения теории Ленгмюра:
1. Адсорбция – процесс локализованный, она вызвана силами, близкими к химическим
2. Адсорбция протекает не на всей поверхности адсорбента, а в активных центрах
3. Каждый активный центр взаимодействует с одной молекулой адсорбата, в результате чего на поверхности адсорбента образуется один слой адсорбированных молекул
4. Адсорбция – процесс обратимый и равновесный
При адсорбционном равновесии скорость адсорбции равна скорости десорбции, она пропорциональна числу ударов молекул адсробтива о поверхность адсорбента, незанятую адсорбированными молекулами. Она равна
Wa = ka (1 – и)p(11)
ka – коэффициент пропорциональности, и – доля поверхности, покрытой адсорбированными молекулами, (1 – и) – доля свободной для адсорбции поверхности адсорбента.
Скорость десорбции:
Wд = kд ни (11)
kд – коэффициент пропорциональности, н – число молекул на 1 м2 при максимальной упаковке.
Так как скорости процессов адсорбции и ресорбции равны, эти уравнения можно приравнять друг другу, и решением полученного уравнения относительно и будет
и = Kp/(1+Kp), K = ka /( kд н) (12)
Исходя из того, что число адсорбированных молекул на единице поверхности равно ин, то количество молей A на единицу поверхности равно
A = ин/NA (13)
Максимальная адсорбция:
A∞ = н/ NA (14)
Тогда уравнение изотермы адсорбции Ленгмюра, связывающее адсорбцию с давлением газа над адсорбентом имеет вид:
A = A∞ Kp/(1+Kp) (15)
Аналогичным путём выводится уравнение изотермы адсорбции Ленгмюра, связывающее адсорбцию с концентрацией:
Г = ГₒC/(C+b) (16),
С – равновесная концентрация адсорбируемого вещества в растворе.
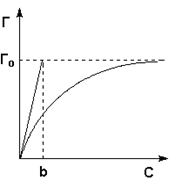
(рис.5)
На рисунке приведена изотерма мономолекулярной адсорбции [2].
Полимолекулярная адсорбция. Уравнение БЭТ
Многие изотермы адсорбции имеют форму, отличную от изотермы адсорбции Ленгмюра. Пример: S-образные кривые, часто наблюдаемые при адсорбции паров:

(рис.6)
С. Брунауэр, П. Эммет, Дж. Теллер предложили теорию, по которой молекулы из газовой фазы могут адсорбироваться поверх уже адсорбированных молекул (Харкинс предложил ей название «теория БЭТ» по первым буквам фамилий авторов). Авторы принимали теорию Ленгмюра о динамическом характере адсорбционного равновесия и справедливость уравнения Ленгмюра для каждого адсорбционного слоя. Уравнение изотермы адсорбции БЭТ:
y/V(1 – y) = 1/CVm + (C – 1)y/Vm C (17)
Уравнение изотермы адсорбции Фрейндлиха
Теория Ленгмюра даёт нам идеальную картину процесса адсорбции. С учётом разности расстояний между активными центрами, зависимости их друг от друга, взаимодействий между адсорбированными молекулами и т.д. вид изотермы адсорбции усложняется.
 (рис.7)
(рис.7) (рис.8)
(рис.8)
Г. Фрейндлих показал, что при T = const удельная адсорбция (число молей адсорбированного газа или растворённого вещества, приходящееся на единицу массы адсорбента), обозначаемая x/m, пропорциональна равновесному давлению (для газов) или равновесной концентрации (для веществ, адсорбируемых из раствора) адсорбируемого вещества, возведённым в степень меньше единицы.
x/m = aCn , x/m = aPn (18)
На рис.7 изображена изотерма адсорбции Фрейндлиха в обычных координатах, на рис.8 – в логарифмических.
Вид изотерм адсорбции по классификации БДДТ
 (рис.9)
(рис.9)
I – изотерма, описываемая уравнением Ленгмюра
II– формирование полислоя на поверхности с высоким адсорбционным потенциалом
III – образование полислоя из газовой среды на твёрдом адсорбенте. Справедлива для тел, потенциал монослоя которых мал и имеет тот же порядок, что и теплота конденсации адсорбтива
IV, V – аналогичны типам II и III для пористых сорбентов, где адсорбция ограничивается объёмом мезопор, петля гистерезиса соответствует дополнительному поглощению пара в результате капиллярной адсорбции.
Ионная адсорбция. Иониты
При адсорбции ионов из раствора адсорбируется чаще всего один тип ионов. Адсорбция может проходить по двум механизмам:
1. Обменная адсорбция. При этом вместо ионов, адсорбируемых из раствора твёрдой фазой, из твёрдой фазы выделяется эквивалентное количество ионов того же знака. Примером такой адсорбции является адсорбция ионов солей ионитами (например, ионообменными смолами).
Иониты – это высокомолекулярные соединения, при диссоциации выделяющие в воду большое количество одноатомных ионов и высокомолекулярный ион противоположного знака. По типу выделяемых ионов они делятся на 2 класса: катиониты и аниониты. При диссоциации катионитов образуется высокомолекулярный анион, в воду выделяется множество катионов. При диссоциации анионитов, соответственно, происходит выделение в воду анионов.
По структуре иониты различают гелевые и макропористые. Гелевые иониты состоят из связанных между собой полимерных цепей. Для осуществления реакции ионного обмена они должны набухнуть. Набухание – это процесс проникновения растворителя в пространство между полимерными цепями ионита. Этот процесс занимает достаточно длительное время, поэтому в практической деятельности чаще применяются макропористые иониты. Их получают, проводя синтез полимера в присутствии соответствующего растворителя. После синтеза растворитель отмывают или отгоняют.
Процесс ионного обмена выглядит следующим образом. Вначале ион, содержащийся в растворе – он называется вытесняющий ион – попадает на поверхность ионита, потом диффундирует в объём ионита туда, где происходит акт обмена. Вытесняемый ион диффундирует из объёма ионита к его поверхности и переходит в раствор.

(рис.9)
2. Специфическая адсорбция заключается в поглощении твёрдой фазой ионов, достраивающих её кристаллическую решётку. При этом вокруг фазы образуется слой противоионов. Формируется двойной электрический слой.
Строение двойного электрического слоя наиболее точно описывается современной теорией Штерна:
1. Поверхность твёрдой фазы адсорбирует ионы, достраивающие её кристаллическую решётку – потенциалопределяющие ионы
2. Адсорбционные силы принимают участие и в образовании первого слоя противоионов – адсорбционного слоя. Ионы этого слоя притягиваются к заряженной поверхности твёрдой фазы электростатическими силами и затем адсорбируются
3. За адсорбционным слоем образуется диффузный слой противоионов. Количество ионов в нём такое, что они полностью нейтрализуют оставшийся противоположный заряд потенциалопределяющих ионов
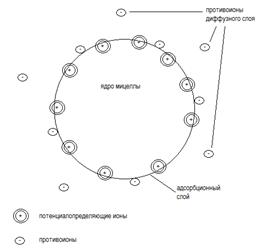
(рис.10)
Потенциал диффузного слоя (ж-потенциал) – это электрокинетический потенциал коллоидной частицы, величина которого имеет большое значение во многих явлениях в коллоидах.
Двойной электрический слой стабилизирует мицеллы – частицы, составляющие дисперсную фазу гидрозолей.
Хроматография
Это разделение веществ в результате сорбционных процессов при движении одной из фаз. Динамическая сорбция в хроматографии осуществляется двумя способами:
1. При фронтальной хроматографии раствор разделяемых веществ непрерывно пропускают через слой сорбента
2. При элютивной хроматографии вводят в начальную часть слоя сорбента смесь разделяемых веществ и затем пропускают растворитель, который «тащит» разделяемые молекулы. Расстояние, пройденное веществом по сорбенту, прямо пропорционально растворимости данного вещества в пропускаемом растворителе. Даёт возможность полностью разделять вещества, входящие в состав разделяемой смеси.
Коллоидная химия
Дисперсные системы – это системы, состоящие из множества частиц одной фазы (дисперсной), распределённых в объёме другой фазы – дисперсионной.
| Дисперсионная среда | Дисперсная фаза | Характеристика по размеру частиц | Название системы |
| газ | Жидкость | Коллоидно-дисперсные (10-7ра -10-9 м) | Аэрозоль |
| Грубодисперсные (10-5 -10-7 м) | Туман | ||
| Твёрдое тело | Кд | Аэрозоль | |
| Гд | Пыль, дым | ||
| Жидкость | Газ | Кд | Пена |
| Гд | |||
| Жидкость | Кд | Эмульсия | |
| Гд | |||
| Твёрдое тело | Кд | Лиозоль | |
| Гд | Суспензия | ||
| Твёрдое тело | Газ | Кд | Твёрдая пена |
| Гд | |||
| Жидкость | Кд | Нет названия | |
| Гд | |||
| Твёрдое тело | Кд | Твёрдый золь | |
| Гд |
Лиофильные и лиофобные золи
Лиофильные системы – это дисперсные системы, образующиеся самопроизвольно, они термодинамически устойчивы. Такими системами являются растворы высокомолекулярных соединений.
Лиофобные золи образуются из пересыщенных растворов или в результате дробления более крупных частиц.
Получение лиофобных золей
1. Конденсационные методы. Из них наиболее распространены метод замены растворителя и метод химической конденсации. Пример первого метода – получение золя канифоли в воде, при этом к спиртовому раствору канифоли постепенно добавляют воду, растворимость канифоли снижается, и образуется лиофобный золь. Пример второго метода – получение золя гидроксида железа путём разложения хлорида железа кипячением раствора
2. Дисперсионный метод – разрушение до коллоидно-дисперсных частиц более крупных агрегатов
3. Пептизация – «расцепление» агрегатов, образовавшихся при коагуляции лиозоля, на отдельные мицеллы; процесс, обратный коагуляции. Возможна, если структура коллоидных частиц не изменена.
Различают опосредованную и непосредственную пептизацию. При непосредственной пептизации к осадку добавляют раствор потенциалопределяющих ионов, в результате чего восстанавливается двойной электрический слой. При опосредованной пептизации потенциалопределяющие ионы выделяются при добавлении какого-либо реактива, высвобождающего их.
Мицеллярная теория коллоидов
Дисперсная фаза золя состоит из мицелл. Мицелла – это частица основного вещества дисперсной фазы, окружённая двойным электрическим слоем. Коллоидно-химическая формула мицеллы (рассмотрим для AgCl) записывается следующим образом:
{(mAgCl* nCl- )* (n-x)H+ }* xH+ или {(mAgCl* nAg+ )* (n-x)NO3 - }* xNO3 -
Особым шрифтом выделена твёрдая частица хлорида серебра – ядро мицеллы. Жирным шрифтом выделены потенциалопределяющие ионы, подчёркнуты в формуле противоионы (двойной чертой – диффузный слой, одной – адсорбционный).
Устойчивость и коагуляция лиофобных золей
По теории Пескова, устойчивость коллоида объясняется присутствием кроме дисперсной фазы и дисперсионной среды третьего вещества – стабилизатора, образующего вокруг коллоидной частицы сольватный слой. Этот процесс – лиофилизация коллоида. Этот процесс можно вызвать адсорбцией поверхностно-активных веществ на поверхности коллоидной частицы.
По физической теории устойчивости и коагуляции электролитами между мицеллами существуют силы притяжения и отталкивания. Силы отталкивания действуют, когда диффузные слои мицелл перекрываются друг другом. Эти силы являются не просто кулоновским взаимодействием. Дерягин показал, что здесь проявляется расклинивающее давление. Притяжение мицелл друг к другу обусловлено Ван-дер-ваальсовыми силами.
Коагуляция – это осаждение дисперсной фазы путём слипания частиц друг с другом. Наиболее важной является коагуляция под действием электролитов. Правила такой коагуляции:
1. Коагуляцию может вызвать любой электролит
2. Минимальная концентрация электролита, с которой начинается коагуляция – порог коагуляции
3. Коагулирующим действием обладает тот ион электролита, который по знаку противоположен заряду гранулы мицеллы
4. Правило Шульце – Гарди: чем больше валентность иона, тем больше его коагулирующая способность
5. В ряду органических ионов коагулирующая способность возрастает с повышением адсорбционной способности
6. В ряду неорганических ионов с одинаковым зарядом их коагулирующая способность возрастает с уменьшением гидратации (например, в ряду однозарядных катионов – от лития к рубидию)
7. В момент начала коагуляции электрокинетический потенциал снижается до критической величины в 0,03 В
8. Ионы, вызвавшие коагуляцию, всегда присутствуют в полученных осадках
Иногда при добавлении избыточного количества коагулирующего электролита происходит перезарядка мицелл. При этом коагулирующий ион становится потенциалопределяющим, формируется новый двойной электрический слой и золь восстанавливается – происходит его пептизация.
Седиментация. Коэффициент Сведберга
Седиментация – это осаждение частиц дисперсной фазы в грубодисперсных системах в поле тяготения. Количественной характеристикой седиментации является коэффициент Сведберга – отношение скорости линейного оседания частицы в радиальном направлении к вызывающему это перемещение центробежному ускорению. 1 S = 10-13 с.
S0 20, w = (зT* (dч –))/(з20, w* (dч – d)) (19)
зT – вязкость растворителя при температуре Т, dч – плотность частицы, d20, w – плотность воды при 200 С, з20, w – вязкость воды при той же температуре, d – плотность растворителя при температуре Т.
На данном эффекте основан исключительно широко распространённый в биохимических и молекулярно-биологических исследованиях метод центрифугирования.
Оптические свойства коллоидов
Поскольку золь состоит из двух разных фаз, его оптические свойства будут отличаться от оптических свойств истинного раствора.
Главное оптическое явление, наблюдаемое у золей – рассеяние света. Именно в гетерогенных системах оно проявляется особенно сильно, хотя из-за флуктуаций плотностей наблюдается и в истинных гомогенных растворах, хотя в гораздо меньшей степени. На интенсивность рассеянного света оказывает влияние его длина волны: при освещении золя белым светом рассеянный свет богаче коротковолновым излучением, а прошедший – длинноволновым. По теории Релея интенсивность света, рассеиваемого частицей (S1 ), определяется по формуле
S1 = (р2 (1+cosи)/2l2 л4 )∙((n2 1 – n2 0 )/(n2 1 + 2n2 0 ))2 ∙V2 I0 (20) – уравнение Релея.
Полная интенсивность света, рассеиваемая частицей во всех направлениях, равна
R1 = 24р3 л4 ∙((n2 1 – n2 0 )/(n2 1 + 2n2 0 ))2 ∙V2 I0 (21)
Мутность системы равна
ф = 24р3 л4 ∙((n2 1 – n2 0 )/(n2 1 + 2n2 0 ))2 ∙N1 V2 (22)
Тогда
RN 1 = фI0 (23)
В этих формулах и – угол между направлением падающего пучка и пучка рассеянного света, l – расстояние от сферической частицы при наблюдении рассеяния, V – объём частицы, n1 и n0 – показатели применения частицы и среды, N1 – число частиц в единице объёма.
Если на золь направить луч света и смотреть на раствор перпендикулярно ходу луча, можно увидеть световой конус, созданный лучом в растворе. Это явление – эффект Фарадея – Тиндаля. Он обусловлен рассеянием света на мицеллах.
Опалесценция – это характерное для гетерогенных систем свечение обычно голубоватых оттенков, возникающее вследствие возбуждения электронов атомов при прохождении света через вещество. В гомогенной среде такое излучение гасится интерференцией, поскольку коэффициент светопреломления в каждой точке однородной среды одинаков. В гетерогенной системе имеются участки с различными величинами коэффициента светопреломления, возникающее излучение гасится не полностью.
Поглощение света в коллоидных системах может осуществляться как дисперсной фазой, так и дисперсионной средой. Если дисперсионная среда для света с данной длиной волны прозрачна, поглощение света осуществляется дисперсной фазой.
Тогда закон поглощения света Бугера-Ламберта-Бера имеет вид:
I = I0 ∙exp (-Elc) (24)
I – интенсивность прошедшего света, I0 – интенсивность упавшего на вещество света, l – толщина поглощающего слоя, с – концентрация поглощающего свет вещества, Е – постоянная абсорбции, отнесённая к выбранной единице концентрации.
Нефелометрия – это аналитический метод определения концентрации частиц, основанный на измерении интенсивности рассеянного света. В этом методе используется зависимость рассеяния света золем от концентрации частиц в нём.
Ультрамикроскопия – это метод, при котором наблюдается свет, рассеянный одиночными частицами. При помощи ультрамикроскопа можно определять и средней размер частиц золя, и их форму (анизодиаметрические частицы вследствие вращательного броуновского движения мерцают).
Броуновское движение
По теории Эйнштейна-Смолуховского направление и скорость теплового движения коллоидных частиц определяются их столкновениями с молекулами дисперсионной среды. Частица, испытывая удары со всех сторон, движется в ту сторону, с которой результирующая сила ударов меньше.
Броуновское движение вследствие этого беспорядочное, частицы постоянно меняют направление. Интенсивность броуновского движения частиц определяют размер движущихся частиц и температура среды (от неё зависит скорость молекул).
Уравнение Эйнштейна-Смолуховского:
Д2 = (2kT/B)∙t(25)
Оценка минимального значения t, при котором это уравнение выполняется, неопределённая.
Броуновское движение присуще гетерогенным системам, в которых частицы достаточно малы, чтобы сила ударов молекул среды о них уравновешивала силу тяжести. Это все дисперсные системы с коллоидно-дисперсными частицами, а также системы с наиболее мелкими грубодисперсными частицами, видимыми в обычный световой микроскоп. Броуновское движение не может быть свойственно истинным растворам, в которых отсутствует твёрдая дисперсная фаза.
Литература
1. В.Н. Захарченко. Коллоидная химия. М: Высшая школа, 1989 г.
2. Интернет-ресурс http://www.physchem.chimfak.rsu.ru
3. Интернет-ресурс http://www.humuk.ru
4. С.А. Калужина. Физическая и коллоидная химия: лабораторный практикум. Воронеж: ЛОП ВГУ, 2001 г.