| Скачать .docx |
Книга: Книга: Дослідження точності впливу ситуативної тривожності на характеристики памяті методом статистични
Міністерство освіти і науки України
Міжнародний економіко-гуманітарний університет
ім. Академіка С. Дем’янчука
ДОСЛІДЖЕННЯ
точності впливу ситуативної тривожності на характеристики пам’яті методом статистичних випробувань Монте Карло
Модель ППП 051- 1
Науковий керівник:
кандидат технічних наук,
доцент Р.М. Літнарович
Рівне, 2007
Абрамович К.П. Дослідження точності впливу ситуативної тривожності на характеристики пам’яті методом статистичних випробувань Монте Карло. Модель ППП О51 – 1.МЕГУ, Рівне, 2007, -30с,
Рецензент: С.В. Лісова, доктор педагогічних наук, професор. Відповідальний за випуск: Й.В. Джунь, доктор фізико-математичних наук, професор.
На основі результатів психологічного експерименту побудована математична модель залежності ситуативної тривожності на характеристики пам’яті у вигляді кубічного поліному по способу найменших квадратів.
В даній роботі генеруються середні квадратичні похибки, які приводяться до заданих нормованих, будується спотворена модель, зрівноважується по способу найменших квадратів. Знаходяться ймовірніші значення коефіцієнтів а, в, с, d кубічного поліному апроксимуючої математичної моделі.
Робиться оцінка точності і даються узагальнюючі висновки. Примінений метод статистичних випробовувань Монте Карло дав можливість провести широкомасштабні дослідження і набрати велику статистику.
Для студентів і аспірантів педагогічних вузів
© Абрамович К.П.
Передмова
За результатами психолого-педагогічного експерименту при дослідженні впливу ситуативної тривожності на характеристики пам’яті, будується математична модель у вигляді поліному третього порядку.
Вихідними даними для проведення досліджень в даній роботі беруться результати психолого-педагогічного експерименту – бали тесту самооцінки тривожності по шкалі Спірбергера (Хі ) і характеристики пам’яті – кількість правильних відповідей на запитання вікторини (Уі ).
За цими даними була побудована математична модель у вигляді поліному третього порядку способом найменших квадратів. Дана модель приймалась за істинну модель.
Генерувались випадкові числа, знаходився коефіцієнт пропорційності К і дані випадкові числа приводилися до середньої квадратичної похибки 0,1 і 0,05, що відповідає ціні найменшої поділки шкали Спірбергера і половині поділки даної шкали.
Будується спотворена модель, яка зрівноважується по способу найменших квадратів.
Дається оцінка точності елементів, зрівноважених процедурою способу найменших квадратів. Робляться узагальнюючі висновки.
1. Представлення істинної моделі
За результатами строгого зрівноваження [6,c.33] отримана емпірична формула залежності характеристик пам’яті Х від ситуативної тривожності У9(істинна модель)
у = -4,717425 Х3 + 33,731505 Х2 – 85,78331 Х + 88,244437. (1.1)
Таблиця 1. Вихідні дані істинної моделі у табличному вигляді [6,c.28]
| Х | 1,6 | 2 | 2,1 | 2,3 | 2,5 | 2,8 | 2,9 | 3 | 3,1 | 3,3 |
| у | 18,021 | 13,864 | 13,167 | 11,986 | 10,898 | 8,949 | 8,101 | 7,108 | 5,939 | 2,965 |
За даними табл.. 1 побудуємо точкову діаграму і графік
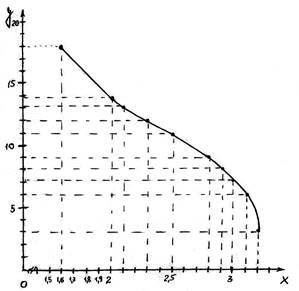
Рис.1. Точкова діаграма і графік
Побудувавши ймовірнішу модель по способу найменших квадратів і зробивши оцінку точності її елементів, в подальшому необхідно провести дослідження точності впливу ситуативної тривожності на характеристики пам’яті методом статистичних випробувань Монте Карло. Для цього необхідно генерувати істинні похибки за допомогою генератора випадкових чисел.
2. Генерування істинних похибок для дослідження математичної моделі методом статистичних випробувань Монте Карло
По шкалі Спірбергера [1] незалежні змінні представляються з точністю 0,1. прийнято, що точність спостережень дорівнює половині шкали.
Тому логічно генерувати випадкові похибки з точністю, яка б дорівнювала 0,05, тобто половині шкали з якою ми працюємо. Але поставимо перед собою задачу ще дослідити математичні моделі з граничною точністю, яку приймемо вдвічі більшу за 0,05, тобто рівну 0,1. При цьому непарні моделі генерують середню квадратичну похибку 0,1, а парні – 0,05.
Сучасні калькулятори мають “вшиті” генератори для генерування випадкових чисел від 0 до 1. але вони генерують числа тільки зі знаком “плюс”.
Приведемо методику розрахунку випадкових чисел, які приймемо в подальшому як істинні похибки для побудови спотвореної моделі.
1. Отримавши ряд випадкових (а точніше псевдовипадкових) чисел ξі , натиском клавіш К, Cч, розраховують середнє арифметичне генерованих псевдовипадкових чисел ξір .
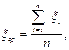(2.1)
де п – сума випадкових чисел.
2. Розраховуються попередні значення істинних похибок Δ΄і за формулою
, (2.2)
3. Знаходять середню квадратичну похибку попередніх істинних похибок за формулою Гаусса
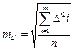
, (2.3)
4. Вичисляють коефіцієнт пропорційності К для визначення істинних похибок необхідної точності
, (2.4)
де С – необхідна нормована константа.
Так, наприклад, при т Δ΄ = 0,28 і необхідності побудови математичної моделі з точністю с=0,1 , будемо мати
,
а при С=0,05 , отримаємо К0,05 = 0,05/0,28 =0,178
5. Істинні похибки розраховуються за формулою
, (2.5)
6. Заключним контролем служить розрахунок середньої квадратичної похибки т ∆ генерованих істинних похибок ∆
, (2.6)
і порівняння
(2.7)
Таблиця 2 . Генерування псевдовипадкових чисел і розрахунок істинних похибок
| № п/п | ξ і | - ξср |  |
∆΄ і 2 |  |
∆і 2 |
| 1 | 0,008 | 0,457 | -0,449 | 0,20174 | -0,207 | 0,04283629 |
| 2 | 0,39 | 0,457 | -0,067 | 0,004457 | -0,031 | 0,00094637 |
| 3 | 0,37 | 0,457 | -0,087 | 0,007527 | -0,04 | 0,00159833 |
| 4 | 0,78 | 0,457 | 0,3232 | 0,104484 | 0,149 | 0,02218548 |
| 5 | 0,47 | 0,457 | 0,0132 | 0,000175 | 0,0061 | 0,00003722 |
| 6 | 0,24 | 0,457 | -0,217 | 0,046985 | -0,100 | 0,00997656 |
| 7 | 0,46 | 0,457 | 0,0032 | 1,05E-05 | 0,00149 | 0,00000223 |
| 8 | 0,61 | 0,457 | 0,1532 | 0,023482 | 0,071 | 0,00498610 |
| 9 | 0,5 | 0,457 | 0,0432 | 0,00187 | 0,01992 | 0,00039699 |
| 10 | 0,74 | 0,457 | 0,2832 | 0,080225 | 0,13052 | 0,01703443 |
| П = 10 | 4,568 | Суми | 8E-16 | 0,470955 | 3,6E-16 | 0,10000000 |
Середня квадратична похибка попередніх істинних похибок
mΔ’
= (0,470955/10)0.5 =0,2170151.
Коефіцієнт пропорційності
.
Середня квадратична похибка при генеруванні випадкових чисел з точністю с=0,1
mΔ ’ =(0.10000000/10)0.5 = 0.1000000.
Таблиця 3 . Побудова спотвореної моделі
| № п/п | Істинна Хіст. | Модель Уіст. | ∆іст. | Хспотв. |
| 1 | 1,6 | 18,021 | -0,207 | 1,393 |
| 2 | 2 | 13,864 | -0,031 | 1,969 |
| 3 | 2,1 | 13,167 | -0,04 | 2,060 |
| 4 | 2,3 | 11,986 | 0,149 | 2,449 |
| 5 | 2,5 | 10,898 | 0,0061 | 2,506 |
| 6 | 2,8 | 8,949 | -0,100 | 2,700 |
| 7 | 2,9 | 8,101 | 0,00149 | 2,901 |
| 8 | 3 | 7,108 | 0,071 | 3,071 |
| 9 | 3,1 | 5,939 | 0,01992 | 3,120 |
| 10 | 3,3 | 2,965 | 0,13052 | 3,431 |
| п = 10 | 25,6 | 100,998 | 3,6E-16 | 25,600 |
По даним спотвореної моделі виконують строге зрівноваження методом найменших квадратів і отримують ймовірніші моделі, яким роблять оцінку точності зрівноважених елементів і дають порівняльний аналіз на основі якого заключають на предмет поширення даної моделі для рішення проблеми в цілому.
3. Представлення системи нормальних рівнянь
В результаті проведеного експерименту ми маємо ряд результатів Хі , Уі , функціональну залежність між якими будемо шукати за допомогою поліному степені К, де коефіцієнти аі являються невідомими.
Тоді, система нормальних рівнянь буде
па0 +а1 [х ]+а2 [х2 ]+...+ат [хт ]- [у ] = 0,
а0
[х
]+а1
[х2
]+а2
[х3
]+...+ат
[хт+1
]- [ху
] = 0,
а0
[х2
]+а1
[х3
]+а2
[х4
]+...+ат
[хт+1
]- [х2у
] = 0,(3.1)
............................
а0 [хт ]+а1 [хт+1 ]+а2 [хт+2 ]+...+ат [х2т ]- [хт у ] = 0,
де знаком [ ] позначена сума відповідного елемента.
Для поліному третього порядку виду
y = ax 3 + bx 2 + cx + d (3.2)
система нормальних рівнянь буде
dn + c [ x ] + b [ x 2 ] + a [ x 3 ] - [ y ] = 0,
d[x] + c[x2 ] + b[x3 ] + a[x4 ] - [xy] = 0, (3.3)
d[x2 ] + c[x3 ] + b[x4 ] + a[x5 ] - [x2 y] = 0,
d[x3 ] + c[x4 ] + b[x5 ] + a[x6 ] - [x3 y] = 0,
або
a[x6 ] + b[x5 ] + c[x4 ] + d[x3 ] – [x3 y]= 0,
a[x5 ] + b[x4 ] + c[x3 ] + d[x2 ] – [x2 y]= 0, (3.4)
a[x4 ] + b[x3 ] + c[x2 ] + d[x] – [xy] = 0,
a [ x 3 ] + b [ x 2 ] + c [ x ] + dn – [ y ]= 0,
В подальшому будемо рішати систему лінійних нормальних рівнянь (3.3) або (3.4) одним із відомих в математиці способів.
4. Встановлення коефіцієнтів нормальних рівнянь
Приведемо розрахункову таблицю, на основі якої отримують коефіцієнти нормальних рівнянь.
Таблиця 4. Розрахунок коефіцієнтів нормальних рівнянь.
| № п/п | xоп | yіст | x˚ | x2 | x3 | x6 | x5 | x4 |
| 1 | 1,393 | 18,021 | 1 | 1,941 | 2,703 | 7,307 | 5,246 | 3,766 |
| 2 | 1,969 | 13,864 | 1 | 3,878 | 7,636 | 58,316 | 29,614 | 15,038 |
| 3 | 2,060 | 13,167 | 1 | 4,244 | 8,742 | 76,424 | 37,099 | 18,009 |
| 4 | 2,449 | 11,986 | 1 | 5,997 | 14,687 | 215,713 | 88,084 | 35,968 |
| 5 | 2,506 | 10,898 | 1 | 6,281 | 15,740 | 247,737 | 98,854 | 39,445 |
| 6 | 2,700 | 8,949 | 1 | 7,291 | 19,686 | 387,521 | 143,520 | 53,153 |
| 7 | 2,901 | 8,101 | 1 | 8,419 | 24,427 | 596,663 | 205,640 | 70,874 |
| 8 | 3,071 | 7,108 | 1 | 9,429 | 28,952 | 838,204 | 272,976 | 88,900 |
| 9 | 3,120 | 5,939 | 1 | 9,734 | 30,369 | 922,284 | 295,611 | 94,749 |
| 10 | 3,431 | 2,965 | 1 | 11,768 | 40,372 | 1629,884 | 475,113 | 138,496 |
| n=10 | 25,600 | 100,998 | 10 | 68,980 | 193,314 | 4980,054 | 1651,756 | 558,398 |
Продовження таблиці 4.
| № п/п | х3 у | х2 у | ху |
| 1 | 48,7148 | 34,97037 | 25,10381 |
| 2 | 105,8723 | 53,76312 | 27,3015 |
| 3 | 115,107 | 55,87662 | 27,1243 |
| 4 | 176,0406 | 71,88419 | 29,35309 |
| 5 | 171,5309 | 68,44533 | 27,31149 |
| 6 | 176,1661 | 65,24388 | 24,16335 |
| 7 | 197,8805 | 68,19956 | 23,50499 |
| 8 | 205,7891 | 67,01892 | 21,82591 |
| 9 | 180,3622 | 57,80981 | 18,52923 |
| 10 | 119,7025 | 34,89342 | 10,17148 |
| n=10 | 1497,166 | 578,105 | 234,389 |
Параметр S розраховується за формулою
S = x + x 2 + x 3 + x 0 - y (4.1)
Таким чином, на основі проведених розрахунків нами отримана слідуюча система нормальних рівнянь
10 d+25,6 c+68,980b+193,314a-101=0,
25 d+68,980c+193,314b+558,398a-234,389=0,
68,980d+193,314c+558,398b+1651,756a-578,105=0 , (4.2)
193,314d+558,398c+1651,756b+4980,054a-1496,166=0,
або
4980,054a+1651,756b +558,398c +193,314d -1496,166=0,
1651,756a+558,398b +193,314c +68,980d-578,105=0,
578,105a+100 ,998 b+68,980c+25,6d-234,389=0 , (4.3)193,314a+68,980b+25,6c+10d-101=0
5. Рішення системи лінійних рівнянь способом Крамера
Нехай, маємо систему лінійних рівнянь
a11 x1 + a12 x2 +…+ am xn = b1 ,
a21 x1 +a22 x2 +…+a2n xn =b2, (5.1)
………………………..
an1 x1 +an2 x2 +…+ann xn =bn .
Для того, щоб із цієї системи визначити невідомі хі , складемо із коефіцієнтів при невідомих визначних Δ, який називається визначником системи рівнянь (5.1)
| Δ= | а11 а12 ........... а1п а21 а22 ........... а2п ................................................ ап1 ап2 ........... апп |
(5.2) |
Помножимо ліву і праву частини рівності (5.2) на хі . В лівій частині будемо мати Δ хі , в правій же частині введемо у всі члени і –го стовпчика визначника акі множник хі
| Δ · хі = | а11 а12 ... а1і хі ... а1п а21 а22 ... а2і хі ... а2п ....................................... ап1 ап2 ...апі хі ... апп |
(5.3) |
Після до і – го стовпчика визначника (5.3) додамо всі остальні стовпчики, помножені відповідно на х1 , х2 , ... , хп . Величина визначника від цього не зміниться. Тоді і -й стовпчик представить собою ліву частину системи рівнянь (5.1).
Замінимо його вільними членами цієї системи і позначимо через Δі
| Δ · хі = Δі = | а11 а12 ... b 1 ... а1п а21 а22 ... b 2 ... а2п ....................................... ап1 ап2 ... bn ... апп |
(5.4) |
Звідки:
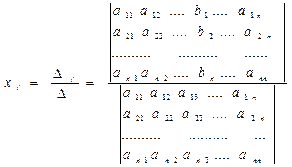(5.5)
Формула (5.5) дає можливість визначити кожне невідоме системи лінійних рівнянь (5.1).
Якщо вільні члени системи лінійних рівнянь рівні нулю, то вона буде системою лінійних однорідних рівнянь.
Система лінійних однорідних рівнянь може мати рішення відмінне від нульового, якщо визначник системи Δ рівний нулю.
Для системи чотирьох лінійних рівнянь
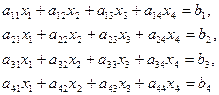(5.6)
якщо визначник системи Δ не дорівнює нулю
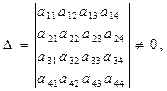(5.7)
то система визначена і по Крамеру її невідомі виражаються формулами
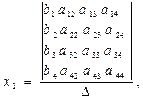(5.8)
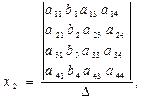(5.9)
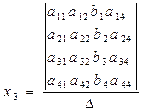, (5.10)
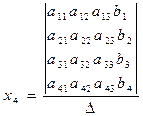, (5.11)
Як бачимо, що
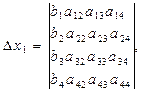(5.12)
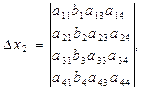(5.13)
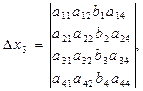(5.14)
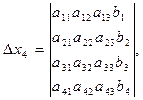(5.15)
Приведемо формулу знаходження визначника четвертого порядку
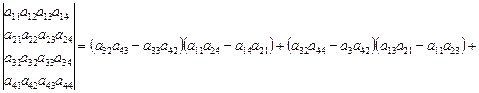
(5.16)
І в нашому випадку
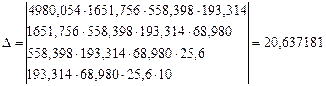
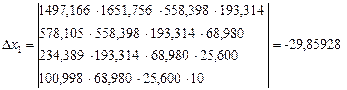
тоді невідомий коефіцієнт а при х3 буде
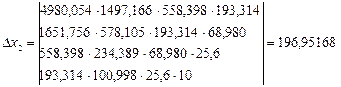
Невідомий коефіцієнт b при х2 буде
;
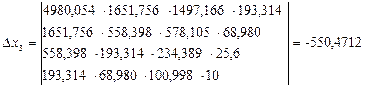
і невідомий коефіцієнт с при х буде:
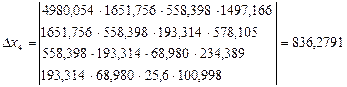
Коефіцієнт d буде
d = Δx4 /Δ =40,522935
Таким чином, на основі проведених досліджень, математична модель впливу ситуативної тривожності хі на характеристики пам’яті уі виражається формулою
(5.17)
6. Контроль зрівноваження
Підставляючи отриманні значення коефіцієнтів а , b , c , d у формули (4.3), отримаємо слідуючі результати.
| х3 ] | x2 ] | x ] | х0 ] | Y | Контроль |
| 4980,054 | 1651,756 | 558,398 | 193,314 | 1496,166 | 1496,166 |
| 1651,756 | 558,398 | 193,314 | 68,980 | 578,105 | 578,105 |
| 558,398 | 193,314 | 68,980 | 25,6 | 234,389 | 234,389 |
| 193,314 | 68,980 | 25,6 | 10 | 100,998 | 100,998 |
| A -1,446868 | B 9,543536 | C -26,67376 | D 40,522935 |
7. Оцінка точності параметрів, отриманих із рішення системи нормальних рівнянь
Середні квадратичні похибки визначаємих невідомих х1 , х2 , х3 , х4 , розраховуються за формулами
, (7.1.)
, (7.2)
, (7.3)
, (7.4)
де тх1 , тх2 , тх3 , тх4 – середні квадратичні похибки невідомих, що визначаємо х1 , х2 , х3 , х4 , т – середня квадратична похибка одиниці ваги, яка розраховується за формулою
, (7.5)
У формулі (7.5) п – число значень факторних і результуючих ознак (х і у ), к – степінь поліному. В нашому випадку п =10; к =3. V - різниця між вихідним значенням уі і вирахуваним значенням у ΄ за отриманою нами формулою (5.17);
, (7.6)
А11 , А22 , А33 , А44 – алгебраїчні доповнення першого, другого, третього і четвертого діагональних елементів
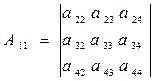, (7.7)
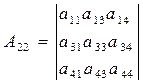, (7.8)
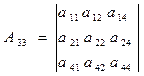, (7.9)
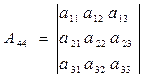, (7.10)
де
(7.11)
Приведемо формулу розкриття визначника третього порядку
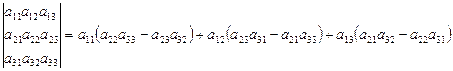. (7.12)
І в нашому випадку отримаємо
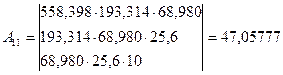
Величина оберненої ваги
(1/Px11
)0.5
= 10.399008.
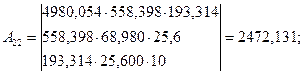
(1/Px2
)0.2
= 71,748385.
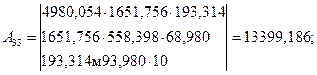
; (1/Px33
)0.5
=843.11354
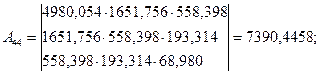
; (1/Px44
)0.5
= 256.49004.
Підставляючи у виведену нами формулу (5.17) значення Х спотвореної моделі, отримаємо розрахункові значення у΄ , які будуть дещо відрізнятись від вихідних значень У .
Таблиця 6 . Порівняльний аналіз результатів строгого зрівноваження.
| № п/п | Хвихідне | Увихідне | У΄зрівноваж.. | V =Уі - Уі ΄ | V 2 |
| 1 | 1,6 | 18,021 | 17,974 | 0,04708 | 0,00222 |
| 2 | 2 | 13,864 | 13,956 | -0,0918 | 0,00843 |
| 3 | 2,1 | 13,167 | 13,426 | -0,2586 | 0,06686 |
| 4 | 2,3 | 11,986 | 11,186 | 0,80025 | 0,6404 |
| 5 | 2,5 | 10,898 | 10,841 | 0,05685 | 0,00323 |
| 6 | 2,8 | 8,949 | 9,5967 | -0,6477 | 0,41946 |
| 7 | 2,9 | 8,101 | 8,1308 | -0,0298 | 0,00089 |
| 8 | 3 | 7,108 | 6,7115 | 0,39646 | 0,15718 |
| 9 | 3,1 | 5,939 | 6,2588 | -0,3198 | 0,10227 |
| 10 | 3,3 | 2,965 | 2,918 | 0,047 | 0,00221 |
| п=10 | 25,6 | 100,998 | 101,00 | 0,000 | 1,403 |
Тоді, середня квадратична похибка одиниці ваги буде
Середня квадратична похибка визначення коефіцієнта а
Середня квадратична похибка визначення коефіцієнта b
Середня квадратична похибка визначення коефіцієнта с
Середня квадратична похибка визначення коефіцієнта d
В исновки.
На основі проведених досліджень в даній роботі:
1. Генеровані випадкові числа, які приведено до нормованої досліджуваної точності.
2. На основі істинної моделі і генерованих істинних похибок побудована спотворена модель впливу ситуативної тривожності на характеристики пам’яті.
3. Математична модель апроксимована по способу найменших квадратів кубічним поліномом.
4. Отримана формула
залежності характеристик пам’яті У
від ситуативної тривожності Х
.
5. Встановлено, що середня квадратична похибка одиниці ваги за результатами зрівноваження складає 
балів по шкалі Спірбергера:
середня квадратична похибка визначення коефіцієнта а при х3 та = 0,676073;
середня квадратична похибка визначення коефіцієнта b при х2 т b = 4,900198;
середня квадратична похибка визначення коефіцієнта с при х тс = 11,4082;
середня квадратична похибка визначення коефіцієнта d тd = 8,472532;
6. Розроблена методика підготовки істинних похибок наперед заданої точності.
7. Дана робота відкриває дорогу для проведення досліджень методом статистичних випробовувань Монте Карло.
8. Вона дає можливість охопити велику аудиторію, тому що генеруються похибки індивідуально і вони не повторюються в других моделях.
9. Робота виконується вперше. Нам невідомі літературні джерела, де б виконувались аналогічні дослідження в царині психології.
Література.
1. Максименко С.Д., Е.Л. Носенко Експериментальна психологія (дидактичний тезаурус). Навчальний посібник –К.: МАУП, 2004, -128 с.
2. Літнарович Р.М. Основи математики. Дослідження впливу ситуативної тривожності на характеристики пам’яті. Навчальний посібник для студентів Педагогічного факультету. Частина 2. МЕГУ, Рівне, 2006,-270.
3. Літнарович Р.М. Основи математики. Дослідження результатів психолого-педагогічного експерименту логарифмічною функцією. Частина 3. МЕГУ, Рівне, 2006 –19с.
4. Літнарович Р.М. Основи математики. Дослідження результатів психолого-педагогічного експерименту експоненціальною функцією. Частина 4. МЕГУ, Рівне, 2006 –17с.
5. Літнарович Р.М. Основи математики. Дослідження результатів психолого-педагогічного експерименту степенною функцією. Частина 5. МЕГУ, Рівне, 2006, - 17с.
6. Літнарович Р.М. Дослідження точності апроксимації результатів психолого-педагогічного експерименту методом статистичних випробувань Монте Карло.Ч.1.МЕГУ, Рівне,2006,-45с.
Додаток 1
Генерування псевдовипадкових чисел, підпорядкування їх нормальному закону розподілу і розрахунок істинних похибок
| 0,008 | 0,457 | -0,449 | 0,20174 | -0,207 | 0,04283629 |
| 0,39 | 0,457 | -0,067 | 0,004457 | -0,031 | 0,00094637 |
| 0,37 | 0,457 | -0,087 | 0,007527 | -0,04 | 0,00159833 |
| 0,78 | 0,457 | 0,3232 | 0,104484 | 0,149 | 0,02218548 |
| 0,47 | 0,457 | 0,0132 | 0,000175 | 0,0061 | 0,00003722 |
| 0,24 | 0,457 | -0,217 | 0,046985 | -0,100 | 0,00997656 |
| 0,46 | 0,457 | 0,0032 | 1,05E-05 | 0,00149 | 0,00000223 |
| 0,61 | 0,457 | 0,1532 | 0,023482 | 0,071 | 0,00498610 |
| 0,5 | 0,457 | 0,0432 | 0,00187 | 0,01992 | 0,00039699 |
| 0,74 | 0,457 | 0,2832 | 0,080225 | 0,13052 | 0,01703443 |
| 4,568 | Суми | 8E-16 | 0,470955 | 3,6E-16 | 0,10000000 |
| A | B | C | D | E | F |
Додаток 2.Побудова спотвореної моделі
| 1,393 | 1,6 | 18,021 | -0,207 | 1,393 |
| 1,969 | 2 | 13,864 | -0,031 | 1,969 |
| 2,060 | 2,1 | 13,167 | -0,04 | 2,060 |
| 2,449 | 2,3 | 11,986 | 0,149 | 2,449 |
| 2,506 | 2,5 | 10,898 | 0,0061 | 2,506 |
| 2,700 | 2,8 | 8,949 | -0,100 | 2,700 |
| 2,901 | 2,9 | 8,101 | 0,00149 | 2,901 |
| 3,071 | 3 | 7,108 | 0,071 | 3,071 |
| 3,120 | 3,1 | 5,939 | 0,01992 | 3,120 |
| 3,431 | 3,3 | 2,965 | 0,13052 | 3,431 |
| 25,600 | 25,6 | 100,998 | 3,6E-16 | 25,600 |
| I | G | H | E | I |
| Хспотв. | Xіст. | Уіст. | Істинні похиб. | Хспотв. |
Додаток 3.Розрахункова таблиця
| 1 | 1,941 | 2,703 | 3,766 | 5,246 | 7,307 | 25,10381 | 34,97037 |
| 1 | 3,878 | 7,636 | 15,038 | 29,614 | 58,316 | 27,3015 | 53,76312 |
| 1 | 4,244 | 8,742 | 18,009 | 37,099 | 76,424 | 27,1243 | 55,87662 |
| 1 | 5,997 | 14,687 | 35,968 | 88,084 | 215,713 | 29,35309 | 71,88419 |
| 1 | 6,281 | 15,740 | 39,445 | 98,854 | 247,737 | 27,31149 | 68,44533 |
| 1 | 7,291 | 19,686 | 53,153 | 143,520 | 387,521 | 24,16335 | 65,24388 |
| 1 | 8,419 | 24,427 | 70,874 | 205,640 | 596,663 | 23,50499 | 68,19956 |
| 1 | 9,429 | 28,952 | 88,900 | 272,976 | 838,204 | 21,82591 | 67,01892 |
| 1 | 9,734 | 30,369 | 94,749 | 295,611 | 922,284 | 18,52923 | 57,80981 |
| 1 | 11,768 | 40,372 | 138,496 | 475,113 | 1629,884 | 10,17148 | 34,89342 |
| 10 | 68,980 | 193,314 | 558,398 | 1651,756 | 4980,054 | 234,389 | 578,105 |
| J | K | L | M | N | O | P | Q |
| X0 | X^2 | X^3 | X^4 | X^5 | X^6 | YX | YX^2 |
Продовження розрахункової таблиці
| 48,7148 | 17,974 | 0,04708 | 0,00222 | 324,7564 |
| 105,8723 | 13,956 | -0,0918 | 0,00843 | 192,2105 |
| 115,107 | 13,426 | -0,2586 | 0,06686 | 173,3699 |
| 176,0406 | 11,186 | 0,80025 | 0,6404 | 143,6642 |
| 171,5309 | 10,841 | 0,05685 | 0,00323 | 118,7664 |
| 176,1661 | 9,5967 | -0,6477 | 0,41946 | 80,0846 |
| 197,8805 | 8,1308 | -0,0298 | 0,00089 | 65,6262 |
| 205,7891 | 6,7115 | 0,39646 | 0,15718 | 50,52366 |
| 180,3622 | 6,2588 | -0,3198 | 0,10227 | 35,27172 |
| 119,7025 | 2,918 | 0,047 | 0,00221 | 8,791225 |
| 1497,166 | 101,00 | 0,000 | 1,403 | 1193,065 |
| R | S | T | U | V |
| YX^3 | Yзрівн. | V=Yi-Yз | VV | YY |
Додаток 5. Розрахунок визначників
| 4980,054 | 1651,756 | 558,398 | 193,314 |
| 1651,756 | 558,398 | 193,314 | 68,980 |
| 558,398 | 193,314 | 68,980 | 25,6 |
| 193,314 | 68,980 | 25,6 | 10 |
| D= | 20,637181 | ||
| 1497,166 | 1651,756 | 558,398 | 193,314 |
| 578,105 | 558,398 | 193,314 | 68,980 |
| 234,389 | 193,314 | 68,980 | 25,600 |
| 100,998 | 68,980 | 25,600 | 10 |
| D1= | -29,85928 | ||
| 4980,054 | 1497,166 | 558,398 | 193,314 |
| 1651,756 | 578,105 | 193,314 | 68,980 |
| 558,398 | 234,389 | 68,980 | 25,6 |
| 193,314 | 100,998 | 25,6 | 10 |
| D2= | 196,95168 | ||
| 4980,054 | 1651,756 | 1497,166 | 193,314 |
| 1651,756 | 558,398 | 578,105 | 68,980 |
| 558,398 | 193,314 | 234,389 | 25,6 |
| 193,314 | 68,980 | 100,998 | 10 |
| D3= | -550,4712 | ||
| 4980,054 | 1651,756 | 558,398 | 1497,166 |
| 1651,756 | 558,398 | 193,314 | 578,105 |
| 558,398 | 193,314 | 68,980 | 234,389 |
| 193,314 | 68,980 | 25,6 | 100,998 |
| D4= | 836,2791 |
Додаток 6.Вільні члени нормальних рівнянь
| 1497,166 |
| 578,105 |
| 234,389 |
| 100,998 |
Додаток 7.Розрахунок коефіцієнтів апроксимуючого поліному
| a=D1/D= | -1,446868 |
| b=D2/D= | 9,543536 |
| c=D3/D= | -26,67376 |
| d=D4/D= | 40,522935 |
| Y=aX^3+bX^2+cX+d | |
Нами виведена формула за результатами теоретичних досліджень
Додаток 8.Знаходження алгебраїчних доповнень
| 4980,054 | 1651,756 | 558,398 | ||
| A44= | 7390,4458 | 1651,756 | 558,398 | 193,314 |
| 558,398 | 193,314 | 68,980 | ||
| 4980,054 | 558,398 | 193,314 | ||
| A22= | 2472,131 | 558,398 | 68,980 | 25,6 |
| 193,314 | 25,600 | 10 | ||
| A33= | 13399,186 | 4980,054 | 1651,756 | 193,314 |
| 1651,756 | 558,398 | 68,980 | ||
| 193,314 | 68,980 | 10 | ||
| 558,398 | 193,314 | 68,980 | ||
| A11= | 47,05777 | 193,314 | 68,980 | 25,6 |
| 68,980 | 25,6 | 10 | ||
Додаток |
9. |
|||
| КОНТРОЛЬ ЗРІВНОВАЖЕННЯ: | ||||
|
||||
| 1,40315 | ||||
| 1,403150 | ||||
| 0,000000 | ||||
Додаток 10.Оцінка точності зрівноважених елементів
| Середня | квадратична похибка одиниці ваги | |||
| m= | 0,447716 | |||
| Середня | квадратична похибка коефіцієнта а | |||
| ma= | 0,676073 | |||
| Се редня квадратична похибка коефіцієнта в | ||||
| mb= | 4,900198 | |||
| Середня квадратична похибка коефіцієнта с | ||||
| mc= | 11,4082 | |||
| Середня квадратична похибка коефіцієнта d | ||||
| md= | 8,472532 | |||
Абрамович К.П.
Дослідження точності впливу ситуативної тривожності на характеристики пам’яті методом статистичних випробувань Монте Карло
Модель ППП 051- 1
Комп’ютерний набір, Верстка і макетування та дизайн в редакторі Microsoft® Office® Word 2003 Абрамович Катерина
Міжнародний Економіко-Гуманітарний Університет ім.акад. С.Дем’янчука
Кафедра математичного моделювання
33027,м.Рівне,вул..акад. С.Дем’янчука,4.