| Скачать .docx |
Реферат: Групповые дисперсии. Агрегатный индекс себестоимости
Задача 1. По данным о производственной деятельности ЗАО определить средние затраты на 1 руб. произведенной продукции в целом по ЗАО.
Таблица 1 - Исходные данные
| Предприятие |
Общие затраты на производство, млн. руб. |
Затраты на 1 руб. произведенной продукции, коп. |
| 1 |
2,12 |
75 |
| 2 |
8,22 |
71 |
| 3 |
4,43 |
73 |
Решение:
Для определения средних затрат на 1 рубль произведенной продукции необходимо воспользоваться средней гармонической, так как у нас известен числитель и неизвестен знаменатель. Для определения средней строим вспомогательную таблицу.
Таблица 2 - Вспомогательная
| Предприятие |
Общие затраты на производство, млн. руб., (Wi) |
Затраты на 1 руб. произведенной продукции, руб. (Xi) |
Объем произведенной продукции, млн руб. (Wi/Xi) |
| 1 |
2,12 |
0,75 |
2,83 |
| 2 |
8,22 |
0,71 |
11,58 |
| 3 |
4,43 |
0,73 |
6,07 |
| Итого: |
14,77 |
20,47 |
Так средние затраты на 1 рубль продукции рассчитываются по формуле
 ,
,
где х
- признак (варианта) - индивидуальные значения усредняемого признака; ![]() показатель, представляющий собой реально существующий экономический показатель равный х∙
f:
показатель, представляющий собой реально существующий экономический показатель равный х∙
f:
Данные берутся из таблицы.

Ответ: Средние затраты на 1 рубль произведенной продукции равны 72 коп.
Задача 2. По данным 10% -го выборочного обследования рабочих по стажу работы, результаты которого приведены ниже, определить:
1) относительную величину структуры численности рабочих;
2) моду и медиану стажа рабочих;
3) средний стаж рабочих цеха;
4) размах вариации;
5) среднее линейное отклонение;
6) дисперсию;
7) среднее квадратическое отклонение;
8) коэффициент вариации;
9) с вероятностью 0,997 пределы, в которых изменяется средний стаж рабочих в целом по предприятию;
10) с вероятностью 0,997 пределы, в которых изменяется доля рабочих, имеющих стаж работы более 10 лет в целом по предприятию. Сделать выводы.
Таблица 3 - Исходные данные
| Группы рабочих по стажу, лет |
До 2 |
2 - 4 |
4 - 6 |
6 - 8 |
8 - 10 |
10 - 12 |
12 - 14 |
| Число рабочих |
6 |
8 |
12 |
24 |
17 |
8 |
5 |
Решение:
1) Находим относительную величину структуры численности рабочих, для этого строим следующую таблицу.
Таблица 4 - Относительная структура численности рабочих
| Группы рабочих по стажу, лет |
Число рабочих |
Структура,% |
| До 2 |
6 |
7,5 |
| 2 - 4 |
8 |
10 |
| 4 - 6 |
12 |
15 |
| 6 - 8 |
24 |
30 |
| 8 - 10 |
17 |
21,25 |
| 10 - 12 |
8 |
10 |
| 12 - 14 |
5 |
6,25 |
| Итого: |
80 |
100 |
2) Находим моду и медиану стажа рабочих. Для этого строим вспомогательную таблицу.
Таблица 5 - Вспомогательная.
| Группы рабочих по стажу, лет |
Число рабочих (fi) |
Середина интервала, (xi) |
xi*fi |
fi. накопл |
| До 2 |
6 |
1 |
6 |
6 |
| 2 - 4 |
8 |
3 |
24 |
14 |
| 4 - 6 |
12 |
5 |
60 |
26 |
| 6 - 8 |
24 |
7 |
168 |
50>40 |
| 8 - 10 |
17 |
9 |
153 |
67 |
| 10 - 12 |
8 |
11 |
88 |
75 |
| 12 - 14 |
5 |
13 |
65 |
80 |
| Итого: |
80 |
564 |
Мода - это наиболее часто встречающееся значение ряда:
![]() ,
,
где ![]() - мода;
- мода; ![]() - нижняя граница модального интервала. Интервал с максимальной частотой является модальным;
- нижняя граница модального интервала. Интервал с максимальной частотой является модальным; ![]() - шаг модального интервала, который определяется разницей его границ; fmo
- частота модального интервала; fmo
-1
- частота интервала, предшествующего модальному; fmo
+1
- частота интервала, последующего за модальным.
- шаг модального интервала, который определяется разницей его границ; fmo
- частота модального интервала; fmo
-1
- частота интервала, предшествующего модальному; fmo
+1
- частота интервала, последующего за модальным.
Медианой является значение признака х , которое больше или равно и одновременно меньше или равно половине остальных элементов ряда распределения. Медиана делит ряд на две равные части:
 ,
,
где xme
- нижняя граница медианного интервала. Интервал, в котором находится порядковый номер медианы, является медианным. Для его определения необходимо подсчитать величину ![]() . Интервал с накопленной частотой равной величине
. Интервал с накопленной частотой равной величине![]() является медианным; i
- шаг медианного интервала, который определяется разницей его границ;
является медианным; i
- шаг медианного интервала, который определяется разницей его границ; ![]() - сумма частот вариационного ряда; Sme
-1
- сумма частот вариационного ряда; Sme
-1
![]() - сумма накопленных частот в домедианном интервале; fme
- частота медианного интервала.
- сумма накопленных частот в домедианном интервале; fme
- частота медианного интервала.
3) Находим средний стаж рабочих цеха:
![]() ,
,
где х - признак (варианта) - индивидуальные значения усредняемого признака, в качестве которого берется середина интервала, определяемая как полусумма его границ;
f - частота, т.е. числа, показывающие, сколько раз повторяется та или иная варианта.
Сравниваем полученные значения, в нашем случае получаем:
![]() ,
,
что говорит о левосторонней асимметрии.
По этим данным можно сделать вывод о том, что средний стаж рабочих составляет 7,05 лет; наиболее часто встречаются рабочие со стажем 7,263 года. Кроме того, половина рабочих имеет стаж более 7,166 лет, а другая - менее 7,166 лет.
4) Находим размах вариации.
Размах вариации:
![]() ,
,
где х max - максимальное значение признака; х min - минимальное значение признака.
Так, разница между максимальным значением признака и минимальным составляет 12.
5) Находим среднее линейное отклонение:
![]() ,
,
где ![]() - индивидуальные значения признака,
- индивидуальные значения признака, ![]() - средняя величина; f
- частота.
- средняя величина; f
- частота.
Строим расчетную таблицу.
Таблица 6 - Расчетная
| Середина интервала, (xi) |
|
Число рабочих (fi) |
|
|
|
| 1 |
6,05 |
6 |
36,3 |
36,60 |
219,62 |
| 3 |
4,05 |
8 |
32,4 |
16,40 |
131,22 |
| 5 |
2,05 |
12 |
24,6 |
4, 20 |
50,43 |
| 7 |
0,05 |
24 |
1,2 |
0,00 |
0,06 |
| 9 |
1,95 |
17 |
33,15 |
3,80 |
64,64 |
| 11 |
3,95 |
8 |
31,6 |
15,60 |
124,82 |
| 13 |
5,95 |
5 |
29,75 |
35,40 |
177,01 |
|
|
80 |
189 |
767,80 |
![]() .
.
Так средний абсолютный разброс значений вокруг средней составил 2,362. То есть работники отличаются по стажу друг от друга в среднем на 2,362 года.
6) Находим дисперсию:
![]()
7) Находим среднее квадратическое отклонение:
 .
.
Средний разброс стажа от среднего стажа в 7,05 лет составляет 3,097.
8) Находим коэффициент вариации:
![]() .
.
Так как коэффициент вариации больше 33%, то это говорит о высокой степени неоднородности совокупности.
9) Находим с вероятностью 0,997 пределы, в которых изменяется средний стаж рабочих в целом по предприятию.
Границы генеральной средней:
![]() ,
,
где ![]() - генеральная средняя,
- генеральная средняя, ![]() - выборочная средняя, Δ
- выборочная средняя, Δ![]() - предельная ошибка выборочной средней:
- предельная ошибка выборочной средней:
 ,
,
где ![]() - коэффициент доверия, зависящий от вероятности исследования: при вероятности 0,954 t
= 2, а при вероятности 0,997 t
= 3; n
- объем выборочной совокупности;
- коэффициент доверия, зависящий от вероятности исследования: при вероятности 0,954 t
= 2, а при вероятности 0,997 t
= 3; n
- объем выборочной совокупности;
N - объем генеральной совокупности;
![]() - доля отбора единиц из генеральной совокупности в выборочную;
- доля отбора единиц из генеральной совокупности в выборочную;
![]() - дисперсия признака выборочной совокупности.
- дисперсия признака выборочной совокупности.
Так, находим предельную ошибку выборочной средней:
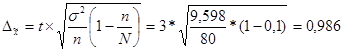 .
.
Тогда пределы, в которых изменяется средний стаж рабочего, будут:
![]()
10) с вероятностью 0,997 пределы, в которых изменяется доля рабочих, имеющих стаж работы более 10 лет в целом по предприятию. Сделать выводы.
Границы генеральной доли:
![]() ,
,
где р
- генеральная доля, ![]() - выборочная доля:
- выборочная доля:
![]() ,
,
где ![]() - число единиц, обладающих данным или изучаемым признаком; n
- объем выборочной совокупности;
- число единиц, обладающих данным или изучаемым признаком; n
- объем выборочной совокупности; ![]() - предельная ошибка доли:
- предельная ошибка доли:
 ,
,
где n - объем выборочной совокупности;
N - объем генеральной совокупности;
![]() - доля отбора единиц из генеральной совокупности в выборочную.
- доля отбора единиц из генеральной совокупности в выборочную.
Тогда доля работников со стажем больше 10 лет будет изменяться в пределах:
![]()
Задача 3. Для установления зависимости между урожайностью и сортом винограда в одном из хозяйств на основе выборки определили урожай на 8 кустах винограда.
Таблица 7 - Исходные данные
| Сорт винограда |
Число проверенных кустов |
Урожай с куста, кг |
||
| № куста винограда |
||||
| 1 |
2 |
3 |
||
| А |
3 |
6 |
5 |
7 |
| Б |
3 |
7 |
6 |
8 |
| В |
2 |
9 |
7 |
- |
Исчислить общую, межгрупповую и среднюю из групповых дисперсий.
Определите связь между сортом и его урожайностью, рассчитав коэффициент детерминации.
Сделать вывод.
Решение:
![]() ,
,
где ![]() - общая дисперсия;
- общая дисперсия; ![]() - средняя из групповых дисперсий;
- средняя из групповых дисперсий; ![]() - межгрупповая дисперсия.
- межгрупповая дисперсия.
Величина общей дисперсии ![]() характеризует вариацию признака под влиянием всех факторов, формирующих уровень признака у единиц совокупности.
характеризует вариацию признака под влиянием всех факторов, формирующих уровень признака у единиц совокупности.
![]()
где ![]() - общая средняя арифметическая для всей изучаемой совокупности;
- общая средняя арифметическая для всей изучаемой совокупности; ![]() _ значение признака (варианта).
_ значение признака (варианта).
Средняя из групповых дисперсий ![]() характеризует случайную вариацию, возникающую под влиянием других неучтенных факторов, и не зависит от условия (признака-фактора), положенного в основу группировки;
характеризует случайную вариацию, возникающую под влиянием других неучтенных факторов, и не зависит от условия (признака-фактора), положенного в основу группировки;
 ,
,
где fi
- число единиц в определенной i - й
группе; ![]() - дисперсия по определенной i - й
группе:
- дисперсия по определенной i - й
группе:
![]() ,
,
где ![]() - средняя по определенной i - й
группе.
- средняя по определенной i - й
группе.
Межгрупповая дисперсия отражает систематическую вариацию, т.е. те различия в величине изучаемого признака, которые возникают под влиянием фактора, положенного в основу группировки:
![]() .
.
Находим среднюю из групповых дисперсий. Для этого находим дисперсию по каждой группе. Строим расчетную таблицу.
Таблица 8 - Расчетная
| Сорт винограда |
Число проверенных кустов (fi) |
Урожай с куста, кг |
Среднее значение |
||
| № куста винограда |
|||||
| 1 |
2 |
3 |
|||
| А |
3 |
6 |
5 |
7 |
6 |
|
|
0 |
-1 |
1 |
||
|
|
0 |
1 |
1 |
Сумма |
|
|
|
0 |
1 |
1 |
2 |
|
| Б |
3 |
7 |
6 |
8 |
7 |
|
|
0 |
-1 |
1 |
||
|
|
0 |
1 |
1 |
Сумма |
|
|
|
0 |
1 |
1 |
2 |
|
| В |
2 |
9 |
7 |
- |
8 |
|
|
1 |
-1 |
|||
|
|
1 |
1 |
Сумма |
||
|
|
1 |
1 |
2 |
||
Получаем следующие значения, которые сводим в таблицу.
Таблица 9 - Десперсии по группам
| Сорт винограда |
Число проверенных кустов (fi) |
|
|
| А |
3 |
0,667 |
2 |
| Б |
3 |
0,667 |
2 |
| В |
2 |
1,000 |
2 |
| Итого: |
8 |
6 |
Рассчитываем среднюю из групповых дисперсий:
 ,
,
Таким образом, разброс значений за счет неучтенных факторов составляет 0,75 кг.
Находим межгрупповую дисперсию.
Для этого строим следующую вспомогательную таблицу.
Таблица 10 - Вспомогательная
| Сорт винограда |
Число проверенных кустов |
Урожай с куста, кг |
Среднее по группе |
|
|
|
||
| № куста винограда |
||||||||
| 1 |
2 |
3 |
||||||
| А |
3 |
6 |
5 |
7 |
6 |
-1 |
1 |
3 |
| Б |
3 |
7 |
6 |
8 |
7 |
0 |
0 |
0 |
| В |
2 |
9 |
7 |
- |
8 |
1 |
1 |
2 |
| Итого |
8 |
Общая средняя |
7 |
2 |
5 |
|||
![]() .
.
Так, из-за того, что виноград разных сортов, урожайность в среднем отклоняется от среднего значения на 0,625 кг.
Находим общую дисперсию:
![]() =0,75+0,625=1,375.
=0,75+0,625=1,375.
Так, под влиянием всех факторов урожайность отклоняется от среднего значения на 1,375 кг.
Задача 4. Имеются следующие данные о выпуске продукции на одном из предприятий.
Таблица 11 - Исходные данные
| Виды продукции |
Затраты на производство, тыс. руб. |
Произведено, тыс. шт. |
||
| I квартал |
II квартал |
I квартал |
II квартал |
|
| А |
5 600 |
5 850 |
80 |
90 |
| Б |
4 060 |
4 675 |
70 |
85 |
| В |
6 500 |
6 860 |
100 |
98 |
Определить:
1) агрегатный индекс себестоимости, агрегатный индекс физического объема продукции и общий индекс затрат на производство;
2) абсолютное изменение затрат на производство - общее и за счет изменения себестоимости единицы продукции и физического объема производства. Сделать выводы.
Решение:
1) Находим агрегатный индекс себестоимости, агрегатный индекс физического объема продукции и общий индекс затрат на производство. Для этого строим расчетную таблицу.
Таблица 12 - Расчетная
| Виды продукции |
Затраты на производство, тыс. руб. |
Произведено, тыс. шт. |
Расчетные показатели |
||||
| I квартал (z0) |
II квартал (z1) |
I квартал (q0) |
II квартал (q1) |
z0*q0 |
z1*q1 |
z0*q1 |
|
| А |
5 600 |
5 850 |
80 |
90 |
448000 |
526500 |
504000 |
| Б |
4 060 |
4 675 |
70 |
85 |
284200 |
397375 |
345100 |
| В |
6 500 |
6 860 |
100 |
98 |
650000 |
672280 |
637000 |
| Итого: |
|
|
|
|
1382200 |
1596155 |
1486100 |
Агрегатный индекс себестоимости:
![]() ,
,
где ![]() - себестоимость в отчетном и базисном периоде соответственно;
- себестоимость в отчетном и базисном периоде соответственно; ![]() - физический объем производства в отчетном периоде;
- физический объем производства в отчетном периоде;
Агрегатный индекс физического объема произведенной продукции:
![]() ,
,
где ![]() ,
q0
- физический объем производства в отчетном и базисном периоде соответственно;
,
q0
- физический объем производства в отчетном и базисном периоде соответственно; ![]() - себестоимость в отчетном периоде;
- себестоимость в отчетном периоде;
Агрегатный индекс затрат на производство равен:
![]() .
.
Таким образом, изменение себестоимости каждого вида продукции увеличили общие затраты производства на 7,4%. Под влиянием изменения объемов производства общие затраты выросли на 7,5%. А под влиянием этих обоих факторов - на 15,4%.
2) Находим абсолютное изменение затрат на производство - общее и за счет изменения себестоимости единицы продукции и физического объема производства.
Общее абсолютное изменение затрат на производство:
![]() =1596155-1382200=213955 млн. руб.
=1596155-1382200=213955 млн. руб.
Абсолютное изменение затрат на производство за счет изменения себестоимости, т.е. роль себестоимости в изменении затрат на производство:
![]() =1596155-1486100=110055 млн. руб.
=1596155-1486100=110055 млн. руб.
Абсолютное изменение затрат на производство за счет изменения физического объема производства, т.е. роль физического объема в изменении затрат на производство:
![]() =1486100-1382200=103900 млн. руб.
=1486100-1382200=103900 млн. руб.
103900+110055=213955
Таким образом, изменение в себестоимости в большей степени повлияло на изменение общих затрат на производство.
Задача 5. Имеются следующие данные о затратах на производство продукции растениеводства.
Таблица 13 - Исходные данные
| Группы сельскохозяйственных культур |
Общие затраты на производство, (тыс. руб.) в периоде |
Индивидуальный индекс себестоимости |
|
| Базисном (z0*q0) |
Отчетном (z1*q1) |
||
| Озимые зерновые |
223,0 |
242,0 |
1,02 |
| Зернобобовые |
47,2 |
49,0 |
1,05 |
Вычислить общие индексы затрат на производство, себестоимости и физического объема. Сделать выводы.
Решение:
Для нахождения индексов строим вспомогательную таблицу.
Таблица 14 - Расчетная
| Группы сельскохозяйственных культур |
Общие затраты на производство, (тыс. руб.) в периоде |
Индивидуальный индекс себестоимости (ip) |
Расчетные показатели |
||
| Базисном (z0*q0) |
Отчетном (z1*q1) |
ip*z0*q0 |
(z1*q1) /ip |
||
| Озимые зерновые |
223 |
242 |
1,02 |
227,46 |
237,25 |
| Зернобобовые |
47,2 |
49 |
1,05 |
49,56 |
46,67 |
| Итого |
270,2 |
291 |
277,02 |
283,92 |
|
Средний арифметический индекс физического объема произведенной продукции:
![]() ,
,
где ![]() - индивидуальный индекс физического объема произведенной продукции; z0,
q0
- себестоимость, физический объем произведенной продукции в базисном периоде соответственно;
- индивидуальный индекс физического объема произведенной продукции; z0,
q0
- себестоимость, физический объем произведенной продукции в базисном периоде соответственно; ![]() - затраты на производство в базисном периоде.
- затраты на производство в базисном периоде.
Так, за счет изменения объемов производства общие затраты на производство выросли на 2,5%.
Средний гармонический индекс себестоимости:
 ,
,
где ![]() - индивидуальный индекс себестоимости; z1,
q1
- себестоимость, физический объем произведенной продукции в отчетном периоде соответственно;
- индивидуальный индекс себестоимости; z1,
q1
- себестоимость, физический объем произведенной продукции в отчетном периоде соответственно; ![]() товарооборот (стоимость) реализованной продукции в отчетном периоде.
товарооборот (стоимость) реализованной продукции в отчетном периоде.
Так, за счет изменения в себестоимости каждой продукции общие затраты на производство продукции выросли на 2,8%.
Общий индекс затрат на производство:
![]()
Изменение затрат под влиянием обоих составит - 5,4%.
Задача 5. Рассчитать:
1) индексы урожайности переменного состава;
2) индекс урожайности постоянного состава;
3) индекс влияния структурных сдвигов. Сделать выводы.
Таблица 15 - Исходные данные
| Сельскохозяйственные предприятия |
Базисный период |
Отчетный период |
||
| Урожайность, ц/га |
Посевная площадь, га |
Урожайность, ц/га |
Посевная площадь, га |
|
| 1 |
35 |
520 |
38 |
650 |
| 2 |
20 |
180 |
22 |
160 |
Решение:
Для решения данной задачи также строим вспомогательную таблицу.
Таблица 16 - Вспомогательная
| Сельскохозяйст-венные предприятия |
Базисный период |
Отчетный период |
Расчетные показатели |
||||
| Урожайность, ц/га (y0) |
Посевная площадь, га (s0) |
Урожайность, ц/га (y1) |
Посевная площадь, га (s1) |
y0*s0 |
y1*s1 |
y0*s1 |
|
| 1 |
35 |
520 |
38 |
650 |
18200 |
24700 |
22750 |
| 2 |
20 |
180 |
22 |
160 |
3600 |
3520 |
3200 |
| Итого |
700 |
810 |
21800 |
28220 |
25950 |
||
Индекс переменного состава представляет собой соотношение средних уровней изучаемого показателя. Индекс урожайности переменного состава:
![]() .
.
Индекс постоянного состава отражает изолированное влияние осредняемого показателя у отдельных единиц совокупности. Индекс урожайности постоянного состава:
![]() .
.
Индекс структурных сдвигов характеризует влияние изменения структуры изучаемой совокупности. Индекс структурных сдвигов:
 .
.
Таким образом, общая урожайность выросла на 19% под влиянием изменения структуры посевных площадей. Под влиянием изменения урожайности каждой посевной площади общая урожайность выросла на 8,8%. В целом под влиянием этих обоих факторов урожайность посевов выросла на 11,8%
Задача 6. По имеющимся данным числе умерших в Хабаровском крае за 2000 - 2005 гг. рассчитать: за каждый год:
1) абсолютный пророст (базисный и цепной);
2) темп роста (базисный и цепной);
3) темпы прироста базисный и цепной);
4) абсолютное значение 1% прироста; в целом за период: 5) средний уровень ряда;
6) средний абсолютный прирост;
7) средний темп роста;
8) средний темп прироста. Сделать выводы.
Таблица 17 - Исходные данные
| Число умерших, чел. |
Год |
|||||
| 2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
|
| 20 745 |
21 639 |
22 513 |
23 290 |
22 745 |
23 074 |
|
Решение:
Для определения абсолютных приростов, темпов роста и темпов прироста строим расчетную таблицу 18. Показатели, заносимые в таблицу, рассчитываются следующим образом:
1. Абсолютный прирост:
А) цепной:
![]() ,
,
где у i - уровень ряда динамики за изучаемый период, у i-1 - уровень ряда динамики за период предшествующий изучаемому;
Б) базисный:
![]() ,
,
где уо - начальный уровень ряда динамики;
2. Темп роста:
А) цепной:
![]() ;
;
Б) базисный:
![]() ;
;
3. Темп прироста: А) цепной:
![]() или
или ![]() ;
;
Б) базисный:
![]() или
или ![]() ;
;
4. Абсолютное значение 1% прироста:
 или
или ![]() .
.
Таблица 18 - Показатели динамики
| Год |
Число умерших, чел. |
Абсолютный прирост |
Темп роста, % |
Темп прироста, % |
Абсолютное значение 1% прироста |
|||
| баз. |
цепн. |
баз. |
цепн. |
баз. |
цепн. |
|||
| 2000 |
20745 |
894 |
894 |
104,30 |
104,30 |
4,309 |
4,309 |
207,45 |
| 2001 |
21639 |
1768 |
874 |
108,52 |
104,03 |
8,523 |
4,039 |
216,39 |
| 2002 |
22513 |
2545 |
777 |
112,26 |
103,45 |
12,268 |
3,451 |
225,13 |
| 2003 |
23290 |
2000 |
-545 |
109,64 |
97,66 |
9,641 |
-2,340 |
232,9 |
| 2004 |
22745 |
2329 |
329 |
111,22 |
101,44 |
11,227 |
1,446 |
227,45 |
| 2005 |
23074 |
894 |
894 |
104,31 |
104,31 |
4,309 |
4,309 |
207,45 |
| Итого |
134006 |
|||||||
Далее рассчитываем средние показатели динамики.
1) средний уровень ряда динамики для интервального ряда:
![]() ,
,
где у i - уровни ряда динамики, n - число уровней ряда динамики;
2) средний абсолютный прирост:
![]() ,
,
где у n - конечный уровень ряда;
3) средний темп роста:
 ,
,
4) средний темп прироста
![]() . =102,1-100=2,1
. =102,1-100=2,1
Так, в среднем за эти годы умирало 22334 человек в год. В среднем количество умерших в год возрастало с каждым годом на 466 человек, или на 2,1%.
Список использованной литературы
1. Елисеева И.И., Юзбашев М.М. Общая теория статистики: учебник / И.И. Елисеева, М.М. Юзбашев. - М.: Финансы и статистика, 2004. - 565 с.
2. Статистика: учеб.-практ. пособие /под ред. М.Г. Назарова. - М.: КНОРУС, 2006 - 480 с.
3. Теория статистики: учебник /под ред. Г.Л. Громыко. - М.: ИНФРА-М., 2000. - 414 с.