| Похожие рефераты | Скачать .zip |
Реферат: Динамическое программирование
Курсовая работа по теории оптимального управления экономическими системами.
Тема : Задача динамического программирования.
I.Основные понятия и обозначения.
Динамическое программирование – это математический метод поиска оптимального управления, специально приспособленный к многошаговым процессам. Рассмотрим пример такого процесса.
Пусть планируется деятельность группы предприятий на N лет. Здесь шагом является один год. В начале 1-го года на развитие предприятий выделяются средства, которые должны быть как-то распределены между этими предприятиями. В процессе их функционирования выделенные средства частично расходуются. Каждое предприятие за год приносит некоторый доход, зависящий от вложенных средств. В начале года имеющиеся средства могут перераспределяться между предприятиями : каждому из них выделяется какая-то доля средств.
Ставится вопрос : как в начале каждого года распределять имеющиеся средства между предприятиями, чтобы суммарный доход от всех предприятий за N лет был максимальным?
Перед нами типичная задача динамического программирования, в которой рассматривается управляемый процесс – функционирование группы предприятий. Управление процессом состоит в распределении (и перераспределении) средств. Управляющим воздействием (УВ) является выделене каких-то средств каждому из предприятий в начале года.
УВ на каждом шаге должно выбираться с учетом всех его последствий в будущем. УВ должно быть дальновидным, с учетом перспективы. Нет смысла выбирать на рассматриваемом шаге наилучшее УВ, если в дальнейшем это помешает получить наилучшие результаты других шагов. УВ на каждом шаге надо выбирать “c заглядыванием в будущее”, иначе возможны серьезные ошибки.
Действительно, предположим, что в рассмотренной группе предприятий одни заняты выпуском предметов потребления, а другие производят для этого машины. Причем целью является получение за N лет максимального объема выпуска предметов потребления. Пусть планируются капиталовложения на первый год. Исходя их узких интересов данного шага (года), мы должны были бы все средства вложить в производство предметов потребления, пустить имеющиеся машины на полную мощность и добиться к концу года максимального объема продукции. Но правильным ли будет такое решение в целом? Очевидно, нет. Имея в виду будущее, необходимо выделить какую-то долю средств и на производство машин. При этом объем продукции за первый год, естественно, снизится, зато будут созданы условия, позволяющие увеличивать ее производство в последующие годы.
В формализме решения задач методом динамического программирования будут использоваться следующие обозначения:
N – число шагов.
![]() –
вектор,описывающий
состояние
системы на k-м
шаге.
–
вектор,описывающий
состояние
системы на k-м
шаге.
![]() –
начальное
состояние, т.
е. cостояние
на 1-м шаге.
–
начальное
состояние, т.
е. cостояние
на 1-м шаге.
![]() –
конечное
состояние, т.
е. cостояние на
последнем шаге.
–
конечное
состояние, т.
е. cостояние на
последнем шаге.
Xk – область допустимых состояний на k-ом шаге.
![]() –
вектор
УВ на k-ом
шаге, обеспечивающий
переход системы
из состояния
xk-1
в состояние
xk.
–
вектор
УВ на k-ом
шаге, обеспечивающий
переход системы
из состояния
xk-1
в состояние
xk.
Uk – область допустимых УВ на k-ом шаге.
Wk – величина выигрыша, полученного в результате реализации k-го шага.
S – общий выигрыш за N шагов.
![]() –
вектор
оптимальной
стратегии
управления
или ОУВ за N
шагов.
–
вектор
оптимальной
стратегии
управления
или ОУВ за N
шагов.
Sk+1(![]() )
– максимальный
выигрыш, получаемый
при переходе
из любого состояния
)
– максимальный
выигрыш, получаемый
при переходе
из любого состояния
![]()
![]() в
конечное состояние
в
конечное состояние
![]() при оптимальной
стратегии
управления
начиная с (k+1)-го
шага.
при оптимальной
стратегии
управления
начиная с (k+1)-го
шага.
S1(![]() )
– максимальный
выигрыш, получаемый
за N
шагов при
переходе системы
из начального
состояния
)
– максимальный
выигрыш, получаемый
за N
шагов при
переходе системы
из начального
состояния
![]() в конечное
в конечное
![]() при реализации
оптимальной
стратегии
управления
при реализации
оптимальной
стратегии
управления
![]() .
Очевидно, что
S = S1(
.
Очевидно, что
S = S1(![]() ),
если
),
если
![]() –фиксировано.
–фиксировано.
Метод динамического программирования опирается на условие отсутствия последействия и условие аддитивности целевой функции.
Условие
отсутствия
последействия.
Состояние
![]() ,
в которое перешла
система за один
k-й
шаг, зависит
от состояния
,
в которое перешла
система за один
k-й
шаг, зависит
от состояния
![]() и выбранного
УВ
и выбранного
УВ
![]() и не зависит
от того, каким
образом система
пришла в состояние
и не зависит
от того, каким
образом система
пришла в состояние
![]() ,
то есть
,
то есть
![]()
Аналогично,
величина выигрыша
Wk
зависит
от состояния
![]() и выбранного
УВ
и выбранного
УВ
![]() ,
то есть
,
то есть
![]()
Условие аддитивности целевой функции. Общий выигрыш за N шагов вычисляется по формуле
![]()
Определение.
Оптимальной
стратегией
управления
![]() называется
совокупность
УВ
называется
совокупность
УВ
![]() ,
то есть
,
то есть
![]() ,
в результате
реализации
которых система
за N
шагов
переходит из
начального
состояния
,
в результате
реализации
которых система
за N
шагов
переходит из
начального
состояния
![]() в конечное
в конечное
![]() и при этом общий
выигрыш S
принимает
наибольшее
значение.
и при этом общий
выигрыш S
принимает
наибольшее
значение.
Условие отсутствия последействия позволяет сформулировать принцип оптимальности Белмана.
Принцип
оптимальности.
Каково бы ни
было допустимое
состояние
системы![]()
![]()
![]()
перед
очередным
i-м
шагом, надо
выбрать допустимое
УВ
![]() на этом
шаге так, чтобы
выигрыш Wi
на i-м
шаге плюс оптимальный
выигрыш на всех
последующих
шагах был
максимальным.
на этом
шаге так, чтобы
выигрыш Wi
на i-м
шаге плюс оптимальный
выигрыш на всех
последующих
шагах был
максимальным.
В качестве
примера постановки
задачи оптимального
управления
продолжим
рассмотрение
задачи управления
финансированием
группы предприятий.
Пусть в
начале i-го
года группе
предприятий
![]() выделяются
соответственно
средства:
выделяются
соответственно
средства:
![]()
![]() совокупность
этих значений
можно считать
управлением
на i-м шаге,
то есть
совокупность
этих значений
можно считать
управлением
на i-м шаге,
то есть
![]() .
Управление
.
Управление
![]() процессом в
целом представляет
собой совокупность
всех шаговых
управлений,
то есть
процессом в
целом представляет
собой совокупность
всех шаговых
управлений,
то есть
![]() .
.
Управление
может быть
хорошим или
плохим, эффективным
или неэффективным.
Эффективность
управления
![]() оценивается
показателем
S.
Возникает
вопрос: как
выбрать шаговые
управления
оценивается
показателем
S.
Возникает
вопрос: как
выбрать шаговые
управления
![]() ,
чтобы величина
S
обратилась
в максимум
?
,
чтобы величина
S
обратилась
в максимум
?
Поставленная
задача является
задачей оптимального
управления,
а управление,
при котором
показатель
S
достигает
максимума,
называется
оптимальным.
Оптимальное
управление
![]() многошаговым
процессом
состоит из
совокупности
оптимальных
шаговых управлений:
многошаговым
процессом
состоит из
совокупности
оптимальных
шаговых управлений:
![]()
Таким образом,
перед нами
стоит задача:
определить
оптимальное
управление
на каждом шаге
![]() (i=1,2,...N)
и, значит, оптимальное
управление
всем процессом
(i=1,2,...N)
и, значит, оптимальное
управление
всем процессом
![]() .
.
II. Идеи метода динамического программирования
Мы отметили, что планируя многошаговый процесс, необходимо выбирать УВ на каждом шаге с учетом его будущих последствий на еще предстоящих шагах. Однако, из этого правила есть исключение. Среди всех шагов существует один, который может планироваться без "заглядыва-ния в будущее". Какой это шаг? Очевидно, последний — после него других шагов нет. Этот шаг, единственный из всех, можно планировать так, чтобы он как таковой принес наибольшую выгоду. Спланировав оптимально этот последний шаг, можно к нему пристраивать предпоследний, к предпоследнему — предпредпоследний и т.д.
Поэтому процесс динамического программирования на 1-м этапе разворачивается от конца к началу, то есть раньше всех планируется последний,
N-й шаг. А как его спланировать, если мы не знаем, чем кончился предпоследний? Очевидно, нужно сделать все возможные предположения о том, чем кончился предпоследний, (N — 1)-й шаг, и для каждого из них найти такое управление, при котором выигрыш (доход) на последнем шаге был бы максимален. Решив эту задачу, мы найдем условно оптимальное управление (УОУ) на N-м шаге, т.е. управление, которое надо применить, если (N — 1)-й шаг закончился определенным образом.
Предположим, что эта процедура выполнена, то есть для каждого исхода
(N — 1)-го шага мы знаем УОУ на N-м шаге и соответствующий ему условно оптимальный выигрыш (УОВ). Теперь мы можем оптимизировать управление на предпоследнем, (N — 1)-м шаге. Сделаем все возможные предположения о том, чем кончился предпредпоследпий, то есть (N — 2)-й шаг, и для каждого из этих предположений найдем такое управление на (N — 1)-м шаге, чтобы выигрыш за последние два шага (из которых последний уже оптимизирован) был максимален. Далее оптимизируется управ чение на (N — 2)-м шаге, и т.д.
Одним словом, на каждом шаге ищется такое управление, которое обеспечивает оптимальное продолжение процесса относительно достигнутого в данный момент состояния. Этот принцип выбора управления , называется принципом оптимальности. Само управление, обеспечивающее оптимальное продолжение процесса относительно заданного состояния, называется УОУ на данном шаге.
Теперь предположим, что УОУ на каждом шаге нам известно: мы знаем, что делать дальше, в каком бы состоянии ни был процесс к началу каждого шага. Тогда мы можем найти уже не "условное", а дейсгвительно оптимальное управление на каждом шаге. |
Действительно, пусть нам известно начальное состояние процесса. Теперь мы уже знаем, что делать на первом шаге: надо применить УОУ, найденное для первого шага и начального сосюяния. В результате этого управления после первого шага система перейдет в другое состояние; но для этого состояния мы знаем УОУ и г д. Таким образом, мы найдем оптимальное управление процессом, приводящее к максимально возможному выигрышу.
Таким образом, в процессе оптимизации управления методом динамического программирования многошаговый процесс "проходится" дважды:
— первый раз — от конца к началу, в результате чего находятся УОУ| на каждом шаге и оптимальный выигрыш (тоже условный) на всех шагах, начиная с данного и до конца процесса;
второй раз — от начала к концу, в результате чего находятся оптимальные управления на всех шагах процесса.
Можно сказать, что процедура построения оптимального управления
методом динамического программирования распадается на две стадии:
предварительную и окончательную. На предварительной стадии для каждого шага определяется УОУ, зависящее от состояния системы (достигнутого в результате предыдущих шагов), и условно оптимальный выигрыш на всех оставшихся шагах, начиная с данного, также зависящий от состояния. На окончательной стадии определяется (безусловное) оптимальное управление для каждого шага. Предварительная (условная) оптимизация производится по шагам в обратном порядке: от последнего шага к первому; окончательная (безусловная) оптимизация — также по шагам, но в естественном порядке: от первого шага к последнему. Из двух стадий оптимизации несравненно более важной и трудоемкой является первая. После окончания первой стадии выполнение второй трудности не представляет: остается только "прочесть" рекомендации, уже заготовленные на первой стадии.
III. Пример задачи динамического программирования
Выбор состава оборудования технологической линии.
Есть технологическая линия , то есть цепочка, последовательность операций.
На каждую операцию можно назначить оборудование только каго-то одного вида, а оборудования, способного работать на данной операции, - несколько видов.
Исходные данные для примера
-
i 1 2 3 j 1 2 1 2 1 2 


10 8 4 5 8 9 
12 8 4 6 9 9 
20 18 6 8 10 12
![]()
Стоимость сырья
Расходы
, связанные
с использованием
единицы оборудования
j-го типа
на i-ой
операции![]()
Производительности,
соответственно,
по выходу и
входу
![]() и
и
![]() для j-готипа
оборудования,
претендующего
на i-ую
операцию.
для j-готипа
оборудования,
претендующего
на i-ую
операцию.
Решение:
Для того, чтобы решить данную задачу методом динамического программирования введем следующие обозначения:
N = 3 – число шагов.
![]() - Технологическая
линия.
- Технологическая
линия.
![]()
![]()
![]() =
(
)
=
(
)
![]() – выбор
оборудования
для i-ой
операции.
– выбор
оборудования
для i-ой
операции.
Ui – область допустимых УВ на i-м шаге.
![]() т.е.
т.е.
Wi – оценка минимальной себестоимости, полученная в результате реализации i-го шага.
S – функция общего выигрыша т. е. минимальная себестоимость .

![]()
![]()
![]() - вектор
УВ на i-ом
шаге, обеспечивающий
переход системы
из состояния
xi-1
в состояние
xi ,
т.е.
оптимальный
выбор оборудования
за N
шагов.
- вектор
УВ на i-ом
шаге, обеспечивающий
переход системы
из состояния
xi-1
в состояние
xi ,
т.е.
оптимальный
выбор оборудования
за N
шагов.
Si+1(![]() )
– максимальный
выигрыш ( в нашем
случае минимальная
себестоимость),
получаемый
при переходе
из любого состояния
)
– максимальный
выигрыш ( в нашем
случае минимальная
себестоимость),
получаемый
при переходе
из любого состояния
![]()
![]() в
конечное состояние
в
конечное состояние
![]() при оптимальной
стратегии
управления
начиная с (k+1)-го
шага.
при оптимальной
стратегии
управления
начиная с (k+1)-го
шага.
S1(![]() )
– максимальный
выигрыш, получаемый
за N
шагов при
переходе системы
из начального
состояния
)
– максимальный
выигрыш, получаемый
за N
шагов при
переходе системы
из начального
состояния
![]() в конечное
в конечное
![]() при реализации
оптимальной
стратегии
управления
при реализации
оптимальной
стратегии
управления
![]() .
Очевидно, что
S = S1(
.
Очевидно, что
S = S1(![]() ),
если
),
если
![]() =
0.
=
0.
Запишем вектора допустимых значений
![]()
![]()
![]()
Запишем вектора допустимых управляющих воздействий
![]()
![]()
![]()
З
![]()
![]()
![]()
![]()
З

![]()
1) Обратный проход
Д

Учитывая то, что этот шаг у нас последний и следующей операции
у
![]()
![]()
возьмем стоимость сырья

![]()
![]()
при
![]() =
=

![]()
![]()
при
![]() =
=
![]()
![]()
т. е.
Для i=2



![]() 115,2
115,2
![]()
при
![]() =
=

![]() 138,04
138,04
![]()
при
![]() =
=
![]() 102,8
102,8
![]()
при
![]() =
=

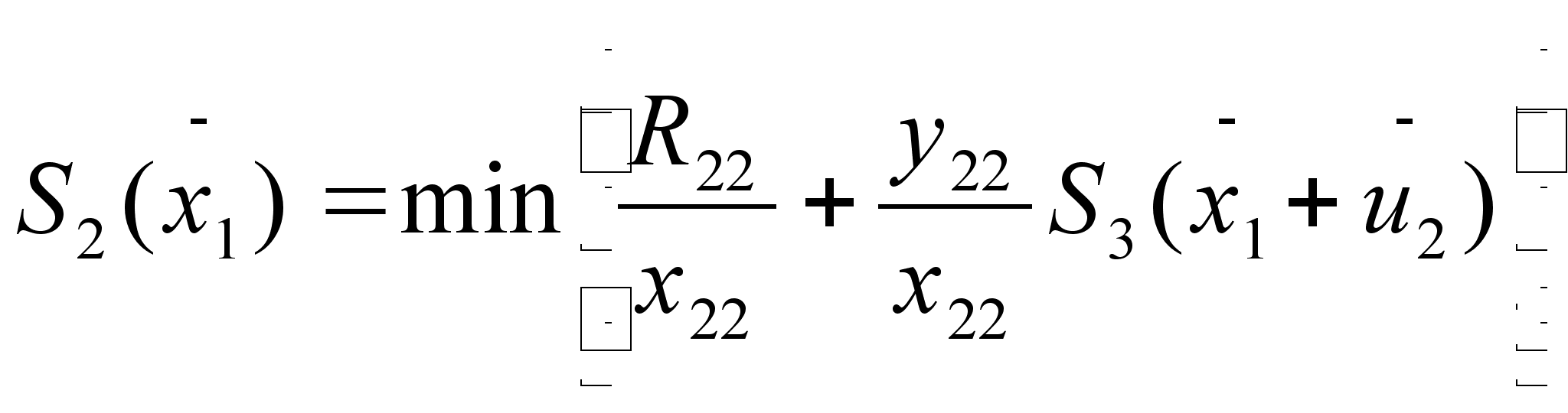
![]() 123,1
123,1
![]()
при
![]() =
=
![]()
![]()
т. е.
Д


![]() 140,2
140,2
![]()
при
![]() =
=

![]() 125,3
125,3
![]()
при
![]() =
=
п

![]() 125,3
125,3
![]()

![]() 125,3
125,3
![]()
при
![]() ==
==

![]() 125,3
125,3
![]()
при
![]() =
=

![]() 125,3
125,3
![]()
при
![]() =
=

![]() 125,3
125,3
![]()
при
![]() =
=

![]() 125,3
125,3
![]()
при
![]() =
=
![]()
![]()
т. е.
П
рямой проход
Учитывая
то,
что
и
![]() =
(0,0,0) имеем
=
(0,0,0) имеем
![]()
![]()
![]()
![]()
i
![]()
![]()
Таким образом оптимальный выбор составаоборудования технологической линии предполагает следующее:
На 1-ую операцию назначим оборудование 2-го вида
На 2-ую операцию назначим оборудование 1-го вида
На 3-ью операцию назначим оборудование 2-го вида
Оценка минимальной себестоимости составит 105,5.
Раздел коллекции : Экономико-математическое моделирование
Автор : Родионов Д.А.
Контактные сведения : dimarik@chel.ru
Наименования работы : Динамическое программирование
Вид работы : курсовая работа
Пожелания : -
Похожие рефераты:
Матричные антагонистические игры с нулевой суммой в чистых стратегиях
Классификация математических моделей, используемых в экономике и менеджменте
Теоретические основы математических и инструментальных методов экономики
Методы оптимизации портфеля бескупонных облигаций
Классификация сейсмических сигналов на основе нейросетевых технологий