| Скачать .docx |
Дипломная работа: Некоторые задачи оптимизации в экономике
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Вятский государственный гуманитарный университет
Математический факультет
Кафедра математического анализа и методики преподавания математики
Выпускная квалификационная работа
Некоторые задачи оптимизации в экономике
Выполнила:
студентка V курса математического факультета
Голомидова Ирина Витальевна
Научный руководитель:
Ст. преподаватель кафедры математического анализа и МПМ
С. А. Фалелеева.
Рецензент:
кандидат педагогических наук, ст. преподаватель кафедры математического анализа и МПМ
Л.В. Караулова.
Допущена к защите в государственной аттестационной комиссии
«___» __________2005 г. Зав. кафедрой М.В. Крутихина
«___»___________2005 г. Декан факультета В.И. Варанкина
Киров
2005
Содержание
Введение................................................................................................... 3
1. Математические модели в экономике................................................. 4
2. Некоторые понятия функций нескольких переменных...................... 6
3. Задача математического программирования
1) Общая постановка задачи.............................................................. 8
2) Задача линейного программирования и способы её решения..... 9
3) Двойственная задача.................................................................... 19
4) Задача нелинейного программирования..................................... 26
5) Задача на условный экстремум.................................................... 31
4. Задача потребительского выбора.
1) Функция полезности. Бюджетное ограничение. Формулировка задачи потребительского выбора................................................................ 34
2) Решение задачи потребительского выбора и его свойства......... 36
3) Общая модель потребительского выбора................................... 39
4) Модель Стоуна ............................................................................ 40
Заключение............................................................................................. 42
Библиографический список................................................................... 43
Введение
Современная математика характеризуется интенсивным проникновением в другие науки, во многом этот процесс происходит благодаря разделению математики на ряд самостоятельных областей. Математика стала для многих отраслей знаний не только орудием количественного расчёта, но также методом точного исследования и средством предельно чёткой формулировки понятий и проблем. Без современной математики с её развитым логическим и вычислительным аппаратом был бы не возможен прогресс в различных областях человеческой деятельности.
Экономика как наука об объективных причинах функционирования и развития общества пользуется разнообразными количественными характеристиками, а поэтому вобрала в себя большое число математических методов.
Актуальность данной темы состоит в том, что в современной экономике используются оптимизационные методы, которые составляют основу математического программирования, теории игр, сетевого планирования, теории массового обслуживания и других прикладных наук.
Изучение экономических приложений математических дисциплин, составляющих основу актуальной экономической математики, позволяет приобрести некоторые навыки решения экономических задач и расширить знания в этой области.
Целью данной работы является изучение некоторых оптимизационных методов, применяемых при решении экономической задач.
При написании дипломной работы были поставлены следующие задачи:
· Рассмотрение некоторых экономических задач и составление математических моделей.
· Изучение некоторых математических методов, применяемых для решения оптимизационных задач в экономике.
· Практическое решение задач.
1. Математические модели в экономике
Современная экономическая теория включает как естественный, необходимый элемент математические модели и методы. Использование математики в экономике позволяет, во-первых, выделить и формально описать наиболее важные, существенные связи. Во-вторых, из чётко сформулированных исходных данных и соотношений можно сделать выводы, адекватные изучаемому объекту в той же мере, что и сделанные предпосылки. В-третьих, методы математики позволяют индуктивным путем получать новые знания об объекте: оценить форму и параметры зависимостей его переменных, в наибольшей степени соответствующие имеющимся наблюдениям. В-четвертых, использование языка математики позволяет точно и компактно излагать положения экономической теории, формулировать её понятия.
Математические модели использовались с иллюстративными исследованиями ещё Ф. Кене (1758г., «Экономическая таблица»), А. Смитом (Классическая макроэкономическая модель), Д. Риккардо (Модель международной торговли). В XIX веке большой вклад в моделирование рыночной экономики внесли математики Л. Вальрас, О. Курно, В. Парето и другие. В XX веке математические методы моделирования применялись очень широко, с их использованием связаны практически все работы, удостоенные Нобелевской премии по экономике (Р. Солоу, В. Леонтьев, Л. Канторович и другие). Развитие макроэкономики, микроэкономики, прикладных дисциплин связано со все более высоким уровнем их формализации. Основу для этого заложил прогресс в области прикладной математики. В России в начале XX века большой вклад в математическое моделирование экономики внесли В.К. Дмитриев и Е.Е. Слуцкий. В 1960-е – 80-е годы экономико-математическое направление было связано, в основном, с попытками формально описать «систему оптимального функционирования социалистической экономики» (Н.П. Федоренко, С.С. Шаталин). Строились многоуровневые системы моделей народно – хозяйственного планирования, оптимизационные модели областей и предприятий.
Математическая модель экономического объекта – это его гомоморфное отображение в виде совокупности уравнений, неравенств, логических отношений, графиков. Иными словами, модель – это условный образ объекта, построенный для упрощения его исследования. Предполагается, что изучение модели дает новые решения в той или иной ситуации.
Можно выделить 3 этапа проведения математического моделирования в экономике:
1. ставятся цели и задачи исследования, проводится качественное описание объекта в виде экономической модели.
2. формируется математическая модель изучаемого объекта, осуществляется выбор методов исследования. Далее исследуется модель с помощью этих методов.
3. осуществляется обработка и анализ полученных результатов.
Математические модели, используемые в экономике, можно подразделить на классы по ряду признаков, относящихся к особенностям моделируемого объекта, цели моделирования и используемого инструментария: модели макро- и микроэкономические, теоретические и прикладные, оптимизационные и равновесные, статические и динамические.
Мы будем рассматривать некоторые оптимизационные модели. К оптимизационным моделям относят следующие: модель линейного программирования, нелинейного, динамического, сетевые модели. Будем рассматривать модели линейного и нелинейного программирования.
2. Некоторые понятия функций нескольких переменных
Многим экономическим явлениям присуща многофакторная зависимость, поэтому при изучении процессов в экономике вводят функции нескольких переменных.
Переменная y называется функцией нескольких переменных x 1 , x 2 ,…, xn , если существует отображение f : Rn → R . Множество всех точек М, участвующих в этом отображении, называется областью определения функции , где М(x 1 , x 2 ,…, xn ).
Наиболее часто встречается функция двух переменных. В экономике для её изучения широко применяются линии уровня.
Линиями уровня функции двух переменных y = f ( x 1 , x 2 ) называется проекция пересечения графика функции y = f ( x 1 , x 2 ) с горизонтальной плоскостью на плоскость Ох1 х2 , причём линия пересечения находится от плоскости Ох1 х2 на высоте С. Уравнение линии уровня имеет вид f ( x 1 , x 2 )=С. Число С в этом случае называется уровнем .
Как и в случае одной переменной, функция y = f ( x 1 , x 2 ) имеет узловые, определяющие структуру графика, точки. В первую очередь это точки экстремума. Точки экстремума функции двух переменных определяются аналогично точкам экстремума функции одной переменной
Сформулируем необходимое условие экстремума – многомерный аналог теоремы Ферма: Пусть точка (
![]() ) -
есть точка экстремума дифференцируемой функции y
=
f
(
x
1
,
x
2
).
Тогда частные производные
) -
есть точка экстремума дифференцируемой функции y
=
f
(
x
1
,
x
2
).
Тогда частные производные![]() (
(
![]() ),
),
![]() (
(
![]() )
в этой точке равны нулю.
)
в этой точке равны нулю.
Точки, в которых выполнены необходимые условия экстремума функции y
=
f
(
x
1
,
x
2
)
, т. е частные производные ![]() равны нулю, называются стационарными.
равны нулю, называются стационарными.
Равенство нулю частных производных выражает лишь необходимое условие, но недостаточное условие экстремума функции нескольких переменных.
|

Достаточное условие экстремума функции двух переменных . Пусть функция y = f ( x 1 , x 2 ) :
a) определена в некоторой окрестности стационарной точки (
![]() )
, в которой
)
, в которой![]() (
(
![]() )
=0
и
)
=0
и ![]() (
(
![]() )=
0;
)=
0;
b) имеет в этой точке непрерывные частные производные второго поряка![]() (
(
![]() )
=А,
)
=А,
![]() (
(
![]() )
=
)
=
![]() (
(
![]() )
=В,
)
=В,
![]() (
(
![]() )
=С.
)
=С.
Тогда, если ![]() =АС-В2
>0
, то в точке (
=АС-В2
>0
, то в точке (
![]() )
функция имеет экстремум, причём, если А>0 минимум, А<0 – максимум. В случае
)
функция имеет экстремум, причём, если А>0 минимум, А<0 – максимум. В случае ![]() =АС-В2
<0
, функция y
=
f
(
x
1
,
x
2
)
экстремума не имеет. Если
=АС-В2
<0
, функция y
=
f
(
x
1
,
x
2
)
экстремума не имеет. Если ![]() =АС-В2
=0
, то вопрос о наличии экстремума остаётся открытым. Требуются другие методы определения экстремума. [11]
=АС-В2
=0
, то вопрос о наличии экстремума остаётся открытым. Требуются другие методы определения экстремума. [11]
В экономических задачах чаще встречаются задачи на условный экстремум. Перейдем к рассмотрению таких задач.
3. Задача математического программирования (ЗМП).
1) Общая постановка задачи
В теории экстремума на независимые переменные x 1 , x 2, …,х n не накладываются никакие дополнительные условия, т.е. не требуется, чтобы переменные удовлетворяли некоторым дополнительным ограничениям.
Рассмотрим другую задачу. Найти максимум (минимум) функции y = f ( x 1 , x 2, …,х n ), при условии, что независимые переменныеx 1 , x 2, …,х n удовлетворяют системе ограничений:
![]() g
1
(
x
1
,
x
2,
…,х
n
)≤
b
1
,
g
1
(
x
1
,
x
2,
…,х
n
)≤
b
1
,
…………………………
gm ( x 1 , x 2, …,х n )≤ bm ,
gm +1 ( x 1 , x 2, …,х n )≥ bm +1 ,
…………………………
gk ( x 1 , x 2, …,х n )≥ bk , (3.1)
gk +1 ( x 1 , x 2, …,х n )= bk +1 ,
…………………………
gp ( x 1 , x 2, …,х n )= bp ,
x 1 , x 2, …,х n ≥0.
Функцию y
=
f
(
x
1
,
x
2,
…,х
n
)
принято называть целевой,
т.к. её максимизация (минимизация) часто есть выражение какой-то цели, систему ограничений (3.1) – специальными ограничениями ЗМП
, неравенстваx
1
≥0 ,
x
≥02,
…, х
n
≥0 – общими ограничениями ЗМП
. Множество всех допустимых решений ЗМП (х
j
≥0,
j
=
![]() )
называется допустимым множеством этой задачи.
)
называется допустимым множеством этой задачи.
Точка (![]() ) называется оптимальным решением
для функции двух переменных, если, во-первых, она есть допустимое решение этой ЗМП, а во-вторых, на этой точке целевая функция достигает максимума (минимума) среди всех точек, удовлетворяющих ограничениям (3.1), причём
) называется оптимальным решением
для функции двух переменных, если, во-первых, она есть допустимое решение этой ЗМП, а во-вторых, на этой точке целевая функция достигает максимума (минимума) среди всех точек, удовлетворяющих ограничениям (3.1), причём
f
(
![]() )≥
f
(
x
1
,
x
2
)
(в случае решения задачи на отыскание максимума),
)≥
f
(
x
1
,
x
2
)
(в случае решения задачи на отыскание максимума),
f
(
![]() ) ≤
f
(
x
1
,
x
2
)
(в случае решения задачи на отыскание минимума).
) ≤
f
(
x
1
,
x
2
)
(в случае решения задачи на отыскание минимума).
Если в ЗМП все функции f ( x 1 , x 2, …,х n ), g i ( x 1 , x 2, …,х n ) линейны, то имеем задачу линейного программирования (ЗЛП), если хотя бы одна из функций нелинейная, имеем задачу нелинейного программирования (ЗЛП). Рассмотрим ЗЛП.
2) ЗЛП и способы её решения .
ЗЛП имеет вид F=c1 x1 +c2 x2 +…+cn xn +c0 →min(max). При этом переменные должны удовлетворять ограничениям:
![]() а11
х1
+ а12
х2
+…+а1
n
х
n
≤
b
1
а11
х1
+ а12
х2
+…+а1
n
х
n
≤
b
1
…………………………
а m 1 х1 + а m 2 х2 +…+a mn x n ≤ bm
а m +11 х1 + а m +12 х2 +…+а m +1 n х n ≥ bm +1
…………………………
а k 1 х1 + а k 2 х2 +…+а kn х n ≥ bk (3.2)
а k 1+1 х1 + а k +12 х2 +…+а k +1 n х n = bk +1
………………………….
а p 1 х1 +а p 2 х2 +…+а pn х n = bp
x 1 , x 2, …,х n ≥0 .
ЗЛП может быть записана в различных формах:
Общий вид : найти минимум (максимум) целевой функции F при ограничениях (3.2) и условии неотрицательности переменных.
Стандартный вид : найти минимум (максимум) целевой функции F и ограничениях, заданных в виде неравенств и добавлены условия о неотрицательности переменных.
Канонический вид : вид, в котором нужно найти минимум (максимум) целевой функции F, где все ограничения заданы в виде равенств и есть условие неотрицательности переменных.
Стандартную задачу можно привести к каноническому виду, путём введения дополнительных неотрицательных переменных. Т.е. свести к системе m линейных уравнений с n переменными.
Любые m переменных системы m линейных уравнений с n переменными (m<n) называются основными (или базисными), если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные m-n переменных называются неосновными или (свободными).
Базисным решением системы m линейных уравнений с n переменными называют решение, в котором все m-n неосновных переменных равны нулю.
Для обоснования свойств ЗЛП и методов её решения, рассмотрим 2 вида записи канонической задачи.
1 вид – матричная форма записи: С=(c1 ,c2 …cn ,c0 ).
Х=![]() А=
А= В=
В=![]() (3.3)
(3.3)
F = CX → min ( max )
AX = B , X ≥0
2 вид – векторная форма записи:
F = CX → min ( max )
р1 x 1 +р2 x 2 +…+р n xn =р. Х≥0 .
р1
=![]() р2
=
р2
=![]() … рn
=
… рn
=![]() .
.
Для того чтобы рассмотреть теоретические основы метода линейного программирования, определим понятие выпуклого множества точек, дав ему определение в аналитической форме:
Множество точек является выпуклым,
если оно вместе с любыми своими двумя точками содержит их произвольную линейную комбинацию. Точка Х является выпуклой линейной комбинацией точек Х1
, Х2
, … Х
n
,если выполняются условия Х=
α
1
x
1
+
α
2
x
2
+…+
αn
xn
,
αj
≥0, (
j
=1,…,
n
)
, ![]() .
.
Теорема 1 . Выпуклый линейный многогранник является выпуклой линейной комбинацией своих угловых точек. (Примем без доказательства).
Теорема 2 . Множество всех допустимых решений системы ограничений ЗЛП является выпуклым .
□ Пусть Х1
=(
x![]() ,
x
,
x![]() ,
…,х
,
…,х
![]() )
и Х2
=(
x
)
и Х2
=(
x![]() ,
x
,
x![]() ,
…,х
,
…,х
![]() )
- два допустимых решения задачи (3.3), заданной в матричной форме. Тогда АХ1
=В
и АХ2
=В
. рассмотрим выпуклую линейную комбинацию решений Х1
и Х2
, т.е. Х=
α
1
Х1
+
α
2
Х2
при α
1
≥0,
α
2
≥0
и α
1
+
α
2
=1
. Покажем, что она также является допустимым решением системы АХ=В
. В самом деле, АХ=А(
α
1
Х1
+
α
2
Х2
)
=α
1
АХ1
+(1-
α
1
)АХ2
= α
1
В+(1-
α
1
)В=В
, т.е. решение удовлетворяет системе ограничений. Но т.к. Х1
≥0, Х2
≥0,
α
1
≥0,
α
2
≥0
, то и Х ≥0
, т.е. решение Х удовлетворяет условию (3.3). ■
)
- два допустимых решения задачи (3.3), заданной в матричной форме. Тогда АХ1
=В
и АХ2
=В
. рассмотрим выпуклую линейную комбинацию решений Х1
и Х2
, т.е. Х=
α
1
Х1
+
α
2
Х2
при α
1
≥0,
α
2
≥0
и α
1
+
α
2
=1
. Покажем, что она также является допустимым решением системы АХ=В
. В самом деле, АХ=А(
α
1
Х1
+
α
2
Х2
)
=α
1
АХ1
+(1-
α
1
)АХ2
= α
1
В+(1-
α
1
)В=В
, т.е. решение удовлетворяет системе ограничений. Но т.к. Х1
≥0, Х2
≥0,
α
1
≥0,
α
2
≥0
, то и Х ≥0
, т.е. решение Х удовлетворяет условию (3.3). ■
Итак, доказано, что множество всех допустимых решений ЗЛП является выпуклым, которое будем называть многогранником решений .
Ответ на вопрос, в какой точке многогранника решений возможно оптимальное решение ЗЛП, даёт следующая теорема.
Теорема 3. Если ЗЛП имеет оптимальное решение, то линейная функция F принимает максимальное (минимальное) значение в одной из угловых точек многогранника решений. Если линейная функция принимает максимальное значение более чем в одной угловой точке, то она принимает его в произвольной точке, являющейся выпуклой линейной комбинацией этих точек .
 □ Будем полагать, что многогранник решений является ограниченным. Обозначим его угловые точки через Х1
,Х2,
…,Х
n
, аоптимальное решение через Х*
. Тогда F
(Х*
) ≥
F
(
X
)
, для всех точек многогранника решений. Если Х*
угловая, то первая часть теоремы доказана. Предположим, что Х*
не является угловой точкой, тогда Х*
,
на основании теоремы 1, можно представить как выпуклую линейную комбинацию угловых точек многогранника решений, т.е. Х*
=
α
1
x
1
+
α
2
x
2
+…+
α
р
x
р
,
αj
≥0, (
j
=1,…,
n
),
□ Будем полагать, что многогранник решений является ограниченным. Обозначим его угловые точки через Х1
,Х2,
…,Х
n
, аоптимальное решение через Х*
. Тогда F
(Х*
) ≥
F
(
X
)
, для всех точек многогранника решений. Если Х*
угловая, то первая часть теоремы доказана. Предположим, что Х*
не является угловой точкой, тогда Х*
,
на основании теоремы 1, можно представить как выпуклую линейную комбинацию угловых точек многогранника решений, т.е. Х*
=
α
1
x
1
+
α
2
x
2
+…+
α
р
x
р
,
αj
≥0, (
j
=1,…,
n
),
![]() . Т.к.
. Т.к.
F (Х* )= F ( α 1 x 1 + α 2 x 2 +…+ α р x р )= α 1 F ( x 1 )+ α 2 F ( x 2 )+…+ α р F ( x р ) . (3.4)
В этом выражении среди значений F ( Xj )( j =1,2,…, p ) выберем максимальное. Обозначим его через М , т.е. М= max F ( Xj ) . Тогда
α 1 F ( x 1 )+ α 2 F ( x 2 ) +…+ α р F ( x р )≤ α 1 М+ α 2 М +…+ α р М = М( α 1 + α 2 +…+ α р ) =М .
Значит F (Х* )≤М . Пусть М= F ( Xk ) , т.е. соответствует угловой точке Xk (1≤к≤р) .
Тогда F (Х* ) ≤ F ( Xk ) . Но по предположению Х* - оптимальное решение, поэтому F (Х* )≥ F ( Xk )=М , следовательно, F (Х* )=М= F ( Xk ) , где Xk - угловая точка. Итак, существует угловая точка Xk , в которой линейная функция принимает максимальное значение.
Для доказательства второй части теоремы допустим, что F (Х) принимает максимальное значение более чем в одной угловой точке, например в точках Х1 , Х2 , … Х q , где 1≤ q ≤ р ; тогда F (Х1 )= F (Х2 )=…= F (Х n )= M .
Пусть Х
выпуклая линейная комбинация этих угловых точек, т.е. Х=
α
1
Х1
+
α
2
Х2
+ …+
αq
Х
q
,
αj
≥0, (
j
=1,…,
q
), ![]() .
В этом случае, учитывая, что функция F
(Х)
– линейная, получим F
(Х)=
F
(
α
1
Х1
+
α
2
Х2
+…+
αq
Х
q
)=
α
1
F
(Х1
)+ +
α
2
F
(Х2
)+…+
αq
F
(Х
q
)=
α
1
M
+
α
2
M
+…+
αq
M
=
M
.
В этом случае, учитывая, что функция F
(Х)
– линейная, получим F
(Х)=
F
(
α
1
Х1
+
α
2
Х2
+…+
αq
Х
q
)=
α
1
F
(Х1
)+ +
α
2
F
(Х2
)+…+
αq
F
(Х
q
)=
α
1
M
+
α
2
M
+…+
αq
M
=
M![]() =
M
, т.е. линейная функция F
принимает максимальное значение в произвольной точке Х
, являющейся выпуклой линейной комбинацией угловых точек Х1
, Х2
, … Х
q
■
=
M
, т.е. линейная функция F
принимает максимальное значение в произвольной точке Х
, являющейся выпуклой линейной комбинацией угловых точек Х1
, Х2
, … Х
q
■
Замечание. Требование ограниченности многогранника решений в теореме является существенным, т.к. в случае неограниченной многогранной области не каждую точку можно представить выпуклой линейной комбинацией её угловых точек.
Доказанная теорема является фундаментальной, т.к. она указывает принципиальный путь решения ЗЛП.
Рассмотрим геометрический метод решения ЗЛП в случае функции двух переменных.
Было доказано, что оптимальное решение ЗЛП находится, по крайней мере, в одной из угловых точек многогранника решений.
Рассмотрим задачу в стандартной форме с двумя переменными.
F=c1 x1 +c2 x2 + с 0 →min(max) ,
![]() При ограничениях а11
х1
+ а12
х2
≤
b
1
,
При ограничениях а11
х1
+ а12
х2
≤
b
1
,
а21 х1 + а22 х2 ≤ b 2 ,
………………
an 1 х1 + а n 2 х2 ≤ bn ,
при условии, что x 1 ≥0 , x 2 ≥0 .
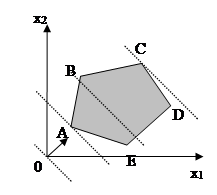
Пусть геометрическим изображением системы ограничений является многоугольник ABCDE. Необходимо среди точек этого многоугольника найти такую точку, в которой линейная функция F = c 1 x 1 + c 2 x 2 +с0 принимает максимальное (или минимальное) значение. Рассмотрим линии уровня функции F или
 c
1
x
1
+
c
2
x
2
=С
( 3.5).
c
1
x
1
+
c
2
x
2
=С
( 3.5).
Это уравнение прямой. Линии уровня функции F параллельны, т.к. их угловые коэффициенты определяются только соотношением между коэффициентами c 1 и c 2 и, следовательно, равны. Т.о., линии уровня функции F – это своеобразные «параллели», расположенные обычно под углом к осям координат.
Важное свойство линий уровня линейной функции состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в другую сторону – только убывает. При фиксированном С рассмотрим линейную функцию. Чем больше значение С, тем больше значение линейной функции. Определив направление возрастания линейной функции, найдём точку, принадлежащую многоугольнику, в которой функция принимает максимальное или минимальное значение.
Геометрическим изображением системы ограничений может служить и многоугольная область. Рассмотрим следующую задачу.
1.В суточный рацион включают два продукта питания П1 и П2 , причём продукта П1 должно войти в дневной рацион не более 200 ед. Стоимость питательных веществ в 1 ед. продукта, минимальные нормы потребления указаны в таблице. Определить оптимальный рацион питания, стоимость которого будет наименьшей .
Питательные вещества |
Минимальная норма потребления |
Содержание питательных веществ в 1 ед. продукта. |
|
| П1 | П1 | ||
А В |
120 160 |
0,2 0,4 |
0,2 0,2 |
Решение .
Обозначим х1 – количество продукта питания П1 ,
х2 – количество продукта питания П2 .
F =2 х1 +4 х2 → min . (суммарная стоимость) При ограничениях
![]() х1
≤ 200,
х1
≤ 200,
0,2 х1 +0,2 х2 ≥120,
0,4 х1 +0,2 х2 ≥160.
 Графическим решением системы ограничений является множество точек плоскости, называемое областью допустимых решений (ОДР). Линии уровня 2х1
+4х2
=0
Графическим решением системы ограничений является множество точек плоскости, называемое областью допустимых решений (ОДР). Линии уровня 2х1
+4х2
=0
![]() х2
=-
х2
=-![]() х1
.
х1
.
Получаем, что минимальное значение, при заданных ограничениях на переменные, достигается в точке А(200;400) . F ( A )=2000.
Ответ : наименьшая стоимость 2000 будет при рационе 200 ед. продукта П1 и 400 ед. продукта П2 .
Не всегда бывает единственное оптимальное решение. Рассмотрим другую задачу.
2. F =4 x 1 +4 x 2 → max . При ограничениях
![]() 2
x
1
+
x
2
≥7,
2
x
1
+
x
2
≥7,
x 1 -2 x 2 ≥-5,
x 1 + x 2 ≤14,
2 x 1 - x 2 ≤18.
Решив, систему ограничений найдём ОДР. Линия уровня будет иметь вид 4
x
1
+4
x
2
=0
![]() x
2
=-
x
1
.
x
2
=-
x
1
.
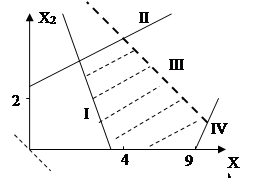 В данной задаче линия уровня с максимальным уровнем совпадает с граничной линией многоугольника решений. Найдём точку пересечения линии IIс линией III:
В данной задаче линия уровня с максимальным уровнем совпадает с граничной линией многоугольника решений. Найдём точку пересечения линии IIс линией III:
![]()
х1
=![]() .
.
Найдём точку пересечения линии IIIс линией IV: 14- х1
=2 х1
-18.
Отсюда х1
= ![]() . Следовательно, х1
=
c
,
x
2
=14-
c
,
c
. Следовательно, х1
=
c
,
x
2
=14-
c
,
c
![]() [
[![]() ;
;![]() ].
Пусть х1
=9
].
Пусть х1
=9 ![]() [
[![]() ;
;![]() ], х2
=5
.
], х2
=5
.
F =4·9+4·5=56.
Ответ
: Fmax
=56 при множестве оптимальных решений х1
=
c
,
x
2
=14-
c
,
где c
![]() [
[![]() ;
;![]() ]
.
]
.
Рассмотренный геометрический метод решения ЗЛП обладает рядом достоинств. Он прост, нагляден, позволяет быстро и легко получить ответ.
Однако есть и недостатки. Возникают «технические» погрешности, которые неизбежно возникают при приближенном построении графиков. Второй недостаток геометрического метода заключается в том, что многие величины, имеющие чёткий экономический смысл (например, такие, как остатки ресурсов производства), не выявляются при геометрическом решении задач. Его можно применять только в том случае, когда число переменных в стандартной задаче равно двум. Поэтому необходимы аналитические методы, позволяющие решать ЗЛП с любым числом переменных и выявить экономический смысл, входящих в них величин.
Одним их таких методов является симплексный метод .
В данном пункте была рассмотрена теорема, из которой следует, что если ЗЛП имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений. Поэтому решение ЗЛП может быть следующим: перебрать конечное число всех угловых точек многогранника решений и выбрать среди них ту, на которой функция цели принимает оптимальное решение. Однако, практическое осуществление такого перебора связано с трудностями, т.к. число решений может быть чрезвычайно велико.
 Пусть ОДР изображается многоугольником ABCDEGH. Предположим,
Пусть ОДР изображается многоугольником ABCDEGH. Предположим,
что его угловая точка соответствует исходному допустимому решению. При беспорядочном наборе пришлось бы перебирать все 7 угловых точек многогранника. Однако, из чертежа видно, что после вершины А выгодно перейти к соседней вершине В, а затем – к оптимальной точке С. Вместо семи перебрали 3 вершины, последовательно улучшая линейную функцию.
Идея последовательного улучшения решения легла в основу универсального метода решения ЗЛП – симплексного метода. Для использования симплексного метода ЗЛП должна быть приведена к каноническому виду. Для реализации симплексного метода необходимо освоить 3 основных элемента:
· способ определения какого – либо первоначального допустимого решения
· правило перехода к лучшему решению
· критерий проверки оптимальности найденного решения.
Алгоритм конкретной реализации этих элементов рассмотрим на примере.
Практические расчёты при решении реальных задач симплексным методом выполняются в настоящее время с помощью компьютера, однако, если расчёты выполняются без ЭВМ, то удобно использовать симплексные таблицы.
Алгоритм составления симплексных таблиц :
1. Система ограничений приводится к каноническому виду.
Для нахождения первоначального базисного решения переменные разбиваются на основные и неосновные. Т.к. определитель, составленный из коэффициентов при дополнительных переменных отличен от нуля, то эти переменные можно взять в качестве основных. При выборе основных переменных не обязательно составлять определитель, достаточно воспользоваться следующим правилом: в качестве основных переменных следует выбрать такие, каждая из которых входит только в одно из уравнений системы ограничений, при этом нет таких уравнений системы, в которые не входит ни одна из этих переменных.
2. Составляют таблицу, где в последней строке указываются коэффициенты функции с противоположным знаком. В левом столбце таблицы записывают основные переменные, в первой строке – все переменные, в последнем столбце свободные члены системы.
3. Проверяют выполнение критерия оптимальности – наличие в последней строке отрицательных коэффициентов. Если таких нет, то решение оптимально, достигнут, например, максимум функции (в правом нижнем углу таблицы), основные переменные при этом принимают значение bi , а неосновные переменные равны нулю, т.е. получается оптимальное базисное решение.
4. Если критерий оптимальности не выполнен, то наибольший по модулю отрицательный коэффициент в последней строке определяет разрешающий столбец S . Составляют оценочные ограничения по следующим правилам:
· ∞, если bi и аis имеют разные знаки;
· ∞, если bi =0и аis <0;
· ∞, если аis =0;
· 0, если bi =0 и аis >0;
· ![]() , если bi
и аis
имеют одинаковые знаки.
, если bi
и аis
имеют одинаковые знаки.
Определяют min![]() . Если конечного минимума нет, то задача не имеет конечного оптимума. Далее выбирают строку с номером q
,
на которой он достигается (любую, если их несколько), и называют её разрешающей строкой
. На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент
аqs
.
. Если конечного минимума нет, то задача не имеет конечного оптимума. Далее выбирают строку с номером q
,
на которой он достигается (любую, если их несколько), и называют её разрешающей строкой
. На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент
аqs
.
5. Переходим к следующей таблице по правилам:
а) в левом столбце записывают новый базис: вместо основной переменной хq - переменную хs , а геометрически произойдёт переход к соседней вершине многоугольника, где значение линейной функции «лучше». Значение линейной функции увеличится, т.к. переменная, входящая в выражение функции, станет основной, т.е. будет принимать не нулевое, а положительное значение;
b) новую строку с номером q получают из старой делением на разрешающий элемент а qs ;
c) все остальные элементы вычисляют по правилу многоугольника:
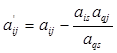 ;
; 
Далее переходим к пункту 3 алгоритма.
Замечание : при отыскании минимума функции Z , полагаем, что F =- Z и учитываем, что Zmin =- Fmax .
Решим задачу симплексным методом.
Для производства трёх изделий А,В и С используются три вида ресурсов. Каждый из них используется в объёме, не превышающем 180, 210 и 236 кг. Нормы затрат каждого из видов ресурсов на одно изделие и цена единицы изделий приведены в таблице.
| Вид ресурса | Нормы затрат ресурсов на 1 изделие, кг | ||
| А | В | С | |
1 2 3 |
4 3 1 |
2 1 2 |
1 3 5 |
| Цена изделия, у.е. | 10 | 14 | 12 |
Определить план выпуска изделий, обеспечивающий получение оптимального дохода.
Решение . х1 - количество выпускаемых изделий А
х2 - количество выпускаемых изделий В
х3 - количество выпускаемых изделий С.
![]() Тогда целевая функция будет иметь вид: F
=10
x
1
+14
x
2
+12 х3
→
max
Тогда целевая функция будет иметь вид: F
=10
x
1
+14
x
2
+12 х3
→
max
при ограничениях: 4 x 1 +2 x 2 +х3 ≤180
3 x 1 + x 2 +3х3 ≤210
x 1 +2 x 2 +5х3 ≤236
Приведём систему к каноническому виду:
![]() 4
x
1
+2
x
2
+х3
+х4
=180
4
x
1
+2
x
2
+х3
+х4
=180
3 x 1 + x 2 +3х3 +х5 =210
x 1 +2 x 2 +5х3 +х6 =236.
Составляем таблицу
| х1 | х2 | х3 | х4 | х5 | х6 | Свободныйчлен | |
х4 х5 х6 |
4 3 1 |
2 1 2 |
1 3 5 |
1 0 0 |
0 1 0 |
0 0 1 |
180 210 236 |
| F’ | -10 | -14 | -12 | 0 | 0 | 0 | 0 |
Определим ведущий элемент: min![]() . Далее выполняем действия, следуя алгоритму.
. Далее выполняем действия, следуя алгоритму.
| х1 | х2 | х3 | х4 | х5 | х6 | Свободныйчлен | |
х2 х5 х6 |
2 1 -3 |
1 0 0 |
1/2 5/2 4 |
1/2 -1/2 -1 |
0 1 0 |
0 0 1 |
90 120 56 |
| F’ | 18 | 0 | -5 | 7 | 0 | 0 | 1260 |
min![]()
| х1 | х2 | х3 | х4 | х5 | х6 | Свободныйчлен | |
х2 х5 х3 |
19/8 23/8 -3/4 |
1 0 0 |
0 0 1 |
5/8 1/8 -1/4 |
0 1 0 |
-1/8 -5/8 1/4 |
83 85 14 |
| F’ | 54/4 | 0 | 0 | 23/4 | 0 | 5/4 | 1330 |
Ответ : Чтобы получить оптимальный доход, нужно выпускать 83 ед. изделия В, 14 ед. изделия С, а изделие А не выпускать. Оптимальный доход составит 1330 у.е. По решению задачи видим, что у предприятия остаются свободными 85 кг. второго вида ресурсов, 1 и 3 вид полностью расходуются [5]
3) Двойственная задача.
Каждой задаче линейного программирования соответствует другая задача, называемая двойственной или сопряжённой
по отношению к исходной. Теория двойственности полезна для проведения качественных исследований ЗЛП. В главе I пункте 2) рассмотрена ![]() задача об использовании ресурсов. Предположим, что некоторая организация решила закупить ресурсы и необходимо установить оптимальные цены на эти ресурсы y
1,
y
2
,
y
3
. Очевидно, что
задача об использовании ресурсов. Предположим, что некоторая организация решила закупить ресурсы и необходимо установить оптимальные цены на эти ресурсы y
1,
y
2
,
y
3
. Очевидно, что
покупающая организация заинтересована в том, чтобы затраты на все ресурсы Z в количествах 180, 210, 236 по ценам соответственно y 1, y 2 , y 3 были минимальными, т.е. Z = 180 y 1 +210 y 2 +236 y 3 → min . С другой стороны, предприятие, продающее ресурсы, заинтересовано в том, чтобы полученная выручка была не мене той суммы, которую предприятие может получить при переработке ресурсов в готовую продукцию. На изготовление единицы продукции А расходуется 4кг . ресурса 1, 3кг . ресурса 2, 1кг . ресурса 3 по цене соответственно y 1, y 2 , y 3 . Поэтому, для удовлетворения требований продавца затраты на ресурсы, потребляемые при изготовлении единицы продукции, должны быть не менее её цены 10у.е ., т.е. 4 y 1 +3 y 2 + y 3 ≥10 .
Аналогично можно составить ограничения в виде неравенств по каждому виду продукции. Экономико-математическая модель исходной задачи и полученной двойственной задачи приведены в таблице.
| Задача I (исходная) | Задача II (двойственная) |
F = 10 x 1 +14 x 2 +12 x 3 → max При ограничениях:
3х1 +х2 +3х3 ≤210 х1 +2х2 +5х3 ≤236 и условие неотрицательности переменных x 1 ≥0, x 2 ≥0, х3 ≥0 . Для производства трёх изделий А, В, С используются три вида сырья. каждый из них используется в объёме, не превышающем 180, 210 и 236кг. Определить план выпуска изделий, обеспечивающий получение оптимального дохода при условии, что потребление ресурсов по каждому виду продукции не превзойдёт имеющихся запасов. |
Z = 180 y 1 +210 y 2 +236 y 3 → min При ограничениях:
y 1 +3 y 2 +5 y 3 ≥12 и условие неотрицательности переменных y 1 ≥0, у2 ≥0, у3 ≥0. Найти такой набор цен ресурсов, при котором общие затраты на ресурсы будут минимальными при условии, что затраты на ресурсы при производстве каждого вида продукции будут не менее прибыли от реализации этой продукции. |
Обе задачи, представленные в таблице обладают следующими свойствами:
1. В одной задаче ищут максимум линейной функции, в другой минимум.
2. Коэффициенты при переменных в линейной функции одной задачи являются свободными членами системы ограничений в другой.
3. Каждая из задач задана в стандартной форме, причём в задаче максимизации – все неравенства вида «≤ », а в задаче минимизации – все неравенства вида «≥ ».
4. Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу.
Для задачи I А= , для задачи II А
, для задачи II А![]() =
=
5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.
6. Условия неотрицательности переменных имеются в обеих задачах.
Две задачи Iи II линейного программирования, обладающие указанными свойствами, называются симметричными взаимодвойственными задачами .
Исходя из определения, можно предложить следующий алгоритм составления двойственной задачи.
1. Приводят все неравенства системы ограничений исходной задачи к одному смыслу: если в исходной задач ищут максимум линейной функции, то все неравенства системы ограничений приводят к виду «≤ », а если минимум – к виду «≥ ».
2. Составляют расширенную матрицу системы А1 , в которую включают матрицу коэффициентов при переменных, столбец свободных членов системы ограничений и строку коэффициентов при переменных в линейной функции.
3. Находят матрицу А![]() , транспонированную к матрице А1
.
, транспонированную к матрице А1
.
4. Формулируют двойственную задачу на основании полученной матрицы А![]() и условия неотрицательности переменных.
и условия неотрицательности переменных.
Связь между оптимальными решениями двойственных задач устанавливается с помощью теорем двойственности. Вначале рассмотрим вспомогательное утверждение.
Основное неравенство теории двойственности
. Пусть имеется пара двойственных задач I и II. Покажем, что для любых допустимых решений Х= (
x
1
,
x
2,
…,х
n
)
и У=
(y
1,
y
2
,…,
ym
)
исходной и двойственной задачи справедливо неравенство F
(
X
) ≤
Z
(
Y
)
или  ≤
≤![]() (3.6)
(3.6)
□ Возьмём неравенства системы ограничений исходной задачи ![]() ≤bi
и умножим соответственно на переменные y
1,
y
2
,…,
ym
и, сложив правые и левые части полученных неравенств, имеем
≤bi
и умножим соответственно на переменные y
1,
y
2
,…,
ym
и, сложив правые и левые части полученных неравенств, имеем
![]()
 ≤
≤![]() .
(3.7)
.
(3.7)
Аналогично умножаем систему ограничений двойственной задачи на переменные x 1 , x 2, …,х n , получим
![]()
![]() ≥
≥![]() (3.8)
(3.8)
Т.к. левые части неравенств (3.7) и (3.8) представляют одно и тоже выражение ![]()
 у
j
, то в силу транзитивности неравенств получим доказываемое неравенство (3.6).■
у
j
, то в силу транзитивности неравенств получим доказываемое неравенство (3.6).■
Теперь докажем признак оптимальности решений.
Достаточный признак оптимальности .
Если X
*
=(
x![]() ,
x
,
x![]() ,…,
x
,…,
x![]() )
и У*
=(у
)
и У*
=(у
![]() , у
, у
![]() ,…, у
,…, у
![]() )
– допустимые решения взаимно двойственных задач, для которых выполняется равенство
)
– допустимые решения взаимно двойственных задач, для которых выполняется равенство
F ( X * ) = Z ( Y * ) (3.9)
то Х* оптимальное решение исходной задачи I, а У* - двойственной задачи II.
□ Пусть Х1 любое допустимое решение исходной задачи I. Тогда на основании основного неравенства (3.6) получим F ( X 1 ) ≤ Z ( Y * ) . Однако Х1 - произвольное решение задачи I. Аналогично доказывается, что решение У* оптимально для задачи II.■
Всегда ли для каждой пары двойственных задач есть одновременно оптимальные решения; возможны ли ситуации, когда одна из двойственных задач имеет решение, а другая нет?
Ответ на эти вопросы даёт следующая теорема.
Первая (основная) теорема двойственности . Если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая, причём оптимальные значения их линейных функций равны:
Fmax = Zmin или F ( X * ) = Z ( Y * ) (3.10)
Если линейная функция одной из задач не ограничена, то система ограничений другой задачи противоречива.
Из первой части утверждения теоремы следует, что равенство (3.9) является не только достаточным, но и необходимым признаком оптимальности взаимно двойственных задач.
□ Докажем утверждение второй части методом от противного. Предположим, что в исходной задаче линейная функция не ограничена, т.е. Fmax =∞, а условия двойственной задачи не являются противоречивыми, т.е. существует хотя бы одно допустимое решение У=( y 1, y 2 ,…, ym ). Тогда в силу основного неравенство теории двойственности (3.6)F ( X ) ≤ Z ( Y ) , что противоречит условию неограниченности F(X). Следовательно, при Fmax =∞ в исходной задаче, допустимых решений в двойственной задаче быть не может. ■
Экономический смысл первой теоремы двойственности состоит в следующем: план производства X
*
=(
x![]() ,
x
,
x![]() ,…,
x
,…,
x![]() )
и набор цен ресурсов У*
=(у
)
и набор цен ресурсов У*
=(у
![]() , у
, у
![]() ,…, у
,…, у
![]() )
оказываются оптимальными тогда и только тогда, когда прибыль от продукции, найденная при ценах с1
, с2
,…, с
n
,«внешних» (известных заранее), равна затратам на ресурсы по «внутренним»(определяемым только из решения задачи) ценамy
1,
y
2
,…,
ym
. Для всех же других планов Х и У обеих задач в соответствии с основным неравенством (3.6) теории двойственности прибыль (выручка) от продукции всегда меньше (или равна) затрат на ресурсы.
)
оказываются оптимальными тогда и только тогда, когда прибыль от продукции, найденная при ценах с1
, с2
,…, с
n
,«внешних» (известных заранее), равна затратам на ресурсы по «внутренним»(определяемым только из решения задачи) ценамy
1,
y
2
,…,
ym
. Для всех же других планов Х и У обеих задач в соответствии с основным неравенством (3.6) теории двойственности прибыль (выручка) от продукции всегда меньше (или равна) затрат на ресурсы.
Экономический смысл первой теоремы двойственности можно интерпретировать и так: предприятию безразлично, производить ли продукцию по оптимальному плану X
*
=(
x![]() ,
x
,
x![]() ,…,
x
,…,
x![]() )
и получать максимальную прибыль Fmax
либо продавать ресурсы по оптимальным ценам У*
=(у
)
и получать максимальную прибыль Fmax
либо продавать ресурсы по оптимальным ценам У*
=(у
![]() , у
, у
![]() ,…, у
,…, у
![]() )
и возместить от продажи равные ей минимальные затраты на ресурсы Zmin
.
)
и возместить от продажи равные ей минимальные затраты на ресурсы Zmin
.
Связь между двумя взаимно двойственными задачами проявляется не только в равенстве оптимальных значений их линейных функций.
Пусть даны две взаимно двойственные задачи I и II. Если каждую из них решать симплексным методом, то необходимо привести их к каноническому виду, для чего в систему ограничений задачи I следует ввести m неотрицательных переменных xn +1 , xn +2 , … , xn + m , а в систему ограничений задачи II - n неотрицательных переменных ym +1 , ym +2 ,…, ym + n . Системы ограничений двойственных задач примут вид:
![]() +xn+i
=bi
, i=1,…,m
(3.11)
+xn+i
=bi
, i=1,…,m
(3.11)![]() -ym+j
=cj
, j=1,…,n
(3.12).
-ym+j
=cj
, j=1,…,n
(3.12).
установим соответствие между первоначальными переменными одной из двойственных задач и дополнительными переменными другой задачи.
| Переменные исходной задачи I | |
| Первоначальные | Дополнительные |
x 1 x 2 … xj … х n ↕ ↕ ↕ ↕ ym +1 ym +2 … ym + j … ym + n |
xn +1 xn +2 … xn + I … xn + m ↕ ↕ ↕ ↕ y 1 y 2 … yj ym |
| Дополнительные | Первоначальные |
| Переменные исходной задачи II | |
Теорема
. Положительным (ненулевым) компонентам оптимального решения одной из взаимно двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи, т.е. для любых i
=1,2,…,
m
и j
=1,2,…,
n
: если ![]() >0, то
>0, то ![]() =0; если
=0; если ![]() >0, то
>0, то![]() =0, и аналогично, если
=0, и аналогично, если ![]() >0, то
>0, то ![]() =0; если
=0; если ![]() >0, то
>0, то![]() =0.
=0.
□ Выразим дополнительные переменные из системы ограничений (3.11) исходной задачи I и (3.12) двойственной задачи, представленных в каноническом виде:
xn+i
=bi
- , i=1,2,…,m
(3.13)
, i=1,2,…,m
(3.13)
ym+j
=![]() -cj
, j=1,…,n.
(3.14)
-cj
, j=1,…,n.
(3.14)
Умножая каждое равенство системы (4.9) на соответствующие переменные уj ≥0 и складывая полученные равенства, найдём
![]() xn
+
i
yi
=
xn
+
i
yi
=![]() bi
yi
-
bi
yi
-![]()
![]() yi
(3.15)
yi
(3.15)
Аналогично, умножая каждое неравенство системы (4.10) на соответствующие переменные xj ≥0 и складывая полученные равенства, найдём
![]() ym
+
j
=
ym
+
j
=![]()
![]() yi
-
yi
-![]() cj
.
(3.16)
cj
.
(3.16)
Равенства (4.11)и(4.12) будут справедливы для любых допустимых значений переменных, в том числе и для оптимальных значений ![]() ,
,![]() ,
,![]() ,
, ![]() . В силу первой теоремы двойственности (3.10)F
(
X
*
) =
Z
(
Y
*
)
или
. В силу первой теоремы двойственности (3.10)F
(
X
*
) =
Z
(
Y
*
)
или  =
=![]() , поэтому из записи правых частей равенств (3.15) и (3.16) следует, что они должны отличаться только знаком. С другой стороны, из неотрицательности выражений
, поэтому из записи правых частей равенств (3.15) и (3.16) следует, что они должны отличаться только знаком. С другой стороны, из неотрицательности выражений ![]() xn
+
i
yi
и
xn
+
i
yi
и ![]() ym
+
j
,
входящие в выражения (3.15) и (3.16), следует, что правые части этих равенств должны быть неотрицательны.
ym
+
j
,
входящие в выражения (3.15) и (3.16), следует, что правые части этих равенств должны быть неотрицательны.
Эти условия могут выполняться одновременно только при равенстве этих правых частей для оптимального значения переменных нулю:
![]()
![]()
![]()
![]() =0,
=0,
![]()
![]()
![]() =0.
(3.17)
=0.
(3.17)
В силу условия неотрицательности переменных каждое из слагаемых в равенстве (4.13) должно равняться нулю:
![]()
![]()
![]() =0
, i=1,2,…,m
=0
, i=1,2,…,m
![]()
![]() =0,
j=1,2,…,n
=0,
j=1,2,…,n
Откуда и вытекает заключение теоремы. ■
Из доказанной теоремы следует, что введённое ранее соответствие между переменными двойственных задач представляет соответствие между основными (как правило не равными нулю) переменными одной из двойственных задач и неосновными (равными нулю) переменными другой задачи, когда они образуют допустимые базисные решения.
Рассмотренная теорема является следствием следующей теоремы.
Вторая теорема двойственности. Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных линейной функции исходной задачи, выраженной через неосновные переменные её оптимального решения.
Метод, при котором вначале симплексным методом решается двойственная задача, а затем оптимум и оптимальное решение исходной задачи находятся с помощью теорем двойственности, называется двойственным симплексным методом . Этот метод бывает выгодно применять, когда первое базисное решение исходной задачи недопустимое или, например, когда число её ограничений m больше числа переменных n.
С помощью теорем двойственности найдём решение задачи II. Получаем следующий набор цен ресурсов (![]()
![]()
![]() ), при котором минимальные затраты составят 1330. [5]
), при котором минимальные затраты составят 1330. [5]
4) Задача нелинейного программирования . (ЗНП)
Рассмотрим ЗНП и способы её решения. Математическая модель ЗНП в общем виде формулируется следующим образом:
f =(x1
,x2,
…,
х
n
)→ min (max)
. При этом переменные должны удовлетворять ограничениям:![]()
![]() g
1
(
x
1
,
x
2,
…,х
n
)≤
b
1
,
g
1
(
x
1
,
x
2,
…,х
n
)≤
b
1
,
…………………………
gm ( x 1 , x 2, …,х n )≤ bm ,
gm +1 ( x 1 , x 2, …,х n )≥ bm +1 ,
…………………………
gk ( x 1 , x 2, …,х n )≥ bk ,
gk +1 ( x 1 , x 2, …,х n )= bk+1 ,
………………………
gp ( x 1, x 2, …,х n )= bp .
x 1 , x 2, …,х n ≥0, где хотя бы одна из функций f, gi нелинейная.
Для ЗЛП нет единого метода решения. В зависимости от вида целевой функции и системы ограничений разработаны специальные методы решения, к которым относятся метод множителей Лагранжа, градиентные методы, приближённые методы решения, графический метод.
Рассмотрим основные идеи графического метода.
Максимум и минимум достигается в точках касания линии уровня с областью допустимых решений (ОДР), которая задается системой ограничений. Например, если линии уровня - прямые, то точки касания можно определить, используя геометрический смысл производной.
Рассмотрим на примерах решение ЗНП.
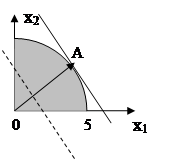
1. Найти экстремумы функции L ( x 1 , x 2 )= x 1 +2 x 2 при ограничениях
![]() ,
, ![]() .
.
|
![]() =-
=-
![]() ; (
; (![]() )
)![]() =-
=-
![]() ;
;
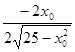 =-
=-
![]() ;
; ![]() x
0
=
x
0
=
![]() ;
x
2
=2
;
x
2
=2
![]() .
.
Тогда L
=
![]() +2∙2
+2∙2
![]() =5
=5
![]() .
.
Ответ
: Минимум достигается в точке О(0;0), глобальный максимум, равный 5
![]() ,
в точке А(
,
в точке А(
![]() ;2
;2
![]() )
.
)
.
2. Найти экстремумы функции L =( x 1 -6)2 +( x 2 -2)2 при ограничениях
![]() x
1
+
x
2
≤8
x
1
+
x
2
≤8
3 x 1 + x 2 ≤15
x 1 + x 2 ≥1
![]() .
.
 Решение.
ОДР – многоугольник ABCDE. Линии уровня представляют собой окружности (
x
1
-6)2
+(
x
2
-2)2
=С
с центром в точке О1
(6;2). Возьмём, например, С=36, видим, что максимум достигается в точке А(0;4), которая лежит на окружности наибольшего радиуса, пересекающую ОДР. L
(
A
)=(0-6)2
+(4-2)2
=40
. Минимум - в точке F, находящейся на пересечении прямой 3
x
1
+
x
2
=15
и перпендикуляра к этой прямой, проведённого из точки О1
. Т.к. угловой коэффициент равен -3, то угловой коэффициент перпендикуляра равен
Решение.
ОДР – многоугольник ABCDE. Линии уровня представляют собой окружности (
x
1
-6)2
+(
x
2
-2)2
=С
с центром в точке О1
(6;2). Возьмём, например, С=36, видим, что максимум достигается в точке А(0;4), которая лежит на окружности наибольшего радиуса, пересекающую ОДР. L
(
A
)=(0-6)2
+(4-2)2
=40
. Минимум - в точке F, находящейся на пересечении прямой 3
x
1
+
x
2
=15
и перпендикуляра к этой прямой, проведённого из точки О1
. Т.к. угловой коэффициент равен -3, то угловой коэффициент перпендикуляра равен ![]() . Из уравнения прямой, проходящей через данную точку О1
с угловым коэффициентом
. Из уравнения прямой, проходящей через данную точку О1
с угловым коэффициентом ![]() , получим (
x
2
-2)=
, получим (
x
2
-2)=
![]() (
x
1
-6).
Найдём координаты точки Е
(
x
1
-6).
Найдём координаты точки Е
![]() х1
-3х2
=0
х1
-3х2
=0
3 x 1 + x 2 =15 .
Решив систему, получаем Е(4.5; 1.5).
L ( E ) = (4.5-6)2 + (1.5-2)2 =2. 5 .
Ответ : Минимум, равный 2.5 достигается в точке (4.5; 1.5) , максимум, равный 40 , в точке (0;4) .
3. Найти экстремумы функции L =( x 1 -1)2 +( x 2 -3)2
при ограничениях
![]() ,
, ![]() .
.
 Решение
: ОДР является часть круга, с центром в начале координат, с радиусом 5, расположенная в I четверти. Линии уровня – это окружности с центром в точке О1
и радиуса С, т.к. (
x
1
-1)2
+(
x
2
-3)2
=С
. Точка О1
– это вырожденная линия уровня, соответствующая минимальному значению С=0. глобальный максимум достигается в точке А, лежащей на пересечении ОДР с линией уровня наибольшего радиуса. При этом
Решение
: ОДР является часть круга, с центром в начале координат, с радиусом 5, расположенная в I четверти. Линии уровня – это окружности с центром в точке О1
и радиуса С, т.к. (
x
1
-1)2
+(
x
2
-3)2
=С
. Точка О1
– это вырожденная линия уровня, соответствующая минимальному значению С=0. глобальный максимум достигается в точке А, лежащей на пересечении ОДР с линией уровня наибольшего радиуса. При этом
L ( A )=(5-1)2 +(0-3)2 =25.
Ответ : Минимум, равный 0 , достигается в точке (1;3) ,
Максимум, равный 25 , - в точке А(5;0) .
4. Предприниматель решил выделить на расширение своего дела 150 тыс.руб. известно, что если на приобретение нового оборудования затратить х тыс. руб., а на зарплату вновь принятых работников у тыс. руб., то прирост объёма продукции составит Q =0.001 x 0.6 · y 0.4 . Как следует распределить выделенные денежные ресурсы, чтобы прирост объёма продукции был максимальным .
![]() Решение
: Целевая функция имеет вид 0.001
x
0.6
·
y
0.4
→
max
при ограничениях x
+
y
≤150
,
Решение
: Целевая функция имеет вид 0.001
x
0.6
·
y
0.4
→
max
при ограничениях x
+
y
≤150
,
![]() .
.
ОДР – треугольник.  Линии уровня будут иметь вид 0.001
x
0.6
·
y
0.4
=С
. Выразив отсюда у
, получим у=
Линии уровня будут иметь вид 0.001
x
0.6
·
y
0.4
=С
. Выразив отсюда у
, получим у=
 . Т.к. максимум достигается в точке касания линии уровня с ОДР, то условие касания имеет вид
. Т.к. максимум достигается в точке касания линии уровня с ОДР, то условие касания имеет вид  =-1.
Найдя производную, получаем
=-1.
Найдя производную, получаем ![]() =-1.
Выразив х
, получим х=
=-1.
Выразив х
, получим х=![]() . у=
. у= =
=![]() .
.
Ответ : Факторы х и у следует распределить в отношении 2:3.
5.Предприятие выпускает изделия А и Б, при изготовлении которых используется сырьё
S
1
и
S
2
. Известны запасы
bi
(
i
=1,2) сырья, нормы его расхода на единицу изделия
aij
(
j
=1,2), оптовые цены
pj
на изделия и их плановая себестоимость с![]() . Как только объём выпускаемой продукции перестаёт соответствовать оптимальному размеру предприятия, дальнейшее увеличение выпуска х
j
ведёт к повышению себестоимости продукции
b
, в первом приближении фактическая себестоимость с
j
описывается функцией с
j
= с
. Как только объём выпускаемой продукции перестаёт соответствовать оптимальному размеру предприятия, дальнейшее увеличение выпуска х
j
ведёт к повышению себестоимости продукции
b
, в первом приближении фактическая себестоимость с
j
описывается функцией с
j
= с![]() + с
+ с![]() х
j
, где с
j
– некоторая постоянная. Все числовые данные приведены в таблице
х
j
, где с
j
– некоторая постоянная. Все числовые данные приведены в таблице
| b1 | b2 | a11 | a12 | a21 | a22 | p1 | p2 | с |
с |
с |
с |
| 90 | 88 | 13 | 6 | 8 | 11 | 12 | 10 | 7 | 8 | 0.2 | 0.2 |
Найти план выпуска изделий, обеспечивающий предприятию наивысшую прибыль в условиях нарушения баланса между объёмом и оптимальным размером предприятия.
Решение : С оставим математическую модель задачи.
Пусть Z – прибыль, получаемая предприятием после реализации х1 выпущенных изделий А и х2 изделий Б.
Z =( 12-( 7+ 0,2 х1 )) х1 +( 10-( 8+ 0,2 х2 )) х2 → max ,
![]() при ограничениях 13 х1
+ 6 х2
≤ 90,
при ограничениях 13 х1
+ 6 х2
≤ 90,
8 х1 + 11 х2 ≤88 ,
![]()
Преобразуя целевую функцию, получим:
Z
=5х1
-0,2х![]() +2 х2
-0,2х
+2 х2
-0,2х![]() →
max
→
max
ОДР – многоугольник ОАВD. Для построения линий уровня функции, приведём функцию к следующему виду:
(х1 -12,5)2 +(х2 -5)2 =181,25-5 Z .
Линиями уровня будут окружности с центром в точке О1
(12,5; 5)
и радиуса ![]() . Окружность наибольшего радиуса будет проходить через точку М, находящейся на пересечении прямой ВD и прямой O1
М, перпендикулярной к BD. Найдём координаты точки М.
. Окружность наибольшего радиуса будет проходить через точку М, находящейся на пересечении прямой ВD и прямой O1
М, перпендикулярной к BD. Найдём координаты точки М.
![]() 13х1
+ 6х2
=90
13х1
+ 6х2
=90
х2 -5=6/13(х1 -12,5). Решив систему, получим, М(6;2) .
Z (М)=30-7,2-2,8+4=26.
Ответ : Для получения предприятием максимальной прибыли, составляющей 26 ден.ед., следует выпустить 6 ед. изделия А и 2 ед. изделия Б.
5) Задача на условный экстремум .
Если система ограничений (3.1) задана в виде равенств, то это задача на условный экстремум. В случае функцииn независимых переменных ( x 1 , x 2, …,х n ) задача на условный экстремум формулируется следующим образом:
L=f(x1 ,x2, …, х n )→max (min)
при условиях: g
i
(
x
1
,
x
2,
…,х
n
)=0,
i
=
![]() .
(
m
<
n
).
.
(
m
<
n
).
В конце XVIIIвека Лагранж предложил остроумный метод решения задачи на условный экстремум. Суть метода Лагранжа состоит в построении функции L
(
x
1
,
x
2,
…,х
n
)=
f
(
x
1
,
x
2,
…,х
n
)+![]() gi
(
x
1
,
x
2,
…,х
n
),
где λ
i
неизвестные постоянные, и нахождении экстремума функции L
.
gi
(
x
1
,
x
2,
…,х
n
),
где λ
i
неизвестные постоянные, и нахождении экстремума функции L
.
Верна следующая теорема: если точка (
![]() )
является точкой условного экстремума функции f
(
x
1
,
x
2,
…,х
n
)
при условии g
(
x
1
,
x
2,
…,х
n
)=0
, то существует значение λi
такие, что точка (
)
является точкой условного экстремума функции f
(
x
1
,
x
2,
…,х
n
)
при условии g
(
x
1
,
x
2,
…,х
n
)=0
, то существует значение λi
такие, что точка (
![]() )
является точкой экстремума функции L
(
)
является точкой экстремума функции L
(
![]() ).
).
Рассмотрим метод Лагранжа для функции двух переменных.
L(x1 ,x2 , λ )= f(x1 ,x2 )+ λ g(x1 ,x2 )
Таким образом, для нахождения условного экстремума функции f ( x 1 , x 2 ) при условии g ( x 1 , x 2 )=0 требуется найти решение системы
![]() L
L![]() =f
=f ![]() (x1
,x2
)+λg
(x1
,x2
)+λg![]() (x1
,x2
)=0,
(3.18)
(x1
,x2
)=0,
(3.18)
L![]() =f
=f ![]() (x1
, x2
) +λg
(x1
, x2
) +λg![]() (x1
, x2) =0,
(x1
, x2) =0,
L![]() =
g
(
x
1
,
x
2
) =0.
[4]
=
g
(
x
1
,
x
2
) =0.
[4]
Есть и достаточные условия, при выполнении которых решение (x
1
,
x
2
,λ
) системы (3.18) определяет точку, в которой функция f достигает экстремума, для этого нужно вычислить значения ![]() и составить определитель
и составить определитель
![]() =-
=- .
.
Если ![]() <0, то функция имеет в точке (
<0, то функция имеет в точке (![]() )
условный максимум, если
)
условный максимум, если ![]() >0 – то условный минимум.
>0 – то условный минимум.
Решим задачу методом множителей Лагранжа.
Общие издержки производства заданы функцией Т=0,5х2 +0,6ху+0,4у2 ++700х+600у+2000, где х и у соответственно количество товаров А и В. Общее количество произведённой продукции должно быть равно 500 единиц. Сколько единиц товара А и В нужно производить, чтобы издержки на их изготовление были минимальными ?
Решение: составим функцию Лагранжа.
L ( x , y , λ) =0,5х2 +0,6ху+0,4у2 ++700х+600у+2000+λ(х+у-500) . Приравнивая к нулю её частные производные, получим
![]() х+0,6у+700+ λ=0,
х+0,6у+700+ λ=0,
0,6х+0,8у+600+ λ=0,
х+у-500=0 .
Решив систему, найдём (0, 500, -1000) .
Воспользуемся достаточным условием для определения найденного значения L![]() (
x
0
,
y
0
)=1,
L
(
x
0
,
y
0
)=1,
L![]() (
x
0
,
y
0
)=0.8,
L
(
x
0
,
y
0
)=0.8,
L![]() (
x
0
,
y
0
)=0.6
. Функция g
= х+у-500
. g
(
x
0
,
y
0
)=0.6
. Функция g
= х+у-500
. g![]() =1
, g
=1
, g![]() =1
.
=1
.
![]() =-(0·
L
=-(0·
L![]() ·
L
·
L![]() +
g
+
g![]() ·
L
·
L![]() ·
g
·
g![]() +
g
+
g![]() ·
g
·
g![]() ·
L
·
L![]() -
g
-
g![]() ·
L
·
L![]() ·
g
·
g![]() -0·
L
-0·
L![]() ·
L
·
L![]() -
g
-
g![]() ·
g
·
g![]() ·
L
·
L![]() )=0,6>0
)=0,6>0
Значит, в точке (0;500) функция L имеет условный минимум.
Ответ : Выгодно производить только 500 ед. товара В, а товар А не производить.
Наиболее простым способом нахождения условного экстремума функции двух переменных является сведение задачи к отысканию экстремума функции одной переменной. Пусть уравнениеg ( x 1 , x 2 )=0 удалось разрешить относительно одной из переменных, например, выразить х2 через х1 : х2 =φ(х1 ). Подставив полученное выражение в функцию, получим y = f ( x 1 , x 2 )= y = f ( x 1 , φ(х1 )) , т.е. функцию одной переменной. Её экстремум и будет условным экстремумом функции y = f ( x 1 , x 2 ).
Проиллюстрируем данный метод на конкретной задаче.
Фирма реализует автомобили двумя способами: через розничную и оптовую торговлю. При реализации х1
автомобилей в розницу расходы на реализацию составляют (4 х1
+х![]() ) у. е., а при продаже х2
автомобилей оптом – х
) у. е., а при продаже х2
автомобилей оптом – х![]() у. е. Найти оптимальный способ реализации автомобилей, минимизирующий суммарные расходы, если общее число, предназначенных для продажи автомобилей составляет 200шт
.
у. е. Найти оптимальный способ реализации автомобилей, минимизирующий суммарные расходы, если общее число, предназначенных для продажи автомобилей составляет 200шт
.
Решение
: Составим функцию L
(х1
,х2
)=4
х1
+х![]() +х
+х![]() и будем находить её минимум. Т.к. для продажи предназначено 200
автомобилей, то х1
+х2
=200. Разрешим данной уравнение относительно переменной х2
: х2
=200-х1
. Подставим полученное выражение в функцию L
, получим L
=4 х1
+ х
и будем находить её минимум. Т.к. для продажи предназначено 200
автомобилей, то х1
+х2
=200. Разрешим данной уравнение относительно переменной х2
: х2
=200-х1
. Подставим полученное выражение в функцию L
, получим L
=4 х1
+ х![]() + (200- х1
)2
=2х
+ (200- х1
)2
=2х![]() --396 х1
+40000
, х1
--396 х1
+40000
, х1
![]() 0.
0.
Найдём экстремум данной функции.
 L
L![]() =4 х1
-396
.
=4 х1
-396
.
Приравняв её к нулю, получим х1 =99 .
Ответ : оптимальный способ реализации автомобилей – это 99 автомобилей в розницу и 101 автомобиль оптом (х2 =200-99) . Расходы составят 20398 р.
В экономических задачах, в которых отыскивается оптимум функции f
=(
x
1
,
x
2,
…,х
n
)
, где n![]() 2, полагают, что найденное единственное решение, удовлетворяющее необходимому условию экстремума, является оптимальным.
2, полагают, что найденное единственное решение, удовлетворяющее необходимому условию экстремума, является оптимальным.
4 . Задача потребительского выбора .
1) Функция полезности. Бюджетное ограничение. Формулировка задачи потребительского выбора .
Будем считать, что потребитель располагает доходом Q, который он полностью тратит на приобретение благ (продуктов) Учитывая структуру цен, доход и собственные предпочтения, потребитель приобретает определённое количество благ, и математическая модель такого его поведения называется моделью потребительского выбора .
В некоторых задачах выделяют один продукт, а вторым считают все остальные. Поэтому сначала рассмотрим модель с двумя видами продуктов. Потребительский набор – это вектор ( x 1 , x 2 ), координата x 1 которого равна количеству единиц первого продукта, а координата x 2 равна количеству единиц второго продукта.
Выбор потребителя характеризуется отношением предпочтения, суть которого состоит в следующем. Считается, что потребитель про каждые два набора может сказать, что либо один из них более желателен, чем другой, либо потребитель не видит между ними разницы. Отношение предпочтения транзитивно, т.е. если набор А=(а1 ,а2 ) предпочтительнее набора B =( b 1 , b 2 ) , а набор B =( b 1 , b 2 ) предпочтительнее набора С=(с1 ,с2 ), то набор А=(а1 ,а2 ) предпочтительнее набора С=(с1 ,с2 ).
На множестве потребительских наборов (
x
1
,
x
2
)
определена функция u
(
x
1
,
x
2
)
(называемая функцией полезности потребителя
), значение u
(
x
1
,
x
2
)
которой на потребительском наборе (
x
1
,
x
2
)
равно потребительской оценке индивидуума для этого набора. Потребительскую оценку u
(
x
1
,
x
2
)
набора (
x
1
,
x
2
)
принято называть уровнем
(или степенью
) удовлетворения потребительского индивидуума, если он приобретает или потребляет данный набор (
x
1
,
x
2
).
Каждый потребитель имеет, вообще говоря, свою функцию полезности. Если набор А ![]() предпочтительнее набора В, то u
(А)>
u
(В).
предпочтительнее набора В, то u
(А)>
u
(В).
Функция полезности удовлетворяет следующим свойствам:
1. Возрастание потребления одного продукта при постоянном потреблении другого продукта ведёт к росту потребительской оценки, т.е. если x![]() >
x
>
x![]() , то u
(
x
, то u
(
x![]() ,
x
2
)>
u
(
x
,
x
2
)>
u
(
x![]() ,
x
2
)
;
,
x
2
)
;
если x![]() >
x
>
x![]() , то u
(
x
1
,
x
, то u
(
x
1
,
x![]() )>
u
(
x
1
,
x
)>
u
(
x
1
,
x![]() ).
).
Иначе говоря, u![]() (
x
1
,
x
2
)=
u
(
x
1
,
x
2
)=
u![]() >0,
u
>0,
u![]() (
x
1
,
x
2
)=
u
(
x
1
,
x
2
)=
u![]() >0.
>0.
Первые частные производные u![]() и u
и u![]() называются предельными полезностями
первого и второго продуктов соответственно.
называются предельными полезностями
первого и второго продуктов соответственно.
2. Предельная полезность каждого продукта уменьшается, если объём его потребления растёт (закон убывания предельной полезности
). Из свойства второй производной следует, что u![]() (
x
1
,
x
2
)<0,
u
(
x
1
,
x
2
)<0,
u![]() (
x
1
,
x
2
)<0.
(
x
1
,
x
2
)<0.
3. Предельная полезность каждого продукта увеличивается, если растёт количество другого продукта. В этом случае продукт, количество которого фиксировано, оказывается относительно дефицитным. Если блага могут замещать друг друга в потреблении, свойство не выполняется. u![]() (
x
1
,
x
2
)=
u
12
>0,
u
(
x
1
,
x
2
)=
u
12
>0,
u![]() (
x
1
,
x
2
)=
u
21
>0.
(
x
1
,
x
2
)=
u
21
>0.
Линия, соединяющая потребительские наборы ( x 1 , x 2 ) , имеющие один и тот же уровень удовлетворения потребностей называется линией безразличия . Линия безразличия есть не что иное, как линия уровня функции полезности. Множество линий безразличия называется картой линий безразличия . Линии безразличия, соответствующие разным уровням удовлетворения потребностей не пересекаются и не касаются. Чем выше и правее расположена линия безразличия, тем большему уровню удовлетворения потребностей она соответствует. Условия 1-3 означают, что линия безразличия убывает и является выпуклой вниз.
Задача потребительского выбора
заключается в выборе такого потребительского набора (х![]() , х
, х![]() ),
который максимизирует его функцию полезности при заданном бюджетном ограничении.
),
который максимизирует его функцию полезности при заданном бюджетном ограничении.
Бюджетное ограничение означает, что денежные расходы на продуктыне могут превышать денежного дохода, т.е. p 1 x 1 + p 2 x 2 ≤ Q , где p1 и p2 –рыночные цены, а Q – доход потребителя, который он готов потратить на приобретение первого и второго продуктов. Величины p 1 , p 2 и Q заданы.
Задача потребительского выбора имеет вид:
u ( x 1 , x 2 )→ max
при ограничении p 1 x 1 + p 2 x 2 ≤ Q
и условие x 1 ≥0, x 2 ≥0.
Допустимое множество (т.е. множество наборов продуктов, доступных для потребителя) представляет собой треугольник, ограниченный осями координат и бюджетной прямой. На этом множестве требуется найти точку, принадлежащую кривой безразличия с максимальным уровнем полезности. Поиск этой точки можно интерпретировать графически как последовательный переход на линии всё более высокого уровня полезности до тех пор, пока эти линии ещё имеют общие точки с допустимым множеством.
|
|
|

2) Решение задачи потребительского выбора и его свойства .
Набор (х![]() , х
, х![]() )
, который является решением задачи потребительского выбора, принято называть оптимальным
для потребителя.
)
, который является решением задачи потребительского выбора, принято называть оптимальным
для потребителя.
Рассмотрим некоторые свойства задачи потребительского выбора. Во – первых, решение задачи (х![]() , х
, х![]() )
сохраняется при любом монотонном (т.е. сохраняющем порядок значении) преобразовании функции полезности u
(
x
1
,
x
2
)
. Поскольку значениеu
(х
)
сохраняется при любом монотонном (т.е. сохраняющем порядок значении) преобразовании функции полезности u
(
x
1
,
x
2
)
. Поскольку значениеu
(х![]() , х
, х![]() ),
было максимальным на всём допустимом множестве, оно остаётся таковым и после монотонного преобразования функции полезности (допустимое множество, определяемое бюджетным ограничением, остаётся неизменным). Таким монотонным преобразованием может быть умножение функции полезности на некоторое положительное число, возведение её в положительную степень, логарифмирование.
),
было максимальным на всём допустимом множестве, оно остаётся таковым и после монотонного преобразования функции полезности (допустимое множество, определяемое бюджетным ограничением, остаётся неизменным). Таким монотонным преобразованием может быть умножение функции полезности на некоторое положительное число, возведение её в положительную степень, логарифмирование.
Во – вторых, решение задачи потребительского выбора не изменится, если все цены и доход увеличиваются (уменьшаются) в одно и то же число раз λ . (λ>0)
Это равнозначно умножению на положительное число λ обеих частей бюджетного ограниченияp 1 x 1 + p 2 x 2 ≤ Q , что даёт неравенство, эквивалентное исходному. Поскольку ни цены, ни доход Q не входят в функцию полезности, задача остаётся той же, что и первоначально.
Если на каком – то потребительском наборе (
x
1
,
x
2
)
бюджетное ограничение p
1
x
1
+
p
2
x
2
≤
Q
будет выполнятся в виде строгого неравенства, то мы можем увеличить потребление какого – либо из продуктов и тем самым увеличить функцию полезности. Следовательно, набор (х![]() , х
, х![]() )
, максимизирующий функцию полезности, должен обращать бюджетное ограничение в равенство, т.е. p
1
х
)
, максимизирующий функцию полезности, должен обращать бюджетное ограничение в равенство, т.е. p
1
х![]() +
p
2
х
+
p
2
х![]() =
Q
.
=
Q
.
Графически это означает, что решение (х![]() , х
, х![]() )
задачи потребительского выбора должно лежать на бюджетной прямой, которая проходит через точки пересечения с осями координат, где весь доход тратиться на один продукт: (0,
)
задачи потребительского выбора должно лежать на бюджетной прямой, которая проходит через точки пересечения с осями координат, где весь доход тратиться на один продукт: (0,
![]() )
и (
)
и (
![]() ,0)
.
,0)
.
Итак, задачу потребительского выбора можно заменить задачей на условный экстремум (ибо решение (х![]() , х
, х![]() )
этих двух задач одно и то же)
)
этих двух задач одно и то же)
u ( x 1 , x 2 )→ max
при условии p 1 x 1 + p 2 x 2 = Q .
Для решения этой задачи применим метод Лагранжа. Выписываем функцию Лагранжа L ( x 1 , x 2, λ)= u ( x 1 , x 2 )+ λ ( p 1 x 1 + p 2 x 2 - Q ), находим её частные производные по переменным x 1 , x 2 и λ и приравниваем к нулю:
![]() L
L![]() = u
= u![]() +λ p1
=0,
+λ p1
=0,
L![]() = u
= u![]() +λ p2
=0,
+λ p2
=0,
L![]() =p1
x1
+p2
x2
-Q =0.
=p1
x1
+p2
x2
-Q =0.
Исключив из полученной системы неизвестную λ, получим систему двух уравнений с двумя неизвестными x 1 , и x 2
![]()
![]() =
=![]() ,
,
p 1 x 1 + p 2 x 2 = Q .
Решение (х![]() , х
, х![]() )
этой системы есть критическая точка функции Лагранжа. Подставив решение (х
)
этой системы есть критическая точка функции Лагранжа. Подставив решение (х![]() , х
, х![]() )
в левую часть равенства
)
в левую часть равенства
 =
=![]() ,
,
получим, что в точке (х![]() , х
, х![]() )
отношение
)
отношение ![]() предельных полезностей u
предельных полезностей u![]() (х
(х![]() , х
, х![]() )
и u
)
и u![]() (х
(х![]() , х
, х![]() )
продуктов равно отношению рыночных цен p
1
и p
2
на эти продукты:
)
продуктов равно отношению рыночных цен p
1
и p
2
на эти продукты:
![]() =
=![]() . (5.1)
. (5.1)
В связи с тем, что отношение ![]() равно предельной норме замены первого продукта вторым в точке локального рыночного равновесия (х
равно предельной норме замены первого продукта вторым в точке локального рыночного равновесия (х![]() , х
, х![]() )
, из (5.1) следует, что эта предельная норма равна отношению рыночных цен
)
, из (5.1) следует, что эта предельная норма равна отношению рыночных цен ![]() на продукты. Приведённый результат играет важную роль в экономической теории.
на продукты. Приведённый результат играет важную роль в экономической теории.
Геометрически решение (х![]() , х
, х![]() )
можно интерпретировать как точку касания линии безразличия функции полезности u
(
x
1
,
x
2
)
с бюджетной прямой p
1
x
1
+
p
2
x
2
=
Q
.
Это определяется тем, что отношение
)
можно интерпретировать как точку касания линии безразличия функции полезности u
(
x
1
,
x
2
)
с бюджетной прямой p
1
x
1
+
p
2
x
2
=
Q
.
Это определяется тем, что отношение ![]() =-
=-![]() показывает тангенс угла наклона линии уровня функции полезности, а отношение -
показывает тангенс угла наклона линии уровня функции полезности, а отношение - ![]() представляет тангенс угла наклона бюджетной прямой. Поскольку в точке потребительского выбора они равны, в этой точке происходит касание данных двух линий.
представляет тангенс угла наклона бюджетной прямой. Поскольку в точке потребительского выбора они равны, в этой точке происходит касание данных двух линий.
Решим задачу потребительского выбора.
Оптимальный набор потребителя составляет 6 ед. продукта х1
и 8 ед. продукта х2. Определите цены потребляемых благ, если известно, что доход потребителя равен 240 руб. Функция полезности потребителя имеет вид:
u
(
x
1
,
x
2
)=
x![]() x
x![]() .
.
Решение . Следуя принципу решения, получаем систему уравнений:
![]()
![]()
![]()
![]() =
=![]() ,
,  =
=![]() ,
, ![]() =
=![]() ,
,
p1 x1 +p2 x2 =240. p1 x1 +p2 x2 =240 . p1 x1 +p2 x2 =240 .
Подставив, вместо х1 – 6 ед ., вместо х2 – 8 ед ., получим: p 1 =10 руб., p 2 =22.5 руб.
3) Общая модель потребительского выбора .
Была рассмотрена модель потребительского выбора с двумя продуктов и её решение с помощью метода множителей Лагранжа. Сейчас рассмотрим свойства задачи потребительского выбора с произвольным числом продуктов и целевой функцией общего вида.
Пусть задана целевая функция предпочтения потребителя u ( x 1 , x 2, …,х n ) , где х i - количество i-го продукта, вектор цен pi =( p 1 , p 2 ,…, pn ) и доход Q. Записав бюджетное ограничение и ограничение на неотрицательность, получаем задачу
u ( x )→ max (5.2)
при условии px ≤ Q , x ≥0
(здесь x =( x 1 , x 2, …,х n ), p = (p 1 , p 2 ,…, pn ), px =( p 1 x 1 +…+ pn xn ) ).
Будем считать, что неотрицательность переменных обеспечивается свойствами целевой функции и бюджетного ограничения. В этом случае можно записать функцию Лагранжа и исследовать её на безусловный экстремум.
L ( x , λ)= u ( x )+ λ ( px - Q ).
Необходимое условие экстремума – равенство нулю частных производных: L![]() =
u
=
u![]() +
λ
pi
=0
для всех i
+
λ
pi
=0
для всех i![]() [1;
n
]
и L
[1;
n
]
и L![]() =
px
-
Q
=0.
Отсюда вытекает, что для всех i в точке х
=
px
-
Q
=0.
Отсюда вытекает, что для всех i в точке х![]() рыночного равновесия выполняется равенство
рыночного равновесия выполняется равенство
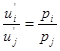 (5.3)
(5.3)
которое получается после перенесения вторых слагаемых, необходимых условий в правую часть и делением i-го равенства на j-ое. Итак, в точке оптимума отношение предельных полезностей любых двух продуктов равно отношению их рыночных цен. Равенство (5.3) можно переписать и в другой форме:
 (5.4)
(5.4)
Это означает, что полезность, приходящаяся на единицу денежных затрат, в точке оптимума одинаковая по всем видам благ. Если бы это было не так, то по крайней мере одну денежную единицу можно было бы перераспределить так, чтобы выросло благосостояние (значение функции полезности) потребителя. Если для некоторых i, j
 ,
,
то некоторое количество денег можно было бы перераспределить от i –го продукта к j-му, увеличив уровень благосостояния.
4) Модель Стоуна . Выведем теперь функцию спроса для конкретной функции потребительского предпочтения, называемой функцией Р.Стоуна. Эта функция имеет вид
u
(
x
)=
![]() →
max
(5.5)
→
max
(5.5)
Здесь а
i
– минимально необходимое количество i-го продукта, которое приобретается в любом случае и не является предметом выбора. Для того чтобы набор {
ai
}
мог быть полностью приобретен, необходимо, чтобы доход Q был больше ![]() - количество денег, необходимого для покупки этого набора. Коэффициенты степени а
i
>0
характеризуют относительную «ценность» продуктов для потребителя.
- количество денег, необходимого для покупки этого набора. Коэффициенты степени а
i
>0
характеризуют относительную «ценность» продуктов для потребителя.
Добавив к целевой функции (5.5) бюджетные ограничения ![]() ≤Q, хi
≥0, получим задачу, называемую моделью Стоуна. Как было сказано на стр. 36, бюджетное ограничение должно обращаться в равенство. Составим функцию Лагранжа L
(
x
1
,
x
2,
…,х
n
,
λ)=
u
(
x
)+ λ (
p
1
x
1
+…+
pn
xn
–
Q
).
≤Q, хi
≥0, получим задачу, называемую моделью Стоуна. Как было сказано на стр. 36, бюджетное ограничение должно обращаться в равенство. Составим функцию Лагранжа L
(
x
1
,
x
2,
…,х
n
,
λ)=
u
(
x
)+ λ (
p
1
x
1
+…+
pn
xn
–
Q
).
Найдём частные производные функции Лагранжа и приравняем их к нулю L![]() =
a
1
(
x
1
-
a
1
)
=
a
1
(
x
1
-
a
1
)
![]() ∙(
x
2
-
a
2
)
∙(
x
2
-
a
2
)
![]() ∙…∙(
xn
-
an
)
∙…∙(
xn
-
an
)
![]() + λ
p
1
.
+ λ
p
1
.
Аналогично получаем остальные частные производные. Т.е.
L![]() =
=
![]()
![]() + λ
pi
=0,
где i=
+ λ
pi
=0,
где i=![]() .
.
Выразив xi
,
получим xi
=
ai
-
![]() . (5.6)
. (5.6)
L
![]() =
=![]() -
Q
=0.
Умножив каждое из равенств (5.6) на λ
pi
и просуммировав их по i, имеем
-
Q
=0.
Умножив каждое из равенств (5.6) на λ
pi
и просуммировав их по i, имеем
![]() =0
(5.7).
=0
(5.7).
Поскольку в точке оптимума бюджетное ограничение выполняется как равенство, заменим ![]() на Q, получим
на Q, получим ![]() =0.
Поделив на λ
, получим
=0.
Поделив на λ
, получим  =-(
Q
-
=-(
Q
-![]() )
. Откуда
)
. Откуда  . Полученное выражение подставляем в равенство (5.6)
. Полученное выражение подставляем в равенство (5.6)
xi
=
ai
+
 (5.8)
(5.8)
Т.е. вначале приобретается минимально необходимое количество продукта ai
.
Затем рассчитывается сумма денег, остающаяся после этого, которая распределяется пропорционально «весам» важности ![]() i
. Разделив количество денег на ценуpi
, получаем дополнительно приобретаемое, сверх минимума, количество i- продукта и добавляем его к а
i
. [1]
i
. Разделив количество денег на ценуpi
, получаем дополнительно приобретаемое, сверх минимума, количество i- продукта и добавляем его к а
i
. [1]
При написании работы мною была изучена литература по данной теме. Были рассмотрены математические модели в экономике, повторены некоторые понятия функций нескольких переменных, необходимых для изучения оптимизационных задач. Также была изучена постановка задач математического программирования и методы их решения. Был рассмотрен симплексный метод, который позволяет решить любую задачу линейного программирования. Для ЗЛП была рассмотрена симметричная взаимодвойственная задача и метод её решения с использованием теорем двойственности. Для задачи нелинейного программирования был рассмотрен геометрический метод решения. А также рассмотрены задачи на условный экстремум.
В работе приводится задача потребительского выбора, решение которой сводится к решению задач на условный экстремум. Также рассмотрен частный случай задачи потребительского выбора - модель Стоуна.
Мною были решены задачи по каждому виду рассмотренных оптимизационных задач. Это ЗЛП симплексным и графическим методом, решена двойственная задача, несколько задач нелинейного программирования, задачи на условный экстремум методом подстановки и методом множителей Лагранжа, задача потребительского выбора.
Я считаю, что знание этой темы может пригодиться не только экономистам и людям, специально занимающимся этой наукой, но и ненаучным работникам, т.к. в жизни часто приходится сталкиваться с решением подобного рода задач.
Библиографический список
1. Замков, О.О. Математические методы в экономике: Учебник/ Под общ. ред. д.э.н., проф. А.В. Сидоровича/ О.О. Замков, А.В. Толстопятенко, Ю.Н. Черемных; МГУ им. Ломоносова.-3-е изд., перераб. – М.: Издательство «Дело и сервис», 2001
2. Ильин, В.А. Математический анализ/ В.А. Ильин, В.А. Садовничий, Б.Х. Сендов. – М.: Наука, 1979
3. Красс, М.С. Основы математики и её приложения в экономическом образовании: Учебник. – 3-е изд. – М.: Дело,2002
4. Кремер, Н.Ш. Высшая математика для экономистов: Учебник для вузов/ Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н Фридман. - М.: ЮНИТИ, 2002.
5. Кремер, Н.Ш. Исследование операций в экономике: Учебное пособие для вузов/ Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера. – М.: Банкиибиржи, ЮНИТИ,1997.
6. Малыхин, В.И. Математика в экономике: Учебное пособие.- М.:ИНФРА - Москва, 2002.
7. Симонов, А.В. Об одном приложении производной к решению экономических задач/ А.С. Симонов, Н.Г. Игнатьев// математика в школе №9, 2001
8. Сборник задач и упражнений по высшей математике: мат. программирование: Учеб. Пособие/ А.В. Кузнецов, В.А. Сакович, Н.И. Холод; Под. общ. ред. А.В. Кузнецова – Мн.: Выш. шк., 2002
9. Сборник задач по высшей математике для экономистов: Учебное пособие/ Под. ред. В.И. Ермакова.- М.: Инфра – Москва, 2002.
10. Сборник задач по микроэкономике. К «Курсу микроэкономики» Р.М. Нуреева/ Гл. ред. д.э.н., проф. Р.М. Нуреев. – М.: Норма, 2003
11. Фихтенгольц, Г.М. основы математического анализа. Часть 1. 4-е изд. – СПб: издательство «Лань», 2002.
12. Онегов, В.А. Исследование операций. Задачи, методы, алгоритмы. – Киров: ВГПУ, 2001.