Реферат: Некоторые особенности психологического восприятия и визуальной интерпретации динамических процессов

«Некоторые особенности психологического восприятия и визуальной интерпретации динамических процессов»

Введение

Я хотел бы в своем выступлении остановиться на некоторых психологических особенностях человеческого восприятия. Использование торговых систем как, впрочем, и подавляющего большинства средств технического анализа, основано на графическом представлении эмпирической информации. Это действительно наиболее эффективный способ анализа данных, однако, на этом пути нас подстерегает ряд опасностей, связанных с субъективной составляющей такого подхода. Информация, которую мы воспринимаем, взаимодействует с некими нашими психологическими моделями, которые присущи человеческой психике в целом и трейдерам в частности. И выясняется, что наши интуитивные ожидания особенно в области оценки вероятностей оказываются не просто искаженными, они оказываются катастрофически ошибочными. Можно рассуждать, почему это происходит, но так как нас интересуют в большей степени практические последствия этих эффектов я перейду к рассмотрению некоторых примеров такого искаженного восприятия, которое, как вы увидите, может оказаться критическим при торговле.

Каким образом меня стала интересовать эта тема? Лет 5 назад, во время не особо активных торгов, мы с одним трейдером играли в примитивную “случайную” игру в кости – используя доску для нард, у каждого игрока по 15 фишек, мы по очереди бросали 2 кубика, считали сумму выпадающих очков - у одного, допустим, 10, у другого 7 – считали разницу очков – в нашем случае равную 3 и тот у кого сумма меньше, передает соответствующее количество фишек противнику. Проигрывает тот, у кого первого заканчиваются фишки. Была некая денежная ставка, она не была большой, но проигрывать было неприятно. В один из дней я проиграл достаточно большое кол-во партий. Несмотря на то, что в трейдинге я никогда не держу проигрывающих позиций в течение последних 10 лет, здесь я задумался, вроде игра случайная, почему бы вместо того, чтобы расплатиться, поиграть еще несколько дней, ставка небольшая, вполне можно и отыграться. Но до следующей нашей игры мне попался известный учебник по теории вероятности Вильяма Феллера «Введение в теорию вероятности и ее приложения», где на очень простом уровне были изложены примеры, связанные со случайными блужданиями. Этот учебник хорош тем, что наряду с аналитическими выкладками Феллер приводит примеры и показывает, насколько наши ожидания вообще не соответствуют тому, что происходит на самом деле со статистической точки зрения.

В качестве простейшего объекта, который рассматривался у Феллера, рассматривалась игра с подбрасыванием идеальной монеты. В случае выпадения «решки» 1 доллар получал первый игрок, в случае выпадения «орла» - второй. В результате получалась траектория, которая представляла собой сальдо счета одного игрока. У второго игрока, естественно, получалась симметричная траектория с обратным знаком. Это простейший вариант случайного блуждания, когда одно приращение равно либо +1, либо –1, вероятности каждого выпадения равны. И как совершенно справедливо указывал автор, результаты, которые аналитически получаются по поводу характеристик такого процесса, оказываются для большинства из нас абсолютно неожиданными.

Попробуем смоделировать аналогичную ситуацию. С помощью примитивной формулы, которая в Excel выглядит так:

0,5 – RAND,

генерируем равномерно распределенную случайную величину от –0,5 до +0,5.

В данном случае мы имеем дело с непрерывной случайной величиной, в отличии от дискретного случая с монетой, но это практически никак не повлияет на интересующие нас характеристики.

Так выглядит полученный таким образом ряд .

РИС.1

Это хаотическая, по крайней мере, внешне, траектория колебаний вокруг нуля в неком диапазоне. В нашем случае в диапазоне от –0,5 до 0,5. Это вполне соответствует нашим представлениям о том, как такой процесс может выглядеть. Дальше мы последовательно суммируем эти точки и получаем следующую картину.

Это процесс, который не имеет никакой памяти, все точки независимы, по крайней мере, если мы считаем, что генератор качественный.

Вот варианты такой траектории при количестве бросков 100 (РИС.2), 1000 (РИС.3),

10000 (РИС.4), и 30000 (РИС.5 и РИС.6)

РИС.2

РИС.3

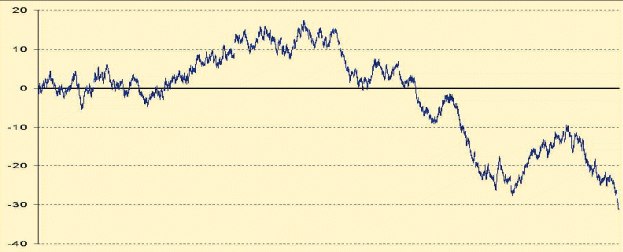
РИС.4

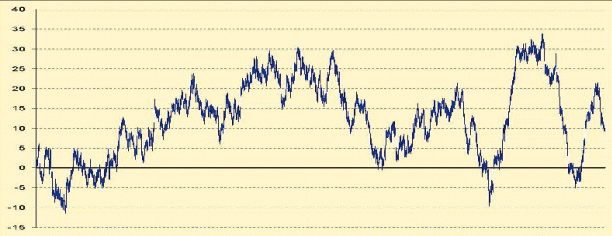
РИС.5

РИС.6

Давайте внимательно посмотрим варианты с 30000 испытаний. Мы сейчас в он-лайне нагенерим пару десятков таких случайных блужданий.

Я понимаю, что тех, кто профессионально занимался случайными блужданиями, эти графики, безусловно, не удивят. Но по моему опыту, у большинства людей при виде такого типа траекторий, создается впечатление, что генератор плохой. Тоже самое происходило, как описывал Феллер, когда он предъявлял свои модельные результаты, по поводу бросания “идеальной” монеты полученные на ЭВМ. 90% опрошенных говорили, что монета “неправильная”.

Специалисты, имеющие соответствующее образование обычно засаживались на несколько дней, пытаясь сделать настоящий, правильный генератор. Улучшение качества генератора в этих картинках не изменяет ничего. И мало того, легко показать, что характеристики идеальных случайных блужданий вполне соответствуют тем графикам, которые мы видим. С точки зрения трейдера в первую очередь, это впечатление их трендовости. Психологически мы ожидаем, что случайное блуждание должно все-таки как-то колебаться вокруг нуля. С какими-то отклонениями, уходами, но количество пересечений нулевой оси должно быть значительно больше. Мало того, в 70-е годы, когда все это описывалось у Феллера, был произведен опрос людей, занимающихся математической статистикой - какое количество в среднем пересечений с нулевой осью они ожидают. Результат опроса на порядок отличался от теоретического. В среднем, в 10 раз больше мы ожидаем пересечение с нулевой осью, т.е. намного менее трендовые графики.

Подсознательно мы себе представляем, что в таком процессе есть некая пружинка, которая возвращает траекторию обратно, несмотря на то, что мы знаем, о том, что в нашем случае броски независимые и такого рода идеальная система не обладает памятью. Естественно это интуитивное представление о некой отрицательной обратной связи неверно, также как и некорекктные ссылки на “закон больших чисел”.

Аналитические результаты в области случайных блужданий в основном базируются на комбинаторном анализе. Вероятности тех или иных сценариев получаются путем сравнения количество всевозможных путей при заданном количестве бросков с теми путями, которые нас интересуют по каким-либо критериям.

В частности выясняется, что независимо от количества бросков наиболее вероятна ситуация, когда график ни разу не пересекает нулевую ось (по сравнению с вероятностями пересечений 1 раз, 2 раза, и т.д.)

Если взять игру со 100 бросками траектория ни разу не пересечет 0 в 16% случаев. 5 пересечений мы будем иметь – в 9%, 9 – в 2,5%, 13 – в 0,5% случаев. Эти результаты абсолютно не соответствуют нашим интуитивным представлениям. Естественно, сразу возникает последствия, связанные с задачами о разорении, противотрендовыми торговыми стратегиями т.д.

Другая интересная характеристика случайных блужданий – количество времени, которое точка проводит на одной стороне графика. Выводы показывают, если количество бросков велико, то в 20% случаев наша траектория будет находиться на одной стороне 97,5% времени, а в 10% - 99,5% времени. Эти цифры говорят сами за себя.

Вышеописанные характеристики случайных блужданий, описываются известным в статистике законом Арксинуса, применительно к нашему последнему примеру – это вероятность того, какую часть от всего отведенного времени точка находится на положительной или отрицательной стороне. Равенство - 50% на положительной стороне и 50% на отрицательной (интуитивно наиболееожидаемый сценарий) – имеет наименьшую вероятность, а максимальную вероятность – сценарий, при котором вся траектория находится либо на одной, либо на другой стороне.

Общий вид распределения вероятностей в зависимости от доли времени нахождения на одной стороне вы видите на Р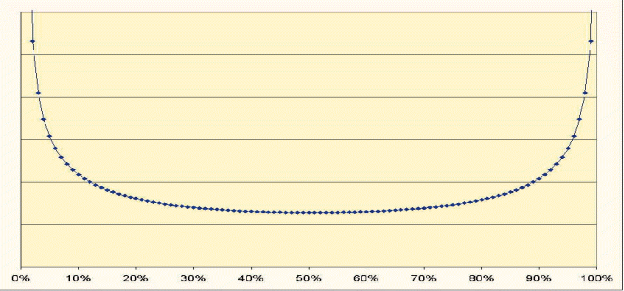ИС.8.

РИС.8

Хочу сразу оговориться, что мое выступление не следует воспринимать как критику технического анализа.

Необходимо просто более объективно воспринимать то, что мы видим в поведении цен и в результатах, которые мы получаем. Приведу пример. Многоуважаемый мною Джон Мерфи, автор наверное лучших книг по техническому анализу в главе, где он дискутирует с приверженцами теории случайных блужданий рынка, коим я ни в коей мере не являюсь, приводит график швейцарского франка за1985 год:

Далее он пишет: «Вот видите какой здесь тренд. О какой случайности может идти речь?» Аргумент, к сожалению, не серьезный, так как случайные блуждания выстраиваться в трендовую последовательность примерно в каждом пятом случае.

Приведу еще один пример искаженных ожиданий. В той же брокерской компании, где я играл в кости, я провел опрос среди трейдеров «Предположим мы возьмем какой-либо актив и будем каждый день подбрасывать монетку. В соответствии с тем, что выпадем орел или решка будем открывать позицию либо вверх, либо вниз. Предположим, что у нас нет комиссии и проскальзывания. Что будет происходить с нашим счетом?».

Все ответили, что счет будет колебаться вокруг нуля. Моделируем такую ситуацию. Возьмем S&P с 1991 года, дальше генерим вышеописанным способом столбец из 1 и –1, которые соответствуют длинной или короткой позициям. Посмотрим на варианты графиков сальдо нашего теоретического счета, управляемого случайной торговой системой.

РИС.7

Тоже самое. Никаких колебаний вокруг 0 нет. Многие из таких траекторий будут опять же иметь тредовый вид. Растущие тренды в данном случае будут соответствовать выигрышным торговым системам.

Надо отдавать себе отчет, что если мы сделали торговую систему и положили ее на какой-то актив пусть даже с очень длинной историей, то велика вероятность, что историческое тестирование случайным образом породит замечательную траекторию EQUITY системы, но этот один эксперимент со статистической точки ничего значить не будет.

Поэтому с точки зрения создания торговых систем очень важно проверять систему на грубость: исследовать чувствительность к параметрам, тестировать на различных активах и т.д. Обо всем об этом неоднократно говорилось, и я думаю, вы прекрасно об этом знаете.

Очевидно, что поведение цен не является случайным блужданием, также как, скажем, и EQUITY конкретной торговой системы. Но надо понимать, что траектории, которые мы видим, существуют на фоне некого пространства случайных блужданий. Это пространство, при прочих равных, обладает свойствами которые сильно отличаются от наших интуитивных ожиданий и что четкое представление об этих свойствах, безусловно, необходимо для того, чтобы объективно оценивать то, чем мы с вами занимаемся.