| Скачать .docx |
Реферат: Постановка и основные свойства транспортной задачи
Транспортная задача (Т-задача) является одной из наиболее распространенных специальных задач ЛП. Частные постановки задачи рассмотрены рядом специалистов по транспорту, например О.Н. Толстым [18; 59].
Первая строгая постановка Т-задачи принадлежит Ф. Хичкоку, поэтому в зарубежной литературе ее называют проблемой Хичкока.
Первый точный метод решения Т-задачи разработан Л.В. Канторовичем и М.К. Гавуриным.
Постановка Т-задачи. Пусть в пунктах А1 ,…,Am производят некоторый однородный продукт, причем объем производства в пункте Ai составляет ai единиц, i = 1,…, m. Допустим, что данный продукт потребляют в пунктах B1 ., Bn , a объем потребления в пункте Вj составляет bj одиниць j = 1., n. Предположим, что из каждого пункта производства возможно транспортировка продукта в любой пунктпотребления. Транспортные издержки по перевозке единицы продукции из пункта Ai в пункт Вj равны cij (i = 1., m; j = 1., n). Задача состоит в определении такого плана перевозок, при котором запросы всех потребителей Вj полностью удовлетворены, весь продукт из пунктов производства вывезен и суммарные транспортные издержки минимальны.
Условия Т-задачи удобно представить в виде табл. 1.1.
Таблица. 1.1.
Пункт потребления Пункт производства |
B1 | B2 | . | Bn | Bj ai |
| A1 | C11 | C12 | . | C1n | a1 |
| A2 | C21 | C22 | . | C2n | a2 |
| Am | Cm1 | Cm2 | . | Cmn | am |
Ai bj |
b1 | b2 | . | bn | Объем производства Объем потребления |
Пусть ![]() количество продукта, перевозимого из пункта Ai
в пункт Вj
.
количество продукта, перевозимого из пункта Ai
в пункт Вj
.
Требуется определить множество переменных ![]() , i = 1., m, j = 1., n, удовлетворяющих условиям
, i = 1., m, j = 1., n, удовлетворяющих условиям
![]() (1.1)
(1.1)
![]() (1.2)
(1.2)
и таких, что целевая функция
![]() (1.3)
(1.3)
достигает минимального значения.
Условие (1.1) гарантирует полный вывоз продукта из всех пунктов производства, а (1.2) означает полное удовлетворение спроса во всех пунктах потребления.
Таким образом, Т-задача представляет собой задачу ЛП с ![]() числом переменных, и (m + n) числом ограничений равенств.
числом переменных, и (m + n) числом ограничений равенств.
Переменные ![]() удобно задавать в виде матрицы
удобно задавать в виде матрицы
 (1.4)
(1.4)
Матрицу X
, удовлетворяющую условиям Т-задачи (1.1) и (1.2) называют планом перевозок, а переменные ![]() – перевозками. План
– перевозками. План ![]() , при котором целевая функция минимальна, называется оптимальным, а матрица С
=
, при котором целевая функция минимальна, называется оптимальным, а матрица С
= ![]() – матрицей транспортных затрат.
– матрицей транспортных затрат.
Графический способ задания Т-задач показан на рис. 1

Рис. 1
Отрезок A i B j называют коммуникацией. На всех коммуникациях ставят величины перевозок xij .
Вектор P ij , компоненты которого состоят из коэффициентов при переменных xij в ограничениях (3.1.1) и (3.1.2), называют вектором коммуникаций:

Вводят также вектор производства-потребления P 0 , где
![]() .
.
Тогда ограничение (3.1.1) и (3.1.2) можно записать в векторной форме
![]() , (1.5)
, (1.5)
Свойства транспортной задачи
1. Для разрешимости Т-задачи необходимо и достаточно, чтобы выполнялось условие баланса
![]() , (1.6)
, (1.6)
то есть, чтобы суммарный объем производства равнялся объему потребления.
Доказательство. Пусть переменные xij
, i = 1., m; j = 1., n удовлетворяют условиям (1.1), (1.2). Суммируя (1.1) по ![]() , а (1.2) по
, а (1.2) по ![]() , получим:
, получим:
![]() .я
.я
Отсюда ![]() , что и доказывает необходимость условия баланса Т-задачи.
, что и доказывает необходимость условия баланса Т-задачи.
Пусть справедливо условие (1.6). Обозначим ![]() , где
, где ![]() .
.
Нетрудно доказать, что хij составляет план задачи. Действительно

Таким образом, доказана достаточность условия баланса для решения Т-задачи.
2. Ранг системы ограничений (1.1), (1.2) равен ![]()
Доказательство. Так как количество уравнений (1.1), (1.2) равно ![]() , то ранг этой системы
, то ранг этой системы ![]() . Пусть, набор
. Пусть, набор ![]() удовлетворяет всем уравнениям, кроме первых. Покажем, что он удовлетворяет также и первому уравнению.
удовлетворяет всем уравнениям, кроме первых. Покажем, что он удовлетворяет также и первому уравнению.
Очевидно
![]()
Так как
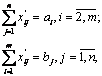 ,
то
,
то
![]()
![]() ,
отсюда
,
отсюда
![]() ,
,
Учитывая условие баланса (1.6), получим
![]() ,
,
т.е. первое уравнение системы (1.1) тоже удовлетворяется.
Таким образом, ранг системы уравнений (1.1), (1.2) ![]() .
.
Докажем, что ранг системы уравнений (1.1), (1.2) равен точно ![]() . Для этого составим матрицу из первых (
. Для этого составим матрицу из первых (![]() ) компонентов векторов
) компонентов векторов ![]()

Очевидно, что эта матрица не вырождена. Поэтому векторы {![]() } образуют базис. Так как базис системы состоит из (
} образуют базис. Так как базис системы состоит из (![]() ) векторов, то и ранг системы (1.1), (1.2)
) векторов, то и ранг системы (1.1), (1.2) ![]() .
.
Двойственная транспортная задача (![]() – задача).
Для Т-задачи, как и для любой задачи ЛП, существует двойственная задача к ней
– задача).
Для Т-задачи, как и для любой задачи ЛП, существует двойственная задача к ней ![]() -задача.
-задача.
Переменные ![]() -задачи обозначим v1
, v 2
., v n
, – u1
, – u2
., – um
…
-задачи обозначим v1
, v 2
., v n
, – u1
, – u2
., – um
…
Теорема 1.
![]() -задача имеет решение и если X
опт
=
-задача имеет решение и если X
опт
= ![]() ,
,
![]() – оптимальные решения T и
– оптимальные решения T и ![]() -задачи соответственно, то
-задачи соответственно, то
![]() . (1.7)
. (1.7)
Если учесть, что ui – стоимость единицы продукции в пункте Аі, а vj – стоимость после перевозки в пункт Bj , то смысл теоремы будет такой:
Суммарные транспортные расходы при оптимальном плане перевозок равны приращению суммарной стоимости продукции после ее перевозки в пункты потребления.
Переменные ui иvj называют потенциалами пунктов Ai иBj для Т-задачи.
Таким образом, теорема 1. утверждает, что при оптимальных решениях значения целевой функции прямой и двойственной Т-задач равны между собой.
Справедливость теоремы 1. следует из основной теоремы двойственной ЛП (теорема 2.5).
Сформулируем необходимые и достаточные условия оптимальности плана Т-задачи.
Теорема 2. Для оптимальности плана Х0 Т-задачи необходимо и достаточно существование таких чисел v1 , v2 ., vn , – u1 , – u2 ., – um , что
vj
– ui
![]() cij
, i = 1., m; j=1., n… (1.8)
cij
, i = 1., m; j=1., n… (1.8)
При этом, если
![]() это vj
–
ui
=
cij
.
это vj
–
ui
=
cij
.
Cправедливость этой теоремы вытекает из общих идей теории двойственности линейного программирования (в частности, теоремы 2.5, 2.7).
Дадим экономическую интерпретацию условий теоремы 2.
Разность между потенциалами пунктов Bj
иAi
,
т.е. величину vj
– ui
, можно рассматривать как приращение ценности единицы продукции при перевозке из пункта Ai
в пункт Bj
. Поэтому, если vj
– ui
< cij
, то перевозка по коммуникации Ai
Bj
нерентабельна, и ![]() . Если vj
– ui
= cij
, то такая перевозка рентабельна, и
. Если vj
– ui
= cij
, то такая перевозка рентабельна, и ![]() (см. Теорему 2.7).
(см. Теорему 2.7).
Транспортная задача с ограниченными пропускными способностями.
Важной в практическом отношении является Тd - задача, в которой существуют ограничения на пропускные способности коммуникаций.
Пусть ![]() - пропускная способность коммуникации Ai
Bj
.
- пропускная способность коммуникации Ai
Bj
.
Тогда ![]() (1.9)
(1.9)
Т-задача состоит в минимизации Ц.Ф. (1.3) при условиях (1.1), (1.2), (1.9). Даже в случае разрешимости Т-задачи, Тd – задача может оказаться неразрешимой, поскольку величины пропускных способностей будут недостаточны для полного вывоза продукта из п. Аі , и полного ввоза продукта в п. Вj . Поэтому для Тd – задачи вводят еще два условия:
![]() (1.10)
(1.10)
![]() (1.11)
(1.11)
Но и при добавочных условиях (1.10), (1.11) Тd – задача не всегда разрешима. Для установления совместимости всех условий делают попытку построить любой план Т-задачи. Если удается, то система уравнений (1.1), (1.2), (1.9) – (1.11) совместна. В противном случае Тd – задача неразрешима.
Теорема 3. Для оптимальности плана Х0 Тd – задачи необходимо и достаточно существование таких чисел v1 , v2 ., vn , – u1 , – u2 ., – um , при которых
![]() если
если ![]() , (1.12)
, (1.12)
![]() если 0 <
если 0 <![]() , (1.13)
, (1.13)
![]() если
если![]() . (1.14)
. (1.14)
Смысл условий оптимальности (1.12) – (1.14) состоит в следующем:
если приращение стоимости продукта vj
– uj
меньше транспортных расходов cij
, то такая перевозка убыточна, а потому ![]() . Если же приращение стоимости продукта vj
– uj
больше транспортных расходов cij
(3.1.14), то эта перевозка прибыльна, а потому ее величина должна быть максимальной, т.е.
. Если же приращение стоимости продукта vj
– uj
больше транспортных расходов cij
(3.1.14), то эта перевозка прибыльна, а потому ее величина должна быть максимальной, т.е. ![]() .
.
Таким образом, теорема 3.3 по существу выражает принцип рентабельности для Td – задачи.
Открытые транспортные модели.
Существует ряд практических задач, в которых условие баланса ![]() не выполняется. Такие модели называются открытыми. Возможные два случая:
не выполняется. Такие модели называются открытыми. Возможные два случая:
1)![]()
2)![]()
В первом случае полное удовлетворение спроса невозможно.
Такую задачу можно привести к обычной транспортной задаче следующим образом. Обозначим через ![]() величину штрафа из-за неудовлетворения запросов на единицу продукта в пункте Bj
.
величину штрафа из-за неудовлетворения запросов на единицу продукта в пункте Bj
.
Тогда требуется минимизировать
![]() (1.15)
(1.15)
при условиях

где ![]() - неудовлетворенный спрос.
- неудовлетворенный спрос.
Задачу (3.1.15) приводят к обычной Т-задаче введением фиктивного пункта производства А
m+1
, с объемом производства ![]() и транспортными издержками
и транспортными издержками ![]() В таком случае Т-задача будет иметь вид
В таком случае Т-задача будет иметь вид
минимизировать ![]()
при условиях

В найденном решении хопт
полагаем все перевозки из фиктивного пункта А
m+1
равными нулю, т.е. ![]() .
.
Рассмотрим теперь второй случай. Введем фиктивный пункт B
n+1
с объемом спроса ![]() . Пусть
. Пусть ![]() - это убытки (штраф) в пункте Аі
за единицу невывезенного продукта. Обозначим через сии,n+1
=
- это убытки (штраф) в пункте Аі
за единицу невывезенного продукта. Обозначим через сии,n+1
= ![]() удельные транспортные издержки на перевозку единицы продукта с А
і
в В
n+1
. Тогда соответствующая Т-задача запишется так:
удельные транспортные издержки на перевозку единицы продукта с А
і
в В
n+1
. Тогда соответствующая Т-задача запишется так:
минимизировать ![]() (1.16)
(1.16)
при условиях
 (1.17) – (1.18)
(1.17) – (1.18)
В найденном решении ![]() все перевозки
все перевозки ![]() в фиктивный пункт Вn+1
считают равными нулю.
в фиктивный пункт Вn+1
считают равными нулю.
Опорные планы Т-задачи
Опорным (базисным) планом Т-задачи называют любое ее допустимое, базисное решение. Понятие опорного плана имеет наглядную геометрическую интерпретацию.
Последовательность коммуникаций
![]() (1.19)
(1.19)
называют маршрутом, соединяющим пункты ![]() (рис. 2).
(рис. 2).



![]()
![]()
![]()
![]()
![]() …
… ![]()
 |
 |
![]()
![]()
![]() .
. ![]()
![]()
Рис. 2
Используя маршрут, составленный из коммуникаций, можно осуществить перевозку продукта из пункта ![]() в пункт
в пункт ![]() , проходя через пункты
, проходя через пункты ![]() .
.
В процессе этого движения коммуникации, стоящие на четных местах в (1.19), будут пройдены в противоположном направлении.
Маршрут (1.19), к которому добавлена коммуникация ![]() называется замкнутым маршрутом или циклом.
называется замкнутым маршрутом или циклом.
Способ проверки произвольного плана Т-задачи на опорность, основан на следующих двух теоремах (прямой и обратной).
Теорема 4.
Система, составленная из векторов ![]() Т-задачи, является линейно независимой тогда и только тогда, когда из коммуникаций, соответствующих этим векторам, нельзя составить замкнутый маршрут.
Т-задачи, является линейно независимой тогда и только тогда, когда из коммуникаций, соответствующих этим векторам, нельзя составить замкнутый маршрут.
![]()
![]()
![]()
![]()
![]() Доказательство. Необходимость
. Пусть векторы
Доказательство. Необходимость
. Пусть векторы ![]() линейно независимы. Если бы существовал замкнутый маршрут из коммуникаций
линейно независимы. Если бы существовал замкнутый маршрут из коммуникаций ![]() и
и ![]() , то, очевидно, начиная движение из пункта
, то, очевидно, начиная движение из пункта ![]() и последовательно проходя все пункты
и последовательно проходя все пункты ![]() по последней коммуникации
по последней коммуникации ![]() мы вернемся в начальный пункт
мы вернемся в начальный пункт ![]() . Тогда справедливое равенство
. Тогда справедливое равенство
![]() (1.20)
(1.20)
которое указывает на линейную зависимость векторов
![]() .
.
Полученное противоречие доказывает необходимость условий теоремы 4.
Достаточность
. Допустим, что из коммуникаций, отвечающих векторам ![]() системы R, нельзя составить замкнутый маршрут. Докажем, что в таком случае R – линейно независимая система. Если предположить противное, т.е. линейную зависимость векторов системы R
, то существуют такие числа
системы R, нельзя составить замкнутый маршрут. Докажем, что в таком случае R – линейно независимая система. Если предположить противное, т.е. линейную зависимость векторов системы R
, то существуют такие числа ![]() , среди которых не все нули, для которых выполняется условие
, среди которых не все нули, для которых выполняется условие
![]() . (1.21)
. (1.21)
Пусть, например ![]() . Перенесем тогда соответствующий вектор вправо и получим
. Перенесем тогда соответствующий вектор вправо и получим
![]() , (1.22)
, (1.22)
где Е1
образуется вычеркиванием в Е пары индексов (![]() ). Компонента с номером
). Компонента с номером ![]() в правой части (3.1.22) не равна нулю.
в правой части (3.1.22) не равна нулю.
Следовательно, это же относится и к левой части этого равенства, т.е. среди
векторов ![]() найдется хотя бы один вектор вида
найдется хотя бы один вектор вида ![]() с
с
коэффициентом ![]() . Перенеся его в правую чатсть равенства (1.22), получим
. Перенеся его в правую чатсть равенства (1.22), получим
![]()
![]() , (1.23)
, (1.23)
где ![]() . Но поскольку
. Но поскольку ![]() , компонента с номером
, компонента с номером ![]() правой части (1.23) отлична от нуля. Поэтому среди векторов левой части (1.23) найдется хотя бы один вектор вида
правой части (1.23) отлична от нуля. Поэтому среди векторов левой части (1.23) найдется хотя бы один вектор вида ![]() , для которого
, для которого ![]() . Перенося его в правую часть (1.23), находим
. Перенося его в правую часть (1.23), находим
![]() (1.24)
(1.24)
где ![]()
Этот процесс переноса векторов в правую часть можно продолжить аналогичным образом и дальше. Допустим, что уже проведено (2k-1) шагов. Тогда имеет место соотношение
![]() (1.25)
(1.25)
где ![]()
Возможные два случая:
1) ![]() при некотором
при некотором ![]()
2) ![]() .
.
В первом случае процесс переноса заканчивается, причем из векторов в правой части (1.25) можно образовать замкнутый маршрут. Таким маршрутом является
![]()
Во втором случае процесс переноса продолжается, и поскольку ![]() , среди векторов Р
ij
, где (i, j)
, среди векторов Р
ij
, где (i, j) ![]() обязательно найдется вектор
обязательно найдется вектор ![]() с коэффициентом
с коэффициентом ![]() .
.
Описанный процесс переноса не может длится бесконечно, так как все вектора, переносимые вправо, различны. Поэтому через конечное число шагов мы обязательно столкнемся со случаем 1, который, как показано выше, ведет к образованию замкнутого маршрута.
Итак, допустив, что система векторов ![]() линейно зависима, мы пришли к противоречию с условием теоремы, согласно которому из коммуникаций
линейно зависима, мы пришли к противоречию с условием теоремы, согласно которому из коммуникаций ![]() системы R нельзя составить замкнутый маршрут. Остается принять, что система R состоит из линейно независимых векторов.
системы R нельзя составить замкнутый маршрут. Остается принять, что система R состоит из линейно независимых векторов.
Достаточность условий теоремы доказана.
Назовем коммуникацию ![]() Т-задачи основной коммуникацией плана Х
, если
Т-задачи основной коммуникацией плана Х
, если ![]() Тогда, используя теорему 3.4, можно сформулировать следующий признак проверки произвольного плана на опорность.
Тогда, используя теорему 3.4, можно сформулировать следующий признак проверки произвольного плана на опорность.
План ![]() Т-задачи является опорным (базисным), если из его основных коммуникаций нельзя составить замкнутый маршрут.
Т-задачи является опорным (базисным), если из его основных коммуникаций нельзя составить замкнутый маршрут.
Теорема 5.
Вектор ![]() является линейной комбинацией векторов системы R
тогда и только тогда, когда из векторов этой системы можно составить маршрут, соединяющий пункты Ak
и
является линейной комбинацией векторов системы R
тогда и только тогда, когда из векторов этой системы можно составить маршрут, соединяющий пункты Ak
и ![]() . Если этот маршрут имеет вид
. Если этот маршрут имеет вид
![]()
то
![]() . (1.26)
. (1.26)
Доказательство этой теоремы основано на теореме 3.4. Пусть ![]() выражен в виде линейной комбинации векторов системы R. Добавив к ней вектор
выражен в виде линейной комбинации векторов системы R. Добавив к ней вектор ![]() , получим систему линейно зависимых векторов. Тогда в силу теоремы 3.4 появляется замкнутый маршрут
, получим систему линейно зависимых векторов. Тогда в силу теоремы 3.4 появляется замкнутый маршрут ![]() . Этот замкнутый маршрут должен содержать коммуникацию
. Этот замкнутый маршрут должен содержать коммуникацию ![]() и, следовательно, все остальные коммуникации должны соединить
и, следовательно, все остальные коммуникации должны соединить ![]() и
и ![]() .
.
Тогда
![]() .
.
Перенеся ![]() в правую часть, получим выражение (1.26), что и требовалось доказать.
в правую часть, получим выражение (1.26), что и требовалось доказать.
| 1 | 2 | 3 | 4 | 5 | 6 | i /j |
| 1 | 1 | |||||
| 1 | 2 | |||||
| X = | 3 | |||||
| 1 | 4 | |||||
| 1 | 1 | 5 | ||||
| Рис. 3.3. | ||||||
Рассмотрим произвольную матрицу ![]() . Между позициями матрицы Х
и векторами
. Между позициями матрицы Х
и векторами ![]() можно установить следующее соответствие. Вектор
можно установить следующее соответствие. Вектор ![]() соответствует элементу
соответствует элементу ![]() матрицы Х.
Тогда можно задать систему из векторов
матрицы Х.
Тогда можно задать систему из векторов ![]() , выделив единицами соответствующие элементы матрицы Х.
Рассмотрим матрицу на рис3. Здесь единицами отмечена система векторов R:
, выделив единицами соответствующие элементы матрицы Х.
Рассмотрим матрицу на рис3. Здесь единицами отмечена система векторов R:
![]() .
.
При использовании матрицы Х
критерий проверки линейной независимости формулируется так: для линейной независимости системы векторов![]() необходимо и достаточно, чтобы из ненулевых элементов матрицы Х
, отвечающих этим векторам, невозможно было составить замкнутый маршрут (цикл).
необходимо и достаточно, чтобы из ненулевых элементов матрицы Х
, отвечающих этим векторам, невозможно было составить замкнутый маршрут (цикл).
Так как из выделенных единицами позиций на рис. 3 нельзя составить замкнутый маршрут, то данная система линейно независима и образует базис.
Введем теперь в систему ![]() вектор
вектор ![]() , отметив его знаком '+'. Чтобы разложить
, отметив его знаком '+'. Чтобы разложить ![]() по векторам системы R, составим цепочку из выделенных элементов, которая замыкается на элементе
по векторам системы R, составим цепочку из выделенных элементов, которая замыкается на элементе ![]() :
:
![]() .
.
При небольших размерах матрицы Х визуальное отыскание замкнутых цепочек в ней представляет значительные трудности. В таком случае прибегают к формализованному методу вычеркивания. Метод вычеркивания позволяет выделить в произвольном плане Х Т-задачи замкнутую цепочку, если она существует.
Этот метод состоит в следующем. Выделив в плане Х множество ненулевых элементов, обозначаемое через S, выясним, существуют ли во множестве элементов S циклы. Для этого просматриваем одну за другой строки плана Х и вычеркиваем строки, не содержащие элементов S, и строки, которые содержат не более одного элемента S (ненулевой элемент). Просмотрев все строки плана Х , переходим к столбцам и вычеркиваем те из них, которые содержат не более одного элемента S.
При этом элементы, содержащиеся в ранее вычеркнутых строках, в расчет не принимают. Далее повторяем весь этот процесс, просматривая сначала строки, а потом столбцы оставшейся после вычеркивания строк и столбцов подматрицы.
После конечного числа шагов этот процесс заканчивается одним из следующих двух исходов: 1) все строки (столбцы) матрицы вычеркнуты; 2) получена подматрица, в каждой строке и столбце которой содержится не менее двух элементов S.
В первом случае из элементов множества S составить цикл невозможно. Следовательно, соответствующий план Х является опорным.
Во втором случае множество S содержит цикл (циклы) и соответствующий план Х не является опорным (базисным). На рис. 4 показаны два плана Т-задачи: небазисный (рис. 4, а) и базисный (рис. 4, б). Номера линий указывают порядок вычеркивания. Звездочками отмечены элементы, которые вычеркнуть нельзя. Они образуют цикл.
1* *1 1* 1* 1 1 *1 *1 Рис. 4. а) |
1 1 9 1 1 2 1 10 1 1 1 3 1 4 1 Рис. 4. б) |
Нахождение начальных опорных планов
Существует несколько методов построения начальных опорных планов Т-задачи. Из них самый распространенный метод северо-западного угла и метод минимального элемента.
Метод северо-западного угла. Основную идею метода рассмотрим на конкретном примере.
Пусть дана Т-задача с четырьмя пунктами производства А1
, А2
, А3
, А4
с объемами производства ![]() и пунктами потребления
и пунктами потребления ![]() с объемами потребления соответственно
с объемами потребления соответственно ![]() .
.
Построим матрицу Х
размером 4х4, причем для удобства вычислений снизу от нее оставим строку bj
, справа столбец ai
. Кроме того, снизу от bj
образуем строки ![]() , где будем записывать неудовлетворенные потребности, а справа от ai
– столбцы
, где будем записывать неудовлетворенные потребности, а справа от ai
– столбцы ![]() , где будем записывать остатки невывезенного продукта (табл. 2).
, где будем записывать остатки невывезенного продукта (табл. 2).
Заполнение таблицы начинают с левого верхнего элемента таблицы X –
x11
, что и обусловило название метода. Сравнив ![]() с
с ![]() и выбрав меньшее из них, получим x11
=1. Записываем это значение в матрицу Х0
. Так как первый выбор произведен по строке, то остальная часть первой строки должна быть заполнена нулями. Во вспомогательном столбце
и выбрав меньшее из них, получим x11
=1. Записываем это значение в матрицу Х0
. Так как первый выбор произведен по строке, то остальная часть первой строки должна быть заполнена нулями. Во вспомогательном столбце ![]() записываем остатки невывезенного продукта,
записываем остатки невывезенного продукта, ![]() , а в строке
, а в строке ![]() – неудовлетворенные потребности после одного шага заполнения.
– неудовлетворенные потребности после одного шага заполнения.
Переходим к второй строке и начинаем заполнение с элемента ![]() (новый северо-западный угол незаполненной части таблицы 2). Сравнивая
(новый северо-западный угол незаполненной части таблицы 2). Сравнивая ![]() выбираем меньшее из них, и потому
выбираем меньшее из них, и потому ![]() . Остальную часть второй строки заполняем нулями. Далее заполняем таблицу аналогично. После окончания процесса заполнения будем иметь начальный план Х0
. Полученный план является базисным (опорным), так как из его ненулевых элементов нельзя составить цикл. Кроме того, он удовлетворяет условиям задачи, так как
. Остальную часть второй строки заполняем нулями. Далее заполняем таблицу аналогично. После окончания процесса заполнения будем иметь начальный план Х0
. Полученный план является базисным (опорным), так как из его ненулевых элементов нельзя составить цикл. Кроме того, он удовлетворяет условиям задачи, так как
![]() .
.
Таблица 2
| Х | ||||||||||
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 3 | 3 | 3 | 1 | 0 | 0 | 0 |
| 0 | 0 | 2 | 2 | 4 | 4 | 4 | 4 | 4 | 2 | 0 |
| 5 | 1 | 2 | 2 | |||||||
| 4 | 1 | 2 | 2 | |||||||
| 0 | 1 | 2 | 2 | |||||||
| 0 | 0 | 2 | 2 | |||||||
| 0 | 0 | 0 | 2 | |||||||
| 0 | 0 | 0 | 0 |
Формальное описание алгоритма. I. Определяют верхний левый элемент матрицы Х :
![]() .
.
Возможные три случая: а) если ![]() то
то ![]() и всю первую строку, начиная со второго элемента, заполняют нулями; б) если
и всю первую строку, начиная со второго элемента, заполняют нулями; б) если ![]() , то
, то ![]() , а все оставшиеся элементы первого столбца заполняют нулями; в) если
, а все оставшиеся элементы первого столбца заполняют нулями; в) если
![]() то
то ![]()
и все оставшиеся элементы первых столбцов и строки заполняют нулями.
Находим
![]()
на этом один шаг метода заканчивается.
2. Пусть уже проделано k шагов. (k+1) – й шаг состоит в следующем. Определяют верхний левый элемент незаполненной части матрицы Х. Пусть это будет элемент
![]()
причем
![]() , (1.27)
, (1.27)
где
 (1.28)
(1.28)
Если ![]() , то заполняем нулями строку
, то заполняем нулями строку ![]() , начиная с (
, начиная с (![]() +1) – го элемента. В противном случае заполняем нулями столбец
+1) – го элемента. В противном случае заполняем нулями столбец ![]() , начиная с элемента (
, начиная с элемента (![]() +1). Если
+1). Если ![]() , то заполняем нулями остаток строки
, то заполняем нулями остаток строки ![]() и столбца
и столбца ![]() . Далее вычисляем
. Далее вычисляем ![]() . На этом (k+1) – й шаг заканчивается. Описанный процесс повторяется до тех пор, пока матрица Х
не будет заполнена полностью.
. На этом (k+1) – й шаг заканчивается. Описанный процесс повторяется до тех пор, пока матрица Х
не будет заполнена полностью.
Метод минимального элемента
Этот метод является вариантом метода северо-западного угла, учитывающим специфику матрицы транспортных затрат С
=![]() . В отличие от метода северо-западного угла данный метод позволяет сразу получить достаточно экономичный план, сокращая общее количество итераций по его дальнейшей оптимизации.
. В отличие от метода северо-западного угла данный метод позволяет сразу получить достаточно экономичный план, сокращая общее количество итераций по его дальнейшей оптимизации.
Формальное описание алгоритма. Элементы матрицы нумеруют, начиная от минимального в порядке возрастания, а затем в этом же порядке заполняют матрицу Х 0 .
Пусть элементом с минимальным порядковым номером оказался ![]() . Возможные три случая: а) если
. Возможные три случая: а) если ![]() , то оставшуюся часть
, то оставшуюся часть ![]() -й строки заполняем нулями; б) если
-й строки заполняем нулями; б) если ![]() , то оставшуюся часть
, то оставшуюся часть ![]() -го столбца заполняем нулями; в) если
-го столбца заполняем нулями; в) если ![]() , то оставшуюся часть
, то оставшуюся часть ![]() -й строки и
-й строки и ![]() -го столбца заполняем нулями.
-го столбца заполняем нулями.
Дале этот процесс повторяют с незаполненной частью матрицы Х 1 .
Пример 1. Найти начальный базисный план методом минимального элемента для Табл. 3. следующей задачи.
Таблица. 3.
| Ai \ Bj | 1 | 2 | 3 | 4 | Bj / ai |
| 1 | 7(10) | 8(11) | 5(7) | 3(5) | 11 |
| 2 | 2(3) | 4(4) | 5(8) | 9(12) | 11 |
| 3 | 6(9) | 3(4) | 1(1) | 2(2) | 8 |
| Ai / bj | 5 | 9 | 9 | 7 | bj \ ai |
Цифры в скобках указывают порядок заполнения элементов в матрице Х0 (табл. 3.4).
Соответствующее значение целевой функции равно
![]() 3*8 + 1*5 + 3*7 + 5*2 + 6*4 + 8*1 = 92
3*8 + 1*5 + 3*7 + 5*2 + 6*4 + 8*1 = 92
Таблица 4
| Х0 | ||||||||
| 0 | 3 | 1 | 7 | 11 | 4 | 3 | 0 | |
| 5 | 6 | 0 | 0 | 11 | 6 | 0 | ||
| 0 | 0 | 8 | 0 | 8 | 0 | |||
| 5 | 9 | 9 | 7 | |||||
| 0 | 3 | 1 | 0 | |||||
| 0 | 0 | |||||||
Решение транспортной задачи при вырожденном опорном плане
Опорный план называется вырожденным, если число его ненулевых перевозок k меньше ранга матрицы ограничений. В процессе построения начального плана или при его улучшении очередной план может оказаться вырожденным.
Рассмотрим два случая.
1. Вырожденный план является начальным Х
0
. Тогда выбирают некоторые нулевые элементы матрицы Х
0
в качестве базисных так, чтобы при этом не нарушалось условие базисного плана. Число этих элементов равняется ![]() . Далее данные элементы заменяют на
. Далее данные элементы заменяют на ![]() (где
(где ![]() – произвольное, бесконечно малое число) и рассматривают их как обычные базисные элементы плана. Задачу решают как невырожденную, а в последнем оптимальном плане Х
k
вместо
– произвольное, бесконечно малое число) и рассматривают их как обычные базисные элементы плана. Задачу решают как невырожденную, а в последнем оптимальном плане Х
k
вместо![]() пишут нули.
пишут нули.
2. Вырожденный план получается при построении плана Х
k+1
на базе Х
k
, если цепочка в плане Х
k
содержит не менее двух минимальных нечетных элементов. В таком случае в матрице Х
k+1
полагают равным нулю только один из этих элементов, а остальные заменяют на ![]() , и далее решают задачу как невырожденную. Если на k-м шаге
, и далее решают задачу как невырожденную. Если на k-м шаге ![]() , то при переходе от Х
k
к Х
k+1
значение целевой функции не изменяется, а в базис вводится элемент
, то при переходе от Х
k
к Х
k+1
значение целевой функции не изменяется, а в базис вводится элемент ![]() , для которого перевозка станет равной
, для которого перевозка станет равной ![]() .
.
Пример 2. Решим Т-задачу со следующими условиями (см. Табл.6)
Проверим условие баланса ![]()
Предварительный этап. Методом минимального элемента строим начальный базисный план Х 0 (Табл. 5)
Таблица 5
| C = | ai bj | 4 | 6 | 8 | 6 |
| 6 | 2(5) | 2(4) | 3(6) | 4(11) | |
| 8 | 6(12) | 4(10) | 3(9) | 1(3) | |
| 10 | 1(1) | 2(6) | 2(7) | 1(2) |

Так как m + n – 1 = 6; k = 4, то план х0 – вырожденный; l = m+ n -1 – k = 2.
Два нулевых элемента Х
0
делаем базисными так, чтобы не нарушить условие опорности. Выберем в качестве базисных элементов ![]() ,
, ![]() и положим их равными .
и положим их равными .
Схема перевозок для плана Х 0 показана на рис. 6.

Рис. 6.
Для вычисления предварительных потенциалов выберем начальный пункт А
1
и допустим, что ![]() . Потенциалы всех остальных пунктов вычисляем по формулам
. Потенциалы всех остальных пунктов вычисляем по формулам
![]() ,
, ![]()
Для проверки оптимальности плана х0 строим матрицу С 1 , элементы которой вычисляем по соотношению
![]()

Так как в матрице С 1 элемент С 23 = – 3 < 0, то план Х 0 – неоптимальный.
Первая итерация. Второй этап.
| *
|
6* | 0 | 0 | | 6 | 0 | 0 | ||||
| X0 = | * | 8 | 0+ | X1 = | 0 | 0 | 6 | | |||
| 4 | 0 | 0 | 6* | 1 = | 4 | 0 | 0 | 6 | |||
![]()
В результате построения Х
1
в базис вводим![]() . План Х
1
является вырожденным (в цепочке есть два минимальных элемента). Поэтому один из этих элементов, например
. План Х
1
является вырожденным (в цепочке есть два минимальных элемента). Поэтому один из этих элементов, например ![]() , в плане Х
1
заменяем на .
, в плане Х
1
заменяем на .
Вторая итерация. Первый этап
| 0 | 2 | 2 | 0 | 0 | -1 | 2 | ||||
| 2 | 0 | -3 | С2 = | 5 | 3 | 0 | 0 | |||
| 0 | 1 | 2 | 0 | 0 | 1 | -1 | 0 | |||
| -3 |
![]()
Второй этап.
| |
6 | 0 | 0 | | 6 | 0 | 0 | |||
| X1 = | 0 | 0 | 8* | * | X2 = | 0 | 0 | 2 | 6 | |
| 4 | 0 | 0+ | 6* | 3 =min {8, 6}= 6 | 4 | 0 | 6 | 0 | ||
Третья итерация. Первый этап.
| -1 | 2 | +1 | 0 | 0 | 0 | 3 | ||||
| С2 = | 5 | 3 | С2 = | 4 | 2 | 0 | 0 | |||
| 1 | -1 | 0 | +1 | 0 | 1 | 0 | 1 | |||
| -1 | -1 |
Так как в матрице С 3 нет отрицательных элементов, план Х 2 – оптимальный.
Венгерский метод для транспортной задачи
Рассмотренная выше задача о назначениях представляет собой частный случай Т-задачи, когда ![]() . Поэтому венгерский метод, применимый для решения транспортной задачи специального вида, можно распространить на общий случай Т-задачи.
. Поэтому венгерский метод, применимый для решения транспортной задачи специального вида, можно распространить на общий случай Т-задачи.
Пусть требуется решить Т-задачу следующего вида
минимизировать ![]()
при условиях

Алгоритм решения Т-задачи, основанный на венгерском методе, состоит из предварительного этапа и конечного числа однотипных итераций.
В результате предварительного этапа вычисляют матрицу ![]() , элементы которой удовлетворяют следующим условиям:
, элементы которой удовлетворяют следующим условиям:
![]() , (1.3.1)
, (1.3.1)
![]() . (1.3.2)
. (1.3.2)
Если в условиях (1.3.1), (1.3.2) строгие равенства, то матрица Х 0 является решением Т-задачи.
Матрицу, построенную в результате k-й итерации, обозначим ![]() . Обозначим также
. Обозначим также
![]() . (1.3.3)
. (1.3.3)
Величина ![]() называется суммарной невязкой для матрицы
называется суммарной невязкой для матрицы ![]() . Она характеризует близость
. Она характеризует близость ![]() к искомому плану Т-задачи. Итерации проводятся до тех пор, пока величина
к искомому плану Т-задачи. Итерации проводятся до тех пор, пока величина ![]() не станет равна нулю.
не станет равна нулю.
Описание алгоритма Венгерского метода
Предварительный этап. В каждом из столбцов матрицы транспортных издержек ![]() отыскивают минимальный элемент, который вычитают из всех элементов этого столбца. Получают матрицу С
'. Далее в каждой строке матрицы С
' выбирают минимальный элемент и вычитают его из всех элементов рассматриваемой строки. Приходят к матрице С
0
(С
0
~ C
), все элементы которой неотрицательны, причем в каждой строке и столбце С
0
имеем по крайней мере, один нуль. Строят матрицу Х
0
так, чтобы ее ненулевые элементы были расположены в позициях нулей матрицы С
0
.
отыскивают минимальный элемент, который вычитают из всех элементов этого столбца. Получают матрицу С
'. Далее в каждой строке матрицы С
' выбирают минимальный элемент и вычитают его из всех элементов рассматриваемой строки. Приходят к матрице С
0
(С
0
~ C
), все элементы которой неотрицательны, причем в каждой строке и столбце С
0
имеем по крайней мере, один нуль. Строят матрицу Х
0
так, чтобы ее ненулевые элементы были расположены в позициях нулей матрицы С
0
.
Пусть ![]() - номер строки, в которой расположен k-й нуль j-го столбца матрицы С
0
. Тогда элементы первого столбца матрицы Х
0
определяют по рекуррентной формуле
- номер строки, в которой расположен k-й нуль j-го столбца матрицы С
0
. Тогда элементы первого столбца матрицы Х
0
определяют по рекуррентной формуле
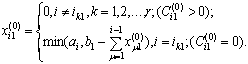 (3.3.4)
(3.3.4)
Т.е. все элементы первого столбца ![]() , которым соответствуют ненулевые элементы в матрицы С
0
, заполняют нулями, а остальные элементы этого столбца заполняют по методу северо-западного угла.
, которым соответствуют ненулевые элементы в матрицы С
0
, заполняют нулями, а остальные элементы этого столбца заполняют по методу северо-западного угла.
Допустим, что столбцы Х 0 от первого до (j-1) – го включительно уже заполнены. Тогда элементы j-го столбца определяют в соответствии с формулой
 (3.3.5)
(3.3.5)
Если ![]() , то Х
0
– оптимальный план Т-задачи. Если
, то Х
0
– оптимальный план Т-задачи. Если ![]() , то переходим к первой итерации.
, то переходим к первой итерации.
(k+1) – я итерация. Каждая итерация состоит из двух или трех этапов. Итерация начинается первым этапом, а заканчивается вторым. Между первым и вторым этапами в общем случае несколько раз могут быть проведены третий и первый этапы.
Допустим, что уже проведено k итераций, причем ![]() . В этом случае необходимо, используя матрицы С
k
и Х
k
, провести следующую (k+1) – ю итерацию. Перед началом итерации выделяют знаком '+' те столбцы матрицы С
k
, для которых невязки по столбцам равны
. В этом случае необходимо, используя матрицы С
k
и Х
k
, провести следующую (k+1) – ю итерацию. Перед началом итерации выделяют знаком '+' те столбцы матрицы С
k
, для которых невязки по столбцам равны
![]() .
.
Первый этап. Если все ненулевые элементы матрицы С
k
окажутся в выделенных столбцах, то переходят к третьему этапу. В противном случае пусть некоторый невыделенный нуль находится в ![]() -й строке и в
-й строке и в ![]() -м столбце. Тогда вычисляют значения невязки
-м столбце. Тогда вычисляют значения невязки ![]() -й строки:
-й строки:
![]() .
.
Возможен один из двух случаев: 1)![]() , 2)
, 2)![]() . В первом случае
. В первом случае ![]() -ю строку С
k
отмечают знаком '+' справа от нее, а сам невыделенный нуль отмечают штрихом. Далее просматривают элементы
-ю строку С
k
отмечают знаком '+' справа от нее, а сам невыделенный нуль отмечают штрихом. Далее просматривают элементы ![]() -й строки, которые лежат в выделенных столбцах и ищут среди них существенные нули (напомним, что существенным нулем С
k
называется такой элемент
-й строки, которые лежат в выделенных столбцах и ищут среди них существенные нули (напомним, что существенным нулем С
k
называется такой элемент ![]() , для которого
, для которого ![]() ). Если таким существенным нулем оказался элемент
). Если таким существенным нулем оказался элемент ![]() , а сам столбец – выделен, то знак выделения '+' над столбцом уничтожают, а сам этот нуль отмечают звездочкой.
, а сам столбец – выделен, то знак выделения '+' над столбцом уничтожают, а сам этот нуль отмечают звездочкой.
Затем просматривают -й столбец и отыскивают в нем нуль (нули), расположенные в отличных от ![]() -й строках. Если такой нуль имеется, то отмечают его штрихом и анализируют невязку его строки.
-й строках. Если такой нуль имеется, то отмечают его штрихом и анализируют невязку его строки.
Далее процесс поиска нулей и выделение их (штрихами или звездочками) продолжается аналогично, и за несколько шагов он заканчивается одним из следующих исходов:
1) найдем очередной невыделенный нуль матрицы С
k
, для которого невязкая в строке ![]() . Тогда отметив его штрихом, переходим ко второму этапу;
. Тогда отметив его штрихом, переходим ко второму этапу;
2) все нули матрицы С
k
оказались выделенными, причем для каждого из нулей, выделяемых штрихом, невязка ![]() . Тогда переходим к третьему этапу.
. Тогда переходим к третьему этапу.
Во втором случае, отметив этот нуль штрихом, сразу переходим к третьему этапу.
Второй этап. Состоит в построении цепочки из нулей матрицы С k , отмеченных штрихами и звездочками, и в последующем переходе к новой матрице Х k+1
Пусть для некоторого нуля со штрихом матрицы С
k
, расположенного, например, в позиции (![]() ), невязка строки
), невязка строки ![]() . Начиная с этого элемента
. Начиная с этого элемента ![]() , строят цепочку из отмеченных нулей матрицы С
k
: двигаясь по столбцу
, строят цепочку из отмеченных нулей матрицы С
k
: двигаясь по столбцу ![]() , выбирают нуль со звездочкой
, выбирают нуль со звездочкой ![]() , далее двигаясь от него по строке
, далее двигаясь от него по строке ![]() , находят нуль со штрихом
, находят нуль со штрихом ![]() . Потом движутся от него по столбцу 2
к следующему нулю со звездочкой и т.д. Такой последовательный переход от 0' к 0*
по столбцу и от 0*
к 0' по строке осуществляют до тех пор, пока это возможно.
. Потом движутся от него по столбцу 2
к следующему нулю со звездочкой и т.д. Такой последовательный переход от 0' к 0*
по столбцу и от 0*
к 0' по строке осуществляют до тех пор, пока это возможно.
Можно доказать, что процесс построения цепочки однозначный и законченный, цепочка не имеет циклов, начинается и заканчивается нулем со штрихом.
После того как цепочка вида
![]()
построена, осуществляют переход к матрице ![]() от матрицы Х
k
по формулам
от матрицы Х
k
по формулам
 (1.3.7)
(1.3.7)
где  (1.3.8)
(1.3.8)
Таким образом, ![]() -минимальный элемент среди совокупности четных элементов цепочки, невязки строки, где начинается цепочка, и столбца, где она заканчивается.
-минимальный элемент среди совокупности четных элементов цепочки, невязки строки, где начинается цепочка, и столбца, где она заканчивается.
Вычисляем невязку для ![]()
На этом (k+1) – я итерация заканчивается.
Третий этап. Итак, допустим, что все нули выделены. Третий этап заключается в переходе от матрицы С
k
к эквивалентной матрице С′
k
, в которой появляется новый невыделенный нуль (или нули). Пусть ![]() , где минимум выбирают из всех невыделенных элементов матрицы С
k
. Тогда из всех элементов невыделенных строк матрицы С
k
вычитают h, а ко всем элементам выделенных столбцов прибавляют h. В результате получают матрицу С
'k
(С
'k
~ C
k
), в которой все существенные нули матрицы С
k
остаются нулями, и кроме того, появляются новые невыделенные нули.
, где минимум выбирают из всех невыделенных элементов матрицы С
k
. Тогда из всех элементов невыделенных строк матрицы С
k
вычитают h, а ко всем элементам выделенных столбцов прибавляют h. В результате получают матрицу С
'k
(С
'k
~ C
k
), в которой все существенные нули матрицы С
k
остаются нулями, и кроме того, появляются новые невыделенные нули.
Далее переходят к первому этапу, и в зависимости от его результата либо переходят ко второму этапу, либо снова возвращаются к третьему этапу. За конечное число повторов пары этапов третий – первый обязательно перейдем ко второму этапу.
Если после выполнения второго этапа ![]() то Х
k+1
– оптимальный план. В противном случае переходим к (k+2) итерации.
то Х
k+1
– оптимальный план. В противном случае переходим к (k+2) итерации.
Отметим некоторые важные особенности венгерского метода.
Поскольку данный метод в отличие от метода потенциалов не использует опорных планов, то явление вырожденности плана для него отсутствует. Это устраняет возможность зацикливания, связанного с вырожденностью планов Т-задачи, которая облегчает программирование метода и его реализацию на ЭВМ.
Метод позволяет на каждой итерации по величине невязки ![]() оценить близость Х
k
к оптимальному плану, а также верхнюю границу необходимого числа оставшихся итераций Nост
:
оценить близость Х
k
к оптимальному плану, а также верхнюю границу необходимого числа оставшихся итераций Nост
:
![]() . (1.3.9)
. (1.3.9)
Эта формула справедлива для целочисленных значений всех переменных ![]() и
и ![]() .
.
Список литературы
1. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа.
2. Вентцель Е.С. Исследование операций. – М.: Наука, 1976.
3. Горелик В.А., Ушаков И.А. Исследование операций. – М: Машиностроение, 1986. – 286 с.
4. Давыдов Э.Т. Исследование операций: Учебное пособие для студентов вузов. – М.: Высшая школа, 1990. – 383 с.
5. Ермолаев Ю.М. Математические методы исследования операций. – К.: Наука, 1979.
6. Кузнецов Ю.Н. Математическое программирование. – М.: Наука, 1976.
7. Минц М. Математическое программирование. Теория и алгоритмы. – М.: Наука, 1990.
8. Таха Х. Введение в исследование операций. – м.: Мир, 1985.
9. Толбатов Ю.А. Эконометрика в Excel. – К.: Четверта хвиля, 1997.

 5 6 11 7 8
5 6 11 7 8