| Скачать .docx |
Реферат: Моделирование хозяйственной деятельности предприятия
Министерство образования и науки РФ
Хабаровская государственная академия экономики и права
Кафедра высшей математики
Факультет «Финансист»
Специальность: «Финансы и кредит»
Специализация: ГМФ
КОНТРОЛЬНАЯ РАБОТА
По дисциплине
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Вариант № 6
Выполнил: Алепов А.В.
студ. 3ФК курса,
г. Южно-Сахалинск 2006 г.
№6
Привести систему к системе с базисом, найти соответствующее базисное решение и сделать проверку, подставив решение в исходную систему:
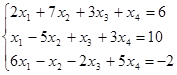
Решение:
Составим таблицу:
| 2 | 7 | 3 | 1 | 6 |
| 1 | -5 | 1 | 3 | 10 |
| 6 | -1 | -2 | 5 | -2 |
| 1 | -5 | 1 | 3 | 10 |
| 2 | 7 | 3 | 1 | 6 |
| 6 | -1 | -2 | 5 | -2 |
| 1 | -5 | 1 | 3 | 10 |
| 0 | 17 | 1 | -5 | -14 |
| 0 | 29 | -8 | -13 | -62 |
| 1 | 1 | -5 | 3 | 10 |
| 0 | 1 | 17 | -5 | -14 |
| 0 | -8 | 29 | -13 | -62 |
| 1 | 0 | -22 | 8 | 24 |
| 0 | 1 | 17 | -5 | -14 |
| 0 | 0 | 165 | -53 | -174 |
| 1 | 0 | 0 | ||
| 0 | 1 | 0 | ||
| 0 | 0 | 1 |
Получили систему с базисом:
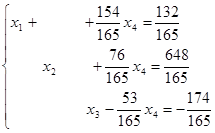
Здесь ![]() ,
, ![]() ,
, ![]() - базисные неизвестные,
- базисные неизвестные, ![]() - свободное неизвестное. Положим
- свободное неизвестное. Положим ![]() . Получим
. Получим ![]() ,
, ![]() ,
, ![]() .
.
Подставим решение в исходную систему:
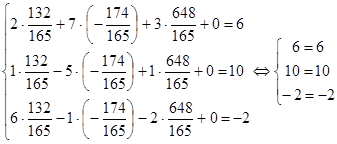 ,
,
решение найдено верно.
№26
Предположим, что для производства двух видов продукции А и В можно использовать только материал трех сортов. При этом на изготовление единицы изделия А расходуется 2 кг материала, 3 кг материала второго сорта, 4 кг материла третьего сорта. На изготовление единицы изделия В расходуется 5 кг материала, 2 кг материала второго сорта, 3 кг материла третьего сорта. На складе фабрики имеется всего материала первого сорта 45 кг, второго сорта - 27 кг, третьего сорта – 38 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль 7 тыс. рублей, а от продукции вида В прибыль составляет 5 тыс. рублей.
Определить максимальную прибыль от реализации всей продукции видов А и В. Решить задачу симплексным методом и графически.
Решение:
1. Решение с помощью симплексного метода.
Составим математическую модель задачи. Обозначим через х1
и х2
выпуск продукции А и В соответственно. Затраты материала первого сорта на план ![]() составят 2х1
+ 5х2
и они недолжны превосходить запасов 45 кг:
составят 2х1
+ 5х2
и они недолжны превосходить запасов 45 кг:
![]()
Аналогично, ограничения по материалу второго сорта
![]()
И по материалу третьего сорта:
![]()
Прибыль от реализации х1 изделий А и х2 изделий В составит
![]()
целевая функция задачи.
Получили модель задачи:
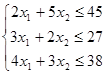
![]()
![]()
Вводом балансовых переменных приводим модель к каноническому виду:
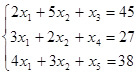
![]()
![]()
Запишем начальное опорное решение:
![]()
Симплекс-таблицу заполняем из коэффициентов при неизвестных из системы ограничений и функции:
| Баз.перем. | С | План | 7 | 5 | 0 | 0 | 0 |
| х1 | х2 | х3 | х4 | х5 | |||
| х3 | 0 | 45 | 2 | 5 | 1 | 0 | 0 |
| х4 | 0 | 27 | 3 | 2 | 0 | 1 | 0 |
| х5 | 0 | 38 | 4 | 3 | 0 | 0 | 1 |
| ∆Z | 0 | -7 | -5 | 0 | 0 | 0 | |
| x3 | 0 | 27 | 0 | 11/3 | 1 | -2/3 | 0 |
| x1 | 7 | 9 | 1 | 2/3 | 0 | 1/3 | 0 |
| х5 | 0 | 2 | 0 | 1/3 | 0 | -4/3 | 1 |
| ∆Z | 63 | 0 | -1/3 | 0 | 7/3 | 0 | |
| x3 | 0 | 5 | 0 | 0 | 1 | 14 | -11 |
| x1 | 7 | 5 | 1 | 0 | 0 | 3 | -2 |
| x2 | 5 | 6 | 0 | 1 | 0 | -4 | 3 |
| ∆Z | 65 | 0 | 0 | 0 | 1 | 1 |
![]()
в индексной строке содержатся две отрицательные оценки , наибольшая по абсолютной величине (-7)
![]()
В индексной строке содержится отрицательная оценка (-1/3).
в индексной строке нет отрицательных оценок
Так как все оценки положительные записываем оптимальное решение:
![]()
При этом плане прибыль от реализации изделий х1 = 5 и х2 = 6 составит Zmax = 65; х4 = 0 и х5 = 0 означает, что материал второго и третьего сорта использован полностью, а х3 = 5 говорит о том, что осталось еще 5 кг материала первого сорта.
Получили Zmax
= 65 тыс. руб. при ![]() .
.
2. Графическое решение:
Рассмотрим систему линейных неравенств.
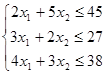
![]()
![]()
Строим область допустимых решений данной задачи. Для этого строим граничные линии в одной системе координат:
![]() (I),
(I),
![]() (II),
(II),
![]() (III),
(III),
х1 = 0 (IV), х2 = 0 (V).
Для построения прямых берем по две точки:
![]()
![]()
![]()
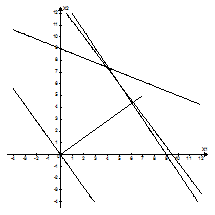
![]()
Областью решений является пятиугольник ABCDO.
Затем строим на графике линию уровня
![]()
и вектор
![]()
или
![]()
Теперь перемещаем линию уровня в направлении вектора ![]() . Последняя точка при выходе из данной области является точка С – в ней функция
. Последняя точка при выходе из данной области является точка С – в ней функция
![]()
достигает своего наибольшего значения.
Определим координаты точки С из системы уравнений (II) и (III):
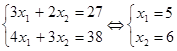
Подставим найденные значения в целевую функцию:
![]() .
.
Т.е. максимальная прибыль от реализации изделий А и В составит 65 тыс. рублей.
№46
Для модели предыдущей задачи составить двойственную, из симплексной таблицы найти ее решение и проверить по основной теореме.
Решение:
Модель предыдущей задачи:
![]()
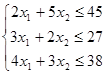
![]()
Двойственная ей задача имеет вид:
![]()
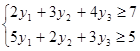
![]()
Для предыдущей задачи ее решение: ![]() при
при ![]()
Следовательно, по основной теореме для двойственной задачи: ![]() при
при ![]()
Проверка:
![]() верно.
верно.
№ 66
Решить транспортную задачу.
![]()
![]()
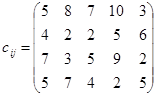
Решение:
1. Занесем данные задачи в таблицу:
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | 5 | 8 | 7 | 10 | 3 | 100 |
| А2 | 4 | 2 | 2 | 5 | 6 | 200 |
| А3 | 7 | 3 | 5 | 9 | 2 | 200 |
| А4 | 5 | 7 | 4 | 2 | 5 | 100 |
| 190 | 100 | 130 | 80 | 100 | 600 |
2. Составляем математическую модель задачи: для этого вводим неизвестные хij , которыми являются количество единиц товара, перевозимого от каждого поставщика к каждому потребителю.
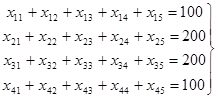 ограничения по поставкам
ограничения по поставкам
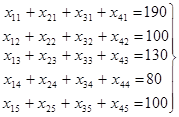 ограничение по потребителям
ограничение по потребителям
![]() (
(![]() ,(
,(![]() ограничения по здравому смыслу.
ограничения по здравому смыслу.
Цель задачи (стоимость всей перевозки) в математической форме:
![]()
Задача разрешима, т.к.
![]() .
.
3. Находим оптимальный план по методу наименьшего элемента
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | 5100 | 87 | 76 | 108 | 33 | 100 |
| А2 | 4 |
270- | 2130 | 53 | 65 | 200 |
| А3 | - 770 | +330 | 52 | 95 | 2100 | 200 |
| А4 | 520 | 76 | 43 | 280 | 55 | 100 |
| 190 | 100 | 130 | 80 | 100 | 600 |
![]() - план невырожденный
- план невырожденный
![]()
Дадим оценку полученному плану методом потенциалов. Каждому поставщику Аi
ставим в соответствие число ![]() (
(![]() , называемое потенциалом поставщика; каждому потребителю Bj
– число
, называемое потенциалом поставщика; каждому потребителю Bj
– число ![]() (
(![]() , называемое потенциалом потребителя. Причем
, называемое потенциалом потребителя. Причем ![]() и
и ![]() выбираем так, чтобы в любой загруженной клетке сумма их равнялась тарифу этой клетки, т.е.
выбираем так, чтобы в любой загруженной клетке сумма их равнялась тарифу этой клетки, т.е. ![]()
Всего занятых клеток m+ n– 1 = 8 (план не вырожденный). Придаем одному из неизвестных значение 0.
Для определения потенциалов составляем систему:
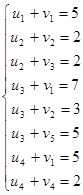
Откуда
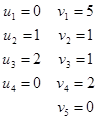
Вычисляем оценки для свободных клеток по формуле
![]()
и запишем их в левом углу свободных клеток. В клетке (2; 1) получили отрицательную оценку. Строим для нее цикл
![]()
вдоль которого перемещаем
![]() .
.
Получаем следующий план перевозок:
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | 5100 | 85 | 74 | 108 | 31 | 100 |
| А2 | 470 | 20 | 2130 | 54 | 65 | 200 |
| А3 | 72 | 3100 | 52 | 97 | 2100 | 200 |
| А4 | 520 | 74 | 41 | 280 | 53 | 100 |
| 190 | 100 | 130 | 80 | 100 | 600 |
![]() - план невырожденный
- план невырожденный
![]()
Дадим оценку полученному плану. Всего занятых клеток m+ n– 2 = 7 (план не вырожденный). Придаем двум из неизвестных значение 0.
Для определения потенциалов составляем систему:
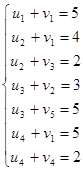 Откуда
Откуда 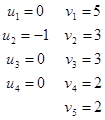
Вычисляем оценки для свободных клеток и записываем их в левом углу свободных клеток.
Все оценки положительны, значит, план оптимален.
Оптимальный план можем представить в виде
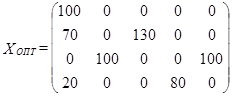
транспортные расходы по этому плану составят
![]() условных единиц.
условных единиц.