| Скачать .docx |
Курсовая работа: Моделирование и прогнозирование естественного прироста населения в РФ
В данной курсовой работе методы и модели эконометрического анализа используется с целью моделирования и прогнозирования естественного прироста населения в Российской Федерации. Значения естественного прироста населения представлены в виде одномерного временного ряда ежемесячных данных в период с января 2006г. по декабрь 2008 г.
Естественный прирост - разность между числами родившихся и умерших.
Актуальность исследования тесно связана со сложившейся тяжелой демографической ситуацией в России. Такая ситуация начала складываться в начале 90-х годов XX века и совпала с экономическим кризисом в стране.
Сокращение населения затронуло практически все территории Российской Федерации и почти все этнические группы. Депопуляция в Российской Федерации обусловливается не только низкой рождаемостью. Крайне острой проблемой является высокая смертность населения. Некоторое улучшение ситуации со смертностью в 1995-1998 годах оказалось непродолжительным. С 1999 года смертность населения страны вновь начала расти.
Данное исследование может послужить основой для формирования демографической политики в субъектах Российской Федерации и разработки региональных планов по улучшению демографической ситуации.
Предметом исследования являются ежемесячные данные об уровне естественного прироста населения в абсолютном выражении, т.к. по абсолютным данным модели и прогнозы являются более достоверными.
Целью данной курсовой работы является описание предмета исследования и эконометрических методов его анализа, моделирование и выявление тенденций изменения изучаемого показателя, прогнозирование и анализ полученных прогнозных значений.
В теоретической части курсовой работы подробно раскрывается содержание вопросов темы - предпрогнозная ориентация (программа исследования), включающая в себя анализ внешней обстановки; анализ внутренней обстановки; подробную характеристику объекта и предмета исследования; определение времени основания и учреждения в прогнозе; обоснование и описание методов, используемых в ходе исследования; организацию проведения исследования; формулирование рабочих гипотез.
В практической части проводится исследование временных рядов естественного прироста населения с помощью мультипликативной и аддитивной моделей, рядов Фурье, адаптивной сезонной модели, фиктивных переменных. По полученным данным определяется наиболее адекватная и точная модель, далее строится итоговый прогноз на период с января 2009г. по декабрь 2009г.
Для нахождения параметров, оценок моделей, проведения тестов на адекватность и значимость, а также для прогнозирования использовались пакеты MicrosoftExcel и STATISTICA.
Программа исследования естественного прироста населения в РФ в период с января 2006г. по декабрь 2008г. предполагает содержание подробной характеристики проблемы состоящую из следующих пунктов:
· анализ внешней обстановки (характеристика экономической, политической, социальной ситуации в государстве);
· анализ внутренней обстановки (тенденции внутри объекта исследования);
· подробная характеристика объекта и предмета исследования;
· определение времени основания и упреждения в прогнозе: текущий, краткосрочный;
· обоснование и описание методов, используемых в ходе исследования;
· формулирование рабочих гипотез.
Остановимся подробнее на каждом пункте исследования.
В России в основном завершен переход к рыночной экономической системе. Создана система базовых правовых норм и других институтов, обеспечивающих развитие рыночных отношений.
Достигнута высокая степень открытости российской экономики. Внешнеторговый оборот в 2007 году составил 45 процентов валового внутреннего продукта, что является одним из наиболее высоких показателей для стран с развитой экономикой.
В целом обеспечена макроэкономическая стабильность. Экономика защищена от внешних шоковых воздействий международными резервными активами Российской Федерации.
Сформировался мощный слой развивающихся компаний, успешно конкурирующих на внутреннем и внешнем рынках и активно привлекающих капитал для своего развития. Российский фондовый рынок стал важным фактором привлечения инвестиций и обеспечения экономического роста страны. В условиях развивающегося мирового финансового кризиса российская финансовая система (при активной поддержке государства) показала свою устойчивость.
Преодолены тенденции социальной конфронтации в обществе, наблюдавшиеся в 90-е годы. Развиваются институты гражданского общества.
Показатели социально-экономического развития Российской Федерации, достигнутая макроэкономическая стабильность и финансовая устойчивость свидетельствуют о результативности проведенных системных преобразований. Последние 5 лет темпы роста российской экономики значительно превышают среднемировой уровень (около 107 процентов и 104,6 процента соответственно).
1.2 Анализ внутренней обстановки
На данный момент существует положительная тенденция естественного прироста населения, о чем свидетельствуют следующие данные:
Январь 2006г. – -99636 чел.
Январь 2007г. – -65331 чел.
Январь 2008г. – -59241 чел.
Декабрь 2008г. – -26179 чел.
Но ситуация остается тяжелой, т.к. естественная убыль населения (отрицательный естественный прирост населения) все еще присутствует.
1.3 Характеристика объекта и предмета исследования
Предметом исследования является демографическая ситуация, сложившаяся в РФ в период с 2006 по 2008гг.
Объектом исследования является динамика изменения естественного прироста населения в РФ.
1.4 Время основания и упреждения прогноза
Основанием для прогноза служит упорядоченная ежемесячная выборка, предоставленная Федеральной службой государственной статистики, в период с января 2006г. по декабрь 2008г. и содержащая 36 наблюдений.
Временем упреждения прогноза является период с января по декабрь 2009 г. – прогноз является краткосрочным.
1.5 Обоснование и описание методов, используемых в ходе исследования
Для данного исследования выбран достаточно широкий диапазон моделей исследования:
· Аддитивная модель;
· Мультипликативная модель;
· Одномерный анализ Фурье;
· Регрессионная модель с переменной структурой (фиктивные переменные);
· Адаптивная сезонная модель.
Выбор производился исходя из особенностей выборки – в исходных данных присутствует тенденция временного ряда, а также наблюдается наличие периодических колебаний. Выбранные модели достаточно хорошо описывают такие процессы.
Для аддитивной и мультипликативной моделей временного ряда необходимо произвести сглаживание методом простой скользящей средней.
Оценка параметров каждой из модели производится методом наименьших квадратов (МНК).
1.6 Формулировка рабочих гипотез
В период с января по декабрь 2009г. динамика изменения естественного прироста населения будет иметь возрастающую тенденцию и, следовательно, значения показателя будут увеличиваться.
Рассмотрим график временного ряда исходных данных естественного прироста населения РФ в период с января 2006 по декабрь 2008 года (Приложение 1). Проанализировав график, делаем вывод о наличии сезонных колебаний с периодичностью 12 месяцев и возрастающей тенденцией, что наглядно отражено в построенном графике сезонной волны (Приложение 2). Подтверждение данному факту отражено в АКФ и ЧАКФ (Таблица 1).
Таблица 1 - Значения АКФ и ЧАКФ
| Лаг | АКФ | ЧАКФ |
| 1 | 0,664 | 0,664 |
| 2 | 0,537 | 0,173 |
| 3 | 0,337 | -0,135 |
| 4 | 0,242 | 0,011 |
| 5 | 0,065 | -0,164 |
| 6 | -0,058 | -0,120 |
| 7 | -0,051 | 0,155 |
| 8 | 0,044 | 0,225 |
| 9 | 0,104 | 0,067 |
| 10 | 0,216 | 0,152 |
| 11 | 0,247 | -0,031 |
| 12 | 0,369 | 0,132 |
| 13 | 0,208 | -0,300 |
| 14 | 0,162 | -0,025 |
| 15 | 0,024 | -0,036 |
Наибольшее значение достигается на 1 лаге, следовательно, присутствует тенденция временного ряда. Выбросы по АКФ – 1 и 12 лаг, по ЧАКФ – 1 и 13 лаг – гипотеза о сезонных колебаниях с периодичностью 12 месяцев подтверждается. Качество каждой модели будем оценивать по показателям среднеквадратической ошибки и средней ошибки аппроксимации. После построения всех моделей сделаем по каждой из них прогноз и проанализируем полученные результаты.
2.2 Аддитивная модель временного ряда
По графику временного ряда можно установить наличие приблизительно равной амплитуды колебаний. Это свидетельствует о соответствии этого ряда аддитивной модели. Рассчитаем ее компоненты.
Расчетная таблица модели приведена в Приложении 3.
Шаг 1. Проведем выравнивание исходных уровней ряда методом простой скользящей средней. Для этого:
· Просуммируем уровни ряда последовательно за каждые 12 месяцев со сдвигом на один момент времени и определим условные годовые объемы показателя;
· Разделив полученные суммы на 12, найдем скользящие средние. Отметим, что полученные таким образом выравненные значения уже не содержат сезонной компоненты;
· Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние.
Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями временного ряда и центрированными скользящими средними. Используем эти оценки для расчета значений сезонной компоненты S. Для этого найдем средние за каждый месяц (по всем годам) оценки сезонной компоненты Si. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем месяцам должна быть равна 0.
Для данной модели имеем:
-20801,292 - 229,292 - 10613,250 - 6961,104 - 11583,625 - 676,625 + 13547,792 + 16693,917 + 13749,417 + 4680,354 - 463,792 - 1198,000 = -3855,500
Определим корректирующий коэффициент:
k = -3855,500 / 12 = -321,292
Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом k:
![]()
Проверим условие равенства нулю суммы значений скорректированной сезонной компоненты:
-20480,000 + 92,000 - 10291,958 - 6639,813 - 11262,333 - 355,333 + 13869,083 + 17015,208 + 14070,708 + 5001,646 - 142,500 - 876,708 = 0
Таким образом получены следующие значения скорректированной сезонной компоненты (Таблица 2):
Таблица 2 - Значения скорректированной сезонной компоненты
| Январь | S1 | -20480,000 | Июль | S7 | 13869,083 |
| Февраль | S2 | 92,000 | Август | S8 | 17015,208 |
| Март | S3 | -10291,958 | Сентябрь | S9 | 14070,708 |
| Апрель | S4 | -6639,813 | Октябрь | S10 | 5001,646 |
| Май | S5 | -11262,333 | Ноябрь | S11 | -142,500 |
| Июнь | S6 | -355,333 | Декабрь | S12 | -876,708 |
Занесем полученные значения для соответствующих месяцев каждого года.
Шаг 3. Элиминируем влияние скорректированной сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим: T + E = Y – S. Эти значения рассчитываются для каждого момента времени и содержат только тенденцию и случайную компоненту.
Шаг 4. Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда (T + E) с помощью линейного тренда. Результаты выравнивания следующие:
T = -63923,013 + 1156,975 ·t; R 2 = 0,889
Таблица 3 - Статистика уравнения тренда
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | -63923,013 | 1487,618 | -42,970 | 3,23251E-31 |
| t | 1156,975 | 70,114 | 16,501 | 8,46925E-18 |
Уравнение описывает на 88,9% вариацию исходного показателя естественного прироста, при этом уравнение является статистически значимым при уровне надежности 95%.
Подставляя в это уравнение значения t = 1,…, 36, найдем уровни T для каждого момента времени.
Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням T значения сезонной компоненты для соответствующих месяцев.
Шаг 6. В соответствие с методикой построения аддитивной модели расчет абсолютной ошибки производится по формуле:
E = Y – (T + S).

Исходя из значений выше приведенных показателей качества, можно сделать вывод о том, что модель обладает высокой точностью и пригодна для прогнозирования.
2.3 Мультипликативная модель временного ряда
Шаг 1. Проведем выравнивание исходных уровней временного ряда методом простой скользящей средней. Методика, применяемая для мультипликативной модели, полностью совпадает с методикой аддитивной модели. Расчетная таблица модели приведена в Приложении 4.
Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние. Используем эти оценки для расчета значений скорректированной сезонной компоненты. Для этого найдем средние за каждый месяц оценки сезонной компоненты. Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений скорректированной сезонной компоненты по всем кварталам должна быть равно числу периодов в цикле, т.е. двенадцати, так как в нашем случае число периодов одного цикла равно 12 месяцам. В результате имеем следующие сезонные компоненты: 1,526 + 1,010 + 1,280 + 1,183 + 1,329 + 1,032 + 0,712 + 0,631 + 0,680 + 0,874 + 1,008 + 1,021 = 12,287.
Определим скорректированные значения сезонной компоненты, умножив ее на средние оценки на корректирующий коэффициент k:
![]()
Проверим условие равенства двенадцати суммы значений скорректированной сезонной компоненты:
1,491 + 0,987 + 1,250 + 1,155 + 1,298 + 1,008 + 0,695 + 0,616 + 0,664 + 0,853 + 0,985 + 0,997 = 12.
Получим следующие значения скорректированной сезонной компоненты (Таблица 4):
Таблица 4 - Значения скорректированной сезонной компоненты
| Январь | S1 | 1,491 | Июль | S7 | 0,695 |
| Февраль | S2 | 0,987 | Август | S8 | 0,616 |
| Март | S3 | 1,250 | Сентябрь | S9 | 0,664 |
| Апрель | S4 | 1,155 | Октябрь | S10 | 0,853 |
| Май | S5 | 1,298 | Ноябрь | S11 | 0,985 |
| Июнь | S6 | 1,008 | Декабрь | S12 | 0,997 |
Занесем полученные значения для соответствующих месяцев каждого года.
Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения скорректированной сезонной компоненты. Получим: T·E = Y / S, которые содержат только тенденцию и случайную компоненту.
Шаг 4. Определим компоненту T в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни (T·E). Результаты аналитического выравнивания:
Т = -64018,071 + 1201,064 · t; R 2 = 0,863
Таблица 5 - Статистика уравнения тренда
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | -64018,071 | 1744,938 | -36,688 | 6,24E-29 |
| t | 1201,064 | 82,242 | 14,604 | 3,27E-16 |
Уравнение описывает на 86,3% вариацию исходного показателя естественного прироста, при этом уравнение является статистически значимым при уровне надежности 95%.
Подставляя в это уравнение значения t = 1,…,36, найдем уровни Т для каждого момента времени.
Шаг 5. Найдем уровни ряда по мультипликативной модели, умножив уровни Т на значения скорректированной сезонной компоненты для соответствующих месяцев.
Шаг 6. Расчет ошибки в мультипликативной модели производится по формуле:
E = Y / (T·S)

Исходя из значений выше приведенных показателей качества, можно сделать вывод о том, что модель обладает высокой точностью и пригодна для прогнозирования.
2.4 Одномерный анализ Фурье
Выполним одномерный анализ Фурье для показателя естественного прироста населения РФ. Расчетная таблица ряда Фурье представлена в Приложении 5.
Переменными для составления модели будут следующие: t, cos(2·Π·t/12); sin(2·Π·t/12); cos(4·Π·t/12); sin(4·Π·t/12); cos(6·Π·t/12); sin(6·Π·t/12).
Значение знаменателя каждой дроби обусловлено периодичностью сезонных колебаний.
Построив модель с включением данных переменных, получаем следующее уравнение:
Ŷt = -64314,412 + 1178,132 · t – 5360,004 ·cos(2·Π·t/12) –12253,175 ·sin(2·Π·t/12) – 4098,437 ·cos(4·Π·t/12) + 1894,178 ·sin(4·Π·t/12) + 933,424 ·cos(6·Π·t/12) –5109,257 ·sin(6·Π·t/12); R 2 = 0,897
Таблица 6 - Статистика уравнения для модели ряда Фурье
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | -64314,412 | 2390,342 | -26,906 | 1,49932E-21 |
| t | 1178,132 | 113,994 | 10,335 | 4,62652E-11 |
| cos(2Pi*t/12) | -5360,004 | 1595,524 | -3,359 | 0,002267582 |
| sin(2Pi*t/12) | -12253,175 | 1647,329 | -7,438 | 4,22248E-08 |
| cos(4Pi*t/12) | -4098,437 | 1595,524 | -2,569 | 0,015828755 |
| sin(4Pi*t/12) | 1894,178 | 1603,648 | 1,181 | 0,247471866 |
| cos(6Pi*t/12) | 933,424 | 1595,524 | 0,585 | 0,56321529 |
| sin(6Pi*t/12) | -5109,257 | 1595,524 | -3,202 | 0,003385848 |
Уравнение описывает на 89,7% вариацию исходного показателя естественного прироста, при этом уравнение является статистически значимым при уровне надежности 95%.
Но коэффициенты перед переменными sin(4·Π·t/12) и cos(6·Π·t/12) не удовлетворяют данному уровню надежности.
Исключим их из модели и перестроим уравнение регрессии.
Ŷt = -64096,083 + 1166,330 · t –5348,202 · cos(2·Π·t/12) –12297,219 · sin(2·Π·t/12) –4086,636 · cos(4·Π·t/12) – 5121,059 · sin(6·Π·t/12); R2 = 0,891
Таблица 7 - Статистика уравнения для модели ряда Фурье
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | -64096,083 | 2361,646 | -27,140 | 1,138E-22 |
| t | 1166,330 | 112,370 | 10,379 | 1,90859E-11 |
| cos(2Pi*t/12) | -5348,202 | 1588,773 | -3,366 | 0,002101931 |
| sin(2Pi*t/12) | -12297,219 | 1639,342 | -7,501 | 2,31486E-08 |
| cos(4Pi*t/12) | -4086,636 | 1588,773 | -2,572 | 0,015299504 |
| sin(6Pi*t/12) | -5121,059 | 1588,773 | -3,223 | 0,003049779 |
Уравнение описывает на 89,1% вариацию исходного показателя естественного прироста, уравнение статистически значимо при уровне надежности 95%. Все коэффициенты уравнения статистически значимы при аналогичном уровне надежности.

Модель имеет высокие показатели среднеквадратической ошибки и средней ошибки аппроксимации, но может быть использована для прогнозирования.
2.5 Регрессионная модель с переменной структурой (фиктивные переменные)
Рассмотрим еще один метод моделирования временного ряда, содержащего сезонные колебания, - построение модели регрессии с включением фактора времени и фиктивных переменных. Количество фиктивных переменных в такой модели должно быть на единицу меньше числа моментов (периодов) времени внутри одного цикла колебаний. В данном случае при моделировании ежемесячных данных модель должна включать двенадцать независимых переменных – фактор времени и одиннадцать фиктивных переменных. Каждая фиктивная переменная отражает сезонную (циклическую) компоненту временного ряда для какого-либо одного периода. Она равна единице для данного периода и нулю для всех остальных периодов.
Построим модель регрессии с включением фактора времени и фиктивных переменных для данных о естественном приросте населения в РФ. В данной модели двенадцать независимых переменных: t, D2, D3, D4, D5, D6, D7, D8, D9, D10, D11, D12 и результативная переменная Y. Составим матрицу исходных данных (Приложение 6).
Уравнение регрессии имеет вид:
Ŷt = -89444,083 + 1132,083 · t + 24047,583 ·D2 + 17218,167 ·D3 + 21431,750 ·D4 + 15077,333 ·D5 + 26904,583 ·D6 + 40734,833 ·D7 + 43809,083 ·D8 + 38606,667 ·D9 + 32848,917 ·D10 + 26662,833 ·D11 + 24437,083 ·D12
R 2 = 0,960
Уравнение описывает на 96,0% вариацию исходного показателя естественного прироста, уравнение статистически значимо при уровне надежности 95%.
Оценим параметры уравнения регрессии обычным МНК. Результаты оценки приведены в Таблице 8.
Таблица 8 - Статистика уравнения для модели с фиктивными переменными
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | -89444,083 | 2879,238 | -31,065 | 2,76051E-20 |
| t | 1132,083 | 79,218 | 14,291 | 6,2844E-13 |
| D2 | 24047,583 | 3803,309 | 6,323 | 1,8825E-06 |
| D3 | 17218,167 | 3805,783 | 4,524 | 0,000152385 |
| D4 | 21431,750 | 3809,903 | 5,625 | 1,00291E-05 |
| D5 | 15077,333 | 3815,664 | 3,951 | 0,000634609 |
| D6 | 26904,583 | 3823,058 | 7,037 | 3,59459E-07 |
| D7 | 40734,833 | 3832,075 | 10,630 | 2,38467E-10 |
| D8 | 43809,083 | 3842,705 | 11,401 | 6,10242E-11 |
| D9 | 38606,667 | 3854,934 | 10,015 | 7,43321E-10 |
| D10 | 32848,917 | 3868,747 | 8,491 | 1,52119E-08 |
| D11 | 26662,833 | 3884,126 | 6,865 | 5,33422E-07 |
| D12 | 24437,083 | 3901,054 | 6,264 | 2,16207E-06 |
Проанализируем эти результаты. Все коэффициенты уравнения и само уравнение статистически значимы при уровне надежности 95%.

Исходя из значений выше приведенных показателей качества, можно сделать вывод о том, что модель обладает высокой точностью и пригодна для прогнозирования.
2.6 Адаптивная сезонная модель Тейла – Вейджа
Рассмотрим аддитивную модель сезонных явлений с линейным ростом, предложенную Г. Тейлом и С. Вейджем. Параметры адаптации определим методом последовательных итераций, исходя из принципа минимизации средней ошибки аппроксимации модели. В результате получим следующие значения: α1 = 0,9; α2 = 0,1; α3 = 0,1.
Тренд – линейный, уравнение тренда выглядит следующим образом:
T = -67660,089 + 1358,979 ·t; R 2 = 0,579
Начальные условия для нулевого цикла представлены в таблице 9:
Таблица 9 -Начальные условия
| i | ĝi0 | i | ĝi0 |
| 1 | -24733,642 | 7 | 14639,816 |
| 2 | -912,954 | 8 | 17487,170 |
| 3 | -7969,267 | 9 | 12057,857 |
| 4 | -3982,580 | 10 | 6073,211 |
| 5 | -10563,892 | 11 | -339,768 |
| 6 | 1036,462 | 12 | -2792,414 |

Исходя из значений выше приведенных показателей качества, можно сделать вывод о том, что модель обладает высокой точностью и пригодна для прогнозирования.
2.7 Прогнозирование естественного прироста населения
Рассмотрим прогнозные значения естественного прироста населения в РФ по вышеописанным моделям, сравним полученные значения с фактическими, и выберем наиболее адекватную и точную модель для целей прогнозирования (Таблица 10).
Для оценки точности каждого прогноза рассчитаем среднюю относительную ошибку прогноза по формуле:

Таблица 10 - Прогнозные значения
| Адд. модель | Мультипл. модель | Ряд Фурье | Модель с фикт. переменными | Адапт. модель Тейла-Вейджа | Фактические значения | |
| Январь 2009 | -41595 | -29184 | -38887 | -47557 | -46805 | -47976 |
| Февраль 2009 | -19866 | -18134 | -31056 | -22377 | -22944 | -24401 |
| Март 2009 | -29093 | -21475 | -21699 | -28075 | -29994 | -32121 |
| Апрель 2009 | -24284 | -18459 | -23375 | -22729 | -26006 | -27017 |
| Май 2009 | -27749 | -19177 | -24958 | -27951 | -32588 | -28463 |
| Июнь 2009 | -15685 | -13678 | -13849 | -14992 | -20989 | -19821 |
| Июль 2009 | -304 | -8598 | -86 | -30 | -7384 | -4237 |
| Август 2009 | 3999 | -6886 | 2590 | 4177 | -4539 | 1050 |
| Сентябрь 2009 | 2212 | -6624 | -348 | 106 | -9968 | -3263 |
| Октябрь 2009 | -5701 | -7484 | -426 | -4519 | -15951 | -12170 |
| Ноябрь 2009 | -9688 | -7452 | -4684 | -9573 | -22368 | -25891 |
| Декабрь 2009 | -9265 | -6350 | -17547 | -10667 | -24818 | -25116 |
| Средняя относит. ошибка прогноза (%) | 66,260 | 111,627 | 56,422 | 62,296 | 74,758 | - |
Исходя из показателя средней относительной ошибки прогноза, можно сделать вывод о том, что показатель естественного прироста населения наиболее точно прогнозируется рядом Фурье.
В ходе работы было проведено моделирование и прогнозирование естественного прироста населения в РФ. Исследование было проведено с помощью следующих моделей:
· Аддитивная модель;
· Мультипликативная модель;
· Одномерный анализ Фурье;
· Регрессионная модель с переменной структурой (фиктивные переменные);
· Адаптивная сезонная модель.
Выдвинутая гипотеза о возрастающей тенденции динамики изменения естественного прироста населения в РФ в 2009 году подтверждается.
По каждой модели сделан прогноз на 2009 год, при этом следует отметить, что наиболее точный прогноз дает модель с использованием ряда Фурье, в тоже время вариацию исходного показателя наиболее точно описывает адаптивная модель Тейла – Вейджа. Также можно сделать вывод о том, что для получения наиболее достоверного прогноза показателя необходимо комбинировать прогнозные значения нескольких наиболее точных моделей.
1. StatSoft // http://www.statsoft.ru/
2. Агентство АКДИ // http://www.akdi.ru/
3. Концепция демографической политики Российской Федерации на период до 2015 года // http://www.akdi.ru/econom/program/demogr.htm
4. Концепция долгосрочного социально-экономического развития Российской Федерации на период до 2020 года // http://www.youngscience.ru/753/820/978/index.shtml
5. МеньшоваИ.В. Моделирование экономических процессов методами регрессионного анализа.- Воскресенск: Издательский дом «Лира», 2009. - 113 с.
6. Президент России молодым ученым и специалистам // http://www.youngscience.ru/
7. Федеральная служба государственной статистики // http://www.gks.ru/
8. Эконометрика: учебник / И.И. Елисеева, С.В. Курышев, Т.В. Костеева и др.; под ред. И.И. Елисеевой. – 2-е изд. - М.: Финансы и статистика, 2007. – 576 с.
Приложение 1

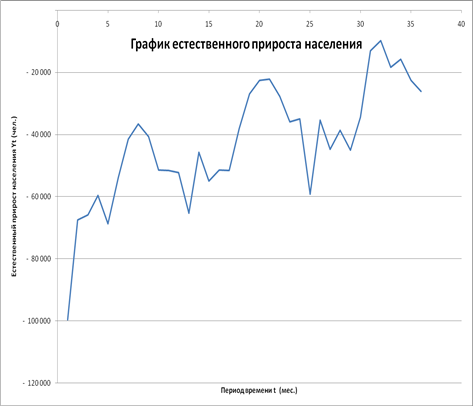
Приложение 2
![]()

Приложение 3
| Год | Месяц | t | Yt | Скользящее среднее | Центрир. скользящее среднее | К-т сезонности | Скорр.сезонная компонента S | Десезон-й естественный прирост | Тренд T | Ошибка E |
| 2006 | Январь | 1 | - 99 636 | -20480,000 | -79156,000 | -62766,038 | -16389,962 | |||
| Февраль | 2 | - 67 539 | 92,000 | -67631,000 | -61609,063 | -6021,937 | ||||
| Март | 3 | - 65 908 | -10291,958 | -55616,042 | -60452,088 | 4836,046 | ||||
| Апрель | 4 | - 59 589 | -6639,813 | -52949,188 | -59295,113 | 6345,925 | ||||
| Май | 5 | - 68 708 | -11262,333 | -57445,667 | -58138,137 | 692,471 | ||||
| Июнь | 6 | - 53 946 | -57460,083 | -355,333 | -53590,667 | -56981,162 | 3390,495 | |||
| Июль | 7 | - 41 476 | -54601,333 | -56030,708 | 14554,708 | 13869,083 | -55345,083 | -55824,187 | 479,104 | |
| Август | 8 | - 36 599 | -52786,417 | -53693,875 | 17094,875 | 17015,208 | -53614,208 | -54667,212 | 1053,003 | |
| Сентябрь | 9 | - 40 643 | -51877,583 | -52332,000 | 11689,000 | 14070,708 | -54713,708 | -53510,237 | -1203,472 | |
| Октябрь | 10 | - 51 480 | -51196,333 | -51536,958 | 56,958 | 5001,646 | -56481,646 | -52353,261 | -4128,384 | |
| Ноябрь | 11 | - 51 660 | -49769,000 | -50482,667 | -1177,333 | -142,500 | -51517,500 | -51196,286 | -321,214 | |
| Декабрь | 12 | - 52 337 | -48446,500 | -49107,750 | -3229,250 | -876,708 | -51460,292 | -50039,311 | -1420,981 | |
| 2007 | Январь | 13 | - 65 331 | -47241,083 | -47843,792 | -17487,208 | -20480,000 | -44851,000 | -48882,336 | 4031,336 |
| Февраль | 14 | - 45 760 | -46072,000 | -46656,542 | 896,542 | 92,000 | -45852,000 | -47725,361 | 1873,361 | |
| Март | 15 | - 55 002 | -44534,667 | -45303,333 | -9698,667 | -10291,958 | -44710,042 | -46568,385 | 1858,344 | |
| Апрель | 16 | - 51 414 | -42556,917 | -43545,792 | -7868,208 | -6639,813 | -44774,188 | -45411,410 | 637,223 | |
| Май | 17 | - 51 580 | -41251,917 | -41904,417 | -9675,583 | -11262,333 | -40317,667 | -44254,435 | 3936,768 | |
| Июнь | 18 | - 38 076 | -39806,750 | -40529,333 | 2453,333 | -355,333 | -37720,667 | -43097,460 | 5376,793 | |
| Июль | 19 | - 27 011 | -39297,000 | -39551,875 | 12540,875 | 13869,083 | -40880,083 | -41940,485 | 1060,401 | |
| Август | 20 | - 22 570 | -38428,917 | -38862,958 | 16292,958 | 17015,208 | -39585,208 | -40783,509 | 1198,301 | |
| Сентябрь | 21 | - 22 195 | -37580,750 | -38004,833 | 15809,833 | 14070,708 | -36265,708 | -39626,534 | 3360,826 | |
| Октябрь | 22 | - 27 747 | -36520,750 | -37050,750 | 9303,750 | 5001,646 | -32748,646 | -38469,559 | 5720,913 | |
| Ноябрь | 23 | - 36 000 | -35978,750 | -36249,750 | 249,750 | -142,500 | -35857,500 | -37312,584 | 1455,084 | |
| Декабрь | 24 | - 34 995 | -35677,750 | -35828,250 | 833,250 | -876,708 | -34118,292 | -36155,609 | 2037,317 | |
| 2008 | Январь | 25 | - 59 214 | -34519,500 | -35098,625 | -24115,375 | -20480,000 | -38734,000 | -34998,633 | -3735,367 |
| Февраль | 26 | - 35 343 | -33456,250 | -33987,875 | -1355,125 | 92,000 | -35435,000 | -33841,658 | -1593,342 | |
| Март | 27 | - 44 824 | -33136,083 | -33296,167 | -11527,833 | -10291,958 | -34532,042 | -32684,683 | -1847,359 | |
| Апрель | 28 | - 38 694 | -32143,917 | -32640,000 | -6054,000 | -6639,813 | -32054,188 | -31527,708 | -526,480 | |
| Май | 29 | - 45 076 | -31024,750 | -31584,333 | -13491,667 | -11262,333 | -33813,667 | -30370,733 | -3442,934 | |
| Июнь | 30 | - 34 464 | -30290,083 | -30657,417 | -3806,583 | -355,333 | -34108,667 | -29213,758 | -4894,909 | |
| Июль | 31 | - 13 112 | 13869,083 | -26981,083 | -28056,782 | 1075,699 | ||||
| Август | 32 | - 9 811 | 17015,208 | -26826,208 | -26899,807 | 73,599 | ||||
| Сентябрь | 33 | - 18 353 | 14070,708 | -32423,708 | -25742,832 | -6680,876 | ||||
| Октябрь | 34 | - 15 841 | 5001,646 | -20842,646 | -24585,857 | 3743,211 | ||||
| Ноябрь | 35 | - 22 570 | -142,500 | -22427,500 | -23428,882 | 1001,382 | ||||
| Декабрь | 36 | - 26 179 | -876,708 | -25302,292 | -22271,906 | -3030,385 |
Приложение 4
| Год | Месяц | t | Yt | Скользящее среднее | Центрир. скользящее среднее | К-т сезонности | Скорр.сезонная компонента S | Десезон-й естественный прирост | Тренд T | Ошибка E |
| 2006 | Январь | 1 | - 99 636 | 1,491 | -66841,949 | -62817,008 | 1,064 | |||
| Февраль | 2 | - 67 539 | 0,987 | -68448,267 | -61615,944 | 1,111 | ||||
| Март | 3 | - 65 908 | 1,250 | -52716,508 | -60414,880 | 0,873 | ||||
| Апрель | 4 | - 59 589 | 1,155 | -51572,821 | -59213,816 | 0,871 | ||||
| Май | 5 | - 68 708 | 1,298 | -52934,959 | -58012,753 | 0,912 | ||||
| Июнь | 6 | - 53 946 | -57460,083 | 1,008 | -53533,646 | -56811,689 | 0,942 | |||
| Июль | 7 | - 41 476 | -54601,333 | -56030,708 | 0,740 | 0,695 | -59681,851 | -55610,625 | 1,073 | |
| Август | 8 | - 36 599 | -52786,417 | -53693,875 | 0,682 | 0,616 | -59371,555 | -54409,561 | 1,091 | |
| Сентябрь | 9 | - 40 643 | -51877,583 | -52332,000 | 0,777 | 0,664 | -61170,468 | -53208,498 | 1,150 | |
| Октябрь | 10 | - 51 480 | -51196,333 | -51536,958 | 0,999 | 0,853 | -60318,449 | -52007,434 | 1,160 | |
| Ноябрь | 11 | - 51 660 | -49769,000 | -50482,667 | 1,023 | 0,985 | -52465,144 | -50806,370 | 1,033 | |
| Декабрь | 12 | - 52 337 | -48446,500 | -49107,750 | 1,066 | 0,997 | -52474,271 | -49605,306 | 1,058 | |
| 2007 | Январь | 13 | - 65 331 | -47241,083 | -47843,792 | 1,366 | 1,491 | -43828,048 | -48404,242 | 0,905 |
| Февраль | 14 | - 45 760 | -46072,000 | -46656,542 | 0,981 | 0,987 | -46376,060 | -47203,179 | 0,982 | |
| Март | 15 | - 55 002 | -44534,667 | -45303,333 | 1,214 | 1,250 | -43993,344 | -46002,115 | 0,956 | |
| Апрель | 16 | - 51 414 | -42556,917 | -43545,792 | 1,181 | 1,155 | -44497,558 | -44801,051 | 0,993 | |
| Май | 17 | - 51 580 | -41251,917 | -41904,417 | 1,231 | 1,298 | -39738,970 | -43599,987 | 0,911 | |
| Июнь | 18 | - 38 076 | -39806,750 | -40529,333 | 0,939 | 1,008 | -37784,954 | -42398,924 | 0,891 | |
| Июль | 19 | - 27 011 | -39297,000 | -39551,875 | 0,683 | 0,695 | -38867,453 | -41197,860 | 0,943 | |
| Август | 20 | - 22 570 | -38428,917 | -38862,958 | 0,581 | 0,616 | -36613,459 | -39996,796 | 0,915 | |
| Сентябрь | 21 | - 22 195 | -37580,750 | -38004,833 | 0,584 | 0,664 | -33404,979 | -38795,732 | 0,861 | |
| Октябрь | 22 | - 27 747 | -36520,750 | -37050,750 | 0,749 | 0,853 | -32510,800 | -37594,669 | 0,865 | |
| Ноябрь | 23 | - 36 000 | -35978,750 | -36249,750 | 0,993 | 0,985 | -36561,076 | -36393,605 | 1,005 | |
| Декабрь | 24 | - 34 995 | -35677,750 | -35828,250 | 0,977 | 0,997 | -35086,786 | -35192,541 | 0,997 | |
| 2008 | Январь | 25 | - 59 214 | -34519,500 | -35098,625 | 1,687 | 1,491 | -39724,389 | -33991,477 | 1,169 |
| Февраль | 26 | - 35 343 | -33456,250 | -33987,875 | 1,040 | 0,987 | -35818,817 | -32790,414 | 1,092 | |
| Март | 27 | - 44 824 | -33136,083 | -33296,167 | 1,346 | 1,250 | -35852,472 | -31589,350 | 1,135 | |
| Апрель | 28 | - 38 694 | -32143,917 | -32640,000 | 1,185 | 1,155 | -33488,710 | -30388,286 | 1,102 | |
| Май | 29 | - 45 076 | -31024,750 | -31584,333 | 1,427 | 1,298 | -34728,070 | -29187,222 | 1,190 | |
| Июнь | 30 | - 34 464 | -30290,083 | -30657,417 | 1,124 | 1,008 | -34200,563 | -27986,159 | 1,222 | |
| Июль | 31 | - 13 112 | 0,695 | -18867,500 | -26785,095 | 0,704 | ||||
| Август | 32 | - 9 811 | 0,616 | -15915,580 | -25584,031 | 0,622 | ||||
| Сентябрь | 33 | - 18 353 | 0,664 | -27622,508 | -24382,967 | 1,133 | ||||
| Октябрь | 34 | - 15 841 | 0,853 | -18560,694 | -23181,903 | 0,801 | ||||
| Ноябрь | 35 | - 22 570 | 0,985 | -22921,763 | -21980,840 | 1,043 | ||||
| Декабрь | 36 | - 26 179 | 0,997 | -26247,663 | -20779,776 | 1,263 |