В курсовом проекте представлена концепция моделирования различных процессов в универсальной системе моделирования на примере конкретно поставленной задачи.

В пояснительной записке содеожится обоснование выбора программного средства, цели выполнения моделирования, постановка с заданными параметрами, а также приведены непосредственно модель и результат ее работы.

Введение

В век компьютерных технологий и всё более глубокого внедрения автоматизированных систем управления на предприятиях особенно востребованным является умение решать задачи, таких как та, которая была дана на курсовое проектирование:

Умение решать задачи по автоматизации технологических процессов подразумевает умение вести научно – исследовательскую и проектно – конструкторскую работу в области исследования и разработки сложных систем; способность ставить и проводить имитационные эксперименты с моделями процессов функционирования систем на современных ЭВМ для оценки вероятностно – временных характеристик систем; принятие экономически и технически обоснованных инженерных решений; анализ научно – технической литературы в области системного моделирования, а также использование стандартов, справочников, технической документации по математическому и программному обеспечению ЭВМ и т.д.

Система GPSS (GeneralPurposeSystemSimulator) предназначена для написания имитационных моделей систем с дискретными событиями. Наиболее удобно в системе GPSS описываются модели систем массового обслуживания, для которых характерны относительно простые правила функционирования составляющих их элементов.

В системе GPSS моделируемая система представляется с помощью набора абстрактных элементов, называемых объектами. Каждый объект принадлежит к одному из типов объектов.

Объект каждого типа характеризуется определенным способом поведения и набором атрибутов, определяемых типом объекта. Например, если рассмотреть работу порта, выполняющего погрузку и разгрузку прибывающих судов, и работу кассира в кинотеатре, выдающего билеты посетителям, то можно заметить большое сходство в их функционировании. В обоих случаях имеются объекты, постоянно присутствующие в системе (порт и кассир), которые обрабатывают поступающие в систему объекты (корабли и посетители кинотеатра). В теории массового обслуживания эти объекты называются приборами и заявками. Когда обработка поступившего объекта заканчивается, он покидает систему. Если в момент поступления заявки прибор обслуживания занят, то заявка становится в очередь, где и ждет до тех пор, пока прибор не освободится. Очередь также можно представлять себе как объект, функционирование которого состоит в хранении других объектов. Каждый объект может характеризоваться рядом атрибутов, отражающих его свойства. Например, прибор обслуживания имеет некоторую производительность, выражаемую числом заявок, обрабатываемых им в единицу времени. Сама заявка может иметь атрибуты, учитывающие время ее пребывания в системе, время ожидания в очереди и т.д. Характерным атрибутом очереди является ее текущая длина, наблюдая за которой в ходе работы системы (или ее имитационной модели), можно определить ее среднюю длину за время работы (или моделирования). В языке GPSS определены классы объектов, с помощью которых можно задавать приборы обслуживания, потоки заявок, очереди и т.д., а также задавать для них конкретные значения атрибутов.

Раздел 1. Постановка задачи

Задача: на регулировочный участок цеха через случайные интервалы времени поступают по два агрегата в среднем через каждые 45 мин. Первичная регулировка осуществляется для двух агрегатов одновременно и занимает около 40 мин. Если в момент прихода агрегатов предыдущая партия не была обработана, поступившие агрегаты на регулировку не принимаются. Агрегаты после первичной регулировки, получившие отказ, поступают в промежуточный накопитель. Из накопителя агрегаты, прошедшие первичную регулировку, поступают попарно на вторичную регулировку, которая выполняется в среднем за 50 мин, а не прошедшие первичную регулировку поступают на полную, которая занимает 120 мин для одного агрегата. Все величины, заданные средними значениями, распределены экспоненциально.

Смоделировать работу участка в течение 240 ч. Определить вероятность отказа в первичной регулировке и загрузку накопителя агрегатами, нуждающимися в полной регулировке. Определить параметры и ввести в систему накопитель, обеспечивающий безотказное обслуживание поступающих агрегатов.

Необходимо исследовать работу регулировочного участка, состоящего из первичной, вторичной и полной регулировок, а также агрегатов поступающих на регулировку. В качестве цели моделирования выберем изучение функционирования системы, а именно оценивание ее характеристик с точки зрения эффективности работы системы, т.е. будет ли обеспечено безотказное обслуживание поступающих агрегатов.

С учетом имеющихся ресурсов в качестве метода решения задачи выберем метод имитационного моделирования, позволяющий не только анализировать характеристики модели, но и проводить структурный, алгоритмический и параметрический синтез модели на ЭВМ при заданных критериях оценки эффективности и ограничениях.

Постановка задачи исследования функционирования регулировочного участка, состоящего из первичной, вторичной и полной регулировок, а также агрегатов поступающих на регулировку, представлена в задании к курсовому проектированию, из которого следует, что необходимо определить:

· вероятность отказа в первичной регулировке;

· загрузку накопителя агрегатами, нуждающимися в полной регулировке.

Раздел 2. Выбор методов решения задачи

В качестве критерия оценки эффективности процесса функционирования системы целесообразно выбрать вероятность отказа в первичной обработке вследствие переполнения очереди, которая должна быть минимальной, при этом загрузка УПД и каждой ЭВМ должна быть максимальной.

Экзогенные (независимые) переменные модели:

· время первичной обработки;

· время вторичной обработки;

· время полной обработки;

· количество обрабатываемых агрегатов на каждой регулировке;

Эндогенные (зависимые) переменные модели:

· вероятность отказа в первичной регулировке;

· загрузка накопителя агрегатами, нуждающимися в полной регулировке;

При построении математической имитационной модели процессов функционирования системы будем использовать непрерывно-стохастический подход на примере типовой Q -схемы, потому что исследуемая система может быть представлена как система массового обслуживания с непрерывным временем обработки параметров.

Формализовав процесс функционирования исследуемой системы в абстракциях Q -схемы, на втором этапе алгоритмизации модели и ее машинной реализации выберем язык имитационного моделирования, потому что высокий уровень проблемной ориентации языка значительно упростит программирование, а специально предусмотренные в нем возможности сбора, обработки и вывода результатов моделирования позволят быстро и подробно проанализировать возможные исходы имитационного эксперимента с моделью. Для получения полной информации о характеристиках процесса функционирования системы необходимо будет провести полный факторный эксперимент, который позволит определить, насколько эффективно функционирует система, и выдать рекомендации по ее усовершенствованию.

Выдвижение гипотез и принятие предположений

Для заполнения пробелов в понимании задачи исследования, а также проверки возможных результатов моделирования при проведении машинного эксперимента выдвигаем следующие гипотезы :

· количество первичных и вторичных обработок будет одинаково, так как они выполняются последовательно;

· количество поступающих агрегатов на полную регулировку будет меньше, чем на первичной регулировке, так как время затрачиваемое на обработку агрегатов на полной регулировке равно 120 минут, тогда как на первичной регулировке затрачивается 40 минут, а также на первичную регулировку агрегаты поступают попарно, а на полную по одному.

Алгоритмизация модели системы и ее машинная реализация

Построение логической схемы модели

Процесс начинает свою работу с выполнения проверки (блок1) на наличие свободных мест на первой регулировке. Если места есть, то агрегаты направляются на первичную регулировку (блок2), после чего происходит постановка агрегатов в очередь в накопитель 2 (блок 3). Если же мест на первичной регулировке не оказалось, то агрегаты становятся в очередь в накопитель 1 (блок 4). Из накопителя 1 агрегаты поступают на полную регулировку (блок 5), после чего покидают систему. Из накопителя 2 агрегаты поступают на вторичную регулировку (блок 6), после которой также покидают систему.

Получение математических соотношений

Для построения машинной модели системы в комбинированном виде, т.е. с использованием аналитико-имитационного подхода, необходимо часть процессов в системе описать аналитически, а другую часть сымитировать соответствующими алгоритмами. На данном этапе построения аналитической модели зададим математические соотношения в виде явных функций.

Загрузку технических средств системы и число циклов выполнения остальных заданий в виде явных функций записать трудно. Эти величины определим с помощью языка имитационного моделирования.

Проверка достоверности модели системы

На данном подэтапе достоверность модели системы проверяется по следующим показателям:

а) возможности решения поставленной задачи:

Решение данной задачи с помощью математических отношений нецелесообразно, так как искомые данные не имеют явных функций. Использование имитационного моделирования решает эти сложности, но для правильной реализации нужно точно и безошибочно определить параметры и переменные модели, обосновать критерии оценки эффективности системы, составить концептуальную модель и построить логическую схему. Все эти шаги построить модель данного процесса;

б) точности отражения замысла в логической схеме:

При составлении логической схемы, важно понимать смысл задачи, до этого построить концептуальную модель. Проверку точности можно выполнить при подробном описании самой схемы, при этом, сопоставлять с описанием концептуальной модели;

в) полноте логической схемы модели:

Проверить наличие всех выше описанных переменных, параметров, зависимостей, последовательности действий;

Раздел 3. Формализация и алгоритмизация модели

Построение концептуальной модели в виде Q -схемы

В качестве типовой математической схемы применяется Q -схема, состоящая из одного источника (И), накопителя (Н), четырех каналов (К₁ , К₂ , К₃ , К₄ ), двух клапанов (рис. 2). После генерации заданий в источнике И, следует их запуск при помощи дисплея, канал К1, работая на нем 55±35 сек. После запуска задание поступают в накопитель Н, а затем в клапан 1, который управляется каналом К2. Если в канале К2 выполняется задание с более высоким приоритетом, то задание поступает в накопитель Н. Если канал К2 свободен, или обрабатывается задание с более низким приоритетом, то начинается обработка поступившего задания в течении 130±40 сек. После обработки задание поступает в канал К3, где выводится на печать в течении 35±13 сек. Затем задание поступает в канал К4, где производится анализ задания в течение 65±23 сек. Клапан 2 принимает задания от канала К4, управляется соответствующим каналом, при этом выполнение задания либо заканчивается N_ВЫП1,2,3 , либо отправляется в накопитель Н для повторной обработки.

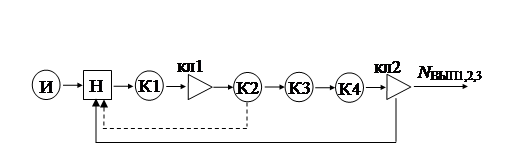
Рис. 2. Концептуальная модель в виде Q -схемы

Формальная модель системы:

Q = { И, Н, К₁ , К₂ , К₃ , К₄ , N _ВЫП1,2,3 , кл₁ , кл₂ }.

Согласно разработанной концептуальной модели окончательные гипотезы и предположения совпадают с ранее принятыми. Выбранная процедура аппроксимации определения средних значений выходных переменных соответствует реальным случайным процессам, протекающим в системе массового обслуживания.

Раздел 4. Описание программы и инструкции по моделированию

Проведение программирования модели

EMKEQU 2;	кол-во мест в очереди
Prov1 BVARIABLE (F$Rem1);	проверка1 на занятость первичной обработки
Prov2 BVARIABLE (F$Rem2);	проверка2 на занятость вторичной обработки
Prov3 BVARIABLE (F$Rem3);	проверка3 на занятость полной обработки
generate 45,2	генерация поступающих агрегатов
TEST E BV$Prov1,0,met1;	обращение к проверке1
QUEUE RemQ1;	встать в очередь на первую регулировку
SEIZE Rem1;	занять рабочее место
DEPART RemQ1;	покинуть очередь
ADVANCE 40,2;	обработка
RELEASE Rem1;	освобождение первичной регулировки
LINK Otst2,FIFO;	отправить в накопитель2
GENERATE ,,,1	генерация поступающих агрегатов
met4	TEST E BV$Prov2,0;	обращение к проверке2
UNLINK Otst2,met3,1;	вывести из накопителя2
ADVANCE 0.001
TRANSFER ,met4
met3	SEIZE Rem2;	занять рабочее место
ADVANCE 50,2;	вторичная регулировка
RELEASE Rem2;	освобождение вторичной регулировки
TERMINATE
GENERATE ,,,1	генерация поступающих агрегатов
met2	TEST E BV$Prov3,0;	обращение к проверке3
UNLINK Otst,met5,1;	вывести из накопителя1
ADVANCE 0.001
TRANSFER ,met2
met5	SEIZE Rem3;	занять рабочее место
ADVANCE 120,2;	полная регулировка
RELEASE Rem3;	освобождение полной регулировки
TERMINATE
met1	SPLIT 1, met6	удваивание количества транзактов
met6	LINK Otst,FIFO;	отправить в накопитель1
generate 14400	генерация работы участка для 240 часов работы
terminate 1	Уничтожение выполненных заданий

Раздел 5. Анализ результатов моделирования

Основные обозначения:

START TIME – время начала моделирования;

END TIME - время окончания моделирования;

BLOCKS - количество блоков, используемых в программе;

FACILITIES – количество одноканальных устройств;

STORAGES – количество многоканальных устройств.

Далее приводится информация о блоках:

LOC – номер блока, назначенный системой;

BLOCK TYPE – название блока;

ENTRY COUNT – количество транзактов, прошедших через блок за время моделирования;

СURRENT COUNT – количество транзактов, задержанных в блоке на момент конца моделирования;

RETRY – количество транзактов, ожидающих специальных условий для прохождения через данный блок;

Отчет о работе устройства:

FACILITY – название устройства;

ENTRIES – количество транзактов, прошедших через устройство;

UTIL . – вероятность загрузки устройства;

AVE . TIME – среднее время обработки одного транзакта устройством;

AVAIL . – состояние готовности устройства на момент конца моделирования (1 –готово к обслуживанию очередной заявки; 0 – не готово);

OWNER – номер последнего транзакта занимающего устройство (если не занималось, то значение 0);

PEND – количество транзактов, ожидающих устройство, и находящихся в режиме прерывания;

INTER – количество транзактов, прерывающих устройство в данный момент;

RETRY – количество транзактов, ожидающих специальных условий, зависящих от состояния объекта типа «устройство»;

DELAY – определяет количество транзактов, ожидающих занятия или освобождения устройства.

Статистика об очередях:

QUEUE – имя очереди;

MAX - максимальная длина очереди;

CONT . – текущая длина очереди;

ENTRY – общее количество входов;

ENTRY (0) - количество «нулевых» входов;

AVE . CONT . – средняя длина очереди;

AVE . TIME – среднее время пребывания транзактов в очереди;

AVE .(-0) – среднее время пребывания в очереди без учета «нулевых» входов;

RETRY – количество транзактов, ожидающих специальных условий.

Информация о списке текущих событий CEC ( Current Events Chain ):

XN – номер транзакта;

PRI – приоритет транзакта (по умолчанию - 0);

M 1 – время пребывания транзакта в системе с момента начал моделирования;

ASSEM - номер семейства транзактов;

CURRENT – номер блока в котором находится транзакт;

NEXT – номер блока в который перейдет транзакт далее;

PARAMETER – номер или имя параметра транзакта;

VALUE – значение параметра.

Информация о списке будущих событий FEC ( Future Events Chain ):

XN – номер транзакта;

PRI – приоритет транзакта;

BDT - таблица модельных событий – абсолютное модельное время выхода транзакта из списка будущих событий и перехода транзакта в список текущих событий;

ASSEM - номер семейства транзактов;

CURRENT - номер блока в котором находится транзакт (0 – если транзакт не вошел в модель);

NEXT - номер блока в который перейдет транзакт далее;

PARAMETER – номер или имя параметра транзакта;

VALUE – значение параметра.

Результаты моделирования Исходный вариант (Первичная регулировка – 40 мин, вторичная – 50 мин, полная-120)

При использовании программы со стандартными значениями получаем следующее:

GPSS World Simulation Report - Kyrs.13.1

Monday, December 27, 2010 22:01:20

START TIME END TIME BLOCKS FACILITIES STORAGES

0.000 14400.000 30 3 0

NAME VALUE

EMK 2.000

MET1 27.000

MET2 19.000

MET3 14.000

MET4 10.000

MET5 23.000

MET6 28.000

OTST 10013.000

OTST2 10009.000

PROV1 10001.000

PROV2 10003.000

PROV3 10005.000

REM1 10002.000

REM2 10004.000

REM3 10006.000

REMQ1 10008.000

LABEL LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY

1 GENERATE 369 0 0

2 TEST 369 0 0

3 QUEUE 210 0 0

4 SEIZE 210 0 0

5 DEPART 210 0 0

6 ADVANCE 210 1 0

7 RELEASE 209 0 0

8 LINK 209 0 0

9 GENERATE 1 0 0

MET4 10 TEST 3978022 0 0

11 UNLINK 3978022 0 0

12 ADVANCE 3978022 0 0

13 TRANSFER 3978022 1 0

MET3 14 SEIZE 209 0 0

15 ADVANCE 209 1 0

16 RELEASE 208 0 0

17 TERMINATE 208 0 0

18 GENERATE 1 0 0

MET2 19 TEST 118312 0 0

20 UNLINK 118312 0 0

21 ADVANCE 118312 0 0

22 TRANSFER 118312 1 0

MET5 23 SEIZE 120 0 0

24 ADVANCE 120 1 0

25 RELEASE 119 0 0

26 TERMINATE 119 0 0

MET1 27 SPLIT 159 0 0

MET6 28 LINK 318 198 0

29 GENERATE 1 0 0

30 TERMINATE 1 0 0

FACILITY ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY

REM1 210 0.583 39.995 1 531 0 0 0 0

REM2 209 0.724 49.867 1 529 0 0 1 0

REM3 120 0.992 119.015 1 206 0 0 1 0

QUEUE MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY

REMQ1 1 0 210 210 0.000 0.000 0.000 0

USER CHAIN SIZE RETRY AVE.CONT ENTRIES MAX AVE.TIME

OTST2 0 0 0.046 209 2 3.186

OTST 198 0 98.781 318 199 4473.123

FEC XN PRI BDT ASSEM CURRENT NEXT PARAMETER VALUE

531 0 14409.239 531 6 7

532 0 14409.933 532 0 1

529 0 14419.678 529 15 16

206 0 14494.321 204 24 25

MET6 2.000

533 0 28800.000 533 0 29

Эти данные говорят, что первичную обработку, за 240 часов работы, прошло 210 агрегатов, вероятность загрузки 58%, при этом среднее время обработки составляет 39.995 мин и отсутствие агрегатов, ожидающих своей очереди. На вторичную регулировку прошло 209 агрегатов, вероятность загрузки составляет 72%, среднее время 49.867 и 1 агрегат, ожидающий своей очереди. На полную регулировку попало 120 агрегатов, вероятность загрузки 99%, среднее время 119.015 мин и 1 агрегат, ожидающий своей очереди.

Результаты моделирования Тест №1 Первичная регулировка – 45 мин, вторичная – 60 мин, полная-100)

FACILITY ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY

REM1 184 0.574 44.940 1 0 0 0 0 0

REM2 184 0.764 59.824 1 552 0 0 1 0

REM3 144 0.994 99.440 1 220 0 0 1 0

QUEUE MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY

REMQ1 1 0 184 184 0.000 0.000 0.000 0

Эти данные говорят, что первичную обработку, за 240 часов работы, прошло 184 агрегатов, вероятность загрузки 57%, при этом среднее время обработки составляет 44 мин и отсутствие агрегатов, ожидающих своей очереди. На вторичную регулировку прошло 184 агрегатов, вероятность загрузки составляет 76%, среднее время 59.824и 1 агрегат, ожидающий своей очереди. На полную регулировку попало 144 агрегатов, вероятность загрузки 99%, среднее время 99.440 мин и 1 агрегат, ожидающий своей очереди.

Результаты моделирования Тест №2 Первичная регулировка – 40 мин, вторичная – 60 мин, полная-120)

FACILITY ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY

REM1 214 0.592 39.849 1 526 0 0 0 0

REM2 213 0.885 59.802 1 524 0 0 1 0

REM3 119 0.992 120.015 1 204 0 0 1 0

QUEUE MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY

REMQ1 1 0 214 214 0.000 0.000 0.000 0

Эти данные говорят, что первичную обработку, за 240 часов работы, прошло 214 агрегатов, вероятность загрузки 59%, при этом среднее время обработки составляет 39,849 мин и отсутствие агрегатов, ожидающих своей очереди. На вторичную регулировку прошло 213 агрегатов, вероятность загрузки составляет 88%, среднее время 59.802 и 1 агрегат, ожидающий своей очереди. На полную регулировку попало 119 агрегатов, вероятность загрузки 99%, среднее время 120 мин и 1 агрегат, ожидающий своей очереди.

Результаты моделирования Тест №3 Первичная регулировка – 40 мин, вторичная – 40 мин, полная-90)

FACILITY ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY

REM1 215 0.596 39.949 1 525 0 0 0 0

REM2 214 0.594 39.999 1 0 0 0 0 0

REM3 159 0.991 89.708 1 277 0 0 1 0

QUEUE MAX CONT. ENTRY ENTRY(0) AVE.CONT.AVE.TIME AVE.(-0) RETRY

REMQ1 1 0 215 215 0.000 0.000 0.0000

Эти данные говорят, что первичную обработку, за 240 часов работы, прошло 215 агрегатов, вероятность загрузки 59%, при этом среднее время обработки составляет 39,949 мин и отсутствие агрегатов, ожидающих своей очереди. На вторичную регулировку прошло 214 агрегатов, вероятность загрузки составляет 59%, среднее время 39,999 и нет агрегатов, ожидающих своей очереди. На полную регулировку попало 159 агрегатов, вероятность загрузки 99%, среднее время 90 мин и 1 агрегат, ожидающий своей очереди.

Заключение

Самым выгодным из предложенных вариантов является тест №2, потому, что регулировку прошло наибольшее количество агрегатов и при этом регулировочные станки вырабатывают наибольшую мощность.

Самым экономически нецелесообразным является тест №1, так как регулировку прошло наименьшее количество агрегатов, но несмотря на это, они выдают, достаточно, высокую мощность.

Список литературы

1. Емельянов А.А., Власов Е.А., Дума Р.В. Имитационное моделирование экономических процессов: Учеб. пособие. Под ред. А.А.Емельянова. – М.: Финансы и статистика, 2004. –368 с.: ил.

2. Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры. 2 изд., испр. – М.: Физматлит, 2001. –320.

3. Антонов А.В. Системный анализ. чебник для вузов. – М.: Высш. шк, 2004. - 454 с.: ил. (главы 4,11 ).

4. Цисарь И.Ф., Нейман В.Г. Компьютерное моделирование экономики. – М.: «Диалог-МИФИ»,2002.- 304 с.

5. Кудрявцев Е.М., Добровольский А.В. Основы работы с универсальной системой моделирования GPSSWorld / Учебное пособие. – Издательство Ассоциации строительных вузов, 2005. – 256 с.