| Скачать .docx |
Курсовая работа: Процесс создания математической модели объекта
Содержание
1. Введение
2. Задание на курсовую работу
1.Обработка исходных данных методом площадей
2.Частотные характеристики
3.По заданному закону регулирования найти математическую модель ЗСАУ
4.Определение устойчивости ЗСАУ
5.Нахождение переходной характеристики ЗСАУ и основных ПКР
6.Функциональная схема
7.Вывод
3. Заключение
4. Список литературы
5. Приложение
Введение
Управление состоянием сложных систем всегда связано с необходимостью получения информации об этом состоянии и его целенаправленных и хаотических изменениях.
В данной работе было предложено смоделировать простую систему регулирования давления. Данные системы используются во многих отраслях промышленности, поэтому исследования их классических моделей являются довольно оправданными. Также, зачастую, проектировщики сталкиваются с тем, что в системе уже внедрены некоторые функции контроля, но их адекватность и качество работы не всегда легко определить. Поэтому было предложено определить объекты регулирования в системах по имеющимся выходным характеристикам, используя метод площадей для определения их передаточных функций, а также внедрение новых регуляторов, с заданными коэффициентами, с проверкой системы на устойчивость.
Подобные исследования в настоящее время проводятся часто, в связи с тем, что утрачивается та или иная документация по системам, и проектировщикам для модернизации необходимо знать, с чем они имеют дело изначально.
Задание на курсовую работу.
1. По экспериментальным данным найти математическую модель объекта (системы) методом площадей в виде звена 2-го или 3-го порядка. Оценить точность аппроксимации.
2. Найти и построить частотные характеристики объекта (АЧХ, ФЧХ, АФЧХ) и провести подробный анализ этих характеристик.
3. По заданному закону регулирования найти математическую модель ЗСАУ.
4. Определить устойчивость ЗСАУ по одному из критериев. Если система неустойчива, то добиться ее устойчивости.
5. Найти переходную функцию ЗСАУ и построить ее. Найти по кривой основные ПКР.
6. Привести структурную схему САУ в соответствии с требованиями ГОСТ.
7. Дать выводы по работе.
| t | 0 | 0.25 | 0.3 | 0.35 | 0,5 | 0,75 | 1 | 1.25 | 1,5 | 1.75 | 2 | 2.25 | 2,5 |
| s | 0 | 0.05 | 0.07 | 0.09 | 0.11 | 0.13 | 0.16 | 0.19 | 0.21 | 0.25 | 0.29 | 0.35 | 0.4 |
| t | 2.7 | 3 | 3,2 | 4,25 | 4.5 | 4.75 | 5 | 5,25 | 5.5 | 5.75 | 6 |
| s | 0.45 | 0.5 | 0.55 | 0.6 | 0.7 | 0.75 | 0.8 | 0.85 | 0.9 | 0.95 | 1 |
Регулятор ПИД: Кп = 1; Ки = 0,5; Тд = 15сек; К=2
Объект регулирования АПЗ-2
1. Обработка исходных данных Методом площадей.
Данный метод был разработан М.П. Симою. Метод служит для определения передаточной функции объекта по экспериментальной кривой разгона.
В основе метода лежит предположение, что исследуемый объект может быть описан линейным дифференциальным уравнением с постоянными коэффициентами:
![]() (2)
(2)
W(p) = S bi pi / S aj pj [-], b0 = 0, a0 = 1
Задача состоит в том, чтобы определить неизвестные коэффициенты
а1 ¸ а n и b 1 ¸ bm .
![]() Коэффициенты ai
будут определяться по следующим формулам:
Коэффициенты ai
будут определяться по следующим формулам:
а1 = F 1 + b 1
а2 = F 2 + b 2 + F 1 b 1
а3 = F 3 + b 3 + b 2 F 1 + b 1 F 2
…………….
а i = Fi + bi + S bj Fi - j
В системе уравнений, приведенной выше i = m + n. Составляющие элементы системы определяются из следующих формул:
F 1 = D t { S (1- s ) – 0.5}
F 2 = F 1 2 D Q { S [1 - s ]*[1 - Q ] – 0.5}
F 3 = F 1 3 D Q { S [1 - s ]*[1 – 2* Q + Q 2 /2] – 0.5}
и т.д.
Для нахождения передаточной функции данного объекта по его кривой переходного процесса, воспользуемся методом площадей (Симою).
По исходной кривой значения Yi для каждого значения времени заносим в таблицу Exсel и находим значения, необходимые для вычисления значений Fi.
Исходя из полученных данных, имеем:
F1 = 3,2875, F2 = 5,31953, F3 = 7,30796. F4 = -7,61321
По полученным значениям видно, что разница между F3 и F4 существенная, при этом F4 является числом отрицательным, что дает нам основание говорить о том, что значение коэффициента а4 = 0.
Исходя из приведенных выше формул нахождения а i , получаем коэффициенты b 1 , a 1 , a 2 , а3 :
b 1 = 1,042; a 1 = 4,32927; a 2 = 8,74435, а3 = 12,8497 .
Передаточная функция имеет вид:
W(p) = (1,042 + 1)/(12,8497р3 + 8,74435р2 + 4,32927р + 1).
Построим данную передаточную функцию в пакете VisSim, получим характеристику и найдем все ошибки (среднеквадратическое отклонение, абсолютную и относительную (приведенную) ошибки). График полученной характеристики приведен в приложении.
| № | t | Уэ | Ур | hi = Уэ – Ур | Dhi 2 |
| 1 | 0,25 | 0,05 | 0,06 | 0,01 | 0,0001 |
| 2 | 0,5 | 0,11 | 0,13 | 0,02 | 0,0004 |
| 3 | 1 | 0,16 | 0,18 | 0,02 | 0,0004 |
| 4 | 1,5 | 0,21 | 0,24 | 0,03 | 0,0009 |
| 5 | 2 | 0,29 | 0,3 | 0,01 | 0,0001 |
| 6 | 3 | 0,5 | 0,518 | 0,018 | 0,000324 |
| 7 | 4,25 | 0,6 | 0,73 | 0,13 | 0,0169 |
| 8 | 4,5 | 0,7 | 0,8 | 0,1 | 0,01 |
| 9 | 5 | 0,8 | 0,85 | 0,05 | 0,0025 |
| 10 | 5,5 | 0,9 | 0,94 | 0,04 | 0,0016 |
| 11 | 5,75 | 0,95 | 0,953 | 0,003 | 0,000009 |
Произведем все необходимые вычисления.
d =√ ∑0,033233⁄11=0,001
абсолютная ошибка D = max {|Yр – Yэ|} = 0,003
относительная ошибка D = D*100% / (|Ymax - Ymin|) = 0,0101 %.
Судя по полученным значениям ошибок, можно сделать вывод, что полученная переходная характеристика модели является достаточно адекватной относительно исходным экспериментальным данным.
2. Частотные характеристики.
Для построения частотных характеристик необходимо полученную передаточную функцию представить в частотном виде путем замены p = jw. После произведенной замены, необходимо выделить реальную и мнимую части данной передаточной функции звена.
Производя простые математические преобразования и вычисления, получаем функцию звена в виде:
W(jw) = Re + jIm
W(jw)=![]()
![]()
По полученному выражению получаем значения для построения АЧХ, ФЧХ и АФЧХ. Для этого вновь воспользуемся программой MSExcel для удобства проведения громоздких расчетов (Таблица значений АЧХ и ФЧХ приведена в приложении). График АФЧХ – есть зависимость Im(Re). По полученным значениям и по виду графика можно видеть, как меняется данная зависимость.
По полученным графикам можно сделать вывод, что данное звено является фильтром низких частот. Оно пропускает амплитуду сигнала на более низких частотах. На высоких частотах это пропускание стремится к нулю. Об этом говорит график АЧХ. График ФЧХ показывает то, что с увеличением частоты подаваемого на вход сигнала, происходит снижение рассогласования фаз выходного и входного значений сигнала. АФЧХ, в свою очередь, имеет интересный вид. График пересекает единичную окружность дважды, и стремится к нулю. Если в случае замкнутой системы это говорит о ее устойчивости по Ляпунову, то в случае разомкнутой это также говорит об устойчивости. Данное утверждение подтверждает и вид переходной характеристики, построенной при помощи пакета VisSim30 (графики АЧХ, ФЧХ, АФЧХ и график переходной характеристики полученного звена приведены в приложении).
3.По заданному закону регулирования найти математическую модель ЗСАУ.
Используя заданный ПИД–регулятор, необходимо найти математическую модель замкнутой системы автоматического управления (ЗСАУ). ПИД – закон имеет следующие заданные параметры и вид передаточной функции:
ПИД – Кп = 0,8 Ки = 0,1 Тд = Кд = 10

Составим структурную схему данной САУ:

ПИД W(P)
Описание работы системы: управляющий сигнал подается на вход регулятора. Регулятор преобразует входной сигнал и преобразованный по своему закону сигнал подает на вход объекта регулирования. Выходной сигнал вновь подается на вход системы, но только на, так называемое, устройство сравнения, и с учетом полученной разности выходного сигнала подается на вход регулятора.
С учетом структуры системы определим передаточную функцию ЗСАУ. Для удобства сначала определим WРСАУ (P) с учетом передаточной функции имеющегося регулятора, а потом запишем передаточную функцию ЗСАУ .
![]()
передаточная функция замкнутой системы будет иметь вид:
![]()
(График переходной характеристики приведен в приложении)
4.Определение устойчивости ЗСАУ.
Составление математической модели системы является важным этапом математического моделирования. Но также не маловажным условием полученной модели является ее устойчивость. Для избежания неблагоприятных последствий во время эксплуатации систем, на стадии моделирования обязательной стадией исследования является исследование модели системы на устойчивость. Для определения устойчивости имеются несколько критериев, названных в честь их создателей: Найквиста, Михайлова, Рауса, Гурвица, Ляпунова. Позднее критерий Гурвица стали называть критерием Рауса – Гурвица, т.к. их способы несколько различаются, но принцип определения идентичен, в обоих случаях для нахождения устойчивости определяется матрица коэффициентов.
В связи с тем, что критерии Найквиста, Михайлова и Ляпунова являются корневыми методами, а мы имеем дело с передаточной функцией 4-го порядка, то для упрощения определения устойчивости воспользуемся критерием Рауса – Гурвица, который не требует нахождения корней.
Теорема Гурвица утверждает, что для того, чтобы действительные части всех корней характеристического уравнения (знаменателя передаточной функции)
![]()
c действительными коэффициентами и b0 >0 были отрицательными, необходимо и достаточно, чтобы были положительными все определители D1, D2, ..., Dm, составленные из коэффициентов уравнения по следующей схеме:
309808 математическая модель метод площадь
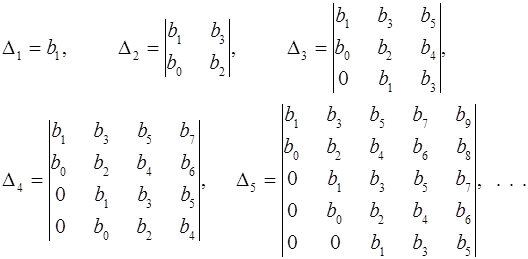 и т. д.
и т. д.
При составлении определителей по указанной схеме, коэффициенты с индексом, превышающим степень характеристического уравнения, заменяют нулями.
Согласно критерию Рауса – Гурвица, найдем определители характеристического уравнения ЗСАУ:
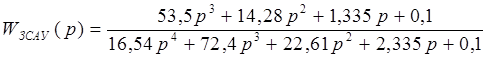
Характеристическое уравнение имеет вид:
![]()
D1 = b1 = 72,4 > 0;

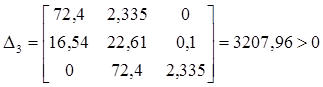
D4 = 0,1*D3 > 0
Так как все определители положительны, то согласно критерию устойчивости Гурвица, замкнутая система автоматического управления является устойчивой.
5. Нахождение переходной функции ЗСАУ и основных ПКР.
Нахождение переходной характеристики ЗСАУ возможно провести двумя способами: решение ДУ классическим методом или методом обратного преобразования Лапласа.
Решим одним из способов (обратным преобразованием Лапласа) полученную передаточную функцию ЗСАУ.
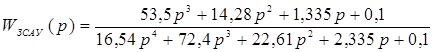
Для начала найдем все возможные корни данного уравнения, воспользовавшись численным методом нахождения корней.
р1 = -4,048, р2 = -0,1878.
Для нахождения оставшихся 2 комплексных корней разделим характеристическое уравнение на квадратный трехчлен, полученный путем умножения двух найденных корней. Разделив, получим корни:
р3,4, = -0,071 ±j0,054
Перепишем исходное уравнение в виде и произведем необходимые вычисления:
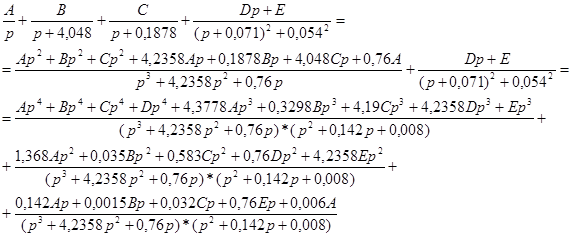
Составим систему уравнений и определим неизвестные коэффициенты А, В, С и D.

Решая полученную систему, получаем коэффициенты:
А = 1, В = -0,8108, С = 0,0029, D = -0,192, Е = -0,0788
Заменяя буквенные значения коэффициентов численными, и производя обратное преобразование Лапласа, получим:

Подставим различные значения t в полученное уравнение и получим переходную характеристику. Для этого снова воспользуемся пакетом MSExcel. График будет иметь вид:

Как показали исследования, график переходной функции построенный в пакете VisSim30 аналогичен приведенному выше. Можно сделать вывод, что полученная переходная функция найдена верно.
Для нахождения основных показателей качества регулирования (ПКР), воспользуемся графиком, полученным при помощи пакета VisSim30.
Основными ПКР являются:
· Время переходного процесса t п/п
· Вид переходного процесса (апериодический, колебательный, монотонный )
· Абсолютное перерегулирование s абс
· Статическая ошибка e ст
· Степень затухания y (определяется в случае колебательного процесса)
1. Время переходного процесса.
Временем переходного процесса считается то время, когда график переходной функции попадает в область значений от 0,95Yуст до 1,05Yуст , т.е. ±5% от установившегося значения и не выходит из этой области. Судя по графику переходного процесса, и по значениям, полученным в результате расчета при построении графика, видно, что время переходного процесса равно 40 секундам (t рег = t п/п = 40 сек ).
2. По графику видно, что переходной процесс является колебательным. Колебания данного процесса настолько малы, что изменения значений относительно Yуст = 1 составляют тысячные доли.
3. Абсолютное перерегулирование s абс = Ymax – Yуст = 0,006218572.
4. Статическая ошибка. Система является статической если e ст >0. Если e ст = 0, то система является астатической. Судя по полученным значениям и по виду переходной характеристики, данная система является астатической, т.к. e ст = 0.
5. Т.к. переходной процесс является колебательным и имеет А1
и А3
(первая и третья амплитуды переходного процесса), то можно найти и степень затухания. ![]()

6. Функциональная схема
Системы Автоматического Управления в общем виде выглядит следующим образом:
 |
7. Вывод
Математическая модель объекта регулирования системы, полученная в работе, является достаточно адекватной исходным данным. Об этом говорят значения полученных абсолютной и относительной погрешностей (D = 0,0001 и D = 0,0101 %). По частотным характеристикам самого объекта можно определить его некоторые свойства (полоса пропускания сигнала, устойчивость, отставание выходного сигнала от входного).
При получении математической модели всей системы был использован ПИД – регулятор. Сигнал измененный по заданному закону подается на объект регулирования и объект работает с измененным сигналом. Полученная замкнутая система является устойчивой.
Показатели качества регулирования, определенные в работе, говорят о том, что переходной процесс имеет: малое перерегулирование, что очень важно в системах подобного рода (контроль температуры и прочее); низкую степень колебательности, что также является показателем качества; система является астатической, т.е. система достигает необходимого выходного значения; что касается времени регулирования, то оно составляет 40 сек. Такое время переходного процесса является негативным в системах реального времени, что же касается систем контроля температуры, то этот показатель является довольно адекватным, т.к. невозможно достигнуть мгновенного изменения температуры в реальных системах.
Заключение
В данной курсовой работе было проведено математическое моделирование системы контроля температуры. Нужно заметить, что данный подход не только возможен, но и с успехом применяется во всех отраслях технического производства и контроля. Этот классический подход к разработке подобных систем основан на простых линейных звеньях. В реальных же системах процессы гораздо сложнее и линейностью не отличаются. Подобная методика расчета позволяет усвоить азы теории управления и углубиться в ее математическую моделирующую сторону. Это дает возможность получить теоретический навык в работе с подобными системами, а главное, что подобные исследования позволяют более смело подходить к различного рода разработкам.
При исследовании системы были получены различные показатели системы, в частности основные ПКР. Были сделаны выводы о качестве регулирования, а по виду переходных характеристик (построенных по исходным данным и полученным в результате исследования) можно было судить об адекватности полученных моделей (об этом говорят различного рода погрешности).
Система, расчет которой был проведен, вряд ли будет работать в реальной среде, в виду того, что приведенные методики расчетов были применены, в данном случае, для систем, на которые не оказываются внешние воздействия. В свою очередь, ход расчета системы, его последовательность вполне реально могут и применяются в настоящее время в исследованиях систем.
Список литературы
1. Курс лекций «Моделирование систем управления», Магомедов М.Я.
2. Курс лекций «Идентификация и диагностика систем», Омаров О.М.-С.
3. Курс лекций «Теория автоматического управления», Омаров М.-С.М.