| Скачать .docx |
Курсовая работа: Улучшение системы выпуска товаров
Содержание
1. Постановка задачи
· Формирование схемы движения. Транспортная задача
· Оптимизация плана выпуска промышленной продукции. Симплекс-метод
2. Транспортная задача
3. Симплекс-метод
1. Постановка задачи
Формирование схемы движения (Транспортная задача)
Задача, решаемая в курсовой работе, относиться к классу оптимизационных, функционал которой имеет экстремум. Поиск экстремума заключается в выборе оптимального варианта из множества вариантов прикрепления пунктов отправления и назначения грузов. Предполагается, что на всех направлениях осуществляются перевозки однородного груза и в этой части проблема сводиться к решению однопродуктовой транспортной задачи.
Необходимо решить задачу связи пунктов отправления и назначения, обеспечив вывоз всех грузов из пункта отправления, ввоз во все пункты назначения требуемых объемов грузов и достижения минимального суммарного грузооборота.
Оптимизация плана выпуска промышленной продукции
В этом разделе разрабатывается оптимальный план выпуска промышленной продукции. Задача формируется следующим образом: для выпуска четырех видов продукции требуются затраты сырья, рабочего времени и оборудования. Сформулировать экономико-математическую модель задачи на максимум прибыли и найти оптимальный план выпуска продукции.
Необходимо определить искомые переменные, расписать математическую постановку задачи и решить ее симплекс-методом.
В заключительном разделе курсовой работы необходимо расшифровать полученные результаты, обосновать оптимальность и допустимость полученного решения и сделать выводы.
Задание №22
Транспортная задача.
Исходные данные:
| Пункты отправления | Объем ввоза, тыс. тонн |
| А | 50 |
| Г | 100 |
| Е | 350 |
| Пункты назначения | Объем ввоза, тыс. тонн |
| К | 70 |
| Л | 130 |
| М | 50 |
| Н | 150 |
| П | 100 |
Расстояния между пунктами, км:
| А-К | 350 | Г-К | 220 | Е-К | 200 |
| А-Л | 400 | Г-Л | 290 | Е-Л | 240 |
| А-М | 340 | Г-М | 160 | Е-М | 235 |
| А-Н | 230 | Г-Н | 260 | Е-Н | 150 |
| А-П | 180 | Г-П | 255 | Е-П | 225 |



Используя метод северо-западного угла, составляем первоначальный план перевозок и проверяем на оптимальность:
| Bj | К=70 | Л=130 | М=50 | Н=150 | П=100 | Ui | |||||
| Ai | |||||||||||
| А=50 | 50 | 350 | - | 400 | - | 340 | - | 230 | - | 180 | 405 |
| Г=100 | 20 | 220 | 80 | 290 | - | 160 | - | 260 | - | 255 | 275 |
| Е=350 | - | 200 | 50 | 240 | 50 | 235 | 150 | 150 | 100 | 225 | 225 |
| Vj | -55 | 15 | 10 | -75 | 0 | ||||||
Определяются потенциальные оценки свободных клеток:
| 12= | 20 | 23= | 125 |
| 13= | 75 | 24= | -60 |
| 14= | 100 | 25= | 55 |
| 15= | 225 | 31= | -30 |
План перевозок не оптимален, поскольку имеются положительные потенциальные оценки, а значение целевой функции:
Z=50*350+20*220+80*290+50*240+50*235+150*150+100*225=113850
Может быть улучшено.
Выбираем цикл с включением в качестве вершины клетки с потенциальной оценкой +125, что позволяет перераспределить перевозки:
| 80 | 80 | - | 30 | 80 | 50 |
| 130 | 50 | 130 | 50 | ||
| 50 | 100 | 50 | 100 | 100 | - |
и получить новый план перевозок в виде очередной таблице:
| Bj | К=70 | Л=130 | М=50 | Н=150 | П=100 | Ui | |||||
| Ai | |||||||||||
| А=50 | 50 | 350 | - | 400 | - | 340 | - | 230 | - | 180 | 405 |
| Г=100 | 20 | 220 | 30 | 290 | 50 | 160 | - | 260 | - | 255 | 275 |
| Е=350 | - | 200 | 100 | 240 | - | 235 | 150 | 150 | 100 | 225 | 225 |
| Vj | -55 | 15 | -115 | -75 | 0 | ||||||
Полученный план так же не оптимален, так как среди потенциальных оценок свободных клеток есть положительные:
| 12= | 20 | 24= | -60 |
| 13= | -50 | 25= | 55 |
| 14= | 100 | 31= | -30 |
| 15= | 225 | 33= | -125 |
При этом значение целевой функции:
Z=50*350+20*220+30*290+100*240+50*160+150*150+100*225=107600
Улучшилось.
Снова выбираем цикл с включением в качестве вершины клетки с потенциальной оценкой +20, что позволяет перераспределить перевозки:
| 50 | 50 | - | 20 | 50 | 30 |
| 70 | 30 | 70 | 30 | ||
| 20 | 50 | 30 | 50 | 50 | - |
и получить новый план перевозок в виде очередной таблице:
| Bj | К=70 | Л=130 | М=50 | Н=150 | П=100 | Ui | |||||
| Ai | |||||||||||
| А=50 | 20 | 350 | 30 | 400 | - | 340 | - | 230 | - | 180 | 385 |
| Г=100 | 50 | 220 | - | 290 | 50 | 160 | - | 260 | - | 255 | 255 |
| Е=350 | - | 200 | 100 | 240 | - | 235 | 150 | 150 | 100 | 225 | 225 |
| Vj | -35 | 15 | -95 | -75 | 0 | ||||||
Полученный план так же не оптимален, так как среди потенциальных оценок свободных клеток есть положительные:
| 13= | -50 | 24= | -60 |
| 14= | 80 | 25= | 55 |
| 15= | 205 | 31= | -30 |
| 22= | -20 | 33= | -125 |
При этом значение целевой функции:
Z=20*350+50*220+30*400+100*240+50*160+150*150+100*225=107000
Улучшилось.
Снова выбираем цикл с включением в качестве вершины клетки с потенциальной оценкой +80, что позволяет перераспределить перевозки:
| 30 | 30 | - | - | 30 | 30 |
| 130 | 150 | 130 | 150 | ||
| 100 | 250 | 150 | 130 | 250 | 120 |
и получить новый план перевозок в виде очередной таблице:
| Bj | К=70 | Л=130 | М=50 | Н=150 | П=100 | Ui | |||||
| Ai | |||||||||||
| А=50 | 20 | 350 | - | 400 | - | 340 | 30 | 230 | - | 180 | 305 |
| Г=100 | 50 | 220 | - | 290 | 50 | 160 | - | 260 | - | 255 | 175 |
| Е=350 | - | 200 | 130 | 240 | - | 235 | 120 | 150 | 100 | 225 | 225 |
| Vj | 45 | 15 | -15 | -75 | 0 | ||||||
Полученный план так же не оптимален, так как среди потенциальных оценок свободных клеток есть положительные:
| 12= | -80 | 24= | -160 |
| 13= | -50 | 25= | -80 |
| 15= | 125 | 31= | 70 |
| 22= | -100 | 33= | -25 |
При этом значение целевой функции:
Z=20*350+50*220+130*240+50*160+30*230+120*150+100*225=104600
Улучшилось.
Снова выбираем цикл с включением в качестве вершины клетки с потенциальной оценкой +125, что позволяет перераспределить перевозки:
| 30 | 30 | - | - | 30 | 30 |
| 150 | 100 | 150 | 100 | ||
| 120 | 220 | 100 | 150 | 220 | 70 |
и получить новый план перевозок в виде очередной таблице:
| Bj | К=70 | Л=130 | М=50 | Н=150 | П=100 | Ui | |||||
| Ai | |||||||||||
| А=50 | 20 | 350 | - | 400 | - | 340 | - | 230 | 30 | 180 | 180 |
| Г=100 | 50 | 220 | - | 290 | 50 | 160 | - | 260 | - | 255 | 50 |
| Е=350 | - | 200 | 130 | 240 | - | 235 | 150 | 150 | 70 | 225 | 225 |
| Vj | 170 | 15 | 110 | -75 | 0 | ||||||
Полученный план так же не оптимален, так как среди потенциальных оценок свободных клеток есть положительные:
| 12= | -205 | 24= | -285 |
| 13= | -50 | 25= | -205 |
| 14= | -125 | 31= | 195 |
| 22= | -225 | 33= | 100 |
При этом значение целевой функции:
Z=20*350+50*220+130*240+50*160+150*150+30*180+70*225=100850
Улучшилось.
Снова выбираем цикл с включением в качестве вершины клетки с потенциальной оценкой +195, что позволяет перераспределить перевозки:
| 20 | 50 | 30 | - | 50 | 50 |
| 20 | 100 | 20 | 100 | ||
| - | 70 | 70 | 20 | 70 | 50 |
и получить новый план перевозок в виде очередной таблице:
| Bj | К=70 | Л=130 | М=50 | Н=150 | П=100 | Ui | |||||
| Ai | |||||||||||
| А=50 | - | 350 | - | 400 | - | 340 | - | 230 | 50 | 180 | 180 |
| Г=100 | 50 | 220 | - | 290 | 50 | 160 | - | 260 | - | 255 | 245 |
| Е=350 | 20 | 200 | 130 | 240 | - | 235 | 150 | 150 | 50 | 225 | 225 |
| Vj | -25 | 15 | -85 | -75 | 0 | ||||||
| 11= | -195 | 22= | -30 |
| 12= | -205 | 24= | -90 |
| 13= | -245 | 25= | -10 |
| 14= | -125 | 33= | -95 |
Z=50*220+20*200+130*240+50*160+150*150+50*180+50*225=96950
Таким образом, получен оптимальный план перевозок.
Симплекс-метод
Исходные данные:
| Тип ресурса | Нормы затрат ресурсов на единицу продукции | Запасы ресурсов | |||
| 1 | 2 | 3 | 4 | ||
| Сырье | 6 | 4 | 3 | 5 | 70 |
| Рабочее время | 23 | 15 | 19 | 31 | 450 |
| Оборудование | 11 | 15 | 8 | 17 | 140 |
| Прибыль на единицу продукции | 31 | 26 | 9 | 17 | |
На основе исходных данных составляется математическая модель задачи:
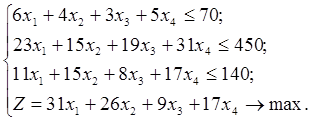
Для решения задачи симплекс-методом необходимы очевидные промежуточные преобразования:

Если выбрать в качестве базисных переменных введенные дополнительные переменные ![]() ,
, ![]() ,
, ![]() то последняя модель переписывается в виде:
то последняя модель переписывается в виде:

В итоге формируется симплекс-таблица следующего вида:
П БП |
1 | ||||
| 6 | 4 | 3 | 5 | 70 | |
| 2 3 | 1 5 | 19 | 31 | 450 | |
| 1 1 | 1 5 | 8 | 1 7 | 140 | |
| -31 | -26 | -9 | -17 | 0 |
Решение не оптимально. В строке Z присутствуют отрицательные коэффициенты. Выбираем разрешающий столбец с максимальным отрицательным значением ![]() . Для выбора разрешающе строки свободные коэффициенты (70, 450, 140) делят на элементы разрешающего столбца. По минимальному положительному отношению выбирается разрешающая строка
. Для выбора разрешающе строки свободные коэффициенты (70, 450, 140) делят на элементы разрешающего столбца. По минимальному положительному отношению выбирается разрешающая строка ![]() . Пересечение разрешающего столбца и строка дает разрешающий инструмент (=6)
. Пересечение разрешающего столбца и строка дает разрешающий инструмент (=6)
| БП/П | (-Х1) | (-Х2) | (-Х3) | (-Х4) | 1 | |
| Х5= | 6 | 4 | 3 | 5 | 70 | 11,6 |
| Х6= | 23 | 15 | 19 | 31 | 450 | 19,56 |
| Х7= | 11 | 15 | 8 | 17 | 140 | 12,72 |
| Z= | -31 | -26 | -9 | -17 | 0 |
При выборе разрешающими столбца ![]() и строки Х5 получаем новую симплекс-таблицу:
и строки Х5 получаем новую симплекс-таблицу:
| БП/П | (-Х5) | (-Х2) | (-Х3) | (-Х4) | 1 | |
| Х1= | 0,16 | 0,66 | 0,5 | 0,83 | 11,66 | 17,66 |
| Х6= | -3,83 | -0,33 | 7,5 | 11,83 | 181,66 | -550,48 |
| Х7= | -1,83 | 7,66 | 2,5 | 7,83 | 11,66 | 1,52 |
| Z= | 5,16 | -5,33 | 6,5 | 8,83 | 361,66 |
| БП/П | (-Х5) | (-Х7) | (-Х3) | (-Х4) | 1 |
| Х1= | 0,32 | -0,08 | 0,28 | 0,152 | 10,65 |
| Х6= | -3,91 | 0,04 | 7,6 | 12,17 | 182,17 |
| Х2= | -0,23 | 0,13 | 0,32 | 1,02 | 1,52 |
| Z= | 3,89 | 0,69 | 8,23 | 14,28 | 369,78 |
Согласно полученным данным оптимальным является распределение заказа между 10,65 станками первого типа и 182,17 станками шестого типа. При минимальных издержках в 369,78 ден. единиц.