Реферат: Основы оценки сложных систем. Понятия и виды шкал. Отработка характеристик, измеряемых в разных шкалах

Министерство просвещения ПМР

Приднестровский государственный университет им. Т.Г. Шевченко

Рыбницкий филиал

Кафедра «Социально – экономических дисциплин»

Реферат

по дисциплине “Теория систем и системного анализа ”

на тему:

«Основы оценки сложных систем. Понятия и виды шкал. Отработка характеристик, измеряемых в разных шкалах»

Выполнила

студентка II курса, з/о

специальности «Менеджмент организации»

Шишкевич О.А.

Проверил:

Павлинов И.А.

г. Рыбница

2011 г.

План работы

Введение

I. Понятие и виды шкал

II. Обработка характеристик, измеряемых в разных шкалах

III. Шкала уровней качества систем с управлением

IV. Методы качественного и количественного оценивания систем

Заключение

Список использованной литературы

Приложение.

Введение

Оценка сложных систем может проводиться для разных целей. Во-первых, для оптимизации - выбора наилучшего алгоритма из нескольких, реализующих один закон функционирования системы. Во-вторых, для идентификации - определения системы, качество которой наиболее соответствует реальному объекту в заданных условиях. В-третьих, для принятия решений по управлению системой. Под оценкой понимают результат, получаемый в ходе процесса, который определен как оценивание.

Выделяют четыре этапа оценивания сложных систем:

Этап 1. Определение цели оценивания. В системном анализе выделяют два типа целей:

Качественной называют цель, достижение которой выражается в номинальной шкале или в шкале порядка;

Количественной называют цель, достижение которой выражается в количественных шкалах. Определение цели должно осуществляться относительно системы, в которой рассматриваемая система является элементом (подсистемой).

Этап 2. Измерение свойств систем, признанных существенными для целей оценивания. Для этого выбираются соответствующие шкалы измерений свойств и всем исследуемым свойствам систем присваивается определенное значение на этих шкалах.

Этап 3. Обоснование предпочтений критериев качества и критериев эффективности функционирования систем на основе измеренных на выбранных шкалах свойств.

Этап 4. Собственно оценивание. Все исследуемые системы, рассматриваемые как альтернативы, сравниваются по сформулированным критериям и в зависимости от целей оценивания ранжируются, выбираются, оптимизируются и т.д.

I. Понятие и виды шкал

сложный система оценивание шкала

В основе оценки лежит процесс сопоставления значений качественных или количественных характеристик исследуемой системы значениям соответствующих шкал. Исследование характеристик привело к выводу о том, что все возможные шкалы принадлежат к одному из нескольких типов, определяемых перечнем допустимых операций на этих шкалах.

Шкала – это средство фиксации результатов измерения свойств объектов путем упорядочивания их в определенную числовую систему, в которой отношение между отдельными результатами выражено в соответствующих числах. В процессе упорядочивания каждому элементу выборки ставится в соответствие определенный балл (шкальный индекс), устанавливающий положение наблюдаемого результата на шкале.

Шкалирование — это операция упорядочивания исходных эмпирических данных путем перевода их в шкальные оценки. Шкала дает возможность упорядочить наблюдаемые явления, при этом каждое из них получает количественную оценку (квантифицируется). Шкалирование помогает определить низшую и высшую ступени исследуемого явления.

Формально шкалой называется кортеж из трех элементов < X, ф, Y>, где X реальный объект, Yшкала, ф гомоморфное отображение X на Y.

В исследованиях применяют классификацию шкал, предложенную С.Стивенсоном (см. рис. 1), согласно которой четыре основных способа измерения, связанные с различными правилами, называют измерительными шкалами (номинальная, порядковая, интервальная и шкала отношений).

Выделяют следующие виды шкал:

1) Самой слабой качественной шкалой является номинальная (шкала наименований, классификационная шкала), по которой объектам х. или их неразличимым группам дается некоторый признак. Основным свойством этих шкал является сохранение неизменными отношений равенства между элементами эмпирической системы в эквивалентных шкалах.

Шкалы номинального типа допускают только различение объектов на основе проверки выполнения отношения равенства на множестве этих элементов. Номинальный тип шкал соответствует простейшему виду измерений, при котором шкальные значения используются лишь как имена объектов, поэтому шкалы номинального типа часто называют также шкалами наименований.

Примерами измерений в номинальном типе шкал могут служить номера автомашин, телефонов, коды городов, лиц, объектов и т. п. Единственная цель таких измерений выявление различий между объектами разных классов. Если каждый класс состоит из одного объекта, шкала наименований используется для различения объектов.

2) Шкала называется ранговой (шкала порядка), если множество Ф состоит из всех монотонно возрастающих допустимых преобразований шкальных значений.

Порядковый тип шкал допускает не только различие объектов, как номинальный тип, но и используется для упорядочения объектов по измеряемым свойствам. Измерение в шкале порядка может применяться, например, в следующих ситуациях:

1. необходимо упорядочить объекты во времени или пространстве. Это ситуация, когда интересуются не сравнением степени выраженности какого-либо их качества, а лишь взаимным пространственным или временным расположением этих объектов;

2. нужно упорядочить объекты в соответствии с каким-либо качеством, но при этом не требуется производить его точное измерение;

3. какое-либо качество в принципе измеримо, но в настоящий момент не может быть измерено по причинам практического или теоретического характера.

Примером шкалы порядка может служить шкала твердости минералов, предложенная в 1811 г. немецким ученым Ф. Моосом и до сих пор распространенная в полевой геологической работе. Другими примерами шкал порядка могут служить шкалы силы ветра, силы землетрясения, сортности товаров в торговле, различные социологические шкалы и т.п.

3) Одним из наиболее важных типов шкал является тип интервалов. Тип шкал интервалов содержит шкалы, единственные с точностью до множества положительных линейных допустимых преобразований вида ф (х) = ах + Ь, где

х € Y шкальные значения из области определения Y; я > 0; Ъ любое значение.

Основным свойством этих шкал является сохранение неизменными отношений интервалов в эквивалентных шкалах.

Примером шкал интервалов могут служить шкалы температур. Переход от одной шкалы к эквивалентной, например от шкалы Цельсия к шкале Фаренгейта, задается линейным преобразованием шкальных значений: t °F = 1,8 t°C + 32.

Шкалы интервалов так же, как номинальная и порядковая, сохраняют различие и упорядочение измеряемых объектов. Однако кроме этого они сохраняют и отношение расстояний между парами объектов. Запись означает, что расстояние между х{я х2 в К раз больше расстояния между х3 и х4 и в любой эквивалентной шкале это значение (отношение разностей численных оценок) сохранится. При этом отношения самих оценок не сохраняются.

4) Шкалой отношений (подобия) называется шкала, если Ф состоит из преобразований подобия ср (х) = ах, а> О, где X&Y- шкальные значения из области определения Y; а - действительные числа.

Нетрудно убедиться, что в шкалах отношений остаются неизменными отношения численных оценок объектов. Действительно, пусть в одной шкале объектам ах и а2 соответствуют шкальные значения хх и х2, а в другой ф (jtj) = ах^ и ф (х2) - ах2 , где а > О - произвольное действительное число. Тогда имеем:

Данное соотношение объясняет название шкал отношений. Примерами измерений в шкалах отношений являются измерения массы и длины объектов. Известно, что при установлении массы используется большое разнообразие численных оценок. Так, производя измерение в килограммах, получаем одно численное значение, при измерении в фунтах - другое и т.д. Однако можно заметить, что в какой бы системе единиц ни производилось измерение массы, отношение масс любых объектов одинаково и при переходе от одной числовой системы к другой, эквивалентной, не меняется. Этим же свойством обладает и измерение расстояний и длин предметов.

Как видно из рассмотренных примеров, шкалы отношений отражают отношения свойств объектов, т.е. во сколько раз свойство одного объекта превосходит это же свойство другого объекта.

5) Шкалы разностей определяются как шкалы, единственные с точностью до преобразований сдвига ср (х) - х + Ь, где х е Y -шкальные значения из области определения Y; Ь действительные числа. Это означает, что при переходе от одной числовой системы к другой меняется лишь начало отсчета.

Шкалы разностей применяются в тех случаях, когда необходимо измерить, насколько один объект превосходит по определенному свойству другой объект. В шкалах разностей неизменными остаются разности численных оценок свойств.

Примерами измерений в шкалах разностей могут служить измерения прироста продукции предприятий (в абсолютных единицах) в текущем году по сравнению с прошлым, увеличение численности учреждений, количество приобретенной техники за год и т. д.

Другим примером измерения в шкале разностей является летоисчисление (в годах). Переход от одного летоисчисления к другому осуществляется изменением начала отсчета.

Как и шкалы отношений, шкалы разностей являются частным случаем шкал интервалов, получаемых фиксированием параметра а: (а = 1), т.е. выбором единицы масштаба измерений. Точка отсчета в шкалах разностей может быть произвольной.

Шкалы разностей, как и шкалы интервалов, сохраняют отношения интервалов между оценками пар объектов, но, в отличие от шкалы отношений, не сохраняют отношения оценок свойств объектов.

6) Абсолютными называют шкалы, в которых единственными допустимыми преобразованиями Ф являются тождественные преобразования:

ф (х) = {е}, где е(х) =х.

Абсолютные шкалы применяются, например, для измерения количества объектов, предметов, событий, решений и т.п. В качестве шкальных значений при измерении количества объектов используются натуральные числа, когда объекты представлены целыми единицами, и действительные числа, если кроме целых единиц присутствуют и части объектов.

Абсолютные шкалы являются частным случаем всех ранее рассмотренных типов шкал, поэтому сохраняют любые соотношения между числами оценками измеряемых свойств объектов: различие, порядок, отношение интервалов, отношение и разность значений и т.д.

II. Обработка характеристик, измеренных в разных шкалах

Особенностью измерения и оценивания качества сложных систем является то, что для одной системы по разным частным показателям качества могут применяться любые из типов шкал от самых слабых до самых сильных. При этом для получения надежного значения показателя может проводиться несколько измерений. Кроме того, обобщенный показатель системы может представлять собой некую осредненную величину однородных частных показателей.

При измерении и оценке физических величин обычно трудностей не возникает, так как перечисленные величины измеряются в абсолютной шкале. Измерение, например, ряда антропометрических характеристик осуществляется в шкале отношений. Более сложной является оценка в качественных шкалах. Однако отдельные показатели в процессе системного анализа уточняются, и, как следствие, появляется возможность от измерения и оценки в качественных шкалах перейти к оценке в количественных шкалах.

В любом случае при работе с величинами, измеренными в разных шкалах, необходимо соблюдать определенные правила, которые не всегда очевидны. Иначе неизбежны грубые просчеты и промахи при оценке систем. Проиллюстрируем широко распространенную ошибку при использовании балльной оценки. Пусть для экспертизы представлены две системы А и Б, оцениваемые по свойствам y1, y2, у3, y4 . Качество каждой системы оценивается как среднеарифметическое по пятибалльной системе, но оценка в баллах является вследствие округления не совсем точной. Так, например, свойства, имеющие фактический уровень 2,6 и 3,4 балла, получат одинаковую оценку 3 балла. Результаты экспертизы приведены в табл. 1.

По фактическому качеству лучшей является система А, а по результатам экспертизы лучшей признают систему Б. Таким образом, способы измерения и обработки их результатов оказывают существенное влияние на результаты.

Избежать ошибок можно, используя результаты, полученные в теории шкалирования, они определяют правила и перечень допустимых операций осреднения характеристик.

Проводить осреднение допускается только для однородных характеристик, измеренных в одной шкале. Это означает, например, что не имеет физического смысла вычисление среднего значения скорости для мобильного абонентского пункта, если слагаемыми являются скорость передачи данных и скорость перемещения этого объекта. Иными словами, осредняются только такие значения уi, i = 1, ..., п, которые представляют собой или оценки различных измерений одной и той же характеристики, или оценки нескольких различных однородных характеристик.

Каждое значение показателя уi может иметь для исследователя различную ценность, которую учитывают с помощью коэффициентов значимости ct, причем

∑ сi = 1.

i=1

Для получения осреднённого значения показателя наиболее часто применяют основные формулы осреднения. ( Таблица 2. смотреть Приложение 2.)

Простая и взвешенные средние величины различаются не только по величине (не всегда), по способу вычисления, но и по своей роли в решении задач системного анализа. При этом средневзвешенные величины используются для сравнения систем с учетом вклада различных факторов в осредненную оценку. Например, среднее количество информации, получаемой из сети Интернет организацией, пользующейся услугами различных прикладных служб. Если эта средняя величина входит в систему показателей себестоимости, протоколов работы, типов используемых линий, то следует применять взвешенное среднее, так как произведение невзвешенного среднего на общую пропускную способность линий не даст количества полученной информации, поскольку служба электронной почты используется, например, значительно реже, чем WWW, и, следовательно, вносит меньший вклад в общее количество получаемой информации. Если же необходимо изучить связь количества получаемой информации с днем недели, то следует применять простое среднее количество информации за сутки, полностью абстрагируясь от различий между типами служб.

Среднеарифметическое используется в случаях, когда важно сравнить абсолютные значения какой-либо характеристики нескольких систем. Например, скорость вывода на печать текстов (лист/мин) для различных печатающих устройств.

Если при замене индивидуальных значений показателя на среднюю величину требуется сохранить неизменной сумму квадратов исходных величин (измерение вариации характеристики в совокупности), то в качестве средней следует использовать среднеквадратичное. Например, при определении местоположения источника радиоизлучения в радиоразведке вычисляется среднеквадратичное отклонение нескольких измерений.

Среднегеометрическое, в свою очередь, используется для определения относительной разности отдельных значений при необходимости сохранения произведения индивидуальных величин тогда, когда среднее значение качественно одинаково удалено от максимального и минимального значений, т.е. когда важны не абсолютные значения, а относительный разброс характеристик. "Например, если максимальная производительность процессора на операциях с данными целочисленного типа составляет для сжатия текстового файла миллион условных единиц, а для сжатия изображений графических объектов сто, то какую величину считать средней? Среднеарифметическое (500 000) качественно однородно с максимальным и резко отлично от минимального. Среднегеометрическое по логике дает верный ответ: 10 000. В статистике среднегеометрическое находит применение при определении средних темпов роста.

Среднегармоническое используется, если необходимо, чтобы неизменной оставалась сумма величин, обратных индивидуальным значениям характеристик. Пусть, например, в режиме обмена данными средняя скорость передачи данных по прямому каналу составляет 64 Кбайт/с, а средняя скорость по обратному каналу 2,4 Кбайт/с. Какова средняя скорость обмена данными? При замене индивидуальных значений скорости у1 = 64 и у2 = 2,4 на среднюю величину необходимо, чтобы неизменной величиной осталось время передачи в обе стороны, иначе средняя скорость может оказаться любой. Таким образом,

Yср = 2(1/64+1 /2,4) -1 ≈ 4,8 Кбайт/с.

Соотношение между разными типами средних величин определяется правилом мажорантности средних

СГр ≤ СГм ≤ СА ≤ СК.

Использование необоснованных способов определения средних величин может привести к искусственному завышению или занижению осредненного значения показателя качества системы. В качестве упражнения обучаемым предлагается определить свой средний балл за прошедшую сессию на основе перечисленных средних величин.

Сводные данные по характеристикам разных шкал и перечень допустимых операций осреднения характеристик приведены в табл. 3, откуда следует, что для величин, измеренных в номинальной шкале, никаких осреднений производить не допускается. Сводные данные по характеристикам разных шкал.Таблица 3. (смотреть в Приложении 3.)

Среднеарифметическое применимо для величин, измеренных в шкалах интервалов, разностей, отношений и абсолютной, но недопустимо для шкалы порядка. Более устойчивой оценкой среднего является медиана (50-процентный квантиль), которая рекомендуется как основной показатель для шкал порядка, интервалов, разностей, отношений и абсолютной.

Математическое ожидание допустимо для шкал интервалов, разнрстей, отношений и абсолютных, но не столь устойчиво, как медиана. Применение математического ожидания для величин, измеренных в шкале порядка, является некорректным. Среднегеометрическое является единственно допустимым средним для степенных и логарифмических шкал, а также одним из допустимых для шкалы отношений. Для шкалы отношений допустимы также средневзвешенное арифметическое, среднегармо-ническое и среднеквадратичное.

Средневзвешенное арифметическое, часто применяемое как обобщенный линейный критерий, допустимо использовать тогда и только тогда, когда значения частных показателей можно представить мультипликативным метризованным отношением линейного порядка или, другими словами, когда они измерены в шкале отношений.

Будущее развития теории шкалирования и ее применения для нужд математического обеспечения ИС связаны с дальнейшим развитием понятия измерения. Наиболее перспективным представляется расширение понимания шкалы путем привлечения понятий нечеткой и лингвистических переменных, используемых в теории нечетких множеств. Обобщение понятия характеристической функции путем перехода к понятию функции принадлежности μn € [0,1], используемой в этой теории, создает базу для введения более тонкой структуры измерения качественных характеристик и учета неопределенностей, свойственных сложным системам, на основе понятия нечеткой шкалы. Например, пусть рассматриваемое нечеткое множество возраст людей. Нечеткими переменными (шкальными значениями), означающими возраст, являются лингвистические переменные «молодой», «средний», «старый» с приписанными им функциями принадлежности, которые можно определить так, как показано на (рис. 2.) При этом 20-летний человек относится к нечеткому подмножеству возраста «молодой» с функцией принадлежности μмол = 0,8, и он же с функцией принадлежности μср = 0,1 относится к нечеткому подмножеству возраста «средний». Рис. 2. Пример нечеткой шкалы. (смотреть Приложение 4.)

III. Шкала уровней качества систем с управлением

При оценивании качества систем с управлением признают целесообразным введение нескольких уровней качества, проранжированных в порядке возрастания сложности рассматриваемых свойств.

Первичным качеством любой системы является ее устойчивость. Для простых систем устойчивость объединяет такие свойства, как прочность, стойкость к внешним воздействиям, сбалансированность, стабильность, гомеостазис (способность системы возвращаться в равновесное состояние при выводе из него внешними воздействиями). Для сложных систем характерны различные формы структурной устойчивости, такие, как надежность, живучесть и т.д.

Более сложным, чем устойчивость, является помехоустойчивость, понимаемая как способность системы без искажений воспринимать и передавать информационные потоки. Помехоустойчивость объединяет ряд свойств, присущих в основном системам управления. К таким свойствам относятся надежность информационных систем и систем связи, их пропускная способность, возможность эффективного кодирования/декодирования информации, электромагнитная совместимость радиоэлектронных средств и т.д.

Следующим уровнем шкалы качества системы является управляемость способность системы переходить за конечное (заданное) время в требуемое состояние под влиянием управляющих воздействий. Управляемость обеспечивается прежде всего наличием прямой и обратной связи, объединяет такие свойства системы, как гибкость управления, оперативность, точность, производительность, инерционность, связность, наблюдаемость объекта управления и др. На этом уровне качества для сложных систем управляемость включает способность принятия решений по формированию управляющих воздействий.

Следующим уровнем на шкале качеств является способность. Это качество системы, определяющее ее возможности по достижению требуемого результата на основе имеющихся ресурсов в заданный период времени. Данное качество характеризуется такими свойствами, как результативность (производительность, мощность и т.п.), ресурсоемкость и оперативность. Итак, способность - это потенциальная эффективность функционирования системы, способность получить требуемый результат при идеальном способе использования ресурсов и в отсутствие воздействий внешней среды.

Наиболее сложным качеством системы является самоорганизация. Самоорганизующаяся система способна изменять свою структуру, параметры, алгоритмы функционирования, поведение для повышения эффективности. Принципиально важными свойствами этого уровня являются свобода выбора решений, адаптируемость, самообучаемость, способность к распознаванию ситуаций.

Введение уровней качества позволяет ограничить исследования одним из перечисленных уровней. Для простых систем часто ограничиваются исследованием устойчивости. Уровень качества выбирает исследователь в зависимости от сложности системы, целей исследования, наличия информации, условий применения системы.

IV. Методы качественного и количественного оценивания систем

Методы оценивания систем разделяются на качественные и количественные.

Качественные методы используются на начальных этапах моделирования, если реальная система не может быть выражена в количественных характеристиках, отсутствуют описания закономерностей систем в виде аналитических зависимостей. В результате такого моделирования разрабатывается концептуальная модель системы.

Простейшей формой задачи оценивания является обычная задача измерения, когда оценивание есть сравнение с эталоном, а решение задачи находится подсчетом числа эталонных единиц в измеряемом объекте. Например, пусть х - отрезок, длину которого надо измерить. В этом случае отрезку сопоставляется действительное число ф (х) - его длина.

Более сложные задачи оценивания разделяются на задачи: парного сравнения, ранжирования, классификации, численной оценки.

Задача парного сравнения заключается в выявлении лучшего из двух имеющихся объектов. Задача ранжирования - в упорядочении объектов, образующих систему, по убыванию (возрастанию) значения некоторого признака. Задача классификации - в отнесении заданного элемента к одному из подмножеств. Задача численной оценки - в сопоставлении системе одного или нескольких чисел.

Перечисленные задачи могут быть решены непосредственно лицом, принимающим решение, или с помощью экспертов - специалистов в исследуемой области. Во втором случае решение задачи оценивания называется экспертизой.

Качественные методы измерения и оценивания характеристик систем, используемые в системном анализе, достаточно многочисленны и разнообразны.

К основным методам качественного оценивания систем относят:

* методы типа мозговой атаки или коллективной генерации идей;

типа сценариев;

* экспертных оценок;

* типа Дельфи;

* типа дерева целей;

* морфологические методы.

Количественные методы используются на последующих этапах моделирования для количественного анализа вариантов системы.

Наличие неоднородных связей между отдельными показателями сложных систем приводит к проблеме корректности критерия превосходства к необходимости идти на компромисс и выбирать для каждой характеристики не оптимальное значение, а меньшее, но такое, при котором и другие показатели тоже будут иметь приемлемые значения.

Для решения проблемы корректности критерия превосходства были разработаны методы количественной оценки систем:

* методы теории полезности;

* методы векторной оптимизации;

* методы ситуационного управления, инженерии знаний.

Методы теории полезности основаны на аксиоматическом использовании отношения предпочтения множества векторных оценок систем.

Методы векторной оптимизации базируются на эвристическом использовании понятия векторного критерия качества систем (многокритериальные задачи) и включают методы главного критерия, лексикографической оптимизации, последовательных уступок, скаляризации, человеко-машинные и другие методы. При решении задач векторной оптимизации векторный (многокомпонентный) критерий эффективности, выраженный через показатели исходов операции, заменяют скалярным на основе какой-либо функции свертки.

Методы ситуационного управления, инженерии знаний основаны на построении семиотических моделей оценки систем. В таких моделях система предпочтений ЛПР формализуется в виде набора логических правил, по которым может быть осуществлен выбор альтернатив. При этом понятие векторного критерия в явном виде не используется.

Рассмотрение указанных подходов в системном анализе основано на трех важных особенностях.

Во-первых, считается, что не существует системы, наилучшей в независящем от ЛПР смысле. Всегда система может быть наилучшей лишь для данного ЛПР. Другое ЛПР в данных условиях может предпочесть альтернативную систему.

Во-вторых, считается, что не существует оптимальной системы для всех целей и воздействий внешней среды. Система может быть эффективной только для конкретной цели и в конкретных условиях. В других условиях и для других целей система может быть неэффективной. Например, конверсия танков в интересах сельского хозяйства показала, что эта техника по сравнению с тракторами неэффективна по показателям ресурсоемкости.

В-третьих, методы исследования операций (линейное, нелинейное, динамическое программирование и др.) не удовлетворяют требованиям, предъявляемым к задачам оценивания сложных организационных систем, поскольку вид целевой функции или неизвестен, или не задан аналитически, или для нее отсутствуют средства решения.

Заключение

Методы оценивания систем разделяются на качественные и количественные.

Список использованной литературы

1. Бусленко Н. П., Калашников В. В,, Коваленко Н. Н. Лекции по теории сложных систем. М., Сов. радио,1973

2. Волкова В. П., Денисов А. А. Основы теории систем и системного анализа. С-П, изд. СПбГТУ, 1999

3. Денисов А. А,,Колесников Д. Н. Теория больших систем управления. Уч. пособие. Л., Энергоиздат, 1982

4. Квейд Э. Анализ сложных систем. М., Сов. радио, 1969

5. Месарович М., Такахара И. Общая теория систем: математические основы. М., Мир, 1978

6. Моисеев Н. Н. Математические задачи системного анализа. М., Наука, 1981

7. Перегудов Ф. И., Тарасенко Ф. П. Введение в системный анализ. Уч. пособие. М., ВШ, 1989

8. Системный анализ в управлении. Учеб. пособие / В.С.Анфилатов, А.А.Емельянов, А.А. Кукушкин; Под ред. А.А.Емельянова. – М.: Финансы и статистика, 2005. – 368 с.

9. Уемов А. И. Системный подход и общая теория систем. М., Мысль, 1978

10. Флейшман Б. С, Основы системологии. М., Радио и связь, 1982

11. Фомин Г.Н.Математические методы и модели в коммерческой деятельности: Учебник. – М.: Финансы и статистика, 2005. – 616 с.

12. Черняк Ю. И. Системный анализ в управлении экономикой. М., Экономика, 1975

Приложение 1

Рис. 1. Классификация шкал по С.Стивенсу.

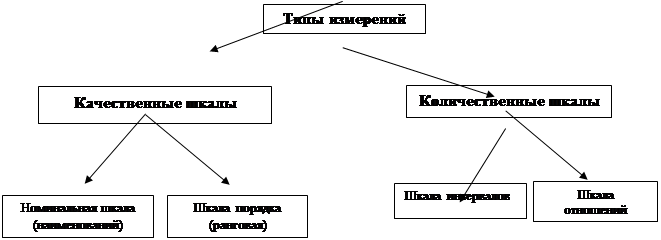
Таблица 1. Пример балльной оценки свойств систем.

Свойство системы	Система А		Система Б
Свойство системы	истинная	в баллах	истинная	в баллах
У\	4,4	4	3,6	4
Уг	3,3	3	3,7	4
Уъ	2,4	2	2,6	3
У*	4,4	4	2,6	3
Суммарная оценка	14,5	13	12,5	14

Приложение 2

Таблица 2. Основные формулы осреднения.

Наименование	Формула
Средневзвешенное арифметическое (СВА)	n Yсва =∑сi yi .i =1
Среднеарифметическое (СА), частный случай СВА при равнозначности измерений (сi = 1/n)	n Yса =1/n ∑yi ………….. i=1
Среднеквадратичное (СК)	n Yck=√ 1/n∑ Yi2 i=1
Средневзвешенное геометрическое (СВГм)	n Yсвгм = П Yi2 i=1
Среднегеометрическое (СГм) частный случай СВГм при сi=1/n	n n Yсгм =√ П Yi i=1
Средневзвешенное гармоническое (СВГр)	n Yсвгр =(∑CiYi-1) -1 i=1
Среднегармоническое (СГр)	n Yсгр =n(∑Yi-1) -1 i=1

Приложение 3

Таблица 3. Сводные данные по характеристикам разных шкал

Исходная эмпирическая система

Параметры, сохраняющиеся при переходе от одной шкалы к другой (из числа допустимых)

Допустимые виды осреднения

Рекомендуемые (да, нет) допустимые (+) и недопустимые (-) виды обработки случайных величин

Отношение порядка

Шкала

Среднее

Другое

Средние

Разброс

Характеристики связи

Медиана

M(x)

Д(x)

Другие

Эквивалентность

Номинальная

Распределение по классам эквивалентности

Нет

Линейный порядок

Порядка

Порядок

Нет

Да

Нет

—

R(ξ , η)

То же, с мультипликативной метрикой

Интервалов

Отношение разностей ф(y1) - ф(y2) = y1 - y2

Ф(y3) - Ф(y4) y3 - y4

Да

Нет

Да

—

corr(ξ, η)

Линейный порядок

Степенная

Отношение разностей логарифмов lnф(y1) - lnф(y2) = lny1 - lny2

lnФ(y3) - lnФ(y4) lny3 - lny5

Нет

Среднегармоническое

—

Линейный порядок

Логарифмическая

Отношение логарифмов lnф(y1) = lny1

lnФ(y2) lny2

Нет

То же

—

То же

Отношений

Отношение оценок ф(y1) = y1

Ф(y2) y3

Да

СВА СГм СГр СК

Да

— +

—

То же, с аддитивной метрикой

Разностей

Разность оценок

ф(y1) - ф(y2) = y1 - y2

Да

—

Да

— +

—

cov(ξ, η)

То же, на числовой оси целых чисел

Абсолютная

Допустимых преобразований нет

Да

—

Да

—

Приложение 4

Рис. 2. Пример нечеткой шкалы

О 10 20 30 40 50 60 70 80 Возраст

Реферат: Основы оценки сложных систем. Понятия и виды шкал. Отработка характеристик, измеряемых в разных шкалах

Похожие рефераты: