| Скачать .docx |
Реферат: Уравнения линейной регрессии
Министерство образования и науки РФ
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Всероссийский заочный финансово-экономический институт
Филиал в г. Туле
Контрольная работа
по дисциплине «Эконометрика»
Тула - 2010 г.
Содержание
Задача 1
Задача 2 (а, б)
Задача 2 в
По предприятиям легкой промышленности получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (Х, млн. руб.) табл. 1.
Табл. 1.1.
| Х | 33 | 17 | 23 | 17 | 36 | 25 | 39 | 20 | 13 | 12 |
| Y | 43 | 27 | 32 | 29 | 45 | 35 | 47 | 32 | 22 | 24 |
Требуется:
1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.
2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков ![]() ; построить график остатков.
; построить график остатков.
3. Проверить выполнение предпосылок МНК.
4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05).
5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (α=0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости α=0,1, если прогнозное значение фактора Х составит 80% от его максимального значения.
7. Представить графически: фактические и модельные значения Y, точки прогноза.
8. Составить уравнения нелинейной регрессии:
гиперболической;
степенной;
показательной.
Привести графики построенных уравнений регрессии.
9. Для указанных моделей найти коэффициенты детерминации и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.
Решение
1. Линейная модель имеет вид:
![]()
Параметры уравнения линейной регрессии найдем по формулам

Расчет значения параметров представлен в табл. 2.
Табл. 1.2.
| t | y | x | yx | |||||||
| 1 | 43 | 33 | 1419 | 1089 | 42,236 | 0,764 | 0,584 | 90,25 | 88,36 | 0,018 |
| 2 | 27 | 17 | 459 | 289 | 27,692 | -0,692 | 0,479 | 42,25 | 43,56 | 0,026 |
| 3 | 32 | 23 | 736 | 529 | 33,146 | -1,146 | 1,313 | 0,25 | 2,56 | 0,036 |
| 4 | 29 | 17 | 493 | 289 | 27,692 | 1,308 | 1,711 | 42,25 | 21,16 | 0,045 |
| 5 | 45 | 36 | 1620 | 1296 | 44,963 | 0,037 | 0,001 | 156,25 | 129,96 | 0,001 |
| 6 | 35 | 25 | 875 | 625 | 34,964 | 0,036 | 0,001 | 2,25 | 1,96 | 0,001 |
| 7 | 47 | 39 | 1833 | 1521 | 47,69 | -0,69 | 0,476 | 240,25 | 179,56 | 0,015 |
| 8 | 32 | 20 | 640 | 400 | 30,419 | 1,581 | 2,500 | 12,25 | 2,56 | 0,049 |
| 9 | 22 | 13 | 286 | 169 | 24,056 | -2,056 | 4,227 | 110,25 | 134,56 | 0,093 |
| 10 | 24 | 12 | 288 | 144 | 23,147 | 0,853 | 0,728 | 132,25 | 92,16 | 0,036 |
| ∑ | 336 | 235 | 8649 | 6351 | 12,020 | 828,5 | 696,4 | 0,32 | ||
| Средн. | 33,6 | 23,5 | 864,9 | 635,1 |
Определим параметры линейной модели ![]()

Линейная модель имеет вид
![]()
Коэффициент регрессии ![]() показывает, что выпуск продукции Y возрастает в среднем на 0,909 млн. руб. при увеличении объема капиталовложений Х на 1 млн. руб.
показывает, что выпуск продукции Y возрастает в среднем на 0,909 млн. руб. при увеличении объема капиталовложений Х на 1 млн. руб.
2. Вычислим остатки ![]() , остаточную сумму квадратов
, остаточную сумму квадратов ![]() , найдем остаточную дисперсию
, найдем остаточную дисперсию ![]() по формуле:
по формуле:
![]()
Расчеты представлены в табл. 2.


Рис. 1. График остатков ε.
3. Проверим выполнение предпосылок МНК на основе критерия Дарбина-Уотсона.
Табл. 1.3.
| 0,584 | |
| 2,120 | 0,479 |
| 0,206 | 1,313 |
| 6,022 | 1,711 |
| 1,615 | 0,001 |
| 0,000 | 0,001 |
| 0,527 | 0,476 |
| 5,157 | 2,500 |
| 13,228 | 4,227 |
| 2,462 | 0,728 |
| 31,337 | 12,020 |


d1=0,88; d2=1,32 для α=0,05, n=10, k=1.
![]() ,
,
значит, ряд остатков не коррелирован.
4. Осуществим проверку значимости параметров уравнения на основе t-критерия Стьюдента. (α=0,05).

![]() для ν=8; α=0,05.
для ν=8; α=0,05.
Расчет значения ![]() произведен в табл. 2. Получим:
произведен в табл. 2. Получим:
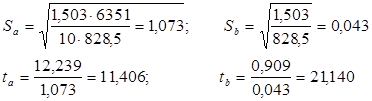
Так как ![]() , то можно сделать вывод, что коэффициенты регрессии a и b с вероятностью 0,95 значимы.
, то можно сделать вывод, что коэффициенты регрессии a и b с вероятностью 0,95 значимы.
5. Найдем коэффициент корреляции по формуле

Расчеты произведем в табл. 2.
![]()
Значит,![]() . Т.о. связь между объемом капиталовложений Х и выпуском продукции Y можно считать тесной, т.к.
. Т.о. связь между объемом капиталовложений Х и выпуском продукции Y можно считать тесной, т.к. ![]() .
.
Коэффициент детерминации найдем по формуле ![]() . Значит, вариация объема выпуска продукции Y на 98,4% объясняется вариацией объема капиталовложений X.
. Значит, вариация объема выпуска продукции Y на 98,4% объясняется вариацией объема капиталовложений X.
Проверим значимость уравнения регрессии с помощью F-критерия Фишера

Fтаб=5,32, т.к. k1=1, k2=8, α=0,05
![]()
т.к. F значительно больше Fтабл, то можно сделать вывод, что уравнение регрессии с вероятностью 95% статистически значимо.
Оценим точность модели на основе использования средней относительной ошибки аппроксимации.

Расчеты произведены в табл. 2.
![]() ,
,
значит, линейную модель можно считать точной, т.к. Е<5%/
6. С помощью линейной модели осуществим прогноз Y при α=0,1 и х=0,8хmax

Определим границы прогноза. t0,1;8=1,86


Найдем границы интервала: ![]()
7. Представим графически фактические и модельные значения Y, точки прогноза.

Рис. 2. Фактические данные, линейная модель и результаты прогнозирования.
8. а) Составим уравнение гиперболической модели. Гиперболическая модель имеет вид
![]() ;
;
Проведем линеаризацию переменной путем замены ![]() .
.

Расчеты произведем в табл. 3.

Модель имеет вид:
![]()
Табл.1.4.
| t | y | x | Х | уХ | |||||
| 1 | 43 | 33 | 0,030 | 1,290 | 0,001 | 36,870 | 6,130 | 37,577 | 0,143 |
| 2 | 27 | 17 | 0,059 | 1,593 | 0,003 | 32,135 | -5,135 | 26,368 | 0,190 |
| 3 | 32 | 23 | 0,043 | 1,376 | 0,002 | 34,683 | -2,683 | 7,198 | 0,084 |
| 4 | 29 | 17 | 0,059 | 1,711 | 0,003 | 32,135 | -3,135 | 9,828 | 0,108 |
| 5 | 45 | 36 | 0,028 | 1,260 | 0,001 | 37,289 | 7,711 | 59,460 | 0,171 |
| 6 | 35 | 25 | 0,040 | 1,400 | 0,002 | 35,260 | -0,260 | 0,068 | 0,007 |
| 7 | 47 | 39 | 0,026 | 1,222 | 0,001 | 37,644 | 9,356 | 87,535 | 0,199 |
| 8 | 32 | 20 | 0,050 | 1,600 | 0,003 | 33,600 | -1,600 | 2,560 | 0,050 |
| 9 | 22 | 13 | 0,077 | 1,694 | 0,006 | 29,131 | -7,131 | 50,851 | 0,324 |
| 10 | 24 | 12 | 0,083 | 1,992 | 0,007 | 28,067 | -4,067 | 16,540 | 0,169 |
| ∑ | 336 | 235 | 0,495 | 15,138 | 0,029 | 297,985 | 1,445 | ||
| Средн | 33,6 | 23,5 | 0,050 | 1,514 | 0,003 |
Найдем индекс корреляции по формуле

![]() ,
,
значит, связь между объемом капиталовложений Х и выпуском продукции Y можно считать тесной, т.к. ![]() .
.
Индекс детерминации найдем по формуле ![]() . Значит, вариация объема выпуска продукции Y на 57,2% объясняется вариацией объема капиталовложений X.
. Значит, вариация объема выпуска продукции Y на 57,2% объясняется вариацией объема капиталовложений X.
Проверим значимость уравнения на основе F-критерия Фишера.
![]()
F>Fтабл (10,692>5,32),
значит, уравнение статистически значимо.
Оценим точность модели на основе средней относительной ошибки аппроксимации.
![]() ,
,
значит, расчетные значения ŷ для гиперболической модели отличаются от фактических значений на 14,45%.
8. б) Построим степенную модель, которая имеет вид
![]()
Проведем линеаризацию переменных путем логарифмирования обеих частей уравнения.

Расчет неизвестных параметров произведем в табл. 5.
Табл. 1.5.
| t | y | x | Y | Х | YХ | |||||
| 1 | 43 | 33 | 1,633 | 1,519 | 2,481 | 2,307 | 42,166 | 0,834 | 0,696 | 0,019 |
| 2 | 27 | 17 | 1,431 | 1,23 | 1,760 | 1,513 | 27,930 | -0,930 | 0,865 | 0,034 |
| 3 | 32 | 23 | 1,505 | 1,362 | 2,050 | 1,855 | 33,697 | -1,697 | 2,880 | 0,053 |
| 4 | 29 | 17 | 1,462 | 1,23 | 1,798 | 1,513 | 27,930 | 1,070 | 1,145 | 0,037 |
| 5 | 45 | 36 | 1,653 | 1,556 | 2,572 | 2,421 | 44,507 | 0,493 | 0,243 | 0,011 |
| 6 | 35 | 25 | 1,544 | 1,398 | 2,159 | 1,954 | 35,488 | -0,488 | 0,238 | 0,014 |
| 7 | 47 | 39 | 1,672 | 1,591 | 2,660 | 2,531 | 46,775 | 0,225 | 0,051 | 0,005 |
| 8 | 32 | 20 | 1,505 | 1,301 | 1,958 | 1,693 | 30,896 | 1,104 | 1,219 | 0,035 |
| 9 | 22 | 13 | 1,342 | 1,114 | 1,495 | 1,241 | 23,644 | -1,644 | 2,703 | 0,075 |
| 10 | 24 | 12 | 1,380 | 1,079 | 1,489 | 1,164 | 22,498 | 1,502 | 2,256 | 0,063 |
| ∑ | 336 | 235 | 15,127 | 13,380 | 20,422 | 18,192 | 12,296 | 0,346 | ||
| Cредн | 33,6 | 23,5 | 1,513 | 1,338 | 2,042 | 1,819 |

Получим ![]()
Перейдем к исходным переменным путем потенцирования данного уравнения.

Найдем индекс корреляции.
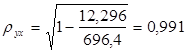 ,
,
значит, связь между объемом капиталовложений Х и выпуском продукции Y тесная, т.к. ![]() .
.
Индекс детерминации найдем по формуле ![]() . Значит, вариация объема выпуска продукции Y на 98,2% объясняется вариацией объема капиталовложений X.
. Значит, вариация объема выпуска продукции Y на 98,2% объясняется вариацией объема капиталовложений X.
Проверим значимость уравнения на основе F-критерия Фишера.
![]()
F>Fтабл (436,448>5,32), значит, уравнение статистически значимо.
Оценим точность модели на основе средней относительной ошибки аппроксимации.
![]() ,
,
значит, расчетные значения ŷ для гиперболической модели отличаются от фактических значений на 3,46%. Модель точная.
8. в) Составим показательную модель, уравнение которой имеет вид:
![]()
Проведем линеаризацию переменных путем логарифмирования обеих частей уравнения.

Табл. 1.6.
| t | y | x | Y | Yx | |||||
| 1 | 43 | 33 | 1,633 | 53,889 | 1089 | 42,343 | 0,657 | 0,432 | 0,015 |
| 2 | 27 | 17 | 1,431 | 24,327 | 289 | 27,220 | -0,220 | 0,048 | 0,008 |
| 3 | 32 | 23 | 1,505 | 34,615 | 529 | 32,126 | -0,126 | 0,016 | 0,004 |
| 4 | 29 | 17 | 1,462 | 24,854 | 289 | 27,220 | 1,780 | 3,168 | 0,061 |
| 5 | 45 | 36 | 1,653 | 59,508 | 1296 | 46,001 | -1,001 | 1,002 | 0,022 |
| 6 | 35 | 25 | 1,544 | 38,600 | 625 | 33,950 | 1,050 | 1,102 | 0,030 |
| 7 | 47 | 39 | 1,672 | 65,208 | 1521 | 49,974 | -2,974 | 8,845 | 0,063 |
| 8 | 32 | 20 | 1,505 | 30,100 | 400 | 29,571 | 2,429 | 5,900 | 0,076 |
| 9 | 22 | 13 | 1,342 | 17,446 | 169 | 24,374 | -2,374 | 5,636 | 0,108 |
| 10 | 24 | 12 | 1,380 | 16,560 | 144 | 23,710 | 0,290 | 0,084 | 0,012 |
| ∑ | 336 | 235 | 15,127 | 365,107 | 6351 | 26,233 | 0,399 | ||
| Средн | 33,6 | 23,5 | 1,513 | 36,511 | 635,1 |

Перейдем к исходным переменным, выполнив потенцирование уравнения.

Найдем индекс корреляции.
![]() ,
,
значит, связь между объемом капиталовложений Х и выпуском продукции Y тесная, т.к. ![]() .
.
Индекс детерминации найдем по формуле ![]() . Значит, вариация объема выпуска продукции Y на 96,2% объясняется вариацией объема капиталовложений X.
. Значит, вариация объема выпуска продукции Y на 96,2% объясняется вариацией объема капиталовложений X.
Проверим значимость уравнения на основе F-критерия Фишера.
![]()
F>Fтабл (202,528>5,32),
значит, уравнение статистически значимо.
Оценим точность модели на основе средней относительной ошибки аппроксимации.
![]() ,
,
значит, расчетные значения ŷ для гиперболической модели отличаются от фактических значений на 3,99%. Модель точная.
9. Сравним полученные модели.
Табл. 1.7.
| Модель регрессии | F-критерий | |||
| Линейная | 0,992 | 0,984 | 492 | 3,2 |
| Гиперболическая | 0,756 | 0,572 | 10,692 | 14,45 |
| Степенная | 0,991 | 0,982 | 436,448 | 3,46 |
| Показательная | 0,981 | 0,962 | 202,528 | 3,99 |
Наилучшей моделью является линейная модель ![]() (по максимуму критерия корреляции, детерминации, F-критерия и минимальной средней ошибке аппроксимации).
(по максимуму критерия корреляции, детерминации, F-критерия и минимальной средней ошибке аппроксимации).
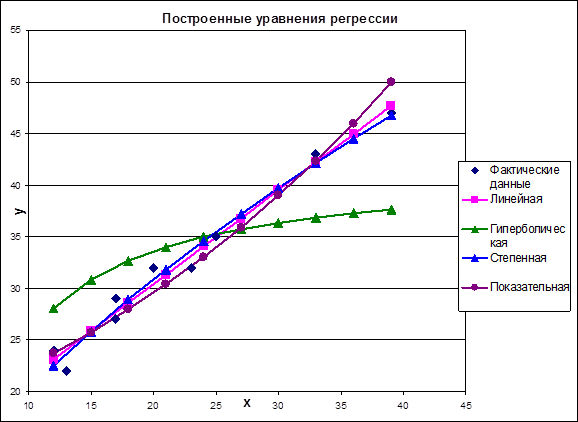
Рис. 3. Построенные уравнения регрессии.
Для каждого варианта даны по две СФМ, которые записаны в виде матриц коэффициентов модели. Необходимо записать системы одновременных уравнений и проверить обе системы на идентифицируемость.
Табл. 2.1.
| Номер варианта | Номер уравнения | Задача 2а | Задача 2б | ||||||||||||
| переменные | переменные | ||||||||||||||
| y1 | y2 | y3 | x1 | x2 | x3 | x4 | y1 | y2 | y3 | x1 | x2 | x3 | x4 | ||
| 6 | 1 | -1 | b12 | b13 | a11 | a12 | 0 | 0 | -1 | 0 | b13 | a11 | a12 | 0 | a14 |
| 2 | b21 | -1 | b23 | a21 | 0 | 0 | a24 | b21 | -1 | 0 | a21 | 0 | a23 | a24 | |
| 3 | 0 | b32 | -1 | a31 | a32 | a33 | 0 | b31 | 0 | -1 | a31 | a32 | 0 | a34 | |
Решение
a) CФМ имеет вид:

Проверим систему на идентифицируемость. Для этого проверим каждое уравнение системы на выполнение необходимого и достаточного условия идентификации.
1) В 1-м уравнении 3 эндогенные переменные y1, y2, y3 (Н=3). В нем отсутствуют экзогенные переменные х3, х4 (D=2). Необходимое условие идентификации

Для проверки на достаточное условие идентификации составим матрицу из коэффициентов при отсутствующих переменных.
| уравнение | Отсутствующие переменные | |
| х3 | х4 | |
| 2 | 0 | а24 |
| 3 | а33 | 0 |
Составим матрицу из коэффициентов

![]()
Определитель матрицы не равен 0, ранг равен 2. достаточное условие идентификации выполняется и 1-е уравнение точно идентифицируемо.
2) Во 2-м уравнении 3 эндогенные переменные y1, y2, y3 (Н=3); отсутствуют экзогенные х2, х3 (D=2).
2+1=3 — необходимое условие идентификации выполнено.
Для проверки на достаточное условие составим матрицу из коэффициентов при отсутствующих переменных.
| уравнение | Отсутствующие переменные | |
| х2 | х3 | |
| 1 | а12 | 0 |
| 3 | а32 | а33 |

![]()
Определитель не равен 0, ранг матрицы равен 2, достаточное условие идентификации выполняется. 2-е уравнение точно идентифицируемо.
3) В 3-м уравнении 2 эндогенные переменные y2, y3 (Н=2); отсутствует 1 экзогенная х4 (D=1).
1+1=2 — необходимое условие идентификации выполняется.
Составим матрицу из коэффициентов при отсутствующих переменных.
| уравнение | Отсутствующие переменные | |
| у1 | х4 | |
| 1 | -1 | 0 |
| 3 | b21 | а24 |

![]()
Определитель не равен 0, ранг матрицы равен 2-м, достаточное условие идентификации выполняется. 3-е уравнение точно идентифицируемо.
Т.о, если все 3 уравнения идентифицируемы, то и СФМ идентифицируема.
б) СФМ имеет вид:

Проверим систему на идентифицируемость, для этого проверим каждое уравнение на выполнение необходимого и достаточного условия идентификации.
1) В 1-м уравнении 2 эндогенных переменных y1, y3 (Н=2); отсутствующая экзогенная переменная х3 (D=1).

Составим матрицу из коэффициентов при отсутствующих переменных.
| уравнение | Отсутствующие переменные | |
| у2 | х3 | |
| 2 | -1 | а23 |
| 3 | 0 | 0 |

![]()
Достаточное условие не выполнено, уравнение не идентифицируемо.
2) Во 2-м уравнении 2 эндогенных переменных y1, y2 (Н=2). Отсутствующая экзогенная переменная х2 (D=1). Необходимое условие D+1=H выполняется.
Составим матрицу из коэффициентов при отсутствующих переменных.
| уравнение | Отсутствующие переменные | |
| у3 | х2 | |
| 1 | b13 | а12 |
| 3 | -1 | a32 |

![]()
Необходимое условие идентификации выполняется. 2-е уравнение точно идентифицируемо.
3) В 3-м уравнении 2 эндогенных переменных y1, y3 (Н=2); отсутствующая экзогенная переменная х3 (D=1). Необходимое условие D+1=H выполняется. Составим матрицу из коэффициентов при отсутствующих переменных.
| уравнение | Отсутствующие переменные | |
| у2 | х3 | |
| 1 | 0 | 0 |
| 2 | -1 | a23 |

![]()
Достаточное условие не выполняется. 3-е уравнение не идентифицируемо.
Т.к. 1-е и 3-е уравнения не идентифицируемы, то и вся СФМ не является идентифицируемой.
Ответ: а) СФМ идентифицируема; б) СФМ не является идентифицируемой.
По данным таблицы для своего варианта, используя косвенный метод наименьших квадратов, построить структурную форму модели вида:

Табл. 2.2.
| Вариант | n | y1 | y2 | x1 | x2 |
| 6 | 1 | 77,5 | 70,7 | 1 | 12 |
| 2 | 100,6 | 94,9 | 2 | 16 | |
| 3 | 143,5 | 151,8 | 7 | 20 | |
| 4 | 97,1 | 120,9 | 8 | 10 | |
| 5 | 63,6 | 83,4 | 6 | 5 | |
| 6 | 75,3 | 84,5 | 4 | 9 |
Решение
Структурную модель преобразуем в приведенную форму модели.

Для нахождения коэффициентов первого приведенного уравнения используем систему нормальных уравнений.

Расчеты произведем в табл. 2.3.
Табл. 2.3.
| n | y1 | y2 | x1 | x2 | |||||||
| 1 | 77,5 | 70,7 | 1 | 12 | 77,5 | 1 | 12 | 930 | 144 | 70,7 | 848,4 |
| 2 | 100,6 | 94,9 | 2 | 16 | 201,2 | 4 | 32 | 1609,6 | 256 | 189,8 | 1518,4 |
| 3 | 143,5 | 151,8 | 7 | 20 | 1004,5 | 49 | 140 | 2870 | 400 | 1062,6 | 3036 |
| 4 | 97,1 | 120,9 | 8 | 10 | 776,8 | 64 | 80 | 971 | 100 | 967,2 | 1209 |
| 5 | 63,6 | 83,4 | 6 | 5 | 381,6 | 36 | 30 | 318 | 25 | 500,4 | 417 |
| 6 | 75,3 | 84,5 | 4 | 9 | 301,2 | 16 | 36 | 677,7 | 81 | 338 | 760,5 |
| ∑ | 557,6 | 606,2 | 28 | 72 | 2742,8 | 170 | 330 | 7376,3 | 1006 | 3128,7 | 7789,3 |
| средн. | 92,933 | 101,033 | 4,667 | 12 |
Подставив полученные значения в систему нормальных уравнений.

Решение этих уравнений дает значения d11=5,233; d12=5,616.
1-e уравнение ПФМ имеет вид:
![]()
Для нахождения коэффициентов d2k второго приведенного уравнения используем следующую систему нормальных уравнений
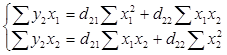
Расчеты произведем в табл. 2.3.
Подставив полученные значения в систему нормальных уравнений, получим

Решение этой системы дает значения d21=9,288; d22=4,696.
2-е уравнение ПФМ имеет вид
![]()
Для перехода от ПФМ к СФМ найдем х2 из второго уравнения.

Подставив это выражение в 1-е уравнение, найдем структурное уравнение.

т.о. b12=1,196; a11=-5,875.
Найдем х1 из 1-го уравнения ПФМ

Подставив это выражение во 2-е уравнение ПФМ, найдем структурное уравнение.

т.о. b21=1,775; a22=-5,272
Свободные члены СФМ находим из уравнений
линейныйрегрессия детерминация аппроксимация квадрат
![]()
![]()
Ответ: окончательный вид СФМ таков
