Реферат: Моделирование работы банка

Введение.

Российские коммерческие банки являются объектом пристального внимания. В настоящий момент банки стали весьма весомым фактором деловой и политической жизни общества, с их деятельностью увязывается решение широкого спектра проблем переходной экономики. Таким образом, банковская система, кроме выполнения своих “обычных функций” , является активным агентом и проводником экономических реформ.

Условия жесткой конкурентной борьбы ставят требования по высокому качеству предоставляемых банку услуг. Следовательно, одной из основных задач является оптимизация внутреннего функционирования. Данный подход предоставляет следующие возможности: проведение расчета и обоснование плановых показателей, входящих в систему планирования;обеспечение контроля выполнения планов и оценки деятельности по результатам за период; обоснование и принятие организационных решений по движению кадров, ликвидации и создании подразделений банка.

С точки зрения методологии, здесь наиболее широко применим метод группировки данных, то есть на основании нескольких экономических критериев выделяется база для расчета доходов и расходов.

На основании этих данных при помощи методов математико-экономического моделирования (в частности, используемая в данной работе динамическая модель стохастического программирования) может быть получено эффективное решение, которое поможет оптимизировать внутреннее функционирование банка. С помощью такого подхода определяется эффективность деятельности филиальной сети и продуктов ее производства.

1.Банковская система.

Наличие эффективной, разветвленной банковской системы - важнейшая черта любой развитой рыночной экономики. В России мы можем наблюдать интереснейший феномен. За считанные месяцы множество банков, объединившись в систему, взяло на себя все обеспечение внутреннего денежного обращения и внешнего оборота страны. При этом их начальный капитал образовался из активов государственных промышленных и торговых предприятий, получивших самостоятельность структурных подразделений Госбанка СССР.

Когда же в 1994 году было прекращено централизованное льготное кредитование производства, коммерческие банки мгновенно взяли на себя и все кредитные операции. В настоящее время, несмотря на определенные признаки кризиса, банковская система является наиболее активным сектором экономики и занимает в ней доминирующее положение.

Главным в сущности банка, его основой, считается организация денежно-кредитного процесса и имитирование денежных знаков.

Одно из определений коммерческого банка: это фирма, имеющая чартер правительства на ведение банковских операций.

К основным видам предоставляемых услуг, согласно [2], можно отнести:

факторинг - ряд комиссионно - посреднических услуг, оказываемых банком клиенту, в процессе осуществления последним расчетов за товары и услуги и сочетающихся как правило с кредитованием его оборотного капитала;

лизинг - банк в данном случае может выступать арендодателем, либо посредником между арендодателем и арендатором;

доверительные услуги - с ценными бумагами, депозитными операциями, управление имуществом;

информационные - о кредитоспособности, о процентной ставке; консультационные услуги - о повышении класса кредитоспособности клиента.

Для обеспечения экономических условий устойчивого функционирования банка, ЦБ России устанавливает следующие экономические нормативы деятельности коммерческих банков:

- нормативы достаточности капитала коммерческого банка;

- нормативы ликвидности баланса коммерческого банка;

- минимальный размер обязательных резервов, депонируемых в ЦБ России;

- максимальный размер риска на одного заемщика.¹

Наиболее часто ликвидность определяют, как способность актива быть переведенным в наличные деньги за непродолжительное время без неопределенности и существенных потерь его стоимости. Однако рыночная структура в цивилизованных странах уже настолько развита ,что даже для самых низколиквидных активов время реализации можно считать малым при долгосрочном планировании и первым признаком ликвидности актива становится степень возможности его использования в качестве средства платежа .

При этом ЦБ применяет нормативы как директивного характера, обязательные для выполнения всеми коммерческими банками, так и оценочные, используемые для анализа их деятельности и финансового состояния.

Деятельность отдельных подразделений , в соответствии с выполнением определенных функций , оценивается при помощи введения системы специальных индивидуальных экономических показателей, как правило, валовых. Функции предварительно не анализируются. При этом работа нескольких подразделений, включенных в одну «технологическую цепочку», может оцениваться совершенно независимо и рассматривается изолированно.

По [8],для банка в целом, может использоваться, к примеру, еще и следующая система показателей:

1)темпы роста прибыли (убытков) за период в результате деятельности;

2)темпы роста валюты баланса; доля накопленной прибыли в валюте баланса;

3)величина и качество работающих активов: доля работающих активов, доля предоставленных кредитов в общей сумме активов;

4)показатели рентабельности: доходы/расходы, прибыль/активы, прибыль/активы работающие, доходы/собственный капитал банка;

5)экономические нормативы деятельности установленные Центральным Банком;

6)основные коэффициенты ликвидности.

Все нормативные таблицы, формулы, можно найти в любом учебнике по банковскому делу. В дальнейшем , при постановке и рассмотрении задачи будем считать естественным выполнение этих ограничений .

Важную роль при конкретизации функционирования банка может играть тип стратегии:

1. продажа освоенных услуг старым клиентам;

2. проникновение (прежние услуги новым клиентам на старом рынке);

3. развитие (продажа старых услуг на новом рынке);

4. сбыт новых услуг (новые услуги на старом рынке);

5. диверсификация (новые услуги на новом рынке).

Существует иерархическая структура целей:

- перспективные цели (максимизация прибыли, выживание, максимизация доходов акционеров, максимизация корпорационного роста и др.)

- среднесрочные цели (увеличение рыночной доли, рост дохода в расчете на акцию, расширение клиентуры, увеличение капитальной базы и др.)

- краткосрочные цели (доходность активов, доходность капитала, доходность инвестиций, повышение квалификации персонала и др.)

Таким образом, мы видим, что все зависит от целей, которые ставит перед собой банк . Обобщим их, будем считать, что банк стремится максимизировать прибыль.

Опираясь на [1],опишем структуру коммерческого банка, она нам понадобится в дальнейшем. (рис.1).

Разумеется, приведенная схема является примерной, так как огромное влияние на структуру аппарата управления банка оказывают масштабы его деятельности, степень специализации, возможность совершать те или иные операции. В ряде случаев банк не выполняет тех или иных услуг, объем его операций слишком незначительный , что бы формировать не только управление, но и отделы. Но мы не будем заострять на этом внимание.

Для эффективного решения непосредственно управленческих задач, достижения устойчивого и прибыльного функционирования банка необхо­димо проведение глубокого анализа всех сторон его деятельности на осно­ве внутренней информации: рентабельности комплекса оказываемых услуг и операций, окупаемости произведенных затрат, прибыльности функциони­рования отдельных подразделений и др. Особую важность подобный ана­лиз приобретает в условиях обострившейся конкуренции на банковских рынках, усиления регулирующих ограничений со стороны государственных органов, участившихся банкротств и отзывов лицензий коммерческих бан­ков.

2.Виды моделей.

2.1.Линейное программирование.

Ответственные решения в современных целенаправленных системах планирования и управления должны быть в некотором смысле экстремальными или близкими к ним. Отступление от этого принципа обычно связано с излишними затратами (часто весьма значительными) и снижает эффективность управления (часто весьма существенно).

Большое число задач планирования, управления и проекти­рования укладывается в схему линейного программирования:

C x  min, (1.1)

Ax  b, (1.2)

X  0. (1.3)

Еще более широкий класс задач выбора эффективного ре­шения укладывается в рамки общей схемы математического программирования.

План, набор команд управления или проект часто могут быть формально представлены в виде системы чисел или функ­ций, удовлетворяющих определенным ограничениям — равен­ствам, неравенствам или логическим соотношениям. План, си­стема команд управления или проект оптимальны, если они, кроме того, обращают в минимум или в максимум (в зависи­мости от постановки задачи) некоторую функцию от искомых параметров — показатель качества решения.

Запись (1.1)—(1.3), вполне осмысленная при детерминиро­ванных значениях параметров условий задачи, теряет опреде­ленность и требует дополнительных разъяснений при случайных значениях исходных данных. Между тем во многих прикладных задачах коэффициенты c_j целевой функции, элементы матрицы условий А или составляющие вектора ограничений b — случай­ные величины.

Исходная информация для планирования, проектирования и управления в экономике, как пра­вило, недостаточно достоверна. Планирование производства обычно ведется в условиях неполной информации об обстановке, в которой будет выполняться план и реализовываться произ­веденная продукция. Во всех случаях в моделях математического программирования, к исследованию которых сводятся задачи планирования, проектирования и уп­равления, отдельные или все параметры целевой функции и ограничений могут оказаться неопределенными или случай­ными, Естественный на первый взгляд путь анализа подобных задач—замена случайных параметров их средними значениями и вычисление оптимальных планов полученных таким образом детерминированных моделей—не всегда оправдан. При сгла­живании параметров условий задачи может быть нарушена адекватность модели изучаемому явлению. Усреднение исходных данных может привести к потере полезной информации и привнести в модель ложную информацию. Решение детерми­нированной задачи с усредненными параметрами может не удовлетворять ограничениям исходной модели при допустимых реализациях параметров условий.

2.2.Стохастическое программирование.

В одних случаях опыт, статистика и изучение процессов, определяющих изменение исходных данных и формирующих условия, в которых реализуется план, проект или система управ­ления, позволяют устанавливать те или иные вероятностные характеристики параметров целевой функции и ограничений задачи. В других случаях нет оснований, для каких бы то ни было суждений о статистических особенностях явлений, способ­ных изменить предполагаемые значения параметров условий задачи. Ситуации первого типа называются ситуациями, связан­ными с риском, а ситуации второго типа—неопределенными. И те, и другие являются предметом исследования стохастического программирования—раздела математического програм­мирования, изучающего теорию и методы решения условных экстремальных задач при неполной информации о параметрах условий задачи.

Постановки задач стохастического программирования суще­ственным образом зависят от целевых установок и информаци­онной структуры задачи.

В приложениях стохастическое программирование исполь­зуется для решения задач двух типов. В задачах первого типа прогнозируются статистические характеристики поведения мно­жества идентичных экстремальных си­стем. Соответствующий раздел стохастического программирова­ния будем называть пассивным стохастическим программиро­ванием. Модели второго типа предназначены для построения методов и алгоритмов планирования и управления в условиях неполной информации. Соответствующий раздел стохастического программирования будем называть активным стохастическим программированием, подчеркивая этим действенную целевую на­правленность моделей.

Подходы к постановке и анализу стохастических экстре­мальных задач существенно различаются в зависимости от того, получена ли информация о параметрах условий задачи (пли об их статистических характеристиках) в один прием или по частям (в два или более этапов). При построении стохастиче­ской модели важно также знать, необходимо ли единственное решение, не подлежащее корректировке, или можно по мере накопления информации один или несколько раз подправлять решение. Другими словами, речь идет о том, какая задача рас­сматривается: статическая или динамическая. В соответствии с этим в стохастическом программировании исследуются одно­этапные, двухэтапные и многоэтапные задачи.

Статические, или одноэтапные, задачи стохастического про­граммирования представляют собой естественные стохастиче­ские аналоги детерминированных экстремальных задач, в кото­рых динамика поступления исходной информации не играет роли, а решение принимается один раз и не корректируется. Одноэтапные стохастические задачи, как те, что порождены де­терминированными моделями стохастического программирова­ния, так и те, что имеют смысл только при случайных парамет­рах условий, различаются характером ограничений и выбором целевой функции.

Разработка предварительного плана и компенсация невя­зок—два этапа решения одной задачи. В соответствии с этим задачи рассматриваемого типа называют двухэтапными за­дачами стохастического программирования.

Естественным обобщением двухэтапных задач являются многоэтапные (динамические) задачи стохастического програм­мирования. Часто в процессе управления представляется воз­можность последовательно наблюдать ряд реализаций парамет­ров условий и соответствующим образом корректировать план. Естественно, что как предварительный план, так и последова­тельные корректировки должны, помимо содержательных огра­ничений, учитывать априорные статистические характеристики случайных параметров условий на каждом этапе.

К анализу многоэтапных задач стохастического программи­рования сводятся формальные исследования численных методов планирования производства и развития экономической системы.

Роль стохастических моделей и методов в исследо­вании закономерностей поведения экономических систем и в разработке количественных методов планирования экономики и управления производством имеет два аспекта — методологический и вычислительный. И тот и другой связаны с одной из важнейших категорий современной матема­тической логики — с понятием сложности, точнее, с понятиями «сложность алгоритма», «сложность вычислений» и «сложность развития».

Роль вычислительного аспекта проблемы определяется тем, что планирование, управление и проектирование происходят, как правило, в условиях неполной информации. Рыночная конъюнктура, спрос на продукцию, изменения в состоянии обо­рудования не могут быть точно предсказаны. В условиях кон­курентной экономики дополнительно возникает направленная дезинформация.

Учет случайных факторов и неопределенности в планировании и управлении — важная задача стохастического программирования.

Однако этим не исчерпывается роль стохастических методов в экономическом анализе. Принципы стохастического програм­мирования дают основание для сопоставления затрат на накоп­ление и хранение информации с достигаемым экономическим эффектом, позволяют аргументировать рациональное разделе­ние задач между человеком и вычислительной машиной и слу­жат теоретическим фундаментом для алгоритмизации управле­ния сложными системами. Принципы стохастического програм­мирования позволяют сблизить точные, но узко направленные формальные математические методы с широкими, но нечеткими содержательными эвристическими методами анализа. И здесь, таким образом, мы переходим к методологической роли стоха­стического программирования в исследовании сложных систем.

В связи с оценками сложности алгоритмов и вычислений представляет смысл условно разделить задачи планирования, управления и проектирования на задачи вычислительного и не вычислительного характера.

Многие задачи управления, должны быть отнесены к классу задач не вычислительного характера. Т.о. необходимо согласование сложности управляемого объекта и управляющего устройства за счет ра­ционального упрощения объекта (разумной переформулировки задачи).

2.3.Формальная постановка стохастической задачи.

Приведем формальную постановку многоэтапной стохастиче­ской задачи. Пусть _i—набор случайных параметров i-го этапа, a x_i —решение, принимаемое на i-м этапе. Обозначим ^k =(₁ , … , _k) , x^k = (x₁ , … ,x_n) ,

k = 1,…,n .

Общая модель многоэтапной задачи стохастиче­ского программирования имеет вид:

M_ⁿ ₀ ( ⁿ , xⁿ )  min, (4.1)

M _k _k ( ^k , x^k ) ^k-1 b_k (^k-1) , (4.2)

x_kG_k ,k=1,…,n. (4.3)

Здесь ₀ (ⁿ , xⁿ) —случайная функция от решений всех этапов,

_k (^k , x^k) -случайная вектор-функция, определяющая ограни­чения k-го этапа; b_k (^k-1) —случайный вектор; G_k —некоторое множество, определяющее жесткие ограничения k-го этапа; M _k _k ^k-1 —условное математическое ожидание _k в пред­положении, что на этапах, предшествующих k-му, реализован набор

^k-1 =(₁ , … , _k-1).

Предполагается, что совместное рас­пределение вероятностей всех случайных параметров условий задано (или, по крайней мере, известно, что оно существует).

Для того чтобы постановка задачи (4.1)—(4.3) была пол­ной, необходимо еще указать, среди какого класса функций (ре­шающих правил x=x() Х) от реализаций случайных исход­ных данных следует разыскивать решение.

К моменту, когда должно быть принято решение k-то этапа, можно успеть обработать результаты наблюдения реализаций случая на этапах 1, ..., s; sk.

В задачах решение на 1-м этапе принимается после реализации случайных параметров условий на предыду­щем (i—1)-м этапе. Решающие правила имеют вид x_i=x_i (^i-1 ) , i = 1,…,n .

Будем называть такие задачи многоэтапными зада­чами стохастического программирования с условными ограниче­ниями и с априорными решающими правилами.

Сведение задачи управления к анализу модели стохастиче­ского программирования позволяет разделить процесс выбора решения на два этапа. Первый—трудоемкий предваритель­ный — использует структуру задачи и априорную статистиче­скую информацию для получения решающего правила (или ре­шающего распределения) —формулы, таблицы или инструкции, устанавливающей зависимость решения (или функции распре­деления оптимального плана) от конкретных значений парамет­ров условий задачи. Второй — нетрудоемкий оперативный этап — использует решающее правило (решающее распределение) и те­кущую реализацию условий для вычисления оптимального плана (или его распределения).[10]

2.4.Методы решения задач стохастического программирования.

Основные классы задач, для решения которых создается вы­числительный комплекс, непосредственно или методами стоха­стического расширения формулируются как модели стохастиче­ского программирования.

Вообще говоря, все модели выбора решения, сформулирован­ные в терминах математического программирования, могут быть (а в практических задачах, отвечающих управлению сложными системами и процессами, должны быть) сформулированы как модели стохастического программирования.

Соответствие формально построенных стохастических моде­лей содержательным постановкам—решающее условие успеш­ного управления в условиях неполной информации. Вряд ли мо­гут быть приведены универсальные рекомендации по выбору информационной структуры модели и статистических характери­стик, используемых для формирования целевого функционала задачи и области его определения.

Анализ опыта решения практических экстремальных задач методами математического программирования свидетельствует о серьезных успехах этого подхода (и о внедрении данных ме­тодов в практику планирования, управления и проектирования) в задачах относительно простой структуры, главным образом одно экстремальных, при не слишком большой размерности задачи, когда число переменных и ограничений (в моделях достаточно общего вида) не превышает сотен или тысяч. Однако методы детерминированного математического программирования не прививаются в системах большой сложности, отвечающих многоэкстремальным задачам или задачам большой размерно­сти.

До сих пор нет достаточно конструктивного метода решения общей (даже линейной) двухэтапной задачи стохастического программирования. Стандартные методы выпуклого программи­рования в общем случае неприменимы для вычисления предва­рительного плана — решения выпуклой задачи первого этапа. Основная трудность в том, что целевая функция и область определения планов первого этапа заданы. вообще говоря, неявно. В случаях, когда область К имеет относительно простую структуру или задача оказывается с простой рекурсией, эффек­тивным, хотя и трудоемким методом вычисления предваритель­ного плана, оказывается метод стохастических градиентов², представляющий собой итеративный метод типа стохастической аппроксимации.

Все это подсказывает путь алгоритмизации решения сложных задач в автоматизированных системах управления—замену трудоемких процедур, отвечающих обоснованным (точным или приближенным) методам решения детерминированных экстремальных задач, относительно простыми «законами управления»—решающими правилами или решающими распределениями стохастического расширения соответствующих задач.

Платой за упрощение задачи и за переход от громоздких алгоритмов к относительно простым решающим механизмам служат трудоемкая предварительная работа по построению «за­конов управления» и некоторая потеря эффективности решения задачи в каждом отдельном случае.

В литературе по стохастическому программированию опи­саны многочисленные модели выбора решений, сформулирован­ные в терминах стохастического программирования. Разнообразные задачи управления запаса­ми—классические примеры стохастических моделей. Синтез си­стем массового обслуживания, удовлетворяющих заданным тре­бованиям и оптимизирующих пропускную способность системы или определяемый ею доход, сводится к решению экстремаль­ных стохастических задач.

3.Динамическая модель работы банка.

3.1.Вводные сведения.

В общем случае, проведение управленческого анализа разбивается на три

основных этапа:

I.Производится группировка банковских услуг и операций по признаку сферы оказания и осуществления, функциональному подразделению, мес­ту выполнения и общей клиентской базе. Подобные комплексы услуг и опе­раций являются источниками прибыли, составляют единую технологиче­скую цепочку и называются бизнес-центрами. Далее следует сбор и аналитическая обработка данных по каждому из бизнес-центров. Методика анализа включает составление портфеля привле­чения и размещения средств, расчета операционных доходов, расходов и прибыли, накладных и обще банковских расходов, конечной прибыли и анализ окупаемости инвестиций в деятельность бизнес-центра. Для продвижения определенного комплекса услуг бизнес-центра требуют­ся капитальные вложения - инвестиции в техническое и программное обес­печение, помещения и оборудование. Данные инвестиции необходимо оце­нить с точки зрения окупаемости и рентабельности, потоков денежных посту­плений и потоков финансовых средств. Для этой цели производится анализ окупаемости инвестиционных проектов. В рамках этого же этапа производится наиболее важный и необходимый анализ рентабельности отдельных услуг и операций, осуществляемых биз­нес-центром.

II. На втором этапе сгруппированные комплексы услуг и операций (биз­несы) локализуются в организационной структуре банка. Происходит "наложение" и увязывание технологических цепочек бизнесов с функционально территориальной структурой организации. Формируются центры более высо­кого уровня - центры ответственности (или центры прибылей), включающие в себя несколько функционально взаимосвязанных и организационно объеди­ненных бизнес-центров. Необходима методика обоснованного перераспределения затрат ин­фраструктурных подразделений по центрам ответственности. Возможно, так­же такого перераспределения не осуществлять, выделяя в конечных продук­тах анализа результаты деятельности инфраструктурных центров. В ходе анализа рассчитываются основные показатели деятельности цен­тров ответственности - конечная прибыль, объемы привлеченных и разме­щенных средств, окупаемость инвестиционных проектов центра ответствен­ности, которые могут включать несколько взаимосвязанных проектов уровня бизнес-центров.

III.Общую сумму прибыли, заработанную банком, необходимо перерас­пределить, во-первых, по осуществляемым отдельным операциям и услугам, во-вторых, по функциональным подразделениям. Данный этап интегрирует результаты двух предыдущих и является наиболее трудоемким.

Данная разбивка финансовых результатов может производиться до уровня любой глубины - вплоть до каждого отдельного вида услуг и функционально­го подразделения - филиала или отдела.

Рассмотрим общий случай.

3.2.Постановка задачи .

Некоторый банк, организационная структура которого построена на базе отделений, ежегодно распределяет ассигнования на выполнение различных работ. Каждое из S отделений представляет руководству банка данные трех видов . Информация первой группы относится к проведению поисковых исследований неопределенного характера . Если на исследования такого рода в отделении j выделяют v_j тысяч долларов, то оценка ожидаемого долгосрочного дохода равна P_j (v_j ) миллионов долларов. Информация второй группы относится к услугам, по которым поисковые исследования уже завершены и для внедрения которых требуется проведение ряда работ и подсчетов. Для таких проектов ассигнования в объеме w_j тысяч долларов, согласно имеющейся оценке, дадут, в конечном счете, доход в размере Q_j (w_j ) миллионов долларов. К третьей группе относится информация , связанная с улучшением качества уже оказываемых услуг . Затраты x_j тысяч долларов, согласно сделанным оценкам, должны принести всего R_j(x_j) миллионов долларов дополнительного дохода.

Правление банка утверждает общую сумму ассигнований на все проекты в размере N тысяч долларов, и верхний предел L_j ассигнований между отделениями j. Следовательно, необходимо распределить ассигнования между отделениями таким образом, чтобы обеспечивалась максимизация общего дохода банка при наложенных ограничениях.

Математическая модель задачи описывается следующими соотношениями:

[P_j (v _j ) + Q _j (w _j ) + R_j (x _j )] (1)

максимизировать, при ограничениях

(v_j + w_j + x_j ) N (2)

общая сумма ассигнований

v_j + w_j + x_j L_j , j=1,2..s (3)

v_j , w_j , x_j (4) неотрицательные целые при любом j .

Поскольку на все управляемые переменные наложено только одно ограничение (2) , а остальные бюджетные и целочисленные ограничения (3) и (4) относятся только к отделению j ,то в данном случае имеет место задача распределения усилий с одним ограничением.³ Таким образом получаем следующее рекуррентное соотношение :

g_j (n) = max [ P_j ( v_j ) + Q_j (w_j ) + R_j (x_j ) + g_j ( n - v_j - w_j - x_j ) ] , j = 1,2...s (5)

где n = 0,1,2...N и максимизация производится только по неотрицательным целочисленным значениям v_j ,w_j и x_j удовлетворяющим условию:

v_j + w_j + x_j min (L_j , n)

На каждом шаге отыскания максимума можно использовать метод решения задачи о распределении усилий, представив этот пример в следующем виде:

P_j ( v_j ) + Q_j (w_j ) + R_j (x_j ) max (6) при ограничениях

v_j + w_j + x_j y , (7)

где v_j ,w_j и x_j должны быть неотрицательными целыми числами. Необходимо получить решение для каждого значения y = 0,1....L_j .

Чтобы использовать рекуррентный подход к задаче (6)-(7) , примем

p _j (y) = P_j (y) , y = 0,1...L_j , (8)

q _j (y) = max [ Q_j (w_j ) + p_j ( y- w_j ) ] , y = 0, 1 ... L_j (9)

w_j

где максимизация производится только по неотрицательным целым значениям

w_j y , и

r _j (y) = max [ Q_j (x_j ) + q _j (y - x_j )] , y = 0,1... L_j (10)

x_j

где максимизация производится только по неотрицательным целым значениям

x_j y .

Далее находится решение по соотношению:

g _j (n) = max [ r _j (y) + g _j ( n - y ) ] , j = 1,2...s, (11)

y

где n = 0,1...N и максимизация производится только по неотрицательным

целым значениям y , удовлетворяющим условию у min (L_j , n) .

Следовательно, для решения этой задачи нужно связать s расчетов

распределения усилий с общей моделью распределения усилий..

Таким образом, в качестве решения мы получим значения v_j , w_j и x_{j -} выделяемые средства на соответствующие проекты, дающие максимизацию общего дохода банка g _j (n) по отделам j = 1,2...s .

Согласно поставленной задачи (динамическая модель) и решения задач «о распределении усилий», была получена программа.⁴ Она опирается на следующие числовые данные:

• число отделов;

• общий объем финансирования;

• максимальное финансирование отдела;

• зависимость доходов от вложений по видам исследований;

• максимальные объемы финансирования отделов.

После распределения средств по отделам, а затем в каждом отделе, получаем эффективное распределение средств. После чего подсчитываем общий доход

подобного финансирования.

Программа настроена на определенную организационную структуру, базирующуюся на отделах. И может работать с любыми данными укладывающимися в эти рамки с соответствующими ограничениями. Таким образом, она может находить решение заданной проблемы для любого предприятия.

4.Нейронные сети.

4.1. Общие положения по нейронным сетям.

Один из возможных подходов к многомерным и зачастую нели­нейным информационным рядам финансового рынка заключается в том, чтобы по возможности подражать образцам поведения участ­ников рынка, используя такие методы искусственного интеллекта, как экспертные системы или нейронные сети.

На моделирование процессов принятия решений этими методами было потрачено много усилий. Оказалось, однако, что экспертные системы в сложных ситуациях хорошо работают лишь тогда, когда системе присуща внутренняя стационарность (т.е. когда на каждый входной вектор имеется единственный не меняющийся со временем ответ). Под такое описание в какой-то степени подходят задачи ком­плексной классификации или распределения кредитов, но оно пред­ставляется совершенно неубедительным для финансовых рынков с их непрерывными структурными изменениями. В случае с финансо­выми рынками едва ли можно утверждать, что можно достичь пол­ного или хотя бы в определенной степени адекватного знания о данной предметной области, в то время как для экспертных систем с алгоритмами, основанными на правилах, это — обычное требова­ние.

Н
ейронные сети предлагают совершенно новые многообещаю­щие возможности для банков и других финансовых институтов, ко­торым по роду своей деятельности приходится решать задачи в усло­виях небольших априорных знаний

о среде.

Рис.2. Блок-схема финансового

прогнозирования при помощи нейронных сетей.

Характер финансовых рынков драматическим образом меняется с тех пор, как вследствие ослабления контроля, приватизации и появления новых финансовых инструментов национальные рынки слились в общемировые, а в большинстве секторов рынка возросла свобода финансовых опера­ций. Очевидно, что сами основы управления риском и доходом не могли не претерпеть изменений, коль скоро возможности диверси­фикации и стратегии защиты от риска изменились до неузнаваемо­сти.

Возможности такого при­менения облегчаются тем, что имеются огромные базы экономиче­ских данных, — ведь сложные модели всегда прожорливы в отноше­нии информации.

Существенными составными частями нового подхода являются: ней­ронные сети (сети компьютерных процессоров, взаимодействие ко­торых построено по образцу процессов обучения, происходящих в человеческом мозге). Общей чертой новых методов является воз­можность распознавания образов и генетические алгоритмы (методы, в которых, исходя из большого набора первоначальных предположений, выра­батывают все более правильные представления о поведении рынка и, в конечном счете, более содержательные рабочие гипотезы). Про ме­тоды обоих видов говорят, что они управляются данными, в проти­воположность подходу, основанному на применении правил, кото­рый принят в экспертных системах. Системы, основанные на знани­ях, обладают тем недостатком, что построенные на их основе методы торговли оказываются довольно негибкими.

Нейронные сети хорошо приспособлены для решения задач классификации и анализа временных рядов. Задача классификации понимается как задача от­несения предъявленного объекта к одному из нескольких попарно непересекающихся множеств. При этом наиболее важным случаем здесь является бинарная классификация — примерами ее могут слу­жить распознавание доходных и недоходных инвестиций или разли­чение компаний, имеющих хорошие шансы выжить, от тех, которые должны обанкротиться. Способность к моделированию нелинейных процессов, работе с зашумленными данными и адаптивность дают возможность приме­нять нейронные сети для решения широкого класса финансовых за­дач. Время обучения зависит от сложности задач, от выбора на­чальных решений и требуемого качества алгоритма.

В связи с этим не представляется возможным рассмотрение модели работа банка , так как полное описание модели требует большого количества переменных и достаточно сложных связей между ними.

Но, тем не менее, есть выход: разбить общую модель на части. Нельзя сказать, что это решит все проблемы .Между тем , такой подход имеет и свои положительные стороны.

Банк аккумулирует временно свободные денежные средства(вклады).Для того, что бы привлечь вкладчиков, необходимо осуществление таких операций и предоставляемых услуг, что бы доход, полученный в результате был бы оптимальным. Одна из предоставляемых услуг : покупка-продажа наличной валюты. Доходы подвержены значительным колебаниям в зависимости от конъюнктуры рынка. В этом случае существенную помощь может оказать, например, прогнозирование курсов валют, ставок.

Рассмотрим прогнозирование ставки доллара к немецкой марке.

4
.2.Прогнозирование ставки доллара к немецкой марке.

Рис.3. Общая схема работы.

Обучение происходило основываясь на информации о 700 дней. Сеть использовала предсказания изменения ставки на 1 день вперед.. Предсказанные значения для ставки показываются черным цветом. Действительные значения - серым. Прямая с квадратиками – проверочное. (рис.4.)

Рис.4.

Рис.5.

Во время обучения сети были построены обобщающие правила, основываясь на которых было осуществлено предсказание на 35 дней торговли.(рис.5)

Сеть выводит пунктиром, в действительности - сплошной линией.

Таким образом, благодаря этой информации, банк может подкорректировать работу валютного отдела , избежать ошибок в выборе стратегий , потери денег.

Заключение.

Коммерческий банк - это кредитное учреждение, реализующее экономические интересы. Банковское дело - как правило, весьма выгодный бизнес, основанный на определенных принципах. Основной - прибыльность. Показатель прибыли официально считается основным показателем деятельности банка. Иначе говоря, размер капитала, т.к. в балансовом отчете в разделе собственные средства (капитал) прибыль занимает не последнее место. Размер капитала банка имеет исключительное значение для его деятельности. Во-первых, регулирующие органы устанавливают мини­мально необходимый размер капитала для вновь созда­ваемых и работающих банков. Во-вторых, капитал бан­ков служит основой (капитальной базой) для установ­ления регулирующими органами нормативов, определя­ющих контролируемые показатели их деятельности. Наконец, чем больше размер капитала банка, тем выше уверенность его вкладчиков, кредиторов и клиентов, поскольку при этом повышается его надежность.

Т.о. для получения наибольшей прибыли предполагается создание и организация:

системы информации;

системы прогнозирования денежных ресурсов;

системы принятия решений;

системы контроля.

Представление динамической модели работы банка в виде программы оправды-вает себя, когда число отделов (S) и объемы финансирования (N) достаточно большие. (Уже при S>4 , N>10)

В этом случае преимущества такого подхода к решению задачи неоспоримы, так

как в ручную рассчитать такой объем информации сложно, и программа дает неплохие результаты.

Программа настроена на определенную организационную структуру, базирующуюся на отделах.

Методика, изложенная в данной работе, может быть применена в любом отдельно взятом банке. Например, в следующих банках: Возрождение, Волгопромбанк, Индустриальный, РусЮгБанк, Сава и др.

Приложение 1.

Модель общего вида задачи распределения усилий.

Такой же динамический под­ход в той же мере справедлив и в случае, когда огра­ничение нелинейно, и в случае, когда огра­ничение является линейным..

Модель описывается следующими соотношениями:

Максимизировать 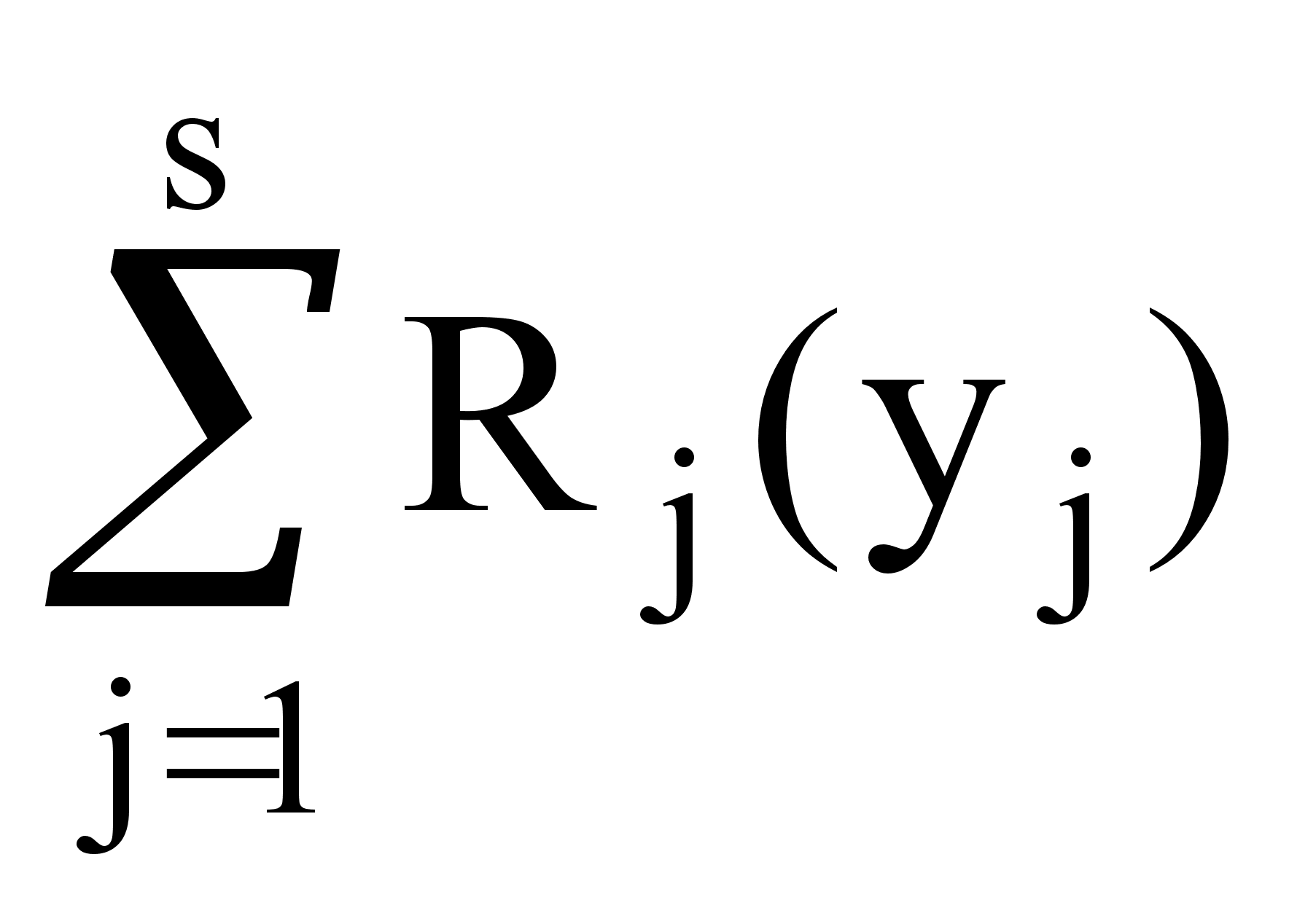(1’)

при ограничениях (2’)

y_j = 0 , 1, 2, ... при любом j. (3’)

Допустим, что каждая функция H_j(y_j) есть неубывающая функция, принимающая целочисленные значения при любом y_j = 0, 1, 2, ... и удовлетворяющая условию H_j(0) = 0. Для упрощения рассужде­ний принимается, что H₁(y₁) = y₁, вследствие чего допустимое решение существует при любом значении N. На каждую величину y_j можно также наложить ограничение сверху.

Рекуррентное соотношение динамического программирования, соответствующее задаче (1’) — (3’), имеет следующий вид:

g_j = max {R_j (y_j) +g_j-1 [ n – H_j(y_j)]}, j = 1,2,...,s, (4’)

g₀ ( n ) ≡ 0, j = 0 , (5’)

где n = 0, 1, ..., N, а максимум берется только по неотрицатель­ным целочисленным значениям y_j, удовлетворяющим условию H_j(y_j) ≤ n. Отыскивается значение g_s(N). Для выполнения вычисле­ний нужно определить по выражению (4’) значения каждой функции g_j(n) при n = 0, 1, ..., N, начиная с j = 1 и заканчивая j=s. [4].

Приложение 2.

Листинг.

{ Динамическая модель работы банка }

program Bank;

uses Crt;

const

S = 10; { Число отделов }

N = 67; { Общий объем финансирования }

Lmax = 17; { Максимальное финансирование отдела }

{ Зависимости доходов от вложений по видам исследований и отделам }

P : array[1..S, 0..Lmax] of integer = (

{0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 }

(0, 0, 3, 1, 1, 22, 10, 17, 2, 9, 10, 6, 6, 17, 14, 10, 10, 10 ),

(0, 0, 3, 1, 1, 2, 10, 17, 9, 2, 11, 7, 6, 13, 13, 13, 13, 13 ),

(0, 0, 3, 8, 1, 20, 17, 6, 6, 6, 6, 7, 7, 8, 8, 8, 8, 8 ),

(0, 1, 3, 1, 1, 22, 10, 17, 3, 9, 20, 6, 6, 17, 14, 10, 10, 10 ),

(0, 1, 30,8, 1, 2, 11, 17, 4, 2, 11,27,26, 33, 33, 33, 33, 33 ),

(0, 1, 3, 7, 1, 14, 17, 6, 6, 6, 6, 7,17, 18, 18, 18, 8, 28 ),

(0, 3, 2, 6, 1, 22, 10, 14, 7, 9, 10, 6, 6, 17, 14, 15, 10, 11 ),

(0, 3, 1, 5, 1, 2, 0, 17, 9, 2, 11, 7, 6, 13, 13, 13, 13, 13 ),

(0, 5, 6, 14,1, 21, 15, 6, 8, 6, 6, 7, 7, 8, 11, 8, 8, 8 ),

(0, 6, 9, 3, 1, 20, 12, 4, 6, 1, 6, 7, 7, 8, 14, 18, 28, 38 )

);

Q : array[1..S, 0..Lmax] of integer = (

{0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 }

(0, 0,13, 3, 3, 23, 30, 15,12,19, 11, 1, 1, 11, 13, 14, 14, 14 ),

(0, 0, 3, 1,11, 2, 10, 17,19, 2, 11, 7, 6, 13, 13, 33, 33, 14 ),

(0, 0, 3, 8,11, 20, 17, 6, 16, 6, 6, 7, 7, 8, 8, 38, 48, 5 ),

(0, 1, 3, 1,11, 22, 10, 17,13, 9, 20, 6, 6, 17, 14, 40, 14, 15 ),

(0, 1, 30,8,11, 2, 11, 17,11, 2, 11,27,26, 33, 33, 32, 34, 35 ),

(0, 1, 3, 7,11, 14, 17, 6, 16,16,16, 17,17, 18, 18, 28, 14, 25 ),

(0, 3, 2, 6,11, 22, 10, 14,17,19, 10, 6,16, 17, 14, 15, 10, 15 ),

(0, 3, 1, 5,11, 2, 0, 17,19,12, 11, 7,16, 13, 13, 13, 15, 13 ),

(0, 5, 6, 14, 11, 21, 15, 6, 18,16,16, 17,17, 8, 11, 18, 18, 18 ),

(0, 6, 9, 3,11, 20, 12, 4, 16,11,16, 7, 7, 8, 14, 18, 28, 38 )

);

R : array[1..S, 0..Lmax] of integer = (

{0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 }

(0, 0, 0, 0, 0, 20, 0, 10, 0, 0, 10, 0, 6, 10, 10, 10, 10, 10 ),

(0, 0,13,11, 1,12, 10, 17,19,12, 11,17,16, 13, 13, 13, 13, 13 ),

(0, 0,13,28,11, 20, 17,16, 16,16,16, 27,37, 38, 38, 18, 18, 8 ),

(0,11,13,21,11, 22, 10, 17, 3, 9, 20, 6, 6, 17, 14, 10, 10, 10 ),

(0,11, 30,8,11,12, 11, 17,14, 2, 11,27,26, 33, 33, 33, 33, 33 ),

(0,11,13,27, 1, 14, 17,16, 16, 6, 6, 7,17, 18, 18, 18, 8, 28 ),

(0,13,12,26, 1, 22, 10, 14,17, 9, 10,26,26, 17, 14, 15, 10, 11 ),

(0,13,11,25,21, 2, 0, 17,19, 2, 11,27,26, 13, 13, 13, 13, 13 ),

(0,15,16,21,21, 21, 15,16, 18, 6, 6, 27,27, 28, 11, 28, 28, 8 ),

(0,16,19,23, 1, 20, 12, 4, 26,21,26, 27,27, 28, 14, 18, 28, 38 )

);

{ Максимальные объемы финансирования отделов }

L : array[1..S] of integer = ( 12, 5, 3, 10, 11, 7, 8, 10, 6, 17 );

function min(a, b : integer) : integer;

begin

if a > b then min := b

else min := a;

end;

var

i, j, y, k, f : integer;

Sum, nn : integer;

pp, qq, rr : array[1..S, 0..Lmax] of integer;

T : array[0..S, 0..N] of record

y, g : integer;

end;

T2 : array[0..3, 0..Lmax] of record

y, g : integer;

end;

Income : array[1..S, 0..3] of integer;

begin

ClrScr;

{ Поиск p(y) }

for j := 1 to S do

for y := 0 to L[j] do

pp[j, y] := P[j, y];

{ Поиск q(y) }

for j := 1 to S do

for y := 0 to L[j] do begin

qq[j, y] := Q[j, 0] + pp[j, y];

for i := 1 to y do

if Q[j, i] + pp[j, y-i] > qq[j, y] then

qq[j, y] := Q[j, i] + pp[j, y-i];

end;

{ Поиск r(y) }

for j := 1 to S do

for y := 0 to L[j] do begin

rr[j, y] := R[j, 0] + qq[j, y];

for i := 1 to y do

if R[j, i] + qq[j, y-i] > rr[j, y] then

rr[j, y] := R[j, i] + qq[j, y-i];

end;

{ Поиск g }

for i := 0 to N do begin

T[0, i].y := 0;

T[0, i].g := 0;

end;

for j := 1 to S do

for i := 0 to N do begin

T[j, i].y := 0;

T[j, i].g := rr[j, 0] + T[j-1, i].g;

for y := 1 to min(L[j], i) do

if rr[j, y] + T[j-1, i-y].g > T[j, i].g then begin

T[j, i].y := y;

T[j, i].g := rr[j, y] + T[j-1, i-y].g;

end;

end;

{ Распределение средств по отделам }

nn := N;

for j := S downto 1 do begin

Income[j, 0] := T[j, nn].y;

nn := nn - Income[j, 0];

end;

{ Распределение средств в каждом отделе }

for k := 1 to S do begin

for i := 0 to Income[k, 0] do begin

T2[0, i].y := 0;

T2[0, i].g := 0;

end;

for j := 1 to 3 do

for i := 0 to Income[k, 0] do begin

T2[j, i].y := 0;

case j of

1 : T2[j, i].g := P[k, 0] + T2[j-1, i].g;

2 : T2[j, i].g := Q[k, 0] + T2[j-1, i].g;

3 : T2[j, i].g := R[k, 0] + T2[j-1, i].g;

end;

for y := 1 to i do begin

case j of

1 : f := P[k, y];

2 : f := Q[k, y];

3 : f := R[k, y];

end;

if f + T2[j-1, i-y].g > T2[j, i].g then begin

T2[j, i].y := y;

T2[j, i].g := f + T2[j-1, i-y].g;

end;

end;

end;

nn := Income[k, 0];

Income[k, 3] := T2[3, nn].y;

nn := nn - Income[k, 3];

Income[k, 2] := T2[2, nn].y;

nn := nn - Income[k, 2];

Income[k, 1] := T2[1, nn].y;

end;

{ Результаты }

WriteLn('Динамическая модель работы банка');

Sum := 0;

for j := 1 to S do begin

for i := 1 to 3 do

WriteLn('y[', j, ', ', i, '] := ', Income[j, i]);

WriteLn('Расход: ', Income[j, 0]);

WriteLn('Доход: ',

P[j, Income[j, 1]] + Q[j, Income[j, 2]] + R[j, Income[j, 3]]);

Sum := Sum + P[j, Income[j, 1]] + Q[j, Income[j, 2]] + R[j, Income[j, 3]];

readkey;

end;

WriteLn('Общий доход: ', Sum);

WriteLn(' Сделанные вложения: ', Sum);

readkey;

end.

Результаты.

y[1,1]=5 y[2,1]=0 y[3,1]=0 y[4,1]=5

y[1,2]=2 y[2,2]=0 y[3,2]=0 y[4,2]=0

y[1,3]=5 y[2,3]=2 y[3,3]=3 y[4,3]=3

Расходы:12 Расходы:2 Расходы:3 Расходы:8

Доходы:55 Доходы:13 Доходы:28 Доходы:43

y[5,1]=2 y[6,1]=0 y[7,1]=5 y[8,1]=0

y[5,2]=2 y[6,2]=4 y[7,2]=0 y[8,2]=0

y[5,3]=2 y[6,3]=3 y[7,3]=3 y[8,3]=5

Расходы:6 Расходы:7 Расходы:8 Расходы: 3

Доходы:12 Доходы:38 Доходы:48 Доходы:25

y[9,1]=3 y[10,1]=5

y[9,2]=1 y[10,2]=5

y[9,3]=1 y[10,3]=3

Расходы:5 Расходы:13

Доходы:34 Доходы:63

Было осуществлено финансирование в размере 67 миллионов долларов.

Общая прибыль составила 437 миллионов долларов.

Итого, чистая прибыль 370 миллионов долларов.

Литература.

1)Банки и банковские операции : Учебник для вузов. / Под редакцией Е.Ф.Жукова.

-М.:Банки и биржи , ЮНИТИ ,1997.

2)Банковское дело / Под редакцией О.И.Лаврушина .-М .: Банковский и биржевой научно- консультационный центр , 1992 .

3)Банковское дело / Под редакцией В.И.Колесникова , Л.П.Кроливецкой .- М.:Финансы и статистика , 1995 .

4)Бэстенс Д.-Э.,Ван Дер Берг В.-М.,Вуд Д. .Нейронные сети и финансовые рынки :принятие решений в торговых операциях. М.:ТВП,Финансы и страховая математика ,т.3.,1997.

5)Вагнер Г. Основы исследования операций.-М.: Мир, т.2 ,1973.

6)Гуриев С.М. ,Поспелов И.Г. .Модель деятельности банка при отсутствии инфляции и экономического роста.// Экономика и математические методы , том 33 , вып.3 ,1997.

7)Киперман Г.Я.,Сурганов Б.С..Популярный экономический словарь .- М.: Экономика , 1993.

8)Перар Ж.Управление международными денежными потоками.- М.:Финансы и статистика,1998.

9)Садвакасов К..Коммерческие банки.Управленческий анализ деятельности .

Планирование и контроль. - М.:Ось-89,1998.

10)Черкасов В.Е.Финансовый анализ в коммерческом банке. – М.:ИНФРА--М, 1995.

11)Юдин Д.Б., Березнева Т.Д.. Статистические и динамические модели стохастического программирования.// Применение исследования операций в экономике.М.:Экономика,1977.

Содержание: Введение................................................................................................1 Глава1.Банковская система.................................................................2 Глава2.Виды моделей..........................................................................6

2.1.Линейное программирование.............................................6

2.2.Стохастическое программирование...................................7

2.3.Формальная постановка стохастической задачи...............9

2.4.Методы решения.................................................................10 Глава3.Динамическая модель работы банка...................................12

3.1.Вводные сведения...............................................................12

3.2.Постановка задачи..............................................................13 Глава4.Нейронные сети......................................................................16

4.1.Общие положения.............................................................16

4.2.Прогнозирование ставки доллара к немецкой марке.....18 Заключение...........................................................................................20 Приложения..........................................................................................21 Литература...........................................................................................27

Министерство общего и профессионального образования

Российской Федерации

Волжский гуманитарный институт

Волгоградского государственного университета

Кафедра информатики и математического моделирования

дипломная работа

на тему: Моделирование работы банка.

Выполнила: студентка 5 курса

ПМФ - 942 группы

Шалимова М.В.___________

(подпись)

Научный руководитель:

к.т.н., доцент

Мирецкий И.Ю.___________

(подпись)

Заведующий кафедрой:

к.ф.-м.н., доцент

Батхин А.Б.________________

(подпись)

Волжский

1999 г.