| Скачать .docx | Скачать .pdf |
Реферат: Кредиты от коммерческого банка на жилищное строительство
Задание 1
Приведены поквартальные данные о кредитах от коммерческого банка на жилищное строительство (в условных единицах) за 4 года (всего 16 кварталов, первая строка соответствует первому кварталу первого года).
Требуется:
1) Построить адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора, приняв параметры сглаживания a 1 =0,3; a 2 =0,6; a 3 =0,3.
2) Оценить точность построенной модели с использованием средней относительной ошибки аппроксимации.
3) Оценить адекватность построенной модели на основе исследования:
- случайности остаточной компоненты по критерию пиков;
- независимости уровней ряда остатков по d -критерию (критические значения d 1 = 1,10 и d 2 = 1,37) и по первому коэффициенту автокорреляции при критическом значении r 1 = 0,32;
- нормальности распределения остаточной компоненты по R/S-критерию с критическими значениями от 3 до 4,21.
4) Построить точечный прогноз на 4 шага вперед, т.е. на 1 год.
5) Отразить на графике фактические, расчетные и прогнозные данные.
Таблица 1
Поквартальные данные о кредитах от коммерческого банка на жилищное строительство (в условных единицах) за 4 года
| t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
2 |
13 |
14 |
15 |
16 |
| Y(t) |
28 |
36 |
43 |
28 |
31 |
40 |
49 |
30 |
34 |
44 |
52 |
33 |
39 |
48 |
58 |
36 |
Решение
Будем считать, что зависимость между компонентами тренд-сезонный временный ряд мультипликативная. Мультипликативная модель Хольта-Уинтерса с линейным ростом имеет следующий вид:
![]() , (1)
, (1)
где k – период упреждения;
Y р ( t ) — расчетное значение экономического показателя для t -гo периода;
a ( t ) , b ( t ) и F ( t ) - коэффициенты модели; они адаптируются, уточняются по мере перехода от членов ряда с номером t -1 к t ;
F ( t + k - L ) - значение коэффициента сезонности того периода, для которого рассчитывается экономический показатель;
L - период сезонности (для квартальных данных L =4 , для месячных – L =12).
Таким образом, если по формуле 1 рассчитывается значение экономического показателя, например за второй квартал, то F ( t + k - L ) как раз будет коэффициентом сезонности второго квартала предыдущего года.
Уточнение (адаптация к новому значению параметра времени t ) коэффициентов модели производится с помощью формул:
![]() ; (2)
; (2)
![]() ; (3)
; (3)
![]() . (4)
. (4)
Параметры сглаживания a 1 , a 2 и a 3 подбирают путем перебора с таким расчетом, чтобы расчетные данные наилучшим образом соответствовали фактическим (т.е. чтобы обеспечить удовлетворительную адекватность и точность модели).
Из формул 1 - 4 видно, что для расчета а (1) и b (1) необходимо оценить значения этих коэффициентов для предыдущего период времени (т.е. для t =1-1=0). Значения а (0) и b (0) имеют смысл этих же коэффициентов для четвертого квартала года, предшествующего первому году, для которого имеются данные в табл. 1.
Для оценки начальных значений а (0) и b (0) применим линейную модель к первым 8 значениям Y ( t ) из табл. 1. Линейная модель имеет вид:
![]() . (5)
. (5)
Метод наименьших квадратов дает возможность определить коэффициенты линейного уравнения а (0) и b (0) по формулам 6 - 9:
 ; (6)
; (6)
![]() ; (7)
; (7)
![]() ; (8)
; (8)
![]() . (9)
. (9)
Применяя линейную модель к первым 8 значениям ряда из таблицы 1 (т.е. к данным за первые 2 года), находим значения а (0) и b (0). Составим вспомогательную таблицу для определения параметров линейной модели:
Таблица 2
| t |
Y(t) |
t-tcp |
Y-Ycp |
(t-tcp )2 |
(Y-Ycp )(t-tcp ) |
|
| 1 |
28 |
-3,5 |
-7,625 |
12,25 |
26,6875 |
|
| 2 |
36 |
-2,5 |
0,375 |
6,25 |
-0,9375 |
|
| 3 |
43 |
-1,5 |
7,375 |
2,25 |
-11,0625 |
|
| 4 |
28 |
-0,5 |
-7,625 |
0,25 |
3,8125 |
|
| 5 |
31 |
0,5 |
-4,625 |
0,25 |
-2,3125 |
|
| 6 |
40 |
1,5 |
4,375 |
2,25 |
6,5625 |
|
| 7 |
49 |
2,5 |
13,375 |
6,25 |
33,4375 |
|
| 8 |
30 |
3,5 |
-5,625 |
12,25 |
-19,6875 |
|
| S |
36 |
285 |
0 |
0 |
42 |
36,5 |
![]()
![]()
![]()
![]()
Уравнение (5) с учетом полученных коэффициентов имеет вид: Yp ( t ) =31,714+0,869·t . Из этого уравнения находим расчетные значения Y р ( t ) и сопоставляем их с фактическими значениями (табл. 3). Такое сопоставление позволяет оценить приближенные значения коэффициентов сезонности I-IV кварталов F (-3) , F (-2) , F (-1) и F (0) для года, предшествующего первому году, по которому имеются данные в табл. 1. Эти значения необходимы для расчета коэффициентов сезонности первого года F (1), F (2), F (3), F (4) и других параметров модели Хольта-Уинтерса по формулам 1 - 4.
Таблица 3
Сопоставление фактических данных Y ( t ) и рассчитанных по линейной модели значений Yp ( t )
| t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| Y(t) |
28 |
36 |
43 |
28 |
31 |
40 |
49 |
30 |
| Yp (t) |
32,583 |
33,452 |
34,321 |
35,190 |
306,060 |
36,929 |
37,798 |
38,667 |
Коэффициент сезонности есть отношение фактического значения экономического показателя к значению, рассчитанному по линейной модели. Поэтому в качестве оценки коэффициента сезонности I квартала F (-3) может служить отношение фактических и расчетных значений Y ( t ) I квартала первого года, равное Y (1) /Y р (1) , и такое же отношение для I квартала второго года (т.е. за V квартал t =5) Y (5)/ Y р(5) . Для окончательной, более точной, оценки этого коэффициента сезонности можно использовать среднее арифметическое значение этих двух величин.
F (-3) = [ Y (1) / Yp (1) + Y (5) / Yp (5) ] / 2=[ 28 / 32,583 + 31 / 36,060 ] / 2 = 0,8595.
Аналогично находим оценки коэффициента сезонности для II, III и IV кварталов:
F (-2) = [Y (2) / Yp (2) + Y (6) / Yp (6) ] / 2 = 1,0797;
F (-1) = [Y (3) / Yp (3) + Y (7) / Yp (7) ] / 2 = 1,2746;
F (0) = [Y (4) / Yp (4) + Y (8) / Yp (8) ] / 2 = 0,7858.
Оценив значения а (0), b (0), а также F (-3), F (-2), F (-1) и F (0), можно перейти к построению адаптивной мультипликативной модели Хольта-Уинтерса с помощью формул 1 - 4.
Из условия задачи имеем параметры сглаживания a 1 =0,3; a 2 =0,6; a 3 =0,3. Рассчитаем значения Yp (t ), a (t ), b (t ) и F (t ) для t =l.
Из уравнения 1, полагая что t =0, k =1, находим Y р (1) :
![]() Из уравнений 2 - 4, полагая что t
=1, находим:
Из уравнений 2 - 4, полагая что t
=1, находим:
![]() ;
;
![]() ;
;
![]() .
.
Аналогично рассчитаем значения Yp ( t ), a ( t ), b ( t ) и F ( t ) для t =2:
![]()
![]() ;
;
![]() ;
;
![]() ;
;
для t =3:
![]()
![]() ;
;
![]() ;
;
![]() ;
;
для t =4:
![]()
![]() ;
;
![]() ;
;
![]() ;
;
для t =5:
![]()
Обратим внимание на то, что здесь и в дальнейшем используются коэффициенты сезонности F ( t - L ) , уточненные в предыдущем году (L =4):
![]() ;
;
![]() ;
;
![]() ;
;
Продолжая аналогично для, t = 6,7,8,…,16 строят модель Хольта-Уинтерса (табл. 4). Максимальное значение t , для которого можно находить коэффициенты модели, равно количеству имеющихся данных по экономическому показателю Y ( t ) . В нашем примере данные приведены за 4 года, то есть за 16 кваралов. Максимальное значение t равно 16.
Таблица 4
Модель Хольта-Уинтерса
| t |
Y ( t ) |
a(t) |
b(t) |
F(t) |
Yp(t) |
Абс.погр., E ( t ) |
Отн.погр., % |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
31,71 |
0,87 |
0,7858 |
||||
| 1 |
28,0 |
32,58 |
0,87 |
0,8594 |
28,01 |
-0,01 |
0,02 |
| 2 |
36,0 |
33,42 |
0,86 |
1,0782 |
36,11 |
-0,11 |
0,32 |
| 3 |
43,0 |
34,11 |
0,81 |
1,2661 |
43,69 |
-0,69 |
1,60 |
| 4 |
28,0 |
35,14 |
0,87 |
0,7924 |
27,44 |
0,56 |
1,99 |
| 5 |
31,0 |
36,03 |
0,88 |
0,8600 |
30,95 |
0,05 |
0,16 |
| 6 |
40,0 |
36,97 |
0,90 |
1,0805 |
39,80 |
0,20 |
0,51 |
| 7 |
49,0 |
38,11 |
0,97 |
1,2778 |
47,94 |
1,06 |
2,17 |
| 8 |
30,0 |
38,72 |
0,86 |
19 |
30,97 |
-0,97 |
3,24 |
| 9 |
34,0 |
39,57 |
0,86 |
0,8596 |
34,04 |
-0,04 |
0,11 |
| 10 |
44,0 |
40,51 |
0,88 |
1,0839 |
43,68 |
0,32 |
0,73 |
| 11 |
52,0 |
41,19 |
0,82 |
1,2687 |
52,90 |
-0,90 |
1,73 |
| 12 |
33,0 |
42,07 |
0,84 |
0,7834 |
32,84 |
0,16 |
0,47 |
| 13 |
39,0 |
43,64 |
1,06 |
0,8800 |
36,88 |
2,12 |
5,43 |
| 14 |
48,0 |
44,58 |
1,02 |
1,0796 |
48,45 |
-0,45 |
0,95 |
| 15 |
58,0 |
45,64 |
1,03 |
1,2700 |
57,85 |
0,15 |
0,25 |
| 16 |
36,0 |
46,45 |
0,97 |
0,7783 |
36,56 |
-0,56 |
1,56 |
Проверка качества модели
Для того чтобы модель была качественной уровни, остаточного ряда E(t) (разности Y(t)-Yp(t) между фактическими и расчетными значениями экономического показателя) должны удовлетворять определенным условиям (точности и адекватности). Для проверки выполнения этих условий составим таблицу 5.
Проверка точности модели
Будем считать, что условие точности выполнено, если относительная погрешность (абсолютное значение отклонения abs {E ( t ) }, поделенное на фактическое значение Y ( t ) и выраженное в процентах 100%·abs {E ( t ) }/Y ( t ) ) в среднем не превышает 5%. Суммарное значение относительных погрешностей (см. гр. 8 табл. 4) составляет 21,25, что дает среднюю величину 21,25/16 = 1,33%.
Следовательно, условие точности выполнено.
Таблица 5
Промежуточные расчеты для оценки адекватности модели
| Квартал, t |
Отклонение, E( t) |
Точки поворота |
E( t) 2 |
[E(t)-E(t-1) ]2 |
E(t)∙E(t-1) |
| 1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
-0,01 |
- |
0,00 |
- |
- |
| 2 |
-0,11 |
0 |
0,01 |
0,01 |
0,00 |
| 3 |
-0,69 |
1 |
0,48 |
0,33 |
0,08 |
| 4 |
0,56 |
1 |
0,31 |
1,56 |
-0,38 |
| 5 |
0,05 |
1 |
0,00 |
0,26 |
0,03 |
| 6 |
0,20 |
0 |
0,04 |
0,02 |
0,01 |
| 7 |
1,06 |
1 |
1,13 |
0,74 |
0,22 |
| 8 |
-0,97 |
1 |
0,95 |
4,14 |
-1,03 |
| 9 |
-0,04 |
0 |
0,00 |
0,87 |
0,04 |
| 10 |
0,32 |
1 |
0,10 |
0,13 |
-0,01 |
| 11 |
-0,90 |
1 |
0,80 |
1,49 |
-0,29 |
| 12 |
0,16 |
0 |
0,02 |
1,11 |
-0,14 |
| 13 |
2,12 |
1 |
4,49 |
3,85 |
0,33 |
| 14 |
-0,45 |
1 |
0,21 |
6,62 |
-0,96 |
| 15 |
0,15 |
1 |
0,02 |
0,36 |
-0,07 |
| 16 |
-0,56 |
- |
0,32 |
0,50 |
-0,08 |
| S |
0,88 |
10 |
8,88 |
21,98 |
-2,27 |
Проверка условия адекватности
Для того чтобы модель была адекватна исследуемому процессу, ряд остатков E ( t ) должен обладать свойствами случайности, независимости последовательных уровней, нормальности распределения.
Проверка случайности уровней . Проверку случайности уровней остаточной компоненты (гр. 2 табл. 5) проводим на основе критерия поворотных точек. Для этого каждый уровень ряда E ( t ) сравниваем с двумя соседними. Если он больше (либо меньше) обоих соседних уровней, то точка считается поворотной и в гр. 3 табл. 5 для этой строки ставится 1, в противном случае в гр. 3 ставится 0. В первой и последней строке гр. 3 табл. 5 ставится прочерк или иной знак, так как у этого уровня нет двух соседних уровней.
Общее число поворотных точек в нашем примере равно р = 10.
Рассчитаем значение q :
![]() .
.
Функция int означает, что от полученного значения берется только целая часть. При N = 16
![]() .
.
Если количество поворотных точек р больше q , то условие случайности уровней выполнено. В нашем случае р = 10, q = 6, значит условие случайности уровней ряда остатков выполнено.
Проверка независимости уровней ряда остатков (отсутствия автокорреляции) . Проверку проводим двумя методами:
1) по d -критерию Дарбина-Уотсона;
2) по первому коэффициенту автокорреляции r (1).
1)  .
.
Примечание . В случае если полученное значение больше 2, значит, имеет место отрицательная автокорреляция. В таком случае величину d уточняют, вычитая полученное значение из 4. Находим уточненное значение d `= 4-2,47=1,53
Полученное (или уточненное) значение d сравнивают с табличными значениями d 1 и d 2 . Для нашего случая d 1 =1,08, а d 2 =1,36.
Если 0<d <d 1 , то уровни автокоррелированы, то есть, зависимы, модель неадекватна.
Если d 1 <d <d 2 , то критерий Дарбина-Уотсона не дает ответа на вопрос о независимости уровней ряда остатков. В таком случае необходимо воспользоваться другими критериями (например, проверить независимость уровней по первому коэффициенту автокорреляции).
Если d 2 <d <2 , то уровни ряда остатков являются независимыми.
В нашем случае d 2 <d ` <2 , следовательно уровни ряда остатков являются независимыми.
2) 
Если модуль рассчитанного значения первого коэффициента автокорреляции меньше критического значения | r (1) | < r та6 , то уровни ряда остатков независимы. Для нашей задачи критический уровень r та6 = 0,32. Имеем: | r (1) | = 0,26 < r таб = 0,32 - значит уровни независимы.
Проверка соответствия ряда остатков нормальному распределению определяем по RS -критерию . Рассчитаем значение RS :
![]() ,
,
где Е max - максимальное значение уровней ряда остатков E ( t ) ;
Emin - минимальное значение уровней ряда остатков E ( t ) (гр. 2 табл. 5):
S - среднее квадратическое отклонение.
Е max =2,12, Emin =-0,97, Е max -Emin = 2,12 - (-0,97) = 3,09;

![]()
Полученное значение RS сравнивают с табличными значениями, которые зависят от количества точек N и уровня значимости. Для N =16 и 5%-го уровня значимости значение RS для нормального распределения должно находиться в интервале от 3,00 до 4,21.
Так как 3,00 < 4,02 < 4,21, полученное значение RS попало в заданный интервал. Значит, уровни ряда остатков подчиняются нормальному распределению.
Расчет прогнозных значений экономического показателя
Составим прогноз на четыре квартала вперед (т.е. на 1 год, с t =17 по t =20). Максимальное значение t , для которого могут быть рассчитаны коэффициенты a ( t ) , b ( t ) определяется количеством исходных данных и равно 16. Рассчитав значения а (16) и b (16) (см. табл. 4), по формуле 1 можно определить прогнозные значения экономического показателя Yp ( t ) . Для t =17 имеем:
![]()
Аналогично находим Yp (18), Yp (19), Yp (20):
![]()
![]()
![]()
Ha нижеприведенном рисунке проводится сопоставление фактических и расчетных данных. Здесь же показаны прогнозные значения цены акции на 1 год вперед. Из рисунка видно, что расчетные данные хорошо согласуются с фактическими, что говорит об удовлетворительном качестве прогноза.

Рис. Сопоставление расчетных и фактических данных
Задание 2
Даны цены (открытия, максимальная, минимальная и закрытия) за 10 дней. Интервал сглаживания принять равным пяти дням. Рассчитать:
- экспоненциальную скользящую среднюю;
- момент;
- скорость изменения цен;
- индекс относительной силы;
- %R , %К и %D .
Расчеты проводить для дней, для которых эти расчеты можно выполнить на основании имеющихся данных.
Таблица 6
| Дни |
Цены |
||
| макс. |
мин. |
закр. |
|
| 1 |
998 |
970 |
982 |
| 2 |
970 |
922 |
922 |
| 3 |
950 |
884 |
902 |
| 4 |
880 |
823 |
846 |
| 5 |
920 |
842 |
856 |
| 6 |
889 |
840 |
881 |
| 7 |
930 |
865 |
870 |
| 8 |
890 |
847 |
852 |
| 9 |
866 |
800 |
802 |
| 10 |
815 |
680 |
699 |
Решение.
Экспоненциальная скользящая средняя (ЕМА). При расчете ЕМА учитываются все цены предшествующего периода, а не только того отрезка, который соответствует интервалу сглаживания. Однако последним значениям цены придается большее значение, чем предшествующим. Расчеты проводятся по формуле:
![]() ,
,
где k =2/(n +1), n – интервал сглаживания;
Ct – цена закрытия t -го дня;
ЕМА t – значения ЕМА текущего дня t .
Составим таблицу рассчитанных значений ЕМА :
Таблица 7
| t |
Цена закрытия, Ct |
EMA t |
| 1 |
982 |
- |
| 2 |
922 |
- |
| 3 |
902 |
- |
| 4 |
846 |
- |
| 5 |
856 |
|
| 6 |
881 |
|
| 7 |
870 |
|
| 8 |
852 |
874,9926 |
| 9 |
802 |
850,6617 |
| 10 |
699 |
800,1078 |
Приведем алгоритм расчета.
1. Выбрать интервал сглаживания n (в нашем случае n = 5).
2. Вычислить коэффициент k (k = 2/(n + 1) = 2/(5 + 1) = 1/3).
3. Вычислить МА для первых 5 дней. Для этого сложим цены закрытия за первые 5 дней. Сумму разделим на 5 и запишем в графу ЕМАt за 5-ый день.
4. Перейти на одну строку вниз по графе ЕМАt . Умножить на k данные по конечной цене текущей строки.
5. Данные по ЕМАt за предыдущий день взять из предыдущей строки и умножить на (1- k ).
6. Сложить результаты, полученные на предыдущих двух шагах. Полученное значение ЕМАt записать в графу текущей строки.
7. Повторить шаги 4, 5 и 6 до конца таблицы.
Построим график ЕМАt .

Момент (МОМ). Момент рассчитывается как разница конечной цены текущего дня Ct и цены n дней тому назад Ct - n .
![]() ,
,
где Ct – цена закрытия t -го дня;
МОМ t – значения МОМ текущего дня t .
Составим таблицу рассчитанных значений МОМ :
Таблица 8
| t |
Цена закрытия, Ct |
МОМ t |
| 1 |
982 |
- |
| 2 |
922 |
- |
| 3 |
902 |
- |
| 4 |
846 |
- |
| 5 |
856 |
856-982 = -126 |
| 6 |
881 |
881-922 = -41 |
| 7 |
870 |
870-902 = -32 |
| 8 |
852 |
852-846 = 6 |
| 9 |
802 |
802-856 = -54 |
| 10 |
699 |
699-881 = -182 |
Построим график МОМ t .

Положительные значения МОМ свидетельствуют об относительном росте цен, отрицательные – о снижении. Движение графика момента вверх из зоны отрицательных значений является слабым сигналом покупки до пересечения с нулевой линией. График момента пересекает нулевую линию в районе 7-8-го дня, а затем снова снижатся.
Скорость изменения цен . Похожий индикатор, показывающий скорость изменения цен (ROC ), рассчитывается как отношение конечной цены текущего дня к цене n дней тому назад, выраженное в процентах.
![]() ,
,
где Ct – цена закрытия t -го дня;
R О Ct – значения R О C текущего дня t .
Составим таблицу рассчитанных значений R О C :
Таблица 9
| t |
Цена закрытия, Ct |
R О C t , % |
| 1 |
982 |
- |
| 2 |
922 |
- |
| 3 |
902 |
- |
| 4 |
846 |
- |
| 5 |
856 |
856 / 982·100 = 87,17 |
| 6 |
881 |
881 / 922·100 = 95,55 |
| 7 |
870 |
870 / 902·100 = 96,45 |
| 8 |
852 |
852 / 846·100 = 100,71 |
| 9 |
802 |
802 / 856·100 = 93,69 |
| 10 |
699 |
699 / 881·100 = 79,34 |
Построим график R О Ct .
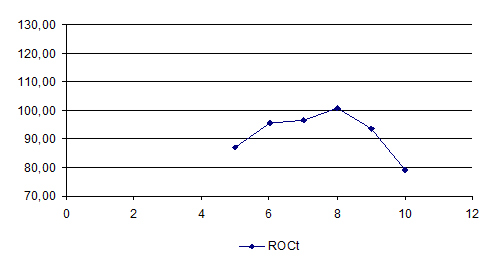
ROC является отражением скорости изменения цены, а также указывает направление этого изменения. Графическое отображение и правила работы ничем не отличаются от момента. В качестве нулевой линии используется уровень 100%. Этот индикатор также показал сигнал к покупке в районе 7-8-го дня.
Индекс относительной силы ( RSI ). Наиболее значимым осциллятором, расчет которого предусмотрен во всех компьютерных программах технического анализа, является индекс относительной силы.
Для расчета применяют формулу:
![]() ,
,
где AU – сумма приростов конечных цен за n последних дней;
AD – сумма убыли конечных цен за n последних дней.
Рассчитывается RSI следующим образом (таблица 10).
1. Выбираем интервал n (в нашем случае n =5).
2. Начиная со 2-го дня до конца таблицы, выполняем следующую процедуру. Вычитаем из конечной цены текущего дня конечную цену предыдущего дня. Если разность больше нуля, то ее записываем в графу «Повышение цены». Иначе абсолютное значение разности записываем в графу «Понижение цены».
3. С 6-го дня и до конца таблицы заполняем графы «Суммы повышений» и «Суммы понижений». Для этого складывают значения из графы «Повышение цены» за последние 5 дней (включая текущий) и полученную сумму записываем в графу «Суммы повышений» (величина AU в формуле). Аналогично находят сумму убыли конечных цен по данным графы «Понижение цены» и записываем в графу «Суммы понижений» (величина AD в формуле).
4. Зная AU и AD, по формуле рассчитываем значение RSI и записываем в графу RSI.
Таблица 10
| t |
Цена закрытия, Ct |
Повышение цены |
Понижение цены |
Сумма повышений |
Сумма понижений |
RSI |
| 1 |
982 |
|||||
| 2 |
922 |
17 |
||||
| 3 |
902 |
|||||
| 4 |
846 |
67 |
||||
| 5 |
856 |
26 |
||||
| 6 |
881 |
36 |
36 |
110 |
24,66 |
|
| 7 |
870 |
22 |
36 |
115 |
23,84 |
|
| 8 |
852 |
1 |
37 |
115 |
24,34 |
|
| 9 |
802 |
38 |
75 |
48 |
60,98 |
|
| 10 |
699 |
57 |
132 |
22 |
85,71 |
Построим график RSI .

Зоны перепроданности располагаются обычно ниже 25-20, а перекупленности – выше 75-80%. Как видно из рисунка, индекс относительной силы вышел из зоны, ограниченной линией 25%, на 7-8 день (сигнал к покупке).
Стохастические линии. Если МОМ, ROC и RSI используют только цены закрытия, то стохастические линии строятся с использованием более полной информации. При их расчете используются также максимальные и минимальные цены. Как правило, применяются следующие стохастические линии: % R , %К и % D .
![]() ,
,
где %К t – значение индекса текущего дня t ;
Ct – цена закрытия t -го дня;
L 5 и H 5 – минимальная и максимальная цены за 5 предшествующих дней, включая текущий (в качестве интервала может быть выбрано и другое число дней).
Похожая формула используется для расчета % R :
![]() ,
,
где % Rt – значение индекса текущего дня t ;
Ct – цена закрытия t -го дня;
L 5 и H 5 – минимальная и максимальная цены за 5 предшествующих дней, включая текущий.
Индекс % D рассчитывается аналогично индексу %К , с той лишь разницей, что при его построении величины (Ct - L 5 ) и (H 5 - L 5 ) сглаживают, беря их трехдневную сумму.

Ввиду того что %D имеет большой статистический разброс, строят еще ее трехдневную скользящую среднюю – медленное %D.
Составим таблицу 11 для нахождения всех стохастических линий.
1. В графах 1-4 приведены дни по порядку и соответствующие им цены (максимальная, минимальная и конечная).
2. Начиная с 5-го дня в графах 5 и 6 записываем максимальную и минимальную цены за предшествующие 5 дней, включая текущий.
3. В графе 7 записываем (Ct - L 5 ) – разность между данными графы 4 и графы 6.
4. Графу 8 составляют значения разности между данными графы 5 и графы 4, т.е. результат разности (H 5 - Ct ).
5. Размах цен за 5 дней (H 5 - L 5 ) – разность между данными графы 5 и графы 6 записываем в графу 9.
6. Рассчитанные по формуле значения %K заносим в графу 10.
7. В графу 11 заносим значения %R, рассчитанные по формуле.
8. Шаги 2-7 повторяем для 6-й, 7-й строки и т.д. до конца таблицы.
9. Для расчета %D, начиная с 7-й строки, складываем значения Ct - L 5 из графы 7 за 3 предыдущих дня, включая текущий (t=5, 6 и 7), и записываем в графе 12. Аналогично значения размаха (H 5 - L 5 ) из графы 9 складываем за 3 предшествующих дня и заносим в графу 13.
10. По формуле, используя данные граф 12 и 13, рассчитываем %D и записываем в графу 14.
11. Шаги 9 и 10 повторяем для 8-й, 9-й и 10-й строк.
12. Медленное %D находим как скользящую среднюю от %D (данные берем из графы 14) с интервалом сглаживания, равным трем. Результат записываем в графу 15.
Таблица 11
| t |
макс. Нt |
мин. Lt |
закр. Ct |
мак. за 5 дн. Н5 |
мин. за 5 дн. L5 |
Ct - L5 |
H5 - Ct |
H5 - L5 |
%К t |
%Rt |
сумма за 3 дн. Ct - L5 |
сумма за 3 дн. H5 – L5 |
%Dt |
медленное%Dt |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 1 |
998 |
970 |
982 |
|||||||||||
| 2 |
970 |
922 |
922 |
|||||||||||
| 3 |
950 |
884 |
902 |
|||||||||||
| 4 |
88 |
823 |
846 |
|||||||||||
| 5 |
920 |
842 |
856 |
998 |
823 |
33 |
142 |
175 |
18,86 |
81,14 |
||||
| 6 |
889 |
840 |
881 |
970 |
823 |
58 |
89 |
147 |
39,46 |
60,54 |
||||
| 7 |
930 |
865 |
870 |
950 |
823 |
47 |
80 |
127 |
37,01 |
62,99 |
138 |
449 |
30,73 |
|
| 8 |
890 |
847 |
852 |
930 |
823 |
29 |
78 |
107 |
27,10 |
72,90 |
134 |
381 |
35,17 |
|
| 9 |
866 |
800 |
802 |
930 |
800 |
2 |
128 |
130 |
1,54 |
98,46 |
78 |
364 |
21,43 |
29,11 |
| 10 |
815 |
680 |
699 |
930 |
680 |
19 |
231 |
250 |
7,60 |
92,40 |
50 |
487 |
10,27 |
22,29 |
Построим стохастические линии:

Смысл индексов %К и %R состоит в том, что при росте цен цена закрытия бывает ближе к максимальной, а при падении цен наоборот – ближе к минимальной. Индексы %R и %К проверяют, куда больше тяготеет цена закрытия.
Задание 3
3.1. Банк выдал ссуду, размером 500 000 руб. Дата выдачи ссуды – 21.01.02, возврата – 11.03.02. Дата выдачи и день возврата считать за один день. Проценты рассчитываются по простой процентной ставке 10% годовых. Найти:
3.1.1) точные проценты с точным числом дней ссуды;
3.1.2) обыкновенные проценты с точным числом дней ссуды;
3.1.3) обыкновенные проценты с приближенным числом дней ссуды.
Решение
Используем формулы ![]() ;
; ![]() :
:
3.1.1) ![]() ,
, ![]() ,
, ![]() руб.
руб.
3.1.2) ![]() ,
, ![]() ,
, ![]() руб.
руб.
3.1.3) ![]() ,
, ![]() ,
, ![]() руб.
руб.
3.2. Через 180 дней после подписания договора должник уплатит 500 000 руб. Кредит выдан под 10% годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт?
Решение
Используем формулу:
 руб.
руб.
Дробь в правой части равенства при величине S
называется дисконтным множителем
. Этот множитель показывает, какую долю составляет первоначальная сумма ссуды в окончательной величине долга. Дисконт суммы S
равен ![]() руб.
руб.
3.3. Через 180 дней предприятие должно получить по векселю 500 000 руб. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке 10% годовых (год равен 360 дням). Определить полученную предприятием сумму и дисконт.
Решение
Используем формулы ![]() ,
, ![]()
![]() .
.
![]() руб.
руб.
![]() руб.
руб.
3.4. В кредитном договоре на сумму 500 000 руб. и сроком на 4 года зафиксирована ставка сложных процентов, равная 10% годовых. Определите наращенную сумму.
Решение
Воспользуемся формулой наращения для сложных процентов:
![]() руб.
руб.
3.5. Ссуда, размером 500 000 руб. предоставлена на 4 года. Проценты сложные, ставка – 10% годовых. Проценты начисляются 2 раза в год. Вычислить наращенную сумму.
Решение
Начисление процентов два раза в год, т.е. m=2. Всего имеется N = 4·2 =8 периодов начислений. По формуле начислений процентов по номинальной ставке:![]() находим:
находим:
![]() руб.
руб.
3.6. Вычислить эффективную ставку процента, если банк начисляет проценты 2 раза в год, исходя из номинальной ставки 10% годовых.
Решение
По формуле ![]() находим:
находим:
![]() , т.е. 10,25%.
, т.е. 10,25%.
3.7. Определить какой должна быть номинальная ставка при начислении процентов 2 раза в год, чтобы обеспечить эффективную ставку 10% годовых.
Решение
По формуле ![]() находим:
находим:
![]() , т.е. 9,76%
, т.е. 9,76%
3.8. Через 4 года предприятию будет выплачена сумма 500 000 руб. Определить ее современную стоимость при условии, что применяется сложная процентная ставка 10% годовых.
Решение
По формуле ![]() находим:
находим:
![]() руб.
руб.
3.9. Через 4 года по векселю должна быть выплачена сумма 500 000 руб. Банк учел вексель по сложной учетной ставке 10% годовых. Определить дисконт.
Решение
Дисконтирование по сложной учетной ставке осуществляется по формуле:
![]() руб.
руб.
Дисконт суммы S равен:
![]() руб.
руб.
3.10. В течение 4 лет на расчетный счет в конце каждого года поступает по 500 000 руб., на которые 2 раза в год начисляются проценты по сложной годовой ставке 10%. Определить сумму на расчетном счете к концу указанного срока.
Решение
По формуле ![]() находим:
находим:
![]() руб.
руб.