| Скачать .docx |
Курсовая работа: Методи фінансового аналізу та його спеціальні прийоми
Метод и фінансового аналізу та його спеціальні прийоми
Вступ
Метод — це шлях дослідження, вивчення. У широкому розумінні метод означає шляхи, способи і засоби пізнання дійсності, сукупність взаємопов’язаних принципів і способів дослідження процесів, явищ, предметів у природі та суспільстві.
Метод науки — це притаманний науці спосіб проникнення у зміст предмета, що вивчається.
Якщо предмет відповідає на запитання «Що вивчається?», то метод дає відповідь на запитання «Як вивчається? Якими прийомами? У які способи?».
Метод фінансового аналізу — це системне, комплексне дослідження, взаємопов’язане вивчення, опрацювання і використання інформації фінансового характеру з метою виявлення і мобілізації резервів ліпшого використання фінансових ресурсів і встановлення оптимальної структури їх джерел.
Практичним додатком до методу фінансового аналізу як науки виступає його методика — сукупність прийомів вивчення та опрацювання фінансової інформації. Оскільки фінансовий аналіз є складовою аналізу фінансово-господарської діяльності підприємства, то він практично повністю використовує його методику.
На теперішній час серед учених-економістів не існує єдиного погляду щодо класифікації способів і прийомів аналізу.
У фінансовому аналізі використовується такий інструментарій.
Абсолютні, відносні та середні величини
Економічні явища, які вивчаються у фінансовому аналізі, мають кількісну визначеність, що виражається в абсолютних і відносних величинах.
Абсолютні величини показують кількісні розміри економічного явища в одиницях міри, ваги, обсягу, площі, вартості тощо безвідносно до розміру інших явищ. Абсолютні величини слугують базою для розрахунку відносних величин.
Відносні величини одержують у разі визначення співвідношень між абсолютними величинами і застосовують у розрахунках рівня виконання плану, координації, структури, інтенсивності змін за певний період.
Так, відносна величина напруженості планового завдання являє собою відношення планового рівня показника поточного року (періоду) до його рівня у минулому році (періоді), а відносна величина виконання планового завдання — відношення фактичного показника звітного року (періоду) до планового його рівня за відповідний період.
Відносні показники структури — це питома вага окремої частини в загальному, яка виражається, як правило, у процентах. Наприклад, питома вага прибутку від реалізації у загальному прибутку сільськогосподарського підприємства.
Відносні величини координації — це співвідношення частин цілого між собою. Наприклад, основного та оборотного капіталу, власного і позикового капіталу.
Відносні величини інтенсивності — це ступінь поширеності, розвитку якогось явища у відповідному середовищі. Наприклад, ступінь неповернення дебіторської заборгованості, ступінь бартерних угод.
Відносні величини ефективності — це співвідношення ефекту з ресурсами, витратами. Наприклад, ефективність використання капіталу характеризується його віддачею (рентабельністю) — відношенням суми прибутку до середньорічної суми основного та оборотного капіталу.
Серед відносних величин у фінансовому аналізі широкого застосування набули проценти, коефіцієнти, індекси.
Щоб отримати відносну величину, виражену в процентах, треба одну абсолютну величину (чисельник) поділити на іншу абсолютну величину (знаменник) і помножити на 100. Так, щоб знайти питому вагу грошових коштів в оборотному капіталі, треба суму грошових коштів поділити на величину оборотного капіталу і помножити на 100. Припустимо, що сума грошових коштів дорівнює 595 тис. грн, величина оборотного капіталу — 4353 тис. грн. Тоді питома вага грошових коштів становить:
![]()
Коефіцієнти характеризують відносні величини двох порівнюваних показників, з яких один беруть за одиницю.
Індекси — це відносні величини, які характеризують зміну показника, що вивчається, у часі або просторі. Їх застосовують для виявлення динаміки різних показників фінансово-господарської діяльності підприємств, виконання планового завдання.
Наприклад, використовуючи індексний метод, необхідно дати оцінку виконання планового завдання по прибутку за такими даними: величина прибутку за планом — 1100 тис. грн, фактично — 1240 тис. грн.
Індекс виконання плану становить:
![]()
Від індексів легко перейти до процентів, і навпаки. Якщо обчислено один з них, немає потреби обчислювати інший. Їх легко перетворити. Так, у нашому прикладі, індекс виконання плану по прибутку становить 1,127, або 112,7 % (1,127 × 100). Якщо відносну величину виражено у процентах, а необхідно отримати індекс, то її слід поділити на 100 (112,7 : 100 = 1,127).
Поряд із абсолютними і відносними показниками часто застосовуються середні величини. Вони використовуються у фінансовому аналізі для узагальненої кількісної характеристики сукупності однорідних явищ за визначеною ознакою. Наприклад, аналізуючи валюти балансу, використовують середню величину підсумку балансу для обчислення коефіцієнта зростання (зниження) валюти балансу; під час аналізу дебіторської заборгованості розраховують середню дебіторську заборгованість для обчислення показників її якості та ліквідності — коефіцієнта оберненості та тривалості одного обороту в днях.
Середні величини показують загальну міру визначеної ознаки у сукупності, що вивчається, тобто одним числом характеризують усю сукупність об’єктів.
Для аналізу фінансово-господарської діяльності застосовують різні типи середніх величин: середньоарифметична, середньохронологічна, середньоквадратична, середньогеометрична тощо. Порядок їх обчислення, а також використання в економічній роботі ґрунтовно розглядаються в курсах теоретичної та галузевої статистики.
У фінансовому аналізі найчастіше використовуються середня арифметична (проста і зважена) та середня хронологічна.
Середня арифметична проста застосовується, коли всі варіанти трапляються один раз або мають однакові частоти в досліджуваній сукупності. Розраховують її діленням підсумку всіх показників на загальне число показників:
![]() ,
,
де ![]() — середня арифметична проста;
— середня арифметична проста;
х1, х2, … , хn — показники;
n — кількість показників.
Наприклад, дебіторська заборгованість на початок року становила 971 тис. грн., на кінець року — 1446 тис. грн.
Середня дебіторська заборгованість розраховуватиметься за простою арифметичною:
![]() ,
,
де ДЗ — середня дебіторська заборгованість;
ДЗ1 — дебіторська заборгованість на початок року;
ДЗ2 — дебіторська заборгованість на кінець року;
2 — кількість показників.
Отже,
ДЗ = (971 000 + 1 446 000) : 2 = 1 208 000 (грн).
![]() Середня арифметична зважена застосовується тоді, коли варіант у досліджуваній сукупності повторюється неоднакову кількість разів. Її знаходять множенням кожного варіанта на число його повторень (частоту, вагу), додають добутки і підсумок ділять на суму повторень показників. Розраховується середня арифметична зважена за формулою
Середня арифметична зважена застосовується тоді, коли варіант у досліджуваній сукупності повторюється неоднакову кількість разів. Її знаходять множенням кожного варіанта на число його повторень (частоту, вагу), додають добутки і підсумок ділять на суму повторень показників. Розраховується середня арифметична зважена за формулою
![]() ,
,
де ![]() — середня арифметична зважена;
— середня арифметична зважена;
х1, х2, … , хn — варіанти;
f1, f2, …, fn — частоти.
Середня хронологічна визначається за показниками, що змінюються у часі. Обчислюючи її крайні показники ряду ділять на 2, а решту беруть цілими. Обчислюється середня хронологічна за формулою
 ,
,
де ![]() — середня хронологічна;
— середня хронологічна;
х1, х2, … , хn — показники на окрему дату;
n — кількість дат.
Наприклад, за середньою хронологічною визначаються середньорічні залишки товарно-матеріальних цінностей на основі даних на перше число кожного місяця.
Використовуючи середні величини, треба зважати на те, що в них згладжуються індивідуальні ознаки. Щоб уникнути неправильних висновків, аналіз середніх величин треба доповнювати дослідженням їх складових.
Заслуговує на увагу використання у фінансовому аналізі індексного методу.
Індексний метод ґрунтується на відносних показниках, що характеризують співвідношення рівня даного (досліджуваного) явища і рівня аналогічного явища, прийнятого за базу. Будь-який індекс обчислюється зіставленням досліджуваної величини з базисною.
Індекси бувають індивідуальні та групові; базисні та ланцюгові. Індивідуальні виражають співвідношення безпосередньо порівнянних величин, групові — співвідношення складних явищ. У разі обчислення базисних індексів певні показники всіх аналізованих періодів відносять до показників базисного року. Обчислюючи ланцюгові індекси кожен наступний показник відносять до попереднього.
База у разі обчислення базисних індексів є постійною, а ланцюгових індексів — змінною. На практиці користуються обома індексами одночасно. Це дає змогу визначити відразу дві характеристики досліджуваного явища, одержати повнішу картину про нього. Базисні індекси показують зміни показників наступних періодів часу щодо рівня показника базисного періоду, а ланцюгові характеризують відхилення показників кожного наступного періоду від показників попереднього.
За допомогою індексного методу, крім оцінювання виконання плану, напруженості планового завдання, зміни показників за певні періоди, можна також виконували й факторний аналіз, у якому широко застосовуються агрегатні індекси.
Розглянемо застосування агрегатних індексів для аналізу виручки від реалізації продукції звітного року порівняно з минулим і розрахунку впливу фактора кількості і фактора цін.
Індекс обсягу реалізації у вартісному вимірі (Ipn):
Ipn ![]() ,
,
де q1, q0 — кількість реалізованої продукції відповідно за звітний і минулий роки;
p1, p0 — ціна реалізації відповідно у звітному і попередньому роках.
Цей індекс показує зміни кількості та ціни. Його ще можна визначити через добуток індексу фізичного обсягу реалізованої продукції (Iq) та індексу ціни (Ip):
Ipn = Iq Ip.
На відхилення виручки від реалізації впливають два фактори: кількість реалізованої продукції (фактор кількості) і ціна реалізації (фактор цін).
Тому, визначаючи індекс обсягу реалізації у кількісному вимірі, необхідно враховувати, що змінюється кількість, а ціна залишається на базисному рівні:
Iq ![]() .
.
У разі обчислення індексу ціни змінюється ціна, а обсяг реалізації залишається на аналізованому рівні:
Ip ![]()
Отже,
Ipn ![]() .
.
Треба пам’ятати: якщо узагальнюючий економічний показник являє собою добуток кількісного та якісного показників — факторів, то при визначенні впливу кількісного фактора якісний показник фіксується на базисному рівні, а впливу якісного фактора кількісний показник фіксується на рівні аналізованого періоду.
Індексний метод дає змогу провести розкладання за факторами не тільки відносних, але й абсолютних відхилень узагальнюючого показника. Якщо від чисельника наведених вище формул відняти знаменники, то отримаємо абсолютні відхилення виручки від реалізації в цілому і за рахунок кожного фактора окремо:
¾ ![]() — загальне відхилення виручки від реалізації звітного року порівняно з минулим;
— загальне відхилення виручки від реалізації звітного року порівняно з минулим;
¾ ![]() — відхилення виручки від реалізації за рахунок зміни кількості реалізованої продукції у звітному році порівняно з минулими;
— відхилення виручки від реалізації за рахунок зміни кількості реалізованої продукції у звітному році порівняно з минулими;
¾ ![]() — відхилення виручки від реалізації за рахунок зміни ціни;
— відхилення виручки від реалізації за рахунок зміни ціни;
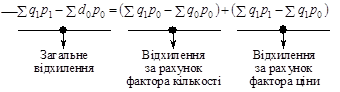
Наведений принцип розкладання абсолютного відхилення узагальнюючого показника за факторами використовується, коли число факторів дорівнює двом (один з них — кількісний, другий — якісний), а аналізований показник виражений як їх добуток.
Розглянемо вплив факторів на відхилення прибутку від реалізації одного виду товарної продукції. У цьому разі застосовуються індивідуальні індекси. У звітному році порівняно із планом на прибуток від реалізації (П) впливають три фактори: q — обсяг реалізованої продукції, p — ціна реалізації, z — собівартість одиниці продукції. Розрахуємо:
1. індекс виконання планового завдання:
![]() ;
;
2. відносне відхилення прибутку за рахунок зміни обсягу реалізації:
![]() ;
;
3. відносне відхилення прибутку за рахунок зміни ціни реалізації:
![]() ;
;
4. відносне відхилення прибутку за рахунок зміни собівартості одиниці продукції:
![]() .
.
Отже,
iп = inq × inp × inz .
Індексний метод застосовується також для факторного аналізу кількох видів продукції.
Порівняння — це один із способів, за допомогою якого людина досліджує всі предмети та явища у природі, суспільстві, в економіці. Порівняння є найдавнішим і найпоширенішим прийомом аналізу. Кожен показник і кожна цифра, отримувані в аналітичному дослідженні, мають значення лише порівняно із відомими показниками і цифрами. Без порівняння взагалі не може бути аналізу.
У разі застосування цього прийому аналізований показник порівнюється з базовим.
У фінансовому аналізі, як правило, досліджуваними найчастіше виступають фактично досягнуті показники. Базою порівняння можуть бути показники:
¾ планові;
¾ минулих періодів;
¾ середньорайонні;
¾ інших окремих однотипових за спеціалізацією господарств;
¾ досягнень наукових установ;
¾ нормативні;
¾ договірних зобов’язань;
¾ розвинених країн.
Порівняння фактичних показників з плановими дає можливість визначити ступінь виконання плану за досліджуваний період часу, а зіставлення даних звітного періоду із минулими — виявити тенденції розвитку економічних процесів господарства.
Зіставленням фактичних показників із середньорайонними, з показниками окремих (кращих) господарств, з досягненнями науки, досвідом роботи передових підрозділів оцінюються результати аналізованого господарства, здійснюються пошук, визначення та мобілізація невикористаних резервів.
Шляхом порівняння фактичних показників з нормативними контролюється за витрачання фінансових ресурсів.
Важливим для підприємств є порівняння фактичних показників з договірними зобов’язаннями.
У сучасних умовах господарювання доцільно фактичні звітні показники порівнювати з досягненнями розвинених країн, щоб встановити існуючий розрив і накреслити шляхи його подолання.
Таке порівняння дає змогу виявити переваги ринкової економіки, приватизації в Україні, визначити конкурентну спроможність підприємств. Крім цього, зазначені показники можна порівнювати між собою, тобто база порівняння і досліджуваний показник можуть змінюватися залежно від мети аналізу.
В окремих випадках (наприклад, при вивченні обґрунтованості та напруженості планових завдань) аналізованими показниками можуть бути планові показники, які порівнюються з базисними — фактично досягнутими за минулий рік або за кілька років. Важливим також є порівняння різних варіантів рішень з метою вибору оптимального.
У разі застосування цього прийому слід пам’ятати про необхідність дотримання умови забезпечення зіставлення показників.
Можна виділити такі вимоги для дотримання зіставлення:
1) єдина методологія розрахунку показників;
2) однаковість оцінювання;
3) однакові складові показників включені у розрахунок;
4) єдині календарні строки при зіставленні у часі;
5) зіставимість вихідних умов діяльності (природних, кліматичних тощо).
Групування — це невід’ємна частина практично будь-якого економічного дослідження. Воно потребує визначення класифікації явищ і процесів, а також причин і факторів, що їх обумовлюють. Групування — це виокремлення із сукупності досліджуваних явищ якісно однорідних типів, груп із суттєвими ознаками.
Групування поділяють на типологічні, структурні та аналітичні.
Типологічні групування застосовуються для виділення певних типів явищ і процесів. Наприклад, групування підприємств за видами фінансової стійкості.
Структурні групування дають змогу вивчати структуру певних явищ та економічних процесів за визначеними ознаками. Наприклад, у процесі дослідження структури капіталу підприємства визначається питома вага кожної його статті.
Аналітичні групування призначені для виявлення взаємозв’язку, взаємообумовленості та взаємодії між досліджуваними явищами. Такі групування широко застосовуються і є основою проведення факторного аналізу.
При побудові аналітичних групувань із двох взаємопов’язаних показників один розглядається як результативний показник, другий — як фактор, що впливає на перший. Але при цьому слід мати на увазі, що залежно від мети проведення аналізу взаємозалежність і взаємовплив факторного і результативного показників у кожному конкретному випадку можуть змінюватися (факторний показник може виступати як результативний, і навпаки). Крім того, варто наголосити, що результативний показник завжди один, а число факторів може бути різним (один, два, три ...).
Перерахування показників. У науковій літературі такий прийом аналізу виділяється окремо. Він використовується для здійснення умови зіставлення. Перерахунок показників полягає у їх коригуванні. Завжди коригуються і перераховуються показники при аналізі виконання плану, динаміки за кілька років (інших періодів часу), двох підприємств, закордонного досвіду, враховуючи зміни, які виникли через перехід до ринкових відносин, аналізу впливу цінового механізму, інфляції. Наприклад, перевиконання плану щодо виробництв продукції потребує додаткового, проти плану, витрачання заробітної плати. Щоб фактичні дані були порівнянні з плановими, необхідно фактичне витрачання заробітної плати зіставити з плановими, перерахованими на фактично вироблену продукцію. Тільки тоді можна правильно визначити, перевитрати чи економія по заробітній платі мали місце під час виробництва фактичного виходу продукції, і робити обґрунтовані висновки щодо подальшого розподілу фінансових ресурсів.
Ряди динаміки — це ряд чисел, що характеризують зміну величин у часі. Аналіз динаміки показників дає змогу виявляти і досліджувати закономірності, тенденції розвитку явищ.
Ряди динаміки характеризуються абсолютними і відносними величинами.
Абсолютні величини поділяються на моментні, що характеризують економічне явище на певний момент часу (наприклад, наявність власних оборотних коштів на початок або кінець року) та інтервальні (періодичні), що характеризують результати за певні періоди (наприклад, виручка від реалізації за перший, другий, третій квартали і в цілому за рік). До абсолютних величин, використованих для аналізу динаміки, належать: абсолютне зростання та абсолютний приріст. Відносними показниками для характеристики динаміки є темп зростання і темп приросту.
Абсолютне зрістання дорівнює величині аналізованого показника.
Абсолютний приріст характеризує, на скільки одиниць змінився (збільшився «+», зменшився «–») аналізований показник щодо базисного. Щоб його розрахувати, треба від аналізованого показника відняти базисний.
Темп зростання показує, у скільки разів аналізований показник більший або менший за базисний. Темп зростання, виражений у процентах, показує, скільки процентів аналізований показник становить щодо базисного, прийнятого за 100 %.
Темп приросту показує, на скільки процентів аналізований показник відхилився від базисного.
Розглянемо методику розрахунку цих показників на такому прикладі.
Чистий прибуток становив:
— у минулому році 11 450 грн.;
— у звітному році — 15 000 грн.
Абсолютне зростання чистого прибутку становить 15 000 грн.
Абсолютний приріст: +3550 грн (15 000 грн. — 11 450 грн.).
Темп зростання дорівнює: 131 % (15 000 : 11 450 ´ 100), тобто треба аналізований показник поділити на базисний і помножити на 100.
Темп приросту: 31 % (![]() , або
, або ![]() , або 131 — 100).
, або 131 — 100).
Отже, темп приросту можна розрахувати в три способи:
¾ від аналізованого показника відняти базисний, отриманий результат поділити на базисний показник і помножити на 100 %;
¾ якщо розраховано абсолютне відхилення, то його треба поділити на базисний рівень показника і помножити на 100 %;
¾ якщо розраховано темп зростання, то від нього треба відняти 100 %.
Останній спосіб — найпростіший і найшвидший.
У сучасних умовах комп’ютерної технології оброблення інформації аналіз динаміки здійснюється за допомогою спеціальної програми «Ряди динаміки».
Аналітичні таблиці. Без аналітичних таблиць проведення фінансово-господарського аналізу неможливе. Таблиці широко застосовуються для унаочнення методики аналітичних розрахунків, отриманих результатів аналізу, групування показників і виявлених резервів.
За допомогою таблиць краще сприймається аналітична інформація під час вивчення явищ і процесів за допомогою згрупованих показників і цифр, розташованих у певному порядку. Таблиця є раціональнішою, компактнішою, наочнішою, яскравішою формою відображення аналітичного процесу, ніж текстовий варіант викладення аналітичного матеріалу. У разі використання таблиць ефект сприйняття інформації пізнавального характеру значно підвищується.
Складання аналітичних таблиць — дуже важка справа, оскільки вони містять у собі систематизований виклад числових результатів збирання та опрацювання матеріалів, відображують зв’язки між досліджуваними показниками.
Для того щоб грамотно скласти аналітичну таблицю, необхідно:
¾ добре знати сутність економічного процесу, явища, окремого показника, що вивчаються;
¾ володіти методикою їх аналізу;
¾ дотримуватися певних правил складання та оформлення аналітичної таблиці.
Існують різні види таблиць, які несуть різноманітну інформацію. Проте кожна таблиця мусить мати свій заголовок, який повинен коротко і чітко визначає її зміст.
Таблиці складаються з горизонтальних рядків (підмет) і вертикальних колонок-граф (присудок). У підметі таблиці наводяться об’єкти, які характеризуються цифровими показниками, а у присудку — показники, що характеризують підмет. На перетині граф і рядків ставиться цифровий матеріал. У таблиці доцільно наводити контрольні підсумки. Це полегшує аналіз і підкріплює висновки. Графи, що містять підмет, нумеруються заголовними літерами в алфавітному порядку, а графи, що містять присудок, — арабськими цифрами.
Якщо таблиця містить показники різних одиниць вимірювання, то вони обов’язково вказуються у змісті таблиці. Якщо таблиця містить показники єдиного вимірювання, то одиниця вимірювання виноситься у заголовок.
В аналітичних таблицях зручно відображати основні характерні риси об’єкта дослідження, порядок обчислення показників, виконання плану та оцінку його напруженості, динаміку показників, структурні зміни показників, методику і розрахунки факторного аналізу, виявлення і підрахунок резервів.
У графах і рядках доцільно наводити методику розрахунку показників (див. аналітичні таблиці).
Графічний спосіб слугує засобом вивчення економіки. У фінансовому аналізі графік є засобом ілюстрування господарських процесів. Це узагальнений рисунок стану і розвитку досліджуваного економічного явища (явищ), який дає змогу наочно дослідити тенденції і зв’язки економічних показників. Є різні способи зображення економічних показників (залежно від особливостей досліджуваних явищ). Різноманітними є і графіки. У фінансовому аналізі найчастіше застосовують лінійні графіки, кругові та стовпчикові діаграми.
Лінійні графіки зручні для відображення зв’язків між досліджуваними показниками. Їх використовують в основному для унаочнення функціональної залежності та для порівняння тенденцій розвитку окремих показників у процесі дослідження підсумків роботи господарств. Лінійні графіки подають за допомогою прямокутних координат. Якщо вивчається функціональна залежність між показниками, то на горизонтальній прямій — осі абсцис (X) — відкладаються значення факторного показника, а на вертикальній прямій — осі ординат (Y) — значення результативного показника у відповідному масштабі. Кожна точка на координатному полі показує сукупність двох чисел. Сукупність двох чисел, що визначає положення точки, називається її координатами.
Якщо на лінійному графіку зображується співвідношення різних взаємопов’язаних показників, рівень їх розвитку у динаміці, то на осі абсцис відкладаються періоди часу через рівні інтервали (наприклад, роки), а по осі ординат — значення досліджуваних показників. Лінійні графіки мають супроводжуватися умовними позначеннями або надписами.
Наочним засобом порівняння абсолютних величин того самого ж найменування є стовпчикова діаграма, на якій порівнюються окремі показники за допомогою співвідношення стовпчиків різної величини. Стовпчики можна заштрихувати або зафарбувати.
Для зображення складу досліджуваного показника, питомої ваги окремих складових у його загальній величині використовують кругові діаграми (їх також називають структурними секторними). У цих діаграмах структура показника подається у вигляді секторів, на які розбито коло, прийняте за 100 %. Величина кожного сектора визначається питомою вагою певної складової. Сектори також можна заштрихувати або зафарбувати різними кольорами, відмічаючи умовні позначення.
Але варто наголосити, що для чіткого ілюстрування графіком висновків, необхідно правильно його побудувати — знайти такі способи зображення, які найліпше відповідають змісту та економічній сутності зображуваних показників.
Треба пам’ятати, що будь-який графік сам по собі не замінює конкретних даних. Тому, якщо графік не включає чисел, то вони мають бути наведені у тексті. Графік повинен бути точним, побудованим відповідно до масштабу, мати пояснення змісту кольорів і штриховок, назви показників. Графік не можна перевантажувати даними — перевантаження ускладнює його читання.
Вивчення взаємозв’язку показників
Проведення фінансового аналізу потребує відповідної послідовності вивчення економічних показників.
На початковій стадії аналізу будь-якого показника вивчення здійснюється від загального до часткового (дедуктивний прийом дослідження). На стадії узагальнення вивчені складові аналізованого показника розглядаються з урахуванням їх впливу на загальні показники (індуктивний прийом дослідження). Дедуктивний та індуктивний прийоми досліджень — це два боки того самого процесу вивчення явищ. У цьому виявляється єдність і нерозривний зв’язок аналізу та синтезу.
Досконало пізнати суть і розвиток будь-якого досліджуваного явища можна лише за умови розкриття внутрішнього його змісту, з’ясування взаємозв’язку його із складовими.
Фінансовий аналіз передбачає проведення факторного аналізу. Під факторним аналізом слід розуміти методику комплексного, системного вивчення та вимірювання впливу факторів на результативний показник.
Результативним називається економічний показник, який визначається як об’єкт дослідження, як ознака, що залежить від факторних ознак і змінюється під їх впливом.
Економічні показники, застосовувані у факторному аналізі як характеристики результативного показника, визначають його поведінку, тобто впливають на результативний показник і обумовлюють його зміну, називаються факторними.
Детермінований факторний аналіз являє собою методику дослідження впливу факторів, зв’язок яких з результативним показником є функціональним. У разі функціональної залежності зі зміною фактора завжди змінюється і результативний показник. Функціональний зв’язок — це зв’язок, за якого кожному значенню фактора відповідає одне і тільки одне значення результативного показника.
У фінансовому аналізі, як і в економічному, вивчення взаємозв’язку господарських явищ — важливий і найскладніший елемент детермінованого факторного дослідження. У завдання детермінованого аналізу економічних показників входить установлення конкретного виду залежності результативного показника від окремих факторів, що впливають на нього, та кількісного їх розміру.
Таку характеристику одержують за допомогою математичного моделювання економічних процесів. При здійсненні детермінованого факторного аналізу в економічних дослідженнях найпоширенішими й доцільнішими є зображення економічних взаємозв’язків у вигляді математичних формул їх також називають аналітичними моделями). Використання моделей дає змогу абстрактно зобразити основні взаємозв’язки, що існують у реальній господарській системі. Аналітичне моделювання, по-перше, дає змогу методично правильно підійти до вивчення господарських процесів, по-друге, без нього неможливе розв’язання аналітичних задач за допомогою сучасної автоматизації розрахунків. Тому дедалі більшого розвитку набуває перспективний напрям фінансово-економічного аналізу — за допомогою так званих виробничих функцій. Особливої актуальності вони набувають при здійсненні стратегічного аналізу діяльності підприємства.
Функція — це математичне поняття, що відбиває залежність одних величин від інших. У разі позначення досліджуваного показника через Y, а фактора, що впливає на нього, через X, такий взаємозв’язок зображується функцією:
Y = f (X).
Але часто на досліджувані економічні показники впливає не один, а декілька факторів. У такому разі:
Y = f (x1, x2, x3, …, xn),
де n — кількість незалежних факторів;
x1, x2, x3, …, xn — величини кожного окремого фактора.
Ця формула дає загальне уявлення про будь-який взаємозв’язок економічних показників.
При аналізі економічного показника вивчення взаємозв’язку факторних показників, що впливають на нього, тобто складання аналітичної моделі аналізованого показника, включає такі етапи:
1. Виявлення конкретних факторів, які впливають на досліджуваний показник.
2. З’ясування послідовності впливу окремих факторів і здійснення розподілу їх на кількісні та якісні.
3. З’ясування виду залежності досліджуваного показника від кожного окремого фактора.
4. Подання конкретного виду взаємозв’язку аналізованого показника з факторами, що впливають на нього (складання аналітичної моделі).
Отже, з’ясувавши склад факторів, послідовність і характер їх впливу на результативний показник, визначають конкретний вид взаємозв’язку — складають аналітичну модель у вигляді певної функції.
Деталізація — важливий елемент методу фінансового аналізу, за допомогою якого відбувається розчленування досліджуваних економічних явищ, показників, факторів. Деталізація дає змогу на основі знань економічної теорії впорядкувати аналіз, сприяє комплексному розгляду факторів впливу, вказує на значущість кожного з них, є основою математичного моделювання взаємозалежності різних показників і факторів.
Економічні показники можна деталізувати за ознаками простору, часу, за окремими спеціальними ознаками і складовими. Часто деталізацію називають розчленуванням.
Слід враховувати, що чим більша і ширша деталізація аналізованих показників, тим глибшим і якіснішим є їх аналіз, тим точніші аналітичні результати вивчення діяльності підприємства.
Детерміноване моделювання факторних систем передбачає послідовне розчленування факторів вихідної системи та їх перетворення. Способи перетворення факторних систем у деталізованому аналізі досить ґрунтовно висвітлюють у сучасній економічній літературі.
Результативні показники можуть бути розкладені на фактори в різні способи і подані у вигляді різних типів детермінованих моделей.
Елімінування — один із найважливіших елементів здійснення детермінованого факторного аналізу. Це прийом, за допомогою якого виключається дія ряду факторів і виокремлює один з них. Елімінування дає змогу визначити величину впливу окремих факторів на досліджуваний показник, оцінити їхню позитивну і негативну роль, вияивти невикористані резерви підвищення ефективності діяльності господарства. Аналітичні результати такого дослідження відіграють важливу роль у розробленні та прийнятті оптимальних управлінських рішень, для обґрунтування яких необхідні проведення факторного аналізу, порівняння звітних показників з минулими періодами, плановими даними, з кращими виробничими результатами інших господарств тощо.
До елімінування належить спосіб ланцюгових підставлянь. Він застосовується, коли існує функціональний зв’язок між аналізованим показником і факторами, тобто є детерміновані факторні моделі.
Суть цього способу полягає в отриманні низки скоригованих значень узагальненого показника шляхом послідовних замін (ланцюгового підставляння) базисних значень факторів на аналізовані.
У першому розрахунку всі фактори знаходяться на базисному рівні. У другому — перший фактор змінюється на аналізований, останні залишаються незмінними (базисний рівень). У третьому розрахунку перший фактор залишається на аналізованому рівні, а з базисного на аналізований змінюється другий фактор, останні знову залишаються незмінними на базисному рівні і т. д., залежно від кількості факторів.
Існує правило: чим більше факторів, тим більше розрахунків; кілька розрахунків на одиницю більша кількості показників у розрахунковій формулі.
Ступінь впливу факторів виявляється послідовним відніманням: із другого розрахунку віднімається перший (визначається вплив першого фактора); із третього розрахунку — другий (визначається вплив другого фактора) і т. д. залежно від кількості факторів є у формулі.
Розглянемо техніку застосування прийому ланцюгових підставлянь для аналізу відхилення y¢ (аналізований рівень) від y0 (базисний рівень) за рахунок впливу факторів x1, x2, x3, … xn.
![]() — базисні значення факторів;
— базисні значення факторів;
![]() — аналізовані значення факторів.
— аналізовані значення факторів.
Перший розрахунок (базисний рівень результативного показника):
![]()
Другий розрахунок (умовне значення результативного показника):
![]()
Третій розрахунок (умовне значення результативного показника):
![]()
Четвертий розрахунок (умовне значення результативного показника):
![]()
![]()
Останній розрахунок (аналізований рівень результативного показника):
![]()
Знаходимо:
¾ вплив зміни першого фактора x1 на відхилення результативного показника
![]()
¾ вплив зміни другого фактора x2 на відхилення результативного показника
![]()
¾ вплив зміни третього фактора x3 на відхилення результативного показника
![]()
¾ вплив останнього фактора xn на відхилення результативного показника
![]()
¾ ![]() результат попереднього умовного значення результативного показника.
результат попереднього умовного значення результативного показника.
Алгебраїчна сума впливу факторів обов’язково має дорівнювати загальному відхиленню результативного показника:
DY = DY (x1) + DY (x2) + DY (x3) + … + DY (xn).
Відсутність такої рівності свідчить про допущені помилки в розрахунках.
Здійснюючи розрахунки впливу зміни факторів на відхилення результативного показника, необхідно завжди ставити математичні знаки «+» і «–» перед одержаним цифровим результатом («+» — зростання, збільшення; «–» — зменшення, спадання, зниження величини результативного показника).
Застосовуючи цей метод, необхідно виконувати такі правила:
· визначення результативного та визначення факторних показників;
· здійснення класифікації факторів на кількісні та якісні. Якщо кількісних факторів більше одного, то спочатку визначаються кількісні фактори першого підпорядкування, потім другого і т. д.
· складання правильної формули залежності результативного показника від факторів, при цьому на перше місце в моделі взаємозв’язку показників ставляться кількісні фактори, далі — якісні. Якщо кількісних факторів більше одного, то спочатку розміщуються кількісні фактори першого підпорядкування, потім другого, третього і т. д.
Отже, використання способу ланцюгових підставлянь потребує знання взаємозв’язку факторів, їх супідрядності, вміння правильно їх класифікувати і систематизувати, чітко робити розрахунки і правильно формулювати висновки.
Прийом абсолютних різниць є різновидом способу ланцюгових підставлянь, проте деякі автори відносять його до окремого, самостійного способу елімінування. Такий прийом застосовують для розрахунку впливу факторів на відхилення результативного показника тільки в мультиплікативних і змішаних моделях, оскільки він простіший, раціональніший, економічніший та ефективніший ніж спосіб ланцюгових підстановлянь.
Використовуючи його спочатку знаходять абсолютні відхилення за кожним фактором. Потім величину впливу факторів обчислюють множенням абсолютного відхилення досліджуваного фактора на базову величину факторів, розміщених в моделі взаємозв’язку показників праворуч від нього, і на аналізовані рівні факторів, розташованих ліворуч від нього. При цьому ніколи не можна змінювати послідовність впливу факторів за формулою.
Тому, враховуючи послідовність впливу на результативний показник окремих факторів у разі застосування цього прийому, виходять з таких загальних правил:
¾ знаходять загальне абсолютне відхилення результативного фактора і за кожним фактором шляхом порівняння визначають абсолютні відхилення величин аналізованих факторів («+» — більше, «–» — менше) від базисних, які позначають знаком D:
![]()
![]()
![]()
![]()
¾ вплив першого фактора дорівнює відхиленню за ним, взятому у співвідношенні з абсолютними базисними величинами решти наступних факторів:
![]()
¾ вплив другого фактора дорівнює добутку аналізованої величини першого фактора, абсолютного відхилення за другим фактором і базисних величин решти наступних факторів:
![]()
¾ вплив третього і кожного наступного факторів дорівнює добутку аналізованих величин факторів, що стоять у формулі перед фактором, вплив якого обчислюється, на його абсолютне відхилення, помноженому на базисні величини решти наступних факторів:
![]()
¾ вплив останнього фактора обчислюється добутком аналізованих величин вже досліджених факторів і абсолютним відхиленням за цим фактором:
![]()
Якщо розрахунки зроблено правильно, то загальне відхилення за результативним показником дорівнюватиме алгебраїчній сумі впливу всіх факторів.
Різні фактори впливають на загальний показник в бік збільшення або зменшення, позитивно або негативно. Тому істотне значення мають не тільки цифрові величини відхилень, а й математичні знаки «+», «–», що характеризують напрям впливу факторів («+» — збільшення, зростання; «–» — зменшення, зниження).
У разі застосування такого прийому також необхідні знання щодо взаємозв’язку факторів, класифікації їх на кількісні та якісні, головні та другорядні, вміння чітко здійснювати розрахунки й правильно формулювати висновки.
Існує ще одне загальне правило для прийому абсолютних різниць, коли у формулі взаємозв’язку показників тільки два фактори: один — кількісний, другий — якісний:
¾ при розрахунку впливу зміни кількісного фактора на відхилення результативного показника необхідно відхилення за кількісним фактором помножити на базисну величину якісного фактора;
¾ при розрахунку впливу зміни якісного фактора на відхилення результативного показника необхідно відхилення за якісним фактором помножити на аналізований рівень кількісного фактора.
За наявності повних вихідних даних для проведення факторного аналізу доцільно застосовувати спосіб абсолютних різниць, а не безпосередньо ланцюгові підстановки, оскільки при цьому:
1. виконується менша кількість розрахунків (не треба обчислювати умовні показники), значно менше витрачається часу на проведення аналізу, можна одразу отримувати результати впливу факторів на досліджуваний показник;
2. володіння абсолютними відхиленнями величини факторів (+, –) і видом функції взаємозв’язку показників уможливлюється без здійснення конкретних розрахунків і отримання конкретних чисел оцінювання напряму впливу зміни факторів на відхилення по результативного показника.
Розглянемо застосування способу ланцюгових підстановок на прикладі аналізу виконання плану по прибутку від реалізації цукрових буряків (табл. № 1.1). Зазначимо, що величина цього прибутку залежить від трьох факторів:
1) кількості реалізованої продукції (К);
2) реалізаційної ціни одиниці продукції (Ц);
3) собівартості одиниці продукції (С).
Таблиця № 1.1
ВИХІДНІ ДАНІ ДЛЯ ФАКТОРНОГО АНАЛІЗУ ПРИБУТКУ ВІД РЕАЛІЗАЦІЇ ЦУКРОВИХ БУРЯКІВ
| Показник | За планом | Умовне позначення | Фактично | Умовне позначення |
| 1. Кількість реалізованої продукції, ц | 100 000 | К0 | 102 000 | К1 |
| 2. Реалізаційна ціна 1 ц, тис. грн | 2,1 | Ц0 | 2,2 | Ц1 |
| 3. Собівартість 1 ц, тис. грн | 1,2 | С0 | 1,5 | С1 |
| 4. Прибуток від реалізації, млн грн | 90,0 | П0 | 71,4 | П1 |
Отже, модель прибутку від реалізації має змішаний вигляд:
П = К (Ц — С).
Для визначення розміру впливу окремих факторів на прибуток здійснюють ланцюгові підставляння:
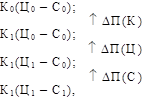
де DП(К) — відхилення прибутку за рахунок зміни кількості реалізованої продукції;
DП(Ц) — відхилення прибутку за рахунок зміни ціни реалізації;
DП(С) — відхилення прибутку за рахунок зміни собівартості одиниці продукції.
Виконаємо розрахунки:
І.100 000 (2,1—1,2) = 90 000;
ІІ.102 000 (2,1—1,2) = 91 800;
ІІІ.102 000 (2,2—1,2) = 102 000;
IV. 102 000 (2,2—1,5) = 71 400;
DП(К) = 91,8 — 90 = +1,8;
DП(Ц) = 102,0 — 91,8 = +10,2;
DП(С) = 71,4 — 102,0 = –30,6;
DП = П1 — П0 = DП(К) +DП(Ц) + DП(С).
Підставимо отримані дані:
71,4 — 90,0 = 1,8 + 10,2 — 30,6;
— 18,6 = — 18,6.
Розглянемо розрахунки впливу факторів за способом абсолютних різниць. Приріст суми прибутку за рахунок зміни:
¾ обсягу реалізації продукції: DП(К) = DК (Ц0 — С0);
¾ ціни реалізації: DП(Ц) = К1 DЦ;
¾ собівартості одиниці продукції: DП(С) = К1 DС.
Розрахунки за наведеними вихідними у табл. 2.1 даними:
DП(К) = (+2000) (2,1 — 1,2) = (+2000) 0,9 = +1800;
DП(Ц) = 102 000 (+0,1) = +10200;
DП(С) = 102 000 (–0,3) = –30600.
План по прибутку не виконано на 18600 тис. грн. Причиною є підвищення собівартості, за рахунок чого прибуток зменшився на 30600 тис. грн. Позитивно вплинули на прибуток збільшення кількості реалізованої продукції та підвищення ціни реалізації (+1800 тис. грн та +10200 тис. грн відповідно).
До елімінування належить також спосіб відносних чисел, до якого вдаються для вимірювання впливу факторів на відхилення результативного показника тільки в мультиплікативних моделях і моделях комбінованого (змішаного) типу. Він використовується, коли вихідні дані містять уже визначені відносні відхилення факторних показників у процентах або коефіцієнтах. Розглянемо методику такого способу на прикладі, коли досліджуваний показник є результатом добутку декількох факторів.
Для визначення впливу першого фактора процент зміни величини цього фактора, поділений на 100, помножується на базисну величину досліджуваного показника.
Для визначення впливу другого і кожного наступного фактора спочатку визначають процент зміни показника, що вивчається, за рахунок відповідного фактора з урахуванням впливу попередніх факторів і потім його помножують на базисний показник, що вивчається.
Вплив останнього фактора визначається так: беруть процент виконання плану за аналізованим показником, віднімають від нього сукупний процент впливу всіх попередніх факторів, одержаний результат помножують на базисну величину аналізованого показника і ділять на 100.
Але треба зазначити, що практично цей спосіб застосовується дуже рідко.
До балансового способу вивчення економічних явищ і процесів вдаються коли необхідно дослідити співвідношення двох груп взаємопов’язаних економічних показників, підсумки яких рівні між собою. Здебільшого він використовується саме у фінансовому аналізі. Так, для визначення платоспроможності підприємства застосовують платіжний баланс, в якому платіжні засоби співвідносяться з платіжними зобов’язаннями.
Бухгалтерський баланс також являє собою приклад застосування балансового способу: актив балансу — групування господарських засобів за їх розміщенням і призначенням — дорівнює його пасиву — джерелам формування господарських засобів підприємства. Бухгалтерський баланс — основне джерело інформації для фінансового аналізу.
Балансовий спосіб широко застосовується для перевірки вихідних даних, на основі яких проводиться аналіз (наприклад, сума загального капіталу = власний капітал + позиковий капітал), для перевірки правильності аналітичних розрахунків (загальне відхилення результативного показника дорівнює алгебраїчній сумі впливу окремих факторів за розв’язування аналітичних задач у детермінованих факторних моделях).
Але слід зауважити, що не всі економічні явища і процеси можна описати функціональною залежністю. В економічних дослідженнях існують стохастичні залежності, які характеризуються приблизністю, невираженістю. У таких випадках виконується стохастичний аналіз, що являє собою методику дослідження факторів, зв’язок яких з результативним показником є неповним, імовірним (кореляційним). У разі кореляційного зв’язку значенню факторної ознаки відповідає не одне певне значення результативного показника, а кілька його значень, тобто відомий розподіл цих значень. Говорять, що у разі кореляційного зв’язку одному значенню фактора відповідає середнє значення результативного показника.
Кореляційний (стохастичний) зв’язок — це неповна, ймовірнісна залежність між економічними показниками, яка виявляється тільки в масі спостережень.
Він класифікується за такими ознаками:
1) за числом факторів:
¾ однофакторний — зв’язок між двома ознаками. Такий зв’язок називають парною кореляцією, що означає зв’язок між одним фактором і результативним показником.
¾ багатофакторний — зв’язок між кількома ознаками. Його називають множинною кореляцією, яка виникає внаслідок взаємодії кількох факторів з результативним показником;
2) за напрямом:
¾ позитивний, коли збільшення (зменшення) фактора веде відповідно до збільшення (зменшення) результативного показника (реалізаційна ціна і виручка);
¾ негативний, коли збільшення (зменшення) фактора веде відповідно до зменшення (збільшення) результативного показника, тобто напрям зміни результативної ознаки не збігається з напрямом зміни фактора (собівартість продукції і прибуток).
3) за аналітичним виразом (за формою):
¾ прямолінійний, — зв’язок може бути виражений прямою лінією;
¾ криволінійний, — зв’язок може бути виражений рівнянням кривої.
При аналізі економічних явищ кореляційний зв’язок має певні особливості:
· він відображується і виявляється не в поодиноких випадках, а в масі явищ, тобто пов’язаний з дією закону великих чисел: лише в достатньо великій кількості факторів індивідуальні особливості та другорядні фактори згладжуються, і незалежність, якщо вона має суттєву силу, виявляється достатньо чітко;
· він є неповним, оскільки звичайно неможливо врахувати всі фактори, що впливають на аналізований показник;
· він оцінює взаємозв’язки в конкретних умовах місця і часу, тобто в ряді випадків залежності, отримані для однієї галузі виробництва, «непрацездатні» в інших галузях;
· стосовно до суспільних явищ і процесів він є незворотним;
· у разі застосування його для розв’язування економічних задач дослідники мають певні труднощі (гранична кількість спостережень; неможливість експерименту на практиці тощо).
Для дослідження стохастичних залежностей використовують кореляційно-регресійний аналіз. Широко застосовуються метод експертних оцінок і рангової кореляції, способи парної і множинної кореляції.
Велику роль у фінансовому аналізі відіграє експертний метод (інша назва — прийом експертних оцінок). Сутність його полягає у збиранні думок спеціалістів щодо поставленої проблеми, подальше опрацювання їх і використання в аналітичній роботі.
Для оцінювання думок експертів про ступінь важливості впливу факторів найчастіше використовується анкетне ранжироване опитування. При цьому розробляється анкета спеціальної форми. Існують певні правила, яких треба дотримуватися під час складання анкет, щоб результати проведеного ранжированого опитування були об’єктивними, достовірними і точними:
¾ в перелік вихідних даних факторів, які впливають на результативний показник, мають включатися всі (на думку дослідників) фактори;
¾ формулювання факторів має бути повним і чітким;
¾ порядок переліку факторів в анкеті має бути довільним;
¾ запитання в анкетах має бути чітко сформульованим, без двоякого тлумачення, щоб опитувані фахівці (експерти) змогли чітко уявити досліджуваний процес;
¾ кількість опитуваних фахівців має в 7—10 разів перевищувати кількість факторів, включених у дослідження;
¾ анкети мають бути невеликими, лаконічними, не потребувати багато часу на їх прочитання і замовлення.
Під час заповнення анкет застосовується метод апріорного ранжування, що вимагає розміщення факторів у порядку зменшення ступеня їх впливу на результативний показник.
Для збирання думок експертів про ступінь впливу факторів на результативний показник використовується приблизно така форма анкети (рис. 1.5).
АНКЕТА ОПИТУВАННЯ
Шановний
_______________________________________________________
Просимо розмістити у таблиці нижченаведені фактори за ступенем їх впливу на ____________________________________.
(назва результативної ознаки)
Цифри графі «Ранги» мають відповідати місцю (номеру), відведеному Вами для даного фактора. Число «один» надається найбільш важливому за ступенем впливу фактору, число «два» — наступному і т. д. Якщо, на Вашу думку, ступінь впливу факторів однаковий, то їм надається однаковий номер-ранг.
ДАНІ ДЛЯ ПРОВЕДЕННЯ АНАЛІЗУ ВПЛИВУ ФАКТОРІВ НА РЕЗУЛЬТАТИВНИЙ ПОКАЗНИК________________________
| № з/п | Фактори | Позначення факторів | Ранг |
| 1 | |||
| 2 | |||
| і т. д. |
Рис. 1.5. Форма анкети опитування
Підготовлені анкети роздаються експертам для заповнення. Результати опитування заносяться у таблицю (табл. 1.2).
Таблиця. 1.2
РЕЗУЛЬТАТИ ОПИТУВАННЯ
| Номер експерта | Ранги факторів, включених в опитування | ||||
| 1 | |||||
| 2 | |||||
| і т. д. | |||||
Така таблиця слугує вихідною інформацією для проведення аналізу.
Першим кроком в обробленні вихідної інформації є перетворення вихідних рангів. По експертах, які надали окремим факторам однакові ранги (зв’язані), здійснюється перетворення рангів. Для цього:
— фактори розміщуються у зростаючий ранжирований ряд за значенням рангів відповідного експерта;
— нумеруються фактори неперервним рядом натуральних чисел (1, 2, 3, ..., п, де п — кількість факторів);
— кожний однаковий ранг фактора для певного експерта замінюється перетвореним, який являє собою середню з відповідних номерів натурального ряду;
— останні ранги факторів замінюються порядковим номером цього фактора у ранжированому ряді.
Наступним кроком є перевірка адекватності (відповідності) початкової і перетвореної таблиць. Перевірку адекватності первісних і перетворених рангів здійснюють таким чином:
1) знаходять суми рангів кожного фактора у вихідній і перетвореній таблицях;
2) установлюють умовні ранги факторів за сумами рангів (мінімальній сумі — ранг 1, наступній за величиною сумі — ранг 2 і т. д. Якщо суми рангів для деяких факторів виявились однаковими, їм присвоюють умовні перетворені ранги);
3) визначають парний ранговий і критичний коефіцієнт Спірмена.
Порівнюють обчислене і критичне значення коефіцієнта. При цьому, якщо обчислене значення більше за критичне значення коефіцієнта, то вихідні та перетворені таблиці адекватні, якщо обчислене значення менше за критичне значення коефіцієнта, то подальший аналіз неможливий, оскільки вихідна та перетворена таблиці не адекватні. У такому разі з’ясовують причини (фахівці слабо орієнтуються в даній проблемі, мала кількість експертів, допустилися помилок під час складання анкет, помилки у процесі збирання інформації, її оброблення тощо).
За умови адекватності таблиць оцінюють ступінь узгодженості експертів. Визначення ступеня узгодженості експертів проводиться шляхом оцінювання значущості коефіцієнта конкордації Кендалла за критерієм хі-квадрат. При цьому погляди експертів узгоджені, якщо обчислене значення критерію більше від табличного. Якщо обчислене значення менше від табличного, роблять висновок про відсутність узгодженості поглядів експертів. У такому разі слід повторити опитування, але вже на більш високому рівні.
Якщо погляди експертів узгоджені, то наступним етапом є оцінювання узгодженості поглядів експертів за кожним фактором. Перевіряють припущення про рівномірність розподілу рангів за кожним фактором, використовуючи критерій Мізеса-Смирнова. Порівнюють обчислене значення критерію з критичним і роблять висновок:
а) якщо обчислене значення критерію менше від критичного, то розподіл рангів фактора не суперечить рівномірному розподілу, тобто щодо цього фактора в експертів немає узгодженої думки. У цьому разі з’ясовується причина одержаного результату і за необхідності проводять повторне опитування;
б) якщо обчислене значення критерію більше від критичного, то розподіл рангів не відповідає рівномірному розподілу, тобто про ступінь впливу аналізованого фактора у експертів існує узгоджена думка.
У разі позитивного вирішення цього етапу наступним є побудова діаграми рангів.
З метою унаочнення розміщення факторів за ступенем впливу будують стовпчикову діаграму рангів. Для цього по осі абсцис відкладають рівні інтервали відповідних факторів в порядку збільшення сум їхніх рангів, а по осі ординат — суми рангів у порядку зменшення їхніх значень. На інтервалах (як на основах) будують прямокутники, висота яких відповідає сумі рангів факторів.
Після побудови спадної діаграми рангів перевіряють, чи немає зменшення випадкового характеру. Для цього за критерієм узгодження хі-квадрат перевіряється припущення про рівномірність розподілу сум рангів. Якщо обчислене значення критерію менше від табличного, то береться припущення про рівномірність розподілу сум рангів. Убування діаграми є випадковим, і робиться висновок, що рівень апріорної інформації відносно поставленої задачі дуже низький і необхідно або провести анкетне опитування на вищому рівні, або включити в дослідження всі фактори, оскільки вони, на думку експертів, усі важливі. Якщо обчислене значення критерію більше від табличного, то припущення про рівномірність розподілу сум рангів відхиляється. Убування рангів має не випадковий характер, і робиться висновок про високий рівень апріорної інформації, про ступінь важливості факторів.
Коли припущення про рівномірність розподілу сум рангів діаграми факторів відхиляється, перевіряється припущення про екс-потенційність убування діаграми рангів за критерієм![]() .
.
Порівнюється обчислене значення критерію з його інтерваль-ним значенням. При цьому, якщо обчислене значення знаходиться поза інтервалом, то відхиляється припущення про експотенційний характер убування рангів. Якщо обчислене значення ![]() входить у табличний інтервал, то береться припущення про експотенційний характер убування діаграми рангів. При цьому чим ближче до середини інтервалу обчислене значення
входить у табличний інтервал, то береться припущення про експотенційний характер убування діаграми рангів. При цьому чим ближче до середини інтервалу обчислене значення ![]() , тим сильніший експотенційний характер убування рангів.
, тим сильніший експотенційний характер убування рангів.
У разі експотенційності убування діаграми рангів виникає можливість розбити фактори на групи за ступенем їхнього впливу на оцінюваний показник. Для цього:
— обчислюють для кожного фактора середні дисперсії, середні квадратичні відхилення;
— визначають обчислене і табличне значення критерію Кокрана;
— обчислене значення критерію порівнюють з табличним. При цьому, якщо воно менше від табличного, то дисперсії однорідні, а якщо більше від табличного — неоднорідні (у разі неоднорідності дисперсій рангів проводять аналіз рангів фактора з найбільшою дисперсією, виявляють причини (допущені помилки в даних, нечітко визначений фактор, експертам важко оцінити його важливість і т. д.);
— знаходять різницю середніх значень для факторів за абсолютною величиною;
— визначають критичне значення різниці, використовуючи t-розподіл Ст’юдента;
— порівнюють різниці середніх від значень факторів з критичними і роблять висновок: якщо різниці менші від критичної, то ці фактори можуть бути об’єднані в одну групу, в протилежному разі — ні;
— формують групи факторів.
Далі визначаються групи експертів з високим і низьким ступенем узгодженості думки. Для виявлення груп, усередині яких узгодженість думки висока, визначають коефіцієнт конкордації ![]() для всіх значень рангів. Виключають із розгляду одного експерта і визначають для залишеної сукупності коефіцієнт конкордації
для всіх значень рангів. Виключають із розгляду одного експерта і визначають для залишеної сукупності коефіцієнт конкордації ![]() . Якщо
. Якщо ![]() >
>![]() , то цей експерт виключається із сукупності, а якщо
, то цей експерт виключається із сукупності, а якщо ![]() — залишається у ній .
— залишається у ній .
Виконавши таку роботу щодо всіх експертів вихідної таблиці, зрештою матимемо групу експертів, усередині якої узгодженість думки висока.
Для виявлення групи експертів з низьким ступенем узгодженості думки визначають коефіцієнт конкордації для всіх експертів ![]() . Виключають із розгляду одного експерта і визначають для залишеної сукупності коефіцієнт конкордації
. Виключають із розгляду одного експерта і визначають для залишеної сукупності коефіцієнт конкордації ![]() . Якщо
. Якщо ![]() то цей експерт залишається із сукупності, а якщо
то цей експерт залишається із сукупності, а якщо ![]() виключається з неї. Виконавши таку роботу щодо всіх експертів вихідної таблиці, зрештою матимемо групу експертів, всередині якої узгодженість думки низька.
виключається з неї. Виконавши таку роботу щодо всіх експертів вихідної таблиці, зрештою матимемо групу експертів, всередині якої узгодженість думки низька.
Оцінювання ступеня узгодженості кожного експерта з усіма іншими експертами проводять таким чином:
— беруть послідовно ранги відповідного експерта (1-го, 2-го і т. д.);
— знаходять суми рангів за факторами для залишених експертів, тобто виключають із підсумовування ранги взятого експерта;
— установлюють для сум рангів залежно від їх величини умовні ранги: найменшій сумі — ранг 1, наступній за величиною сумі — ранг 2 і т. д. У разі однакових сум їм присвоюють однакові (зв’язані) ранги, визначені як середні з порядкових номерів, які мають ці суми в ранжированому ряді;
— знаходять величину рангового коефіцієнта Спірмена для рангів вибраного експерта та умовних рангів, одержаних за сумами рангів, використовуючи співвідношення, наведені раніше;
— аналізують значення обчисленого коефіцієнта Спірмена і роблять висновок. Якщо коефіцієнт Спірмена невід’ємний, то це вказує на оригінальність судження фахівця в оцінці поставленої проблеми (задачі). Додатне значення коефіцієнта рангової кореляції Спірмена вказує на узгодженість думки експерта з думкою усіх інших експертів.
Оцінювання ступеня узгодженості (або оригінальності, тобто несхожості думки кожного експерта з усіма іншими), а також кількісне оцінювання рівня компетентності експерта відносно всіх інших експертів виконують на основі даних табл. 1.3.
Таблиця 1.3
АНАЛІЗ ДУМКИ ЕКСПЕРТА
| Вид аналізу думки експерта |
Значення коефіцієнта Спірмена | ||||
| 0,0...0,3 | 0,3...0,5 | 0,5...0,7 | 0,7...0,9 | 0,9 | |
| Ступінь узгодженості думки | Слабкий | Помірний | Помітний | Високий | Дуже високий |
| Ступінь відмінності думки | Слабкий | Помірний | Помітний | Високий | Дуже високий |
| Ступінь компетентності | 1 | 2 | 3 | 4 | 5 |
Описані процедури реалізації експертних оцінок можна подати у вигляді схеми, наведеної на (рис. 1.6).
Прийом аналізу відбору та оцінювання впливу факторів на результативний показник шляхом анкетного ранжированого опитування швидко реалізується в умовах комп’ютеризації.
На нашу думку, наприклад, у разі аналізу:
— рівня прибутку (Y) факторами, що впливають на нього (X), виступатимуть такі ознаки: обсяг випуску продукції, якість продукції, ритмічність виробництва, ритмічність реалізації, коефіцієнт асортиментності, коефіцієнт структури, використання основних засобів (фондовіддача), матеріаловіддача тощо;

Рис. 1.6. Схема реалізації експертних оцінок шляхом анкетного ранжированого опитування
— рівня рентабельності (Y) — фактори впливу (X): виконання плану реалізації, фондовіддача основних засобів, продуктивність праці, питома вага забракованої продукції, питома вага активної частини основних засобів і т.д.;
— наявності власних оборотних коштів (Y) — фактори впливу (X): прибуток, фондовіддача, ритмічність випуску продукції;
— коефіцієнта оборотності капіталу (Y) — фактори впливу (X): обсяг запасів ТМЦ, матеріаловіддача, показники використання устаткування, продуктивність праці, ритмічність поставок насіння, палива, добрив, якість продукції, обсяг незавершеного виробництва;
— рівня кредиторської заборгованості (Y) — фактори впливу (X): обсяг реалізації продукції, коефіцієнт асортиментності, коефіцієнт структури продукції, продуктивність праці, фондовіддача, якість продукції, рівень дебіторської заборгованості, рентабельність і т. д.;
— фінансової стійкості (Y) — фактори впливу (X): фондовіддача, матеріаловіддача, продуктивність праці, рівень товарної продукції, прибуток, питома вага активної частини основних фондів, втрати від браку і т. д.
Набув поширення прийом парної кореляції (прийом парного кореляційно-регресійного аналізу). Вихідними даними тут є пара значень: результативний показник (Y) і фактор, який на нього впливає (X).
На основі вихідних даних визначаються статистичні характеристики сукупностей. Далі вибирається вид рівняння регресії, тобто відповідний тип математичного рівняння, що найліпше відображує характер досліджуваного зв’язку. Від правильного визначення виду рівняння регресії залежать розв’язання задачі й результати розрахунків.
Кореляційно-регресійний аналіз полягає в побудові статистичної моделі у вигляді рівняння регресії (рівняння кореляційного зв’язку).
Однією з проблем, яку доводиться розв’язувати перед тим, як перейти до побудови рівняння регресії, є вибір типу функції, що описує оцінювану залежність.
Розв’язання цієї проблеми здійснюється в один із таких способів:
· теоретичний аналіз досліджуваного процесу;
· використання раніше отриманих (іншими дослідниками) залежностей;
· аналіз раніше отриманих рівнянь та економічного змісту досліджуваного показника;
· аналіз поля кореляції;
· вибір із кількох рівнянь одного, яке найбільше підходить за визначеним критерієм.
Теоретичний аналіз досліджуваного процесу полягає в тому, що виходячи із знань конкретних умов процесу виробництва, шляхом логічних міркувань та економічних обґрунтувань, спираючись на теоретичні основи явищ, встановлюють вид рівняння.
Використання раніше отриманих залежностей дає зтогу обрати необхідне рівняння зв’язку на основі результатів аналізу інформації (літературні джерела, дослідження інших авторів тощо).
Аналіз раніше отриманих залежностей та економічного змісту нового показника полягає в тому, що на базі раніше отриманого рівняння здійснюється його перетворення й отримується новий вид рівняння для певного економічного показника.
Аналіз поля кореляції — найбільш поширений у практиці прийом, за допомогою якого визначають вид рівняння регресії. При цьому:
— на основі існуючих даних будують поле кореляції (будується прямокутна система координат, на осі абсцис відкладається рівномірна масштабна шкала для фактора впливу X, а на осі ординат — для результативного показника Y, при цьому масштабні шкали на осях припускається починати не з «0», а з будь-якого зручного для конкретного випадку числа. Перебираючи послідовно пари вихідних значень, будують на координатній площині точки. Сукупність побудованих точок являє собою поле кореляції, тобто графік взаємозв’язку між показниками);
— проводиться лінія, навколо якої групуються точки поля кореляції. Таким чином оцінюється напрямок основної тенденції зміни значень результативного показника із зміною значень фактора;
— за видом лінії на полі кореляції, що відображує основну тенденцію зміни, обирається загальний вид рівняння отриманої лінії.
Метод вибору рівняння з кількох залежностей полягає у такому. Якщо є кілька рівнянь, якими, на думку дослідника, можна описати результативний показник, вибирається одне, яке має найкращі оціночні показники. Оцінивши надійність одержаних рівнянь регресії, відкидають ті рівняння, які з низьким рівнем надійності описують взаємозв’язок, який вивчається. За значенням коефіцієнта детермінації беруть відповідне рівняння.
Для розв’язання практичних завдань описані способи застосовуються у взаємозв’язку, доповнюючи й уточнюючи один одного.
Після вибору взаємозв’язку у вигляді загального рівняння визначають числові значення невідомих коефіцієнтів, використовуючи метод найменших квадратів. Суть цього методу полягає в тому, що коефіцієнти регресії визначають так, щоб забезпечити мінімум суми квадратів відхилень значень результативної ознаки q, обчисленої за рівнянням, і значень, одержаних у результаті спостереження.
Цю умову можна забезпечити, якщо невідомі коефіцієнти визначити виходячи із системи рівнянь, одержаної диференціюванням суми квадратів відхилень за кожним невідомим коефіцієнтом рівняння, і прирівняти результат до нуля.
Використовуючи одержані значення рівняння, визначають показники, які характеризують адекватність регресійного рівняння:
— розрахункове значення відхилення розрахункових і вихідних значень Y;
— відносну помилку апроксимації (відношення абсолютного лінійного відхилення до розрахункового значення);
— середню лінійну помилку;
— середню відносну помилку;
— коефіцієнт кореляції для прямолінійної залежності та індекс кореляції для криволінійної;
— коефіцієнт детермінації, що визначає у процентах ту частину закономірності, яка описується одержаним рівнянням;
— середню квадратичну помилку.
Зазначені оціночні показники використовують для оцінювання адекватності рівняння.
Залежно від призначення одержаного рівняння регресії проводять візуальне оцінювання адекватності:
— аналізують величину візуальних значень, відхилень ![]() результативної ознаки і роблять висновок про ступінь «близькості» вихідних і розрахованих за рівнянням значень, а у кінцевому підсумку — про адекватність вихідних даних одержаному рівнянню регресії щодо абсолютних відхилень
результативної ознаки і роблять висновок про ступінь «близькості» вихідних і розрахованих за рівнянням значень, а у кінцевому підсумку — про адекватність вихідних даних одержаному рівнянню регресії щодо абсолютних відхилень ![]() ;
;
— аналізують візуальну величину відносних помилок апроксимації, роблять висновок про адекватність рівняння щодо відносних помилок апроксимації;
— аналізуючи величину середнього лінійного відхилення, роблять висновок про адекватність рівняння регресії вихідним даним щодо величини середньої лінійної помилки, якщо вона не перевищила 5—10 % середнього значення у результативної ознаки;
— аналізуючи середнє значення відносної помилки апроксимації, роблять висновок про адекватність одержаного рівняння регресії вихідним даним щодо величини середньої відносної помилки апроксимації, беручи умовно значення середньої відносної помилки не більше 5—10%. Якщо допустиму помилку апроксимації задано, то розрахована для рівняння середня відносна помилка апроксимації порівнюється з нею. Приймають припущення про адекватність рівняння регресії, якщо розрахована відносна помилка апроксимації менша від допустимої її величини.
У разі прямолінійного рівняння регресії аналізується значущість коефіцієнта кореляції за t-критерієм Ст’юдента. При цьому визначають розраховане і табличне значення t-критерію Ст’юдента. Порівнюють одержане значення з табличним і роблять висновок про значущість коефіцієнта (індексу) кореляції (адекватності) рівняння, якщо ![]() .
.
Коефіцієнт кореляції (індексу) вважається незначним, якщо ![]()
У процесі практичних досліджень немає потреби визначати всі показники надійності рівняння. За всієї різноманітності показників надійності одержаного рівняння регресії остаточний висновок роблять на основі економічної інтерпретації отриманого взаємозв’язку, а також на основі мети, яку поставив дослідник.
Аналіз одержаного рівняння регресії дає можливість зробити такі практичні висновки:
· за значенням коефіцієнта (індексу) кореляції (табл. 1.4) одержується якісна оцінка щільності взаємозв’язку;
Таблиця № 1.4
ХАРАКТЕРИСТИКИ ЩІЛЬНОСТІ ЗВ’ЯЗКУ
| Значення коефіцієнта(індексу) кореляції | 0,1 ... 0,3 | 0,31 ... 0,5 | 0,51 ... 0,7 | 0,71 ... 0,9 | 0,91 ... 0,99 |
| Характеристикащільності зв’язку | Слабка | Помірна | Помітна | Висока | Дуже висока |
· за коефіцієнтом детермінації визначається процент закономірності, що описує одержаним рівнянням досліджуваний взаємозв’язок; (закономірності);
· визначається коефіцієнт еластичності, який показує, на скільки процентів змінюється середнє значення результативної ознаки у разі зміни на 1 % середнього значення фактора, що на нього впливає.
Якщо залежність прямолінійна, то визначають:
— величину зміни результативної ознаки Y при зміні факторної ознаки X на одиницю;
— значення результативної ознаки Y при нульовому значенні фактора X;
— граничні помилки розрахункових значень, на основі яких будують довірчі зони при мінімальних ![]() , максимальних
, максимальних ![]() і середніх (X) значеннях факторної ознаки.
і середніх (X) значеннях факторної ознаки.
Багатофакторний кореляційний аналіз виконується за методами множинного кореляційно-регресійного аналізу. Він здійснюється в кілька етапів (рис. 1.7).
Добір факторів для множинного кореляційного аналізу — дуже важливий етап. Від його правильності залежать достовірність і точність висновків за отриманими результатами. Загальний принцип регресійного аналізу: чим більше вихідних даних, тим краще. Але це правило не може бути орієнтиром у разі стохастичних залежностей. Охопити всі умови вивчених обставин практично неможливо. Чим більше факторів, тим складніше встановити модель взаємозв’язку факторів, визначити вид рівняння регресії.
Вибораючи фактори, слід дотримуватися таких вимог:
· враховувати причинні зв’язки між результативним показником і факторами, що впливають на нього, оскільки вони розкривають сутність економічного явища;
· не включати в кореляційну модель фактори, зв’язок яких з результативним показником має функціональний характер;
· усі фактори мусять мати одиницю величини (вимірювання);
· залучати до аналізу найбільш значущі фактори, що мають вагомий вплив на результативний показник;
· не включати в модель взаємозалежні фактори.
Важливим етапом фінансового аналізу є узагальнення отриманих результатів. Взагалі узагальнення в аналізі має досить творчий характер, залежить від професійних знань спеціалістів, їх уміння усвідомити аналітичну інформацію. Правильно зроблені висновки мають велике практичне значення для поліпшення діяльності підприємства. У фінансовому аналізі узагальнення інформації найчастіше здійснюються у підсумковий спосіб, факторним підрахунком резервів, у конструктивно-варіантний спосіб.
Підсумковий спосіб використовується для підрахунку однорідних показників за відповідною їх сукупністю, що характеризують окремі сторони або об’єкт діяльності підприємства. Факторний підрахунок резервів застосовується для визначення можливого рівня аналізованого показника. Суть його полягає в тому, що, виходячи з пофакторних відхилень,визначають можливий рівень показника за умови закріплення позитивного впливу та запобігання негативному впливу факторів. Для цього підсумовують від’ємні величини факторів і на цю суму коригують фактично досягнутий результативний показник.

Рис. 1.7. Етапи багатофакторното кореляційного аналізу (множинного кореляційно-регресійного аналізу)
Конструктивно-варіантний спосіб застосовується для розроблення різних варіантів господарських процесів і вибору з них оптимальних. Техніка його полягає у конструюванні кращого варіанта результативного показника шляхом відбору позитивних факторів з декількох варіантів і поєднання їх в одне ціле.