| Скачать .docx |
Реферат: Производственная функция. Изокванта, предельная норма технологического замещения одного фактора
Негосударственное (частное) образовательное учреждение
высшего профессионального образования
«Южно-Сахалинский институт экономики, права и информатики»
Кафедра «Экономики и логистики»
КОНТРОЛЬНАЯ РАБОТА
По дисциплине: «Экономическая теория» 1 часть
На тему № 7: «Производственная функция. Изокванта, предельная норма технологического замещения одного фактора производства другим»
Выполнила: студентка 1 курса
заочного факультета группы ФК-18
специальности «Финансы и кредит»
Зыбина Ирина Владимировна
Адрес: г. Южно-Сахалинск,
ул. Сахалинская, 25А-8, т. 89241909559
Проверила: Гадеудина Елена Дмитриевна
Южно-Сахалинск
2010
ОГЛАВЛЕНИЕ
стр.
Введение 3
1. Производственная функция 3 - 10
2. Изокванта, предельная норма технологического замещения одного фактора производства другим 10 - 13
Заключение 13 - 14
Практическое задание. Задачи 4, 8, 14, 23 15 - 21
Список литературы 22
Введение
В условиях современного общества ни один человек не может потреблять только то, что он сам производит. Для наиболее полного удовлетворения своих потребностей люди вынуждены обмениваться тем, что они производят. Без постоянного производства благ не было бы потребления. Поэтому большой интерес представляет анализ закономерностей, действующих в процессе производства благ, которые формируют в дальнейшем их предложение на рынке. Производственный процесс - это основное и первоначальное понятие экономики.
Актуальность настоящей работы обусловлена, с одной стороны, большим интересом к теме "Производственная функция. Изокванта, предельная норма технологического замещения одного фактора производства другим" в современной науке, с другой стороны, ее недостаточной разработанностью.
Рассмотрению обозначенного вопроса посвящено множество работ. В основном материал, изложенный в учебной литературе, носит общий характер, а многочисленные монографии данную тематику рассматривают более узко.
Целью исследования является изучение темы "Производственная функция. Изокванта, предельная норма технологического замещения одного фактора производства другим".
В рамках достижения цели поставлены следующие задачи:
1. Рассмотреть понятие «производственная функция».
2. Проанализировать, что представляет собой изокванта, как количественное выражение производственной функции и предельная норма технологического замещения одного фактора производства другим.
По результатам работы был вскрыт ряд проблем, имеющих отношение к рассматриваемой теме, и сделаны выводы о необходимости дальнейшего изучения улучшения состояния вопроса.
Глава 1. Производственная функция.
Общий результат трудовой деятельности – объем созданной продукции – является зависимым от действия основных факторов производства, их количественного и качественного уровня. Эта связь выражается математической формулой, получившей название производственная функция. [1] Она была разработана в 1890 году английским математиком А. Берри, помогавшим А. Маршаллу при подготовке математического приложения к работе «Принципы экономической науки».[2] В ней показывается количественная зависимость объема выпуска продукции от трех факторов – капитала (средств производства), труда и технического прогресса. Если рассматриваемую функцию выразить в показателях среднегодовых темпов прироста факторов, то она примет следующий вид:
Y= αK + βL + r,
где Y, K, L соответственно темп прироста капитала, продукции и рабочей силы, r – комплексный показатель роста совокупной экономической эффективности всех факторов. α и β – коэффициенты эластичности объема производства соответственно по капиталу и по труду (или коэффициенты, характеризующие прирост объема выпуска продукции, приходящейся на 1 % прироста соответствующего фактора). Производственная функция имеет постоянную эластичность замещения производственных факторов, равную единице. Это означает, что, скажем увеличение численности рабочих (соответственно рост фонда заработной платы) равноценно увеличению основного капитала, т.е. вызовет точно такое же повышение выпуска продукции.[3]
В соответствии с различием между технологической и экономической эффективностью выбор оптимального производственного процесса часто описывается как инженерно-техническое решение, за которым следует экономическое решение. Инженер или технический эксперт отбирает технологические процессы, характеризующиеся минимальными потребностями в ресурсах, отбрасывая все те, которые являются технологически неэффективными. Затем наступает очередь бизнесмена принимать экономическое решение, т.е. выбрать технически эффективный процесс, характеризующийся наименьшими издержками, и, следовательно, являющийся экономически эффективным.[4] Производственная функция учитывает, что факторы могут использоваться в различных пропорциях, а значит, продукция может выпускаться разными способами. Например, вино можно произвести трудоемким способом, топча виноград ногами или капиталоемким, с применением машин. Производственная функция показывает, что является технологически осуществимым при условии, что фирма работает эффективно, т.е. использует каждое сочетание производственных факторов наилучшим образом. Поскольку производственная функция описывает максимально возможный объем выпуска для заданного набора факторов при технологически эффективном способе производства, ресурсы, снижающие выпуск продукции, не будут использоваться никогда. Предположение о том, что производство всегда технологически эффективно, не всегда справедливо, но есть основания ожидать, что стремящиеся к максимальной прибыли фирмы не будут расходовать ресурсы впустую.[5]
Если производство обусловлено только одним фактором, производственная функция (далее ПФ) – это функция, независимая переменная которой принимает значения используемого ресурса (фактора производства), а зависимая переменная – значения объемов выпускаемой продукции
y=f(x).
В этой формуле y есть функция одной переменной x. В связи с этим производственная функция (ПФ) называется одноресурсной или однофакторной. Ее область определения – множество неотрицательных действительных чисел. Символ f является характеристикой производственной системы, преобразующей ресурс в выпуск. В микроэкономической теории принято считать, что y – максимально возможный объем выпуска продукции, если ресурс затрачивается или используется в количестве x единиц.
Возьмем ПФ f в виде f(x)=axb
, где х – величина затрачиваемого ресурса (например, рабочего времени), f(x) – объем выпускаемой продукции (например, число готовых к отправке холодильников). Величины а и b – параметры ПФ f. Здесь a и b – положительные числа и число b![]() 1, вектор параметров есть двумерный вектор (a,b). ПФ у=axb
является типичным представителем широкого класса однофакторных ПФ.
1, вектор параметров есть двумерный вектор (a,b). ПФ у=axb
является типичным представителем широкого класса однофакторных ПФ.
График ПФ изображен на рисунке 1
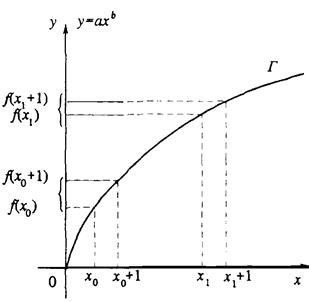
Рис. 1.
На графике видно, что с ростом величины затрачиваемого ресурса y растет, однако при этом каждая дополнительная единица ресурса дает все меньший прирост объема y выпускаемой продукции. Отмеченное обстоятельство (рост объема у и уменьшение прироста объема у с ростом величины х) отражает фундаментальное положение экономической теории (хорошо подтверждаемое практикой), называемое законом убывающей эффективности (убывающей производительности или убывающей отдачи). [6]
В качестве простого примера возьмем однофакторную производственную функцию, характеризующую производство фермером какого-либо сельскохозяйственного продукта. Пусть все факторы производства, такие как величина земельных угодий, наличие у фермера сельскохозяйственной техники, посевного материала, количество труда, вложенного в производство продукта, остаются из года в год постоянными величинами. Меняется только один фактор – количество применяемых удобрений. В зависимости от этого изменяется величина получаемого продукта. Вначале, с ростом переменного фактора, она увеличивается достаточно быстро, затем рост общего продукта замедляется, а начиная с определенных объемов применяемых удобрений, величина получаемого продукта начинает убывать. Дальнейшее увеличение переменного фактора не дает увеличения продукта.[7]
ПФ могут иметь разные области использования. Принцип "затраты-выпуск" может быть реализован как на микро-, так и на макроэкономическом уровне. Сначала остановимся на микроэкономическом уровне. ПФ у=axb , рассмотренная выше, может быть использована для описания взаимосвязи между величиной затрачиваемого или используемого ресурса х в течении года на отдельном предприятии (фирме) и годовым выпуском продукции у этого предприятия (фирмы). В роли производственной системы здесь выступает отдельное предприятие (фирма) – имеем микроэкономическую ПФ (МИПФ). На микроэкономическом уровне в роли производственной системы может выступать также отрасль, межотраслевой производственный комплекс. МИПФ строятся и используются в основном для решения задач анализа и планирования, а также задач прогнозирования.
Точное толкование понятий затрачиваемого или используемого ресурса и выпускаемой продукции, а также выбор единиц их измерения зависят от характера и масштаба производственной системы, особенностей решаемых задач, наличия исходных данных. На микроэкономическом уровне затраты и выпуск могут измеряться как в натуральных, так и в стоимостных единицах (показателях). Годовые затраты труда могут быть измерены в человеко-часах или в рублях выплаченной заработной платы; выпуск продукции может быть представлен в штуках или в других натуральных единицах или в виде своей стоимости.[8]
В теории производства традиционно используются двухфакторная производственная функция, в которой объем производства, является функцией использования ресурсов труда и капитала. Производственная функция нескольких переменных – это функция, независимые переменные которой принимают значения объемов затрачиваемых или используемых ресурсов (число переменных n равно числу ресурсов), а значение функции имеет смысл величин объемов выпуска:
y=f(x)=f(x1 ,…,хn ),
здесь у (у![]() 0) – скалярная, а х – векторная величина, x1
,…,хn
--координаты вектора х, то есть f(x1
,…,хn
) есть числовая функция нескольких переменных x1
,…,хn
. В связи с этим ПФ f(x1
,…,хn
) называют многоресурсной или многофакторной. Более правильной является такая символика f(x1
,…,хn
,а), где а – вектор параметров ПФ.
0) – скалярная, а х – векторная величина, x1
,…,хn
--координаты вектора х, то есть f(x1
,…,хn
) есть числовая функция нескольких переменных x1
,…,хn
. В связи с этим ПФ f(x1
,…,хn
) называют многоресурсной или многофакторной. Более правильной является такая символика f(x1
,…,хn
,а), где а – вектор параметров ПФ.
Для отдельного предприятия (фирмы), выпускающего однородный продукт, ПФ f(x1 ,…,хn ) может связывать объем выпуска с затратами рабочего времени по различным видам трудовой деятельности, различных видов сырья, комплектующих изделий, энергии, основного капитала. ПФ такого типа характеризуют действующую технологию предприятия (фирмы).
ПФ y=f(x1 ,x2 ) называется статической, если ее параметры и ее характеристика f не зависят от времени t, хотя объемы ресурсов и объем выпуска могут зависеть от времени t, то есть могут иметь представление в виде временных рядов: x1 (0), x1 (1),…, x1 (Т); x2 (0), x2 (1),…, x2 (Т); y(0), y(1),…,y(T); y(t)=f(x1 (t), x2 (t)). Здесь t – номер года, t=0,1,…,Т; t= 0 – базовый год временного промежутка, охватывающего годы 1,2,…,Т.
Для моделирования отдельного региона или страны в целом (то есть для решения задач на макроэкономическом, а также на микроэкономическом уровне) часто используется ПФ вида y= ![]() , где а0
, а1
, а2
– параметры ПФ. Это положительные постоянные (часто а1
и а2
таковы, что а1
+а2
=1). ПФ только что приведенного вида называется ПФ Кобба-Дугласа (ПФКД) по имени двух американских экономистов, предложивших ее использовать в 1929 г.[9]
, где а0
, а1
, а2
– параметры ПФ. Это положительные постоянные (часто а1
и а2
таковы, что а1
+а2
=1). ПФ только что приведенного вида называется ПФ Кобба-Дугласа (ПФКД) по имени двух американских экономистов, предложивших ее использовать в 1929 г.[9]
Хотя ПФ различны для разных видов производств, все они обладают общими свойствами:
1. Существует предел увеличения объема производства, который может быть достигнут увеличением затрат одного ресурса при прочих равных условиях. Это значит, что на фирме при данном количестве станков и производственных помещений есть предел увеличения производства посредством привлечения большего количества рабочих. Прирост выпуска при увеличении численности занятых будет приближаться к нулю.
2. Существует определенная взаимодополняемость (комплементарность) факторов производства, но без сокращения объемов производства возможна и определенная взаимосвязь этих факторов. Например, эффективен труд работников, если они обеспечены всеми необходимыми орудиями труда. При отсутствии таких орудий объем может быть сокращен или увеличен при росте числа занятых. В данном случае происходит замена одного ресурса другим.
3. Способ производства А считается технически более эффективным, по сравнению со способом Б , если он предполагает использование хотя бы одного ресурса в меньшем, а всех остальных – не в большем количестве, чем способ Б. Технически неэффективные способы не используются рациональными производителями.
4. Если способ А предполагает использование одних ресурсов в большем, а других – в меньшем количестве, чем способ Б , эти способы несравнимы по технической эффективности. В этом случае оба способа считаются технически эффективными и включаются в производственную функцию. Какой из них выбирать – зависит от соотношения цен применяемых ресурсов. Этот выбор основывается на критериях экономической эффективности. Следовательно, техническая эффективность не тождественна экономической эффективности.[10]
Таким образом, производственная функция является основным инструментом анализа производства. Она задает максимальный объем выпуска продукции, который фирма может произвести при любом заданном наборе ресурсов и показывает результаты использования альтернативных технологически эффективных способов производства. ПФ может быть как однофакторной, так и многофакторной, а так же имеет ряд одинаковых свойств.
Глава 2. Изокванта, предельная норма технологического замещения одного фактора производства другим.
В графической форме производственная функция фирмы может быть представлена группой изоквант. Изокванта представляет собой кривую, которая показывает все сочетания производственных факторов, дающих определенный объем выпуска продукции. Таким образом, каждая изокванта отражает какой-то конкретный объем производства для данной технологии (например, объем выпуска – 1000 единиц продукции). И тогда производственная функция фирмы – это карта изоквант с различными уровнями объема производства.
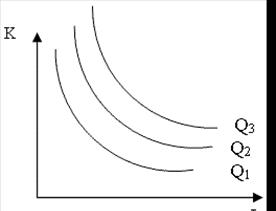
L Рис. 2
Q1; Q2; Q3 - карта изоквант.[11]
Карта изоквант представляет собой набор изоквант, каждая из которых показывает максимальный выпуск продукции, возможный при соответствующем наборе факторов. Карта изоквант является альтернативным способом описания производственной функции, точно так же как карта кривых безразличия представляет собой один из способов описания функции полезности. Изокванты показывают множество возможностей, имеющихся у фирм, когда они принимают решение о производстве, - обычно они могут обеспечить желаемый объем выпуска продукции, используя различные сочетания факторов.[12] Изокванты являются подобием кривых безразличия с той лишь разницей, что они отражают ситуацию не в сфере потребления, а в сфере производства. Так же как и кривые безразличия, отражающие альтернативные варианты потребительского выбора продуктов, обеспечивающие определенный уровень полезности, изокванты отражают альтернативные варианты затрат ресурсов для производства определенного объема продукции.
Чем дальше расположена изокванта от начала координат, тем больше объем выпуска. Изокванты могут проходить через любую точку пространства, где находятся два фактора производства. Вогнутость изоквант указывает на то, что предельные производительности факторов разнонаправлены и в каждой точке будут иметь разную предельную производительность. Это говорит о том, что одно и то же приращение одного фактора будет замещаться убывающим количеством другого фактора. Величина, отражающая необходимые количественные изменения одного фактора в зависимости от единичных измерений другого фактора при сохраненном объеме выпуска, называется Предельной нормой технического замещения факторов (MRTS). Таким образом, при обеспечении постоянного объема выпуска, соотношение замены одного фактора другим выражается предельной нормой технического замещения, при равенстве которой соотношению предельных продуктов факторов достигается оптимальная их комбинация.
Изокванты строятся на основе эмпирических данных, полученных в результате анализа того или иного производственного процесса и несут в себе его характеристики. Во-первых, сама форма изокванты отражает возможности замещения факторов, т.е. пределы возможности комбинаций факторов. Во-вторых, изокванта показывает максимальное значение выпуска для каждой отдельной комбинации факторов. В-третьих, являясь вогнутой кривой, она отражает действие закона убывающей отдачи[13] (по мере увеличения одного фактора и относительном уменьшении другого, предельная производительность первого падает). В-четвертых, изокванты имеют отрицательный наклон, что свидетельствует о разнонаправленном изменении факторов (увеличение одного предполагает уменьшение другого).
Отрицательный наклон изоквант объясняется тем, что увеличение использования одного фактора при определенном объеме выпуска продукта всегда будет сопровождаться уменьшением количества другого фактора. Крутизна наклона изокванты характеризуется предельной нормой технологического замещения факторов производства (MRTS).[14]
Угловой коэффициент любой изокванты показывает возможность замены одного из факторов другим при сохранении постоянного объема выпуска. Предельная норма технологического замещения одного фактора производства другим – величина, на которую может быть сокращен один фактор за счет использования одной дополнительной единицы другого фактора при постоянном объеме выпуска продукции. MRTS всегда является положительной величиной. Изокванты выпуклы – MRTS уменьшается по мере движения вниз вдоль изокванты. Уменьшение MRTS свидетельствует о том, что эффективность использования любого производственного фактора ограничена. С замещением в производственном процессе капитала все большим количеством труда производительность труда снижается. аналогичным образом, когда труд замещается все большим количеством капитала, отдача от капитала снижается. Производству требуется сбалансированное сочетание обоих факторов.[15]
Итак, линия на графике, показывающая разные сочетания производственных ресурсов и данный объем выпуска, называется изоквантой. Эти сочетания ресурсов (технологии) являются наиболее эффективными, т.к. любая точка на изокванте соответствует минимальным объемам ресурсов, необходимых для получения заданного объема готовой продукции. Изокванта обычно выпукла к началу координат вследствие предполагающейся взаимозаменяемости ресурсов. Когда ресурсы являются взаимодополняемыми, изокванта имеет L-образную форму. Когда ресурсы представляют собой совершенные субституты, она принимает форму прямой линии. Совокупность изоквант, отражающая максимально достижимый выпуск продукции при любом заданном наборе факторов производства называется картой изоквант. Предельная норма технологического замещения одного фактора производства другим – величина, на которую может быть сокращен один фактор за счет использования одной дополнительной единицы другого фактора при постоянном объеме выпуска продукции.
Заключение
Производственная функция является основным инструментом анализа производства. Производственные функции позволяют количественно проанализировать важнейшие экономические зависимости в сфере производства. Они дают возможность оценить среднюю и предельную эффективность различных ресурсов производства, эластичность выпуска по различным ресурсам, предельные нормы замещения ресурсов, эффект от масштаба производства и многое другое.
Линия на графике, показывающая разные сочетания производственных ресурсов и данный объем выпуска, называется изоквантой. Эти сочетания ресурсов (технологии) являются наиболее эффективными, т.к. любая точка на изокванте соответствует минимальным объемам ресурсов, необходимых для получения заданного объема готовой продукции. Изокванта обычно выпукла к началу координат вследствие предполагающейся взаимозаменяемости ресурсов. Когда ресурсы являются взаимодополняемыми, изокванта имеет L-образную форму. Когда ресурсы представляют собой совершенные субституты, она принимает форму прямой линии. Совокупность изоквант, отражающая максимально достижимый выпуск продукции при любом заданном наборе факторов производства называется картой изоквант. Предельная норма технологического замещения одного фактора производства другим – величина, на которую может быть сокращен один фактор за счет использования одной дополнительной единицы другого фактора при постоянном объеме выпуска продукции. В данной работе тема «Производственная функция. Изокванта, предельная норма технологического замещения одного фактора производства другим» раскрыта лишь частично, что открывает широкие возможности для более детального дальнейшего изучения ее в рамках другой работы.
Практическое задание
Задача 4
Предположим, данные таблицы характеризуют кривую безразличия покупателя:
| Количество единиц товара А |
Количество единиц товара В |
| 16 |
6 |
| 12 |
8 |
| 8 |
12 |
| 4 |
24 |
Начертите эту кривую (товар А – по вертикали, товар В – по горизонтали). Исходя из того, что цена товара А - 1,5 долл., цена товара В – 1 долл., а мистер Чен намерен потратить 24 долл., добавьте к графику бюджетную линию.
В какой комбинации покупатель приобретает товары А и В? Покажите графически и рассчитайте алгебраически.
Решение:
Мистеру Чену принесут одинаковую полезность такие комбинации товаров А и В, как:
16 ед. товара А и 6 ед. товара В;
12 ед. товара А и 8 ед. товара В;
8 ед. товара А и 12 ед. товара В;
4 ед. товара А и 24 ед. товара В.
При этом, если он решит потратить все 24 дол. на товар А, то он сможет купить 16 его единиц:
24 : 1,5 = 16 ед. товара А.
Если же он потратит все 24 дол. на товар В, то он сможет купить 25 ед. товара В:
24 : 1 = 24 ед. товара В.
Получим следующую кривую безразличия и бюджетную линию:
![]() товар А
товар А
![]()
![]()
![]()
![]()
![]()
![]() 16
16

![]() 12
12

![]() 8
8
кривая безразличия
![]() 4
4
бюджетная линия
0 6 8 12 24 товар В
Таким образом, как видно из графика, кривая безразличия пересекается с бюджетной линией в точке, соответствующей набору из 8 ед. товара А и 12 ед. товара В, следовательно, именно такой выбор и будет делать мистер Чен.
Проверим алгебраически:
8 * 1,5 + 12 * 1 = 24 долл.
Задача 8
Составьте производственную сетку. На её основе изобразите карту изоквант. Подробно объясните рассуждения.
Решение:
Графически на производственной сетке каждая изокванта представляет множество минимально необходимых комбинаций производственных ресурсов для производства определенного объема продукции. Чем дальше от начала координат расположена изокванта, тем больший объем выпуска она представляет:
![]() К
К
![]()
![]()
![]()
![]()
![]()
![]() 5 А
5 А
 |
![]() 3 В
3 В
![]() С
С
![]() D
D
![]() 1 2 L
1 2 L
Если К – это капитал, а L – труд, то рисунок демонстрирует, что одинаковый объем производства можно получить используя то или иное сочетание ресурсов капитала и труда, например, 5 ед. капитала и 1ед. труда (точка А на средней изокванте), или 3 ед. капитала и 2 ед. труда и т.д.
Точка А показывает, что для производства данного объема продукции в большей степени используется капитал, т.е. это более механизированный способ производства (капитал вкладывается в механизацию производства, в развитие технологии). Точка D отражает использование в большей степени человеческого труда и в незначительной степени использование капитала.
Та изокванта, которая расположена дальше от начала координат, демонстрирует наибольший размер производства.
Задача 14
Фирма работает в условиях совершенной конкуренции в краткосрочном периоде. Даны:
| Выпуск продукции в единицу времени (Q) |
Общие издержки (ТС) |
| 0 |
9 |
| 1 |
11 |
| 2 |
15 |
| 3 |
21 |
| 4 |
29 |
| 5 |
39 |
В отрасли таких 1000 фирм.
| Количество спрашиваемой продукции этих фирм (Qd ) |
При цене (Р) |
| 3000 |
2 |
| 2000 |
4 |
| 1500 |
6 |
| 1000 |
8 |
1. Найти равновесную цену и равновесный объем продаж фирмы.
2. В длительном (долгосрочном) периоде будут ли фирмы уходить из отрасли или не будут? Почему?
Решение:
1. Равновесная цена и равновесный объем совершенно конкурентной фирмы в краткосрочном периоде достигается при равенстве предельных издержек, предельного дохода и средних издержек:
МС=МR = АС.
Рассчитаем средние и предельные издержки:
| Q |
ТС |
АС |
МС |
| 0 |
9 |
- |
|
| 1 |
11 |
11 |
2 |
| 2 |
15 |
7,5 |
4 |
| 3 |
21 |
7 |
6 |
| 4 |
29 |
7,25 |
8 |
| 5 |
39 |
7,8 |
10 |
Расчет предельного дохода:
| Q |
Р |
ТR |
МR |
| 0 |
- |
0 |
|
| 1 |
8 |
8 |
8 |
| 1,5 |
6 |
9 |
2 |
| 2 |
4 |
8 |
-2 |
| 3 |
2 |
6 |
-2 |
Таким образом, ни при одном объеме производства требуемое равенство не соблюдается, поэтому определить параметры равновесия не представляется возможным.
2. Рассчитаем, какую прибыль имеет каждая фирма:
| Q |
ТС |
ТR |
Прибыль |
| 0 |
9 |
0 |
-9 |
| 1 |
11 |
8 |
-3 |
| 2 |
15 |
8 |
-7 |
| 3 |
21 |
6 |
-15 |
| 4 |
29 |
- |
- |
| 5 |
39 |
- |
- |
Ни один из объемов производства не позволяет фирмам даже покрыть издержки, следовательно, они несут убытки, и будут уходить из отрасли.
Задача 23
Ниже дана таблица спроса на труд для фирмы, нанимающей данный ресурс в условиях совершенной конкуренции и реализующей свою продукцию на совершенно конкурентном рынке:
| Единицы труда |
Совокупный продукт |
| 1 |
17 |
| 2 |
31 |
| 3 |
43 |
| 4 |
53 |
| 5 |
60 |
| 6 |
65 |
Если цена на единицу продукции 2 $, сколько рабочих будет нанимать фирма при ставке зарплаты около 20 $ в день? При ставке зарплаты около 28 $ в день?
Представьте графически кривую спроса и предложения на услуги труда данной фирмы.
Решение:
Увеличивать найм рабочих целесообразно до тех пор, пока дополнительный доход от каждого дополнительно нанятого рабочего (предельный доход) будет выше, чем затраты на оплату труда этого дополнительно нанятого рабочего (предельных издержек) Как только предельные издержки поравняются предельному доходу найм рабочих необходимо прекратить.
Рассчитаем предельный доход:
| L (труд) |
Совокупный продукт |
TR |
MR |
| 1 |
17 |
17*2=34 |
- |
| 2 |
31 |
31*2= 62 |
28 |
| 3 |
43 |
43*2=86 |
24 |
| 4 |
53 |
53*2= 106 |
20 |
| 5 |
60 |
60*2=120 |
14 |
| 6 |
65 |
65*2=130 |
10 |
Если цена составляет 230 долларов, тои предельные издержки будут равны 20 долларам, т.к. каждый дополнительно нанятый рабочий потребует дополнительных затрат в 20 долларов. Как видно из последнего столбца таблицы, предельному доходу в 20 долларов соответствует количество рабочих в 4 человека.
Если цена труда составит 28 долларов, то предельные издержки будут равны 28 долларам. Условие равенства предельных издержек и предельного дохода при 28 долларах оплаты труда наблюдается при найме 2 рабочих и поэтому фирма будет нанимать при данной зарплате только 2-х рабочих.
Кривые спроса и предложения на рынке труда будут иметь вид:

![]() Р
Р
![]()
![]()
![]()
![]()
![]()
![]()
![]() 168 предложение при 28 дол.
168 предложение при 28 дол.


![]() 140
140
![]() 120
120
![]() 112 предложение при 20 дол.
112 предложение при 20 дол.
![]() 84
84
![]() 60 спрос
60 спрос
![]() 56
56
![]() 40
40
![]() 28
28
0 1 2 3 4 5 6 L
Список литературы
1. Учебники и монографии.
1.1. Борисов Е.Ф. Экономическая теория: Учебник. 3-е издание переработанное и дополненное. - М.: Юрайт-Издат, 2005. – 399 с.
1.2. Замков О.О., Толстопятенко А.В., Черемных Ю.П. Математические методы в экономике: Учебник. – М.: ДИС, 1997. – 368 с.
1.3. Маршалл А. Принципы экономической науки. - М.: Мысль, 1993. – 594 с.
1.4. Микроэкономика/ Под ред. Проф. Яковлевой Е.Б. – М.: СПб. Поиск, 2002. – 358 с.
1.5. Овчинников Г.П. Микроэкономика. – Спб: Изд-во им. Володарского, 1997. – 751 с.
1.6. Пиндайк Роберт С.Ю, Рубинфельд Дэниел Л, Микроэкономика: Пер. с англ.- М.:Дело, 2000. – 771 с.
1.7. Стенли Фишер, Рудигер Дорнбуш, Ричард Шмалензи Экономика: Пер. с английского. - М.: Дело Лтд, 1995. – 868 с.
1.8. Чечевицына Л.Н. «Микроэкономика. Экономика предприятия (фирмы). Изд. 3-е доп. и перераб. – Рост н/Д: «Феникс», 2003 – 400 с.
1.9. Экономика. Учебник под ред. Архипова А.И., А.Н. Нестеренко А.К. Большакова. - М. Изд-во Проспект, 1999. – 792 с.
2. Электронные ресурсы.
2.1. Экономика: электронный учебник. [Электронный ресурс]//Режим доступа: http://economy.bases.ru/index.html.
[1] Борисов Е.Ф. Экономическая теория: Учебник. 3-е издание переработанное и дополненное. М.: Юрайт-Издат, 2005. – С. 183.
[2] Маршалл А. Принципы экономической науки. М.: Мысль, 1993.- С.
[3] Борисов Е.Ф. Экономическая теория: Учебник. 3-е издание переработанное и дополненное. М.: Юрайт-Издат, 2005. - С.183
[4] Стенли Фишер, Рудигер Дорнбуш, Ричард Шмалензи Экономика: Пер. с английского М.: Дело Лтд, 1995. – С. 282.
[5] Пиндайк Роберт С.Ю, Рубинфельд Дэниел Л, Микроэкономика: Пер. с англ.-М.:Дело, 2000 – С. 209.
[6] Овчинников Г.П.. Микроэкономика. – Спб: Изд-во им. Володарского, 1997. – С.189.
[7] Овчинников Г.П.. Микроэкономика. – Спб: Изд-во им. Володарского, 1997. – С.189-190.
[8] Замков О.О., Толстопятенко А.В., Черемных Ю.П. Математические методы в экономике: Учебник. – М.: ДИС, 1997. – С. 236.
[9] Микроэкономика/ под ред. Проф. Яковлевой Е.Б. – М.: СПб. Поиск, 2002. – С. 236.
[10] Чечевицына Л.Н. «Микроэкономика. Экономика предприятия (фирмы). Изд. 3-е доп. и перераб. – Рост н/Д: «Феникс», 2003. – С. 168.
[11] Экономика: электронный учебник.[Электронный ресурс]//Режим доступа: http://economy.bases.ru/index.html
[12] Пиндайк Роберт С.Ю, Рубинфельд Дэниел Л, Микроэкономика: Пер. с англ.-М.:Дело, 2000 – С. 209.
[13] Стенли Фишер, Рудигер Дорнбуш, Ричард Шмалензи Экономика: Пер. с английского.- М.: Дело Лтд, 1995. – С. 284.
[14] Экономика. Учебник под ред. Архипова А.И., А.Н. Нестеренко А.К. Большакова. - М. Изд-во Проспект, 1999. – С. 354.
[15] Стенли Фишер, Рудигер Дорнбуш, Ричард Шмалензи Экономика: Пер. с английского.- М.: Дело Лтд, 1995. – С. 284.