| Скачать .docx | Скачать .pdf |
Реферат: Основные свойства природных газов
Задание №1.
Основные свойства природных газов. Уравнение состояния реальных газов.
Природные углеводородные газы представляют собой смесь предельных УВ вида Сn Н2 n +2 . Основным компонентом является метан СН4 , содержание которого в природных газах достигает 98%. Наряду с метаном в состав природных газов входят более тяжелые УВ, а также неуглеводородные компоненты: азот N, углекислый газ СО2 , сероводород H2 S, гелий Не, аргон Аг.
Природные газы подразделяют на следующие группы.
1. Газ, добываемый из чисто газовых месторождений и представляющий собой сухой газ, свободный от тяжелых УВ.
2. Газы, добываемые вместе с нефтью (растворенные или попутные газы). Это физические смеси сухого газа, пропан-бутановой фракции (жирного газа) и газового бензина.
3. Газы, добываемые из газоконденсатных месторождений,— смесь сухого газа и жидкого углеводородного конденсата. Углеводородный конденсат состоит из большого числа тяжелых УВ (С5 + высш., С6 + высш. и т.д.), из которых можно выделить бензиновые, лигроиновые, керосиновые, а иногда и более тяжелые масляные фракции.
4. Газы газогидратных залежей.
Компонентный состав и свойства отдельных компонентов природного газа приведены в таблице 1.
Таблица 1. Основные свойства компонентов природных газов в стандартных условиях.
| Свойства | Обозна чение | СН1 | С2 Н6 | С3 Н8 | i-С4 Н10 | n-С4 Н10 |
Молекулярная масса Объём 1 кг газа, м Плотность по воздуху Масса 1 м3 газа, кг Критическое давление, МПа Критическая температура, К |
М 22,4 М М 28,97 М 22,4 ркр Ткр |
16,04 1,40 0,554 0,714 4,58 191 |
30,07 0,74 1,038 1,35 4,86 305 |
44,10 0,508 1,522 1,97 4,34 370 |
58,12 0,385 2,006 2,85 3,82 407 |
58,12 0,385 2,006 2,85 3,57 425 |
Во многих случаях состав природных углеводородных газов определяется не полностью, а лишь до бутана (С4 Н10 ) или гексана (С6 Н14 ) включительно, а все остальные компоненты объединяются в остаток (или псевдокомпонент) С5 + высш., С7 + высш.
Газ, в составе которого тяжелые УВ (С3 , С4 ) составляют не более 75 г/м3 , называют сухим. При содержании тяжелых УВ более 150 г/м3 газ называют жирным.
Газовые смеси характеризуются массовыми или молярными концентрациями компонентов. Для характеристики газовой смеси необходимо знать ее среднюю молекулярную массу, среднюю плотность в килограммах на кубический метр или относительную плотность по воздуху.
Молекулярная масса М природного газа:
![]() ,
,
где М – молекулярная масса i-го компонента; xi – объемное содержание i-го компонента, доли ед.
Для реальных газов обычно М=16 – 20.
Плотность газа ρг рассчитывается по формуле:
![]() ,
,
где Vм – объем 1 моля газа при стандартных условиях.
Обычно ρг находится в пределах 0,73 – 1,0 кг/м3 .
Плотность газа в значительной степени зависит от давления и температуры, и поэтому для практического применения этот показатель неудобен. Чаще пользуются относительной плотностью газа по воздуху ρг.в. , равной отношению плотности газа ρг к плотности воздуха ρв , взятой при тех же давлении и температуре:
ρг.в. = ρг / ρв ,
Если ρг и ρв определяются при стандартных условиях, то ρв = 1,293 кг/м3 и ρг.в. = ρг / 1,293.
Плотность нефтяных газов колеблется от 0,554 (для метана) до 2,006 (для бутана) и выше.
Вязкость газа характеризует силы взаимодействия между молекулами газа, которые преодолеваются при его движении. Она увеличивается при повышении температуры, давления и содержания углеводородных компонентов. Однако при давлениях выше 3МПа увеличение температуры вызывает понижение вязкости газа.
Вязкость нефтяного газа незначительна и при 0о С составляет 0,000131 пз; вязкость воздуха при 0о С равна 0,000172 пз.
Уравнения состояния газов используются для определения многих физических свойств природных газов. Уравнением состояния называется аналитическая зависимость между параметрами газа, описывающая поведение газа. Такими параметрами являются давление, объем и температура.
Состояние идеальных газов в условиях высоких давления и температуры определяется уравнением Клапейрона — Менделеева:
![]() ,
,
где р — давление; Vи — объем идеального газа, N— число киломолей газа; R— универсальная газовая постоянная; Т — температура.
Идеальным называется газ, силами взаимодействия между молекулами которого пренебрегают. Реальные углеводородные газы не подчиняются законам идеальных газов. Поэтому уравнение Клапейрона—Менделеева для реальных газов записывается в виде:
pV = ZNRT,
где Z— коэффициент сверхсжимаемости реальных газов, зависящий от давления, температуры и состава газа и характеризующий степень отклонения реального газа от закона для идеальных газов.
Коэффициент сверхсжимаемости Zреальных газов — это отношение объемов равного числа молей реального Vи идеального Vи газов при одинаковых термобарических условиях (т. е. при одинаковых давлении и температуре):
Z=V/Vи
Значения коэффициентов сверхсжимаемости наиболее надежно могут быть определены на основе лабораторных исследований пластовых проб газов. При отсутствии таких исследований (как это чаще всего бывает на практике) прибегают к расчетному методу оценки Zпо графику Г. Брауна (рис.1). Для пользования графиком необходимо знать так называемые приведенные псевдокритическое давление и псевдокритическую температуру. Критической называется такая температура, выше которой газ не может быть превращен в жидкость ни при каком давлении. Критическим давлением называется давление, соответствующее критической точке перехода газа в жидкое состояние.
С приближением значений давления и температуры к критическим свойства газовой и жидкой фаз становятся одинаковыми, поверхность раздела между ними исчезает и плотности их уравниваются.
С появлением в системе двух и более компонентов в закономерностях фазовых изменений возникают особенности, отличающие их поведение от поведения однокомпонентного газа. Не останавливаясь на подробностях, следует отметить, что критическая температура смеси находится между критическими температурами компонентов, а критическое давление смеси всегда выше, чем критическое давление любого компонента.
Для определения коэффициента сверхсжимаемости Z реальных газов, представляющих собой многокомпонентную смесь, находят средние из значений критических давлений и температур каждого компонента. Эти средние называются псевдокритическим давлением pп.кр. и псевдокритической температурой Тп.кр. Они определяются из соотношений:
![]() ;
; ![]() ;
;
где ркр. и Ткр. – критические давления и температура i-го компонента; xi – доля i-го компонента в объеме смеси (в долях единицы).
Приведенные псевдокритические давление и температура, необходимые для пользования графиком Брауна, представляют собой псевдокритические значения, приведенные к конкретным давлению и температуре (к пластовым, стандартным или каким-либо другим условиям):
Рпр. = р/рп.кр. ; Тпр. = Т/Тп.кр. ;
где р и Т – конкретные давления и температура, для которых определяется Z.
Коэффициент сверхсжимаемости Z обязательно используется при подсчете запасов газа для правильного определения изменения объема газа при переходе от пластовых условий к поверхностным, при прогнозировании изменения давления в газовой залежи и при решении других задач.

Рис. 1. Графики зависимости коэффициента сверхсжимаемости Z углеводородного газа от приведенных псевдокритических давления рпр. и температуры Тпр. (по Г.Брауну).
Задание №2.
Задача:
Определить плотность и относительную плотность данной смеси по воздуху.
Дано: состав газа
| название | формула | Объемное содержание Хi ,% |
Молекулярная масса Mi , кг |
| метан | СН4 | 80 | 16,04 |
| этан | С2 Н6 | 7 | 30,07 |
| пропан | С3 Н8 | 3 | 44,1 |
| изобутан | С4 Н10 | 3 | 58,12 |
| Н-бутан | С4 Н10 | 1,5 | 58,12 |
| изопентан | С5 Н12 | 1 | 72,15 |
| Н-пентан | С5 Н12 | 0,4 | 72,15 |
| гексан | С6 Н14 | 2 | 86,18 |
| азот | N2 | 2,1 | 28,01 |
Решение.
Плотность газовой смеси ρсм – масса m единицы объема V или отношение молекулярной массы М к объему моля Vм
ρсм = m / V = М / Vм =М / 22,4 кг/м3
Молекулярная масса М – отношение массы молекулы вещества к 1/12 массы атома изотопа углерода 12 С.
Молекулярная масса природного газа (газовой смеси)
![]() , где
, где
Мi – молекулярная масса i-того компонента смеси;
хi – объемное содержание i- того компонента.
Относительная плотность природного газа ρотн (по воздуху) – отношение плотности смеси ρсм к плотности воздуха ρв , взятых при одинаковых температуре и давлении (при стандартных условиях: t = 0 °С, Р = 0,1013 МПа):
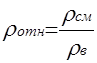
При стандартных условиях ρв = 1,293 кг/м3
Найдем общую молекулярную массу газовой смеси:
![]()
=22,197кг


Ответ: ρсм = 0,991 кг/м3 ; ρотн = 0,766 кг/м3 .
Задание №3.
Задача:
Определить коэффициент сверхсжимаемости для газа.
Дано: состав газа
| Состав газа | формула | Объемное содержание хi , % | Критическая температура , К | Критическое давление , МПа | Рср МПа |
Тср ° С |
| Метан | СН4 | 62 | 191 | 4,58 | 8 | 35 |
| Этан | С2 Н6 | 15 | 305 | 4,86 | ||
| Пропан | С3 Н8 | 10 | 370 | 4,34 | ||
| Азот | N2 | 10 | 124,9 | 3,46 | ||
| углекислота | CO2 | 3 | 304,1 | 7,50 |
Решение.
Коэффициент сверхсжимаемости реальных газов – это отношение объемов равного числа молей реального и идеального газов при одинаковых термобарических условиях:

Наиболее достоверные значения коэффициентов сверхсжимаемости получаются на основе лабораторных исследований пластовых проб газов. В случае отсутствия этих исследований прибегают к расчетному методу оценки по графику Г. Брауна. Для использования графика необходимо знать приведенное псевдокритическое давление Рпр и приведенную псевдокритическую температуру Тпр данного газа.
При известном компонентном составе рассчитывают псевдокритические (средние критические) давление и температуру:
![]()
![]()
Затем находят приведенные псевдокритические давление и температуру при данных давлении Р и температуре Т.

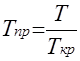
![]()
![]()
По кривым Р.Брауна (рис. 1) находим коэффициент сжимаемости Z , который составляет ≈ 0,78.
Ответ: Z ≈ 0,78.
Литература.
1. Гиматудинов Ш.К. Физика нефтяного и газового пласта. Изд. «Недра». М. 1971г.
2. Гиматудинов Ш.К., Ширковский А.И. Физика нефтяного и газового пласта. Изд. «Недра». М. 1982г.
3. Котяхов Ф.И. Физика нефтяного и газового коллектора. Изд. «Недра». М. 1997г.
4. Мирзаджанзаде А.Х., Аметов И.М., Ковалев А.Г. Физика нефтяного и газового пласта. Изд. «Недра». М. 1982г.