| Скачать .docx | Скачать .pdf |
Реферат: Теория пары снимков
1. Формулы связи координат точек местности и их изображений на тереопаре снимков (прямая фотограмметрическая засечка)
На рис.1 показана стереопара снимков Р1 и Р2, на которых точка местности М изобразилась соответственно в точках m1 и m2 . Будем считать, что элементы внутреннего и внешнего ориентирования снимков известны.
 |
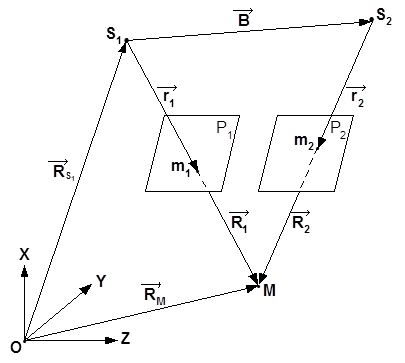Рис.1 . Выведем формулы связи координат точек местности и координат их изображений на стереопаре снимков.
Из рис.1 следует, что векторы 
определяют соответственно положение точки местности М и центра проекции S1
снимка Р1
относительно начала системы координат объекта OXYZ. Вектор 
определяет положение центра проекции S2
снимка Р2
относительно центра проекции S1
.
Векторы 
определяют положение точек m1
и М относительно центра проекции S1
. Векторы 
определяют положение точек m2
и М относительно центра проекции S2
.
Из рис.1 следует, что
(1 )
Так как векторы 
коллинеарны, то
; ( 2)
где N – скаляр.
С учетом ( 2) выражение (1.8.1) будет иметь вид
. ( 3)
В координатной форме выражение (1.7.3) будет иметь вид
; ( 4)
где X1
’,Y1
’,Z1
’ –координаты вектора 
в системе координат объекта OXYZ.
.
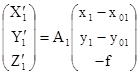Найдем значение N, входящее в выражение ( 4). Из рис.1 следует, что
;
или с учетом (2)
. ( 5)
Так как векторы коллинеарны, то их векторное произведение
. ( 6)
С учетом (5) выражение ( 6) можно представить в виде
;
Или
. ( 7)
В координатной форме выражение (7) имеет вид
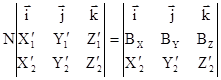
или
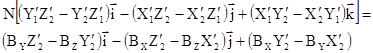, ( 8),
где:
- орты, совпадающие с осями координат X,Y,Z системы координат объекта OXYZ;
BX
, BY
, BZ
, X1
’, Y1
’, Z1
’, X1
’, Y1
’, Z1
’ – координаты векторов 
в системе координат объекта OXYZ.
,
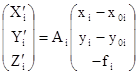где i – номер снимка, а
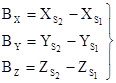. (9)
Так как векторы 
коллинеарны ( так как векторы 
компланарны), значение N можно найти как отношение их модулей, то есть
; (10)
В координатной форме выражение (10) с учетом (8) имеет вид
; (11)
У коллинеарных векторов отношение их координат равно отношению их модулей, поэтому можно записать, что:
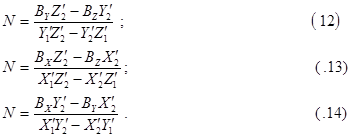
Таким образом, если известны элементы внутреннего и внешнего ориентирования стереопары снимков и измерены на этих снимках координаты соответственных точек x1,y1 и x2,y2, то сначала надо определить по одной из формул ( 12)-( 14) значение скаляра N, а затем по формуле ( 4) вычислить координаты точки местности X,Y,Z.
2. Формулы связи координат точек местности и координат их изображений на стереопаре снимков идеального случая съемки
В идеальном случае съемки угловые элементы ориентирования снимков стереопары w1 =a1 =À1 =w2 =a2 =À2 =0, а базис фотографирования параллелен оси Х системы координат объекта OXYZ.
В этом случае координаты базиса 
будут равны BX
=B, BY
=BZ
=O (B-модуль ).
Примем, что 
, то есть начало системы координат объекта OXYZ совмещено с точкой S1
), f1
=f2
=f, ax0
i
=y0
i
=0.
Так как угловые элементы ориентирования снимков равны нулю, то
,
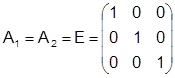а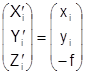 
,
где i – номер снимка.
При этом выражение (1 .13) примет вид
, (1)
а выражение (1 .4), которое мы представим в виде
будет иметь вид
, (2)
а с учетом ( 1)
. (3)
Так как из третьего уравнения выражения (3) следует, что
,
то формулы связи координат (3) можно представить в виде
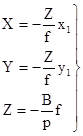(4)
3. Определение координат точек местности по стереопаре снимков методом двойной обратной фотограмметрической засечки
Для определения координат точек местности по стереопаре снимков методом прямой фотограмметрической засечки необходимо, чтобы были известны элементы внешнего ориентирования снимков. В большинстве случаев практики их значения не известны. В этом случае определение координат точек местности по стереопаре снимков выполняют методом двойной обратной фотограмметрической засечки.
Решение задачи по этому методу выполняется в следующей последовательности:
1. Определяют элементы взаимного ориентирования снимков. Пять элементов взаимного ориентирования снимков определяют взаимную угловую ориентацию стереопары снимков и базиса фотографирования. Для их определения необходимо измерить не менее пяти соответственных точек на стереопаре снимков;
2. Строят фотограмметрическую модель объекта по измеренным на стереопаре снимков координатам изображений соответственных точек и значениям элементов взаимного ориентирования снимков. Построенная модель подобна сфотографированному объекту, но имеет произвольный масштаб и произвольно расположена и ориентирована относительно системы координат объекта;
3. Определяют элементы внешнего ориентирования фотограмметрической модели по опорным точкам. Эти семь элементов определяют масштаб модели, ее положение и ориентацию относительно системы координат объекта. Для их определения достаточно трех опорных точек, не лежащих на одной прямой. По значениям элементов внешнего ориентирования фотограмметрической модели и элементов взаимного ориентирования можно определить элементы внешнего ориентирования стереопары снимков;
4. По координатам точек, определенных в системе координат модели, и элементам внешнего ориентирования модели определяют координаты точек в системе координат объекта.
4. Условие, уравнения и элементы взаимного ориентирования снимков
На рис. 1 представлена стереопара снимков Р1 и Р2 в положении, которое они занимали в момент фотографирования.
Любая пара соответственных лучей в этом случае пересекается в точке М местности и лежит в плоскости, проходящей через базис фотографирования 
(базисной плоскости).
Очевидно, что в этом случае векторы , лежащие в базисной плоскости, компланарны.
 |
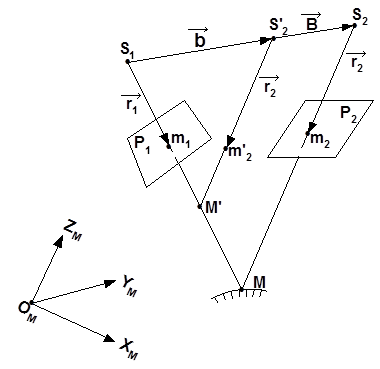Рис. 1
Как известно из аналитической геометрии, смешанное произведение компланарных векторов равно нулю.
. ( .1)
Условие компланарности в координатной форме имеет вид:
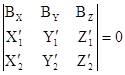. ( 2)
В уравнении ( 2) 
координаты векторов в системе координат фотограмметрической модели ОМ
ХМ
YM
ZM
, в общем случае произвольно расположенной и ориентированной.
В дальнейшем эту систему координат будем называть просто системой координат модели.
Условие ( 2) связывает между собой только направления векторов и выполняется при любых значениях их модулей. Поэтому значение модуля вектора 
можно выбрать произвольно. Направление вектора определяется двумя независимыми величинами. В качестве этих величин можно выбрать координаты bz
и bу
вектора 
, коллинеарного вектору , задав величину координаты bx
произвольно.
В частном случае величину bx можно выбрать равной 1.
При этом направление вектора будут определять величины:
и 
.
Выражение (2) в этом случае будет иметь вид:
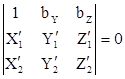( 3)
В уравнении (3)
,
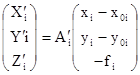где i – номер снимка, а А’1 – ортогональная матрица, элементы aij которой являются функциями угловых элементов ориентирования i-го снимка wi ’,ai ’,Ài ’ относительно системы координат модели ОМ ХМ YM ZM .
В выражении (3), которое является уравнением взаимного ориентирования в общем виде, куда кроме координат соответственных точек, измеренных на стереопаре снимков, и элементов внутреннего ориентирования входят 8 параметров by , bz , w1 ’, a1 ’, À1 ’, w2 ’, a2 ’, À2 ’, которые определяют угловую ориентацию базиса фотографирования и стереопары снимков относительно системы координат модели ОМ ХМ YM ZM .
Причем параметры w1 ’ и w2 ’ определяют поворот снимков стерепары вокруг оси ХМ , параметры bz , a1 ’, a2 ‘ – поворот базиса фотографирования и стереопары снимков вокруг оси YM , а параметры by , À1 ’, À2 ‘– поворот базиса фотографирования и стереопары снимков вокруг оси ZM .
Однако, из этих 8 параметров только 5 определяют взаимную угловую ориентацию базиса фотографирования и стереопары снимков.
Условие (3) выполняется при любой ориентации системы координат модели ОМ ХМ YM ZM . Следовательно, ее можно ориентировать таким образом, чтобы 3 из 8 параметров стали равны нулю.
Очевидно, что в общем случае можно сделать равным нулю только один из параметров, входящих в три группы параметров:
– w1 ’, w2 ’;
– bz , a1 ’, a2 ‘;
– by , À1 ’, À2 ’.
–
Таким образом, в качестве элементов взаимного ориентирования можно выбрать любую комбинацию из восьми параметров by , bz , w1 ’, a1 ’, À1 ’, w2 ’, a2 ’, À2 ’, кроме комбинаций, в которые одновременно входят две тройки параметров bz , a1 ’, a2 ‘ и by , À1 ’, À2 ’, а также пара параметров w1 ’ и w2 ’.
Рассмотрим наиболее распространенные системы элементов взаимного ориентирования:
Система a 1 ’, À 1 ’, w 2 ’, a 2 ’, À 2 ’ . Если принять при этом, что by =bz = w1 ’=0, то уравнение (3) имеет вид:
. ( 4)
Система by , bz , w2 ’, a2 ’, À2 ’. Если при этом принять, что w1 ’= a1 ’= À1 ’=0, то уравнение (3) будет иметь вид:
; ( 5)
так как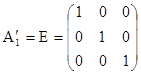 
.
Комментарий. 3 оставшихся из 8 параметров после выбора 5 элементов взаимного ориентирования задают ориентацию системы координат модели ОМ ХМ YM ZM . Например, выбрав систему элементов взаимного ориентирования by , bz , w2 ’, a2 ’, À2 ’ и приняв, что w1 ’= a1 ’= À1 ’ =0, мы таким образом задаем систему координат модели ОМ ХМ YM ZM , которой параллельны осям x, y, z системы координат первого снимка стереопары S1 x1 y1 z1 . В общем случае значения трех параметров можно задавать произвольно.
5. Определение элементов взаимного ориентирования
Для определения элементов взаимного ориентирования в качестве исходного используют уравнения взаимного ориентирования ( 4.3)
.
Каждая точка, измеренная на стереопаре снимков, позволяет составить одно уравнение (4.3), в которое, помимо измеренных координат точек на стереопаре снимков, элементов внутреннего ориентирования и трех параметров, задающих ориентацию системы координат модели, входят 5 неизвестных элементов взаимного ориентирования.
Очевидно, что для определения элементов взаимного ориентирования необходимо измерить на стереопаре снимков не менее 5 точек.
В качестве примера рассмотрим определение элементов взаимного ориентирования by , bz , w2 ’, a2 ’, À2 ’.
В связи с тем, что уравнения ( 4.3) не линейны, их предварительно приводят к линейному виду и переходят к уравнению поправок:
. ( 1)
В уравнении поправок коэффициенты ai частные производные от функции ( 4.3) по соответствующим аргументам, а ℓ– свободный член.
Значения коэффициентов аi в уравнении ( 1) вычисляют по следующим известным значениям:
– измеренным координатам точек на стереопаре снимков – хi , yi ;
– элементам внутреннего ориентирования снимков fi , x0 i , y0 i ;
– 3 параметрам, задающим ориентацию системы координат модели (в нашем случае w1 ’, a1 ’, À1 ’) и приближенным значениям элементов взаимного ориентирования.
Свободный член ℓ вычисляется по формуле ( 4.3) таким же образом.
Полученную систему уравнений поправок решают методом приближений, а в случае, если измерено более 5 точек по методу наименьших квадратов (под условием VT PV=min). В результате решения находят значения элементов взаимного ориентирования.
Критерием, по которому принимается решение о завершении итерраций, могут являться величины поправок к определяемым неизвестным или величины остаточных поперечных параллаксов, которые для каждой измеренной точки вычисляются по формулам:
; ( 2)
где 
.
Величина q ост представляет собой разность ординат измеренных точек на стереопаре снимков, приведенных к идеальному случаю съемки, то есть q=y1 -y2 .
Необходимо отметить, что при отсутствии ошибок построения снимка и ошибок измерений величина q должна быть равна 0.
При определении элементов взаимного ориентирования оптимальным вариантом считается измерение 12-18 точек на стереопаре снимков, расположенных парами или тройками в 6 стандартных зонах (рис. 1).
 |
Рис. 1
 |
- главная точка снимка
- стандартно расположенная зона
В этом случае получается наиболее точное и надежное определение элементов взаимного ориентирования и появляется возможность локализации грубых измерений.
6. Построение фотограмметрической модели
Построение фотограмметрической модели заключается в определении координат точек объекта по измеренным на стереопаре снимков координатам их изображений в системе координат модели ОМ ХМ YM ZM .
Определение координат точек модели производится по формулам прямой фотограмметрической засечки (см. раздел 1).
При этом координаты центра проекции S принимаются произвольными (обычно 
0). Также произвольно (но не равной 0) выбирается величина ВХ
. В большинстве случаев практики величину ВХ
принимают равной:
;
где b – базис фотографирования в масштабе снимка,
m – знаменатель масштаба снимка.
Остальные значения элементов внешнего ориентирования определяют по 8 параметрам by , bz , w1 ’, a1 ’, À1 ’, w2 ’, a2 ’, À2 ’, 5 из которых являются элементами взаимного ориентирования, а 3 определяют ориентацию системы координат модели.
При этом
.
Например, если были определены элементы взаимного ориентирования a1 ’, À1 ’, w2 ’, a2 ’, À2 ’ и при этом величины параметров by , bz , w1 ’ были приняты равными нулю (by =bz =w1 ’=0), то BY =BZ =0, w1 =0, a1 =a1 ’, À1 =À1 ’, w2 =w2 ’, a2 =a2 ’, À2 =À2 ’.
Если были определены элементы взаимного ориентирования by , bz , w2 ’, a2 ’, À2 ’, а величины параметров w1 ’, a1 ’, À1 ’ были приняты равными нулю (w1 ’= a1 ’= À1 ’=0), то
.
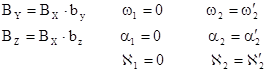7. Внешнее ориентирование модели. Элементы внешнего ориентирования модели
 |
Рис. 1
На рис.1: OXYZ- система координат объекта, ОМ ХМ YM ZM - система координат фотограмметрической модели , А – точка объекта ,АМ -точка фотограмметрической модели, соответствующая точке А объекта .
Векторы 
определяют положение начала системы координат модели ОМ
ХМ
YM
ZM
и точки А местности относительно начала системы координат объекта OXYZ.
Векторы 
определяют соответственно положение точек АМ
и А относительно системы координат фотограмметрической модели.
Из рис. 1 следует, что
. ( 1)
Векторы 
коллинеарны, поэтому
; ( 2)
где t – знаменатель масштаба модели.
С учетом ( 2) выражение ( 1) имеет вид:
; ( .3)
В координатной форме выражение ( 3) имеет вид:
; ( 4)
Или
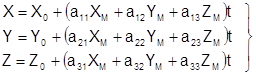. ( .5)
В выражениях ( 4) и ( 5):
X, Y, Z – координаты точки объекта в системе координат объекта;
ХМ ,YM ,ZM - координаты соответствующей точки модели в системе координат фотограмметрической модели;
АМ – матрица преобразования координат, элементы aij которой являются функциями углов wМ , aМ , ÀМ , определяющих ориентацию системы координат модели относительно системы координат объекта;
t – знаменатель масштаба модели.
7 параметров: 
- называют элементами внешнего ориентирования модели.
8. Определение элементов внешнего ориентирования модели по опорным точкам
Для определения элементов внешнего ориентирования модели по опорным точкам в качестве исходных используют уравнения ( 7.5), которые представим в виде:
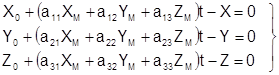. ( 1)
Каждая планово-высотная опорная точка (X,Y,Z) позволяет составить 3 уравнения ( 1), в которых неизвестными являются 7 элементов внешнего ориентирования модели. Каждая плановая опорная точка (X,Y) позволяет составить два первых уравнения из выражения ( 1), а каждая высотная опорная точка (Z) – третье уравнение из выражения ( 1).
Для определения элементов внешнего ориентирования модели необходимо составить систему не менее чем из 7 уравнений. Очевидно, что для этого необходимо иметь не менее двух планово-высотных и одной высотной опорной точки. Задачу можно также решить, если иметь две плановые и три высотные опорные точки.
Так как уравнения ( 1) не линейны, их приводят к линейному виду и переходят к уравнениям поправок.
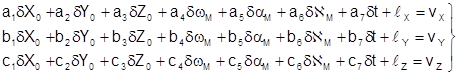. ( 2)
В уравнении поправок:
ai , bi , ci – частные производные от уравнений ( 1) по соответствующим переменным ;
ℓX , ℓY , ℓZ – свободные члены.
Значения коэффициентов уравнений поправок ai , bi , ci вычисляют по известным значениям координат ХМ ,YM ,ZM и X, Y, Z и приближенным значениям неизвестных. Значения свободных членов ℓX , ℓY , ℓZ вычисляют таким же образом по формулам ( .1).
Полученную таким образом систему уравнений поправок решают методом последовательных приближений. Если количество уравнений поправок в системе больше семи, то ее решают по методу наименьших квадратов (под условием VT PV=min).
9. Определение элементов внешнего ориентирования снимков стереопары
По элементам внешнего ориентирования модели и элементам взаимного ориентирования можно определить элементы внешнего ориентирования снимков стереопары.
Линейные элементы внешнего ориентирования снимков 
определяют по формулам:
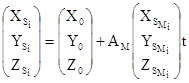; ( 1)
в которых - координаты центра проекции i-го снимка стереопары в системе координат модели.
Угловые элементы внешнего ориентирования снимков wi , ai , Ài определяют в следующей последовательности:
1. Сначала получают матрицу преобразования координат i-го снимка
; ( 2)
АМ – матрица, в которой элементы aij вычисляют по угловым элементам внешнего ориентирования модели wМ , aМ , ÀМ ;
Ai ’ – матрица, в которой элементы aij вычисляют по угловым элементам взаимного ориентирования i-го снимка wi ’, ai ’, Ài ’.
2. Затем по элементам aij матрицы Ai вычисляют угловые элементы внешнего ориентирования i-го снимка стереопары:
.
10. Точность определения координат точек объекта по стереопаре снимков
Для предрасчета точности определения координат точек местности по стереопаре аэрофотоснимков, учитывая, что углы наклона снимков не превышают 1°- 3°, а базис фотографирования практически горизонтален, воспользуемся формулами связи координат точек местности и координат их изображений на стереопаре снимков идеального случая съемки ( 2.4):
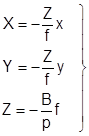. ( 2.4)
Сначала получим среднюю квадратическую ошибку определения высоты точки Z местности. Для этого продифференцируем третью формулу выражения (1.8.4) по аргументу р.
.
 |
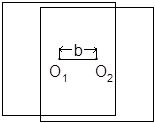Заменим величину р на b – базис в масштабе снимка.
Рис.1
На рис.1 О1 и О2 – главные точки снимка.
В результате получим
.
Перейдя к средним квадратическим ошибкам получим формулу:
. ( 1)
Для получения средних квадратических ошибок определения координат Х и Y точки местности продифференцируем первые две формулы выражения (1.8.4) по аргументам x, y, Z и перейдем к средним квадратическим ошибкам.
В результате получим
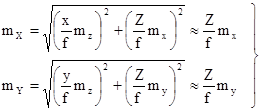. ( 2)
В качестве примера вычислим величины mX , mY и mZ точек местности, определенных по стереопаре снимков масштаба 1:5000, полученной АФА с f =150 мм и форматом кадра 23х23 см, с продольным перекрытием 60%.
Будем считать, что на стереопаре снимков точки были измерены с ошибками
.
В этом случае высота фотографирования
;
а базис фотографирования в масштабе снимка
.
Средние квадратические ошибки определения координат точки местности, вычисленные по формулам ( 1) и ( 2) будут равны:
.