Реферат: Речное хозяйство р Мура

Значение гидрологии, гидрометрии и регулирования стока определяется главными задачами водного хозяйства как отрасли науки и техники, охватывающей учет, изучение, использование, охрану водных ресурсов, а также борьбу с вредным действием вод.

Гидрология - это наука, изучающая гидросферу, включая океаны и моря, реки, озера, болота, почвенные и грунтовые воды, снег и ледники, влагу атмосферы, а также ее свойства и протекающие в ней процессы и явления во взаимосвязи с атмосферой, литосферой (земной корой) и биосферой.

Вода - основная среда, обеспечивающая обмен веществ и развитие организмов. С древнейших времен жизнь человека и развитие культуры связаны с водой. Она широко используется в промышленности, энергетике, сельском и рыбном хозяйстве, в медицине и т.д. Вода - объект изучения физики, химии, механики и других наук.

Гидрология тесно связана с метеорологией - наукой об атмосфере и происходящих в ней процессах, и в первую очередь с той ее частью, которая исследует влагооборот и испарение с поверхности воды. Взаимосвязь гидросферы с литосферой наиболее отчетливо проявляется в процессах формирования земной поверхности под влиянием деятельности воды. В свою очередь, рельеф земной поверхности оказывает существенное влияние на образование водных потоков. Поэтому гидрология имеет много общего с геоморфологией - наукой, изучающей закономерности возникновения и развития форм земной поверхности.

Раздел гидрологии, изучающий поверхностные воды, называется гидрологией суши или континентальной гидрологией . Раздел гидрологии по изучению воды океанов и морей называют гидрологией океанов и морей или океанологией .

Гидрология грунтовых (подземных) вод называется гидрогеологией . В гидрологию входят те разделы гидрогеологии, которые изучают взаимодействие поверхностных и подземных вод, питание рек грунтовыми водами и др. Разделы гидрогеологии, изучающие способы поиска и добычи грунтовых вод, их взаимодействие с горными породами, относят к геологии.

Различают гидрологию рек (речная гидрология , или потамология ), озер (лимнология ), болот (тельматология ), водохранилищ , ледников (гляциология ). Речная гидрология и речная гидравлика, изучающие движение воды в речных руслах и их формирование, дополняют друг друга. Речную гидравлику можно рассматривать как раздел гидрологии суши и как раздел гидравлики.

Гидрология, занимающаяся решение различных инженерных задач (в гидротехнике, гидромелиорации, гидроэнергетике, водоснабжении, строительстве мостов, автомобильных и железнодорожных дорог и т.д.) называется инженерной .

В результате широкого применения в гидрологии теории вероятностных процессов сформировалась стохастическая гидрология .

Гидрометрия - это наука о методах и средствах определения величин, характеризующих движение и состояние жидкости и режим водных объектов. В задачу гидрометрии входят определения: уровней, глубин, рельефа дна и свободной поверхности потока; напоров и давлений; скоростей и направлений течения жидкости, пульсаций скоростей и давлений; параметров волн; гидравлических уклонов; расходов жидкости; мутности потока; расходов наносов и пульпы; элементов термического и ледового режимов потоков.

Регулирование речного стока - это наука о перераспределении (увеличение или уменьшение) во времени объемов речного стока в замыкающем створе реки по сравнению с ходом поступления воды на поверхность водосбора.

1. Характеристики водности рек

Цель занятия - изучить и определить основные характеристики речного бассейна, связанные с ее гидрологическим режимом.

Задачи: освоить основные понятия гидрологических характеристик бассейна реки; изучить основные характеристики, отображающие водный режим реки. Исходные данные: река и пункт наблюдений (р. Мура - п. Ирба); площадь водосбора (F=9320 км² ); расход воды (Q=24,3 м³ /с); высота годового слоя осадков (x=405 мм).

Требуется: вычислить модуль стока (q, л/с∙км² ); определить высоту слоя стока (y, мм); рассчитать объем годового стока (V, км³ ); найти коэффициент стока (η). Порядок выполнения работы:

Река Мура впадает в Ангару, являясь её левым притоком. Площадь водосбора - 9320 км² . Высший уровень воды за год - 537 см, низший - 209 см, средний уровень воды за год - 388 см. Наибольший расход воды за год 33,9 м³ /сек, наименьший - 13,1 м³ /сек, средний расход воды за год - 23,7 м³ /сек. Годовой слой стока - 81 мм. Средняя продолжительность половодья 55 суток, за это время стекает 84% от годового стока вод. Паводок длится 13суток. Наивысшая температура воды в году 21,9єС приходится на 17 июля. С первой декады ноября по последнюю декаду апреля река находится под ледяным покровом, толщина которого достигает 112 см.

Модуль стока:

Слой стока:

Объём стока:

Коэффициент стока:

Выводы

В 4 варианте дана р. Мура в пункте наблюдения Ирба. Имея данные: площадь водосбора - 9320 км² , расход воды - 24,3 м³ /сек, высота годового слоя осадков - 405 мм, мы получили следующие характеристики водности рек: модуль стока - 2,61 л/с∙км² ; высота слоя стока - 82,22 мм; объем годового стока - 0,77 м³ ; коэффициент стока - 0, 203.

Последний показатель отражает, в районе с какой влажностью находится пункт наблюдения, в данном случае с. Ирба. Исходя из полученных данных можно сказать, что район относится к засушливым, так как в таких районах коэффициент стока уменьшается до нуля, а в районах избыточного увлажнения возрастает до 0,7. В данном случае =0, 203.

2. Расчеты испарения

Цель - рассчитать испарение с поверхности воды и с поверхности суши различными методами.

Задача - определить испарение:

1) с малого водоема при отсутствии данных наблюдений.

2) с суши с помощью карты изолиний испарения.

3) с суши по уравнению связи водного и теплового балансов.

2.1 Определение испарения с малого водоема при отсутствии данных наблюдений

Исходные данные: площадь водоема, расположенного вблизи г. Иркутска S = 4,5 км² , средняя глубина H= 3,0 м, средняя длина разгона воздушного потока D = 4,5 км, средняя высота препятствий на берегу h= 12 м.

Требуется: вычислить среднемноголетнее испарение.

Порядок выполнения.

Среднемноголетнее испарение с малых водоемов, расположенных в равнинных условиях определяют по выражению:

где - среднемноголетнее испарение с эталонного бассейна площадью 20 м² ,мм;

к_н , к_з , к_Ώ - поправочные коэффициенты соответственно на глубину водоема, на защищенность водоема от ветра древесной растительностью, строениями, крутыми берегами и другими препятствиями, а также на площадь водоема.

Среднемноголетнее испарение с бассейна площадью 20 м² находят на карте изолиний. Так, для Муры Е₂₀ = 350 мм.

Поправочный коэффициент на глубину водоема находят в зависимости от местоположения водоема и средней глубины. Для р. Мура, расположенной в лесостепной зоне, при = 3,0 м, к_н = 0,995.

Поправочный коэффициент к_з определяют в зависимости от отношения средней высоты (м) препятствий h_р к средней длине (м) разгона воздушного потока D, следовательно,

; К= 0,98

Поправочный коэффициент на площадь водоема к_Ώ для лесостепной зоны при Ω = 4,5 км² равен 1,25.

Находим среднемноголетнее испарение:

Е_в = 350∙0,995∙0,98∙1,25 = 427 мм

2.2 Определение испарения с суши с помощью карты изолиний испарения

Исходные данные: карта среднегодового слоя испарения с суши.

Требуется: определить среднемноголетнее годовое испарение.

Порядок выполнения.

По карте находим расположение Иркутского района и замечаем, что изолиния проходит на отметке 350 мм. Следовательно, для Иркутского района среднемноголетнее годовое испарение (норма) равно 350мм.

2.3 Определение испарения с суши по уравнению связи теплового и водного балансов

Исходные данные: среднемноголетний слой осадков х = 405 мм, радиационный баланс R = 120 кДж/см² , сумма среднемесячных положительных температур воздуха за год равна 54,3.

Требуется: определить среднемноголетнее годовое испарение.

Порядок выполнения.

1. По номограмме находим, что при х = 405 мм и R = 120 кДж/см² среднемноголетний слой испарения Е_с = 320 мм.

2. Для расчета испарения используют уравнение В.С. Мезенцева, которое имеет следующий вид:

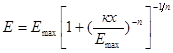где - максимально возможное испарение, мм;

- общее увлажнение, мм;

- параметр, учитывающий гидравлические условия стока.

3. Для определения максимально возможного испарения используем формулу И.В. Карнацевича:

Где Σt- сумма среднемесячных положительных температур воздуха за год.

мм

4. Находим испарение для Ирбы

мм

Вывод: данные расчеты испарения приобретают важное значение в связи с оценкой водного баланса. В результате расчетов получили:

среднемноголетнее испарение с поверхности воды Е_в = 427 мм;

среднемноголетнее испарение с поверхности суши Е_с = 320 мм.

3. Вычисление расхода воды аналитическим способом

Цель - найти основные гидрометрические характеристики реки.

Задача: вычислить расход воды.

Исходные данные: выписка из книжки для записи измерения расхода воды на реке.

Требуется: найти ширину реки (В, м); найти среднюю скорость реки (, м/с); найти максимальную глубину (h_max , м); найти среднюю глубину (, м); найти расход воды (Q, м³ /сек); найти смоченный периметр (ψ, м); найти гидравлический радиус (R, м); найти максимальную скорость реки (V _max , м/сек); найти площадь живого сечения (ω, м² ).

Порядок выполнения работы.

Таблица. Вычисление расхода воды аналитическим способом

№ вертикалей		Расстояние от постоянного начала, м	Глубина, м		Расстояние между промерными вертикалями	Площадь живого сечения, м²		Средняя скорость, м/c		Расход воды между скоростными вертикалями
Промерных	Скоростных	Расстояние от постоянного начала, м	Средняя	между промерными вертикалями	Расстояние между промерными вертикалями	между промерными вертикалями	между скоростными вертикалями	на вертикали	между скоростными вертикалями	Расход воды между скоростными вертикалями
1	2	3	4	5	6	7	8	9	10	11
Урез пб	2	0
0,39	2	0,78
1	4	0,78	3,44	0,39	1,35
1,33	2	2,66
2	I	6	1,88
2,09	2	4,18	0,56
3	8	2,3
2,37	2	4,74	14,01	0,65	9,04
4	10	2,44
2,55	2	5,09
5	II	12	2,65
2,44	2	4,87	0,73
6	14	2,22	9,16	0,70	6,41
2,15	2	4,29
7	III	16	2,07
1,99	2	3,97	0,67
8	18	1,9
1,78	2	3,55	11,40	0,47	5,35
9	20	1,65
0,83	4,7	3,88
Урез лб	24,7	0	0,0
38,01	38,01	22,14

Столбцы 1, 2, 3, 4, 9 - известны.

Столбец 5 - глубина между промерными вертикалями - среднее значение между средними глубинами на урезе правого берега и первой промерной вертикалью и так далее.

Столбец 7 - площадь между промерными вертикалями - произведение столбца 5 - глубина между промерными вертикалями, и столбца 6 - расстояние между промерными вертикалями.

Столбец 8 - площадь между скоростными вертикалями - сумма площадей между соответствующими промерными вертикалями. Общая площадь водного сечения получена как сумма частичных площадей между промерными или скоростными вертикалями.

Столбец 10 - скорость между скоростными вертикалями - между урезами воды и первой или последней промерной вертикалью это произведение средней скорости на вертикали и коэффициента 0,7; между остальными скоростными вертикалями - их среднее значение.

Столбец 11 - расход воды между скоростными вертикалями -произведение значений столбца 8 - площадь сечения между скоростными вертикалями, и столбца 10 - средняя скорость между скоростными вертикалями. Общий расход определяется как сумма всех расходов между скоростными вертикалями. Ширина реки - расстояние между геодезическим прибором и урезом левого берега вычесть расстояние между геодезическим прибором и урезом правого берега:

В = 24,7 м - 2 м = 22,7 м

Средняя скорость реки определяется по формуле:

Среднюю глубину реки находим с помощью выражения:

Смоченный периметр - ломаная линия по дну реки. Смоченный периметр всегда больше ширины реки (Ψ>В).

В нашем случае: ψ₁ =2,15 м, ψ₂ =2,28 м, ψ₃ =2,04 м, ψ₄ =2,00 м, ψ₅ =2,01 м, ψ₆ =2,05 м, ψ₇ =2,01 м, ψ₈ =2,01 м, ψ₉ =2,02 м, ψ₁₀ =4,98 м

Гидравлический радиус определяем по формуле:

Выводы: из работы видно, что:

расход воды на реке (Q) равен 22,14 м³ /сек;

площадь водного сечения (ω) - 38,01 м² ;

ширина реки (В) - 22,7 м.;

средняя глубина () - 1,67 м.;

максимальная глубина (h_max ) - 2,65 м.;

средняя скорость течения () - 0,58 м/сек;

максимальная скорость (V _max ) - 0,73 м/сек;

смоченный периметр (ψ) - 23,55 м.;

гидравлический радиус (R) - 1,61 м.

4. Расчёт годового стока

Цель: изучить закон вероятности гамма-распределения.

Задачи: построить эмпирическую кривую; найти статистические параметры ряда; построить аналитические кривые обеспеченности гамма-распределения.

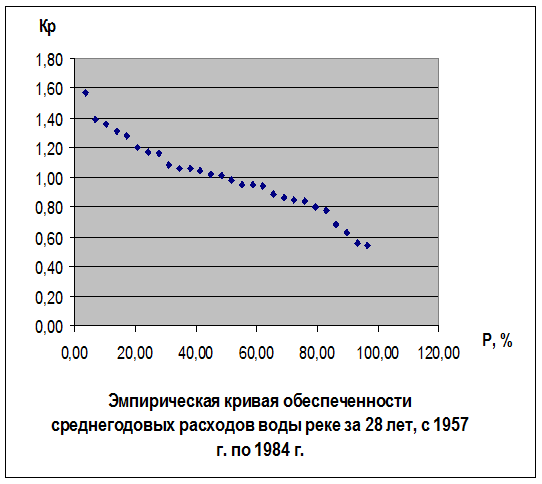
Задание 1 Построение эмпирической кривой обеспеченности среднегодовых расходов воды.

Исходные данные: среднегодовые расходы воды на реке по данным наблюдений за 28 лет.

Требуется: построить эмпирическую кривую обеспеченности среднегодовых расходов воды.

Порядок выполнения работы.

Чтобы построить эмпирическую кривую нужно заполнить таблицу.

Таблица 1 Вычисление эмпирической обеспеченности среднегодовых расходов воды

№ п/п	Год	Q, мі/сек	К_i	P	Kp	Рг
1	1957	15,2	0,63	3,45	1,57	2,09
2	1958	19,4	0,80	6,90	1,39	6,81
3	1959	33,9	1,39	10,34	1,36	8,53
4	1960	28,2	1,16	13,79	1,31	11,10
5	1961	28,4	1,17	17,24	1,28	13,05
6	1962	25,7	1,06	20,69	1, 20	20,06
7	1963	26,4	1,09	24,14	1,17	23,51
8	1964	20,5	0,84	27,59	1,16	24,44
9	1965	21	0,86	31,03	1,09	33,78
10	1966	31,2	1,28	34,48	1,06	37,88
11	1967	24,7	1,02	37,93	1,06	37,88
12	1968	13,5	0,56	41,38	1,05	39,09
13	1969	33	1,36	44,83	1,02	43,47
14	1970	16,7	0,69	48,28	1,02	44,11
15	1971	23,2	0,95	51,72	0,98	49,99
16	1972	24,8	1,02	55,17	0,95	54,01
17	1973	31,9	1,31	58,62	0,95	54,68
18	1974	21,5	0,88	62,07	0,95	55,36
19	1975	29,2	1, 20	65,52	0,88	65,40
20	1976	13,1	0,54	68,97	0,86	68,65
21	1977	25,7	1,06	72,41	0,85	70,56
22	1978	23,1	0,95	75,86	0,84	71,82
23	1979	23	0,95	79,31	0,80	78,34
24	1980	23,8	0,98	82,76	0,78	80,53
25	1981	20,7	0,85	86,21	0,69	90,77
26	1982	19	0,78	89,66	0,63	95,10
27	1983	38,2	1,57	93,10	0,56	98,01
28	1984	25,5	1,05	96,55	0,54	98,44
Q_ср = 24,30

Модульный коэффициент К _i находим по формуле:

Для каждого модульного коэффициента вычисляем соответствующую ему эмпирическую обеспеченность Р по формуле:

В последнем столбце располагаем ранжированные в порядке убывания значения модульных коэффициентов К_р .

Эмпирическая кривая представляет собой зависимость К_р от Р .

Задание 2. Определение статистических параметров ряда.

Исходные данные: среднегодовые расходы воды на реке по данным наблюдений за 28 лет.

Требуется: найти среднеарифметическое ; отклонение σ; коэффициент асимметрии с_s; коэффициент вариации с_v.

Порядок выполнения работы.

Находим статистические параметры.

Таблица 2 Статистические параметры

Среднее	24,3
Стандартная ошибка	1,2
Медиана	24,3
Мода	25,7
Стандартное отклонение	6,1
Дисперсия выборки	37,7
Эксцесс	-0,1
Асимметричность	0,2
Интервал	25,1
Минимум	13,1
Максимум	38,2
Сумма	680,5
Счет	28,0

Из последней таблицы следует:

среднеарифметическое Q_i _:

м³ /сек;

стандартное отклонение σ :

м³ /сек;

коэффициент асимметрии С _S :

коэффициент вариации С _V :

Задание 3. Построение аналитических кривых обеспеченности гамма-распределения.

Исходные данные: эмпирическая обеспеченность и ранжированный в порядке убывания модульный коэффициент.

Требуется: построить аналитическую кривую обеспеченности и вычислить расход воды при 75-процентной и 95-процентной обеспеченности при гамма-распределении.

Порядок выполнения работы.

Для построения аналитических кривых заполняем таблицу ниже.

Таблица 3

Kp	P	Рг
1,57	3,45	2,09
1,39	6,90	6,81
1,36	10,34	8,53
1,31	13,79	11,10
1,28	17,24	13,05
1, 20	20,69	20,06
1,17	24,14	23,51
1,16	27,59	24,44
1,09	31,03	33,78
1,06	34,48	37,88
1,06	37,93	37,88
1,05	41,38	39,09
1,02	44,83	43,47
1,02	48,28	44,11
0,98	51,72	49,99
0,95	55,17	54,01
0,95	58,62	54,68
0,95	62,07	55,36
0,88	65,52	65,40
0,86	68,97	68,65
0,85	72,41	70,56
0,84	75,86	71,82
0,80	79,31	78,34
0,78	82,76	80,53
0,69	86,21	90,77
0,63	89,66	95,10
0,56	93,10	98,01
0,54	96,55	98,44

К_р - ранжированный в порядке убывания модульный коэффициент. Р - эмпирическая обеспеченность.

Р_Г - значения обеспеченности при гамма-распределении, которое определяется формулой:

;

Для нахождения Р_Г в Excel пользуемся функцией ввода формул: гаммарасп.При этом x - первое значение k_p ; альфа - ; бетта = ; интегральное - 1.

Пользуясь диаграммой, расположенной ниже, мы находим значение расхода воды при 75-процентной и 95-процентной обеспеченности, но данные значения не совсем точные, поэтому для определения расхода воды при 75-процентной и 95-процентной обеспеченности пользуемся следующими формулами:

Теперь мы находим К_75Г и К_95Г. Получаем, что: К_75Г =0,82, а К_95Г =0,63.

Следовательно:

Выводы: используя данные значения, мы построили эмпирическую кривую обеспеченности, а также аналитическую кривую обеспеченности при гамма-распределении среднегодовых расходов воды реке. Нашли расход воды при 75-процентной и 95-процентной обеспеченности гамма-распределения: Q_75Г = 19,93 м³ /сек , Q_95Г = 15,31 м³ /сек. Также получили статистические параметры:

среднеарифметическое	24,3
отклонение σ	6,1
коэффициент асимметрии с_s	0,2
коэффициент вариации с_v	0,25

Заключение

Из первой выполненной работы имея данные: площадь водосбора - 9320 км² , расход воды - 24,3 м³ /сек, высота годового слоя осадков - 405 мм, мы получили следующие характеристики водности рек:

модуль стока - 2,61 л/с∙км² ;

высота слоя стока - 82,22 мм;

объем годового стока - 0,77 м³ ;

коэффициент стока - 0, 203.

Во второй работе данные расчеты испарения приобретают важное значение в связи с оценкой водного баланса. В результате расчетов получено:

среднемноголетнее испарение с поверхности воды Е_в = 427 мм;

среднемноголетнее испарение с поверхности суши Е_с = 320 мм.

Из третьей работы видно, что:

расход воды на реке равен 22,14 м³ /сек;

площадь водного сечения - 38,01 м² ;

ширина реки - 22,7 м.;

средняя глубина - 1,67 м.;

максимальная глубина - 2,65 м.;

средняя скорость течения - 0,58 м/сек;

максимальная скорость - 0,73 м/сек;

смоченный периметр - 23,55 м.;

гидравлический радиус - 1,61 м.

В четвертой работе используя данные значения, мы построили эмпирическую кривую обеспеченности, а также аналитические кривые обеспеченности при гамма-распределении среднегодовых расходов воды. Нашли расход воды при 75 - и 95-процентной обеспеченности гамма-распределения: Q_75Г = 19,93 м³ /сек , Q_95Г = 15,31 м³ /сек.

Список использованной литературы

1. Гидрология, гидрометрия и регулирование стока: Учебники и учебные пособия для высших сельскохозяйственных учебных заведений/ Г.В. Железняков, Т.А. Неговская, Е.Е. Овчаров. - М. "Колос", 1984.

2. Практикум по гидрологии, гидрометрии и регулированию стока: Учебники и учебные пособия для студентов высших учебных заведений/ под редакцией Е.Е. Овчарова. - М. ВО"Агропромиздат", 1988.

3. Статистика с применением Exsel: Учебное пособие. / Под ред. Я.М. Иваньо, А. Ф Зверева. - Иркутск, 2006. - 137 с.